Данный материал посвящен такому понятию, как угол между двумя пересекающимися прямыми. В первом пункте мы поясним, что он из себя представляет, и покажем его на иллюстрациях. Потом разберем, какими способами можно найти синус, косинус этого угла и сам угол (отдельно рассмотрим случаи с плоскостью и трехмерным пространством), приведем нужные формулы и покажем на примерах, как именно они применяются на практике.
Что такое угол между пересекающимися прямыми
Для того чтобы понять, что такое угол, образующийся при пересечении двух прямых, нам потребуется вспомнить само определение угла, перпендикулярности и точки пересечения.
Мы называем две прямые пересекающимися, если у них есть одна общая точка. Эта точка называется точкой пересечения двух прямых.
Каждая прямая разделяется точкой пересечения на лучи. Обе прямые при этом образуют 4 угла, из которых два – вертикальные, а два – смежные. Если мы знаем меру одного из них, то можем определить и другие оставшиеся.
Допустим, нам известно, что один из углов равен α. В таком случае угол, который является вертикальным по отношению к нему, тоже будет равен α. Чтобы найти оставшиеся углы, нам надо вычислить разность 180°-α. Если α будет равно 90 градусам, то все углы будут прямыми. Пересекающиеся под прямым углом линии называются перпендикулярными (понятию перпендикулярности посвящена отдельная статья).
Взгляните на рисунок:
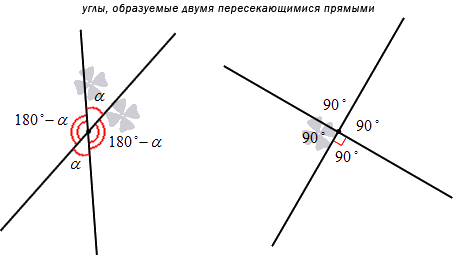
Перейдем к формулированию основного определения.
Угол, образованный двумя пересекающимися прямыми – это мера меньшего из 4-х углов, которые образуют две эти прямые.
Из определения нужно сделать важный вывод: размер угла в этом случае будет выражен любым действительным числом в интервале (0, 90]. Если прямые являются перпендикулярными, то угол между ними в любом случае будет равен 90 градусам.
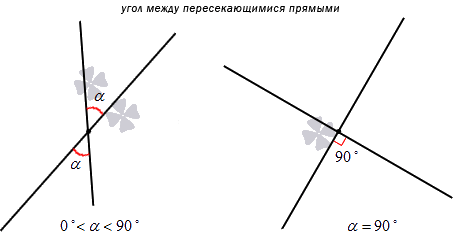
Как найти угол между пересекающимися прямыми на плоскости
Умение находить меру угла между двумя пересекающимися прямыми полезно для решения многих практических задач. Метод решения можно выбрать из нескольких вариантов.
Для начала мы можем взять геометрические методы. Если нам известно что-то о дополнительных углах, то можно связать их с нужным нам углом, используя свойства равных или подобных фигур. Например, если мы знаем стороны треугольника и нужно вычислить угол между прямыми, на которых эти стороны расположены, то для решения нам подойдет теорема косинусов. Если у нас в условии есть прямоугольный треугольник, то для подсчетов нам также пригодится знание синуса, косинуса и тангенса угла.
Координатный метод тоже весьма удобен для решения задач такого типа. Поясним, как правильно его использовать.
У нас есть прямоугольная (декартова) система координат Oxy, в которой заданы две прямые. Обозначим их буквами a и b. Прямые при этом можно описать с помощью каких-либо уравнений. Исходные прямые имеют точку пересечения M. Как определить искомый угол (обозначим его α) между этими прямыми?
Начнем с формулировки основного принципа нахождения угла в заданных условиях.
Нам известно, что с понятием прямой линии тесно связаны такие понятия, как направляющий и нормальный вектор. Если у нас есть уравнение некоторой прямой, из него можно взять координаты этих векторов. Мы можем сделать это сразу для двух пересекающихся прямых.
Угол, образуемый двумя пересекающимися прямыми, можно найти с помощью:
- угла между направляющими векторами;
- угла между нормальными векторами;
- угла между нормальным вектором одной прямой и направляющим вектором другой.
Теперь рассмотрим каждый способ отдельно.
1. Допустим, что у нас есть прямая a с направляющим вектором a→=(ax, ay) и прямая b с направляющим вектором b→(bx, by). Теперь отложим два вектора a→ и b→ от точки пересечения. После этого мы увидим, что они будут располагаться каждый на своей прямой. Тогда у нас есть четыре варианта их взаимного расположения. См. иллюстрацию:
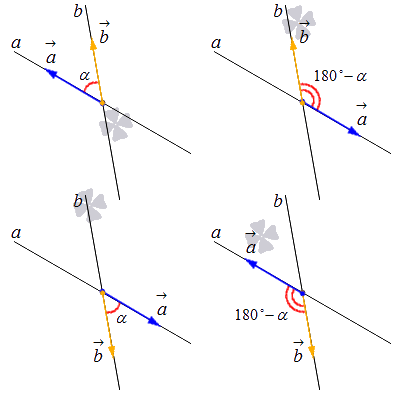
Если угол между двумя векторами не является тупым, то он и будет нужным нам углом между пересекающимися прямыми a и b. Если же он тупой, то искомый угол будет равен углу, смежному с углом a→, b→^. Таким образом, α=a→, b→^ в том случае, если a→, b→^≤90° , и α=180°-a→, b→^, если a→, b→^>90°.
Исходя из того, что косинусы равных углов равны, мы можем переписать получившиеся равенства так: cos α=cos a→, b→^, если a→, b→^≤90°; cos α=cos180°-a→, b→^=-cosa→, b→^, если a→, b→^>90°.
Во втором случае были использованы формулы приведения. Таким образом,
cos αcosa→, b→^, cosa→, b→^≥0-cosa→, b→^, cosa→, b→^<0⇔cos α=cosa→, b→^
Запишем последнюю формулу словами:
Косинус угла, образованного двумя пересекающимися прямыми, будет равен модулю косинуса угла между его направляющими векторами.
Общий вид формулы косинуса угла между двумя векторами a→=(ax, ay) и b→=(bx, by) выглядит так:
cosa→, b→^=a→, b→^a→·b→=ax·bx+ay·byax2+ay2·bx2+by2
Из нее мы можем вывести формулу косинуса угла между двумя заданными прямыми:
cos α=ax·bx+ay·byax2+ay2·bx2+by2=ax·bx+ay·byax2+ay2·bx2+by2
Тогда сам угол можно найти по следующей формуле:
α=arccosax·bx+ay+byax2+ay2·bx2+by2
Здесь a→=(ax, ay) и b→=(bx, by) – это направляющие векторы заданных прямых.
Приведем пример решения задачи.
В прямоугольной системе координат на плоскости заданы две пересекающиеся прямые a и b. Их можно описать параметрическими уравнениями x=1+4·λy=2+λλ∈R и x5=y-6-3. Вычислите угол между этими прямыми.
Решение
У нас в условии есть параметрическое уравнение, значит, для этой прямой мы сразу можем записать координаты ее направляющего вектора. Для этого нам нужно взять значения коэффициентов при параметре, т.е. прямая x=1+4·λy=2+λλ∈R будет иметь направляющий вектор a→=(4, 1).
Вторая прямая описана с помощью канонического уравнения x5=y-6-3. Здесь координаты мы можем взять из знаменателей. Таким образом, у этой прямой есть направляющий вектор b→=(5, -3).
Далее переходим непосредственно к нахождению угла. Для этого просто подставляем имеющиеся координаты двух векторов в приведенную выше формулу α=arccosax·bx+ay+byax2+ay2·bx2+by2. Получаем следующее:
α=arccos4·5+1·(-3)42+12·52+(-3)2=arccos1717·34=arccos12=45°
Ответ: данные прямые образуют угол в 45 градусов.
Мы можем решить подобную задачу с помощью нахождения угла между нормальными векторами. Если у нас есть прямая a с нормальным вектором na→=(nax, nay) и прямая b с нормальным вектором nb→=(nbx, nby), то угол между ними будет равен углу между na→ и nb→ либо углу, который будет смежным с na→, nb→^. Этот способ показан на картинке:
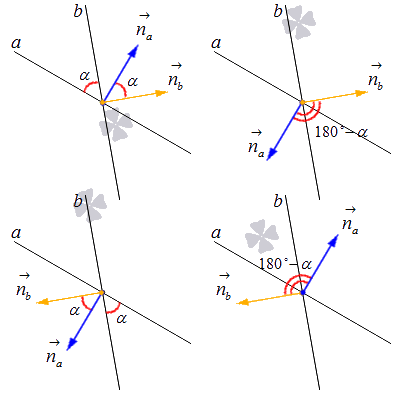
Формулы для вычисления косинуса угла между пересекающимися прямыми и самого этого угла с помощью координат нормальных векторов выглядят так:
cos α=cosna→, nb→^=nax·nbx+nay+nbynax2+nay2·nbx2+nby2α=arccosnax·nbx+nay+nbynax2+nay2·nbx2+nby2
Здесь na→ и nb→ обозначают нормальные векторы двух заданных прямых.
В прямоугольной системе координат заданы две прямые с помощью уравнений 3x+5y-30=0 и x+4y-17=0. Найдите синус, косинус угла между ними и величину самого этого угла.
Решение
Исходные прямые заданы с помощью нормальных уравнений прямой вида Ax+By+C=0. Нормальный вектор обозначим n→=(A, B). Найдем координаты первого нормального вектора для одной прямой и запишем их: na→=(3, 5). Для второй прямой x+4y-17=0 нормальный вектор будет иметь координаты nb→=(1, 4). Теперь добавим полученные значения в формулу и подсчитаем итог:
cos α=cosna→, nb→^=3·1+5·432+52·12+42=2334·17=23234
Если нам известен косинус угла, то мы можем вычислить его синус, используя основное тригонометрическое тождество. Поскольку угол α, образованный прямыми, не является тупым, то sin α=1-cos2α=1-232342=7234.
В таком случае α=arccos23234=arcsin7234.
Ответ: cos α=23234, sin α=7234, α=arccos23234=arcsin7234
Разберем последний случай – нахождение угла между прямыми, если нам известны координаты направляющего вектора одной прямой и нормального вектора другой.
Допустим, что прямая a имеет направляющий вектор a→=(ax, ay), а прямая b – нормальный вектор nb→=(nbx, nby). Нам надо отложить эти векторы от точки пересечения и рассмотреть все варианты их взаимного расположения. См. на картинке:
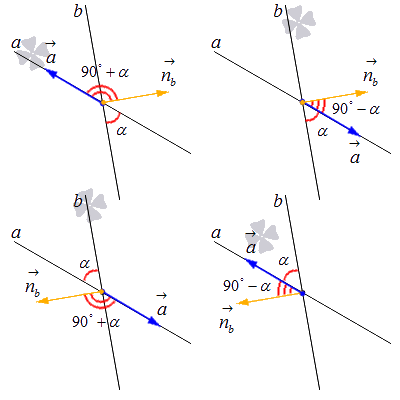
Если величина угла между заданными векторами не более 90 градусов, получается, что он будет дополнять угол между a и b до прямого угла.
a→, nb→^=90°-α в том случае, если a→, nb→^≤90°.
Если он менее 90 градусов, то мы получим следующее:
a→, nb→^>90° , тогда a→, nb→^=90°+α
Используя правило равенства косинусов равных углов, запишем:
cosa→, nb→^=cos(90°-α)=sin α при a→, nb→^≤90°.
cosa→, nb→^=cos90°+α=-sin α при a→, nb→^>90°.
Таким образом,
sin α=cosa→, nb→^, a→, nb→^≤90°-cosa→, nb→^, a→, nb→^>90°⇔sin α=cosa→, nb→^, a→, nb→^>0-cosa→, nb→^, a→, nb→^<0⇔⇔sin α=cosa→, nb→^
Сформулируем вывод.
Чтобы найти синус угла между двумя прямыми, пересекающимися на плоскости, нужно вычислить модуль косинуса угла между направляющим вектором первой прямой и нормальным вектором второй.
Запишем необходимые формулы. Нахождение синуса угла:
sin α=cosa→, nb→^=ax·nbx+ay·nbyax2+ay2·nbx2+nby2
Нахождение самого угла:
α=arcsin=ax·nbx+ay·nbyax2+ay2·nbx2+nby2
Здесь a→ является направляющим вектором первой прямой, а nb→ – нормальным вектором второй.
Две пересекающиеся прямые заданы уравнениями x-5=y-63 и x+4y-17=0. Найдите угол пересечения.
Решение
Берем координаты направляющего и нормального вектора из заданных уравнений. Получается a→=(-5, 3) и n→b=(1, 4). Берем формулу α=arcsin=ax·nbx+ay·nbyax2+ay2·nbx2+nby2 и считаем:
α=arcsin=-5·1+3·4(-5)2+32·12+42=arcsin7234
Обратите внимание, что мы взяли уравнения из предыдущей задачи и получили точно такой же результат, но другим способом.
Ответ: α=arcsin 7234
Приведем еще один способ нахождения нужного угла с помощью угловых коэффициентов заданных прямых.
У нас есть прямая a, которая задана в прямоугольной системе координат с помощью уравнения y=k1·x+b1, и прямая b, заданная как y=k2·x+b2. Это уравнения прямых с угловым коэффициентом. Чтобы найти угол пересечения, используем формулу:
α=arccosk1·k2+1k12+1·k22+1, гдеk1 и k2 являются угловыми коэффициентами заданных прямых. Для получения этой записи были использованы формулы определения угла через координаты нормальных векторов.
Есть две пересекающиеся на плоскости прямые, заданные уравнениями y=-35x+6 и y=-14x+174. Вычислите величину угла пересечения.
Решение
Угловые коэффициенты наших прямых равны k1=-35 и k2=-14. Добавим их в формулу α=arccosk1·k2+1k12+1·k22+1 и подсчитаем:
α=arccos-35·-14+1-352+1·-142+1=arccos23203424·1716=arccos23234
Ответ: α=arccos23234
В выводах этого пункта следует отметить, что приведенные здесь формулы нахождения угла не обязательно учить наизусть. Для этого достаточно знать координаты направляющих и/или нормальных векторов заданных прямых и уметь определять их по разным типам уравнений. А вот формулы для вычисления косинуса угла лучше запомнить или записать.
Как вычислить угол между пересекающимися прямыми в пространстве
Вычисление такого угла можно свести к вычислению координат направляющих векторов и определению величины угла, образованного этими векторами. Для таких примеров используются такие же рассуждения, которые мы приводили до этого.
Допустим, что у нас есть прямоугольная система координат, расположенная в трехмерном пространстве. В ней заданы две прямые a и b с точкой пересечения M. Чтобы вычислить координаты направляющих векторов, нам нужно знать уравнения этих прямых. Обозначим направляющие векторы a→=(ax, ay, az) и b→=(bx, by, bz). Для вычисления косинуса угла между ними воспользуемся формулой:
cos α=cosa→, b→^=a→, b→a→·b→=ax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2
Для нахождения самого угла нам понадобится эта формула:
α=arccosax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2
У нас есть прямая, заданная в трехмерном пространстве с помощью уравнения x1=y-3=z+3-2. Известно, что она пересекается с осью Oz. Вычислите угол пересечения и косинус этого угла.
Решение
Обозначим угол, который надо вычислить, буквой α. Запишем координаты направляющего вектора для первой прямой – a→=(1, -3, -2). Для оси аппликат мы можем взять координатный вектор k→=(0, 0, 1) в качестве направляющего. Мы получили необходимые данные и можем добавить их в нужную формулу:
cos α=cosa→, k→^=a→, k→a→·k→=1·0-3·0-2·112+(-3)2+(-2)2·02+02+12=28=12
В итоге мы получили, что нужный нам угол будет равен arccos12=45°.
Ответ: cos α=12, α=45°.
Геометрия, 11 класс
Урок № 3. Координатный метод решения задач
Перечень вопросов, рассматриваемых в теме:
- специфика и преимущества решения задач в пространстве координатным методом;
- типы задач, решаемые координатным методом;
- этап решения задачи координатным методом;
- решение несложных задач методом координат.
Глоссарий по теме
Уравнение вида  задает в пространстве плоскость α.
задает в пространстве плоскость α.
При этом вектор  – это вектор, перпендикулярный плоскости α. Его называют вектор нормали, или нормальный вектор, или нормаль. Очевидно, что нормалью является любой вектор, коллинеарный вектору
– это вектор, перпендикулярный плоскости α. Его называют вектор нормали, или нормальный вектор, или нормаль. Очевидно, что нормалью является любой вектор, коллинеарный вектору  .
.
Вектор  и любой коллинеарный ему вектор называются направляющим векторами прямой
и любой коллинеарный ему вектор называются направляющим векторами прямой  и прямой
и прямой  соответственно.
соответственно.
Основная литература:
Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. Учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 163-170.
Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 353-260.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Работа по теме урока. Объяснение новой темы
Мы рассмотрели несложную задачу на применение метода координат в пространстве.
Векторы  , угол между которыми мы искали, называются направляющими векторами прямой
, угол между которыми мы искали, называются направляющими векторами прямой  и прямой
и прямой  соответственно.
соответственно.
Рассмотрим этот метод более подробно.
Суть метода координат на плоскости и в пространстве заключается в следующем.
- Ввести систему координат удобным образом (исходя их свойств заданной фигуры)
- Записать условие задачи в координатах, определив во введенной системе координат координаты точек и/или векторов
- Используя алгебраические преобразования, решить задачу
- Интерпретировать полученный результат в соответствии с условием данной задачи
В рассмотренном нами примере, поскольку был дан куб, мы могли ввести систему координат с центром в любой его вершине.
В координатах удобно решать задачи, связанные с поиском расстояний и углов. Но для того чтобы его использовать, нужно знать некоторые формулы:
- Угол между прямыми
- Угол между прямой и плоскостью
- Угол между плоскостями
- Расстояние от точки до плоскости
- Расстояние от точки до прямой в пространстве
- Расстояние между скрещивающимися прямыми
Расстояние между параллельными плоскостями определяется как расстояние от точки, лежащей в одной плоскости, до другой плоскости.
Мы рассмотрим только первые четыре формулы.
Введем их.
Угол между прямыми
Если прямая задана двумя точками A и B, то известен направляющий вектор этой прямой  с координатами {
с координатами { }. Пусть вторая прямая имеет направляющий вектор
}. Пусть вторая прямая имеет направляющий вектор  . Тогда угол между векторами вычисляется по формуле:
. Тогда угол между векторами вычисляется по формуле:
 .
.
Дальше ищется арккосинус от найденного числа. Заметим, что если косинус получился отрицательным, то это значит, что угол между векторами тупой. Поэтому мы берем модуль получившегося числа.
Фактически мы уже рассмотрели пример вычисления угла между прямыми в пространстве.
Угол между прямой и плоскостью
Сначала рассмотрим уравнение плоскости, проходящей через три точки.
 .
.
Вам известно, что в пространстве плоскость задается уравнением, аналогичным тому, которое на плоскости задает прямую.
Если линейное уравнение вида  на плоскости задает прямую l, то уравнение вида
на плоскости задает прямую l, то уравнение вида  задает в пространстве плоскость α. При этом вектор
задает в пространстве плоскость α. При этом вектор  – это вектор, перпендикулярный плоскости α. Его называют вектор нормали, или нормальный вектор, или нормаль.
– это вектор, перпендикулярный плоскости α. Его называют вектор нормали, или нормальный вектор, или нормаль.
Вам известно, что три точки в пространстве определяют единственную плоскость. Поэтому, если заданы три точки, то мы можем найти уравнение плоскости
Мы можем подставить координаты заданных точек в уравнение плоскости и решить систему из трех уравнений с тремя переменными:

В этой системе четыре неизвестных, однако, мы можем избавиться от одной, если разделим все уравнения на D:
 .
.
Для изучения данного способа в 11 классе на базовом уровне введение понятий матрица, определитель матрицы не желателен, данные понятия не входят в базовый курс изучения геометрии.
Иногда эта система оказывается несложной. Но иногда бывает трудно ее решить, и тогда можно использовать следующую формулу:
Обозначение |M| означает определитель матрицы М.
В нашем случае матрица представляет собой таблицу 3х3 элемента. И определитель |M| вычисляется следующим образом:
 .
.
Таким образом, уравнение плоскости будет записано так:



Пример 1:
Написать уравнение плоскости, проходящей через точки K(1; -2; 3), L (0; 1; 1), M (1; 0; 1).
Составим систему.
 .
.
Решая ее, получим значения А, В и С:  . То есть уравнение плоскости имеет вид:
. То есть уравнение плоскости имеет вид:
 .
.
Ответ:  .
.
Теперь запишем формулу угла между прямой и плоскостью.
Пусть дано уравнение плоскости:  и известен
и известен  – направляющий вектор прямой.
– направляющий вектор прямой.
Тогда  – синус угла между прямой и плоскостью.
– синус угла между прямой и плоскостью.
Пример 2:
Найдем угол между прямой и плоскостью. В качестве плоскости возьмем ту, уравнение которой мы только что написали:

Прямая проходит через точки Т(2; -1; 4) и Р(3; 2; 2).
Направляющий вектор прямой:  .
.
Найдем синус угла между прямой и плоскостью:
 .
.
Угол между прямой и плоскостью  .
.
Ответ:  .
.
Угол между плоскостями
Пусть:
уравнение первой плоскости: 
уравнение второй плоскости: 
Тогда  – косинус угла между этими плоскостями.
– косинус угла между этими плоскостями.
Пример 3:
Найдем угол между плоскостями:
 и
и  .
.
Найдем косинус угла между плоскостями:
 .
.
Угол между плоскостями: 
Ответ: 
Расстояние от точки до плоскости
Пусть координаты точки:  , уравнение плоскости:
, уравнение плоскости:  .
.
Тогда Расстояние от точки до плоскости вычисляется по формуле:  .
.
Пример 4.
Найдем расстояние от точки М(4; 3; 4) до плоскости  .
.
 .
.
Теперь рассмотрим решение задачи координатным методом с использованием рассмотренных формул.
Пример 5.
АВС…D1 – куб с ребром 4. Найти расстояние от точки А до плоскости ЕКС (Е – середина D1C1, K – середина C1B1)
Введем систему координат с началом в вершине А так, как показано на рисунке:

Интересующие нас точки будут иметь координаты:
A(0; 0; 0), C(4; 4; 0), E(4; 2; 4), K(2; 4; 4).
Напишем уравнение плоскости ЕКС:
 .
.
Решая ее, получим значения А, В, С и D:  .
.
Уравнение плоскости имеет вид: 
Теперь найдем расстояние от точки А до плоскости ЕКС:  .
.
Ответ:  .
.
Рассмотрим задачу (№14 из варианта ЕГЭ).
В кубе ABC…D1 все рёбра равны 4. На его ребре BB1 отмечена точка K так, что KB = 3. Через точки K и C1 построена плоскость α, параллельная прямой BD1.
а) Докажите, что A1P : PB1 = 2 : 1, где P — точка пересечения плоскости α с ребром A1B1.
б) Найдите угол наклона плоскости α к плоскости грани BB1C1C.
Решение:
Переформулируем первый пункт этой задачи таким образом:
Проведем плоскость через точки Р, K и C1 и докажем, что она параллельна прямой BD1.
Введем систему координат так, как показано на рисунке:

Найдем координаты точек  :
:
Р( ; 0; 4), К(4; 0; 3),
; 0; 4), К(4; 0; 3), (4; 4; 4).
(4; 4; 4).
Напишем уравнение плоскости  :
:
 ;
;

Решая ее, получим значения А, В, С и D:  .
.
 – уравнение плоскости
– уравнение плоскости
Теперь докажем, что плоскость  параллельна прямой BD1.
параллельна прямой BD1.
Найдем угол между прямой BD1 и плоскостью  .
.
Точки В и D1 имеют координаты: В (4; 0; 0), D1 (0; 4; 4).
Направляющий вектор прямой BD1 – это вектор  .
.
Он имеет координаты  .
.
Теперь найдем синус угла между вектором  и плоскостью
и плоскостью  .
.

 .
.
В этом случае нам не нужно считать знаменатель дроби. Так как числитель получился равен 0, то дробь равна 0, то есть синус угла между плоскостью и прямой равен 0, значит, плоскости параллельны или совпадают. Но, так как точка В, например, в плоскости, очевидно, не лежит, то плоскости параллельны.
Это значит, что плоскость, параллельная прямой BD1 и проходящая через точки  действительно пересекает ребро A1B1в точке Р так, что A1P : PB1 = 2 : 1. Что и требовалось доказать.
действительно пересекает ребро A1B1в точке Р так, что A1P : PB1 = 2 : 1. Что и требовалось доказать.
Теперь рассмотри второй пункт задачи. Уравнение плоскости  у нас есть. Плоскость BB1C1 параллельна координатной плоскости YOZ и проходит через точку
у нас есть. Плоскость BB1C1 параллельна координатной плоскости YOZ и проходит через точку
В(4; 0; 0). Поэтому она имеет уравнение  .
.
То есть ее коэффициенты  .
.
Найдем угол между плоскостями, используя формулу


Ответ:  .
.
Содержание материала
- Определение угла между скрещивающимися прямыми
- Как найти угол между скрещивающимися прямыми
- Видео
- Примеры задач на вычисления угла между прямыми на плоскости
- Как вычислить угол между пересекающимися прямыми в пространстве
Определение угла между скрещивающимися прямыми
Пересечение двух линий на плоскости говорит о наличии у них одной общей точки. Она же является центром их пересечения и делит их на лучи.
Лучи формируют четыре угла, которые являются неразвернутыми. Зная о размере одного из них, можно вычислить значение и остальных. Точно можно утверждать, что если один из них – прямоугольный, то остальные три равнозначны ему, а линии будут перпендикулярными.
Рис. 1 Графическое отображение пересечения прямых
Как найти угол между скрещивающимися прямыми
Для определения угла между двумя скрещивающимися линиями можно воспользоваться специальным онлайн-калькулятором или применить традиционный математический алгоритм для вычислений.
Предположим, что две бесконечные линии задаются уравнениями общего вида:
A1 + B1 + C1 = 0
A2 + B2 + C2 = 0
Искомое значение следует обозначить как φ. Численная величина угла измеряется в градусах от 0 до 90°, т. е. угол будет острым или прямоугольным. Необходимо ввести еще одно понятие– угол ψ между нормальными векторами данных прямых:

Если он меньше, либо равен 90°, то непосредственно сам искомый угол будет соответствовать его градусной мере. В случае когда ψ больше 90°, для вычисления φ необходимо применить известную формулу:
φ = 180 — ψ.
Для обоих вариантов достоверно утверждение, что cos φ = lcos ψl. Выполнив необходимые вычисления, можно рассчитать искомое значение:

Если по условию задачи существует некий прямоугольный треугольник с известными сторонами, расположенными на двух прямых, то для вычисления угла между этими прямыми необходимо знать синус, тангенс и косинус искомого угла.
Для нахождения значения синуса угла, образованного в результате пересечения двух прямых, вычисляют модуль косинуса этого угла, образованного направляющими векторами данных прямых.
Видео
Примеры задач на вычисления угла между прямыми на плоскости
 Пример 1. Найти угол между прямыми y = 2x — 1 и y = -3x + 1.
Пример 1. Найти угол между прямыми y = 2x — 1 и y = -3x + 1.
Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:
tg γ =
k1 — k21 + k1·k2
=
2 — (-3)1 + 2·(-3)
=
5-5
= 1
Ответ. γ = 45°
 Пример 2. Найти угол между прямыми y = 2x — 1 и x = 2t + 1y = t.
Пример 2. Найти угол между прямыми y = 2x — 1 и x = 2t + 1y = t.
Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.
Для первой прямой направляющий вектор {1; 2}, для второй прямой направляющий вектор {2; 1}
cos φ =
|1 · 2 + 2 · 1|12 + 22 · 22 + 12
=
45 · 5
= 0.8
Ответ. φ ≈ 36.87°
Пример 3 Найти угол между прямыми 2x + 3y = 0 и
x — 23
=
y4
.
Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.
Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.
2x + 3y = 0 => y = —23x (k1 = —23)
x — 23 = y4 => y = 43x — 83 (k2 = 43)
tg γ =
k1 — k21 + k1·k2
=
—23 — 431 + (-23)·43
=
—631 — 89
= 18
Ответ. γ ≈ 86.82°
Как вычислить угол между пересекающимися прямыми в пространстве
Вычисление такого угла можно свести к вычислению координат направляющих векторов и определению величины угла, образованного этими векторами. Для таких примеров используются такие же рассуждения, которые мы приводили до этого.
Допустим, что у нас есть прямоугольная система координат, расположенная в трехмерном пространстве. В ней заданы две прямые a и b с точкой пересечения M. Чтобы вычислить координаты направляющих векторов, нам нужно знать уравнения этих прямых. Обозначим направляющие векторы a→=(ax, ay, az) и b→=(bx, by, bz). Для вычисления косинуса угла между ними воспользуемся формулой:
cos α=cosa→, b→^=a→, b→a→·b→=ax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2
Для нахождения самого угла нам понадобится эта формула:
α=arccosax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2
У нас есть прямая, заданная в трехмерном пространстве с помощью уравнения x1=y-3=z+3-2. Известно, что она пересекается с осью Oz. Вычислите угол пересечения и косинус этого угла.
Решение
Обозначим угол, который надо вычислить, буквой α. Запишем координаты направляющего вектора для первой прямой – a→=(1, -3, -2). Для оси аппликат мы можем взять координатный вектор k→=(, , 1) в качестве направляющего. Мы получили необходимые данные и можем добавить их в нужную формулу:
cos α=cosa→, k→^=a→, k→a→·k→=1·-3·-2·112+(-3)2+(-2)2·2+2+12=28=12
В итоге мы получили, что нужный нам угол будет равен arccos12=45°.
Ответ: cos α=12, α=45°.
Всё ещё сложно? Наши эксперты помогут разобраться Все услуги
Теги
Определение угла между прямыми

Две прямые называются пересекающимися, если они имеют единственную общую точку. Эта точка называется точкой пересечения прямых. Прямые разбиваются точкой пересечения на лучи, которые образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Если известен размер одного из углов, образованных пересекающимися прямыми, то легко определить размер остальных углов. Если один из углов прямой, то все остальные тоже прямые, а прямые перпендикулярны.
Определение Угол между прямыми – размер наименьшего из углов, образованных этими прямыми.
Угол между прямыми на плоскости
Угол между прямыми заданными уравнениями с угловым коэффициентом
Если две прямые заданы уравнениями с угловым коэффициентом
y = k1x + b1,
y = k2x + b2,
то угол между ними можно найти, используя формулу:
Если знаменатель равен нулю (1 + k1·k2 = 0), то прямые перпендикулярны.

Доказательство. Если прямые заданы уравнениями с угловыми коэффициентами, то легко найти углы между этими прямыми и осью OX
tg α = k1
tg β = k2
Соответственно легко найти угол между прямыми
γ = α – β
tg γ = tg (α – β) = tg α – tg β1 + tg α ·tg β = k1 – k21 + k1·k2
Угол между прямыми через направляющие векторы этих прямых

Если a – направляющий вектор первой прямой и b – направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если уравнение прямой задано параметрически
x = l t + ay = m t + b
то вектор направляющей имеет вид {l; m}
Если уравнение прямой задано как
A x + B y + C = 0
то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = -CB значит точка на прямой имеет координаты K(0, -CB), при y = 0 => x = -CA значит точка на прямой имеет координаты M(-CA, 0). Вектор направляющей KM = {-CA; CB}.
Если дано каноническое уравнение прямой
x – x0 l = y – y0m
то вектор направляющей имеет вид {l; m}
Если задано уравнение прямой с угловым коэффициентом
y = kx + b
то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b). Вектор направляющей KM = {1; k}
Угол между прямыми через векторы нормалей этих прямых

Если a – вектор нормали первой прямой и b – вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если уравнение прямой задано как
A x + B y + C = 0
то вектор нормали имеет вид {A; B}
Если задано уравнение прямой с угловым коэффициентом
y = kx + b
то вектор нормали имеет вид {1; –k}
Угол между прямыми через направляющий вектор и вектор нормали этих прямых

Если a – направляющий вектор первой прямой и b – вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
sin φ = |a · b||a| · |b|
Примеры задач на вычисления угла между прямыми на плоскости

Пример 1. Найти угол между прямыми y = 2x – 1 и y = -3x + 1.
Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:
tg γ =
k1 – k21 + k1·k2
=
2 – (-3)1 + 2·(-3)
=
5-5
= 1
Ответ. γ = 45°

Пример 2. Найти угол между прямыми y = 2x – 1 и x = 2t + 1y = t.
Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.
Для первой прямой направляющий вектор {1; 2}, для второй прямой направляющий вектор {2; 1}
cos φ =
|1 · 2 + 2 · 1|12 + 22 · 22 + 12
=
45 · 5
= 0.8
Ответ. φ ≈ 36.87°
Пример 3 Найти угол между прямыми 2x + 3y = 0 и
x – 23
=
y4
.
Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.
Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.
2x + 3y = 0 => y = -23x (k1 = -23)
x – 23 = y4 => y = 43x – 83 (k2 = 43)
tg γ =
k1 – k21 + k1·k2
=
-23 – 431 + (-23)·43
=
-631 – 89
= 18
Ответ. γ ≈ 86.82°
Угол между прямыми в пространстве
Если a – направляющий вектор первой прямой, а b – направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если дано каноническое уравнение прямой
x – x0 l = y – y0m = z – z0n
то направляющий вектор имеет вид {l; m; n}
Если уравнение прямой задано параметрически
x = l t + ay = m t + bz = n t + c
то направляющий вектор имеет вид {l; m; n}
Пример 4. Найти угол между прямыми
x = 2t + 1y = tz = -t – 1
и
x = t + 2y = -2t + 1z = 1
.
Решение: Так как прямые заданы параметрически, то {2; 1; -1} – направляющий вектор первой прямой, {1; -2; 0} направляющий вектор второй прямой.
cos φ =
|2 · 1 + 1 · (-2) + (-1) · 0|22 + 12 + (-1)2 · 12 + (-2)2 + 02
=
06 · 5
= 0
Ответ. φ = 90°
Пример 5 Найти угол между прямыми
x – 23
=
y4
=
z – 35
и –
x – 22
= 1 – 3y =
3z – 52
.
Решение: Для решения этой задачи найдем направляющие векторы этих прямых.
Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор {3; 4; 5}.
Преобразуем второе уравнение к каноническому вид.
–x – 22 = x – 2-2
1 – 3y = 1 + y-1/3 = y – 1/3-1/3
3z – 52 = z – 5/32/3
Получено уравнение второй прямой в канонической форме
x – 2-2 = y – 1/3-1/3 = z – 5/32/3
{-2; -13; 23} – направляющий вектор второй прямой.
cos φ =
3·(-2) + 4·(-13) + 5·2332 + 42 + 52 · (-2)2 + (-13)2 + (23)2
=
-6 – 43 + 1039 + 16 + 25 · 4 + 19 + 49
=
-450 · 41/9
=
12582
=
682205
Ответ. φ ≈ 74.63°
Вы уже знакомы с понятиями угла между прямыми и угла
между векторами. А также знаете, что такое двугранный угол и угол между прямой
и плоскостью.
Сегодня мы научимся вычислять углы между прямыми, а
также между прямой и плоскостью.
Но для начала введём понятие направляющего вектора.
Определение:
Ненулевой вектор называется направляющим
вектором прямой а, если он лежит либо на прямой а, либо
на прямой, параллельной прямой а.
Понятно, что таких векторов бесконечно много и все
они коллинеарны.
Задача:
найти угол между прямыми, если известны координаты направляющих векторов этих
прямых.
Будем работать с прямыми а и b.
Для прямой a направляющим является
вектор p, а для прямой b
— вектор q.
Итак, возможны два случая.
Если угол между
направляющими векторами острый, то он равен углу между прямыми .
И если угол между
направляющими векторами тупой, то угол между
прямыми равен 180о – .
Так как в первом случае косинус угла между прямыми
равен косинусу угла между направляющими векторами, то мы можем вычислить его по
известной формуле косинуса угла между векторами.
Ну, а во втором случае записан косинус угла смежного
с углом .
Косинусы смежных углов противоположны по знаку, поэтому мы получим выражение
противоположное тому, которое было получено в первом случае.
Угол между прямыми всегда меньше либо равен 90о,
поэтому его косинус соответственно будет являться числом неотрицательным. Тогда
оба случая можно объединить в один и записать, что косинус угла между прямыми
равен частному модуля скалярного произведения направляющих векторов и
произведения их длин.
А сейчас найдём угол между прямой и плоскостью, если
известны координаты направляющего вектора к прямой и координаты ненулевого
вектора, перпендикулярного к плоскости.
Вам уже известно, что углом между прямой и
плоскостью является угол между прямой и её проекцией на эту плоскость.
Обозначим этот угол за .
А угол между направляющим вектором и вектором, перпендикулярным к плоскости
обозначим за .
Эти углы в сумме дают 90о (то есть углы и
являются
дополнительными). А нам известно, что синус угла равен косинусу дополнительного
угла. Это означает, что .
Ну, а между
векторами и
мы
без труда найдём по уже известной формуле:
Но ведь возможен и случай, когда угол между
векторами и
тупой.
Тогда углы и
являются
дополнительными, то есть их сумма равна .
Отсюда можно записать, что .
Ну, а формула косинуса угла между векторами нам уже
известна.
Чтобы объединить две полученных формулы в одну,
можно вспомнить, что синус угла от нуля до 180о является числом
неотрицательным. Тогда можно записать, что
Таким образом, мы получили формулы косинуса угла
между прямыми и синуса угла между прямой и плоскостью. Причём правые части эти
формул абсолютно совпадают.
Отличие лишь в том, что две прямые задают
направляющие векторы.
А прямую и плоскость — направляющий вектор прямой и
вектор, перпендикулярный к плоскости.
Такой вектор называют нормальным вектором к
плоскости.
Решим несколько задач.
Задача:
прямоугольный
параллелепипед, где . Найти
и
.
Решение:
ранее в таких случаях мы пытались по рисунку находить величины углов.
Но теперь мы владеем формулой косинуса угла между
прямыми.
Только для этого необходимо знать координаты
направляющих векторов прямых. В данном случае, для прямой направляющим
может является вектор ,
а для прямой
—
вектор .
Для удобства изобразим прямоугольную систему
координат так, чтобы точка совпадала
с точкой начала координат. Взяв длину рёбер и
за
единичные отрезки, можно утверждать, что длина отрезка равна
2.
Тогда не трудно определить координаты точек ,
,
и
.
Точка .
Точка .
Точка .
А точка .
Теперь не трудно найти координаты векторов и
как
разности соответствующих координат конца и начала вектора.
Получаем, что вектор .
А вектор .
Теперь можем воспользоваться формулой косинуса угла
между прямыми. Подставим координаты направляющих векторов.
А теперь, пользуясь фрагментом из таблицы Брадиса,
найдём величину данного угла, помня о том, что поправка для косинуса имеет знак
минус:
Итак, угол между прямыми .
Теперь найдём угол между прямыми и
.
В качестве направляющих векторов для данных прямых
удобно взять векторы и
.
Найдём координаты точек ,
и
.
Точка А имеет координаты .
Точка .
А точка .
Тогда вектор .
А вектор .
Подставим значения координат направляющих векторов в
формулу косинуса угла между прямыми.
В ходе вычислений получаем
Вычислив примерное значение этой дроби, можем
воспользоваться таблицей Брадиса:
Так получаем, что угол между прямыми .
Вот так по координатам направляющих векторов находят
величину угла между прямыми.
Задача:
тетраэдр.
.
,
а .
Вычислить синус угла между прямой, проходящей через
середины рёбер и
,
и плоскостью: а) ;
б) ;
в) .
Решение:
По условию рёбра ,
и
взаимно
перпендикулярны. Поэтому можно изобразить прямоугольную систему координат так,
чтобы точка совпадала
с точкой начала координат.
Тогда зная длины рёбер ,
и
не
трудно отметить единичные отрезки и определить координаты всех вершин.
Мы с вами будем находить синус угла между прямой и
каждой из данных плоскостей.
Сначала разберёмся с прямой. Она проходит через
середины рёбер и
,
пусть это будут точки и
.
И для вычисления синуса угла нужно знать координаты направляющего вектора. В
качестве направляющего вектора можно взять вектор .
Координаты точки найдём
как координаты середины отрезка .
Каждая из них равна полусумме соответствующих координат точек и
.
Так получаем,
,
.
Аналогично найдём координаты точки ,
как полусумму соответствующих координат точек и
.
Получаем ,
.
Теперь можем найти координаты вектора как
разности соответствующих координат.
Получаем, что направляющий вектор данной прямой
имеет координаты .
Также для вычисления синуса угла между прямой и
плоскостью необходимо знать координаты нормального вектора к плоскости, то есть
перпендикулярного к ней.
Задача:
Доказать, что угол между скрещивающимися прямыми, одна из которых содержит
диагональ куба, а другая — диагональ грани куба, равен .
Решение:
изобразим прямоугольную координатную плоскость так, чтобы координатные оси
совпадали с рёбрами куба.
Обозначим буквами вершины куба, через которые проходят
данные скрещивающиеся прямые. Найдём угол между прямыми .
Пусть длина единичных отрезков на осях равна длине
ребра куба.
Тогда в такой системе координат нетрудно найти
координаты точек О, О1, О2 и О3.
А теперь найдём координаты векторов ОО1 и
О2О3, которые являются направляющими для данных прямых.
Вектор .
А вектор .
Найдём косинус угла между данными прямыми, подставив
в формулу координаты направляющих векторов.
В ходе вычислений получаем, что
А значит, угол между прямыми .
Что и требовалось доказать.
Итоги:
На этом уроке мы получили формулу вычисления
косинуса угла между прямыми по координатам их направляющих векторов. А также
формулу вычисления синуса угла между прямой и плоскостью по координатам
направляющего вектора данной прямой и нормального вектора данной плоскости.
