Всего: 29 1–20 | 21–29
Добавить в вариант
В параллелограмме ABCD высота, опущенная на сторону AB, равна 4,
Найдите синус угла B.
Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.
Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен
Найдите меньшее основание.
Найдите площадь ромба, если его высота равна 2, а острый угол 30°.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.
Площадь боковой поверхности конуса в
раз больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.
На клетчатой бумаге с размером клетки 1×1 изображён угол. Найдите синус этого угла.
Источник: ЕГЭ по математике — 2015. Досрочная волна, вариант ФИПИ
Всего: 29 1–20 | 21–29
Один из типов задач в задании 3 – это задачи на нахождение углов.
На клетчатой решетке изображен угол, величину которого надо найти.
Это могут быть самые разнообразные углы:
Методы вычисления могут быть разные.
Принцип большинства заданий – найти прямоугольный треугольник и вычислить у него стороны и найти угол используя синус или косинус или тангенс (в зависимости от задания)
Если необходимо найти тангенс тупого угла, то в начале находим тангенс смежного острого угла и применяем формулу приведения (в ответе появится минус). Напомню, что синус тупого и острого угла имеет один и тот же знак, а вот косинус, так же как и тангенс, тупого и острого угла имеет противоположные знаки.
Если так не получается, то начинаем искать отрезки, треугольники и вычислять стороны. Применять свойство равнобедренных треугольников или теорему косинусов.
Если совсем непонятно, что делать, то встройте угол в прямоугольник и посчитайте все стороны и решение придет
Мы рассмотрели один из типов задач. Главное, поймите принцип, а тогда решите любую задачу.
Синусом угла в прямоугольном треугольнике называют отношение противолежащего катета к гипотенузе.
Катетами являются стороны, которые образуют прямой угол в треугольнике, соответственно, гипотенузой является третья (самая длинная) сторона.
Для простоты запоминания можно дать такое определение: синус угла — это отношение дальнего от рассматриваемого угла катета к гипотенузе.
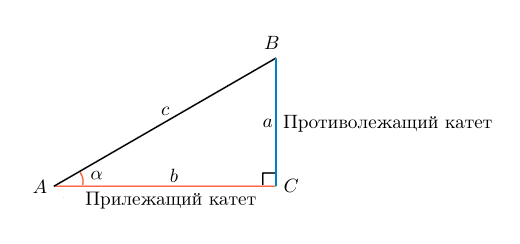
В случае с рисунком, описанным выше: sinα=acsinalpha=frac{a}{c}
В треугольнике, один из углов которого равен 90 градусам, известен катет при угле αalpha и равен он 3 см3text{ см}. Также дано произведение длин катетов и равно 12 см212text{ см}^2. Найдите синус угла αalpha.
Решение
Сначала нужно найти длину неизвестного нам катета. Для этого воспользуемся данным нам произведением. Обозначим неизвестный катет за xx. Тогда, по условию задачи:
3⋅x=123cdot x=12
x=123=4x=frac{12}{3}=4
a=x=4a=x=4
По теореме Пифагора найдем гипотенузу:
a2+b2=c2a^2+b^2=c^2
42+32=c24^2+3^2=c^2
25=c225=c^2
c=5c=5
sinα=ac=45=0.8sinalpha=frac{a}{c}=frac{4}{5}=0.8
Ответ
0.80.8
Вычислите синус 45 градусов.
Решение
Для этого воспользуемся тригонометрической таблицей углов. Находим, что:
sin45∘=π4=0.785sin 45^circ=frac{pi}{4}=0.785
Ответ
0.7850.785
Если в задаче известен косинус угла и нужно найти его синус, то наличие известных длин катетов и гипотенузы не обязательны. Достаточно просто воспользоваться основным тригонометрическим тождеством, которое имеет следующий вид:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
αalpha — любой угол.
Квадрат косинуса угла в треугольнике равен 0.8. Найдите синус данного угла.
Решение
Воспользуемся основным тригонометрическим тождеством:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
sin2α+0.8=1sin^2alpha+0.8=1
sin2α=0.2sin^2alpha=0.2
sinα=0.2sinalpha=sqrt{0.2}
sinα≈0.447sinalphaapprox0.447
Ответ
0.4470.447
Испытываете проблемы с вычислением синуса? Оформите задачу по математике на заказ у наших экспертов!
Тест по теме «Вычисление синуса»
6. Геометрия на плоскости (планиметрия). Часть II
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Вычисление синуса, косинуса и тангенса угла треугольника
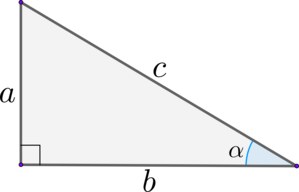
В прямоугольном треугольнике:
(blacktriangleright) Синус острого угла равен отношению противолежащего катета к гипотенузе: [{large{sin alpha =
dfrac{a}{c}}}]
(blacktriangleright) Косинус острого угла равен отношению прилежащего катета к гипотенузе: [{large{cos alpha =
dfrac{b}{c}}}]
(blacktriangleright) Тангенс острого угла равен отношению противолежащего катета к прилежащему: [{large{mathrm{tg}, alpha
= dfrac{a}{b}}}]
(blacktriangleright) Котангенс острого угла равен отношению прилежащего катета к противолежащему: [{large{mathrm{ctg},
alpha =dfrac{b}{a}}}]
Важные формулы:
[{large{begin{array}{|lcl|} hline sin^2 alpha+cos^2 alpha
=1&qquad& mathrm{tg}, alpha cdot mathrm{ctg}, alpha
=1\ &&\
mathrm{tg}, alpha=dfrac{sin alpha}{cos
alpha}&&mathrm{ctg}, alpha
=dfrac{cos alpha}{sin alpha}\&&\
hline
end{array}}}]
[begin{array}{|c|c|c|c|c|c|}
hline & phantom{000}, 0^circ phantom{000}& phantom{000},
30^circ phantom{000} &
phantom{000}, 45^circ phantom{000} & phantom{000}, 60^circ phantom{000}
& phantom{000}, 90^circ phantom{000}\[1ex]
hline sin & 0 ½&frac{sqrt2}2&frac{sqrt3}2 & 1\[1ex]
hline cos & 1 & frac{sqrt3}2&frac{sqrt2}2½ & 0\[1ex]
hline mathrm{tg} & 0 & frac{sqrt3}3&1&sqrt3 & text{не сущ.}\[1ex]
hline mathrm{ctg}& text{не сущ.} &sqrt3&1&frac{sqrt3}3 & 0\[1ex]
hline
end{array}]
Задание
1
#612
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 90^{circ}), (sin {angle BAC} = dfrac{2}{3}). Найдите (AC), если (AB = 6sqrt{5}).
Синус острого угла в прямоугольном треугольнике равен отношению противолежащего этому углу катета к гипотенузе, тогда [dfrac{BC}{AB} = dfrac{2}{3}qquadRightarrowqquad BC = dfrac{2}{3}AB = 4sqrt{5}.]
По теореме Пифагора (AC^2 = AB^2 – BC^2 = 36cdot 5 – 16cdot 5 = 20cdot 5 = 10^2), тогда (AC = 10).
Ответ: 10
Задание
2
#2098
Уровень задания: Равен ЕГЭ
Дан прямоугольный треугольник (ABC), причем (angle C=90^circ). Известно, что (cos angle B=dfrac13), (AB=9). Найдите (BC).

По определению косинуса [cosangle B=dfrac{BC}{AB}=dfrac13 quad
Leftrightarrow quad BC=dfrac13cdot AB=dfrac13cdot 9=3]
Ответ: 3
Задание
3
#2099
Уровень задания: Равен ЕГЭ
Дан треугольник (ABC), причем (angle C=90^circ). Найдите длину его гипотенузы, если (AC=8, cos angle A=dfrac45).

По определению косинуса [cos angle A=dfrac{AC}{AB}=dfrac45
quad Leftrightarrow quad AB=ACcdot dfrac54=10]
Ответ: 10
Задание
4
#3320
Уровень задания: Равен ЕГЭ
Большее основание равнобедренной трапеции равно (34). Боковая сторона равна (14). Синус острого угла равен (dfrac{2sqrt{10}}7). Найдите меньшее основание.

Проведем (BHperp AD). Из (triangle ABH): [dfrac{2sqrt{10}}7=sinangle A=dfrac{BH}{AB}quadRightarrowquad
BH=4sqrt{10}] Тогда по теореме Пифагора [AH=sqrt{14^2-(4sqrt{10})^2}=6] Так как (AH=0,5(AD-BC)), то (BC=AD-2AH=34-12=22).
Ответ: 22
Задание
5
#3305
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C=90^circ), (CH) – высота, (AB=13), (mathrm{tg},angle A=0,2). Найдите (AH).
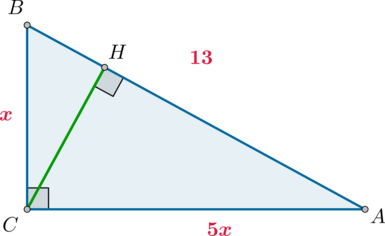
Так как по определению из (triangle ABC): [dfrac{BC}{AC}=mathrm{tg},angle A=dfrac 15] то можно принять (BC=x), (AC=5x). Следовательно, по теореме Пифагора [BC^2+AC^2=AB^2quadRightarrowquad x^2+(5x)^2=13^2quadRightarrowquad
x^2=dfrac{13}2] Из (triangle AHC): [cos angle A=dfrac{AH}{AC}] Из (triangle ABC): [cos angle A=dfrac{AC}{AB}] Следовательно: [dfrac{AH}{AC}=dfrac{AC}{AB}quadRightarrowquad
AH=dfrac{AC^2}{AB}=dfrac{(5x)^2}{13}=dfrac{25}2=12,5]
Ответ: 12,5
Задание
6
#3306
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C=90^circ), (CH) – высота, (AB=26), (mathrm{tg},angle B=5). Найдите (AH).
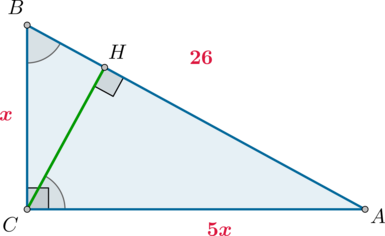
По определению из (triangle ABC): [dfrac{AC}{BC}=mathrm{tg},angle B=dfrac 51] Следовательно, можно принять (AC=5x), (BC=x). Тогда по теореме Пифагора (x^2+(5x)^2=26^2), откуда (x=sqrt{26}).
Тогда [sinangle B=dfrac{AC}{AB}=dfrac5{sqrt{26}}] По свойству прямоугольного треугольника (angle B=angle HCA). Следовательно, из (triangle HCA): [dfrac5{sqrt{26}}=sin angle HCA=dfrac{AH}{AC}quadRightarrowquad
AH=25]
Ответ: 25
Задание
7
#3307
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C=90^circ), (AB=17), (mathrm{tg},angle A=0,25). Найдите высоту (CH).
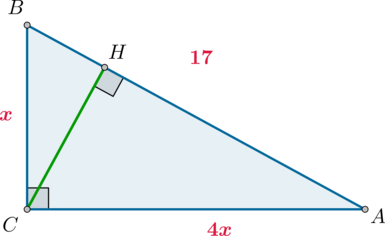
По определению из (triangle ABC): [dfrac{BC}{AC}=mathrm{tg},angle A=dfrac 14] Следовательно, можно принять (AC=4x), (BC=x). Тогда по теореме Пифагора (x^2+(4x)^2=17^2), откуда (x=sqrt{17}).
Так как площадь прямоугольного треугольника (ABC), с одной стороны, равна (0,5CHcdot AB), а с другой стороны, равна (0,5BCcdot AC), то [CHcdot AB=BCcdot ACquadRightarrowquad CH=dfrac{4x^2}{AB}=4]
Ответ: 4
Уметь оперативно и правильно решать задачи ЕГЭ на вычисление элементов многоугольника необходимо всем выпускникам вне зависимости от того, базовый или профильный уровень экзамена они сдают. Причем этой теме традиционно посвящается несколько заданий. Поэтому, если учащийся рассчитывает получить достойные баллы по итогам прохождения ЕГЭ, то ему обязательно стоит уделить внимание задачам, в которых требуется найти синус, косинус и тангенс угла треугольника.
Вместе с образовательным порталом «Школково» вы сможете восполнить пробелы в знаниях и отточить необходимый навык. Весь теоретический и практический материал составлен и изложен таким образом, чтобы все выпускники могли без особых затруднений справляться с задачами ЕГЭ, в которых требуется вычислить тангенс, синус или косинус угла треугольника.
Основные моменты
Первое, что нужно сделать при решении подобных задач в ЕГЭ, – вспомнить, что такое тангенс, косинус и синус угла треугольника. Далее рекомендуется следовать такому алгоритму:
- Выделяем треугольник, в который входит сторона или угол, который требуется найти.
- Определяем известные элементы и выявляем тригонометрическую функцию, которая их связывает.
- Записываем получившееся соотношение и применяем подходящую формулу.
Научившись правильно выполнять упражнения на вычисление элементов многоугольника, а также, например, по теме «Окружность, описанная около многоугольника», которые представлены в данном разделе образовательного портала «Школково», вы сможете закрепить материал и без труда справляться с подобными заданиями на аттестационном экзамене.

УСТАЛ? Просто отдохни
Синус угла. Таблица синусов.
Синус угла через градусы, минуты и секунды
Синус угла через десятичную запись угла
Как найти угол зная синус этого угла
У синуса есть обратная тригонометрическая функция – arcsin(y)=x
sin(arcsin(y))=y
Пример sin(30°) = 1/2; arcsin(1/2) = 30°
Рассчитать арксинус
Определение синуса
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Синусом угла α называется ордината точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.

sin(α) = BC/AB
sin(-α) = -sin(α)
Периодичность синуса
Функция y = sin(x) периодична, с периодом 2π
sin(α ± 2π) = sin(α)
Пример sin(5π) = sin(4π + π) = sin(π)
Таблица синусов в радианах
sin(0°) = 0sin(π/12) = sin(15°) = 0.2588190451sin(π/6) = sin(30°) = 0.5sin(π/4) = sin(45°) = 0.7071067812sin(π/3) = sin(60°) = 0.8660254038sin(5π/12) = sin(75°) = 0.9659258263sin(π/2) = sin(90°) = 1sin(7π/12) = sin(105°) = 0.9659258263sin(2π/3) = sin(120°) = 0.8660254038sin(3π/4) = sin(135°) = 0.7071067812sin(5π/6) = sin(150°) = 0.5sin(11π/12) = sin(165°) = 0.2588190451sin(π) = sin(180°) = 0sin(13π/12) = sin(195°) = -0.2588190451sin(7π/6) = sin(210°) = -0.5sin(5π/4) = sin(225°) = -0.7071067812sin(4π/3) = sin(240°) = -0.8660254038sin(17π/12) = sin(255°) = -0.9659258263sin(3π/2) = sin(270°) = -1sin(19π/12) = sin(285°) = -0.9659258263sin(5π/3) = sin(300°) = -0.8660254038sin(7π/4) = sin(315°) = -0.7071067812sin(11π/6) = sin(330°) = -0.5sin(23π/12) = sin(345°) = -0.2588190451
Таблица Брадиса синусы
| sin(0) = 0 | sin(120) = 0.8660254038 | sin(240) = -0.8660254038 |
| sin(1) = 0.01745240644 | sin(121) = 0.8571673007 | sin(241) = -0.8746197071 |
| sin(2) = 0.0348994967 | sin(122) = 0.8480480962 | sin(242) = -0.8829475929 |
| sin(3) = 0.05233595624 | sin(123) = 0.8386705679 | sin(243) = -0.8910065242 |
| sin(4) = 0.06975647374 | sin(124) = 0.8290375726 | sin(244) = -0.8987940463 |
| sin(5) = 0.08715574275 | sin(125) = 0.8191520443 | sin(245) = -0.906307787 |
| sin(6) = 0.1045284633 | sin(126) = 0.8090169944 | sin(246) = -0.9135454576 |
| sin(7) = 0.1218693434 | sin(127) = 0.79863551 | sin(247) = -0.9205048535 |
| sin(8) = 0.139173101 | sin(128) = 0.7880107536 | sin(248) = -0.9271838546 |
| sin(9) = 0.156434465 | sin(129) = 0.7771459615 | sin(249) = -0.9335804265 |
| sin(10) = 0.1736481777 | sin(130) = 0.7660444431 | sin(250) = -0.9396926208 |
| sin(11) = 0.1908089954 | sin(131) = 0.7547095802 | sin(251) = -0.9455185756 |
| sin(12) = 0.2079116908 | sin(132) = 0.7431448255 | sin(252) = -0.9510565163 |
| sin(13) = 0.2249510543 | sin(133) = 0.7313537016 | sin(253) = -0.956304756 |
| sin(14) = 0.2419218956 | sin(134) = 0.7193398003 | sin(254) = -0.9612616959 |
| sin(15) = 0.2588190451 | sin(135) = 0.7071067812 | sin(255) = -0.9659258263 |
| sin(16) = 0.2756373558 | sin(136) = 0.6946583705 | sin(256) = -0.9702957263 |
| sin(17) = 0.2923717047 | sin(137) = 0.6819983601 | sin(257) = -0.9743700648 |
| sin(18) = 0.3090169944 | sin(138) = 0.6691306064 | sin(258) = -0.9781476007 |
| sin(19) = 0.3255681545 | sin(139) = 0.656059029 | sin(259) = -0.9816271834 |
| sin(20) = 0.3420201433 | sin(140) = 0.6427876097 | sin(260) = -0.984807753 |
| sin(21) = 0.3583679495 | sin(141) = 0.629320391 | sin(261) = -0.9876883406 |
| sin(22) = 0.3746065934 | sin(142) = 0.6156614753 | sin(262) = -0.9902680687 |
| sin(23) = 0.3907311285 | sin(143) = 0.6018150232 | sin(263) = -0.9925461516 |
| sin(24) = 0.4067366431 | sin(144) = 0.5877852523 | sin(264) = -0.9945218954 |
| sin(25) = 0.4226182617 | sin(145) = 0.5735764364 | sin(265) = -0.9961946981 |
| sin(26) = 0.4383711468 | sin(146) = 0.5591929035 | sin(266) = -0.9975640503 |
| sin(27) = 0.4539904997 | sin(147) = 0.544639035 | sin(267) = -0.9986295348 |
| sin(28) = 0.4694715628 | sin(148) = 0.5299192642 | sin(268) = -0.999390827 |
| sin(29) = 0.4848096202 | sin(149) = 0.5150380749 | sin(269) = -0.9998476952 |
| sin(30) = 0.5 | sin(150) = 0.5 | sin(270) = -1 |
| sin(31) = 0.5150380749 | sin(151) = 0.4848096202 | sin(271) = -0.9998476952 |
| sin(32) = 0.5299192642 | sin(152) = 0.4694715628 | sin(272) = -0.999390827 |
| sin(33) = 0.544639035 | sin(153) = 0.4539904997 | sin(273) = -0.9986295348 |
| sin(34) = 0.5591929035 | sin(154) = 0.4383711468 | sin(274) = -0.9975640503 |
| sin(35) = 0.5735764364 | sin(155) = 0.4226182617 | sin(275) = -0.9961946981 |
| sin(36) = 0.5877852523 | sin(156) = 0.4067366431 | sin(276) = -0.9945218954 |
| sin(37) = 0.6018150232 | sin(157) = 0.3907311285 | sin(277) = -0.9925461516 |
| sin(38) = 0.6156614753 | sin(158) = 0.3746065934 | sin(278) = -0.9902680687 |
| sin(39) = 0.629320391 | sin(159) = 0.3583679495 | sin(279) = -0.9876883406 |
| sin(40) = 0.6427876097 | sin(160) = 0.3420201433 | sin(280) = -0.984807753 |
| sin(41) = 0.656059029 | sin(161) = 0.3255681545 | sin(281) = -0.9816271834 |
| sin(42) = 0.6691306064 | sin(162) = 0.3090169944 | sin(282) = -0.9781476007 |
| sin(43) = 0.6819983601 | sin(163) = 0.2923717047 | sin(283) = -0.9743700648 |
| sin(44) = 0.6946583705 | sin(164) = 0.2756373558 | sin(284) = -0.9702957263 |
| sin(45) = 0.7071067812 | sin(165) = 0.2588190451 | sin(285) = -0.9659258263 |
| sin(46) = 0.7193398003 | sin(166) = 0.2419218956 | sin(286) = -0.9612616959 |
| sin(47) = 0.7313537016 | sin(167) = 0.2249510543 | sin(287) = -0.956304756 |
| sin(48) = 0.7431448255 | sin(168) = 0.2079116908 | sin(288) = -0.9510565163 |
| sin(49) = 0.7547095802 | sin(169) = 0.1908089954 | sin(289) = -0.9455185756 |
| sin(50) = 0.7660444431 | sin(170) = 0.1736481777 | sin(290) = -0.9396926208 |
| sin(51) = 0.7771459615 | sin(171) = 0.156434465 | sin(291) = -0.9335804265 |
| sin(52) = 0.7880107536 | sin(172) = 0.139173101 | sin(292) = -0.9271838546 |
| sin(53) = 0.79863551 | sin(173) = 0.1218693434 | sin(293) = -0.9205048535 |
| sin(54) = 0.8090169944 | sin(174) = 0.1045284633 | sin(294) = -0.9135454576 |
| sin(55) = 0.8191520443 | sin(175) = 0.08715574275 | sin(295) = -0.906307787 |
| sin(56) = 0.8290375726 | sin(176) = 0.06975647374 | sin(296) = -0.8987940463 |
| sin(57) = 0.8386705679 | sin(177) = 0.05233595624 | sin(297) = -0.8910065242 |
| sin(58) = 0.8480480962 | sin(178) = 0.0348994967 | sin(298) = -0.8829475929 |
| sin(59) = 0.8571673007 | sin(179) = 0.01745240644 | sin(299) = -0.8746197071 |
| sin(60) = 0.8660254038 | sin(180) = 0 | sin(300) = -0.8660254038 |
| sin(61) = 0.8746197071 | sin(181) = -0.01745240644 | sin(301) = -0.8571673007 |
| sin(62) = 0.8829475929 | sin(182) = -0.0348994967 | sin(302) = -0.8480480962 |
| sin(63) = 0.8910065242 | sin(183) = -0.05233595624 | sin(303) = -0.8386705679 |
| sin(64) = 0.8987940463 | sin(184) = -0.06975647374 | sin(304) = -0.8290375726 |
| sin(65) = 0.906307787 | sin(185) = -0.08715574275 | sin(305) = -0.8191520443 |
| sin(66) = 0.9135454576 | sin(186) = -0.1045284633 | sin(306) = -0.8090169944 |
| sin(67) = 0.9205048535 | sin(187) = -0.1218693434 | sin(307) = -0.79863551 |
| sin(68) = 0.9271838546 | sin(188) = -0.139173101 | sin(308) = -0.7880107536 |
| sin(69) = 0.9335804265 | sin(189) = -0.156434465 | sin(309) = -0.7771459615 |
| sin(70) = 0.9396926208 | sin(190) = -0.1736481777 | sin(310) = -0.7660444431 |
| sin(71) = 0.9455185756 | sin(191) = -0.1908089954 | sin(311) = -0.7547095802 |
| sin(72) = 0.9510565163 | sin(192) = -0.2079116908 | sin(312) = -0.7431448255 |
| sin(73) = 0.956304756 | sin(193) = -0.2249510543 | sin(313) = -0.7313537016 |
| sin(74) = 0.9612616959 | sin(194) = -0.2419218956 | sin(314) = -0.7193398003 |
| sin(75) = 0.9659258263 | sin(195) = -0.2588190451 | sin(315) = -0.7071067812 |
| sin(76) = 0.9702957263 | sin(196) = -0.2756373558 | sin(316) = -0.6946583705 |
| sin(77) = 0.9743700648 | sin(197) = -0.2923717047 | sin(317) = -0.6819983601 |
| sin(78) = 0.9781476007 | sin(198) = -0.3090169944 | sin(318) = -0.6691306064 |
| sin(79) = 0.9816271834 | sin(199) = -0.3255681545 | sin(319) = -0.656059029 |
| sin(80) = 0.984807753 | sin(200) = -0.3420201433 | sin(320) = -0.6427876097 |
| sin(81) = 0.9876883406 | sin(201) = -0.3583679495 | sin(321) = -0.629320391 |
| sin(82) = 0.9902680687 | sin(202) = -0.3746065934 | sin(322) = -0.6156614753 |
| sin(83) = 0.9925461516 | sin(203) = -0.3907311285 | sin(323) = -0.6018150232 |
| sin(84) = 0.9945218954 | sin(204) = -0.4067366431 | sin(324) = -0.5877852523 |
| sin(85) = 0.9961946981 | sin(205) = -0.4226182617 | sin(325) = -0.5735764364 |
| sin(86) = 0.9975640503 | sin(206) = -0.4383711468 | sin(326) = -0.5591929035 |
| sin(87) = 0.9986295348 | sin(207) = -0.4539904997 | sin(327) = -0.544639035 |
| sin(88) = 0.999390827 | sin(208) = -0.4694715628 | sin(328) = -0.5299192642 |
| sin(89) = 0.9998476952 | sin(209) = -0.4848096202 | sin(329) = -0.5150380749 |
| sin(90) = 1 | sin(210) = -0.5 | sin(330) = -0.5 |
| sin(91) = 0.9998476952 | sin(211) = -0.5150380749 | sin(331) = -0.4848096202 |
| sin(92) = 0.999390827 | sin(212) = -0.5299192642 | sin(332) = -0.4694715628 |
| sin(93) = 0.9986295348 | sin(213) = -0.544639035 | sin(333) = -0.4539904997 |
| sin(94) = 0.9975640503 | sin(214) = -0.5591929035 | sin(334) = -0.4383711468 |
| sin(95) = 0.9961946981 | sin(215) = -0.5735764364 | sin(335) = -0.4226182617 |
| sin(96) = 0.9945218954 | sin(216) = -0.5877852523 | sin(336) = -0.4067366431 |
| sin(97) = 0.9925461516 | sin(217) = -0.6018150232 | sin(337) = -0.3907311285 |
| sin(98) = 0.9902680687 | sin(218) = -0.6156614753 | sin(338) = -0.3746065934 |
| sin(99) = 0.9876883406 | sin(219) = -0.629320391 | sin(339) = -0.3583679495 |
| sin(100) = 0.984807753 | sin(220) = -0.6427876097 | sin(340) = -0.3420201433 |
| sin(101) = 0.9816271834 | sin(221) = -0.656059029 | sin(341) = -0.3255681545 |
| sin(102) = 0.9781476007 | sin(222) = -0.6691306064 | sin(342) = -0.3090169944 |
| sin(103) = 0.9743700648 | sin(223) = -0.6819983601 | sin(343) = -0.2923717047 |
| sin(104) = 0.9702957263 | sin(224) = -0.6946583705 | sin(344) = -0.2756373558 |
| sin(105) = 0.9659258263 | sin(225) = -0.7071067812 | sin(345) = -0.2588190451 |
| sin(106) = 0.9612616959 | sin(226) = -0.7193398003 | sin(346) = -0.2419218956 |
| sin(107) = 0.956304756 | sin(227) = -0.7313537016 | sin(347) = -0.2249510543 |
| sin(108) = 0.9510565163 | sin(228) = -0.7431448255 | sin(348) = -0.2079116908 |
| sin(109) = 0.9455185756 | sin(229) = -0.7547095802 | sin(349) = -0.1908089954 |
| sin(110) = 0.9396926208 | sin(230) = -0.7660444431 | sin(350) = -0.1736481777 |
| sin(111) = 0.9335804265 | sin(231) = -0.7771459615 | sin(351) = -0.156434465 |
| sin(112) = 0.9271838546 | sin(232) = -0.7880107536 | sin(352) = -0.139173101 |
| sin(113) = 0.9205048535 | sin(233) = -0.79863551 | sin(353) = -0.1218693434 |
| sin(114) = 0.9135454576 | sin(234) = -0.8090169944 | sin(354) = -0.1045284633 |
| sin(115) = 0.906307787 | sin(235) = -0.8191520443 | sin(355) = -0.08715574275 |
| sin(116) = 0.8987940463 | sin(236) = -0.8290375726 | sin(356) = -0.06975647374 |
| sin(117) = 0.8910065242 | sin(237) = -0.8386705679 | sin(357) = -0.05233595624 |
| sin(118) = 0.8829475929 | sin(238) = -0.8480480962 | sin(358) = -0.0348994967 |
| sin(119) = 0.8746197071 | sin(239) = -0.8571673007 | sin(359) = -0.01745240644 |
Похожие калькуляторы
