Как найти синус угла шестиугольной пирамиде

2023-02-20   

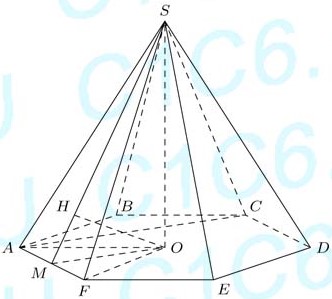
В правильной шестиугольной пирамиде $SABCDEF$ с основанием $ABCDEF$ найдите синус угла между прямой $AB$ и плоскостью $SBC$, если известно, что стороны основания равны 1, а боковые рёбра равны 2.

Решение:

Пусть $O$ – центр основания $ABCDEF$. Прямая $OC$ параллельна прямой $AB$, поэтому угол $alpha$ между прямой $AB$ и плоскостью $SBC$ равен углу между $OC$ и этой плоскостью.
Опустим перпендикуляр $OH$ из точки $O$ на апофему $SM$ пирамиды, лежащую в плоскости $SBC$. Прямая $BC$ перпендикулярна двум пересекающимся прямым $OM$ и $SM$ плоскости $SOM$, содержащей прямую $OH$, значит, $BCperp OH$. Таким образом, прямая $OH$ перпендикулярна двум пересекающимся прямым $BC$ и $SM$ плоскости $SBC$. Следовательно, $OH$ – перпендикуляр к плоскости $SBC$, а $CH$ – ортогональная проекция наклонной $OC$ к этой плоскости. Значит, угол между прямой $OC$ и плоскостью $SBC$ – это угол $OCH$.
В прямоугольном треугольнике $OMS$ известно, что

$OM=BMtg60^{circ}=frac{1}{2}cdotsqrt{3}=frac{sqrt{3}}{2},~SO=sqrt{SB^{2}-OB^{2}}=sqrt{4-1}=sqrt{3},$

$SM=sqrt{SB^{2}-BM^{2}}=sqrt{4-frac{1}{4}}=frac{sqrt{15}}{2}.$

Записав двумя способами площадь треугольника $SOM$, получим, что $frac{1}{2}OMcdot SO=frac{1}{2}SMcdot OH$, откуда

$OH=frac{OMcdot SO}{SM}=frac{frac{sqrt{3}}{2}cdotsqrt{3}}{frac{sqrt{15}}{2}}=frac{3}{sqrt{15}}=frac{sqrt{15}}{5}.$

Следовательно,

$sinalpha=sinangle OCH=frac{OH}{OA}=frac{frac{sqrt{15}}{5}}{1}=frac{sqrt{15}}{5}.$

BC II AD; Пусть начало координат O в середине AD; Ось OX вдоль AD, ось OY -перпендикулярно (проходит через середины BC и EF), ось OZ  вдоль OS;
Плоскость SAF пересекает оси OX в точке A (0, -1, 0) OY в точке M (0, -√3, 0) и OZ в точке S (0, 0, √3);
Координаты M и S очень легко вычислить, потому что OM = OS = OA*tg(60°) (треугольник ASD очевидно равносторонний).
Уравнение плоскости SAF выглядит так
– x – y/√3 + z/√3 = 1;
откуда вектор, нормальный к этой плоскости N = (-√3, -1, 1) (или любой ему пропорциональный).
Теперь надо найти угол между N и осью OX
cos(Ф) = Nx/INI = -√(3/5); по сути это ответ, знак косинуса не важен, его надо просто отбросить (минус означает, что вектор N “смотрит налево”, не более того, но можно выбрать и противоположный ему вектор в качестве нормального)
Ф = arccos(√(3/5));
В задаче надо найти угол между BC и плоскостью SAF. Определение этого угла зависит от того, откуда и в какую сторону считать, но если выбрать ориентацию нормали и определить угол с плоскостью так, чтобы они оба были острые, то ясно, что угол с нормалью и угол с плоскостью вместе составляют 90°; отсюда нужный угол равен arcsin(√(3/5));

Вы находитесь на странице вопроса В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите синус угла между прямой AB и плоскостью SBC? из категории Геометрия.
Уровень сложности вопроса рассчитан на учащихся 5 – 9 классов. На странице
можно узнать правильный ответ, сверить его со своим вариантом и обсудить
возможные версии с другими пользователями сайта посредством обратной связи.
Если ответ вызывает сомнения или покажется вам неполным, для проверки
найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте
новый вопрос, используя ключевые слова: введите вопрос в поисковую строку,
нажав кнопку в верхней части страницы.

Условие

Решение

Написать комментарий