ЗАДАЧА
Прежде чем приступить к решению задачи, мы:
– рассмотрим трапецию, вспомним ее основные характеристики;
– перенесем данные задачи на чертеж;
– внимательно прочитаем вопрос.
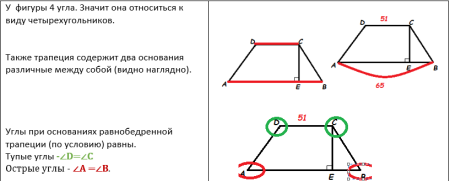
Как мы видим нам дана трапеция АВСD. Что мы знаем об этой фигуре? Давайте рассуждать:
По условию задачи СЕ- высота трапеции.
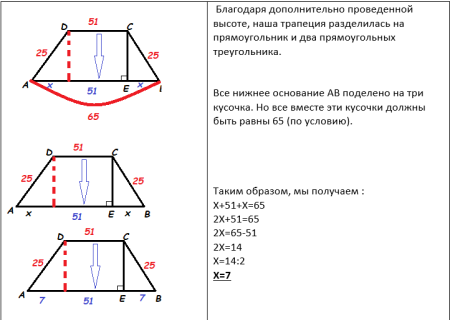
Проведем ещё одну высоту из точки D. Что нам это даст? Во- первых отметим ,что эти высоты равны друг другу. Во- вторых, построенная нами высота «отрезает» из нижнего основания кусочек равный 51. Наглядно это выглядит так;
Напомню, по условию, нам нужно найти синус острого угла трапеции. В нашей трапеции, как мы определили ранее, острые углы – А и В. Рассмотрим подробнее угол В в прямоугольном треугольнике СЕВ. Также вспомним, что синус острого угла – это отношение противоположного катета к гипотенузе прямоугольного ∆. Продолжение решения…..
Найдите синус острого угла трапеции, изображённой на рисунке
мая белых
Ученик
(165),
на голосовании
7 лет назад

Голосование за лучший ответ
блабла ???
Мастер
(2156)
7 лет назад
Проведём высоту трапеции . Она = 4. Найдём гипотенузу
Х^2=4^2+3^2
Х^2=25
Х=5
Синус- отношение противолежащего катета к гипотенузе
Sin =4/5=0.8
Ответ: sin=0.8
Один из типов задач в задании 3 – это задачи на нахождение углов.
На клетчатой решетке изображен угол, величину которого надо найти.
Это могут быть самые разнообразные углы:
Методы вычисления могут быть разные.
Принцип большинства заданий – найти прямоугольный треугольник и вычислить у него стороны и найти угол используя синус или косинус или тангенс (в зависимости от задания)
Если необходимо найти тангенс тупого угла, то в начале находим тангенс смежного острого угла и применяем формулу приведения (в ответе появится минус). Напомню, что синус тупого и острого угла имеет один и тот же знак, а вот косинус, так же как и тангенс, тупого и острого угла имеет противоположные знаки.
Если так не получается, то начинаем искать отрезки, треугольники и вычислять стороны. Применять свойство равнобедренных треугольников или теорему косинусов.
Если совсем непонятно, что делать, то встройте угол в прямоугольник и посчитайте все стороны и решение придет
Мы рассмотрели один из типов задач. Главное, поймите принцип, а тогда решите любую задачу.