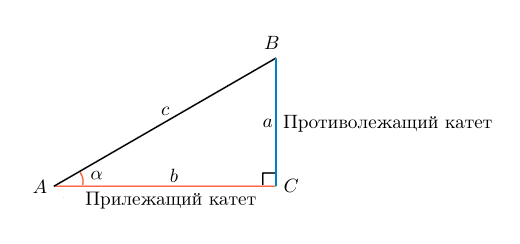
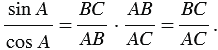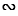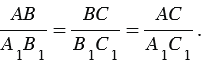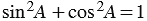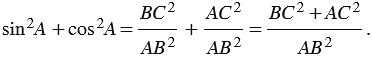Как найти синус угла в прямоугольнике

Как найти синус угла в прямоугольнике

Определение синуса угла

Синусом угла в прямоугольном треугольнике называют отношение противолежащего катета к гипотенузе.

Катетами являются стороны, которые образуют прямой угол в треугольнике, соответственно, гипотенузой является третья (самая длинная) сторона.

Для простоты запоминания можно дать такое определение: синус угла — это отношение дальнего от рассматриваемого угла катета к гипотенузе.

1.png

В случае с рисунком, описанным выше: sin⁡α=acsinalpha=frac{a}{c}

Задача 1

В треугольнике, один из углов которого равен 90 градусам, известен катет при угле αalpha и равен он 3 см3text{ см}. Также дано произведение длин катетов и равно 12 см212text{ см}^2. Найдите синус угла αalpha.

Решение

Сначала нужно найти длину неизвестного нам катета. Для этого воспользуемся данным нам произведением. Обозначим неизвестный катет за xx. Тогда, по условию задачи:

3⋅x=123cdot x=12

x=123=4x=frac{12}{3}=4

a=x=4a=x=4

По теореме Пифагора найдем гипотенузу:

a2+b2=c2a^2+b^2=c^2

42+32=c24^2+3^2=c^2

25=c225=c^2

c=5c=5

sin⁡α=ac=45=0.8sinalpha=frac{a}{c}=frac{4}{5}=0.8

Ответ

0.80.8

Задача 2

Вычислите синус 45 градусов.

Решение

Для этого воспользуемся тригонометрической таблицей углов. Находим, что:

sin⁡45∘=π4=0.785sin 45^circ=frac{pi}{4}=0.785

Ответ

0.7850.785

Если в задаче известен косинус угла и нужно найти его синус, то наличие известных длин катетов и гипотенузы не обязательны. Достаточно просто воспользоваться основным тригонометрическим тождеством, которое имеет следующий вид:

Основное тригонометрическое тождество

sin⁡2α+cos⁡2α=1sin^2alpha+cos^2alpha=1

αalpha — любой угол.

Задача 3

Квадрат косинуса угла в треугольнике равен 0.8. Найдите синус данного угла.

Решение

Воспользуемся основным тригонометрическим тождеством:

sin⁡2α+cos⁡2α=1sin^2alpha+cos^2alpha=1

sin⁡2α+0.8=1sin^2alpha+0.8=1

sin⁡2α=0.2sin^2alpha=0.2

sin⁡α=0.2sinalpha=sqrt{0.2}

sin⁡α≈0.447sinalphaapprox0.447

Ответ

0.4470.447

Испытываете проблемы с вычислением синуса? Оформите задачу по математике на заказ у наших экспертов!

Тест по теме «Вычисление синуса»

Источник

Что такое синус в треугольнике? Как найти синус острого угла в прямоугольном треугольнике?

Определение.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

sinus v treugolnike   Например,

для угла A треугольника ABC

противолежащий катет — это BC.

Соответственно, синус угла A в треугольнике ABC — это

    [sin angle A = frac{{BC}}{{AB}}]

sinus ugla v treugolnike   Для угла B треугольника ABC

противолежащим является катет AC.

Соответственно,  синус угла B в треугольнике ABC

равен отношению AC к AB:

    [sin angle B = frac{{AC}}{{AB}}]

Таким образом, синус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины противолежащего катета на длину гипотенузы. Длины отрезков выражаются положительными числами, поэтому синус угла треугольника также является положительным числом.

Поскольку длина катета всегда меньше длины гипотенузы, то синус острого угла прямоугольного треугольника — число, меньшее единицы.

Вывод:

Синус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:

    [0 < sin angle A < 1]

Синус угла треугольника зависит не от длин сторон треугольника, а от отношения этих длин.

Например,

1) В треугольнике ABC катет BC=3 см, а гипотенуза AB=5 см.

Тогда

    [sin angle A = frac{{BC}}{{AB}} = frac{3}{5}.]

2) В треугольнике ABC катет BC=21 дм, гипотенуза AB=35 дм.

Тогда

    [sin angle A = frac{{BC}}{{AB}} = frac{{21}}{{35}} = frac{3}{5}.]

Длины сторон треугольника изменилось, но отношения длин остались прежними, поэтому и значение синуса угла A не изменилось.

Угол A в обоих треугольниках одинаков.

Источник

  • Прямоугольный треугольник заключает в себе великое множество различных отношений между всеми своими составляющими. Один из углов в таком треугольнике имеет величину 90°, за счет чего и появляются его особенные свойства. Стороны, прилегающие к прямому углу, называются катетами прямоугольного треугольника, а сторона, лежащая напротив него – гипотенузой. Прямой угол в основе треугольника регулирует отношение сторон таким образом, что зная их можно рассчитать любой острый угол. Отношение противолежащего углу α катета a к гипотенузе c называется синусом угла α и записывается следующим образом:

    Разделив катет на гипотенузу, мы получим значение синуса, соответствующее определенной градусной мере, найти которую можно в таблице синусов. Таблица основных значений синусов приведена ниже, а полную версию можно найти по ссылке.

    Стороны и угол sin прямоугольного треугольника

    Свойства

    Синус угла sin(α) — есть отношение противолежащего катета a к гипотенузе c.

    Таблица синусов

    Синус угла 0° градусов   0   0.000
    Синус угла 30° градусов   1/2   0.500
    Синус угла 45° градусов   √2/2   0.707
    Синус угла 60° градусов   √3/2   0.866
    Синус угла 90° градусов   1   1
Источник
  1. Главная
  2. Справочники
  3. Справочник по геометрии 7-9 класс
  4. Подобные треугольники
  5. Синус, косинус и тангенс острого угла прямоугольного треугольника

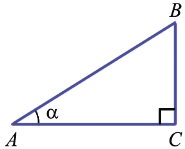
Рассмотрим прямоугольный треугольник АВС с прямым углом С:

Катет ВС этого треугольника является противолежащим углу А, а катет АС – прилежащим к этому углу.

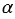
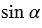
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Синус угла, который равен , обозначается символом , читается: “синус альфа”.

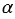
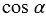
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Косинус угла, который равен , обозначается символом , читается: “косинус альфа”.

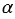
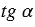
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету. Тангенс угла, который равен , обозначается символом , читается: “тангенс альфа”.

На рисунке

                             (1)

                            (2)

                               (3)

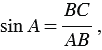
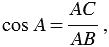
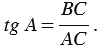
Из формул (1) и (2) получаем:

Сравнивая с формулой (3), находим:

                              (4)

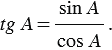
Получили, что тангенс угла равен отношению синуса к косинусу этого угла.

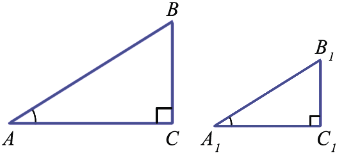
Докажем, что если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.

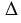
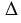
Дано: АВС, А1В1С1, С = С1 = 900, А = А1.

Доказать: sin A = sin A1, cos A = cos A1, tg A = tg A1.

Доказательство:

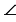
АВС А1В1С1 по первому признаку подобия треугольников (т.к. С = С1 = 900, А = А1). Из подобия треугольников следует пропорциональность сходственных сторон, поэтому мы можем записать:

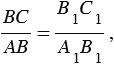
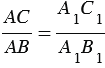
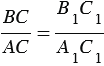
Из этих равенств следует, что т.е. sin A = sin A1. Аналогично , т.е. cos A = cos A1, и , т.е. tg A = tg A1, что и требовалось доказать.

Мы получили, что синус, косинус и тангенс острого угла зависит только от величины этого угла.

Докажем основное тригонометрическое тождество:

Из формул (1) и (2) получаем

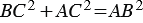
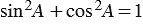
По теореме Пифагора , поэтому .

Советуем посмотреть:

Пропорциональные отрезки

Определение подобных треугольников

Отношение площадей подобных треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Средняя линия треугольника

Пропорциональные отрезки в прямоугольном треугольнике

Практические приложения подобия треугольников

О подобии произвольных фигур

Значение синуса, косинуса и тангенса для углов 30, 45 и 60

Подобные треугольники


Правило встречается в следующих упражнениях:

7 класс

Задание 642,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1033,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1034,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1036,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1037,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 6,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1133,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1238,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1239,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1307,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Гипотенуза прямоугольного треугольника – это сторона, лежащая напротив прямого угла.

Катеты – стороны, лежащие напротив острых углов. Катет (a), лежащий напротив угла (alpha), называется противолежащим (по отношению к углу (alpha)). Другой катет (b), который лежит на одной из сторон угла (alpha), называется прилежащим.

Синус острого угла в прямоугольном треугольнике равен отношению противоположного катета к гипотенузе: (sin∠A=​frac{a}{​c} ​​).

Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе: (cos∠A=frac{b}{c} ​​).

В прямоугольном треугольнике синус одного острого угла равен косинусу другого, и наоборот:

(sin∠A=cos∠B; sin angle A=cos angle B; sin∠A=cos∠B; \ sin∠B=cos∠A; sin angle B=cos angle A; sin∠B=cos∠A.)

Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: (tg ∠A=​frac{a}{b} ​​).

Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу: (tgangle A=frac{sinangle A}{cosangle A}).

Котангенс острого угла в прямоугольном треугольнике равен отношению прилежащего катета к противолежащему: (ctg ∠A=​frac{b}{a} ​​).

Котангенсом острого угла называется отношение косинуса к синусу: (ctgangle A=frac{cosangle A}{sinangle A}).

Таблица значений синуса, косинуса, тангенса и котангенса:

(varphi) (0^{circ}) (30^{circ}) (45^{circ}) (60^{circ}) (90^{circ})
(sin varphi) (0) (begin{aligned} frac{1}{2} end{aligned}) (begin{aligned} frac{sqrt 2}{2} end{aligned}) (begin{aligned} frac{sqrt 3}{2} end{aligned})

(1)

(cos varphi)

 (1) (begin{aligned} frac{sqrt 3}{2} end{aligned}) (begin{aligned} frac{sqrt 2}{2} end{aligned}) (begin{aligned} frac{1}{2} end{aligned})

(0)
(rm tg varphi) (0) (begin{aligned} frac{1}{sqrt 3} end{aligned}) (1) (begin{aligned} sqrt 3 end{aligned})

(color{red}-)
(rm ctg varphi) (color{red}-) (begin{aligned} sqrt 3 end{aligned}) (1) (begin{aligned} frac{1}{sqrt 3} end{aligned})

(0)
Источник

Добавить комментарий