Содержание:
- § 1 Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника
- § 2 Решение задачи по теме урока
§ 1 Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника
В этом уроке мы познакомимся с такими понятиями, как синус, косинус, тангенс и котангенс острого угла в прямоугольном треугольнике, выведем несколько тригонометрических формул, а также рассмотрим решение задачи.
Начертим прямоугольный треугольник АВС с прямым углом С.
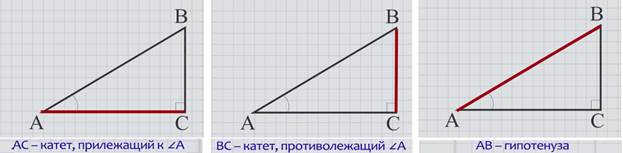
Сторона треугольника АС является катетом, прилежащим к углу А, сторона ВС – катетом, противолежащим углу А, АВ – гипотенуза.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Обозначается sin A.
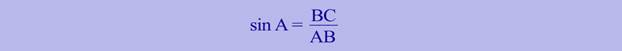
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Обозначается: cos A.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету. Обозначается tg А.
![]()
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету. Обозначается сtg А.
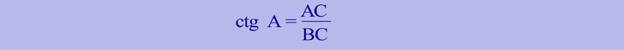

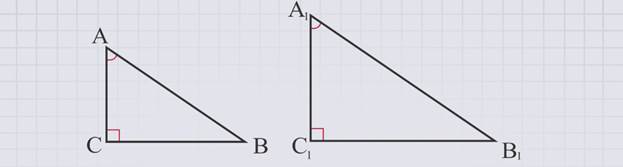
Докажем, что если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы, косинусы и тангенсы этих углов равны.

§ 2 Решение задачи по теме урока
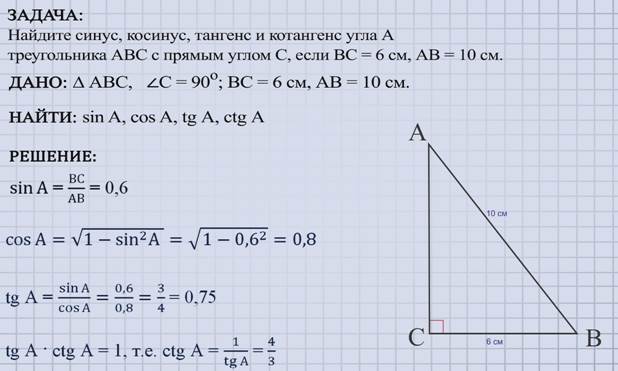
В этом уроке мы познакомились с синусом, косинусом, тангенсом и котангенсом острого угла в прямоугольном треугольнике, вывели тригонометрические формулы и решили задачу, используя полученные знания.
Список использованной литературы:
- Л.С. Атанасян. Учебник. 8 класс.
- Н.Ф. Гаврилова. Поурочные разработки по геометрии. 8 класс. – Москва: «Вако», 2005.
- Л.С. Атанасян и др. Методические рекомендации к учебнику. – Москва: «Просвещение», 2001.
- Д.А. Мальцева. Математика. 9 класс. ГИА 2014. – Москва: Народное образование, 2013.
- О.В. Белицкая. Геометрия. 8 класс. Тесты. – Саратов: «Лицей», 2009.
- С.П. Бабенко, И.С. Маркова. Геометрия 8. Комплексная тетрадь для контроля знаний. – Москва: «Аркти», 2014.
Использованные изображения:
Вспомним,
что синусом угла называется ордината точки
, полученной поворотом точки
вокруг начала координат на угол
.
Косинусом угла называется абсцисса точки
, полученной поворотом точки
вокруг начала координат на угол
.
Тангенсом угла называется отношение синуса угла
к его косинусу.
Котангенсом угла называется отношение косинуса угла
к его синусу.
Теперь приступим к рассмотрению новой темы. Итак,
пусть на координатной плоскости изображена единичная окружность с центром в
начале координат. Точка совершает поворот против часовой стрелки на угол
и оказывается в точке
. По определению синуса и косинуса можем сказать,
что абсцисса точки равна
, а ордината –
. Затем точка
совершает поворот на угол
, противоположный углу
, и оказывается в точке
.
Тогда абсцисса точки равна
, а ордината равна
? Верно.
Посмотрите на угол . Ось
делит
его пополам, а значит, точки и
симметричны относительно оси
. Тогда абсциссы этих точек совпадают, а ординаты
имеют противоположные значения, то есть можем записать, что , а
. Сразу отметим, что формулы
и
справедливы при любых значениях
.
А что можно сказать про тангенс противоположных углов? По
определению тангенса угла можем записать, что . По формуле
числитель запишем как
, по формуле
знаменатель запишем как
:
. Таким образом, мы получили, что
. Отметим, что здесь
,
, так как ранее мы с вами говорили, что тангенс этих углов не
определён.
Как быть с котангенсом противоположных углов? По определению
котангенса угла запишем: . По формуле
числитель запишем как
, а знаменатель по формуле
запишем как
:
. Таким образом, получили, что
. Здесь
,
, так как котангенс этих углов не определён.
Полученные формулы позволяют перейти от вычисления синуса,
косинуса, тангенса и котангенса отрицательных углов к вычислению их значений
для положительных углов.
Давайте найдём ,
,
,
.
Итак, вычислим . Воспользуемся формулой
и запишем
.
По формуле :
.
По формуле :
.
И вычислим . Воспользуемся формулой
и запишем
.
А теперь выполним несколько заданий.
Задание первое. Вычислите:
а) ; б)
; в)
; г)
.
Решение.
Второе задание. Упростите
выражения: а) ; б)
;
.
Решение.

© 2007 – 2023 Сообщество учителей-предметников “Учительский портал”
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены 
Георгий Черняк
85
24.08.2018
Войдите
в Мой Мир, чтобы комментировать
Лежать!
Супер топ
55 705
12.05.2023
Нравится16Нравится16 людям
Войдите
в Мой Мир, чтобы комментировать
Дайте две!
Супер топ
19 122
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
Милота
Супер топ
12 389
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
Медведь практикует первую помощь
Супер топ
9 252
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
Закрыл обратно!
Супер топ
8 331
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
Мама – лучший матрас
Супер топ
6 986
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
Щекотно же!
Супер топ
5 593
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
Деревья-стулья
Супер топ
5 932
12.05.2023
Нравится1Нравится1 человеку
Войдите
в Мой Мир, чтобы комментировать
Антипобег
Супер топ
5 939
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
Рыбное место
Супер топ
5 213
12.05.2023
Нравится1Нравится1 человеку
Войдите
в Мой Мир, чтобы комментировать
Кормушка
Супер топ
4 688
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
Поднимают рояль
Супер топ
4 077
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
Лис на охоте
Супер топ
3 851
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
Битбокс – это просто!
Супер топ
2 953
12.05.2023
Нравится1Нравится1 человеку
Войдите
в Мой Мир, чтобы комментировать
Калибровка воланчика
Супер топ
2 524
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
Как же круто
Супер топ
3 033
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
Командная работа
Супер топ
2 933
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
А когда на море качка…
Супер топ
2 577
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
В яблочко
Супер топ
2 947
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
Водяной эквалайзер
Супер топ
2 372
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
Всё не то, чем кажется
Супер топ
2 294
12.05.2023
Нравится1Нравится1 человеку
Войдите
в Мой Мир, чтобы комментировать
Всем повезло
Супер топ
2 369
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
Замена лампочки
Супер топ
2 352
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
Ласка творит чудеса
Супер топ
2 494
12.05.2023
Войдите
в Мой Мир, чтобы комментировать
Как найти синус видеоурок

ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, Котангенс
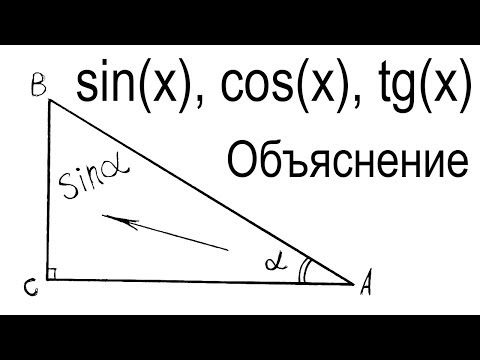
Что такое синус, косинус, тангенс и котангенс объяснение

