Высота – перпендикуляр исходящий из вершины угла на противоположенную сторону
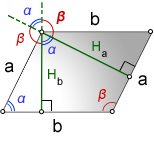a, b – стороны параллелограмма
Hb – высота на сторону b
Ha – высота на сторону a
α, β – углы параллелограмма
Формулы длины высоты параллелограмма, через сторону и угол, ( Hb, Ha):
Острый угол пересечения высот, равен острому углу параллелограмма.
Тупой угол пересечения высот, равен тупому углу параллелограмма.
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства биссектрисы параллелограмма
– Биссектриса по определению делит угол пополам
– Биссектриса отсекает равнобедренный треугольник (в данном случае треугольники ABF и DKC)
– Биссектрисы смежных углов, пересекаются под прямым углом (90°)
– Биссектрисы противоположных углов, равны и параллельны
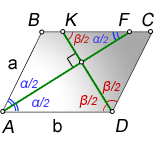AF – биссектриса из острого угла
DK – биссектриса из тупого угла
α – острый угол
β – тупой угол
a – меньшая сторона
b – большая сторона
Так как треугольники ABF и DKC, равнобедренные, следовательно справедливы тождества:
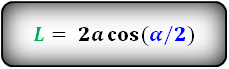
Длина биссектрисы параллелограмма
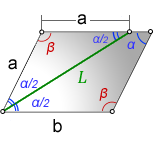
L – биссектриса параллелограмма
a, b – стороны
α, β – углы
Формулы длины биссектрисы через сторону и углы, (L):
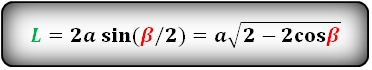
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства углов между диагоналями параллелограмма:
1. Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β <0
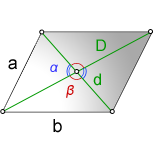
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α – острый угол между диагоналями
β – тупой угол между диагоналями
Формулы косинуса острого и тупого углов между диагоналями, через стороны и диагонали (по теореме косинусов):
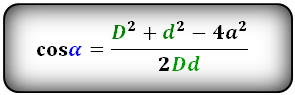
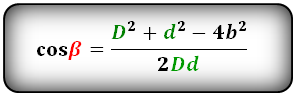
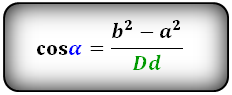
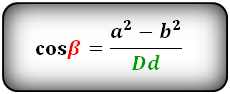
Формула синуса острого и тупого углов через площадь (S) и диагонали:
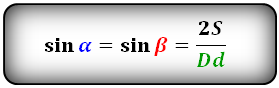
Формулы соотношения острого и тупого углов между диагоналями:
Для определения величины угла в градусах или радианах, используем функции arccos и arcsin
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства углов параллелограмма:
1. Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β <0
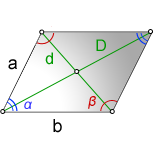
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α – острый угол
β – тупой угол
Формулы косинуса острого и тупого углов через стороны и диагонали (по теореме косинусов):
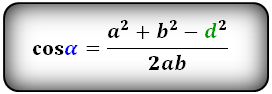
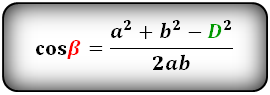
Формула синуса острого и тупого углов через площадь (S) и стороны:
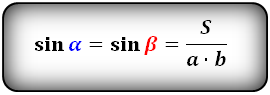
Формулы соотношения острого и тупого углов:
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α, β – углы параллелограмма
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), (D, d):
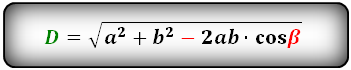
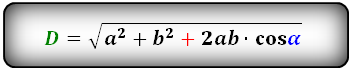
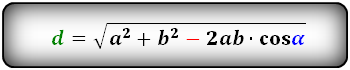
Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), (D, d):
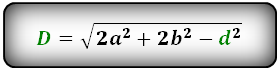
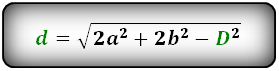
2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.
D – большая диагональ
d – меньшая диагональ
α, β – углы между диагоналями
S – площадь параллелограмма
Формулы диагонали через площадь, известную диагональ и угол между диагоналями, (D, d):
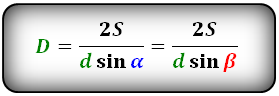
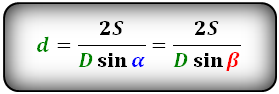
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Формулы длины сторон через диагонали и угол между ними.
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α, β – углы между диагоналями
Формулы сторон параллелограмма через диагонали и угол между ними (по теореме косинусов), (a, b):
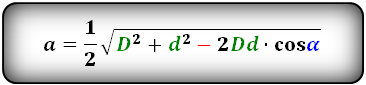
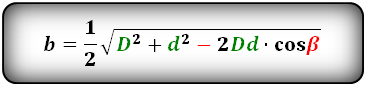
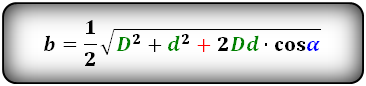
Формулы сторон параллелограмма через диагонали и сторону, (a, b):
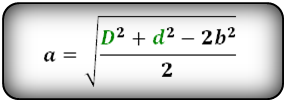
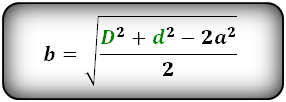
Формулы сторон параллелограмма , (a, b):
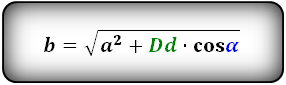
2. Формулы длины сторон параллелограмма через высоту.
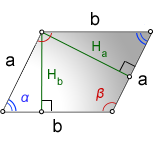
a, b – стороны параллелограмма
Hb – высота на сторону b
Ha – высота на сторону a
α, β – углы параллелограмма
Формулы сторон параллелограмма через высоту, (a, b):
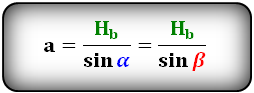
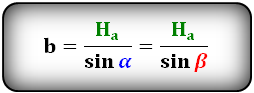
3. Дополнительные, интересные формулы параллелограмма:
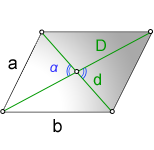
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α – острый угол между диагоналями
Формула суммы квадратов диагоналей:
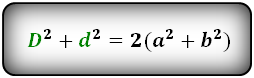
Формула разности квадратов сторон:
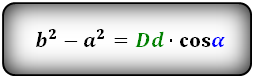
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Углы параллелограмма. Здравствуйте! В этой публикации представлена группа заданий с параллелограммами. Требуется вычислить синус (косинус) заданного угла, сторону или высоту. Всё решение сводится к работе с прямоугольным треугольником. То есть вполне достаточно помнить определения тригонометрических функций и уметь применять их на практике. Задачи решаются в одно действие, многие ученики после построения эскиза, наверняка, смогут решить их устно.
Что ещё стоит отметить? Один факт (свойство синуса), который очень пригодится. Это то, что синусы смежных углов равны, подробнее об этом было написано в этой статье. Если озвучить кратко и простыми словами, то синусы углов сумма которых равна 1800 равны. Это видно и по формуле приведения:
*а также по тригонометрической окружности (при построении таких углов).
Как это применяется в задачах ниже? Как известно, сумма соседних углов параллелограмма равна 1800. И если будет дан синус любого из углов, то это означает, что синусы соседних с ним углов имеют такое же значение.
Рассмотрим задачи:
27433.В параллелограмме ABCD высота, опущенная на сторону AB равна 4, AD=8. Найдите синус угла B.
Построим высоту:
Синус угла В равен синусу угла А, так как известно, что синусы смежных углов равны (указанные углы в сумме равны 180 градусам).
В прямоугольном треугольнике ADE:
Ответ: 0,5
27434. В параллелограмме ABCD высота, опущенная на сторону AB, равна 4, sinA=2/3. Найдите AD.
Построим указанную высоту:
В прямоугольном треугольнике ADE:
Ответ: 6
27435. В параллелограмме ABCD sinС=3/7. AD=21. Найдите высоту, опущенную на сторону AB.
Построим параллелограмм:
Угол С равен углу А. Рассмотрим прямоугольный треугольник ADE:
Ответ: 9
27436. В параллелограмме ABCD AB=3, AD=21, sinA=6/7. Найдите большую высоту параллелограмма.
Построим параллелограмм соблюдая соотношения сторон (АВ<AD):
Большей будет высота, которая проведена к меньшей стороне. Рассмотрим прямоугольный треугольник ADE:
Ответ: 18
27438. В параллелограмме ABCD cosA=(√51)/10. Найдите sinB.
Как уже сказано, синусы смежных углов равны. Для того, чтобы найти sinB, достаточно вычислить sinА. Из основного тригонометрического тождества следует, что:
Ответ: 0,7
27437. В параллелограмме ABCD sinA=(√21)/5. Найдите cosB.
*Посмотрите решение внимательно, есть важные нюансы.
Посмотреть решение
Этом всё. Есть ещё много задач с параллелограммами, их тоже рассмотрим, не пропустите. Успеха вам!
С уважением, Александр Крутицких.
Материалы принесли вам пользу? Расскажите о сайте в социальных сетях!
(Улитка)
Ученик
(74),
закрыт
13 лет назад
Sabcd=AB*AD sin a
Как находить этот синус?
Как найти площадь, если известны диаганали и стороны??
Объясните, пожалуйста
Лучший ответ
Elena Schatz
Высший разум
(140343)
13 лет назад
Решение:
1)Найти косинус угла между данными сторонами по т. косинусов:
BD²=AB²+AD²-2*AB*AD*cosA=>cosA=(AB²+AD²-BD²)/(2*AB*AD) .
2)Зная косинус угла, найти его синус:
sin²A=1-cos²A
3)Найти площадь пар-ма по известной формуле.
Остальные ответы
Похожие вопросы
Для расчёта всех основных параметров параллелограмма воспользуйтесь калькулятором.
Признаки и свойства параллелограмма
- Противоположные стороны параллельны и равны.
- Противоположные углы равны
- Точка пересечения диагоналей делит их пополам.
- Сумма углов четырехугольника прилегающих к любой стороне равна 180°
- В четырехугольнике сумма квадратов диагоналей равна сумме квадратов его сторон
- Сумма углов параллелограмма равна 360°
- Каждая диагональ делит параллелограмма на два равных треугольника
- Биссектрисы противоположных углов параллелограмма всегда параллельны
- Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°)
Формулы стороны параллелограмма
Длины сторон через диагонали и угол между ними
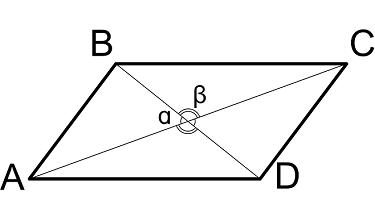
$$
AB = {1 over 2} * sqrt{AC^2 + BD^2 – 2 * AC * BD * cos(α)}
$$
$$
AB = {1 over 2} * sqrt{AC^2 + BD^2 + 2 * AC * BD * cos(β)}
$$
$$
BC = {1 over 2} * sqrt{AC^2 + BD^2 – 2 * AC * BD * cos(β)}
$$
$$
BC = {1 over 2} * sqrt{AC^2 + BD^2 + 2 * AC * BD * cos(α)}
$$
Длина стороны через диагонали и известную сторону
$$
AB = sqrt{AC^2 + BD^2 – 2 * BC^2 over 2}
$$
$$
BC = sqrt{AC^2 + BD^2 – 2 * AB^2 over 2}
$$
Длины сторон через высоты и угол между сторонами
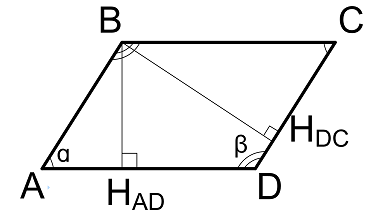
$$
AB = {BH_{AD} over sin(α)} = {BH_{AD} over sin(β)}
$$
$$
BC = {BH_{DC} over sin(α)} = {BH_{DC} over sin(β)}
$$
Формулы диагоналей параллелограмма
Длина диагонали через стороны и углы между ними
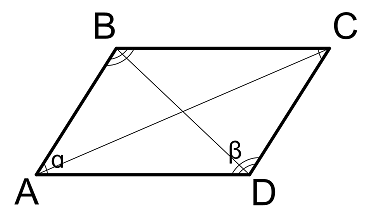
$$
AC = sqrt{AB^2 + BC^2 – 2 * AB * BC * cos(β)}
$$
$$
AC = sqrt{AB^2 + BC^2 + 2 * AB * BC * cos(α)}
$$
$$
BD = sqrt{AB^2 + BC^2 + 2 * AB * BC * cos(β)}
$$
$$
BD = sqrt{AB^2 + BC^2 – 2 * AB * BC * cos(α)}
$$
Длина диагонали через стороны и известную диагональ
$$
AC = sqrt{2 * AB^2 + 2 * BC^2 – BD^2}
$$
$$
BD = sqrt{2 * AB^2 + 2 * BC^2 – AC^2}
$$
Длина диагонали через площадь параллелограмма, известную диагональ и угол между диагоналями
$$
AC = {2 * S over BD * sin(α)} = {2 * S over BD * sin(β)}
$$
$$
BD = {2 * S over AC * sin(α)} = {2 * S over AC * sin(β)}
$$
Формулы углов параллелограмма
Косинус острого угла
$$
cos(α) = {AB^2 + BC^2 – BD^2 over 2 * AB * BC}
$$
Косинус тупого угла
$$
cos(β) = {AB^2 + BC^2 – AC^2 over 2 * AB * BC}
$$
Синус острого и тупого угла через площадь и стороны параллелограмма
$$
sin(α) = sin(β) = {S over AB * BC}
$$
Формулы углов между диагоналями параллелограмма
Косинус острого угла через стороны и диагонали
$$
cos(α) = {AC^2 + BD^2 – 4 * AB^2 over 2 * AC * BD}
$$
$$
cos(α) = {BC^2 – AB^2 over AC * BD}
$$
Косинус тупого угла через стороны и диагонали
$$
cos(β) = {AC^2 + BD^2 – 4 * BC^2 over 2 * AC * BD}
$$
$$
cos(β) = {AB^2 – BC^2 over AC * BD}
$$
Синус острого и тупого угла через площадь и диагонали
$$
sin(α) = sin(β) = {2 * S over AC * BD}
$$
Формула высоты параллелограмма
$$
BH_{AD} = AB * sin(α) = AB * sin(β)
$$
$$
BH_{DC} = BC * sin(α) = BC * sin(β)
$$
Формула биссектрисы параллелограмма
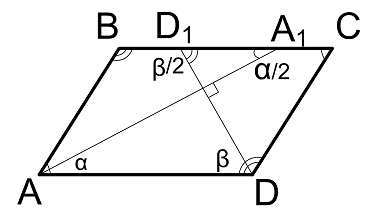
$$
AA_1 = 2 * AB * sin({β over 2}) = AB * sqrt{2 – 2 * cos(β)}
$$
$$
AA_1 = 2 * AB * cos({α over 2})
$$
$$
DD_1 = 2 * AB * sin({β over 2}) = AB * sqrt{2 – 2 * cos(β)}
$$
$$
DD_1 = 2 * AB * cos({α over 2})
$$
У параллелограмма 4 угла, это частный случай четырехугольника, у которого противоположные стороны
попарно параллельны. Из этого свойства вытекает равенство противоположных сторон, равенство
противоположных углов и равенство суммы смежных углов двум прямым. Свойства параллелограмма широко
используются в быту и технике.
- Острый угол параллелограмма через боковую сторону и
высоту - Острый угол параллелограмма через высоту, сторону и
периметр - Острый угол параллелограмма через площадь и две стороны
- Острый угол параллелограмма через две стороны и короткую
диагональ - Тупой угол параллелограмма через две стороны и длинную
диагональ
Острый угол параллелограмма через боковую сторону и высоту
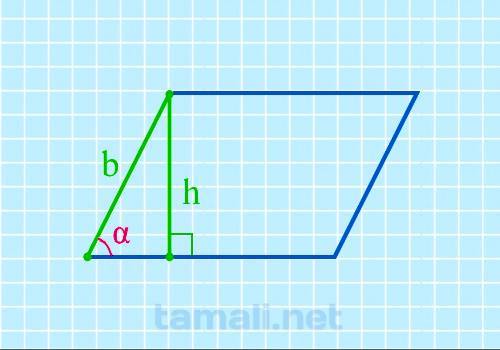
Если известна боковая сторона и высота, то можно найти острый угол параллелограмма по формуле:
sin α = h / b
где α – острый угол, h – высота, b – боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Пусть h = 4 см, b = 8 см. sin α = h / b = 8 / 4 = 2. α = 90°.
Острый угол параллелограмма через площадь и две стороны
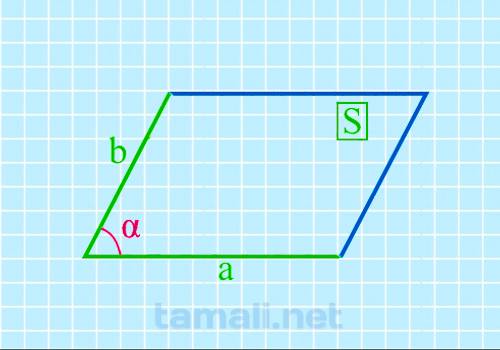
Если известна площадь и две стороны, то можно найти острый угол параллелограмма по формуле:
sin α= S / ab
где α – острый угол, S — площадь параллелограмма, a и b – его стороны.
Цифр после
запятой:
Результат в:
Пример. Пусть S=50 м², a=10 м, b=5 м. sin α= S / ab = 50 / (10 * 5) = 1. α = 90°.
Угол прямой, смежные стороны не равны, имеем дело с прямоугольником.
Острый угол параллелограмма через высоту, сторону и периметр
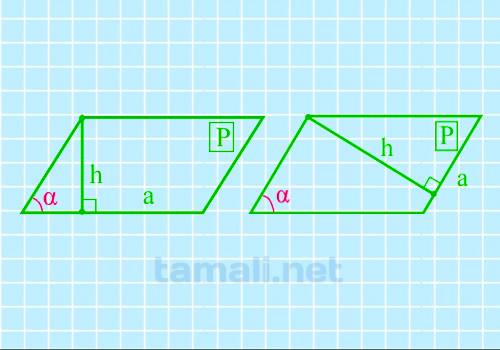
Если известна высота, сторона и периметр, то можно найти острый угол параллелограмма по формуле:
sin α = (2h + a) / P
где α – острый угол, h — высота, a — сторона, P — периметр.
Цифр после
запятой:
Результат в:
Высота опускается на известную и подставляемую в формулу сторону a. Параллелограмм с заданным
периметром приходится строить, если, например, периметр определен длиной веревки, которую требуется
растянуть на местности в форме параллелограмма.
Пример. Пусть h=10 м, a=15 м, P=70 м. sin α=(2h + a) / P= (2 * 10 + 15) / 70 = 0,5. α = 30°.
Острый угол параллелограмма через две стороны и короткую диагональ
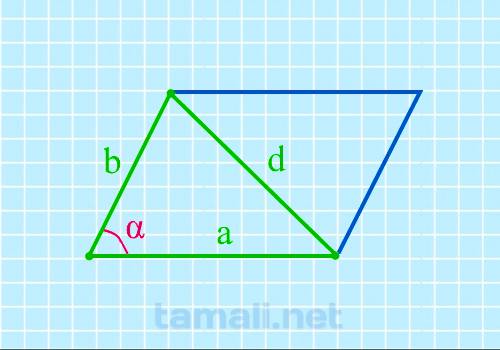
Если известны две стороны и короткая диагональ, то можно найти острый угол параллелограмма по
формуле:
cos α = (a² + b² — d²) / 2ab
где α – острый угол, a и b – стороны параллелограмма, d – его короткая диагональ.
Цифр после
запятой:
Результат в:
Пример расчета: в данном частном случае 2 прилежащие стороны и короткая диагональ
равны, а именно: a = b = d = 26 мм. cos α=(a² + b² — d²) / 2ab = (26² + 26² — 26²) / (2 * 26 * 26) = 0,5. α=60°.
Из равенства прилежащих сторон следует, что это ромб, а результат расчета показывает, что острый угол
в ромбе равен 60°. Знаете, что это за ромб с подобными размерами? Это нагрудный академический знак
для лиц, окончивших советские высшие учебные заведения, установленный с 1961 года.
Тупой угол параллелограмма через две стороны и длинную диагональ
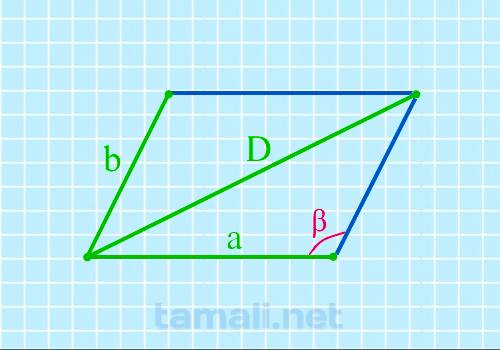
Если известны две стороны и длинная диагональ, то можно найти тупой угол параллелограмма по
формуле:
cos β = (a² + b² — D²) / 2ab
где α – тупой угол, a и b – стороны параллелограмма, D – его длинная диагональ.
Цифр после
запятой:
Результат в:
Пример расчета: вновь ромб со сторонами a = b = 26 мм и длинной диагональю D=43 мм.
cos β = (a² + b² — D²) / 2ab = (26² + 26² — 43²) / (2 * 26 * 26) = -0,368. α = 112°.
Это опять-таки нагрудный академический знак из предыдущего примера, небольшое отличие полученного
результата от 120° (при остром угле 60° по предыдущему примеру) объясняется округлением исходных
данных до целого числа миллиметров.
Свойства параллелограмма
У любого выпуклого четырехугольника сумма всех внутренних углов равна 360°, исходя из общей формулы
суммы внутренних углов выпуклого многоугольника в градусах s = 180 (n — 2), где n – количество
сторон. Следовательно, если хотя-бы 1 угол параллелограмма равен прямому (90°), остальные 3 угла
также являются прямыми, и параллелограмм вырождается в свой частный вид – прямоугольник.
Если 2 смежные стороны параллелограмма равны, то равны все его 4 стороны, и параллелограмм
вырождается в ромб. И, наконец, если у параллелограмма равны 2 смежные стороны, а угол между ними
прямой, параллелограмм является одновременно и прямоугольником, и ромбом, и вырождается в квадрат.
Зачастую возникает необходимость определения неизвестных характеристик параллелограмма через
известные. Выше ряд примеров подобного рода.
Самый наглядный пример параллелограмма – пантограф электропоезда. При подключении опущенного
пантографа к контактной сети железной дороги изменяется конфигурация пантографа при сохранении длин
сторон, в результате изменяется вертикальная диагональ и происходит касание с подачей электрического
тока.
Форму параллелограмма имеет автомобильный реечный домкрат, велосипедная рама (с
диагональю для увеличения жесткости). Ведь параллелограмм — фигура нежесткая, в отличие от
треугольника. Из нежесткости параллелограмма следует, что знания одних длин сторон недостаточно для
вычисления площади фигуры. Так, пантограф электропоезда можно «сложить» до нулевой площади.
Стеклоочиститель лобового стекла автобуса также представляет собой параллелограмм, и именно
нежесткость фигуры позволяет стеклоочистителю «ометать» при движении стекло.
