Коэффициент реактивной мощности sin фи
Коэффициент реактивной мощности sin фи формула
- sin(φ)=√(1-cos²φ)
Коэффициент реактивной мощности sin фи онлайн калькулятор
cos φ:
sin φ:
Поделиться в соц сетях:
Расчет коэффициента мощности (cosφ)
Популярные сообщения из этого блога
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi Как найти тангенс фи, если известен косинус фи формула: tg φ = (√(1-cos²φ))/cos φ Калькулятор онлайн – косинус в тангенс cos φ: tg φ: Поделиться в соц сетях: Найти синус φ, если известен тангенс φ Найти косинус φ, если известен тангенс φ
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о “Использование сердечного индекса Руфье в медико-спортивном контроле”. Проба Руфье – представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор – онлайн tg φ: cos φ: ± Поделиться в соц сетях:

Переменный ток (англ. alternating current — AC) — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным.
В быту для электроснабжения переменяется переменный, синусоидальный ток.
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону (Рисунок 1):
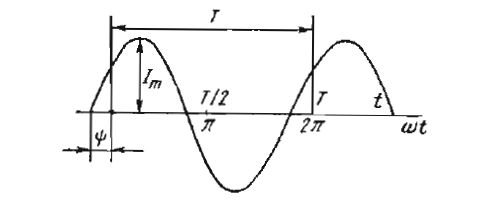

Максимальное значение функции называют амплитудой. Её обозначают с помощью заглавной (большой) буквы и строчной буквы m — максимальное значение. К примеру:
- амплитуду тока обозначают lm;
- амплитуду напряжения Um.
Период Т— это время, за которое совершается одно полное колебание.
Частота f равна числу колебаний в 1 секунду (единица частоты f — герц (Гц) или с-1)
f = 1/T
Угловая частота ω (омега) (единица угловой частоты — рад/с или с-1)
ω = 2πf = 2π/T
Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.
Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой (ω) и начальной фазой Ψ (пси)
В странах СНГ и Западной Европе наибольшее распространение получили установки синусоидального тока частотой 50 Гц, принятой в энергетике за стандартную. В США стандартной является частота 60 Гц. Диапазон частот практически применяемых синусоидальных токов очень широк: от долей герца, например в геологоразведке, до миллиардов герц в радиотехнике.
Синусоидальные токи и ЭДС сравнительно низких частот (до нескольких килогерц) получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых или полупроводниковых генераторов (подробно рассматриваемых в курсе радиотехники и менее подробно — в курсе ТОЭ). Источник синусоидальной ЭДС и источник синусоидального тока обозначают на электрических схемах так же, как и источники постоянной ЭДС и тока, но обозначают их е и j (или e(t) и j(t)).
Обратите внимание! При обозначении величин на схемах или в расчетах важен регистр букв, то есть заглавные буквы (E,I,U…) или строчные (e, i ,u…). Так как строчными буквами принято обозначать мгновенное значение, а заглавными могут обозначаться действующее значение величины (подробнее о действующем значении в следующей статье).
-
Цепи синусоидального тока ( общие понятия и формулы ).
Синусоидальный ток представляет собой
ток, изменяющийся во

времени
по синусоидальному закону: i
= ImSIN(
2πt / T + ψ ) =
ImSIN(
ωt + ψ ).
Максимальное значение функции называется
амплитудой. Ее обозначают: Im.
Период Т – это время, за которое
совершается одно колебание. Частота
равно числу колебаний за
одну секунду. ( ωt + ψ
) – называется фазой. Фаза
характеризует
состояние колебания в любой момент
времени. Под средним
значением
синусоидально изменяющейся величины
понимают ее среднее значение за
полпериода. Среднее
значение тока:
![]()
,
т. е. среднее значение синусоидального
тока составляет 2 / π = 0,638 от амплитудного.
Аналогично, Еср
= 2Еm
/ π; Uср
= 2Um
/ π.
Широко
применяют понятие действующего значения
синусоидально изменяющейся величины
(его называют также эффективным или
среднеквадратичным). Действующее
значение тока:

,
следовательно,
действующее значение синусоидального
тока равно 0,707 от амплитудного. Аналогично,
E
= Em
/ √2 и U
= Um
/ √2.
Действующее
значение синусоидального тока численно
равно значению такого постоянного тока,
который за время, равное периоду
синусоидального тока, выделяет такое
же количество теплоты, что и
синусоидальный ток.
Коэффициент
амплитуды
kа
— это отношение амплитуды периодически
изменяющейся функции к ее действующему
значению. Для синусоидального тока:
ka
= Im
/ I
= √2
Под
коэффициентом формы
kф
понимают отношение действующего
значения периодически изменяющейся
функции к ее среднему за полпериода
значению. Для синусоидального тока: kф
= I
/ Icp
= π
/ 2√2 = 1,11. Существует формула: Imej(ωt
+ ψ
)
= Imejψ
= Im*,
где Im*
-комплексная величина, модуль которой
равен Im
, Ψ –угол, под котором вектор Im*
проведен к оси +1 на комплексной плоскости,
равный начальной фазе. Величину Im*
называют комплексной
амплитудой
тока i.
Скорость поступления энергии по участка
цепи характеризуется мощностью. Под
мгновенным значением мощности, или
под
мгновенной
мощностью,
понимают
произведение мгновенного значения
напряжения и на участке цепи на мгновенное
значение тока
i,
протекающего
по этому участку: p
= ui,
где
р
—
функция времени.
-
Резистивный элемент ( активное сопротивление ) в цепи синусоидального тока.

Резистивный
элемент — это
идеализированный схемный
элемент, учитывающий
выделение теплоты в том
или ином
элементе реальной электрической цепи.
Его характеризуют
зависимостью напряжения
и на нем
от протекающего по нему
тока (вольтамперной
характеристикой) или сопротивлением
R
= u
/ i.
На схемах его
изображают, как и резистор.
Положительные направления
отсчета u
и i
совпадают. Пусть: i
= ImSINωt.
По закону Ома: u
= iR
= RImSINωt
= UmSINωt.
и Um
= RIm.
На рис. в даны
кривые мгновенных значений тока i,
напряжения u
и мощности р
= UmImSIN2ωt
= UmIm*(
1 – COS2ωt
) /2 . Мгновенная
мощность р имеет
постоянную составляющую UmIm
/ 2 и составляющую
UmIm*COS2ωt
/ 2, изменяющуюся с
частотой 2ω. Потребляемая от источника
питания за время dt
энергия равна pdt.
-
Индуктивный элемент в цепи синусоидального
тока.
Индуктивный элемент позволяет
учитывать явление наведения ЭДС,
изменяющимся во времени магнитным
потоком, и явление накопления энергии
в магнитном поле реальных элементов
электрической цепи. Его характеризуют
зависимостью потокосцепления ψ от тока
I
(вебер-амперной характеристикой) или
индуктивностью L
= ψ
/ i.
На схеме замещения реальную индуктивную
катушку можно представить в виде
последовательно соединенных индуктивного
и резистивного элементов. Направления
тока, ЭДС самоиндукции и напряжение на
нем совпадают по направлению. i
= ImSINωt,
UL
= L*di / dt,
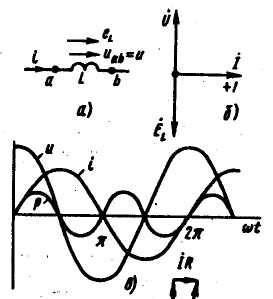
u
= ωLImSIN(ωt
+ 90) = Um
SIN(ωt + 90), Um
= ωLIm,
UL*
= ωLI*ejπ
/ 2.
Произведение ωL
обозначается XL,
называется индуктивным
сопротивлением
и измеряется в омах
(Ом): XL
= ωL.
Таким
образом, индуктивный элемент
(индуктивная катушка, у которой
R
= 0) при синусоидальном токе обладает
сопротивлением,
модуль которого XL
= ωL
прямо пропорционален частоте ω. На
рис. 3.6, б вектор напряжений
опережает вектор тока I
на 90°.
Комплекс ЭДС самоиндукции
EL
находится в противофазе с
комплексом напряжений U.
Графики мгновенных значений i,
u,
р
изображены на рис. в.
Мгновенная мощность рассчитывается по
формуле:
p
= ui
= UmCOSωt*ImSINωt
= UmImSIN2ωt
/ 2.
Мгновенная мощность проходит
через нулевое значение, когда через
нуль проходит либо i,
либо u.
За первую четверть периода, когда u
и i
положительны, р также положительна.
Площадь, ограниченная кривой р и осью
абсцисс за это время, представляет
собой энергию, которая взята от источника
питания на создание энергии магнитного
поля в индуктивной катушке. Во вторую
четверть периода, когда ток в цепи
уменьшается от максимума до нуля, энергия
магнитного поля отдается обратно
источнику питания, при этом мгновенная
мощность отрицательна. За третью четверть
периода у источника снова забирается
энергия, за четвертую отдается и т. д.
Следовательно, энергия периодически
то забирается индуктивной катушкой от
источника, то отдается ему обратно.
Падение напряжения на
реальной индуктивной катушке равно
сумме напряжений на L
и на R.
Угол между напряжением U
на катушке и током I
равен 900
— σ, причем
tgσ
= R
/ ωL
= l
/ QL,
где QL
— добротность реальной индуктивной
катушки. Чем больше QL,
тем меньше σ.
-
Емкостной элемент ( конденсатор ) в
цепи синусоидального тока.
Емкостный элемент
— это идеализированный схемный элемент,
позволяющий учесть протекание токов
смещения и явление накопления энергии
в электрическом поле реальных элементов
электрической цепи. Его характеризует
зависимость заряда q
от напряжения и (кулон-вольтная
характеристика) или емкость C
= q
/ u.
Положительные направления отсчета u
и i
совпадают. Если приложенное к конденсатору
напряжение u
не изменяется во времени, то заряд q
= Сu
на одной его обкладке и заряд — q
на другой (С — емкость конденсатора)
неизменны, и ток через конденсатор не
проходит (i
= dq
/ dt
=0). Если же напряжение на конденсаторе
изменяется во времени по синусоидальному
закону: u
= UmSINωt,
то по синусоидальному
закону будет меняться и заряд q
конденсатора:
q
= Сu
= CUmSINωt
, т. е. конденсатор будет периодически
перезаряжаться. Периодическая
перезарядка конденсатора сопровождается
протеканием через него зарядного тока:
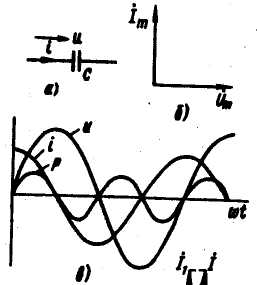
i
= dq / dt = ωCUmCOSωt
= ωCUmSIN(
ωt + 900
). Ток
через
конденсатор опережает
по фазе напряжение
на конденсаторе на 90°,
поэтому на векторной
диаграмме (рис. б) вектор Im
опережает вектор
напряжения Um
на 90°. Амплитуда тока Im
равна амплитуде напряже
ния Um,
деленной на емкостное сопротивление:
Xc
= 1 / ωC
,
Im
= Um
/ Xc
. Емкостное сопротивление обратно
пропорционально
частоте. Единица емкостного сопротивления
— Ом. Графики
мгновенных значений и, i,
p
изображены на рис. в. Мгновенная
мощность рассчитывается
по формуле: p
= UmImSIN2ωt
/ 2. За первую четверть
периода конденсатор потребляет от
источника питания энергию, которая
идет на создание электрического поля
в нем. Во вторую четверть периода
напряжение на конденсаторе уменьшается
от максимума до нуля, и запасенная в
электрическом поле энергия отдается
источнику (мгновенная мощность
отрицательна). За третью четверть периода
энергия снова запасается, за четвертую
отдается и т. д. i
= C*du
/ dt,
u
= ∫idt
/ C.
-
Основы символического метода расчета
цепей синусоидального тока.
Очень широкое распространение на
практике получил символический, или
комплексный, метод расчета цепей
синусоидального тока.
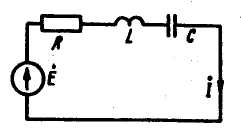
Сущность
символического метода расчета состоит
в том, что при (синусоидальном токе можно
перейти от уравнений, составленных для
мгновенных значений и являющихся
дифференциальными уравнениями к
алгебраическим уравнениям, составленным
относительно комплексов тока и ЭДС.
Этот переход основан на том, что в
уравнении, составленном но законам
Кирхгофа для установившегося процесса,
мгновенное значение тока i
заменяют комплексной амплитудой
тока Im;
мгновенное значение напряжения на
резисторе сопротивлением R,
равное Ri,—
комплексом RIm,
no
фазе совпадающим с током Im;
мгновенное значение напряжения на
индуктивной катушке uL
= L*di
/ dt
–комплексом Im*jωL,
опережающим ток на 90°; мгновенное
значение напряжения на конденсаторе
uc
= ∫idt
/ C
— комплексом Im(
-j
/ ωC
) отстающим от тока на 90°; мгновенное
значение ЭДС е — комплексом Еm.
Пример. Найти Im*
для схемы на рисунке. Решение. Схему
на
рисунке можно описать в виде: uR
+ uL +
uc = e
или
iR + L*di
/ dt + ∫idt / C
= e. в комплексной форме
это выглядит:
Im*R
+ Im*jωL
+ Im*(
-j / ωC ) = Em*.
Если вынести Im*
за скобку, то:
Im**(
R + jωL + ( -j / ωC )) = Em*.
Тогда

.
-
Комплексное сопротивление. Закон Ома
для цепи синусоидального тока.
Множитель R+
jωL
– (-j
/ ωC
) представляет собой комплекс, имеет
размерность сопротивления и обозначается
через Z.
Его называют комплексным сопротивлением:
Z
= zejφ
= R+
jωL
– 1 / ωC.
Комплекс, Z
можно записать в показательной форме.
Модуль комплексного сопротивления
принято обозначать через z.
Точку над Z
не ставят, потому что принято ставить
ее только над такими комплексными
величинами, которые отображают
синусоидальные функции времени.
Уравнение Im**(
R + jωL + ( -j
/ ωC )) = Em*
можно записать так: ImZ
= Em*
. Разделим обе его части на √2 и перейдём
от комплексных амплитуд Im*
и Em*
к комплексам действующих значений I*
и Е*:
I*
= E*
/ Z.
Уравнение Im**(
R + jωL + ( -j
/ ωC )) = Em*
представляет собой закон
Ома для цепи синусоидального тока.
В общем случае Z
имеет некоторую действительную часть
R
и некоторую мнимую часть jХ:
Z
= R
+ jX,
где R
— активное сопротивление; X
— реактивное сопротивление.
-
Комплексная проводимость.
Под комплексной проводимостью
Y
понимают величину, обратную комплексному
сопротивлению Z:
Y
= 1 / Z
= g
– jb
= ye–jφ.
Единица комплексной проводимости — См
или
(Ом-1 ).
Действительную часть ее обозначают
через g,
мнимую — через b.
Так как
![]()
,
то
![]()
Если X
положительно, то и b
положительно. При X
отрицательном b
также отрицательно.
При использовании комплексной
проводимости закон Ома записывают в
виде: I*
= U*Y,
или I*
= U*g
– jU*b
= Ia*
+ Ir*,
где Ia*
— активная составляющая тока; Ir*—
реактивная составляющая тока; U
— напряжение на участке цепи, сопротивление
которого равно Z.
-
Активная, реактивная и полная мощность.
Под активной
мощностью Р понимают
среднее значение мгновенной мощности
р за период Т:
![]()
.
Если ток i
= ImSINωt,
напряжение на участке цепи
u
= UmSIN(ωt
+ φ
), то
![]()
.
Активная мощность физически представляет
собой энергию, которая выделяется в
единицу времени в виде теплоты на участке
цепи в сопротивлении R.
Тогда: P
= U*COSI
= I2R.
Единица активной
мощности — Вт.
Под реактивной
мощностью Q
понимают произведение напряжения U
на участке цепи на ток I
по этому участку и на синус угла φ между
напряжением U
и током I:
Q
= UI*SINφ.
Единица реактивной
мощности — вольт-ампер
реактивный (ВАр). Если SINφ
>0, то Q
>0, если SINφ
<0, то Q
<0. Реактивная мощность Q
пропорциональна среднему за четверть
периода значению энергии, которая
отдается источником питания на создание
переменной составляющей электрического
и магнитного поля индуктивной катушки
и конденсатора. За один период переменного
тока энергия WМЭСР
дважды отдается генератором в цепь и
дважды он получает ее обратно, т. е.
реактивная мощность является энергией,
которой обмениваются генератор и
приемник.
Полная мощность
рассчитывается по формуле:
S
= UI.
Единица полной
мощности — В*А.
Мощности P,
Q
и S
связаны следующей
зависимостью:
P2
+ Q2
= S2.
На щитке любого источника энергии
переменного тока указывается значение
S,
характеризующее ту мощность, которую
этот источник может отдавать потребителю,
если последний работает при COSφ
= 1 (т. е. если потребитель представляет
собой чисто активное сопротивление).
-
Выражение мощности в комплексной
форме записи.
Мощность в комплексной форме записи
имеет формулу:
Š = U*I#
= Uejφu
*Ie-jφi
= UICOSφ + jUISINφ = P + jQ.
Значок ~ (тильда) над
S
обозначает комплекс (а не сопряженный
комплекс) полной мощности, составленный
при участии сопряженного комплекса
тока I#.
Таким образом, активная мощность Р есть
действительная часть (Re),
а реактивная мощность Q
— мнимая часть (Im)
произведения U*I#:
P
= Re
U*I#,
Q
= U*I#.
Пример.
Определить активную, реактивную и полную
мощности по данным: e
= 141SINωt
В, R1
= 3 Ом, R2
= 2 Ом, L
= 0,00955 Гн, ω = 314 рад /с.
Решение. Напряжение
на входе всей схемы равно ЭДС U
= E
= 100 В. Ток в цепи I*
= 17,2е–j31
А. Сопряженный комплекс тока I#
= 17,2еj31
А. Комплекс полной мощности S
= U*I#
= 100*17,2ej31
=
= 1720*COS310
+j*1720*SIN310
= 1475 + j*886; P = 1475; Q = 886.
Следовательно,
активная мощность P
= 1470 Вт, реактивная Q
= 886 ВАр и S
= 1720 B*A.
-
Измерение мощности ваттметром.
Измерение мощности производят обычно
с помощью ваттметра электродинамической
системы, в котором имеются две катушки
— неподвижная и подвижная.
Подвижная катушка, выполненная
из очень тонкого провода, имеет практически
чисто активное сопротивление и называется
параллельной обмоткой.
Ее включают параллельно
участку цепи, подобно вольтметру. Жестко
скрепленная со стрелкой (указателем),
она может вращаться в магнитном поле,
создаваемом неподвижной катушкой.
Неподвижная катушка, выполненная из
довольно толстого привода, имеет
очень малое активное сопротивление и
называется последовательной обмоткой.
Ее включают в цепь последовательно,
подобно амперметру.

Вращающий
момент ваттметра, а следовательно, и
его показания пропорциональны
действительной части произведения
комплексного напряжения Uаb
на параллельной обмотке ваттметра на
сопряженный комплекс
тока I#,
втекающего в конец последовательной
(токовой) обмотки ваттметра и снабженной
точкой: ReUab*I#
= UabI*COS(UabI).
Напряжение на параллельной обмотке
берут равным разности
потенциалов между ее концом, имеющим
точку (точка а), и ее концом, не
имеющим точки (точка b).
Предполагается, что ток I
втекает в конец
последовательной обмотки,
у которого поставлена точка.
Цена деления ваттметра определяется
как частное от деления
произведения номинального
напряжения на номинальный ток на число
делений шкалы.
-
Двухполюсник в цепи синусоидального
тока.
Если мы имеем пассивный
двухполюсник, то входное сопротивление
двухполюсника Zвх
= Е / I.
В общем случае: Zвх
= Rвх
+j
Xвх
= zejφ.
При Хвх
> 0 входное сопротивление имеет
индуктивный характер (φ > 0), при Хвх
< 0 — емкостный и при Хвх
= 0 — чисто активный.
Входная проводимость Y,
представляет собой величину, обратную
входному сопротивлению: Yвх
= l
/ Zвх.
Входное сопротивление
можно определить расчетным путем, если
известна схема внутренних соединений
двухполюсника и характер и значения
сопротивлений, либо опытным путем.
При опытном определении
входного сопротивления двухполюсника
собирают схему рис. а, в которой амперметр
измеряет ток I,
вольтметр — напряжение Uab
= U
на входе двухполюсника.
Ваттметр измеряет
Re{Uab*I#
}, т. е. активную мощность Р = UIcosφ.
Модуль входного сопротивления
z
= U
/ I.
При делении Р на произведение UI
получают косинус угла между напряжением
и током: COSφ
= P
/ UI.
По косинусу угла находят
SINφ
и затем находят Rвх
= z*COSφ
и Xвх
= Z*SINφ
.

Так
как косинус есть функция четная,
т. е. cos(
-φ ) = соsφ,
то измерения
необходимо дополнить еще одним опытом,
который позволил бы путем сопоставлений
показаний амперметра в двух опытах
выявить знак угла φ. Для
определения знака
угла φ можно воспользоваться
специальным
прибором — фазометром либо
при его отсутствии, проделав следующий
опыт: параллельно исследуемому
двухполюснику путем замыкания ключа К
подключают небольшую емкость С (рис.
а). Если
показания амперметра при замыкании
ключа К станут меньше, чем они были при
разомкнутом ключе, то угол φ положителен
и входное сопротивление Z
= zejφ
имеет индуктивный характер (рис. б). Если
показания амперметра при замыкании
ключа станут больше, то φ отрицательно
и входное сопротивление имеет емкостный
характер (рис. в).
Пример.
В схеме рис. a
U
= 120 В; I
= 5 А; Р = 400 Вт. Замыкание ключа К приводит
к уменьшению показаний амперметра.
Определить входное сопротивление
двухполюсника.
Решение.
Модуль входного сопротивления: z
= U
/ I
= 24 Ом; COSφ
= P
/ UI
= 400 / 120*5 = 0,666; SINφ
= 0,745. Таким образом: Rвх
= z*COSφ
= 24*0,666 = 16 Ом;
Xвх
= z*SINφ
= 24*0,745 = 17,9 Ом. Комплекс входного
сопротивления: Zвх
= 16 + j17,9
Ом.
-
Резонансный режим работы двухполюсника.
Пусть двухполюсник
содержит один или несколько индуктивных
элементов и один или несколько
конденсаторов. Под резонансным
режимом (режимами)
работы такого двухполюсника понимают
режим (режимы), при котором входное
сопротивление двухполюсника является
чисто активным. (Следовательно, для
определения условий наступления
резонанса следует приравнять нулю
мнимую часть комплекса входного
сопротивления двухполюсника. Такой
способ справедлив, если не пренебрегать
активными сопротивлениями индуктивных
катушек. )
По отношению к внешней цени двухполюсник
в резонансном режиме ведет себя как
активное сопротивление, поэтому ток и
напряжение на его входе совпадают
по фазе. Реактивная мощность двухполюсника
при этом равна нулю.
Различают две основные разновидности
резонансных режимов: резонанс токов и
резонанс напряжений.
-

Резонанс
токов.
Явление резонанса в схеме рис. а,
образованное
двумя параллельными ветвями с
разнохарактерными
реактивными сопротивлениями, называют
резонансом токов.
Пусть первая ветвь содержит активное
сопротивление R1
и индуктивное ωL.,
а вторая ветвь — активное R2
и емкостное 1 / ωС.
Ток I1*
в первой ветви отстает от напряжения U
= Uab
(рис. б) и может быть записан как:
I1*
= U*Y1
= U*(g1
– jb1
). Ток
I2
во второй ветви опережает напряжение:
I2*
= U*Y2
= U*(g2
– jb2
). Ток
в неразветвленной части цепи:
I*
= I1*
+ I1*
= U*(
g1
+ g2
) – jU*(
b1
+ b2
). По определению
резонансного режима ток I*
должен совпадать по фазе с напряжением
U.
Это будет при условии, что сумма реактивных
проводимостей ветвей равна нулю: b1
+ b2
= 0. b1
и b2
можно рассчитать:
![]()
,
следовательно, условие
наступления режима резонанса токов
можно записать так:

.
На рис. б изображена векторная диаграмма
для резонансного режима. Из рисунка
следует, что если R2
= 0, то резонанс наступит при:
ωL
/ ( R22
+ ω2L2
) = ωC.
В еще более частном случае, когда R2
= 0 и R1
<< L,
резонанс наступит при: ω2LC
≈ 1. Резонанса можно достичь путем
изменения ω, L,
С или R1
и R2.
Числовое значение тока в неразветвленной
части схемы может быть меньше токов в
ветвях схемы. При R2
= 0, R1
≈ 0 ток I
может оказаться ничтожно малым по
сравнению с токами I1
и I2.
В идеализированном, практически не
выполнимом режиме работы, когда R1
= R2
= 0, ток в неразветвленной части схемы
равен нулю и входное сопротивление
равно ∞.
Пример.
В схеме на рис. а R1
= 30 Ом, ωL
= 40 Ом, R2
= 0, ω/
= 103
рад /с. При каком значении емкости
конденсатора в схеме будет резонанс
токов? Решение.

![]()
-
Резонанс напряжений.
Резонанс в схеме
последовательного соединения
R,
L,
С (рис. а) называют резонансом напряжений.
При
резонансе ток в цепи должен совпадать
по фазе с ЭДС
Е*.
Это возможно, если входное сопротивление
схемы Z
= R
+ j(
ωL
— 1 / ωС) будет чисто активным:
Условие наступления резонанса
в схеме: ω0L
= 1 / ω0C,
где ω0
–резонансная частота. При этом I*
= E*
/ R.
Напряжение на индуктивном элементе при
резонансе равно напряжению на емкостном:
UL
= UC
= ω0LI
= ω0LE
/ R.
Отношение: ω0L
/ R
= √(L
/ C
) / R
= Q
называют
добротностью резонансного контура.
Добротность показывает, во сколько
раз напряжение на индуктивном (емкостном)
элементе превышает напряжение на входе
схемы в резонансном режиме. Векторная
диаграмма для режима резонанса изображена
на рис. б.
Характеристическим
сопротивлением q
для схемы (рис. а) называют отношение
напряжения на L
и С в режиме резонанса к току в этом
режиме: q
= QR
= √(L
/ C
) .
-
Частотные характеристики двухполюсников.
Входное сопротивление
и входная проводимость двухполюсника
в общем случае являются функциями
частоты ω. Под частотными характеристиками
(ЧХ) понимают следующие типы характеристик:
1) зависимость модуля входного сопротивления
(проводимости) от частоты ω; 2)
зависимость действительной или мнимой
части входного сопротивления (проводимости)
от частоты ω. ЧХ могут быть получены
расчетным (если известна схема, характер
элементов и их числовые значения)
либо опытным (в этом случае схему
двухполюсника и характер составляющих
ее элементов можно и не знать) путем.
При снятии ЧХ опытным путем на вход
двухполюсника подают напряжение, частоту
которого изменяют в широких пределах,
начиная с нуля, и по результатам
измерений подсчитывают модуль входного
сопротивления (проводимости) или
действительную (мнимую) часть входного
сопротивления (проводимости).

В
общем случае двухполюсники содержат
резистивные и реактивные элементы.
В частном случае двухполюсники могут
состоять только из реактивных элементов,
тогда их называют реактивными
двухполюсниками. Применительно к ним
под ЧХ понимают зависимости X
= f(ω)
или b
= f(ω).
Качественно построим
характеристику z
= f(ω)
для
двухполюсника рис. а
(рис. б). При ω = 0 (конденсатор
представляет собой разрыв)
z
= R
+ R1.
При ω ∞
сопротивление конденсатора
1 / ωC
0,
а индуктивное
сопротивление ωL
∞.
Поэтому при ω
∞, z
= R
+ R2.
При ω = ω0/
имеет место режим резонанса токов и
потому входное сопротивление имеет
максимум. В области частот от 0 до ω0/
z
–имеет индуктивный характер, в области
от ω0/
до ∞ -емкостной . Если R1
= R2
<< L
/ C,
то ω0/
≈ L
/ C*2R1.
Рассмотрим вопрос о построении
частотных характеристик реактивных
двухполюсников, не содержащих резистивных
сопротивлений.
Входное сопротивление
их
Z
= jX,
а входная проводимость Y=
1 / Z
= -j
/ X
= – jb,
тогда b
= 1 / X.
Частотная

характеристика
таких
двухполюсников —это
зависимость
X
(ω) или b
(ω). Эти зависимости
взаимно обратны.
Для индуктивного
элемента Х(ω) = ωL
(рис. а), а
b(ω)
= 1 / ωL
(рис. б). Для емкостного элемента b(ω)
= – ωС (рис. в), а Х(ω) = -1 / ωC
(рис. г). Для получения Х(ω)
последовательно соединенных элементов
надо сложить ординаты кривых Х(ω) этих
элементов.
-
Двухполюсники.

1.
Случай. ( сопротивление
и
емкость соединены последовательно ).
ЧХ последовательно соединенных
L1
и С1
(рис. д) построена на рис. е в
виде кривой 3 (прямая 1 — это
ЧХ L1
, а кривая 2 — ЧХ С1
).
Зависимость b(ω)
для схемы рис. д
изображена на рис. ж. При
частоте ω0
= 1 / √L1C1
кривая Х(ω)
пересекает ось абсцисс, а
кривая
b(ω)
претерпевает разрыв от -∞ до +∞.
При этой частоте имеет место
резонанс напряжений.
Основные формулы: Zвх
= R +jX,
если R = 0, то Zвх
= jX = j*( ωL
– 1 / ωC ).
Yвх
= 1 / Zвх = 1 / ( R +jX ) = R
/ ( R2
+ X2 )
– jX / ( R2
+ X2 )
= g – jb = g – j /X.
2. Случай. При
параллельном соединении элементов
проводимости их надо сложить, то
ясно, что для получения кривой b(ω)
параллельно соединенных элементов надо
сложить ординаты кривых b(ω)
этих элементов. Зависимость b(ω)
для схемы рис. з изображена на рис.к,
а обратная ей зависимость Х(ω) — на рис.
и. При
частоте ω о/
= 1 / √L2C2
кривая b(ω)
пересекает ось абсцисс, а Х(ω)
претерпевает разрыв от
+∞ до -∞. При этой частоте имеет место
резонанс токов в цепи (рис. з).
Основные формулы:

;
![]()
3. Случай.
На рис. л последовательно соединены два
двухэлементных ранее рассмотренных
двухполюсника. Так как Х(ω) каждого
из этих двухполюсников построена, то
результирующее Х(ω) схемы рис. л
получим, суммируя ординаты Х(ω) этих
двухполюсников (т. е. кривых рис. е, и).
Зависимость X(ω)
для схемы рис. л см. рис. м, a
b(ω)
— на рис. н. При плавном увеличении
частоты в схеме (рис. ж), начиная с ω = 0,
сначала возникает резонанс напряжений
при частоте ω1
, затем резонанс токов при ω2,
после этого резонанс напряжений при ω3
. При дальнейшем увеличении ω резонансов
возникать не будет.
Сделаем следующие выводы:
1) режимы резонанса токов
и резонанса напряжений чередуются;
2) число резонансных
частот для канонических схем на единицу
меньше числа реактивных элементов;
3) если в схеме есть путь
для прохождения постоянного тока, то
при плавном увеличении частоты, начиная
с нуля, первым наступит резонанс токов,
если нет — резонанс напряжений.
Это следует из того, что
если есть путь для постоянного тока, то
при ω = 0 характеристика X
= f(ω)
начинается с нуля, затем X
увеличивается, а при некоторой ω кривая
претерпевает разрыв, который и
соответствует резонансу токов.
-

Передача
энергии от активного двухполюсника в
нагрузку.
К зажимам ab
активного двухполюсника (рис. а) подключена
Нагрузка
Zн
= Rн
+jXн.
Требуется выяснить, при соблюдении
каких условий в
нагрузке выделяется максимальная
активная мощность.
По методу эквивалентного
генератора ток в нагрузке: I*
= Uabx*
/ ( Zвх
+ Zн
),
где Zвх
= Rвх
+ jXвх
— входное сопротивление двухполюсника
по отношению к зажимам ab,
поэтому: I*
= Uabx*
/ ( Rвх
+ Rн
+j*(
Xвх
+Xн
)). По
условию, Rвх
и Хвх
заданы и изменять их нельзя. Изменять
можно лишь Rн
и Хн.
Выберем такое Хн
, чтобы ток в цепи был максимальным; это
возможно, если Хвх
+ Хн
=0. При этом двухполюсник работает в
резонансном режиме — ток через нагрузку
по фазе совпадает с напряжением Uфbx:
I
= Uabx
/ ( Rвх
+ Rн
). Как
и в цепи постоянного тока, если взять
Rн
= Rвх
выделяющаяся в нагрузке мощность
максимальна: Pmax
= Uabx2
/ 4Rвх
. Таким
образом, чтобы выделить в нагрузке,
присоединяемой к активному двухполюснику
с входным сопротивлением Rn
+ jXвx,
максимально возможную мощность,
необходимо выбрать следующие
сопротивления нагрузки.: Хн
= -Хвх,
RH
= Rвх.
При этом Zн
= Zвх#,
а КПД составит 50%.
-
Расчет электрических цепей при наличии
в них магнитносвязных катушек.

В
состав электрических цепей могут входить
катушки, магнитно-связанные с другими
катушками. Поток одной из них пронизывает
другие и наводит в них ЭДС взаимоиндукции,
которые должны быть учтены при расчете.
При составлении уравнений для
магнитно-связанных цепей необходимо
знать, согласно или встречно направлены
потоки самоиндукции и взаимоиндукции.
Правильное заключение об этом можно
сделать, если
известно направление намотки
катушек на сердечнике и
выбрано положительное
направление токов в них. На
рис. а
катушки включены согласно, на рис. б —
встречно. Чтобы не
загромождать чертеж,
сердечники катушек на электрических
схемах обычно не изображают, ограничиваясь
тем, что
одноименные зажимы (например,
начала катушек) помечают одинаковыми
значками, например точками. (
Схема рис. в эквивалентна
схеме рис. а, а схема рис. г
– схеме рис. б.
)

Если
на электрической схеме токи двух
магнитно-связанных катушек одинаково
ориентированы относительно одноименно
обозначенных зажимов, например оба
направлены к точкам или оба направлены
от точек, то имеет место согласное
включение, в противном случае —
встречное. Если магнитно
связано несколько катушек, то начало и
конец размечают для каждой пары катушек
отдельно.
Пример.
Показать пример расчета для схемы.
Решение.

Введем обозначение: М –взаимная
индуктивность.
|
UL1 |
R1i1 |
|
UL2 |
-R2i2 |
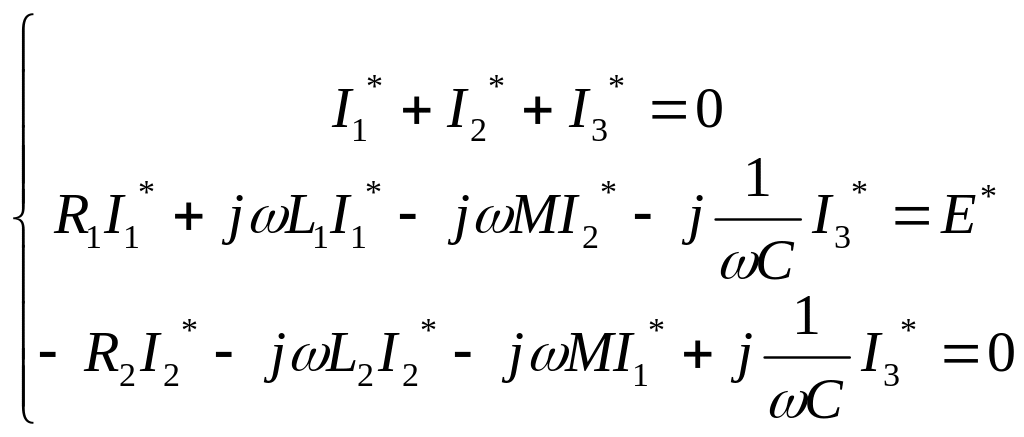
-
Последовательное соединение двух
магнитно-связных катушек.

На
рис. 1 изображена схема последовательного
согласованного включения двух катушек,
а на рис.2 —
последовательного встречного включения
тех же катушек.
При согласном включении:

iR1
+ L1*di
/ dt + M*di / dt + L2*di
/ dt + M*di / dt + iR2
= e.
В комплексной форме записи:
I*(
R1
+ R2
+ jω*( L1
+ L2
+ 2M )) = E*
;
I*Zсогл
= E*,
Zсогл
= R1
+ R2
+ jω*( L1
+ L2
+ 2M )
Векторная диаграмма для
согласного включения изображена на
рис. 3,


где
U1
— напряжение на первой катушке; U2
— на второй.
При встречном включении:
iR1
+ L1*di
/ dt – M*di / dt + L2*di
/ dt – M*di / dt + iR2
= e.
В комплексной форме записи:
I*Zсогл
= E*,
Zсогл
= R1
+ R2
+ jω*( L1
+ L2
– 2M )
Векторная диаграмма для встречного
включения при
L1
> M
и L2
> M
изображена на рис. 4.
-
Определение взаимной индуктивности
опытным путем.
Первый способ.
Проделаем два опыта. В первый из них
включим катушки последовательно и
согласно. Измерим ток и напряжение на
входе и активную мощность цепи. Во втором
те же катушки включим последовательно
и встречно и также измерим I,
U,
Р. По результатам измерений найдем:
Xcorл,
= ω(
Ll
+ L3
+ 2M);
Xвстр
= ω
( Ll
+ L2
– 2M).
Разность Хсогл
— Хвстр
= 4 ωМ,
следовательно,
М
= ( Хсогл
– Хвстр
) / 4ω
.

Второй
способ. Подключим
первую катушку к источнику синусоидальной
ЭДС через амперметр как на рисунке, а к
зажимам второй катушки
присоединим вольтметр с большим
внутренним сопротивлением.
Измерим ток I1
и напряжение U2.
Мгновенное значение
напряжения u2
= M*di1
/ dt.
Его
действующее значение U2
= ωMI1
. Следовательно, M
= U2
/ ωI1.
Пример.
В схеме на рисунке вольтметр показал
100 В,
амперметр 10 А; ω
= 314 рад/с. Определить М. Решение.
По формуле из второго способа, М = 100 / (
314*10 ) = 0,0319 Гн.
-
Трансформатор. Вносимое сопротивление.
Трансформатор представляет
собой статическое (т. е. не имеющее
подвижных
частей) устройство,
служащее для преобразования числового
значения переменного во времени
напряжения, а также для электрического
разделения цепей и преобразования
числовых значений сопротивлений.
Передача энергии из одной цепи в другую
производится трансформатором благодаря
явлению взаимоиндукции. Трансформатор
имеет две обмотки, находящиеся на общем
сердечнике. Магнитную проницаемость
сердечника будем полагать постоянной.
Параметры первичной обмотки R1
и L1
, вторичной — R2
b
L2.
Взаимная индуктивность между обмотками
М. Сопротивление
нагрузки, подключенной к зажимам
вторичной обмотке, равно Zн.
Выберем положительные
направления токов I1*
и I2*.
Обозначим
напряжение на нагрузке Uн*.
Запишем уравнения в комплексной форме:
для первичной цепи:
I1*R1
+ I1*jωL1
+ I2*jωM
= E*.
для вторичной цепи:
I2*R2
+ I2*jωL2
+ I1*jωM
+ Uн
= 0.

На
рис. б качественно построим
векторную диаграмму, полагая, что
нагрузка
Zн
= zнejφ
имеет индуктивный характер.
Ток I2*
направим по оси +1. Напряжение на
нагрузке Uн
опережает ток I2*
на угол φ
Падение напряжения I2*R2
совпадает по фазе
стоком I2*
. Вектор I2*jωL2
опережает вектор тока I2*
на 90 °.
В соответствии с уравнением
для вторичной цепи вектор I1*jωM
проводим так, чтобы геометрическая
сумма падений напряжений во вторичной
цепи равнялась нулю.
Вектор тока I1*
отстает от вектора I1*jωM
на 900.
Вектор I1*R1
совпадает с вектором тока I1*
по фазе, а вектор I1*jωL1
опережает вектор I1*
на 90°.
Вектор I2*jωM
опережает вектор I2*
на 90°. В соответствии с уравнением
дял первичной цепи геометрическая сумма
I1*R1
+ I1*jωL1
+ I2*jωM
дает E1*.
Основные формулы:
Uн*
= I2*Zн
= I2*(
Rн
+ jXн
); I1*
= E1*
/ (( R1
+ Rвн
) + j(
X1
– Xвн
)),
где Rвн
и Xвн
–вносимые из вторичного контура в
первичный активное и реактивное
сопротивление.
![]()
и
![]()
Вносимые сопротивления
представляют собой такие сопротивления,
которые следоало бы “внести” в
первичную цепь (включить последовательно
с R1
и X1
), чтобы учесть влияние нагрузки вторичной
цепи трансформатора на ток в его первичной
цепи (рис. в).

-
Топографическая диаграмма.
Топографическая диаграмма
–совокупность точек комплексной
плоскости, изображающих комплексные
потенциалы одноименных точек цепи.
Пример. Построить
топографическую
диаграмму для схемы на рис.
а к этому
вопросу, совместив ее с
векторной диаграммой токов. Две ветви
схемы связаны магнитно. Значения
параметров: ωL1
= 3 Ом; ωL2
= 4 Ом; ωМ
= 3 Ом; R1
= R2
= 2 Ом; E*
= 100 В. Решение.
Обозначим токи в ветвях через I1*
и I2*
и ток в неразветвленной части схемы —
через I*.
Составим уравнения по второму закону
Кирхгофа для согласного включения
катушек: I1*(
R1
+jωL1
) + I2*jωM
= E*;
I1*jωM
+ I2*(
R2
+jωL2
) = E*.
Совместное решение их дает: I1*
= 16e–j60
A,
I2*
= 14,27e–j86,5.
Топографическая диаграмма, совмещенная
с векторной диаграммой токов, изображена
на рис. 6.
Изначально электрический ток получали с помощью гальванических элементов и это был постоянный ток, то есть он протекал от плюсового источника тока к минвсовому при постоянной величине, ну немного уменьшаясь из-за разряда батареи. Потом появились электрические генераторы, в которых вращающееся магнитное поле генерировало ток и этот ток был переменный, так как магнит по кругу двигался около катушки или катушка двигалась, а магнит был неподвижный, не важно, главное в том, что при движении рамки в магнитном поле ток увеличивается от нуля до максимума, затем от максимума до нуля, затем меняет направление и снова уменьшается, а затем снова возрастает от отрицательного минмума до нуля и все это за один оборот ротора.
Закон изменения тока в электрической машине как раз и описывается функцией синуса. Для выпрямления тока использовали коллекторы, которые переключали отдельные катушки при повороте так, чтобы направление тока всегда было в одну сторону, а за счет увеличения числа катушек уменьшалась пульсация.
Когда же был изобретен трансформатор, то от постоянного тока для передачи на большие расстояния отказались, так как переменный ток лего трансформируется с малого напряжения на большое, затем передается с минимальными потерями по ЛЭП и снова трансформируется на месте потребления до нужных малых напряжений. Везде сейчас используется переменный ток, во всех домах, для освещения улиц, в станках на заводах и фабриках. В России сейчас в быту применяется однофазная сеть с напряжением 220 Вольт и частотой 50 Герц. Это означает, что в розетке по одному проводу подведено напряжение, а второй провод является нулем. Но для объяснения, для чего нужен ноль еще нужно рассказать устройство трехфазной сети, но это уже к теме не относится. Для нас важно, что если к фазному и нулевому проводам подключить прибор, напримпр, лампу, то через него начнет протекать электрический ток, изменяемый по синусоиде. За одну секунду будет 50 положительных полупериодов, и столько отрицательных, а 100 раз вообще ток не будет течь, будет нулевое напряжение. Но мы это мерцание не увидим, так как нить накаливания в лампе не успевает остыть. А вот люминесцентные лампы дествительно потухают 100 раз в секунду и снова разгораются, что не совсем полезно для зрения.
Содержание:
Электрические цепи синусоидального тока:
В общем случае цепь переменного тока характеризуется тремя параметрами: активным сопротивлением R, индуктивностью L и емкостью С. В технике часто применяются цепи переменного тока, в которых преобладает один или два из этих параметров.
При анализе работы и расчетах цепей исходят из того, что для мгновенных значений переменного тока можно использовать все правила и законы постоянного тока.
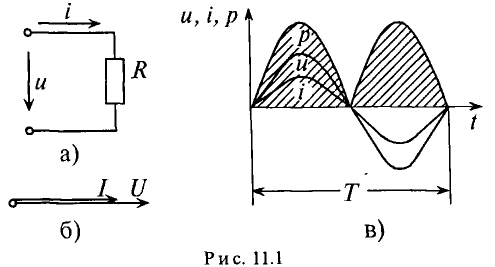
Цепь с активным сопротивлением
Активным сопротивлением R обладают элементы, которые нагреваются при прохождении через них тока (проводники, лампы накаливания, нагревательные приборы и т.д.).
Если к активному сопротивлению R (рис. 11.1) приложено синусоидальное напряжение 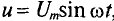
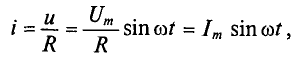
где 
Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, так как начальные фазы их равны (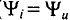 = 0). Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 11.16, временная диаграмма изображена на рис. 11.1в.
= 0). Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 11.16, временная диаграмма изображена на рис. 11.1в.
Математическое выражение закона Ома для цепи переменного тока с активным сопротивлением имеет вид:

Это вытекает из выражения (11.1), если левую и правую части уравнения разделить на 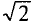 =1,41.
=1,41.
Таким образом, действующее значение синусоидального тока I пропорционально действующему значению синусоидального напряжения U и обратно пропорционально сопротивлению R участка цепи, к которому приложено напряжение U. Такая интерпретация закона Ома справедлива как для мгновенных, так и для действующих и амплитудных значений синусоидального тока.
Активная мощность
Мгновенная мощность в цепи с активным сопротивлением определяется произведением мгновенных значений напряжения ка, т. е. р = ui. Это действие производится над кривыми тока и ряжения в определенном масштабе (рис. 11.1в). В результате учена временная диаграмма мгновенной мощности р. Как видно из временной диаграммы, мощность в цепи с активным сопротивлением изменяется по величине, но не изменяется по направлению (рис. 11.1в). Эта мощность (энергия) необратима. От источника она поступает на потребитель и полностью преобразуется в другие виды мощности (энергии), т.е. потребляется. Такая потребляемая мощность называется активной.
Поэтому и сопротивление R, на котором происходит подобное образование, называется активным сопротивлением, цепи с активным сопротивлением мгновенная мощность характеризует скорость преобразования электрической энергии в другие виды энергии.
Количественно мощность в цепи с активным сопротивлением определяется следующим образом:
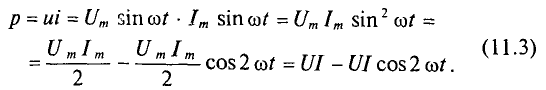
Мгновенная мощность в цепи синусоидального тока с активным сопротивлением представляет собой сумму двух величин -постоянной мощности UI и переменной 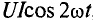 , изменяющейся с двойной частотой.
, изменяющейся с двойной частотой.
Средняя за период мощность, равная постоянной составляющей мгновенной мощности UI, является активной мощностью Р. Среднее за период значение переменной составляющей, как и всякой синусоидальной величины, равно нулю, то есть
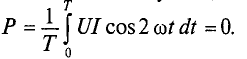
Таким образом, величина активной мощности в цепи синусоидального тока с активным сопротивлением с учетом закона Ома определяется выражением:
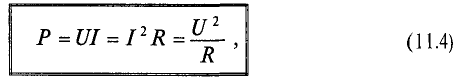
где U- действующее значение напряжения; I— действующее значение тока.
Единицей активной мощности является ватт:
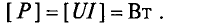
Поверхностный эффект и эффект близости
Сопротивление проводника постоянному току 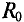 называют омическим сопротивлением и определяют выражением (2.8)
называют омическим сопротивлением и определяют выражением (2.8)  Сопротивление проводника переменному току R называют активным.
Сопротивление проводника переменному току R называют активным.
Оказывается, что сопротивление проводника переменному току больше его омического сопротивления за счет так называемого поверхностного эффекта и эффекта близости, т. е. 
Увеличение активного сопротивления вызвано неодинаковой плотностью тока в различных сечениях проводника (рис. 11.2а).
На рис. 11.2а изображено магнитное поле проводника цилиндрического сечения. Если по проводнику проходит переменный ток, то он создает переменный магнитный поток внутри и вне проводника. Этот поток в различных сечениях проводника индуктирует ЭДС самоиндукции, которая, согласно правилу Ленца. противодействует изменению тока как причине создания ЭДС Очевидно, центр проводника охвачен большим количеством магнитных линий (большее потокосцепление), чем слои, близкие к поверхности. Следовательно, в центре проводника ЭДС (сопротивление) больше, чем на поверхности проводника. Плотность на поверхности больше, чем в центре. Поэтому это явление и называется поверхностным эффектом.
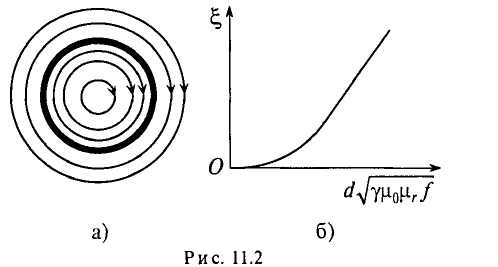
Таким образом, поверхностный эффект уменьшает сечение проводника для переменного тока, а следовательно, увеличивает активное сопротивление R.
Отношение активного сопротивления проводника к его сопротивлению определяет коэффициент поверхностного эффекта 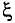 (кси)
(кси)
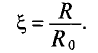
График зависимости коэффициента поверхностного эффекта от параметра проводника d, его удельной проводимости 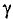 , магнитной проницаемости материала проводника
, магнитной проницаемости материала проводника 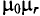 и частоты переменного тока
и частоты переменного тока  , проходящего по проводнику, показан на рис. 11.26.
, проходящего по проводнику, показан на рис. 11.26.
При токах большой частоты  (радиочастотах) ток в центре проводника отсутствует. Поэтому такие проводники делают трубчатыми, т.е. полыми.
(радиочастотах) ток в центре проводника отсутствует. Поэтому такие проводники делают трубчатыми, т.е. полыми.
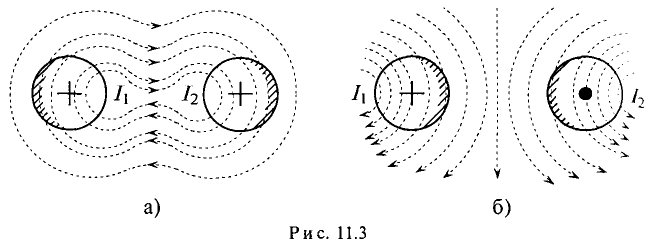
На величину активного сопротивления проводника R оказывает влияние и эффект близости.
Если токи в двух параллельных проводах, расположенных близко друг к другу, направлены в одну сторону, то элементы сечения водников, удаленных на большее расстояние друг от друга, цепляются с меньшим магнитным потоком и имеют большую плотность тока (заштриховано на рис. 11.3а), чем элементы сечения проводников, расположенные близко друг к другу.
Если же токи в близко расположенных параллельных проводах направлены в различные стороны, то большая плотность тока на-дается в элементах сечения проводников, расположенных ближе друг к другу (заштриховано на рис. 11.36).
Таким образом, эффект близости в проводниках также влияет активное сопротивление проводников за счет наведения в различных элементах сечений проводников различных ЭДС взаимоиндукции, направление которых определяется правилом Ленца.
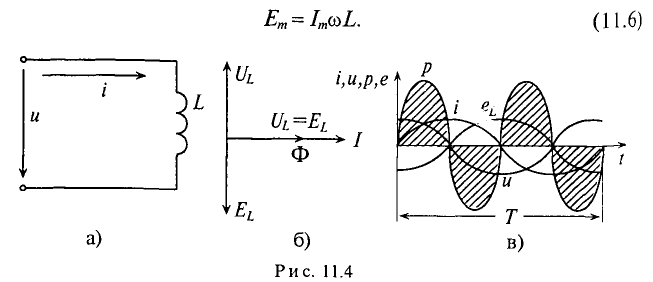
Цепь с идеальной индуктивностью
Идеальной называют индуктивность L такой катушки, активным сопротивлением R и емкостью С которой можно пренебречь, т.е. R= О и С=0.
Если в цепи идеальной катушки индуктивностью L (рис. 11.4а) проходит синусоидальный ток 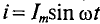 , то этот ток создает в катушке синусоидальный магнитный поток
, то этот ток создает в катушке синусоидальный магнитный поток 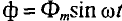 , который индуктирует в катушке ЭДС самоиндукции, равную согласно (9.11)
, который индуктирует в катушке ЭДС самоиндукции, равную согласно (9.11)
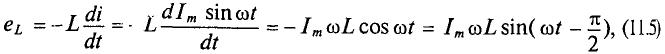
так как 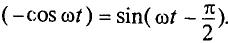
Очевидно, эта ЭДС достигает своего амплитудного значения 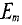 тогда, когда
тогда, когда 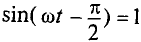 :
:
Тогда 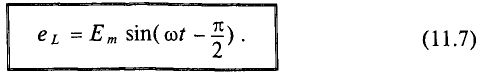
Таким образом, ЭДС самоиндукции в цепи с идеальной индуктивностью L, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстает от тока по фазе на угол 90° = 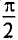 (рис. 11.46, в).
(рис. 11.46, в).
По второму закону Кирхгофа для мгновенных значений можно записать

Откуда 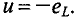
Тогда напряжение, приложенное к цепи с идеальной индуктивностью (см. (11.5)):
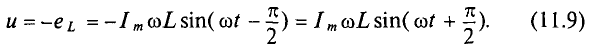
Очевидно, напряжение достигает своего амплитудного значения Um тогда, когда 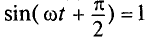 :
:

Следовательно, 
Таким образом, напряжение, приложенное к цепи с идеальной ин-ивностью, как и ток в этой цепи, изменяется по синусоидально-жону, но опережает ток по фазе на угол 90°= 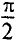 (рис. 11.46, в).
(рис. 11.46, в).
Резюмируя все вышесказанное, можно сделать вывод: для существования тока в цепи с идеальной индуктивностью необходимо ожить к цепи напряжение, которое в любой момент времени но по величине, но находится в противофазе с ЭДС, вызванной таким током (рис. 11.46, в).
Временная диаграмма (рис. 11.4в) еще раз иллюстрирует правило Ленца: ЭДС 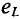 противодействует изменению тока.
противодействует изменению тока.
Если уравнение (11.10) разделить на 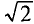 =1,41, то получается
=1,41, то получается 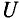 =
=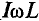 , откуда
, откуда

Это уравнение (11.12а) и есть математическое выражение закона Ома для цепи синусоидального тока с идеальной индуктивностью. Очевидно, знаменатель этого уравнения есть не что иное, как сопротивление, которое называют индуктивным сопротивлением XL.
Таким образом,

Закон Ома для этой цепи можно записать иначе:

Индуктивное сопротивление XL — это противодействие, которое ЭДС самоиндукции eL оказывает изменению тока.
Реактивная мощность в цепи с индуктивностью
Мгновенная мощность для цепи синусоидального тока с идеальной катушкой равна произведению мгновенных значений напряжения и тока
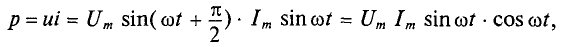
где 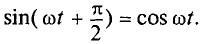
Следовательно, 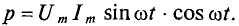
Полученное уравнение умножают и делят на 2:
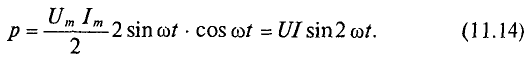
Таким образом, мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой.
Следовательно, среднее значение этой мощности за период Яс, как и любой синусоидальной величины, т. е. активная потребляемая мощность, в этой цепи равна нулю, Р= 0.
Временная диаграмма (рис. 11,4в) подтверждает этот вывод. На диаграмме видно, что мгновенная мощность (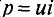 ) в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой.
) в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой.
То есть в 1-ю и 3-ю четверти периода мощность (энергия) источника накапливается в магнитном поле индуктивности. Максимальное значение накапливаемой в магнитном поле идеальной катушки энергии по (9.12) равно
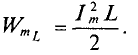
Во 2-ю и 4-ю четверти периода эта мощность (энергия) из магнитного поля идеальной катушки возвращается к источнику.
Таким образом, в цепи переменного тока с идеальной катушки мощность не потребляется (Р= 0), а колеблется между источником и магнитным полем индуктивности, загружая источник и провода.
Такая колеблющаяся мощность (энергия), в отличие от активной, потребляемой, называется реактивной.
Обозначается реактивная мощность буквой Q и измеряется в варах, т.е. [Q]=вар (вольт-ампер реактивный).
Величина реактивной мощности в рассматриваемой цепи определяется выражением
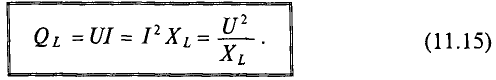
Так как реактивная мощность QL имеет место в цепи с индуктивным сопротивлением, то индуктивное сопротивление считается реактивным сопротивлением X индуктивного характера, т. е. XL.
Цепь с емкостью
Если конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора ходит в цепи очень короткое время, пока напряжение на конденсаторе Uc не станет равным напряжению источника U.
Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I=0).
Если же конденсатор подключить к источнику с синусоидальным напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжена конденсаторе Uc отстает по фазе от напряжения источника и зарядке, и при разрядке конденсатора. Например, пока напряжение на конденсаторе достигает значения 1, напряжение источника достигнет значения 2 (рис. 11.5в), т. е. конденсатор заряжается; пока конденсатор зарядится до напряжения 2, напряжение источника уменьшится до напряжения 3 – конденсатор разряжается на источник и т.д. Однако ток проходит только в цепи конденсатора. Через диэлектрик конденсатора ток не проходит.
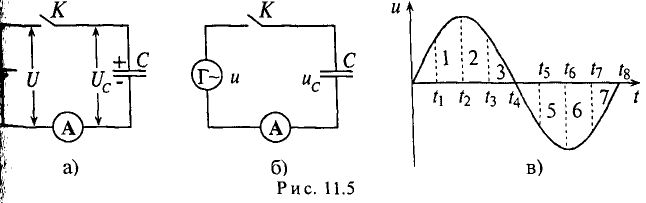
Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение 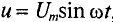 , то в цепи конденсатора проходит ток i (рис. 11.6а):
, то в цепи конденсатора проходит ток i (рис. 11.6а):
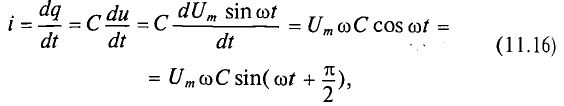
где q= Си согласно (6.3).
Очевидно, ток в цепи конденсатора достигает амплитудного значения тогда, когда 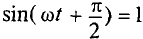 :
:

Тогда 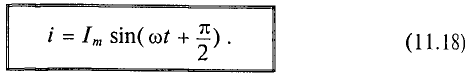
Как видно, ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90°=
Следовательно, напряжение отстает по фазе от тока на 90° =  (рис. 11.66).
(рис. 11.66).
Если уравнение (11.17) разделить на 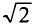 = 1,41, то получится равенство
= 1,41, то получится равенство 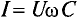 или
или

Это равенство (11.19а) и является математическим выражением закона Ома для цепи переменного тока с емкостью.
Очевидно, знаменатель этого равенства является сопротивлением конденсатора Хс, которое называется емкостным сопротивлением:

Когда закон Ома для цепи с конденсатором можно записать:

Емкостное сопротивление – это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11,5а).
Реактивная мощность в цепи с конденсатором
Если в цепи конденсатора емкостью 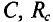 = 0 (рис. 11.6а) проходит ток i, изменяющийся по синусоидальному закону:
= 0 (рис. 11.6а) проходит ток i, изменяющийся по синусоидальному закону:
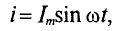
Напряжение и, приложенное к этому конденсатору (рис. 11.6), будет равно
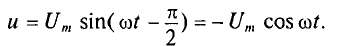
Мгновенная мощность в цепи с конденсатором
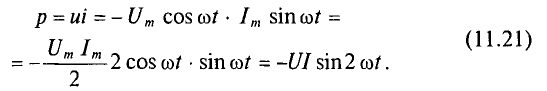
Мощность в цепи с конденсатором, подключенным к источнику с синусоидальным напряжением, изменяется по синусоидальному закону с двойной частотой (рис. 11.6в).
Следовательно, активная мощность Р в рассматриваемой цепи 1С. 11.6а), равная среднему значению мгновенной мощности за период, имеет нулевое значение, Р= 0.
Это следует и из временной диаграммы (рис. 11.6в). На временной диаграмме видно, что изменение мгновенной мощности р по синусоидальному закону происходит с двойной частотой: 2-ю и 4-ю четверти периода мощность (энергия) источника накапливается в электрическом поле конденсатора.
Максимальное значение энергии, накапливаемой в электрическом поле конденсатора, равно
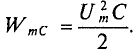
В 1-ю и 3-ю четверти периода эта мощность (энергия) из электрического поля конденсатора возвращается к источнику.
Таким образом, в цепи переменного тока с конденсатором происходит колебание мощности (энергии) между источником и электрическим полем конденсатора. Такая колеблющаяся, но не потребляемая мощность называется реактивной мощностью.
Величина реактивной мощности в цепи конденсатора определяется выражением
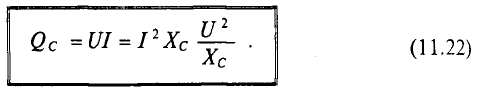
Из временных диаграмм (рис. 11.4в, 11.6в) видно, что реактивная мощность в цепи конденсатора изменяется в противофазе с реактивной мощностью в цепи с идеальной катушкой. Отсюда и знак «минус» в уравнении (11.21) – аналитическом выражении мгновенной мощности в цепи с конденсатором.
Так как реактивная мощность Qc имеет место в цепи с емкостным сопротивлением, то это емкостное сопротивление считается реактивным сопротивлением Х емкостного характера (Хс).
Расчет линейных электрических цепей синусоидального тока
Расчет электрических цепей синусоидального тока производится преимущественно с помощью векторных диаграмм. В нашей главе рассматривается расчет неразветвленных цепей синусоидального тока, содержащих активное сопротивление R, активность L и емкость С в различных сочетаниях.
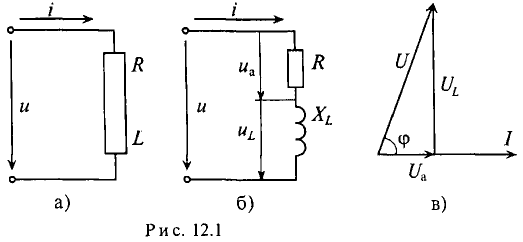
Цепь с активным сопротивлением и индуктивностью
Если по цепи с реальной катушкой, обладающей активным сопротивлением R и индуктивностью L, проходит синусоидальный ток 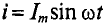 (рис. 12.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки
(рис. 12.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки 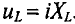
Следовательно, по второму закону Кирхгофа, для мгновенных значений, приложенное к реальной катушке напряжение можно записать

Это равенство справедливо для неразветвленной цепи синусоидального тока с последовательно включенными активным сопротивлением R и индуктивным сопротивлением XL (рис. 12.16).
Активное напряжение (рис. 11.16) совпадет по фазе с током и может быть записано 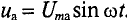 . Индуктивное напряжение
. Индуктивное напряжение 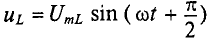 опережает ток на угол 90° =
опережает ток на угол 90° = 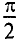 .
.
Мгновенное значение напряжения, приложенного к цепи, определяется алгебраической суммой мгновенных значений напряжений 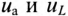 согласно (12.1). А действующее значение этого напряжения U определяется геометрической суммой их действующих значений
согласно (12.1). А действующее значение этого напряжения U определяется геометрической суммой их действующих значений
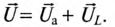
Это равенство лежит в основе построения векторной диаграммы (рис. 12.1 в).
Из векторной диаграммы (рис. 12.1 в) видно, что напряжение U, приложенное к реальной катушке, опережает по фазе ток 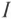 на угол ф. Мгновенное значение этого напряжения может быть записано:
на угол ф. Мгновенное значение этого напряжения может быть записано:
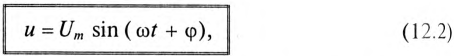
где ф — это международное обозначение угла сдвига фаз между током и напряжением для любой цепи переменного тока.
Воспользовавшись теоремой Пифагора для определения гипотенузы прямоугольного треугольника, по векторной диаграмме (рис. 12.1 в) определяется напряжение
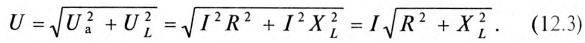
Откуда

Равенство (12.4) является математическим выражением закона Ома для цепи синусоидального тока с активным R и индуктивным XL сопротивлениями в неразветвленной цепи.
Знаменатель этого равенства является сопротивлением этой цепи, которое называется полным, или кажущимся, сопротивлением цепи синусоидального тока. Обозначается кажущееся (полное) сопротивление любой цепи переменного тока буквой Z:

где Zk — полное, или кажущееся, сопротивление реальной катушки.
Тогда закон Ома для любой цепи переменного тока в общем виде можно записать

где Z — кажущееся сопротивление этой цепи.
Треугольники напряжений, сопротивлений, мощностей
Треугольник, все стороны которого изображены векторами напряжений, называется треугольником напряжений. Пользуясь векторной диаграммой для неразветвленной цепи с активным и индуктивным сопротивлениями (рис. 12.1в), выделяем треугольник напряжений (рис. 12.2а).
Связь между напряжениями в данной цепи можно рассматривать как соотношение между сторонами и углами прямоугольного треугольника:
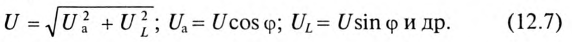
Если все стороны треугольника напряжений разделить на ве-1ину тока в цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают сопротивления цепи, т. е. получится треугольник составлений (рис. 12.16). Сопротивления не являются векторными величинами. Из треугольника сопротивлений можно определить:
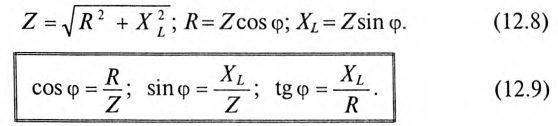
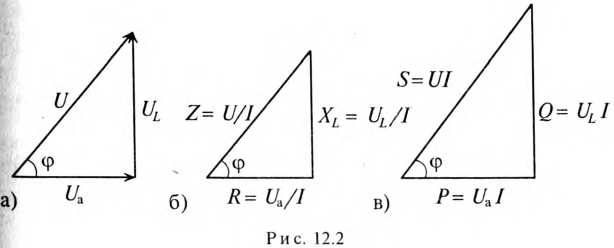
Обычно тригометрические функции угла ф определяются из треугольника сопротивлений отношением (12.9).
Если все стороны треугольника напряжений умножить на величину тока цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают мощности цепи, т.е. получится треугольник мощностей (рис. 12.2в).
Произведение напряжения и тока цепи характеризует полную мощность цепи

которая измеряется в вольт-амперах, т.е. 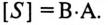
Однако потребляется в цепи только часть полной мощности – активная мощность
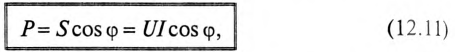
где cos ф показывает, какая часть полной мощности 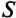 потребляется в цепи, поэтому cos ф называют коэффициентом мощности:
потребляется в цепи, поэтому cos ф называют коэффициентом мощности:

Полная мощность цепи S называется кажущейся. Из того же треугольника мощностей (рис. 12.2в) записать:
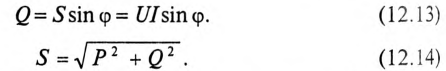
Построив треугольники напряжений, сопротивлений и мощностей для любой цепи синусоидального тока, по выражениям (12.7)—(12.14) можно рассчитать параметры этой цепи.
Цепь с активным сопротивлением и емкостью
Если в цепи с последовательно включенными активным сопротивлением R и емкостью С протекает синусоидальный ток 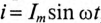 , то он создает падение напряжения на активном сопротивлении
, то он создает падение напряжения на активном сопротивлении 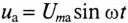 и на емкостном сопротивлении
и на емкостном сопротивлении 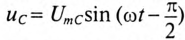 . Векторная диаграмма для этой цепи изображена на рис. 12.36.
. Векторная диаграмма для этой цепи изображена на рис. 12.36.
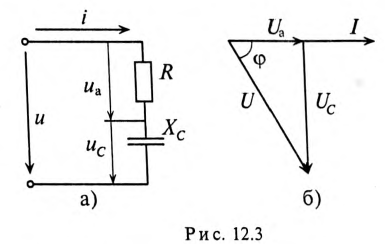
Напряжение цепи изменяется, как и ток, по синусоидальному закону и отстает по фазе от тока на угол ф < 90°, т. е.

Действующее значение напряжения U, приложенного к этой цепи, определяется по векторной диаграмме (рис. 12.3):
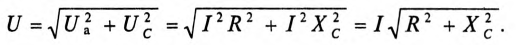
Откуда математическое выражение закона Ома для этой цепи:
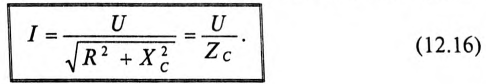
Пример 12.1
К цепи с последовательно включенными сопротивлениями R= 8 Ом и Хс= 6 Ом (рис. 12.3а) приложено напряжение U= 220 В. Определить ток цепи I, напряжение на активном 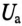 и реактивном Up участках, полную S, активную Р и реактивную Q мощности.
и реактивном Up участках, полную S, активную Р и реактивную Q мощности.
Решение
Для определения тока вычислим полное сопротивление цепи
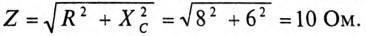
Тогда ток будет равен
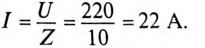
Напряжения на участках:
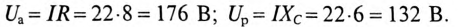
Полная мощность 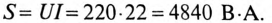
Активная мощность 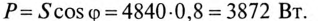
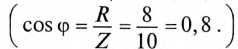
Реактивная мощность 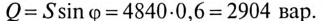
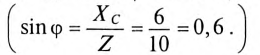
Неразветвленная цепь с активным сопротивлением, индуктивностью и емкостью
Если в неразветвленной цепи с R, L и С (рис. 12.4а) протекает синусоидальный ток 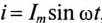 , то он создает падение напряжения на всех участках цепи:
, то он создает падение напряжения на всех участках цепи: 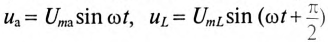 и
и 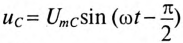 .
.
Мгновенное значение напряжения цепи определяется по формуле
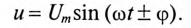
Так как в рассматриваемой цепи включены два реактивных сопротивления XL и Хс, то возможны три режима работы цепи: 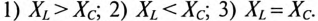
Векторная диаграмма цепи для режима 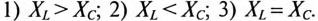 изображена на рис. 12.46.
изображена на рис. 12.46.
Знак перед углом сдвига фаз ф зависит от режима работы цепи Если в рассматриваемой цепи преобладает индуктивное напряжение (сопротивление), т. е.  , то цепь имеет индуктивный характер и напряжение U опережает по фазе ток
, то цепь имеет индуктивный характер и напряжение U опережает по фазе ток  .
.
Если в цепи преобладает емкостное напряжение (сопротивление), т.е. 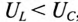 , то цепь имеет емкостной характер и напряжение U отстает по фазе от тока I (—ф).
, то цепь имеет емкостной характер и напряжение U отстает по фазе от тока I (—ф).
Из векторной диаграммы (рис. 12.46) следует:
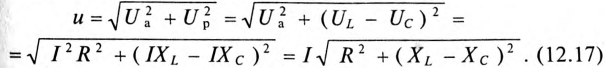
Сопротивление R может включать в себя сопротивление самостоятельного резистора или активное сопротивление реальной катушки и конденсатора.
Математическое выражение закона Ома для неразветвленной цепи с активным сопротивлением, индуктивностью и емкость:
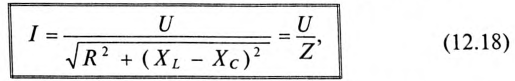
где Z — полное (или кажущееся) сопротивление неразветвленной цепи с R, L и С, т. е.
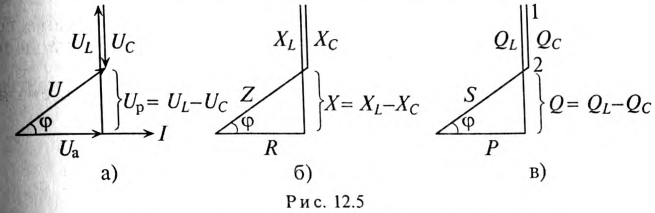
На рис. 12.5 изображены треугольники напряжений, сопротивлений и мощностей для рассматриваемой цепи.
Знак и значение угла ф можно определить из треугольника сопротивлений (рис. 12.56):
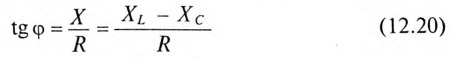
или
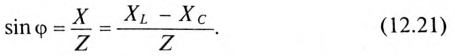
Из выражений (12.20) и (12.21) видно, что если 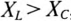 , то угол ф положителен (+ф), если
, то угол ф положителен (+ф), если 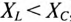 , то угол ф отрицательный (—ф).
, то угол ф отрицательный (—ф).
Из треугольника мощностей (рис. 12.5в) видно, что в цепи с R, L и С кроме активной мощности 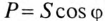 имеется реактивная мощность
имеется реактивная мощность 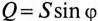 . Кроме того, в цепи происходит колебание мощности (меньшей из двух реактивных, в нашем случае Uc) между электрическим полем конденсатора С и магнитным полем катушки индуктивности L, так как мощности QL и Qc изменяются в противофазе. Но эта мощность (1—2 на рис. 12.5в) не считается реактивной, так как она не загружает источник и провода.
. Кроме того, в цепи происходит колебание мощности (меньшей из двух реактивных, в нашем случае Uc) между электрическим полем конденсатора С и магнитным полем катушки индуктивности L, так как мощности QL и Qc изменяются в противофазе. Но эта мощность (1—2 на рис. 12.5в) не считается реактивной, так как она не загружает источник и провода.
Из треугольника мощностей (рис. 12.5в) видно, что реактивная мощность, которая загружает источник и провода, Q= QL– Qc. Эта реактивная мощность (энергия) колеблется между источником и магнитным полем катушки индуктивности, так как 
Полная мощность цепи определяется по формуле

Колебательный контур
Электрические цепи, в которых происходят периодические изменения токов, напряжений, энергии называются колебательными.
Для того чтобы исследовать резонансные явления, необходимо иметь представления о процессах в колебательном контуре, состоящем из идеальной катушки и конденсатора без потерь.
Если конденсатор емкостью С зарядить до напряжения Um, то в электрическом поле этого конденсатора накопится энергия, максимальное значение которой согласно выражению (6.21):
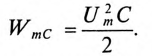
Если к заряженному конденсатору подключить индуктивность L замыканием ключа К (рис. 12.6), то конденсатор будет
разряжаться через индуктивность переменным током i. При этом в индуктивности L создается ЭДС самоиндукции eL, и в магнитном поле ее накапливается энергия, максимальное значение которой (9.12):
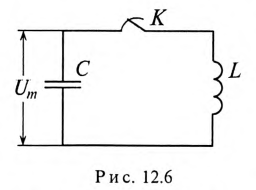
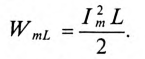
Источником энергии в этом контуре является конденсатор. Ток в контуре, состоящем из индуктивности L и конденсатора С, не прекращается даже когда конденсатор полностью разрядится. За счет ЭДС самоиндукции и энергии, накопившейся в магнитном поле индуктивности, конденсатор будет заряжаться, и энергия магнитного поля индуктивности переходит в электрическое поле конденсатора. При этом источником энергии в этом контуре является индуктивность. Дальше процесс повторяется.
Таким образом, в замкнутом контуре, состоящем из индуктивности и емкости, происходит колебание энергии между электрическим полем конденсатора С и магнитным полем индуктивности L. Поэтому такой замкнутый контур называется колебательным контуром.
Колебание энергии в колебательном контуре происходит с определенной частотой 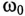 , которую называют частотой собственных колебаний контура. Частоту собственных колебаний со0 определяют из условия равенства энергии электрического и магнитного полей:
, которую называют частотой собственных колебаний контура. Частоту собственных колебаний со0 определяют из условия равенства энергии электрического и магнитного полей:
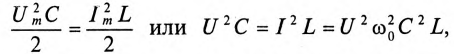
так как из (11.19) в цепи переменного тока с емкостью 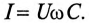
Откуда
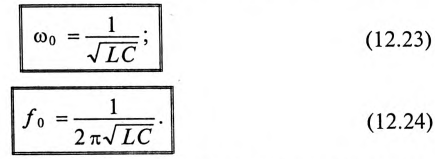
Таким образом, частота собственных колебаний колебательного контура определяется параметрами этого контура L и С.
Если в колебательном контуре отсутствуют потери (идеальный контур), то колебания в нем будут незатухающими с неизменной амплитудой. Если в колебательном контуре имеется активное сопротивление, т.е. возникают потери, то колебания энергии в нем будут затухающие, с уменьшающейся амплитудой, если эти потери не компенсируются.
Резонанс напряжений
Если в цепи синусоидального тока с последовательно соединенными конденсатором емкостью С и катушкой с сопротивлением R И индуктивностью L (рис. 12.7а) равны реактивные сопротивления, то в цепи наступает резонанс напряжений. Равенство реактивных сопротивлений является условием резонанса напряжений.

Из (12.25) следует 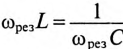 , тогда частота резонанса опреляется выражением
, тогда частота резонанса опреляется выражением

Из (12.26) следует, что резонанс напряжений имеет место в неразветвленной цепи с L и С тогда, когда частота вынужденных колебаний (частота источника) 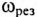 будет равна частоте собственных колебаний резонансного контура
будет равна частоте собственных колебаний резонансного контура 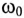 . Следовательно, добиться резонанса напряжений можно изменением частоты источника
. Следовательно, добиться резонанса напряжений можно изменением частоты источника 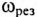 или изменением параметров колебательного контура L или С. т. е. изменением частоты собственных колебаний
или изменением параметров колебательного контура L или С. т. е. изменением частоты собственных колебаний 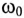 .
.
Полное (кажущееся) сопротивление цепи (рис. 12.7а) при резонансе напряжений определяется по формуле
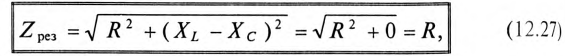
так как XL-Xc=0.
То есть полное сопротивление неразветвленной цепи при резонансе напряжений 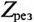 становится минимальным и равным активному сопротивлению цепи R.
становится минимальным и равным активному сопротивлению цепи R.
Следовательно, ток в неразветвленной цепи при резонансе напряжений максимальный:

Реактивные сопротивления при резонансе напряжений равны между собой, т. е.
(12.29)
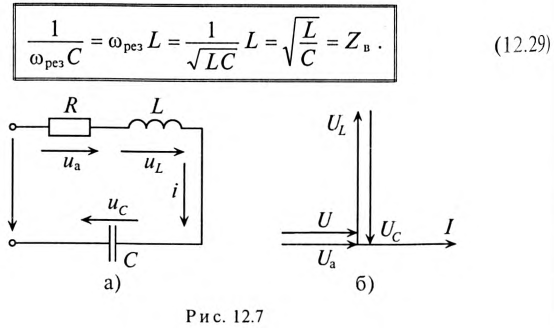
Таким образом, реактивные сопротивления при резонансе напряжений равны (каждое) волновому сопротивлению 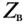 , которое называют характеристическим сопротивлением:
, которое называют характеристическим сопротивлением:
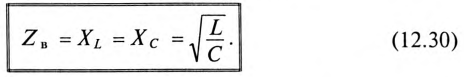
Напряжения на индуктивности UL и на емкости Uc при резонансе напряжений равны между собой, так как равны сопротивления, см. (12.25).
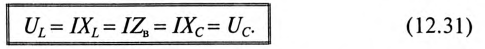
Равенство (12.31) определяет название «резонанс напряжений».
Так как UL и Uc изменяются в противофазе, то напряжение в резонансном режиме равно напряжению на активном сопротивлении 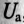 , т. е.
, т. е. 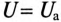 , что видно на векторной диаграмме (рис. 12.76).
, что видно на векторной диаграмме (рис. 12.76).
При резонансе напряжений каждое из реактивных напряжений UL и Uc может оказаться большим, чем напряжение цепи U.
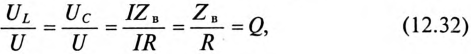
где Q — добротность резонансного контура.
Добротность контура Q показывает, во сколько раз напряжение на индуктивности UL и емкости Uc (каждое) больше напряжения цепи U.
Высокая добротность резонансного контура (при малом активном сопротивлении контура) нашла широкое применение в радиотехнике, в частности в антенном контуре.
Из векторной диаграммы (рис. 12.76) видно, что при резонансе напряжение цепи U совпадает по фазе с током 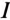 , угол между
, угол между 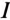 и U ф = 0 и cos ф = 1. Следовательно, кажущаяся мощность цепи S при резонансе вся потребляется, т. е. является активной:
и U ф = 0 и cos ф = 1. Следовательно, кажущаяся мощность цепи S при резонансе вся потребляется, т. е. является активной:

Колеблющаяся между магнитным полем индуктивности и электрическим полем емкости мощность ( ) не является реактивной, так как не загружает источник и провода.
) не является реактивной, так как не загружает источник и провода.
Из выражения (12.33) следует, что при отсутствии активной Мощности Р (активного сопротивления R) резонансный контур становится при резонансе идеальным колебательным контуром. Следовательно, при наличии активного сопротивления R источник расходует свою мощность на компенсацию потерь в контуре, за счет чего колебания в цепи будут незатухающими.
Кроме активного сопротивления R резонансной цепи и напряжения, приложенного к ней, все параметры резонансной цепи (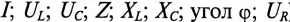 ) изменяются с изменением частоты сети
) изменяются с изменением частоты сети 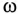 .
.
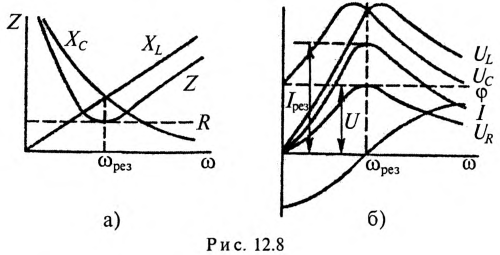
Эти изменения параметров резонансной цепи наглядно иллюстрируются резонансными кривыми, изображенными на рис. 12.8.
На резонансных кривых четко просматриваются значения этих параметров при частоте резонанса 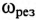 .
.
Общий случай неразветвленной цепи
Для неразветвленной цепи, содержащей несколько активных и реактивных сопротивлений различного характера (рис. 12.9а), справедливо геометрическое равенство напряжений (баланс напряжений)
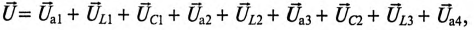
которое лежит в основе построения векторной диаграммы (рис. 12.96).
Таким образом, напряжение цепи равно геометрической сумме напряжений на всех участках этой цепи.
Из векторной диаграммы следует (рис. 12.96)
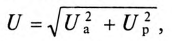
где 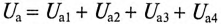 — активное напряжение цепи равно арифметической сумме напряжений на активных участках цепи;
— активное напряжение цепи равно арифметической сумме напряжений на активных участках цепи; 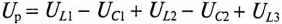 — реактивное напряжение цепи равно алгебраической сумме напряжений на реактивных участках цепи.
— реактивное напряжение цепи равно алгебраической сумме напряжений на реактивных участках цепи.
Те же рассуждения можно отнести и к сопротивлениям:
– полное сопротивление цепи 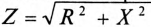 ;
;
– активное сопротивление цепи 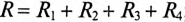 ;
;
– реактивное сопротивление цепи 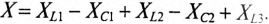
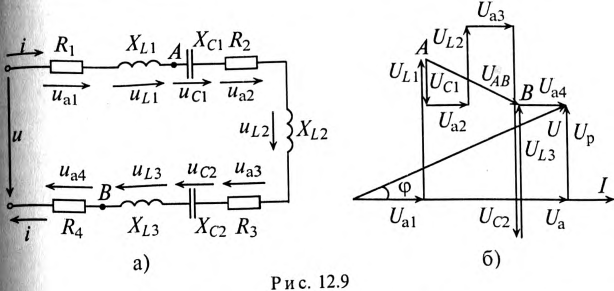
Напряжение на каком-либо участке неразветвленной цепи (рис. 12.9а), например на участке АВ, определяется так:_
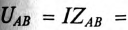
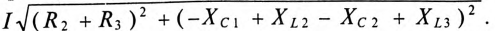
Вектор напряжения UAB показан на векторной диаграмме (рис. 12.96).
Пример 12.2
Напряжение, приложенное к неразветвленной цепи (рис. 12.10) U=220 В, частота тока сети f = 50 Гц. Начальная фаза тока 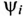 = 0.
= 0.
Сопротивление участков цепи: 
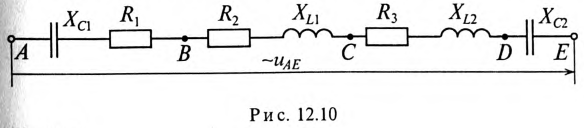
Требуется:
1. Вычислить ток цепи I и записать его мгновенное значение.
2. Записать мгновенное значение напряжения цепи иАЕ, определив предварительно угол ср и характер цепи.
3. Определить напряжение между точками АВ и CD.
4. Построить в масштабе векторную диаграмму цепи, определив едварительно напряжение на каждом сопротивлении.
5. Определить мощности S, Р и Q цепи.
6. Определить частоту, при которой в цепи наступит резонанс напряжений, и ток при резонансе.
7. Определить максимальную энергию, запасенную в магнитном поле катушек WmL и электрическом поле конденсаторов WmC. Как нужно изменить емкость конденсаторов, чтобы в цепи пил резонанс напряжений при частоте f = 50 Гц?
Решение
1. Для определения тока цепи I необходимо вычислить полное сопротивление цепи:
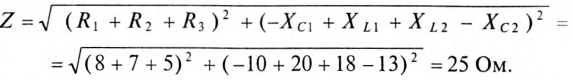
Действующее значение тока 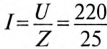 = 8,8 А, а амплитудное значение тока
= 8,8 А, а амплитудное значение тока 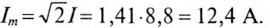
Угловая частота 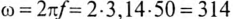 рад/с.
рад/с.
Мгновенное значение тока цепи:
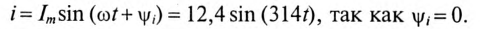
2. Угол сдвига фаз ф и характер цепи определяется через tg ф:
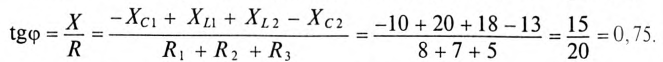
Таким образом, угол ф = 37° (из таблицы), характер цепи индуктивный (+ф).
Тогда мгновенное значение напряжения цепи
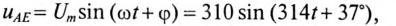
где 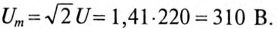
3. Напряжение на участках:
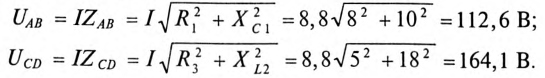
4. Для построения векторной диаграммы определяются напряжения:
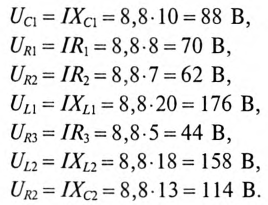
Векторная диаграмма цепи (отображает только характер участков, но не величины напряжений на них) изображена на рис. 12.11.
5. Полная мощность цепи 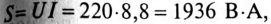 активная мощность Р=
активная мощность Р=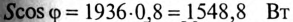 (так как
(так как 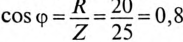 ), реактивная мощность
), реактивная мощность 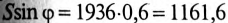 вар, (так как
вар, (так как 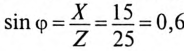 ).
).
6. Для определения частоты резонанса вычисляется индуктивность L и емкость С цепи:
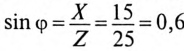
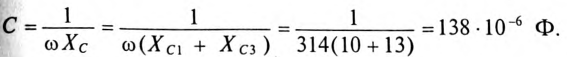
Тогда
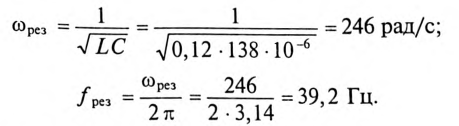
Ток цепи при резонансе 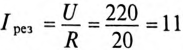 А.
А.
7. Максимальная энергия, запасенная в магнитном поле катушек:
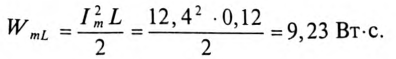
Максимальная энергия, запасенная в электрическом поле конденсаторов:
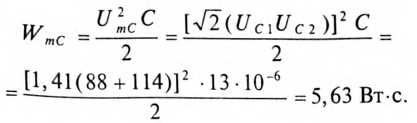
8. Условие резонанса XL = XC.
По условию задачи 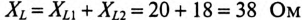 , а
, а 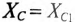
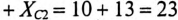 Ом. Этому Хс соответствует емкость С =
Ом. Этому Хс соответствует емкость С = 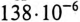 Ф при f = 50 Гц. Для того чтобы выполнить условие резонанса при сохранении частоты 50 Гц, необходимо Хс увеличить до 38 Ом. Чтобы емкостное сопротивление равнялось 38 Ом, величина емкости С должна быть равна
Ф при f = 50 Гц. Для того чтобы выполнить условие резонанса при сохранении частоты 50 Гц, необходимо Хс увеличить до 38 Ом. Чтобы емкостное сопротивление равнялось 38 Ом, величина емкости С должна быть равна
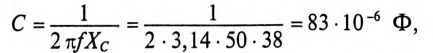
т. е. емкость конденсаторов нужно уменьшить на
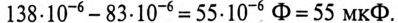
Разветвленная цепь синусоидального тока
Активный и реактивный токи:
Для расчета разветвленных цепей синусоидального тока вводятся расчетные величины активного и реактивного токов цепи.
Если к цепи, содержащей активное сопротивление R и индуктивное XL (рис. 13.1а), приложено синусоидальное напряжение  , то синусоидальный ток в цепи, вызванный этим напряжением, отстает от него по фазе на угол ф (рис. 12.1 в),
, то синусоидальный ток в цепи, вызванный этим напряжением, отстает от него по фазе на угол ф (рис. 12.1 в), 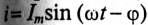 .
.
Векторная диаграмма в этом случае изображена на рис. 13.16.
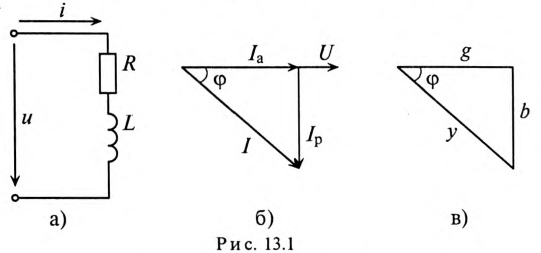
Ток цепи I (рис. 13.16) раскладывается на две составляющие, одна из которых  совпадает по фазе с напряжением, другая
совпадает по фазе с напряжением, другая  — сдвинута на 90°. Составляющая тока
— сдвинута на 90°. Составляющая тока  , совпадающая по фазе с напряжением, называется активной составляющей, или активным током. Составляющая тока
, совпадающая по фазе с напряжением, называется активной составляющей, или активным током. Составляющая тока  , имеющая относительно напряжения сдвиг по фазе на угол 90°, называется реактивной составляющей, или реактивным током.
, имеющая относительно напряжения сдвиг по фазе на угол 90°, называется реактивной составляющей, или реактивным током.
Активный и реактивный токи физического смысла не имеют. Они являются расчетными величинами, так как в неразветвленной цепи (рис. 13.1а) ток на всех участках имеет одинаковое значение. Однако понятия активный  и реактивный
и реактивный  токи значительно облегчают расчет разветвленных цепей синусоидального тока. Соотношения между токами определяются из треугольника токов (рис. 13.16)
токи значительно облегчают расчет разветвленных цепей синусоидального тока. Соотношения между токами определяются из треугольника токов (рис. 13.16)
13.2. Проводимости
Из треугольника токов для рассматриваемой цепи (рис. 13.16) следует: 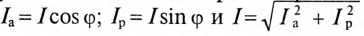 .
.
С другой стороны, известно, что 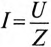 (см. (12.6)), a
(см. (12.6)), a 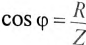 и
и 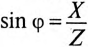 (см. (12.9)).
(см. (12.9)).
Тогда
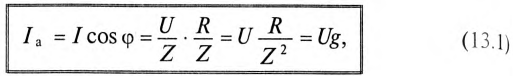
где g — активная проводимость цепи, равная

Величина, на которую умножают напряжение, чтобы получить ток, называют проводимостью.
А так как g определяет активный ток 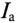 , то ее и называют активной проводимостью.
, то ее и называют активной проводимостью.
Таким образом, активная проводимость g определяется величиной активного сопротивления, деленного на квадрат полного (кажущегося) сопротивления цепи.
Величина реактивного тока определяется выражением
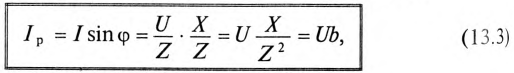
где b — реактивная проводимость цепи, равная

Величина полного тока цепи равна
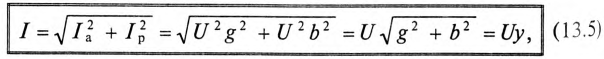
где 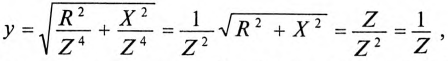 так как для цепи синусоидального тока с
так как для цепи синусоидального тока с 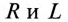 (рис. 13.1а)
(рис. 13.1а) 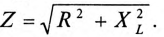
Таким образом, у — полная, или кажущаяся, проводимость цепи:

Полная (кажущаяся) проводимость цепи «у» является обратной величиной полного (кажущегося) сопротивления цепи.
Активная 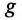 и реактивная
и реактивная 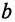 проводимости являются соответственно обратными величинами активного R и реактивного X сопротивлений только в том случае, если эти сопротивления (R и X) являются единственными в цепи или ветви, т. е.
проводимости являются соответственно обратными величинами активного R и реактивного X сопротивлений только в том случае, если эти сопротивления (R и X) являются единственными в цепи или ветви, т. е. 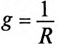 и
и 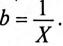
Если же в неразветвленной цепи (или ветви) включены сопротивления 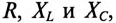 то для определения проводимостей можно воспользоваться выражениями (13.2), (13.4), (13.6). Треугольник проводимостей для рассматриваемой цепи (рис. 13.1а) изображен на рис. 13.1 в. Соотношения между проводимостями определяются из этого треугольника.
то для определения проводимостей можно воспользоваться выражениями (13.2), (13.4), (13.6). Треугольник проводимостей для рассматриваемой цепи (рис. 13.1а) изображен на рис. 13.1 в. Соотношения между проводимостями определяются из этого треугольника.
Параллельное соединение катушки и конденсатора
Если к источнику синусоидального напряжения 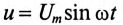 подключить параллельно реальную катушку с активным сопротивлением
подключить параллельно реальную катушку с активным сопротивлением 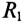 и индуктивным
и индуктивным 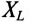 и конденсатор с активным сопротивлением
и конденсатор с активным сопротивлением 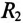 и емкостным
и емкостным 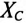 (рис. 13.2а), то токи в параллельных ветвях этой цепи изменяются по синусоидальному закону:
(рис. 13.2а), то токи в параллельных ветвях этой цепи изменяются по синусоидальному закону:
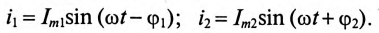
Действующие значения этих токов будут соответственно равны
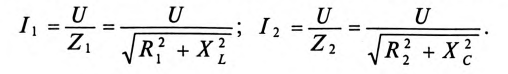
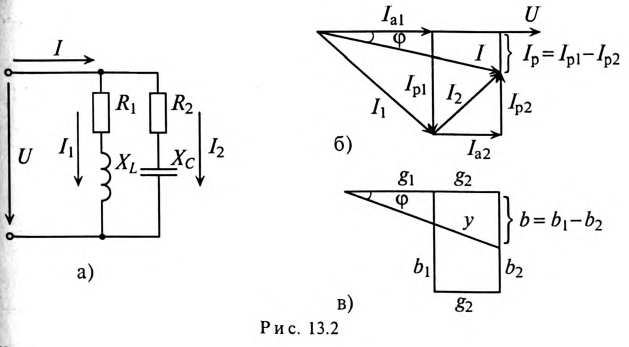
Ток в неразветвленной цепи  равен геометрической сумме токов в ветвях, так как токи не совпадают по фазе:
равен геометрической сумме токов в ветвях, так как токи не совпадают по фазе:
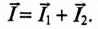
Для определения этого тока строится векторная диаграмма цепи (рис. 13.26), из которой следует:
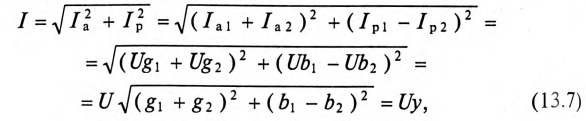
где 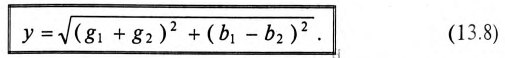
Таким образом, ток в неразветвленной части цепи 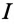 определяется произведением напряжения U и полной проводимости цепи
определяется произведением напряжения U и полной проводимости цепи 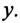
Реактивные проводимости в ветвях имеют различные знаки, так как сопротивления в ветвях различного характера (индуктивное и емкостное).
Треугольник проводимостей рассматриваемой цепи изображен на рис. 13.2в.
Характер разветвленной цепи определяется так же, как и неразветвленной. Если ток цепи 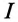 отстает от напряжения
отстает от напряжения 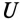 (как в рассматриваемом случае), то цепь индуктивного характера, если же ток
(как в рассматриваемом случае), то цепь индуктивного характера, если же ток 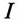 опережает напряжение
опережает напряжение 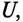 то цепь емкостного характера.
то цепь емкостного характера.
Резонанс токов
Резонанс токов в цепи (рис. 13.2а) с параллельным включением катушки и конденсатора (в различных ветвях) возникает при равенстве реактивных проводимостей в ветвях:
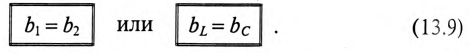
Выражение (13.9) является условием резонанса токов в разветвленных цепях синусоидального тока. Полная (кажущаяся) проводимость при этом условии
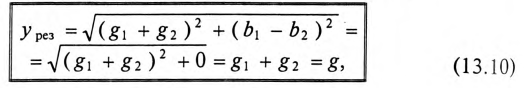
так как 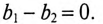
Таким образом, полная проводимость цепи при резонансе токов 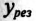 минимальна по величине и равна активной проводимости
минимальна по величине и равна активной проводимости  Следовательно, и ток в неразветвленной части цепи при резонансе токов имеет минимальную величину
Следовательно, и ток в неразветвленной части цепи при резонансе токов имеет минимальную величину

Реактивные токи в ветвях при резонансе токов равны между собой

Это равенство и определяет название «резонанс токов».
На основании равенства (13.12) строится векторная диаграмма при резонансе токов (рис. 13.3). Реактивные токи находятся в противофазе, поэтому ток в неразветвленной части цепи 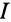 при резонансе токов равен активному току
при резонансе токов равен активному току 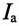 и совпадает по фазе с напряжением, т.е.
и совпадает по фазе с напряжением, т.е. 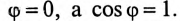 Следовательно, вся мощность цепи 5 при резонансе токов является активной Р:
Следовательно, вся мощность цепи 5 при резонансе токов является активной Р:
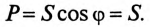
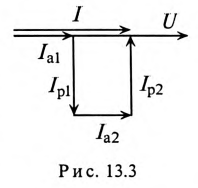
Эта активная мощность компенсирует потери на активном сопротивлении в параллельном резонансном контуре. Мощность (энергия), которая колеблется между электрическим полем конденсатора и магнитным полем индуктивности при резонансе, не является реактивной, так как не загружает источник и провода.
Частота резонанса токов в параллельном резонансном контуре может быть определена из условия резонанса токов, т. е. равенства реактивных проводимостей в ветвях 
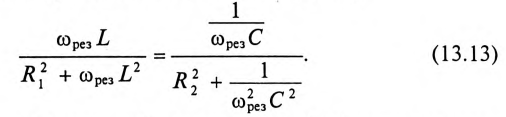
После ряда преобразований равенства (13.13) определяется частота резонанса токов
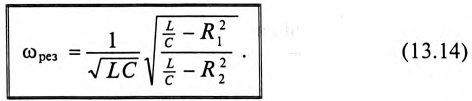
Резонансная частота зависит не только от параметров колебательного контура  но и от активных сопротивлений в ветвях реального резонансного контура.
но и от активных сопротивлений в ветвях реального резонансного контура.
Если в резонансном контуре отсутствуют активные сопротивления в ветвях, то частота резонанса токов  становится равной частоте собственных колебаний идеального резонансного контура
становится равной частоте собственных колебаний идеального резонансного контура
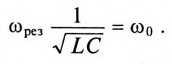
Если в резонансном контуре 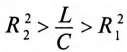 или
или 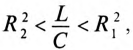 то резонанса токов добиться невозможно.
то резонанса токов добиться невозможно.
Резонанс токов нашел широкое применение в радиотехнике и выпрямительной технике (в резонансных фильтрах) и др.
Пример 13.1
Напряжение, приложенное к параллельно включенным катушке и конденсатору (рис. 13.4а),  частота сети
частота сети 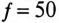 Гц. Параметры цепи:
Гц. Параметры цепи: 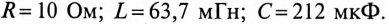 Определить:
Определить:
1) токи всех участков цепи: 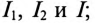
2) углы сдвига фаз этих токов относительно напряжения: 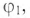
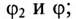
3) полную S, активную Р и реактивную Q мощности цепи;
4) частоту, при которой наступит резонанс токов в этой цепи. Построить векторную диаграмму.
Решение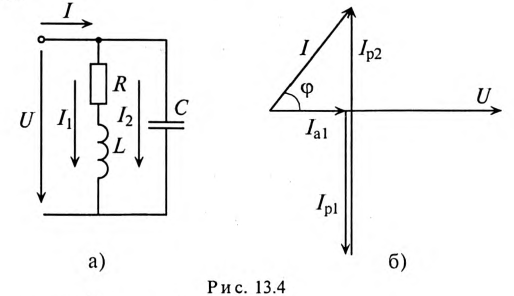
1. Сопротивление участков цепи:
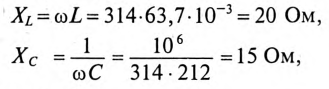
где 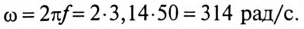
Сопротивление 1-й ветви:
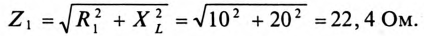
Токи в ветвях соответственно равны
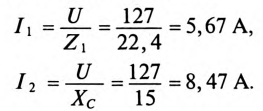
Для определения тока 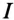 в неразветвленной части цепи определяются проводимости:
в неразветвленной части цепи определяются проводимости:
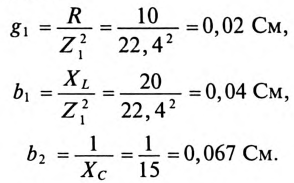
Тогда полная проводимость цепи будет равна
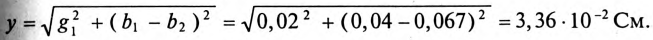
Ток в неразветвленной части цепи
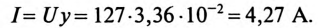
2. Углы сдвига фаз:
.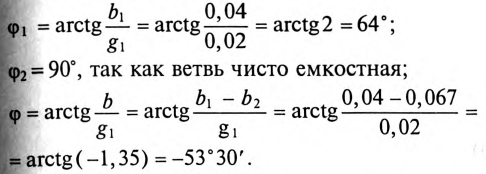
Знак «минус» перед значением угла  параллельного контура означает, что цепь имеет емкостной характер, так как
параллельного контура означает, что цепь имеет емкостной характер, так как 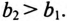
3. Полная мощность цепи 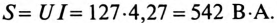
Активная мощность цепи 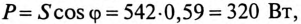 так как
так как 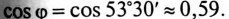
Реактивная мощность цепи 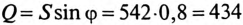 вар, так как
вар, так как 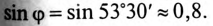
4. Угловая частота резонанса токов в цепи равна
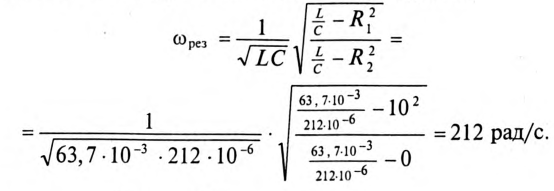
Откуда 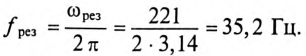
Для построения векторной диаграммы определяют активные и реактивные токи в ветвях:

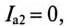 так как в ветви с емкостью отсутствует активное сопротивление, т.е.
так как в ветви с емкостью отсутствует активное сопротивление, т.е. 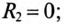
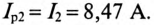
Векторная диаграмма для рассматриваемой цепи изображена на рис. 13.46.
На векторной диаграмме видно, что ток I опережает напряжение U на угол 53°30′ (цепь емкостного характера).
Коэффициент мощности
Номинальные параметры, т.е. мощность источника 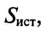 мощность потребителя
мощность потребителя 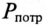 и коэффициент мощности
и коэффициент мощности 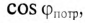 связаны следующим соотношением
связаны следующим соотношением

Из (13.15) следует, что чем меньше 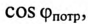 тем большую мощность
тем большую мощность 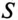 должен иметь источник для питания этого потребителя, т. е. тем больше его габариты, вес, расход материалов, стоимость и др.
должен иметь источник для питания этого потребителя, т. е. тем больше его габариты, вес, расход материалов, стоимость и др.
Ток в цепи потребителя с определенным 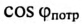 согласно выражению (12.11) равен
согласно выражению (12.11) равен
Из (13.16) видно, что чем меньше 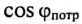 , тем больше ток потребителя
, тем больше ток потребителя 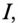 тем больший ток проходит по проводам линий электропередачи, тем больше потери энергии в этой линии и меньше КПД ее и всей системы (3.11). Кроме того, увеличение тока требует для его передачи проводов большего сечения, т. е. большего расхода цветных металлов.
тем больший ток проходит по проводам линий электропередачи, тем больше потери энергии в этой линии и меньше КПД ее и всей системы (3.11). Кроме того, увеличение тока требует для его передачи проводов большего сечения, т. е. большего расхода цветных металлов.
Таким образом, низкий коэффициент мощности потребителя 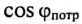 приводит к увеличению мощности источника, питающего этот потребитель, уменьшению КПД линии электропередачи и к увеличению сечения проводов линий электропередачи. 4В России установлен минимально допустимый коэффициент мощности не менее 0,93, т.е.
приводит к увеличению мощности источника, питающего этот потребитель, уменьшению КПД линии электропередачи и к увеличению сечения проводов линий электропередачи. 4В России установлен минимально допустимый коэффициент мощности не менее 0,93, т.е.  должен быть равен или больше 0,93
должен быть равен или больше 0,93 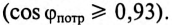
Однако  большинства электрических потребителей переменного тока меньше этой нормы. Так, например,
большинства электрических потребителей переменного тока меньше этой нормы. Так, например,  асинхронных двигателей, в зависимости от нагрузки, составляет
асинхронных двигателей, в зависимости от нагрузки, составляет 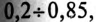 трансформаторов –
трансформаторов – 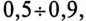 выпрямителей –
выпрямителей – 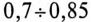 и т.д. Следовательно, коэффициент мощности этих потребителей необходимо повышать.
и т.д. Следовательно, коэффициент мощности этих потребителей необходимо повышать.
Так как большинство потребителей представляет собой нагрузку индуктивного характера, то для улучшения  параллельно с ним подключаются конденсаторы (рис. 13.5а).
параллельно с ним подключаются конденсаторы (рис. 13.5а).
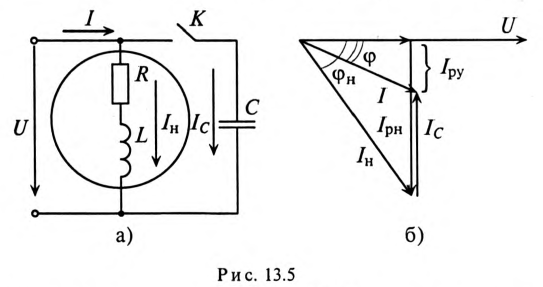
Из векторной диаграммы (рис. 13.56) видно, что с подключением конденсатора С (ключ К замкнут) появляется  за счет которого уменьшается угол
за счет которого уменьшается угол  и увеличивается
и увеличивается 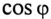 установки. При этом уменьшается ток цепи
установки. При этом уменьшается ток цепи 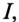 который до подключения конденсатора был равен току нагрузки
который до подключения конденсатора был равен току нагрузки 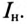
Для повышения коэффициента мощности 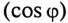 конденсатор можно включить последовательно с потребителем индуктивного характера. Однако при этом нарушается режим работы (напряжение) потребителя. Поэтому для улучшения
конденсатор можно включить последовательно с потребителем индуктивного характера. Однако при этом нарушается режим работы (напряжение) потребителя. Поэтому для улучшения 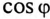 конденсатор подключают параллельно с нагрузкой (рис. 13.5а).
конденсатор подключают параллельно с нагрузкой (рис. 13.5а).
Коэффициент мощности можно повысить, увеличив активную нагрузку. При этом увеличивается потребляемая энергия, что экономически нерационально (уменьшается КПД установки).
Пример 13.2
Асинхронный двигатель, включенный в сеть с напряжением 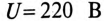 и частотой
и частотой 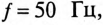 развивает на валу мощность
развивает на валу мощность 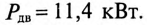 КПД двигателя
КПД двигателя 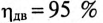 при
при 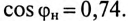 Определить емкость конденсатора С, который необходимо включить параллельно с двигателем (рис. 13.5а), чтобы повысить
Определить емкость конденсатора С, который необходимо включить параллельно с двигателем (рис. 13.5а), чтобы повысить 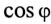 установки до 0,95.
установки до 0,95.
Решение
Мощность, потребляемая двигателем из сети:
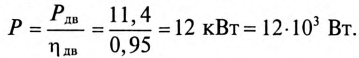
Ток нагрузки 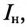 т.е. ток двигателя (рис. 13.5а), равен
т.е. ток двигателя (рис. 13.5а), равен
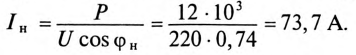
Реактивная составляющая тока двигателя 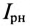 (рис. 13.56)
(рис. 13.56)
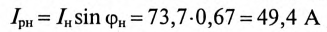
(по таблице 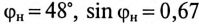 ).
).
Ток установки  при подключении конденсатора, т. е. при
при подключении конденсатора, т. е. при 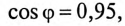 будет равен
будет равен

При 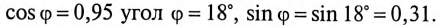 Реактивная составляющая тока установки (рис. 13.56)
Реактивная составляющая тока установки (рис. 13.56)
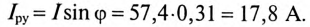
Ток конденсатора 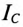 (рис. 13.56)
(рис. 13.56)
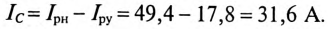
Емкостное сопротивление конденсаторов
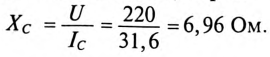
Емкость конденсаторов, которые нужно подключить параллельно двигателю для улучшения 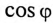 до 0,95:
до 0,95:
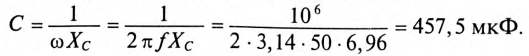
- Электрические цепи несинусоидального тока
- Несинусоидальный ток
- Электрические цепи с распределенными параметрами
- Резистивные электрические цепи и их расчёт
- Резонанс токов
- Трехфазные симметричные цепи
- Трехфазные несимметричные цепи
- Вращающееся магнитное поле
