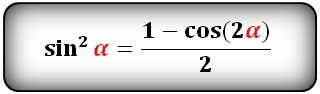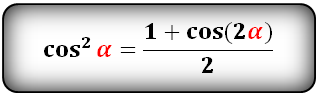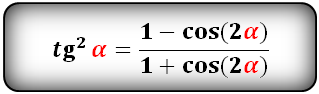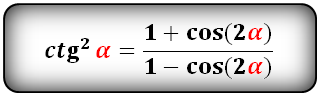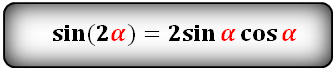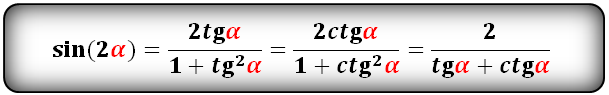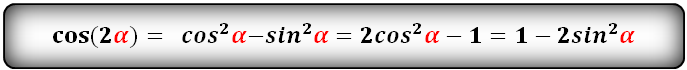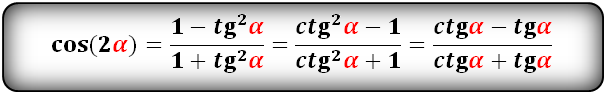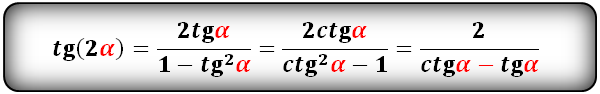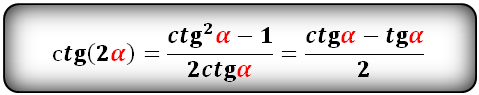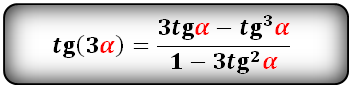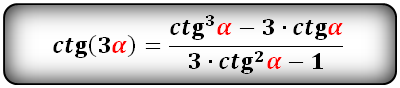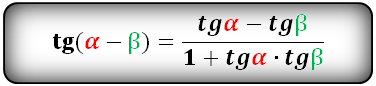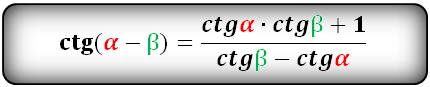чему равен синус в квадрате икс?
любовь будникова
Ученик
(83),
на голосовании
12 лет назад
Голосование за лучший ответ
apd
Гуру
(2828)
12 лет назад
Один минус косинус в квадрате икс.
(основное тригонометрическое правило)
Ерасыл Туркестанов
Знаток
(294)
12 лет назад
1-cos x(2)
Похожие вопросы
Уравнения разложения тригонометрических функций:квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.
Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)
sin(2α)- через sin и cos:
sin(2α)- через tg и ctg:
cos(2α)- через sin и cos:
cos(2α)- через tg и ctg:
tg(2α) и сtg(2α):
Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):
Тригонометрические формулы преобразования разности аргументов
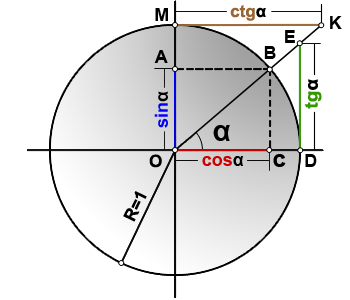
sin(α)=OA
cos(α)=OC
tg(α)=DE
ctg(α)=MK
R=OB=1
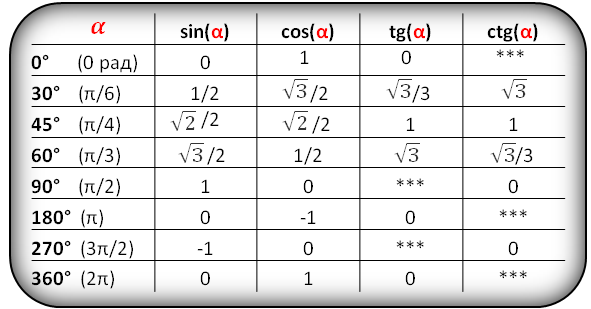
Значения функций для некоторых углов, α
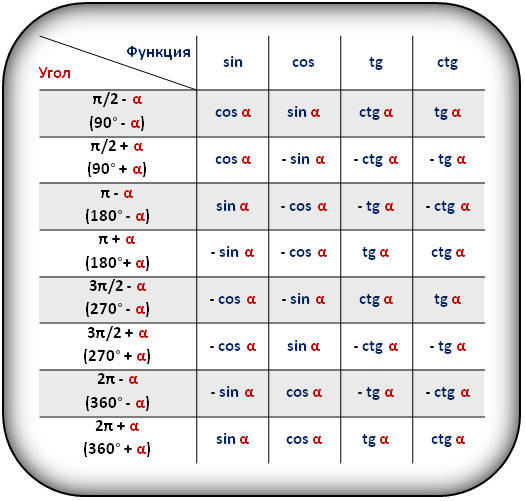
В таблице показаны формулы приведения для тригонометрических функций (sin, cos, tg, ctg).
п.1. Решение простейших тригонометрических уравнений
Про аркфункции (обратные тригонометрические функции) и их свойства – см. §9-11 данного справочника.
Обобщим результаты решения простейших уравнений, полученные в этих параграфах.
| Уравнение | ОДЗ | Решение |
| $$ sinx=a $$ | $$ -1leq aleq 1 $$ | begin{gather*} x=(-1)^k arcsin a+pi kLeftrightarrow\ Leftrightarrow left[ begin{array} {l l} x_1=arcsin a+2pi k\ x_2=pi-arcsin a+2pi k end{array} right. end{gather*} |
| $$ cosx=a $$ | $$ -1leq aleq 1 $$ | begin{gather*} x=pm arccos a+2pi k end{gather*} |
| $$ tgx=a $$ | $$ ainmathbb{R} $$ | begin{gather*} x=arctga+pi k end{gather*} |
| $$ ctgx=a $$ | $$ ainmathbb{R} $$ | begin{gather*} x=arcctga+pi kLeftrightarrow\ Leftrightarrow x=arctgfrac1a+pi k end{gather*} |
Частные случаи, для которых запись результата отличается от общей формулы:
| a=0 | a=-1 | a=1 | |
| $$ sinx=a $$ | $$ x=pi k $$ | $$ -fracpi2+2pi k $$ | $$ fracpi2+2pi k $$ |
| $$ cosx=a $$ | $$ x=fracpi2+pi k $$ | begin{gather*} pi+2pi k end{gather*} | begin{gather*} 2pi k end{gather*} |
Например:
п.2. Решение уравнений с квадратом тригонометрической функции
К простейшим также можно отнести уравнения вида:
| Уравнение | ОДЗ | Решение |
| $$ sin^2x=a $$ | $$ 0leq aleq 1 $$ | begin{gather*} x=pm arcsinsqrt{a}+pi k end{gather*} |
| $$ cos^2x=a $$ | $$ 0leq aleq 1 $$ | begin{gather*} x=pm arccossqrt{a}+pi k end{gather*} |
| $$ tg^2x=a $$ | $$ ageq 0 $$ | begin{gather*} x=pm arctgsqrt{a}+pi k end{gather*} |
| $$ ctg^2x=a $$ | $$ ageq 0 $$ | begin{gather*} x=pm arcctgsqrt{a}+pi k end{gather*} |
Например:
п.3. Различные формы записи решений
Как известно, в тригонометрии все функции связаны между собой базовыми отношениями (см. §12 данного справочника). Если нам известна одна из функций, мы можем без труда найти все остальные. Преобразования в уравнениях приводят к тому, что решение может быть записано через любую из этих функций.
Кроме того, понижение степени или универсальная подстановка (см. §15 данного справочника) приводят к увеличению или уменьшению исходного угла в 2 раза, и ответ может оказаться очень непохожим на решения, полученные другими способами для того же уравнения.
Например:
 |
Решим уравнение (sin^2x=0,64) Для квадрата синуса решение имеет вид: begin{gather*} x=pm arcsinsqrt{0,64}+pi k=\ =pm arcsin0,8+pi k end{gather*} На числовой окружности этому решению соответствуют 4 базовых точки, которые можно представить по-разному: begin{gather*} x=pm arcsin0,8+pi k=\ =pm arccos0,6+pi k=\ =pm arctgfrac43+pi k end{gather*} |
Если решать уравнение с помощью формулы понижения степени, получаем: begin{gather*} sin^2x=frac{1-cos2x}{2}=0,64Rightarrow 1-cos2x=1,28Rightarrow cos2x=-0,28Rightarrow\ Rightarrow 2x=pm arccos(-0,28)+2pi kRightarrow x=pmfrac12 arccos(-0,28)+pi k end{gather*} Если же решать уравнение с помощью универсальной подстановки: begin{gather*} sin^2x=left(frac{2tgfrac{x}{2}}{1+tg^2frac{x}{2}}right)^2=0,64Rightarrowfrac{2tgfrac{x}{2}}{1+tg^2frac{x}{2}}=pm 0,8Rightarrow 1+tg^2frac{x}{2}=pm 2,5tgfrac{x}{2}Rightarrow\ left[ begin{array}{l l} tg^2frac{x}{2}+2,5tgfrac{x}{2}+1=0\ tg^2frac{x}{2}-2,5tgfrac{x}{2}+1=0 end{array} right. Rightarrow left[ begin{array}{l l} left(tgfrac{x}{2}+2right)left(tgfrac{x}{2}+frac12right)=0\ left(tgfrac{x}{2}-2right)left(tgfrac{x}{2}-frac12right)=0 end{array} right. Rightarrow left[ begin{array}{l l} tgfrac{x}{2}=pm 2\ tgfrac{x}{2}=pmfrac12 end{array} right. Rightarrow\ Rightarrow left[ begin{array}{l l} x=pm arctg2+2pi k\ x=pm 2arctgfrac12+2pi k end{array} right. end{gather*} Таким образом, решая одно и то же уравнение, мы получаем очень разные по виду ответы. Однако, при проверке, все полученные множества решений совпадают.
Внимание!
При решении тригонометрических уравнений разными способами полученные ответы могут значительно отличаться по виду, но при этом они описывают одно и то же множество решений, т.е. являются равносильными.
п.4. Примеры
Пример 1. Решите уравнение обычным способом и с помощью универсальной подстановки. Сравните полученные ответы и множества решений. Сделайте вывод.
a) (sin x=frac{sqrt{3}}{2})
 |
Обычный способ: begin{gather*} x=(-1)^k arcsinfrac{sqrt{3}}{2}+pi k=(-1)^kfracpi3 +pi k Leftrightarrow\ Leftrightarrow left[ begin{array}{l l} x=fracpi3+2pi k\ x=frac{2pi}{3}+2pi k end{array} right. end{gather*} 2 базовых точки на числовой окружности. |
Универсальная подстановка: begin{gather*} sinx=frac{2tgfrac{x}{2}}{1+tg^2frac{x}{2}}Rightarrow 1+tg^2frac{x}{2}=frac{2tgfrac{x}{2}}{sqrt{3}/2}Rightarrow tg^2frac{x}{2}-frac{4}{sqrt{3}}tgfrac{x}{2}+1=0\ D=left(-frac{4}{sqrt{3}}right)^2-4=frac{16}{3}-4=frac43, tgfrac{x}{2}=frac{frac{4}{sqrt{3}}pmfrac{2}{sqrt{3}}}{2}Rightarrow left[ begin{array}{l l} tgfrac{x}{2}=frac{1}{sqrt{3}}\ tgfrac{x}{2}=sqrt{3} end{array} right. \ left[ begin{array}{l l} frac{x}{2}=fracpi6+pi k\ frac{x}{2}=fracpi3+pi k end{array} right. Rightarrow left[ begin{array}{l l} x=fracpi3+2pi k\ x=frac{2pi}{3}+2pi k end{array} right. Leftrightarrow x=(-1)^kfracpi3+pi k end{gather*} Ответы и множества решений совпадают.
Ответ: ((-1)^kfracpi3+pi k)
б) (cos2x=frac12)
 |
Обычный способ: begin{gather*} 2x=pm arccosfrac12+2pi kRightarrow\ x=pmfrac12left(arccosfrac12+2pi kright)=\ =pmfrac12cdotfracpi3+pi k=pmfracpi6+pi k end{gather*} 4 базовых точки на числовой окружности. |
Универсальная подстановка: begin{gather*} cos2x=frac{1-tg^2x}{1+tg^2x}=frac12Rightarrow 2(1-tg^2x)=1+tg^2xRightarrow 3tg^2x=1Rightarrow tgx=pmfrac{1}{sqrt{3}}\ x=pmfracpi6+pi k end{gather*} Ответы и множества решений совпадают.
Ответ: (pmfracpi6+pi k)
в) (sinleft(frac{x}{2}+fracpi3right)=1)
Обычный способ: begin{gather*} frac{x}{2}+fracpi3=fracpi2+2pi kRightarrow frac{x}{2}=fracpi2-fracpi3+2pi k=fracpi6+2pi kRightarrow x=fracpi 3+4pi k end{gather*} Одна базовая точка на числовой окружности с периодом (4pi).
Универсальная подстановка: begin{gather*} sinleft(frac{x}{2}+fracpi3right)=frac{2tgfrac{frac{x}{2}+fracpi3}{2}}{1+tg^2frac{frac{x}{2}+fracpi3}{2}}=1Rightarrow tg^2left(frac{x}{4}+fracpi6right)-2tgleft(frac{x}{4}+fracpi6right)-2tgleft(frac{x}{4}+fracpi6right)+1=0Rightarrow\ left(tgleft(frac{x}{4}+fracpi6right)-1right)^2=0Rightarrow tgleft(frac{x}{4}+fracpi6right)=1Rightarrow frac{x}{4}+fracpi6=frac{pi}{4}+pi kRightarrow\ Rightarrow frac{x}{4}=fracpi4-fracpi6+pi kRightarrow frac{x}{4}=frac{pi}{12}+pi kRightarrow x=fracpi3+4pi k end{gather*} Ответы и множества решений совпадают.
Ответ: (fracpi3+4pi k)
г*) (tgleft(3x+fracpi3right)=0)
Обычный способ: begin{gather*} 3x+fracpi3=arctg0+pi k=pi kRightarrow 3x=-fracpi3+pi kRightarrow x=-fracpi9+frac{pi k}{3} end{gather*} Универсальная подстановка: begin{gather*} tgleft(3x+fracpi3right)=frac{2tgfrac{3x+fracpi3}{2}}{1-tg^2frac{3x+fracpi3}{2}}=0Rightarrow tgfrac{3x+fracpi3}{2}=0Rightarrowfrac{3x+fracpi3}{2}=pi kRightarrow\ Rightarrow 3x+fracpi3=2pi k=3x=-fracpi3+2pi kRightarrow=-fracpi9+frac{2pi}{3} end{gather*} При использовании универсальной подстановки потеряна половина корней (период увеличился в 2 раза). Это связано с тем, что мы отбросили еще одно решение: (tgfrac{3x+fracpi3}{2}rightarrowinfty) – значение тангенса у асимптот. Действительно, в этом случае дробь стремится к 0, что удовлетворяет уравнению. Получаем: begin{gather*} frac{3x+fracpi3}{2}=fracpi2+pi kRightarrow 3x+fracpi3=pi+2pi kRightarrow 3x=frac{2pi}{3}+2pi kRightarrow x=frac{2pi}{9}+frac{2pi k}{3} end{gather*} Таким образом, мы получили два семейства решений: begin{gather*} left[ begin{array}{l l} x=-fracpi9+frac{2pi k}{3}\ x=frac{2pi}{9}+frac{2pi}{3} end{array} right. end{gather*} Представим последовательности решений в градусах, подставляя возрастающие значения (k): begin{gather*} left[ begin{array}{l l} x=-20^{circ}+120^{circ}k=left{…,-20^{circ},100^{circ},220^{circ},…right}\ x=40^{circ}+120^{circ}k=left{…,40^{circ},160^{circ},280^{circ},..right} end{array} right. end{gather*} Теперь представим полученное обычным способом решение в градусах: $$ x=-fracpi9+frac{pi k}{3}=-20^{circ}+60^{circ}k=left{…,-20^{circ},40^{circ},100^{circ},160^{circ},220^{circ},280^{circ},…right} $$ Получаем, что: begin{gather*} left[ begin{array}{l l} x=-fracpi9+frac{2pi k}{3}\ x=frac{2pi}{9}+frac{2pi}{3} end{array} right. Leftrightarrow x=-fracpi9+frac{pi k}{3} end{gather*} Ответы и множества решений после учета значений у асимптот совпадают.
Ответ: (-fracpi9+frac{pi k}{3})
Вывод: при использовании универсальной подстановки нужно быть аккуратным и помнить о возможности потерять корни. Семейство бесконечных решений для тангенса (frac{x}{2}=fracpi2+pi k), т.е. (x=pi+2pi k) нужно проверять как возможное решение для исходного уравнения отдельно.
Внимание!
При использовании универсальной подстановки можно потерять часть корней исходного тригонометрического уравнения.
Поэтому вместе с универсальной подстановкой проверяется также дополнительное возможное решение для бесконечного тангенса половинного угла: (x=pi+2pi k). begin{gather*} f(sin(x), cos(x),…)=0Leftrightarrow\ left[ begin{array}{l l} fleft(tgleft(frac{x}{2}right)right)=0\ (?) x=pi+2pi k end{array} right. end{gather*} где слева – исходное уравнение, а справа – универсальная подстановка и дополнительное возможное (не обязательное) семейство решений.
Пример 2.Решите уравнение обычным способом и с помощью формул понижения степени. Сравните полученные ответы и множества решений. Сделайте вывод.
a) (sin^2x=frac34)
 |
Обычный способ: begin{gather*} x=pm arcsinsqrt{frac34}+pi k=pm arcsinfrac{sqrt{3}}{2}+pi k=pmfracpi3+pi k end{gather*} |
Формулы понижения степени: begin{gather*} sin^2x=frac{1-cos2x}{2}=frac34Rightarrow 1-cos2x=frac32Rightarrow cos2x=-frac12Rightarrow\ Rightarrow 2x=pm arccosleft(-frac12right)+2pi k=pmfrac{2pi}{3}+2pi kRightarrow x=pmfracpi3+pi k end{gather*} Ответы и множества решений совпадают.
Ответ: (pmfracpi3+pi k)
б) (cos^2 2x=1)
 |
Обычный способ: begin{gather*} 2x=pm arccossqrt{1}+pi k=pm 0+pi k=pi kRightarrow x=frac{pi k}{2} end{gather*} Формулы понижения степени: begin{gather*} cos^2 2x=frac{1+cos4x}{2}=1Rightarrow 1+cos4x=2Rightarrow\ cos4x=1Rightarrow 4x=0+2pi k=2pi kRightarrow x=frac{pi k}{2} end{gather*} |
Ответы и множества решений совпадают.
Ответ: (frac{pi k}{2})
в) (sin^2left(frac{x}{2}+fracpi3right)=frac14)
 |
Обычный способ: begin{gather*} frac{x}{2}+fracpi3=pm arcsinsqrt{frac14}+pi k=pm arcsinfrac12+pi=pmfracpi6+pi k\ frac{x}{2}=-fracpi3pmfracpi6+pi k= left[ begin{array}{l l} fracpi2+pi k\ -fracpi6+pi k end{array} right. Rightarrow x= left[ begin{array}{l l} -pi+2pi k\ -fracpi3+2pi k end{array} right. end{gather*} |
Формулы понижения степени: begin{gather*} sin^2left(frac{x}{2}+fracpi3right)=frac{1-cosleft(2left(frac{x}{2}+fracpi3right)right)}{2}=frac14Rightarrow 1-cosleft(x+frac{2pi}{3}right)=frac12Rightarrow\ Rightarrow cosleft(x+frac{2pi}{3}right)=frac12Rightarrow x+frac{2pi}{3}=pm arccosleft(frac12right)+2pi kRightarrow\ Rightarrow x=-frac{2pi}{3}pmfracpi3+2pi k= left[ begin{array}{l l} -pi+2pi k\ -fracpi3+2pi k end{array} right. end{gather*} Ответы и множества решений совпадают.
Ответ: (-pi+2pi k, -fracpi3+2pi k)
г) (tg^2left(x+fracpi4right)=1)
 |
Обычный способ: begin{gather*} x+fracpi4=pm arctgsqrt{1}+pi k=pmfracpi4+pi kRightarrow\ Rightarrow x=-fracpi4pmfracpi4+pi k= left[ begin{array}{l l} -fracpi2+pi k\ pi k end{array} right. end{gather*} |
Формулы понижения степени: begin{gather*} cos^2left(x+fracpi4right)=frac{1}{1+underbrace{tg^2left(x+fracpi4right)}_{=1}}=frac12\ cos^2left(x+fracpi4right)=frac{1+cosleft(2left(x+fracpi4right)right)}{2}=frac12 Rightarrow cosleft(2x+fracpi2right)=0Rightarrow\ Rightarrow -sin2x=0Rightarrow sin2x=0 Rightarrow 2x=pi kRightarrow x=frac{pi k}{2} end{gather*} Из чертежа видно, что begin{gather*} left[ begin{array}{l l} -fracpi2+pi k\ pi k end{array} right. Leftrightarrow x=frac{pi k}{2} end{gather*} Оба решения соответствуют 4 базовым точкам на числовой окружности через каждые 90°. Множества решений совпадают. Ответы не совпадают, но являются равнозначными.
Ответ: (frac{pi k}{2})
Вывод: формулы понижения степени не расширяют и не урезают множество корней исходного уравнения. Полученные ответы либо совпадают, либо нет, но всегда являются равнозначными.
Синус в квадрате
Синус (sin) — это тригонометрическая функция, геометрически представляющая отношение противолежащего катета к гипотенузе в прямоугольном треугольнике.
sin 2 (x)=sin(x)*sin(x)
Значение синуса находится в диапазоне от -1 до +1.
Смотрите также калькулятор вычисления синуса угла.
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор вычисления квадрата синуса (синуса в квадрате). С помощью этого калькулятора вы в один клик сможете вычислить квадрат синуса любого угла.
Косинус в квадрате и синус в квадрате
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс — «x», что не меняет сути).
Синус угла альфа (sin ∠α) — это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin 2 α = 1 — cos 2 α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos 2 α = 1 — sin 2 α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Добавить интересную новость
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
user->isGuest) »]) . ‘ или ‘ . Html::a(‘зарегистрируйтесь’, [‘/user/registration/register’], [‘class’ => »]) . ‘ , чтобы получать деньги $$$ за каждый набранный балл!’); > else user->identity->profile->first_name) || !empty(Yii::$app->user->identity->profile->surname))user->identity->profile->first_name . ‘ ‘ . Yii::$app->user->identity->profile->surname; > else echo ‘Получайте деньги за каждый набранный балл!’; > ?>—>
Формулы двойного угла в тригонометрии
Формулы двойного угла служат для выражения синусов, косинусов, тангенсов, котангенсов угла со значением 2 α , используя тригонометрические функции угла α . Данная статья познакомит со всеми формулами двойного угла с доказательствами. Будут рассмотрены примеры применения формул. В заключительной части будут показаны формулы тройного, четверного углов.
Список формул двойного угла
Для преобразования формул двойного угла следует помнить о том, что углы в тригонометрии имеют вид n α записи, где n является натуральным числом, значение выражение записывается без скобок. Таким образом, считается, что запись sin n α имеет то же значение, что и sin ( n α ) . При обозначении sin n α имеем аналогичную запись ( sin α ) n . Использование записи применимо для всех тригонометрических функций со степенями n .
Ниже приведены формулы двойного угла:
sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α — sin 2 α , cos 2 α = 1 — 2 · sin 2 α , cos 2 α = 2 · cos 2 α — 1 t g 2 α = 2 · t g α 1 — t g 2 α c t g 2 α — c t g 2 α — 1 2 · c t g α
Отметим, что данные формулы sin и cos применимы с любым значением угла α . Формула тангенса двойного угла справедлива при любом значении α , где t g 2 α имеет смысл, то есть α ≠ π 4 + π 2 · z , z является любым целым числом. Котангенс двойного угла существует при любом α , где c t g 2 α определен на α ≠ π 2 · z .
Косинус двойного угла имеет тройную запись двойного угла. Все они являются применимыми.
Доказательство формул двойного угла
Доказательство формул берет начало из формул сложения. Применим формулы синуса суммы:
sin ( α + β ) = sin α · cos β + cos α · sin β и косинуса суммы cos ( α + β ) = cos α · cos β — sin α · sin β . Предположим, что β = α , тогда получим, что
sin ( α + α ) = sin α · cos α + cos α · sin α = 2 · sin α · cos α и cos ( α + α ) = cos α · cos α — sin α · sin α = cos 2 α — sin 2 α
Таким образом доказываются формулы синуса и косинуса двойного угла sin 2 α = 2 · sin α · cos α и cos 2 α = cos 2 α — sin 2 α .
Остальные формулы cos 2 α = 1 — 2 · sin 2 α и cos 2 α = 2 · cos 2 α — 1 приводят к виду cos 2 α = cos 2 α = cos 2 α — sin 2 α , при замене 1 на сумму квадратов по основному тождеству sin 2 α + cos 2 α = 1 . Получаем, что sin 2 α + cos 2 α = 1 . Так 1 — 2 · sin 2 α = sin 2 α + cos 2 α — 2 · sin 2 α = cos 2 α — sin 2 α и 2 · cos 2 α — 1 = 2 · cos 2 α — ( sin 2 α + cos 2 α ) = cos 2 α — sin 2 α .
Для доказательства формул двойного угла тангенса и котангенса применим равенства t g 2 α = sin 2 α cos 2 α и c t g 2 α = cos 2 α sin 2 α . После преобразования получим, что t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α и c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos α . Разделим выражение на cos 2 α , где cos 2 α ≠ 0 с любым значением α , когда t g α определен. Другое выражение поделим на sin 2 α , где sin 2 α ≠ 0 с любыми значениями α , когда c t g 2 α имеет смысл. Чтобы доказать формулу двойного угла для тангенса и котангенса, подставим и получим:
t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α = 2 · sin α · cos α cos 2 α cos 2 α — sin 2 α cos 2 α = 2 · sin 2 α cos 2 α 1 — sin 2 α cos 2 α = 2 · t g α 1 — t g 2 α c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos = cos 2 α — sin 2 α sin 2 α 2 · sin α · cos α sin 2 α = cos 2 α sin 2 α — 1 2 · cos α sin α = c t g 2 α — 1 2 · c t g α
Примеры использования формул двойного угла
Данный пункт показывает несколько примеров решения с формулами двойного угла. Конкретные примеры помогут глубже понять изучаемый материал. Чтобы убедиться в справедливости формул 2 α для α = 30 ° , применим значения тригонометрических функций для этих углов. Если α = 30 ° , тогда 2 α = 60 ° . Проверим значения sin 60 ° = 2 · sin 30 ° · cos 30 ° , cos 60 ° = cos 2 30 ° — sin 2 30 ° .
Подставив значения, получим t g 60 ° = 2 · t g 30 ° 1 — t g 2 30 ° и c t g 60 ° = c t g 2 30 ° — 1 2 · c t g 30 ° . .
Известно, что sin 30 ° = 1 2 , cos 30 ° = 3 2 , t g 30 ° = 3 3 , c t g 30 ° = 3 и
sin 60 ° = 3 2 , cos 60 ° = 1 2 , t g 60 ° = 3 , c t g 60 ° = 3 3 , тогда отсюда видим, что
2 · sin 30 ° · cos 30 ° = 2 · 1 2 · 3 2 = 3 2 , cos 2 30 ° — sin 2 30 ° = ( 3 2 ) 2 — ( 1 2 ) 2 = 1 2 , 2 · t g 30 ° 1 — t g 2 30 ° = 2 · 3 2 1 — ( 3 3 ) = 3
и c t g 2 30 ° — 1 2 · c t g 30 ° = ( 3 ) 2 — 1 2 · 3 = 3 3
Проведя вычисления, можно сделать вывод, что справедливость для α = 30 ° подтверждена.
Основное использование тригонометрических формул двойного угла – это преобразования тригонометрических выражений. Рассмотрим пример применения двойного угла, года имеем угол, отличный от 2 α . В примере допускается применение формулы двойного угла 3 π 5 . Тогда его необходимо преобразовать, в результате чего получим α = 3 π 5 : 2 = 3 π 10 . Отсюда следует, что формула двойного угла для косинуса будет иметь вид cos 3 π 5 = cos 2 3 π 10 — sin 2 3 π 10 .
Представить sin 2 α 3 через тригонометрические функции, при α 6 .
Заметим, что из условия имеем 2 α 3 = 4 · α 6 . Тогда использовав 2 раза формулу двойного угла, выразим sin 2 α 3 через тригонометрические функции угла α 6 . Применяя формулу двойного угла, получим sin 2 α 3 = 2 · sin α 3 · cos α 3 . После чего к функциям sin α 3 и cos α 3 применим формулы двойного угла: sin 2 α 2 = 2 · sin α 3 · cos α 3 = 2 · ( 2 · sin α 5 · cos α 6 ) · ( cos 2 α 6 — sin α 6 ) = = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6
Ответ: sin 2 α 3 = 4 · sin α 6 · cos 3 α 6 — 4 · sin 3 α 6 · cos α 6 .
Формулы тройного, четверного и т.д. угла
Таким же образом выводятся формулы тройного, четверного и т.д. углов. Формулы тройного угла можно вывести из формул сложения двойного угла.
sin 3 α = sin ( 2 α + α ) = sin 2 α · cos α + cos 2 α · sin α = 2 · sin α · cos α · cos α + ( cos 2 α — sin 2 α ) · sin α = = 3 · sin α · cos 2 α — sin 3 α
При замене cos 2 α на 1 — sin 2 α из формулы sin 3 α = 3 · sin α · cos 2 α — sin 3 α , она будет иметь вид sin 3 α = 3 · sin α — 4 · sin 3 α .
Так же приводится формула косинуса тройного угла:
cos 3 α = cos ( 2 α + α ) = cos 2 α · cos α — sin 2 α · sin α = = ( cos 2 α — sin 2 α ) · cos α — 2 · sin α · cos α · sin α = cos 3 α — 3 · sin 2 α · cos α
При замене sin 2 α на 1 — cos 2 α получим формулу вида cos 3 α = — 3 · cos α + 4 · cos 3 α .
При помощи полученных формул преобразуем формулу тройного угла для тангенса и котангенса тройного угла:
t g 3 α = sin 3 α cos 3 α = 3 · sin α · cos 2 α — sin 3 α cos 3 α — 3 · sin 2 α · cos α = 3 · sin α · cos 2 α — sin 3 α cos 3 α cos 3 α — 3 · sin 2 α · cos α cos 3 α = = 3 · sin α cos α — sin 3 α cos 3 α 1 — 3 · sin 2 α cos 2 α = 3 · t g α — t g 3 α 1 — 3 · t g 2 α ; c t g 3 α = cos 3 α sin 3 α = cos 3 α — 3 · sin 2 α · cos α 3 · sin α · cos 2 α — sin 3 α = cos 3 α — 3 · sin 2 α · cos α sin 3 α 3 · sin α · cos 2 α — sin 3 α sin 3 α = = cos 3 α sin 3 α — 3 · cos α sin α 3 · cos 2 α sin 2 α — 1 = c t g 3 α — 3 · c t g α 3 · c t g 2 α — 1
Чтобы выводить формулы четвертой степени, имеет смысл представить 4 α как 2 · 2 α , тогда имеет место использование формулы двойного угла два раза. Для выводы формулы 5 степени, представляем 5 α в виде 3 α + 2 α , что позволит применить формулы тройного и двойного углов для ее преобразования. Таким же образом делаются преобразования разных степеней тригонометрических функций. Их применение достаточно редкое в тригонометрии.
Косинус в квадрате и синус в квадрате
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Редактировать этот урок и/или добавить задание Добавить свой урок и/или задание
Добавить интересную новость
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
При правильном ответе Вы получите 8 баллов
Упростить выражение с квадратом косинуса:
Выберите всего один правильный ответ.
Добавление комментариев доступно только зарегистрированным пользователям
Lorem iorLorem ipsum dolor sit amet, sed do eiusmod tempbore et dolore maLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborgna aliquoLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempbore et dLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborlore m mollit anim id est laborum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Lorem ipsum dolor sit amet, consectetu sed do eiusmod qui officia deserunt mollit anim id est laborum.
Lorem ipsum dolor sit amet, consectetur adipisicing sed do eiusmod tempboLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod temLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborpborrum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Источник
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение тригонометрических уравнений.
Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Немного теории.
Тригонометрические уравнения
Уравнение cos(х) = а
Уравнение cos x = а, где ( |a| leqslant 1 ), имеет на отрезке ( 0 leqslant x leqslant pi ) только один корень. Если ( a geqslant 0 ), то корень заключён в промежутке ( left[ 0; ; frac<pi> <2>right] ); если a
Уравнение sin(х) = а
Уравнение tg(х) = а
Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.
Решение тригонометрических уравнений
Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.
Уравнения, сводящиеся к квадратным
Уравнение вида a sin(x) + b cos(x) = c
Используя формулы ( sin(x) = 2sinfrac <2>cosfrac<2>, ; cos(x) = cos^2 frac <2>-sin^2 frac <2>) и записывая правую часть уравпения в виде ( 2 = 2 cdot 1 = 2 left( sin^2 frac <2>+ cos^2 frac <2>right) ) получаем
В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях ( a neq 0, ; b neq 0, ; c neq 0, ; c^2 leqslant b^2+c^2 ) можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на ( sqrt ):
Решить уравнение 4 sin(x) + 3 cos(x) = 5
Здесь a = 4, b = 3, ( sqrt = 5 ). Поделим обе части уравнения на 5:
Уравнения, решаемые разложением левой части на множители
Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.
Источник
Формула косинус квадрат икс
‘);> //–>
Косинус (cos) – это тригонометрическая функция, геометрически представляющая отношение прилежащего катета к гипотенузе в прямоугольном треугольнике.
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор вычисления квадрата косинуса (косинуса в квадрате). С помощью этого калькулятора вы в один клик сможете вычислить квадрат косинус любого угла.
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза – сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза – это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс – «x», что не меняет сути).
Синус угла альфа (sin ∠α) – это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) – отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза – это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin 2 α = 1 – cos 2 α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos 2 α = 1 – sin 2 α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Редактировать этот урок и/или добавить задание и получать деньги постоянно* Добавить свой урок и/или задания и получать деньги постоянно
Добавить новость и получить деньги
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
При правильном ответе Вы получите 8 баллов
Упростить выражение с квадратом косинуса:
Выберите всего один правильный ответ.
Добавление комментариев доступно только зарегистрированным пользователям
Lorem iorLorem ipsum dolor sit amet, sed do eiusmod tempbore et dolore maLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborgna aliquoLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempbore et dLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborlore m mollit anim id est laborum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Lorem ipsum dolor sit amet, consectetu sed do eiusmod qui officia deserunt mollit anim id est laborum.
Lorem ipsum dolor sit amet, consectetur adipisicing sed do eiusmod tempboLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod temLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborpborrum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Основные формулы тригонометрии – это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.
Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Формулы приведения
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.
Формулы приведения являются следствием периодичности тригонометрических функций.
Тригонометрические формулы сложения
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
Тригонометрические формулы сложения
sin α ± β = sin α · cos β ± cos α · sin β cos α + β = cos α · cos β – sin α · sin β cos α – β = cos α · cos β + sin α · sin β t g α ± β = t g α ± t g β 1 ± t g α · t g β c t g α ± β = – 1 ± c t g α · c t g β c t g α ± c t g β
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Формулы кратного угла: двойного, тройного и т.д.
Формулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
Формулы половинного угла
sin 2 α 2 = 1 – cos α 2 cos 2 α 2 = 1 + cos α 2 t g 2 α 2 = 1 – cos α 1 + cos α c t g 2 α 2 = 1 + cos α 1 – cos α
Формулы понижения степени
sin 2 α = 1 – cos 2 α 2 cos 2 α = 1 + cos 2 α 2 sin 3 α = 3 sin α – sin 3 α 4 cos 3 α = 3 cos α + cos 3 α 4 sin 4 α = 3 – 4 cos 2 α + cos 4 α 8 cos 4 α = 3 + 4 cos 2 α + cos 4 α 8
Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
Общий вид формул понижения степени
sin n α = C n 2 n 2 n + 1 2 n – 1 ∑ k = 0 n 2 – 1 ( – 1 ) n 2 – k · C k n · cos ( ( n – 2 k ) α ) cos n α = C n 2 n 2 n + 1 2 n – 1 ∑ k = 0 n 2 – 1 C k n · cos ( ( n – 2 k ) α )
sin n α = 1 2 n – 1 ∑ k = 0 n – 1 2 ( – 1 ) n – 1 2 – k · C k n · sin ( ( n – 2 k ) α ) cos n α = 1 2 n – 1 ∑ k = 0 n – 1 2 C k n · cos ( ( n – 2 k ) α )
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Сумма и разность тригонометрических функций
Произведение тригонометрических функций
Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход – от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.
Формулы произведения тригонометрических функций
sin α · sin β = 1 2 · ( cos ( α – β ) – cos ( α + β ) ) cos α · cos β = 1 2 · ( cos ( α – β ) + cos ( α + β ) ) sin α · cos β = 1 2 · ( sin ( α – β ) + sin ( α + β ) )
Универсальная тригонометрическая подстановка
Все основные тригонометрические функции – синус, косинус, тангенс и котангенс, – могут быть выражены через тангенс половинного угла.
Универсальная тригонометрическая подстановка
sin α = 2 t g α 2 1 + t g 2 α 2 cos α = 1 – t g 2 α 2 1 + t g 2 α 2 t g α = 2 t g α 2 1 – t g 2 α 2 c t g α = 1 – t g 2 α 2 2 t g α 2
Источник