Как найти синус в треуголнике

Что такое синус в треугольнике? Как найти синус острого угла в прямоугольном треугольнике?

Определение.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

   Например,

для угла A треугольника ABC

противолежащий катет — это BC.

Соответственно, синус угла A в треугольнике ABC — это

   

   Для угла B треугольника ABC

противолежащим является катет AC.

Соответственно,  синус угла B в треугольнике ABC

равен отношению AC к AB:

   

Таким образом, синус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины противолежащего катета на длину гипотенузы. Длины отрезков выражаются положительными числами, поэтому синус угла треугольника также является положительным числом.

Поскольку длина катета всегда меньше длины гипотенузы, то синус острого угла прямоугольного треугольника — число, меньшее единицы.

Вывод:

Синус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:

   

Синус угла треугольника зависит не от длин сторон треугольника, а от отношения этих длин.

Например,

1) В треугольнике ABC катет BC=3 см, а гипотенуза AB=5 см.

Тогда

   

2) В треугольнике ABC катет BC=21 дм, гипотенуза AB=35 дм.

Тогда

   

Длины сторон треугольника изменилось, но отношения длин остались прежними, поэтому и значение синуса угла A не изменилось.

Угол A в обоих треугольниках одинаков.

Синус в треугольнике

Что такое синус в треугольнике? Как найти синус острого угла в прямоугольном треугольнике?

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

для угла A треугольника ABC

противолежащий катет — это BC.

Соответственно, синус угла A в треугольнике ABC — это

Для угла B треугольника ABC

противолежащим является катет AC.

Соответственно, синус угла B в треугольнике ABC

равен отношению AC к AB:

Таким образом, синус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины противолежащего катета на длину гипотенузы. Длины отрезков выражаются положительными числами, поэтому синус угла треугольника также является положительным числом.

Поскольку длина катета всегда меньше длины гипотенузы, то синус острого угла прямоугольного треугольника — число, меньшее единицы.

Синус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:

Синус угла треугольника зависит не от длин сторон треугольника, а от отношения этих длин.

1) В треугольнике ABC катет BC=3 см, а гипотенуза AB=5 см.

2) В треугольнике ABC катет BC=21 дм, гипотенуза AB=35 дм.

Длины сторон треугольника изменилось, но отношения длин остались прежними, поэтому и значение синуса угла A не изменилось.

Синус угла. Таблица синусов.

Синус угла через градусы, минуты и секунды

Синус угла через десятичную запись угла

Как найти угол зная синус этого угла

У синуса есть обратная тригонометрическая функция – arcsin(y)=x

Пример sin(30°) = 1/2; arcsin(1/2) = 30°

Определение синуса

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Синусом угла α называется ордината точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.

Периодичность синуса

Функция y = sin(x) периодична, с периодом 2π

Теорема синусов

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Доказательство теоремы синусов

Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Нарисуем стандартный треугольник и запишем теорему формулой:

Формула теоремы синусов:

Докажем теорему с помощью формулы площади треугольника через синус его угла.

Из этой формулы мы получаем два соотношения:

На b сокращаем, синусы переносим в знаменатели:

bc sinα = ca sinβ

Из этих двух соотношений получаем:

Теорема синусов для треугольника доказана.

Эта теорема пригодится, чтобы найти:

• Стороны треугольника, если даны два угла и одна сторона.
• Углы треугольника, если даны две стороны и один прилежащий угол.

Доказательство следствия из теоремы синусов

У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.

где R — радиус описанной около треугольника окружности.

Так образовались три формулы радиуса описанной окружности:

Основной смысл следствия из теоремы синусов заключен в этой формуле:

Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.

Для доказательства следствия теоремы синусов рассмотрим три случая.

1. Угол ∠А = α — острый в треугольнике АВС.

Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.

Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.

Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.

BA1 = 2R, где R — радиус окружности

Следовательно: R = α/2 sinα

Для острого треугольника с описанной окружностью теорема доказана.

2. Угол ∠А = α — тупой в треугольнике АВС.

Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.

Следовательно, ∠А1 = 180° – α.

Вспомним свойство вписанного в окружность четырёхугольника:

Также известно, что sin(180° – α) = sinα.

В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:

α = 2R sin (180° – α) = 2R sinα

Следовательно: R = α/2 sinα

Для тупого треугольника с описанной окружностью теорема доказана.

Часто используемые тупые углы:

• sin120° = sin(180° – 60°) = sin60° = 3/√2;
• sin150° = sin(180° – 30°) = sin30° = 1/2;
• sin135° = sin(180° – 45°) = sin45° = 2/√2.

3. Угол ∠А = 90°.

В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.

Для прямоугольного треугольника с описанной окружностью теорема доказана.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Теорема о вписанном в окружность угле

Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.

Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.

Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.

∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.

Формула теоремы о вписанном угле:

Следствие 1 из теоремы о вписанном в окружность угле

Вписанные углы, опирающиеся на одну дугу, равны.

∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).

Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:

На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.

Следствие 2 из теоремы о вписанном в окружность угле

Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.

ВС — диаметр описанной окружности, следовательно ∠COB = 180°.

Следствие 3 из теоремы о вписанном в окружность угле

Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:

Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.

Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.

Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.

Следовательно: α + γ = 180°.

Поэтому: ∠A + ∠C = 180°.

Следствие 4 из теоремы о вписанном в окружность угле

Синусы противоположных углов вписанного четырехугольника равны. То есть:

sinγ = sin(180° – α)

Так как sin(180° – α) = sinα, то sinγ = sin(180° – α) = sinα

Примеры решения задач

Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.

Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.

Согласно теореме о сумме углов треугольника:

∠B = 180° – 45° – 15° = 120°

Сторону AC найдем по теореме синусов:

Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.

В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:

Значит x = sin (4/5) ≈ 53,1°.

Ответ: угол составляет примерно 53,1°.

Запоминаем

Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.

>

Расширенная теорема: в произвольном треугольнике справедливо следующее соотношение:

[spoiler title=”источники:”]

http://calc-best.ru/matematicheskie/trigonometriya/sinus-ugla?n1=3

http://skysmart.ru/articles/mathematic/teorema-sinusov

[/spoiler]

Что такое синус, косинус, тангенс, котангенс

18 мая 2022

Сегодня мы узнаем, что такое синус, косинус, тангенс и котангенс. Это первый и самый важный урок по тригонометрии на всём сайте.

Содержание:

1. Ключевые определения: синус, косинус, тангенс, котангенс.
2. Почему эти значения зависят только от углов?
3. Стандартные углы: 30°, 45°, 60°.
4. Простейшие свойства синуса, косинуса, тангенса, котангенса.
5. Тригонометрия на координатной сетке.

Никаких сложных формул и длинных решений. Всё расписано максимально подробно. Изучите этот урок — и никаких проблем с тригонометрией не будет. Погнали!

1. Ключевые определения

Рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:

Мы видим, что острый угол $alpha $ образован гипотенузой $c$ и катетом $b$. Такой катет будем называть прилежащим. А катет $a$, который не участвует в формировании угла $alpha $, назовём противолежащим:

Это общепринятые названия: как только в прямоугольном треугольнике отмечен острый угол, для него немедленно можно указать прилежащий катет и противолежащий. И тут мы переходим к ключевым определениям.

1.1. Синус, косинус, тангенс, котангенс

Итак, пусть дан прямоугольный треугольник с острым углом $alpha $.

Тогда:

Определение 1. Синус угла $alpha $ — это отношение противолежащего катета к гипотенузе:

[sin alpha =frac{text{противолежащий катет}}{text{гипотенуза}}=frac{a}{c}]

Определение 2. Косинус угла $alpha $ — это отношение прилежащего катета к гипотенузе:

[cos alpha =frac{text{прилежащий катет}}{text{гипотенуза}}=frac{b}{c}]

Определение 3. Тангенс угла $alpha $ — это отношение противолежащего катета к прилежащему:

[operatorname{tg}alpha =frac{text{противолежащий катет}}{text{прилежащий катет}}=frac{a}{b}]

Определение 3. Котангенс угла $alpha $ — это отношение прилежащего катета к противолежащему:

[operatorname{ctg}alpha =frac{text{прилежащий катет}}{text{противолежащий катет}}=frac{b}{a}]

Вот так всё просто! Берём один катет, делим его на гипотенузы (или на другой катет) — и получаем выражение для синуса, косинуса, тангенса и котангенса. Все эти выражения называются тригонометрическими («тригонометрия» = «треугольники измеряю»).

Рассмотрим пару примеров.

Задача 1. Дан треугольник $ABC$. Найдите синус, косинус и тангенс угла $alpha $.

Решение. Это классический прямоугольный треугольник с катетами 3 и 4 и гипотенузой 5. Угол $alpha $ (он же — угол $A$ или угол $BAC$) образован прилежащим катетом $AB=3$гипотенузой $AC=5$. Следовательно катет $BC=4$ — противолежащий.

Имеем:

[begin{align}sin alpha& =frac{BC}{AC}=frac{5}{4} \ cos alpha& =frac{AB}{AC}=frac{3}{5} \ operatorname{tg}alpha& =frac{BC}{AB}=frac{4}{3} end{align}]

Далеко не всегда будут получаться такие красивые ответы. Чаще они будут содержать корни — это следствие теоремы Пифагора. Но важно понимать: как только мы находим длины катетов и гипотенузу, мы сразу можем найти и синусы, косинусы, тангенсы.

Далее в примерах мы не будем считать котангенсы, потому что из формулы котангенса очевидно, что они легко выражаются через тангенсы:

[operatorname{ctg}alpha =frac{1}{operatorname{tg}alpha }]

Но об этом чуть позже.

Задача 2. Дан треугольник $ABC$. Найдите синус, косинус и тангенс угла $alpha $.

Это равнобедренный прямоугольный треугольник с катетами $AB=BC=1$. Найдём гипотенузу по теореме Пифагора:

[begin{align}{{ AC}^{2}} & ={{AB}^{2}}+{{BC}^{2}}=1+1=2 \ AC & =sqrt{2} \ end{align}]

Теперь найдём синус, косинус и тангенс:

[begin{align}sin alpha &=frac{BC}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ cos alpha &=frac{AB}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ operatorname{tg}alpha&=frac{BC}{AB}=frac{1}{1}=1 end{align}]

Простое правило, чтобы не запутаться, где прилежащий катет, а где противолежащий. Просто помните: приставка «ко» означает «вместе», «сообща». Поэтому «косинус» — это «катет, лежащий рядом, к гипотенузе», «котангенс» — это «катет, лежащий рядом, к противолежащему». И никак иначе.:)

1.2. Задачи для тренировки

Перед тем как переходить к следующей части урока, предлагаю 4 примера для тренировки.

Задача 3. ►

Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.

Решение.

[begin{align}sin alpha &=frac{5}{13} \ cos alpha &=frac{12}{13} \ operatorname{tg}alpha &=frac{5}{12} \ end{align}]

Задача 4. ►

Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.

Решение.

[begin{align}sin alpha &=frac{8}{17} \ cos alpha &=frac{15}{17} \ operatorname{tg}alpha &=frac{8}{15} \ end{align}]

Задача 5. ►

Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.

Прилежащий катет по теореме Пифагора:

[begin{align}{{l}^{2}}&={{3}^{2}}-{{1}^{2}}=9-1=8 \ l&=sqrt{8}=2sqrt{2} \ end{align}]

Синус, косинус и тангенс:

[begin{align}sin alpha&=frac{1}{3} \ cos alpha&=frac{2sqrt{2}}{3} \ operatorname{tg}alpha&=frac{1}{2sqrt{2}}=frac{sqrt{2}}{4} \ end{align}]

Задача 6. ►

Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.

Прилежащий катет по теореме Пифагора:

[begin{align}{{l}^{2}} &={{2}^{2}}-{{1}^{2}}=4-1=3 \ l &=sqrt{3} \ end{align}]

Синус, косинус и тангенс:

[begin{align}sin alpha&=frac{1}{2} \ cos alpha&=frac{sqrt{3}}{2} \ operatorname{tg}alpha&=frac{1}{sqrt{3}}=frac{sqrt{3}}{3} \ end{align}]

Как видим, считать синусы, косинусы и тангенсы совсем несложно. Перейдём теперь к принципиально важному вопросу: а зачем вообще всё это нужно?

2. Теорема о единственности

Ключевая идея: синус, косинус, тангенс и котангенс зависят только от величины угла $alpha $ и никак не зависят от прямоугольного треугольника, в котором идут вычисления.

Такого не произойдёт. Потому что есть теорема о единственности.

2.1. Формулировка теоремы

Теорема. Значение синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике определяются только величиной этого угла и никак не зависят от самого треугольника.

2.2. Доказательство

Рассмотрим произвольный острый угол $alpha $. Для удобства обозначим его вершину буквой $A$:

А затем впишем в него два произвольных прямоугольных треугольника — $ABC$ и $AMN$. Любым удобным способом. Например, можно вписать эти треугольники вот так:

А можно и вот так — это не имеет никакого значения:

Рассмотрим треугольники $ABC$ и $AMN$. Угол $A$ у них общий; углы [angle ABC=angle AMN=90{}^circ ] по условию. Следовательно, треугольники $ABC$ и $AMN$ подобны по двум углам:

[Delta ABCsim Delta AMN]

Из подобия треугольников следует двойное равенство

[frac{AB}{AM}=frac{BC}{MN}=frac{AC}{AN}]

Выпишем второе равенство — получим пропорцию

[frac{BC}{MN}=frac{AC}{AN}]

Попробуем выразить $sin alpha $. Вспомним основное свойство пропорции: произведение крайних членов равно произведению средних. Поэтому

[BCcdot AN=MNcdot AC]

Разделим обе части равенства на длину каждой гипотенузы — $AN$ и $AC$:

[begin{align}frac{BCcdot AN}{ANcdot AC} &=frac{MNcdot AC}{ANcdot AC} \ frac{BC}{AC} &=frac{MN}{AN} end{align}]

Однако по определению синуса имеем:

[begin{align}sin BAC &=frac{BC}{AC} \ sin MAN &=frac{MN}{AN} \ end{align}]

Получается, что $sin BAC=sin MAN$. Другими словами, вне зависимости от выбора треугольника для данного угла $alpha $ мы всегда будем получать одно и то же значение $sin alpha $.

То же самое касается и $cos alpha $, $operatorname{tg}alpha $ и $operatorname{ctg}alpha $ — они зависят лишь от градусной меры угла $alpha $ и никак не зависят от конкретного прямоугольного треугольника, в котором они находятся. Теорема доказана.

3. Стандартные углы

Итак, значения $sin alpha $, $cos alpha $, $operatorname{tg}alpha $ и $operatorname{ctg}alpha $ однозначно определяются величиной угла $alpha $. Нам не важен треугольник — важна только градусная мера угла. Можно один раз посчитать синусы, косинусы и т.д. для нужных углов, а затем просто подставлять их.

Но тут мы сталкиваемся с проблемой, из-за которой многие как раз и не понимают тригонометрию. Проблема состоит из двух пунктов:

1. Для большинства углов $alpha $ нельзя найти точные значения $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
2. Верно и обратное: для большинства «красивых» $sin alpha $, $cos alpha $ и т.д. нельзя подобрать подходящий угол $alpha $.

Звучит немного непонятно, поэтому разберём каждый пункт на конкретных примерах.

3.1. Три стандартных угла

Существует лишь три острых угла, для которых легко считаются синусы, косинусы и т.д. Это 30°, 45°, 60°. Вот их синусы, косинусы и тангенсы:

[begin{array}{c|ccc} alpha& 30{}^circ& 45{}^circ & 60{}^circ \ hlinesin alpha & frac{1}{2} & frac{sqrt{2}}{2} & frac{sqrt{3}}{2} \ cos alpha & frac{sqrt{3}}{2} & frac{sqrt{2}}{2} & frac{1}{2} \ operatorname{tg}alpha& frac{sqrt{3}}{3} & 1 & sqrt{3} \ end{array}]

Чтобы понять, чем эти углы такие особенные, просто посчитаем все эти синусы, косинусы и тангенсы. Начнём с $alpha =45{}^circ $. Для этого рассмотрим равнобедренный прямоугольный треугольник. Мы уже встречались с ним:

Поскольку в равнобедренном треугольнике $angle A=angle B=45{}^circ $, получим:

[begin{align}sin 45{}^circ &=sin A=frac{BC}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ cos 45{}^circ &=sin A=frac{AB}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ operatorname{tg}45{}^circ&=sin A=frac{BC}{AB}=frac{1}{1}=1 end{align}]

Это именно те значения, которые указаны в таблице!

Теперь разберёмся с углами $alpha =30{}^circ $ и $alpha =60{}^circ $. Здесь рассуждения будут чуть сложнее. Сначала рассмотрим равносторонний треугольник $ABC$ со стороной $AB=2$ (просто так удобнее) и проведём высоту $BH$:

Мы знаем, что высота $BH$ — ещё и медиана, и биссектриса. Поэтому $AH=CH=1$, $angle ABH=angle CBH=30{}^circ $.

Следовательно, треугольник $ABH$ — прямоугольный, да ещё и с острыми углами 30° и 60°. По теореме Пифагора легко найти $BH=sqrt{3}$. Нанесём все данные на чертёж:

Разберёмся с углом 60°:

[begin{align} sin{60}^circ &=sin A=frac{BH}{AB}=frac{sqrt{3}}{2} \ cos{60}^circ&=cos A=frac{AH}{AB}=frac{1}{2} \ operatorname{tg}{60}^circ&=operatorname{tg}A=frac{BH}{AH}=sqrt{3} \ end{align}]

И с углом 30°:

[begin{align} sin{30}^circ &=sin ABH=frac{AH}{AB} =frac{1}{2} \ cos{30}^circ &=cos ABH=frac{BH}{AB} =frac{sqrt{3}}{2} \ operatorname{tg}{30}^circ &=operatorname{tg} ABH=frac{AH}{BH} =frac{1}{sqrt{3}} =frac{sqrt{3}}{3} \ end{align}]

Попробуйте повторить все эти рассуждения самостоятельно. Это очень полезное упражнение!

Возникает вопрос: как быть с другими углами? Например, можно ли найти $sin {50}^circ $? Или, быть может, $cos {10}^circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти.

Поэтому идём дальше и посмотрим на ситуацию с другой стороны: как подобрать угол к заданному синусу, косинусу, тангенсу?

3.2. Что с другими углами?

Взгляните ещё раз на «классический» прямоугольный треугольник, с которого мы начинали наши рассуждения:

Катеты 4 и 3, гипотенуза 5 — вполне обычный треугольник. Для него можно посчитать, например, синус острого угла $alpha $:

[sin alpha =sin A=frac{BC}{AB}=frac{3}{5}=0,6]

Итак, мы знаем синус. Внимание, вопрос: каким должен быть угол $alpha $, чтобы $sin alpha =0,6$? Сколько градусов должно быть в угле $alpha $? Ответ: неизвестно.:)

Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $alpha $, чтобы $sin alpha =0,6$. Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует.

Из всех этих рассуждений сделаем важный вывод. В тригонометрии мы:

• Либо берём угол и считаем для него синусы, косинусы и т.д. Но лишь для трёх острых углов — 30°, 45°, 60° — всё будет считаться быстро и красиво. Такие углы называются табличными.
• Либо берём синус, косинус или тангенс и для него пытаемся подобрать острый угол. Но лишь для табличных значений мы сможем подобрать такие углы. И да: это будут углы 30°, 45°, 60°.

Ещё раз:

Мы можем посчитать лишь синус, косинус и тангенс для трёх табличных углов.

Например, $sin 30{}^circ $, $cos 45{}^circ $, $operatorname{tg}60{}^circ $ и т.д. А всякие $sin 15{}^circ $, $cos 25{}^circ $ или $operatorname{tg}89,5{}^circ $ — не сможем. По крайней мере пока.:)

И наоборот:

Зная $sin alpha $, $cos alpha $ или $operatorname{tg}alpha $, мы сможем назвать точный угол $alpha $ только в том случае, если все эти синусы, косинусы и тангенсы — среди табличных значений.

Например, мы точно знаем, что если $sin alpha =frac{sqrt{2}}{2}$, то $alpha =45{}^circ $. Но когда $sin alpha =0,6$, мы уже не можем назвать угол $alpha $ (хотя всегда можем построить такой угол).

С этой мыслью мы и переходим к следующему пункту — свойства тригонометрических выражений.

4. Свойства синуса, косинуса, тангенса

Мы разберём три ключевых свойства:

1. Связь между синусом, косинусом и тангенсом.
2. Связь между острыми углами прямоугольного треугольника.
3. Основное тригонометрическое тождество.

Свойствам 2 и 3 далее в курсе будут посвящены отдельные уроки. Но основные идеи полезно взять на вооружение уже сейчас.

4.1. Связь между синусом, косинусом и тангенсом

Рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:

Выразим синус, косинус:

[sin alpha =frac{a}{c};quad cos alpha =frac{b}{c}]

А теперь выразим тангенс и заметим, что

[operatorname{tg}alpha =frac{a}{b}=frac{a}{c}cdot frac{c}{b}=frac{sin alpha }{cos alpha }]

Точно так же можно выразить и котангенс:

[operatorname{ctg}alpha =frac{b}{a}=frac{b}{c}cdot frac{c}{a}=frac{cos alpha }{sin alpha }]

Более того, сам тангенс и котангенс тоже связаны:

[operatorname{tg}alpha cdot operatorname{ctg}alpha =frac{a}{b}cdot frac{b}{a}=1]

Мы получили три важнейших тригонометрических формулы:

Основные формулы тригонометрии:

[operatorname{tg}alpha =frac{sin alpha }{cos alpha };quad operatorname{ctg}alpha =frac{cos alpha }{sin alpha };quad operatorname{tg}alpha cdot operatorname{ctg}alpha =1]

Эти формулы нужно знать наизусть. И понимать, откуда они берутся.

4.2. Связь между острыми углами

Рассмотрим прямоугольный треугольник $ABC$, где $angle C=90{}^circ $. Пусть градусная мера $angle A=alpha $ градусов:

Мы помним, что сумма острых углов прямоугольного треугольника равна 90°. Поэтому если $angle A=alpha $, то угол $angle B=90{}^circ -alpha $. Но тогда:

[sin alpha =sin A=frac{BC}{AB}=cos B=cos left( 90{}^circ -alpha right)]

То же самое и с косинусами:

[cos alpha =cos A=frac{AC}{AB}=sin B=sin left( 90{}^circ -alpha right)]

И даже с тангенсами и котангенсами:

[begin{align} operatorname{tg}alpha&=operatorname{tg}A=frac{BC}{AC} =operatorname{ctg}B=operatorname{ctg}left( {90}^circ -alpharight) \ operatorname{ctg}alpha&=operatorname{ctg}A=frac{AC}{BC} = operatorname{tg}B=tgleft( {90}^circ -alpha right) \ end{align}]

Другими словами, если вместо $alpha $ поставить ${90}^circ -alpha $, то исходная тригонометрическая функция поменяется на ко-функцию:

[begin{align}sin left( {90}^circ-alpharight) &=cos alpha \ cos left( {90}^circ-alpharight) &=sin alpha \ operatorname{tg}left( {90}^circ-alpharight) &=operatorname{ctg}alpha\ operatorname{ctg}left( {90}^circ-alpharight) &=operatorname{tg}alphaend{align}]

Но это ещё не всё. Есть гораздо более интересная формула.

4.3. Основное тригонометрическое тождество

Вновь рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:

Запишем выражения для $sin alpha $ и $cos alpha $:

[sin alpha =frac{a}{c};quad cos alpha =frac{b}{c}]

Далее заметим, что

[begin{align} {{sin }^{2}}alpha +{{cos }^{2}}alpha&={{left( frac{a}{c} right)}^{2}}+{{left( frac{b}{c} right)}^{2}}= \ & =frac{{{a}^{2}}}{{{c}^{2}}} +frac{{{b}^{2}}}{{{c}^{2}}}= \ & =frac{{{a}^{2}}+{{b}^{2}}}{{{c}^{2}}} end{align}]

В числителе можем применить теорему Пифагора: ${{a}^{2}}+{{b}^{2}}={{c}^{2}}$, поэтому

[{{sin }^{2}}alpha +{{cos }^{2}}alpha =frac{{{c}^{2}}}{{{c}^{2}}}=1]

Правая часть этой формулы вообще не зависит от угла $alpha $.

Основное тригонометрическое тождество:

[{{sin }^{2}}alpha +{{cos }^{2}}alpha =1]

Это равенство связывает синус и косинус одного и того же угла и верно для всех $alpha $.

С помощью основного тригонометрического тождества можно вычислять косинус, зная синус, и наоборот.

Задача 7. Найдите $18cos alpha $ для острого угла $alpha $, если $sin alpha =frac{sqrt{65}}{9}$.

Решение. Запишем основное тригонометрическое тождество:

[{{sin }^{2}}alpha +{{cos }^{2}}alpha =1]

Подставим указанное значение $sin alpha $ и выразим $cos alpha $:

[begin{align}{{left( frac{sqrt{65}}{9} right)}^{2}}+{{cos }^{2}}alpha &=1 \ frac{65}{81}+{{cos }^{2}}alpha &=1 \ {{cos }^{2}}alpha &=frac{16}{81} \ cos alpha&=pm frac{4}{9} end{align}]

Поскольку косинус угла в прямоугольном треугольнике не может быть отрицательным, выбираем вариант $cos alpha ={4}/{9};$. Остаётся сделать финальный шаг:

[18cos alpha =18cdot frac{4}{9}=2cdot 4=8]

Вот и всё! Ответ: 8.

В следующем примере мы уже не будем подробно расписывать каждый шаг. Оформим всё так, как надо оформлять на контрольных и экзаменах.

Задача 8. Найдите $48operatorname{tg}alpha $ для острого угла $alpha $, если $cos alpha =frac{8}{sqrt{113}}$.

Решение. Найдём $sin alpha $:

[begin{align}{{sin }^{2}}alpha &=1-{{cos }^{2}}alpha = \ & =1-{{left( frac{8}{sqrt{113}} right)}^{2}}= \ & =1-frac{64}{113}=frac{49}{113} \ sin alpha&=pm frac{7}{sqrt{113}} end{align}]

Но ${0}^circ lt alpha lt {90}^circ $, поэтому $sin alpha gt 0$. Следовательно

[sin alpha =frac{7}{sqrt{113}}]

Найдём $operatorname{tg}alpha $:

[operatorname{tg}alpha =frac{sin alpha }{cos alpha }=frac{7}{sqrt{113}}cdot frac{sqrt{113}}{8}=frac{7}{8}]

Окончательный ответ:

[48operatorname{tg}alpha =48cdot frac{7}{8}=6cdot 7=42]

Ответ: 42.

Заметка на будущее: замечание о том, что угол $alpha $ острый, весьма существенно. То, как мы сейчас определяем синусы, косинусы и тангенсы (через прямоугольный треугольник), называется геометрической тригонометрией. Её проходят в 8—9 классе.

Но в 10—11 классах появится алгебраическая тригонометрия, где синусы, косинусы и т.д. вполне могут быть отрицательными. И уже не получится просто так избавиться от минуса.

Но всё это будет чуть позже. А сейчас потренируемся.

Задача 9. ►

Найдите $52cos alpha $ для острого угла $alpha $, если $sin alpha =frac{5}{13}$.

Решение. Найдём $cos alpha $:

[begin{align}{{cos }^{2}}alpha &=1-{{sin }^{2}}alpha = \ &=1-frac{25}{169}=frac{144}{169} \ cos alpha&=pm frac{12}{13} end{align}]

Поскольку $cos alpha gt 0$ для острых $alpha $, выбираем $cos alpha ={12}/{13};$. Итого

[52cos alpha =52cdot frac{12}{13}=48]

Ответ: 48.

Задача 10. ►

Найдите $1+2operatorname{tg}alpha $ для острого угла $alpha $, если $cos alpha =frac{1}{sqrt{26}}$.

Решение. Найдём $sin alpha $:

[begin{align}{{sin }^{2}}alpha &=1-{{cos }^{2}}alpha = \ & =1-frac{1}{26}=frac{25}{26} \ sin alpha&=pm frac{5}{sqrt{26}} end{align}]

Поскольку $sin alpha gt 0$ для острых $alpha $, выбираем

[sin alpha =frac{5}{sqrt{26}}]

Считаем $operatorname{tg}alpha $:

[operatorname{tg}alpha =frac{sin alpha }{cos alpha }=frac{5}{sqrt{26}}cdot frac{sqrt{26}}{1}=5]

Откуда

[1+2operatorname{tg}alpha =1+2cdot 5=11]

Ответ: 11.

5. Тригонометрия на координатной сетке

Задачи, которые мы сейчас разберём, вполне могут встретиться в ОГЭ и даже ЕГЭ. Часто в них нет прямоугольного треугольника — есть лишь угол, в который этот треугольник предлагается вписать.

Для решения задач на координатной сетке достаточно посмотреть, через какие узлы сетки проходят интересующие нас лучи. И понять, какие из этих узлов имеет смысл соединить дополнительными построениями.

Звучит страшно, но на практике всё легко.:)

Задача 11. Найдите тангенс угла $ABC$, изображённого на координатной сетке:

Решение. Дополнительное построение: $AHbot BC$ — перпендикуляр из точки $A$ на луч $BC$.

Треугольник $BAH$ — прямоугольный, причём угол $ABC$ — один из его острых углов. Поэтому

[operatorname{tg}ABC=frac{AH}{BH}=frac{3}{4}=0,75]

Это и есть искомый тангенс.

Ответ: 0,75.

Ещё раз: важно, чтобы основание перпендикуляра попадало в узел сетки. Иначе нахождение длины катетов резко усложняется. Попробуйте сами:

Задача 12. ►

Найдите тангенс угла $ABC$, изображённого на координатной сетке:

Решение.

Дополнительное построение: $AHbot BC$ — перпендикуляр из точки $A$ к лучу $BC$.

Треугольник $BAH$ — прямоугольный с острым углом $ABC$. Поэтому

[operatorname{tg}ABC=frac{AH}{BH}=frac{2}{4}=frac{1}{2}]

Ответ: 0,5.

Разумеется, это были совсем простые задачи. Потому что один из лучей был параллелен линиям сетки.

Куда интереснее (и полезнее) рассмотреть ситуации, где лучи направлены под углом к сетке. Суть та же: ищем и соединяем узлы на лучах. Но тут уже нужна наблюдательность.

Задача 13. Найдите тангенс угла $MNK$, изображённого на координатной сетке:

Решение. Луч $KN$ содержит лишь две точки в узлах координатной сетки — собственно, $K$ и $N$. Понятно, что если продолжить луч за точку $K$, мы найдём ещё много таких точек, но будем решать задачу с тем, что есть.

Заметим, что прямая $MN$ наклонена к линиям сетки под углом 45° и образует диагонали квадратов. Это значит, что перпендикуляр к ней тоже будет наклонён под углом 45°.

Дополнительное построение: отрезок $KH$ — диагональ одного из квадратов сетки.

Очевидно, что угол $NHK$ прямой, поэтому треугольник $KHN$ прямоугольный и содержит искомый острый угол $MNK$. Находим тангенс:

[operatorname{tg}MNK=frac{HK}{HN}=frac{sqrt{2}}{2sqrt{2}}=frac{1}{2}=0,5]

Здесь мы предположили, что сторона квадрата сетки равна 1. Но с тем же успехом можно считать, что сторона квадрата $a$:

[operatorname{tg}MNK=frac{HK}{HN}=frac{asqrt{2}}{2asqrt{2}}=frac{1}{2}=0,5]

Ответ: 0,5.

Подобные задачи считаются довольно сложными. По статистике большинство выпускников 9 классов не способны их решать. Но вы-то теперь точно справитесь. Попробуйте:

Задача 14. ►

Найдите тангенс угла $DEF$, изображённого на координатной сетке:

Решение.

Дополнительное построение: отрезок $DH$.

Очевидно, $EH=DH$, угол $EHD$ прямой. Следовательно, треугольник $EDH$ — прямоугольный и равнобедренный. Поэтому $operatorname{tg}DEF=1$.

Либо можно посчитать «напролом», полагая, что сторона квадрата сетки равна $a$:

[operatorname{tg}DEF=frac{asqrt{10}}{asqrt{10}}=1]

Ответ: 1.

Вообще, поиск «правильных» узлов на координатной сетке — это своего рода искусство. И если углубляться в эту тему, то можно быстро выйти на «полуолимпиадные» задачи.

К тому же не существует «самого правильного» дополнительного построения. Задачу на координатной сетке всегда можно решить множеством различных способов. Так, в последнем примере можно было провести перпендикуляр вот так:

И даже так (хотя вряд ли этот способ можно назвать рациональным):

Во всех случаях ответ будет один и тот же. Поэтому не бойтесь экспериментировать. И переходите к следующему уроку — к действительно важным и полезным свойствам синусов, косинусов, тангенсов и котангенсов.:)

Смотрите также:

1. Радианная и градусная мера угла
2. Как быстро запомнить таблицу синусов и косинусов
3. Сложные логарифмические неравенства
4. Сложные выражения с дробями. Порядок действий
5. Задача B5: площадь фигур с вершиной в начале координат
6. Обход точек в стереометрии — 2

Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой нужной науки внесли ученые Ближнего Востока и Индии, которые придумали наиболее важные понятия, объяснили многие свойства, предложили варианты измерения и др.

Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии без таблиц и графиков.

Синус, косинус, тангенс и котангенс. Определения

Зачем разделять понятия синуса, косинуса, тангенса и котангенса?

Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Данные определения даны для острого угла прямоугольного треугольника!

Синус и косинус можно представить через экспоненту (экспоненциальная функция).

Приведем иллюстрацию. 

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Означения синуса, косинуса, тангенса и котангенса позволяют вычислять (находить) значения этих функций по известным длинам сторон треугольника.

Что и почему важно и принято помнить в ходе такого нахождения?

Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тг и ктг – вся числовая прямая, то есть эти функции могут принимать любые значения.

Как найти синус? Для начала нужно определиться, какой перед нами треугольник: прямоугольный или произвольный. В первом случае можно использовать обычный тригонометрический метод, а во втором – теорему косинусов.

Как найти косинус? Соответственно, нам нужно знать значения прилежающего катета и гипотенузы. 

Как найти тангенс? Если треугольник прямоугольный, то тангенс вычисляется при помощи значений противоположного катета и прилежащего (в уравнении нужно поделить одно на другое). Если речь идет о числах, тупых, развернутых углов и углов, превышающих 360 градусов, то тангенс определяется при помощи синуса и косинуса (посредством их отношения и деления).

Теорема синусов и косинусов используется для того чтобы искать элементы в произвольном треугольнике. Такой поиск используется часто.

Угол поворота

Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞. 

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность (круг) с центром в начале декартовой системы координат.

                                                                 

Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y). 

Синус угла поворота α – это ордината точки A1(x , y). sin α=y

Косинус угла поворота α – это абсцисса точки A1(x , y). cos α=икс

Тангенс угла поворота α – это отношение ординаты точки A1(x , y) к ее абсциссе. tg α=yx

Котанг угла поворота α – это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy

Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, -1). В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогична ситуация с котангенсом. Отличие состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.

При решении практических примеров не говорят “синус угла поворота α”. Слова “угол поворота” просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь. 

Числа

Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?

Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.

Например, синус числа 10π равен синусу угла поворота величиной 10π рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Начальная точка на окружности – точка A c координатами (1, 0).

Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.

Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t=y

Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t=x

Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. tg t=yx=sin tcos t

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.

Тригонометрические функции углового и числового аргумента

Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k ,   k ∈ Z   ( α = π 2 + π · k ,   k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k ,   k ∈ Z   ( α = π · k ,   k ∈ Z ). 

Можно сказать, что sin α, cos α, tg α, ctg α – это функции угла альфа, или функции углового аргумента. 

Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k ,   k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k ,   k ∈ Z.

Синус, косинус, тангенс и котангенс – основные тригонометрические функции.

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело. 

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью  соотношений сторон прямоугольного треугольника. Покажем это.

                                                                     

Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A(1,0) на угол величиной до 90 градусов и проведем из полученной точки A1(x,y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A1OH равен углу поворота α, длина катета OH равна абсциссе точки A1(x,y). Длина катета, противолежащего углу, равна ординате точки A1(x,y), а длина гипотенузы равна единице, так как она является радиусом единичной окружности. 

В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе. 

sin α=A1HOA1=y1=y

Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.

Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.

Синус, косинус, тангенс и котангенс: основные формулы

​​​​​​​

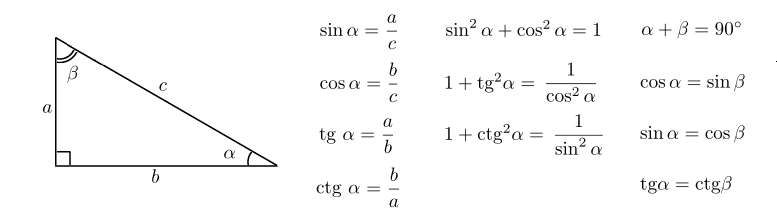
Исторический термин «решение треугольников» (лат. solutio triangulorum) обозначает решение следующей тригонометрической задачи: найти остальные стороны и/или углы треугольника по уже известным^[1]. Существуют также обобщения этой задачи на случай, когда заданы другие элементы треугольника (например, медианы, биссектрисы, высоты, площадь и т. д.), а также на случай, когда треугольник располагается не на евклидовой плоскости, а на сфере (сферический треугольник), на гиперболической плоскости (гиперболический треугольник) и т. п. Данная задача часто встречается в тригонометрических приложениях — например, в геодезии, астрономии, строительстве, навигации.

Решение плоских треугольников[править | править код]

У треугольника^[2] общего вида имеется 6 основных элементов: 3 линейные (длины сторон ) и 3 угловые (). Сторону, противолежащую углу при вершине, традиционно обозначают той же буквой, что и эта вершина, но не заглавной, а строчной (см. рисунок). В классической задаче плоской тригонометрии заданы 3 из этих 6 характеристик, и нужно определить 3 остальные. Очевидно, если известны только 2 или 3 угла, однозначного решения не получится, так как любой треугольник, подобный данному, тоже будет решением, поэтому далее предполагается, что хотя бы одна из известных величин — линейная^[3].

Алгоритм решения задачи зависит от того, какие именно характеристики треугольника считаются известными. Поскольку вариант «заданы три угла» исключён из рассмотрения, остаются 5 различных вариантов^[4]:

• три стороны;
• две стороны и угол между ними;
• две стороны и угол напротив одной из них;
• сторона и два прилежащих угла;
• сторона, противолежащий угол и один из прилежащих.

Основные теоремы[править | править код]

Стандартным методом решения задачи является использование нескольких фундаментальных соотношений, выполняющихся для всех плоских треугольников^[5]:

Теорема косинусов

Теорема синусов

Сумма углов треугольника

Из других иногда полезных на практике универсальных соотношений следует упомянуть теорему тангенсов, теорему котангенсов, теорему о проекциях и формулы Мольвейде.

Замечания[править | править код]

1. Для нахождения неизвестного угла надёжнее использовать теорему косинусов, а не синусов, потому что значение синуса угла при вершине треугольника не определяет однозначно самого угла, поскольку смежные углы имеют один и тот же синус^[6]. Например, если то угол может быть как , так и , потому что синусы этих углов совпадают. Исключением является случай, когда заранее известно, что в данном треугольнике тупых углов быть не может — например, если треугольник прямоугольный. С косинусом такие проблемы не возникают: в интервале от до значение косинуса определяет угол однозначно.
2. При построении треугольников важно помнить, что зеркальное отражение построенного треугольника тоже будет решением задачи. Например, три стороны однозначно определяют треугольник с точностью до отражения.
3. Все треугольники подразумеваются невырожденными, то есть длина стороны не может быть нулевой, а величина угла — положительное число, меньшее, чем .

Три стороны[править | править код]

Пусть заданы длины всех трёх сторон . Условие разрешимости задачи — выполнение неравенства треугольника, то есть каждая длина должна быть меньше, чем сумма двух других длин:

Чтобы найти углы , надо воспользоваться теоремой косинусов^[7]:

Третий угол сразу находится из правила, что сумма всех трёх углов должна быть равна

Не рекомендуется второй угол находить по теореме синусов, потому что, как указано в замечании 1, существует опасность спутать тупой угол с острым. Этой опасности не возникнет, если первым определить, по теореме косинусов, наибольший угол (он лежит против наибольшей из сторон) — два других угла точно являются острыми, и применение к ним теоремы синусов безопасно.

Ещё один метод вычисления углов по известным сторонам — использование теоремы котангенсов.

Две стороны и угол между ними[править | править код]

Пусть для определённости известны длины сторон и угол между ними. Этот вариант задачи всегда имеет единственное решение. Для определения длины стороны применяется теорема косинусов^[8]:

Фактически задача сведена к предыдущему случаю. Далее ещё раз применяется теорема косинусов для нахождения второго угла:

Третий угол находится из теоремы о сумме углов треугольника: .

Две стороны и угол напротив одной из них[править | править код]

В этом случае решений может быть два, одно или ни одного. Пусть известны две стороны и угол . Тогда уравнение для угла находится из теоремы синусов^[9]:

Для краткости обозначим (правая часть уравнения). Это число всегда положительно. При решении уравнения возможны 4 случая, во многом зависящие от D^[10][11].

1. Задача не имеет решения (сторона «не достаёт» до линии ) в двух случаях: если или если угол и при этом
2. Если существует единственное решение, причём треугольник прямоугольный:

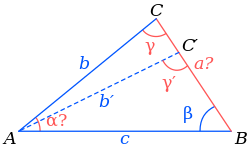
2. Если то возможны 2 варианта.
   1. Если , то угол имеет два возможных значения: острый угол и тупой угол . На рисунке справа первому значению соответствуют точка , сторона и угол , а второму значению — точка , сторона и угол .
   2. Если , то (большей стороне треугольника соответствует больший противолежащий угол). Поскольку в треугольнике не может быть двух тупых углов, тупой угол для исключён и решение единственно.

Третий угол определяется по формуле . Третью сторону можно найти по теореме синусов:

Сторона и два угла[править | править код]

Пусть задана сторона и два угла. Эта задача имеет единственное решение, если сумма двух углов меньше . В противном случае задача решения не имеет.

Вначале определяется третий угол. Например, если даны углы , то . Далее обе неизвестные стороны находятся по теореме синусов^[12]:

Решение прямоугольных треугольников[править | править код]

В этом случае известен один из углов — он равен 90°. Необходимо знать ещё два элемента, хотя бы один из которых — сторона. Возможны следующие случаи:

• два катета;
• катет и гипотенуза;
• катет и прилежащий острый угол;
• катет и противолежащий острый угол;
• гипотенуза и острый угол.

Вершину прямого угла традиционно обозначают буквой , гипотенузу — . Катеты обозначаются и , а величины противолежащих им углов — и соответственно.

Расчётные формулы существенно упрощаются, так как вместо теорем синусов и косинусов можно использовать более простые соотношения — теорему Пифагора:

и определения основных тригонометрических функций:

Ясно также, что углы и  — острые, так как их сумма равна . Поэтому любой из неизвестных углов однозначно определяется по любой из его тригонометрических функций (синусу, косинусу, тангенсу и др.) путём вычисления соответствующей обратной тригонометрической функции.

При корректной постановке задачи (если заданы гипотенуза и катет, то катет должен быть меньше гипотенузы; если задан один из двух непрямых углов, то он должен быть острый) решение всегда существует и единственно.

Два катета[править | править код]

Гипотенуза находится по теореме Пифагора:

Углы могут быть найдены с использованием функции арктангенса:

или же по только что найденной гипотенузе:

Катет и гипотенуза[править | править код]

Пусть известны катет и гипотенуза — тогда катет находится из теоремы Пифагора:

После этого углы определяются аналогично предыдущему случаю.

Катет и прилежащий острый угол[править | править код]

Пусть известны катет и прилежащий к нему угол .

Гипотенуза находится из соотношения

Катет может быть найден либо по теореме Пифагора аналогично предыдущему случаю, либо из соотношения

Острый угол может быть найден как

Катет и противолежащий острый угол[править | править код]

Пусть известны катет и противолежащий ему угол .

Гипотенуза находится из соотношения

Катет и второй острый угол могут быть найдены аналогично предыдущему случаю.

Гипотенуза и острый угол[править | править код]

Пусть известны гипотенуза и острый угол .

Острый угол может быть найден как

Катеты определяются из соотношений

Решение сферических треугольников[править | править код]

Сферический треугольник общего вида полностью определяется тремя из шести своих характеристик (3 стороны и 3 угла). Стороны сферического треугольника принято измерять не линейными единицами, а величиной опирающихся на них центральных углов.

Решение треугольников в сферической геометрии имеет ряд отличий от плоского случая. Например, сумма трёх углов зависит от треугольника; кроме того, на сфере не существует неравных подобных треугольников, и поэтому задача построения треугольника по трём углам имеет единственное решение. Но основные соотношения: две сферические теоремы косинусов и сферическая теорема синусов, — используемые для решения задачи, аналогичны плоскому случаю.

Из других соотношений могут оказаться полезными формулы аналогии Непера^[13] и формула половины стороны^[14].

Три стороны[править | править код]

Если даны (в угловых единицах) стороны , то углы треугольника определяются из теоремы косинусов^[15]:

,

,

,

Две стороны и угол между ними[править | править код]

Пусть заданы стороны и угол между ними. Сторона находится по теореме косинусов^[15]:

Углы можно найти так же, как в предыдущем случае, можно также использовать формулы аналогии Непера:

Две стороны и угол не между ними[править | править код]

Пусть заданы стороны и угол . Чтобы решение существовало, необходимо выполнение условия:

Угол получается из теоремы синусов:

Здесь, аналогично плоскому случаю, при получаются два решения: и .

Остальные величины можно найти из формул аналогии Непера^[16]:

,

.

Сторона и прилежащие углы[править | править код]

В этом варианте задана сторона и углы . Угол определяется по теореме косинусов^[17]:

Две неизвестные стороны получаются из формул аналогии Непера:

или, если использовать вычисленный угол , по теореме косинусов:

Два угла и сторона не между ними[править | править код]

В отличие от плоского аналога данная задача может иметь несколько решений.

Пусть заданы сторона и углы . Сторона определяется по теореме синусов^[18]:

Если угол для стороны острый и , существует второе решение:

Остальные величины определяются из формул аналогии Непера:

Три угла[править | править код]

Если заданы три угла, стороны находятся по теореме косинусов:

,

,

.

Другой вариант: использование формулы половины угла^[19].

Решение прямоугольных сферических треугольников[править | править код]

Изложенные алгоритмы значительно упрощаются, если известно, что один из углов треугольника (например, угол ) прямой. Прямоугольный сферический треугольник полностью определяется двумя элементами, остальные три находятся при помощи мнемонического правила Непера или из нижеприведённых соотношений^[20]:

Вариации и обобщения[править | править код]

Во многих практически важных задачах вместо сторон треугольника задаются другие его характеристики — например, длина медианы, высоты, биссектрисы, радиус вписанного или описанного круга и т. д. Аналогично вместо углов при вершинах треугольника в задаче могут фигурировать иные углы. Алгоритмы решения подобных задач чаще всего комбинируются из рассмотренных выше теорем тригонометрии.

Примеры:

Примеры практического применения[править | править код]

Триангуляция[править | править код]

Чтобы определить расстояние от берега до недоступной точки — например, до удалённого корабля,— нужно отметить на берегу две точки, расстояние между которыми известно, и измерить углы и между линией, соединяющей эти точки, и направлением на корабль. Из формул варианта «сторона и два угла» можно найти длину высоты треугольника^[23]:

Этот метод используется в каботажном судоходстве. Углы при этом оцениваются наблюдениями с корабля известных ориентиров на земле. Аналогичная схема используется в астрономии, чтобы определить расстояние до близкой звезды: измеряются углы наблюдения этой звезды с противоположных точек земной орбиты (то есть с интервалом в полгода) и по их разности (параллаксу) вычисляют искомое расстояние^[23].

Другой пример: требуется измерить высоту горы или высокого здания. Известны углы наблюдения вершины из двух точек, расположенных на расстоянии . Из формул того же варианта, что и выше, получается^[24]:

Расстояние между двумя точками на поверхности земного шара[править | править код]

Надо вычислить расстояние между двумя точками на земном шаре^[25]:

Точка : широта долгота

Точка : широта долгота

Для сферического треугольника , где  — северный полюс, известны следующие величины:

Это случай «две стороны и угол между ними». Из приведенных выше формул получается:

,

где  — радиус Земли.

История[править | править код]

Зачатки тригонометрических знаний можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая. Главным достижением этого периода стало соотношение, позже получившее имя теоремы Пифагора; Ван дер Варден считает, что вавилоняне открыли его между 2000 и 1786 годами до н. э.^[26]

Общая постановка задачи решения треугольников (как плоских, так и сферических) появилась в древнегреческой геометрии^[27]. Во второй книге «Начал» Евклида теорема 12 представляет собой словесный аналог теоремы косинусов для тупоугольных треугольников^[28]:

В тупоугольных треугольниках квадрат на стороне, стягивающей тупой угол, больше [суммы] квадратов на сторонах, содержащих тупой угол, на дважды взятый прямоугольник, заключённый между одной из сторон при тупом угле, на которую падает перпендикуляр, и отсекаемым этим перпендикуляром снаружи отрезком при тупом угле.

Следующая за ней теорема 13 — вариант теоремы косинусов для остроугольных треугольников. Аналога теоремы синусов у греков не было, это важнейшее открытие было сделано гораздо позднее^[29]: древнейшее из дошедших до нас доказательств теоремы синусов на плоскости описано в книге Насир ад-Дин Ат-Туси «Трактат о полном четырёхстороннике», написанной в XIII веке^[30].

Первые тригонометрические таблицы составил, вероятно, Гиппарх в середине II века до н. э. для астрономических расчётов. Позднее астроном II века Клавдий Птолемей в «Альмагесте» дополнил результаты Гиппарха. Первая книга «Альмагеста» — самая значимая тригонометрическая работа всей античности. В частности, «Альмагест» содержит обширные тригонометрические таблицы хорд для острых и тупых углов, с шагом 30 угловых минут. В таблицах Птолемей приводит значение длин хорд с точностью до трех шестидесятиричных знаков^[31]. Такая точность примерно соответствует пятизначной десятичной таблице синусов с шагом 15 угловых минут^[1].

Птолемей явно не формулирует теорему синусов и косинусов для треугольников. Тем не менее он всегда справляется с задачей решения треугольников, разбивая треугольник на два прямоугольных^[32].

Параллельно с развитием тригонометрии плоскости греки, под влиянием астрономии, далеко продвинули сферическую тригонометрию^[33]. Решающим этапом в развитии теории стала монография «Сферика» в трёх книгах, которую написал Менелай Александрийский (около 100 года н. э.). В первой книге он изложил теоремы о сферических треугольниках, аналогичные теоремам Евклида о плоских треугольниках (см. I книгу «Начал»). По сообщению Паппа, Менелай первым ввёл понятие сферического треугольника как фигуры, образованной отрезками больших кругов^[34]. Несколько десятилетий спустя Клавдий Птолемей в своих трудах «География», «Аналемма» и «Планисферий» даёт подробное изложение тригонометрических приложений к картографии, астрономии и механике.

В IV веке, после упадка античной науки, центр развития математики переместился в Индию. Сочинения индийских математиков (сиддханты) показывают, что их авторы были хорошо знакомы с трудами греческих астрономов и геометров^[35]. Чистой геометрией индийцы интересовались мало, но их вклад в прикладную астрономию и расчётные аспекты тригонометрии очень значителен. В частности, индийцы первыми ввели в использование косинус^[36]. Кроме того, индийцы знали формулы для кратных углов , для . В «Сурья-сиддханте» и в трудах Брахмагупты при решении задач фактически используется сферический вариант теоремы синусов, однако общая формулировка этой теоремы в Индии так и не появилась^[37].

В VIII веке учёные стран Ближнего и Среднего Востока познакомились с трудами древнегреческих и индийских математиков и астрономов. Их астрономические трактаты, аналогичные индийским сиддхантам, назывались «зиджи»; типичный зидж представлял собой сборник астрономических и тригонометрических таблиц, снабжённый руководством по их использованию и (не всегда) изложением общей теории^[38]. Сравнение зиджей периода VIII—XIII веков показывает быструю эволюцию тригонометрических знаний. Самые ранние из сохранившихся трудов принадлежат ал-Хорезми и ал-Марвази (IX век), которые рассмотрели, наряду с известными ещё индийцам синусом и косинусом, новые тригонометрические функции: тангенс, котангенс, секанс и косеканс^[36].

Сабит ибн Курра (IX век) и ал-Баттани (X век) первыми открыли фундаментальную теорему синусов для частного случая прямоугольного сферического треугольника. Для произвольного сферического треугольника доказательство было найдено (разными способами и, вероятно, независимо друг от друга) Абу-л-Вафой, ал-Худжанди и ибн Ираком в конце X века^[29]. В другом трактате ибн Ирака сформулирована и доказана теорема синусов для плоского треугольника^[39]. Сферическая теорема косинусов в общем виде сформулирована в странах ислама не была, однако в трудах Сабита ибн Курры, ал-Баттани и других астрономов имеются эквивалентные ей утверждения^[40].

Фундаментальное изложение тригонометрии как самостоятельной науки (как плоской, так и сферической) дал персидский математик и астроном Насир ад-Дин ат-Туси в 1260 году^[41]. Его «Трактат о полном четырёхстороннике» содержит практические способы решения типичных задач, в том числе труднейших, решенных самим ат-Туси — например, построение сторон сферического треугольника по заданным трём углам^[42]. Таким образом, к концу XIII века были открыты базовые теоремы, необходимые для эффективного решения треугольников.

В Европе развитие тригонометрической теории стало чрезвычайно важным в Новое время, в первую очередь для артиллерии, оптики и навигации при дальних морских путешествиях. В 1551 году появились 15-значные тригонометрические таблицы Ретика, ученика Коперника, с шагом 10″^[43]. Потребность в сложных тригонометрических расчётах вызвала в начале XVII века открытие логарифмов, причём первые логарифмические таблицы Джона Непера содержали только логарифмы тригонометрических функций. Среди других открытий Непера — эффективный алгоритм решения сферических треугольников, получивший название «формулы аналогии Непера»^[44]. Алгебраизация тригонометрии, начатая Франсуа Виетом, была завершена Леонардом Эйлером в XVIII веке, после чего алгоритмы решения треугольников приобрели современный вид.

См. также[править | править код]

• Признаки подобия треугольников
• Площадь треугольника
• Сферическая тригонометрия
• Сферический треугольник
• Триангуляция
• Тригонометрические тождества
• Тригонометрические функции
• Формулы Мольвейде

Примечания[править | править код]

Литература[править | править код]

Теория и алгоритмы

• Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. Геометрия: 7—9 классы. Учебник для общеобразовательных учреждений. — 19-е изд. — М.: Просвещение, 2009. — 384 с. — ISBN 978-5-09-021136-9.
• Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
• Гельфанд И. М., Львовский С. М., Тоом А. Л. Тригонометрия, учебник для 10 класса. — М.: МЦНМО, 2002. — ISBN 5-94057-050-X.
• Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
• Мензел Д. (ред.). Основные формулы физики. Глава 1. Основные математические формулы. — М.: Изд. иностранной литературы, 1957. — 658 с.
• Основные понятия сферической геометрии и тригонометрии // Энциклопедия элементарной математики (в 5 томах). — М.: Физматгиз, 1963. — Т. 4. — С. 518—557. — 568 с.
• Степанов Н. Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948.

История

• Глейзер Г. И. История математики в школе. VII-VIII классы. Пособие для учителей. — М.: Просвещение, 1982. — С. 76—95. — 240 с.
• Глейзер Г. И. История математики в школе. IX-X классы. Пособие для учителей. — М.: Просвещение, 1983. — 352 с.
• История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука.
  • История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
  • Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
  • Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
• Матвиевская Г. П. Очерки истории тригонометрии: Древняя Греция. Средневековый Восток. Позднее Средневековье. — Изд. 2-е. — М.: Либроком, 2012. — 160 с. — (Физико-математическое наследие: математика (история математики)). — ISBN 978-5-397-02777-9.
• Рыбников К. А. История математики в двух томах. — М.: Изд. МГУ, 1960. — Т. I.
• Сираждинов С. Х., Матвиевская Г. П. Абу Райхан Беруни и его математические труды. Пособие для учащихся. — М.: Просвещение, 1978. — 95 с. — (Люди науки).
• Цейтен Г. Г. История математики в древности и в средние века. — М.—Л.: ГТТИ, 1932. — 230 с.
• Цейтен Г. Г. История математики в XVI и XVII веках. — М.—Л.: ОНТИ, 1938. — 456 с.