Для нахождения элементов в произвольном треугольнике используется теорема синусов или теорема косинусов.
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов:
asinA=bsinB=csinC
(в решении задачи одновременно пишутся две части, они образуют пропорцию).
Теорема синусов используется для вычисления:
-
неизвестных сторон треугольника, если даны два угла и одна сторона;
-
неизвестных углов треугольника, если даны две стороны и один прилежащий угол.
Так как один из углов треугольника может быть тупым, значение синуса тупого угла находится по формуле приведения
sin180°−α=sinα
.
Наиболее часто используемые тупые углы:
sin120°=sin180°−60°=sin60°=32;sin150°=sin180°−30°=sin30°=12;sin135°=sin180°−45°=sin45°=22.
Радиус описанной окружности

, где (R) — радиус описанной окружности.
Выразив радиус, получаем
R=a2sinA
, или
R=b2sinB
, или
R=c2sinC
.
Для вычисления элементов прямоугольного треугольника достаточно (2) данных величин (две стороны или сторона и угол).
Для вычисления элементов произвольного треугольника необходимо хотя бы (3) данных величины.
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Также теорема исполняется для любой стороны треугольника:
Теорема косинусов используется для вычисления:
-
неизвестной стороны треугольника, если даны две стороны и угол между ними;
-
вычисления косинуса неизвестного угла треугольника, если даны все стороны треугольника.
Значение косинуса тупого угла находится по формуле приведения
cos180°−α=−cosα
.
Наиболее часто используемые тупые углы:
cos120°=cos180°−60°=−cos60°=−12;cos150°=cos180°−30°=−cos30°=−32;cos135°=cos180°−45°=−cos45°=−22.
Если необходимо найти приблизительное значение синуса или косинуса другого угла или вычислить угол по найденному синусу или косинусу, то используется таблица или калькулятор.
Источники:
Рис. 1-3. Треугольник, окружность, © ЯКласс.
Свойства тригонометрических функций
Отсюда вытекает много интересных свойств и тригонометрических формул.
Во-первых, надеюсь, все знают, что в прямоугольном треугольнике самая большая сторона – это гипотенуза.
Поэтому из определения синуса и косинуса ((sin(alpha)=frac{a}{c}; quad cos(alpha)=frac{b}{c})) следует, что они всегда меньше единицы, ведь мы катет (меньшую сторону) делим на гипотенузу (большую сторону треугольника). И как мы узнаем позже, синус и косинус всегда больше минус единицы. То есть синус и косинус могут принимать только значения из промежутка:
$$ sin(alpha) in [-1;1];$$
$$ cos(alpha) in [-1;1];$$
Для тангенса и котангенса никаких ограничений нет, они могут принимать абсолютно любые значения.
Теперь выведем несколько формул, без которых нам точно потом не обойтись. Например, можно обратить внимание, что тангенс выражается через деление синуса на косинус, просто расписав их по определению:
$$frac{sin(alpha)}{cos(alpha)}=frac{frac{a}{c}}{frac{b}{c}}=frac{a}{c}*frac{c}{b}=frac{a}{b};$$
А последняя формула есть ни что иное, как определение тангенса:
$$ tg(alpha)=frac{a}{b};$$
Значит
$$ tg(alpha)=frac{sin(alpha)}{cos(alpha)}.$$
Аналогичные рассуждения можно провести для котангенса:
$$frac{cos(alpha)}{sin(alpha)}=frac{frac{b}{c}}{frac{a}{c}}=frac{b}{c}*frac{c}{a}=frac{b}{a};$$
А котангенс по определению:
$$ctg(alpha)=frac{b}{a};$$
Значит
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)}.$$
Кроме этого, легко заметить, что функции тангенса и котангенса взаимно обратны:
$$tg(alpha)*ctg(alpha)=frac{a}{b}*frac{b}{a}=1.$$
А теперь мы подобрались к не самой очевидной тригонометрической формуле, но одной из самых главных во всей тригонометрии. Основное тригонометрическое тождество:
$$sin^2(alpha)+cos^2(alpha)=1. qquad (1)$$
Выводится оно тоже из определений синуса и косинуса с использованием теоремы Пифагора (гипотенуза в прямоугольном треугольнике равна сумме квадратов катетов (c^2=a^2+b^2;)):
$$sin^2(alpha)+cos^2(alpha)=left(frac{a}{c}right)^2+left(frac{b}{c}right)^2=left(frac{a^2}{c^2}right)+left(frac{b^2}{c^2}right)=frac{a^2+b^2}{c^2}=frac{c^2}{c^2}=1.$$
С основным тригонометрическим тождеством вы будете сталкиваться постоянно и в 9-м и в 10-м классах.
И разберем еще две важные формулы:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
Выводится она очень легко, опять же, используя определения тангенса и косинуса. Рекомендую потренироваться и сделать это самим.
$$1+left(frac{a}{b}right)^2=frac{1}{frac{b^2}{c^2}};$$
$$left(frac{b^2}{b^2}right)+left(frac{a^2}{b^2}right)=1*frac{c^2}{b^2};$$
$$frac{b^2+a^2}{b^2}=frac{c^2}{b^2};$$
Используем теорему Пифагора:
$$frac{c^2}{b^2}=frac{c^2}{b^2};$$
Получили верное равенство, значит формула верна.
И вторая аналогичная формула для котангенса:
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)};$$
Вывод один в один, сделайте сами.
Для удобства соберем все формулы вместе.
$$sin^2(alpha)+cos^2(alpha)=1. qquad(1)$$
$$ tg(alpha)=frac{sin(alpha)}{cos(alpha)}. qquad(2)$$
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)}. qquad(3)$$
$$tg(alpha)*ctg(alpha)=1.qquad(4)$$
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)}. qquad(5)$$
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)}. qquad(6)$$
Это далеко не все тригонометрические формулы, их гораздо больше. Но для начала и для 9-го класса этого вполне достаточно.
Зачем же они нужны? Оказывается, эти формулы помогают связать тригонометрические функции между собой. Посмотрите внимательно на первую формулу (1): зная, например, чему равен косинус, можно легко найти синус, и наоборот.
Пример 1
Пусть (cos(alpha) =frac{1}{2}), найдите (sin(alpha)=?)
Берем основное тригонометрическое тождество (формула (1)) и подставляем в него известный по условию задачи (cos(alpha)=frac{1}{2}:)
$$sin^2(alpha)+cos^2(alpha)=1;$$
$$sin^2(alpha)+left(frac{1}{2}right)^2=1;$$
А дальше просто решаем получившееся уравнение относительно синуса:
$$sin^2(alpha)=1-left(frac{1}{2}right)^2;$$
$$sin^2(alpha)=1-frac{1}{4};$$
Приводим к общему знаменателю:
$$sin^2(alpha)=frac{4}{4}-frac{1}{4};$$
$$sin^2(alpha)=frac{3}{4};$$
И здесь внимательно решаем квадратное уравнение:
$$sin(alpha)=pmfrac{sqrt{3}}{2};$$
Обратите внимание на (pm). Синус может быть как положительным, так и отрицательным, так как при подстановке и возведении в квадрат минус сгорает. Значит здесь получается два ответа.
Ответ:(sin(alpha)=pmfrac{sqrt{3}}{2}.)
Аналогично, зная хотя бы одну тригонометрическую функцию, можно найти все остальные, используя тригонометрические формулы. Рассмотрим еще пример:
Пример 2
Пусть (sin(alpha) =frac{1}{3}), найдите (ctg(alpha)=?)
Смотрим на наш список формул и находим такую, в которой есть и синус и котангенс – это формула (6):
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)}.$$
Подставляем известный из условия синус (sin(alpha) =frac{1}{3}):
$$1+сtg^2(alpha)=frac{1}{left(frac{1}{3}right)^2}.$$
Перевернем правую часть:
$$1+сtg^2(alpha)=left(frac{3}{1}right)^2.$$
$$1+сtg^2(alpha)=9.$$
Теперь решим уравнение и найдем котангенс:
$$сtg^2(alpha)=8.$$
$$сtg(alpha)=pmsqrt{8}=pmsqrt{4}*sqrt{2}=pm2sqrt{2}.$$
Ответ:(сtg(alpha)=pm2sqrt{2}).
Выглядит пугающе, но учить вам это НЕ НУЖНО! В некоторых школах есть изверги, которые заставляют учить такую таблицу, но в этом совершенно нет необходимости. В дальнейшем мы научимся сами выводить все значения тригонометрических функций только из маленькой таблицы.
Обратите внимание, что синус некоторого угла в треугольнике всегда положителен, неважно, тупой или острый угол. А вот косинус, тангенс и котангенс в треугольнике положительны только от острых углов и отрицательны от тупых.
Тут может возникнуть вопрос, как может существовать синус, косинус, тангенс или котангенс от тупого угла, большего чем (90^o), если мы давали определение всех тригонометрических функций через прямоугольный треугольник, в котором нет углов больших (90^o). Ну что ж, да тригонометрические функции существуют для любых углов и острых, и тупых, но для самого начала тригонометрии определения через прямоугольный треугольник нам более чем достаточно. Просто запомните выводы, которые мы сделали в предыдущем абзаце.
Рассмотрим пример на тригонометрию по типу схожий с заданиями ОГЭ. Обычно задачи сводятся просто к нахождению тригонометрической функции некоторого угла, нарисованного на рисунке:
Пример 2
По рисунку определить значение (sin(alpha)=?)
По определению синус в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе. Первым делом достроим наш синий угол (angle{ABC}) до прямоугольного треугольника, для этого опустим из точки (A) высоту (AH) к (BC). Получили прямоугольный треугольник (AHB). Теперь можем воспользоваться определением синуса:
$$sin(alpha)=frac{AH}{AB};$$
По клеточкам на рисунке найдем длину отрезка (AH=15). А гипотенузу (AB) найти по клеточкам не выйдет, так как она идет по диагонали. Но мы можем найти опять по клеточкам второй катет в прямоугольном треугольнике (BH=12) и применить теорему Пифагора:
$$AB^2=AH^2+BH^2;$$
$$AB^2=15^2+12^2=225+144=369;$$
$$AB=sqrt{369}=3sqrt{41};$$
Подставим в формулу для синуса и найдем его:
$$sin(alpha)=frac{AH}{AB}=frac{15}{3sqrt{41}};$$
Ответ: (sin(alpha)= frac{15}{3sqrt{41}}.)
Разберем еще примеры посложнее на нахождение тригонометрических функций друг через друга. Некоторые даже будут из реального ЕГЭ:
Пример 3
Пусть (tg(alpha)=sqrt{3}), найти (cos(alpha)=?), если известно, что (alpha<90^o).
Задание из ЕГЭ по профильной математике.
Условие аналогично условию в примерах №1 и 2, но появилось еще какое-то ограничение на угол (alpha), пока не будем обращать на него внимания, и решаем как обычно. Воспользуемся формулой (5), в ней есть и косинус, и тангенс, как раз одна из функций нам дана, а другую надо найти:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
$$1+(sqrt{3})^2=frac{1}{cos^2(alpha)};$$
$$1+3=frac{1}{cos^2(alpha)};$$
$$4=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{4};$$
$$cos(alpha)=pmfrac{1}{2}.$$
У нас опять получилось два ответа из-за квадрата. В условии сказано, что задание из первой части ЕГЭ, а значит два ответа быть не может. Для этого нам и дано, что (alpha<90^o). Это означает, что угол (alpha) острый, а значит косинус у острого угла обязательно должен быть положительный.
Ответ: (cos(alpha)=frac{1}{2}.)
Пример 4
Пусть (tg(alpha) =-2), найти (sin(alpha)=?), при (90^o<alpha<180^o).
Опять обратимся к нашим формулам (1-6) и пытаемся найти такую, в которой есть и синус и тангенс. И тут оказывается, что такой формулы нет. Но нам никто не запрещает, зная тангенс и используя формулу (5), найти косинус:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
$$1+(-2)^2=frac{1}{cos^2(alpha)};$$
$$5=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{5};$$
$$cos^2(alpha)=pmsqrt{frac{1}{5}};$$
Так как согласно условию (alpha>90^o), то значение косинуса должно быть отрицательным:
$$cos(alpha)=-sqrt{frac{1}{5}};$$
А потом, уже зная косинус, по основному тригонометрическому тождеству (1) можно найти требуемый в задаче синус:
$$sin^2(alpha)+cos^2(alpha)=1;$$
$$sin^2(alpha)+left(-sqrt{frac{1}{5}}right)^2=1;$$
$$sin^2(alpha)+frac{1}{5}=1;$$
$$sin^2(alpha)=-frac{1}{5}+1;$$
$$sin^2(alpha)=frac{4}{5};$$
$$sin(alpha)=pmsqrt{frac{4}{5}};$$
Синус у нас положительный и при острых ((alpha<90^o)) и при тупых углах ( (90<alpha<180) ):
$$sin(alpha)=sqrt{frac{4}{5}};$$
Ответ: (sin(alpha)=sqrt{frac{4}{5}}.)
Итак, зная значение хотя бы одной из четырех тригонометрических функций, при помощи формул (1-6) можно найти три оставшихся, именно для этого формулы и нужны.
Зная угол (angle{A}=60^o), мы знаем все тригонометрические функции от этого угла. Смотрите в таблицу (1):
$$sin(60^o)=frac{sqrt{3}}{2};$$
$$cos(60^o)=frac{1}{2};$$
$$tg(60^o)=sqrt{3};$$
$$ctg(60^o)=frac{1}{sqrt{3}};$$
С другой стороны, можно расписать функции по определению через отношение сторон в прямоугольном треугольнике:
$$sin(angle{A})=frac{BC}{AB};$$
$$cos(angle{A})=frac{AC}{AB};$$
$$tg(angle{A})=frac{BC}{AC};$$
$$ctg(angle{A})=frac{AC}{BC};$$
Не пугайтесь, все нам не понадобится. Воспользуемся пока формулами:
$$cos(60^o)=frac{1}{2};$$
$$cos(angle{A}=60^o)=frac{AC}{AB};$$
Нам известны косинус (angle{A}) и сторона (AC), а значит, мы можем найти гипотенузу (AB):
$$frac{1}{2}=frac{5}{AB};$$
$$AB=frac{5}{frac{1}{2}}=5*frac{2}{1}=10;$$
Нашли гипотенузу, теперь найдем последнюю сторону (BC). Для этого нам нужна любая формула с (BC), например:
$$sin(angle{A})=frac{BC}{AB};$$
Синус знаем, (AB) только что нашли – выражаем (BC):
$$BC=AB*sin(60^o)=10*frac{sqrt{3}}{2}=5*sqrt{3}.$$
Ответ: (AB=10;) (BC=5*sqrt{3}.)
Подведем итоги. Зная любую сторону в прямоугольном треугольнике и хотя бы один из острых углов, можно найти все остальные стороны при помощи тригонометрии.
Рассмотрим задачу посложнее.
Пример 6
Дан прямоугольный треугольник (bigtriangleup{ABC}), в котором угол (angle{C}=90^o), угол (tg(angle{A})=frac{1}{5}), сторона (AB=13). В треугольнике из прямого угла (angle{C}) проведена высота (CH). Найти (AH).
Первым делом обратите внимание на один очень важный факт. Если провести высоту в прямоугольном треугольнике из прямого угла, то она поделит треугольник еще на два прямоугольных. В нашем случае (bigtriangleup{ACH}) и (bigtriangleup{CHB}) тоже будут прямоугольными. А значит в них выполняются все соотношения для тригонометрических функций.
Например, в (bigtriangleup{ACH}) для угла (angle{A}) противолежащим катетом будет (CH), а прилежащим – сторона (AH), гипотенуза будет соответственно (AC). А значит можно записать формулы, следующие из определения тригонометрических функций:
$$sin(angle{A})=frac{CH}{AC};$$
$$cos(angle{A})=frac{AH}{AC};$$
$$tg(angle{A})=frac{CH}{AH};$$
$$ctg(angle{A})=frac{AH}{CH};$$
Аналогичные соотношения можно записать и для (bigtriangleup{CHB}) и (bigtriangleup{ABC}). Не буду нагромождать, запишите эти соотношения сами в качестве тренировки.
Следующий важный момент, на который следует обратить внимание – это углы в получившихся треугольниках. Обозначим угол (angle{CAB}=alpha). Тогда, так как (angle{CHA}=90^o), можно выразить угол:
$$angle{ACH}=180-angle{CAB}-angle{CHA}=180-alpha-90=90-alpha;$$
Напомню, что треугольник (bigtriangleup{ABC}) прямоугольный с прямым углом (angle{ACB}=90^o).
Значит
$$angle{HCB}=angle{ACB}-angle{ACH}=90-(90-alpha)=alpha=angle{CAB};$$
Важный факт: (angle{HCB}=angle{CAB})! А равенство этих углов само собой означает и равенство всех тригонометрических функций. То есть, например, (sin(angle{HCB})=sin(angle{ACB})). Точно так же у них равны и косинусы, и тангенсы, и даже котангенсы!
Аналогичные рассуждения можно провести для углов (angle{ACH}=angle{CBA}).
Запомните это!
А теперь приступим непосредственно к решению задачи. Нам известна гипотенуза (AB) и (tg(alpha)). По определению тангенса в (bigtriangleup{ABC}):
$$tg(angle{A})=frac{CB}{AC};$$
Либо из (bigtriangleup{ACH}):
$$tg(angle{A})=frac{CH}{AH};$$
В этих формулах есть проблема: нет известной нам стороны, гипотенузы (AB). А значит, у нас две неизвестные, и решить мы не можем.
Но зная тангенс, мы легко можем найти косинус по формуле:
$$1+tg(alpha)^2=frac{1}{cos^2(alpha)};$$
$$1+left(frac{1}{5}right)^2=frac{1}{cos^2(alpha)};$$
$$1+frac{1}{25}=frac{1}{cos^2(alpha)};$$
$$frac{26}{25}=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{frac{26}{25}}=1*frac{25}{26}=frac{25}{26};$$
$$cos(alpha)=pmsqrt{frac{25}{26}}=pmfrac{5}{sqrt{26}};$$
Так как (anglealpha) это острый угол из прямоугольного треугольника, то его косинус точно будет положительным:
$$cos(alpha)=frac{5}{sqrt{26}}.$$
Не самый приятный косинус, но что делать, будем решать так, как есть.
С другой стороны, из (bigtriangleup{ABC}):
$$cos(alpha)=frac{AC}{AB};$$
Подставим известное (AB):
$$frac{5}{sqrt{26}}=frac{AC}{13};$$
$$AC=13*frac{5}{sqrt{26}}=frac{13*5}{sqrt{26}};$$
Либо косинус еще можно расписать в (bigtriangleup{ACH}):
$$cos(alpha)=frac{AH}{AC}=frac{5}{sqrt{26}};$$
Подставим найденное (AC):
$$frac{AH}{frac{13*5}{sqrt{26}}}=frac{5}{sqrt{26}};$$
$$AH=frac{5}{sqrt{26}}*frac{13*5}{sqrt{26}}=frac{5*13*5}{26}=frac{25}{2}=12,5.$$
Ответ: (AH=12,5.)
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂

Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .
Угол A обозначается соответствующей греческой буквой .

Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла
, называется противолежащим (по отношению к углу
). Другой катет
, который лежит на одной из сторон угла
, называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
sin A
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
cos A
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
tg A
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
tg A
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
ctg A
Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

| sin |
sin |
|
| cos |
1+tg |
cos |
| tg |
1+ctg |
sin |
| ctg |
tg |
Давайте докажем некоторые из них.
- Сумма углов любого треугольника равна
. Значит, сумма двух острых углов прямоугольного треугольника равнa
.
- С одной стороны,
как отношение противолежащего катета к гипотенузе. С другой стороны,
, поскольку для угла
катет а будет прилежащим. Получаем, что
. Иными словами,
.
- Возьмем теорему Пифагора:
. Поделим обе части на
получаем
то есть
Мы получили основное тригонометрическое тождество. - Поделив обе части основного тригонометрического тождества на
, получим:
Это значит, что если нам дан тангенс острого угла
, то мы сразу можем найти его косинус. Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?

С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до
.
| 0 | |||||
| sin |
0 | ||||
| cos |
0 | ||||
| tg |
0 | − | |||
| ctg |
− | 0 |
Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Докажем теорему:
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и
и равными острыми углами А и

Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому
Из этих равенств следует, что т. е. sin А = sin
Аналогично, т. е. cos А = cos
и
т. е. tg A = tg
Это значит, что синус, косинус и тангенс зависят только от величины угла.
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
Задача 1. В треугольнике ABC угол C равен , sin A = 0,1. Найдите cos B.
Задача решается за четыре секунды.
Поскольку , sin A = cos B = 0,1.
Задача 2. В треугольнике угол
равен
,
,
.
Найдите .

Решение:
Отсюда
Найдем AC по теореме Пифагора.
Ответ: 4,8.
Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.
Решение:

Для угла А противолежащий катет – это ВС,
АВ является гипотенузой треугольника, лежит против Значит, sin A
Катет, прилежащий к – это катет АС, следовательно, cos А
Длину катета АС найдем по теореме Пифагора:
Тогда
cos А
tg A
Ответ: 0,92; 0,42.
Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.
Задача 4. В треугольнике АВС угол С равен AC = 2, sin A=
Найдите BC.
Решение:

AC = b = 2, BC = a, AB = c.
Так как sin A
По теореме Пифагора получим
Ответ: 0,5.
Задача 5. В треугольнике АВС угол С равен
tg A =
Найдите AB.

Решение:
AC = b = 4, tg A
Ответ: 7.
Задача 6.
В треугольнике АВС угол С равен CH – высота, AB = 13, tg A =
Найдите AH.

Решение:
AВ = с = 13, tg A = тогда b = 5a.
По теореме Пифагора ABC:
тогда
(по двум углам), следовательно
откуда
Ответ: 12,5.
Задача 7. В треугольнике АВС угол С равен
CH – высота, BC = 3, sin A =
Найдите AH.

Решение:
Так как sin A = тогда
c = АВ = 18.
sin A = = cos B =
Рассмотрим BHC:
=
получим
тогда BH = = 0,5,
AH = AB – BH = 18 – 0,5 = 17,5.
Ответ: 17,5.
Задача 8. В треугольнике АВС угол С равен 90 CH — высота, BC = 3, cos A =
Найдите АH.

Решение:
Так как для АВС:
A =
sin В =
а для ВНС: sin В =
=
, откуда СН =
По теореме Пифагора найдем ВН:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для АВС получим:
тогда
Ответ: 17,5.
Задача 9. В треугольнике АВС угол С равен 90 CH — высота, СН = 24 и BН = 7. Найдите sin A.

Решение:
По определению sin A= =
=
Рассмотрим BHC :
ВС найдем по теореме Пифагора:
ВС=
тогда а значит и sin A =
= 0,28.
Ответ: 0,28.
Задача 10. В треугольнике АВС угол С равен 90 CH — высота, СН = 8 и BН = 4. Найдите tg A.

Решение:
По определению sin A = =
=
cos A =
=
=
тогда tg A = который найдем из
BHC:
Ответ: 0,5.
Задача 11. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, tg A =
Найдите АН.

Решение:
По определению tg A=
Для BHC:
, значит
СН =
Для АHC: tg A=
то
AH =
Ответ: 27.
Задача 12. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, sin A =
Найдите АВ.
Решение:

Так как cos В = = sin A =
Из СВН имеем cos В =
=
тогда ВС =
В АВС имеем sinA =
=
тогда AВ =
Ответ: 27.
Задача 13. В треугольнике АВС угол С равен 90 из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.
Решение:

Найдем НВ по теореме Пифагора из ВСН:
sin В = =
Для АВС: cos A =
получили cos A = 0,6.
Найдем АС и АВ несколькими способами.
1-й способ.
Так как cos A = то пусть АС = 3х, АВ = 5х,
тогда по теореме Пифагора получим
х = 5 ( так как х0). Значит,
2-й способ.
(по двум углам), значит
или
k = тогда
АС =
;
АВ =
3-й способ.
(высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда
АН = 144:16 = 9.
АВ = АН + НВ = 9 + 16 = 25.
По теореме Пифагора найдем АС:
=
Ответ: cos A = 0,6; АС = 15, АВ = 25.
Задача 14.
Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.
Найдите АВ и cos А.
Решение:

Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:
ВС = =
cos C =
Для АВС: sin А =
= cos C =
Для АНВ: sin А =
=
то
=
АВ =
Из основного тригонометрического тождества найдем
cos A =
Ответ: АВ = 40, cos A = 0,8.
Задача 15.
Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А =
Найдите площадь треугольника.
Решение:

В прямоугольном АСЕ sin А =
значит
= 14.
Второй катет найдем, используя теорему Пифагора:
Площадь прямоугольного треугольника равна S =
поэтому
Ответ: 336.
Задача 16.
В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.
Найдите sin Результат округлите до сотых.
Решение:

A-общий,
),
значит sin
Найдем АС по теореме Пифагора из САВ:
Тогда sin
Ответ: 0,38.
Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = Найдите высоту СН.
Решение:

Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда
высота СН является медианой, то есть АН = НВ =
Поскольку АСН — прямоугольный,
cos A =
то есть
АС =
По теореме Пифагора тогда
Ответ: 15.
Задача 18. В треугольнике АВС угол С равен 90 sin A =
AC = 10
Найдите АВ.
Решение:

1-й способ.
Поскольку sin A =
то можно обозначить
ВС = 11х, АВ = 14х.
По теореме Пифагора
(14х- 11х)(14х + 11х) = 3 100;
учитывая, что длина стороны положительна, х = 2,
следовательно, АВ = 14 2 = 28.
2-й способ.
Воспользуемся основным тригонометрическим тождеством
cos A =
По определению cos A = значит
Так как АС=10 то
откуда АВ =
= 28.
Ответ: 28.
Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 и 4.
Решение:

Пусть ВАО =
Диагонали ромба делят его углы пополам, значит, =
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = а катет ВО =
Поэтому tg откуда
Ответ:
Часто в задачах встречаются треугольники с углами и
или с углами
и
. Основные соотношения для них запоминайте наизусть!

Для треугольника с углами и
катет, лежащий напротив угла в
, равен половине гипотенузы.
Треугольник с углами и
— равнобедренный. В нем гипотенуза в
раз больше катета.
Задача 20.
В треугольнике АВС угол С равен 90 угол А равен 30
АВ = 2
Найдите высоту CH.
Решение:

Рассмотрим АВС:
По свойству катета, лежащего против угла имеем ВС =
АВ =
В BHC:
то
следовательно, ВН =
BC =
По теореме Пифагора найдем НС:
Ответ: 1,5.
Задача 21.
В треугольнике АВС угол С равен 90 CH — высота, АВ = 2,
Найдите АH.
Решение:

Из АВС найдем ВС =
АВ = 1 (по свойству катета, лежащего против угла 30
),
то
Из ВСН:
то
следовательно,
ВН = ВС =
АН = АВ — НВ = 2 – = 1,5.
Ответ: 1,5.
Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.

Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Если вам понравился разбор данной темы – записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Синусом угла в прямоугольном треугольнике называют отношение противолежащего катета к гипотенузе.
Катетами являются стороны, которые образуют прямой угол в треугольнике, соответственно, гипотенузой является третья (самая длинная) сторона.
Для простоты запоминания можно дать такое определение: синус угла — это отношение дальнего от рассматриваемого угла катета к гипотенузе.
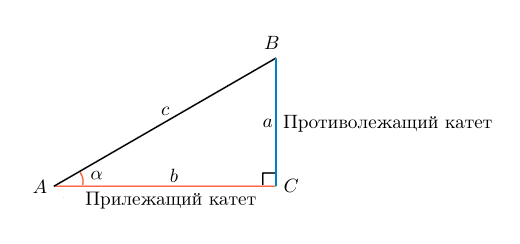
В случае с рисунком, описанным выше: sinα=acsinalpha=frac{a}{c}
В треугольнике, один из углов которого равен 90 градусам, известен катет при угле αalpha и равен он 3 см3text{ см}. Также дано произведение длин катетов и равно 12 см212text{ см}^2. Найдите синус угла αalpha.
Решение
Сначала нужно найти длину неизвестного нам катета. Для этого воспользуемся данным нам произведением. Обозначим неизвестный катет за xx. Тогда, по условию задачи:
3⋅x=123cdot x=12
x=123=4x=frac{12}{3}=4
a=x=4a=x=4
По теореме Пифагора найдем гипотенузу:
a2+b2=c2a^2+b^2=c^2
42+32=c24^2+3^2=c^2
25=c225=c^2
c=5c=5
sinα=ac=45=0.8sinalpha=frac{a}{c}=frac{4}{5}=0.8
Ответ
0.80.8
Вычислите синус 45 градусов.
Решение
Для этого воспользуемся тригонометрической таблицей углов. Находим, что:
sin45∘=π4=0.785sin 45^circ=frac{pi}{4}=0.785
Ответ
0.7850.785
Если в задаче известен косинус угла и нужно найти его синус, то наличие известных длин катетов и гипотенузы не обязательны. Достаточно просто воспользоваться основным тригонометрическим тождеством, которое имеет следующий вид:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
αalpha — любой угол.
Квадрат косинуса угла в треугольнике равен 0.8. Найдите синус данного угла.
Решение
Воспользуемся основным тригонометрическим тождеством:
sin2α+cos2α=1sin^2alpha+cos^2alpha=1
sin2α+0.8=1sin^2alpha+0.8=1
sin2α=0.2sin^2alpha=0.2
sinα=0.2sinalpha=sqrt{0.2}
sinα≈0.447sinalphaapprox0.447
Ответ
0.4470.447
Испытываете проблемы с вычислением синуса? Оформите задачу по математике на заказ у наших экспертов!
Тест по теме «Вычисление синуса»
Содержание:
Пусть в прямоугольном треугольнике гипотенуза равна с, один из острых углов равен 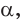
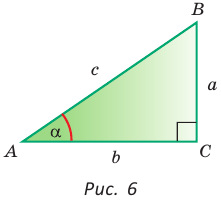
Определения синуса, косинуса, тангенса и котангенса острого угла
Определение. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:
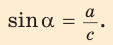
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
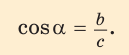
Определение. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:
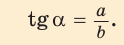
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему:
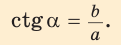
Пример:
Угол К в 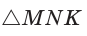 равен 90° (рис. 7).
равен 90° (рис. 7).
Тогда:
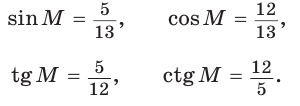
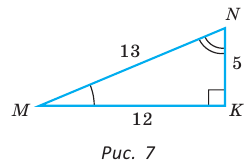
Для угла N катет МК — противолежащий, а катет NK — прилежащий (см. рис. 7, с. 11). Поэтому согласно определениям получаем:
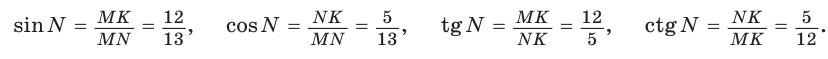
Можно заметить, что синус острого угла а прямоугольного треугольника и косинус другого острого угла этого треугольника, содержащего 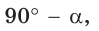 равны, т. е.
равны, т. е. 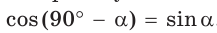 . Так же
. Так же 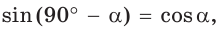
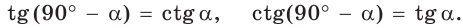 Например,
Например, 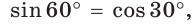
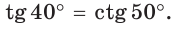
А теперь выполните Тест 1 и Тест 2.
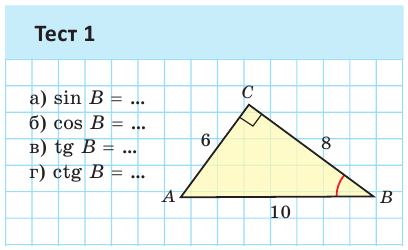
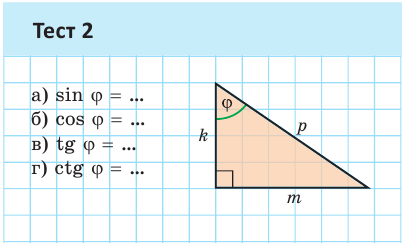
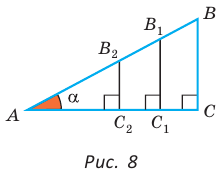
Значение синуса острого угла, а также косинуса, тангенса и котангенса зависит только от величины угла и не зависит от размеров и расположения прямоугольного треугольника с указанным острым углом.
Это следует из того, что прямоугольные треугольники с равным острым углом подобны, а у подобных треугольников соответствующие стороны пропорциональны. Так, в 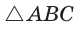 (рис. 8)
(рис. 8) 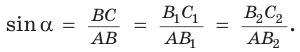
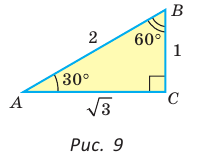
Значения синуса, косинуса, тангенса и котангенса углов 30°, 45°, 60°
Рассмотрим прямоугольный треугольник АВС, у которого 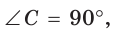
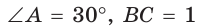 (рис. 9). Так как катет, лежащий против угла в 30°, равен половине гипотенузы, то АВ = 2. По теореме Пифагора
(рис. 9). Так как катет, лежащий против угла в 30°, равен половине гипотенузы, то АВ = 2. По теореме Пифагора
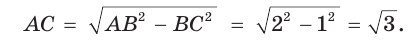 Тогда:
Тогда:
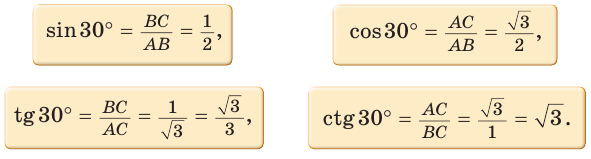
Так как 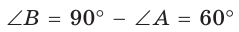 (см. рис. 9), то
(см. рис. 9), то

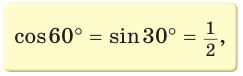
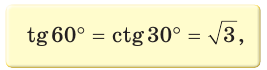
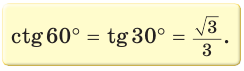
Рассмотрим равнобедренный прямоугольный треугольник АВС, у которого 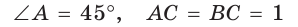 (рис. 10). По теореме Пифагора
(рис. 10). По теореме Пифагора
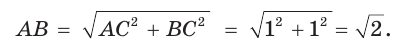
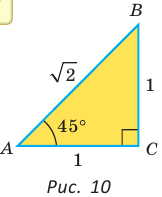
Тогда:
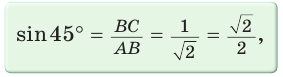
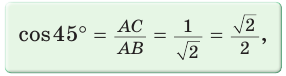
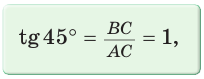
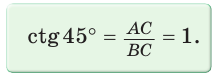
Составим таблицу значений синусов, косинусов, тангенсов и котангенсов для углов 30°, 45° и 60°.
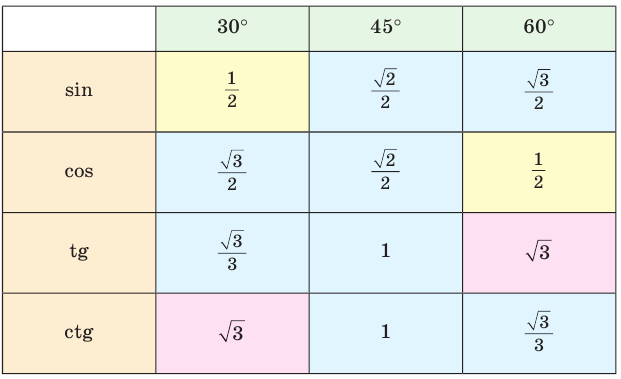
Нахождение значений тригонометрических функций
Значения синуса, косинуса, тангенса и котангенса данного угла можно приближенно находить при помощи специальных тригонометрических таблиц* либо калькулятора.
Например, с помощью калькулятора, компьютера или мобильного телефона (смартфона) находим: sin45° = 0,707106… . Приближенное значение тригонометрических функций при решении задач будем брать с округлением до четырех знаков после запятой: sin45° = 0,7071.
Итак, точное значение sin 45° равно 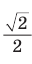 . а приближенное — 0,7071.
. а приближенное — 0,7071.
Таблицы и калькулятор также позволяют находить величину острого угла по значению синуса, косинуса или тангенса. Например, найдем острый угол, синус которого равен 0,4175. Выбрав на компьютере вид калькулятора «инженерный», далее «градусы», нужно ввести последовательно  . На экране появится ответ: 24,676… . Округлим его до десятых долей градуса и получим 24,7°. Учитывая, что 1° содержит 60 угловых минут, получим: 0,7° = 0,7 • 60′ = 42′. Искомый угол, синус которого 0,4175, приближенно равен 24°42′.
. На экране появится ответ: 24,676… . Округлим его до десятых долей градуса и получим 24,7°. Учитывая, что 1° содержит 60 угловых минут, получим: 0,7° = 0,7 • 60′ = 42′. Искомый угол, синус которого 0,4175, приближенно равен 24°42′.
А теперь выполните Тест 3.

Тригонометрические функции острого угла
Синус, косинус, тангенс и котангенс являются функциями угла, так как каждому острому углу 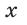 соответствует единственное значение синуса, косинуса, тангенса и котангенса. Они называются тригонометрическими функциями и записываются так:
соответствует единственное значение синуса, косинуса, тангенса и котангенса. Они называются тригонометрическими функциями и записываются так: 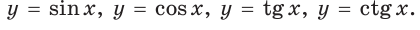
Поскольку в прямоугольном треугольнике катет меньше гипотенузы, то для острого угла 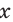 справедливо:
справедливо: 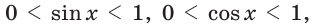 следовательно синус и косинус острого угла положительны и меньше 1.
следовательно синус и косинус острого угла положительны и меньше 1.
Тангенс и котангенс острого угла могут принимать любое положительное значение. Например, tg85° ~ 11,4.
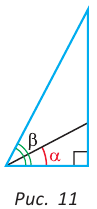
С увеличением острого угла синус и тангенс возрастают, а косинус и котангенс убывают (рис. 11), то есть если 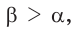 то
то
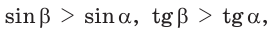 но
но 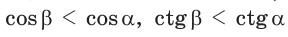 (cm. c. 28, задачу 2*). Это гарантирует, что синус (косинус, тангенс и котангенс) острого угла определяют этот угол однозначно.
(cm. c. 28, задачу 2*). Это гарантирует, что синус (косинус, тангенс и котангенс) острого угла определяют этот угол однозначно.
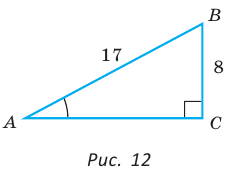
Пример №1
В прямоугольном треугольнике АВС, где 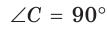 , катет ВС равен 8 см, гипотенуза АВ равна 17 см. Найти косинус угла А (рис. 12).
, катет ВС равен 8 см, гипотенуза АВ равна 17 см. Найти косинус угла А (рис. 12).
Решение:
По теореме Пифагора найдем катет 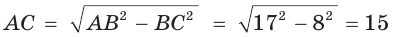 (см). Косинус острого угла прямоугольного треугольника равен от ношению прилежащего катета к гипотенузе. Тогда
(см). Косинус острого угла прямоугольного треугольника равен от ношению прилежащего катета к гипотенузе. Тогда 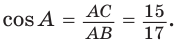
Ответ: 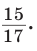
Пример №2
Гипотенуза АВ прямоугольного треугольника АВС равна 20 см, 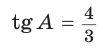 (рис. 13). Найти площадь треугольника.
(рис. 13). Найти площадь треугольника.
Решение:
Так как 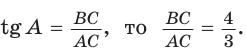 Обозначим
Обозначим 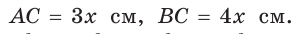 По теореме Пифагора
По теореме Пифагора 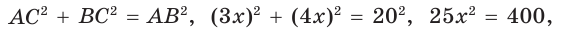
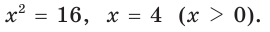 Тогда
Тогда 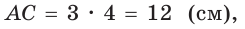 ВС = 4 • 4 = 16(см),
ВС = 4 • 4 = 16(см), 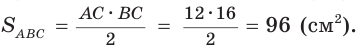
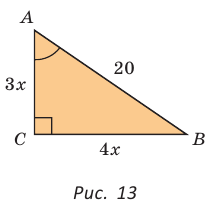
Ответ: 96 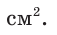
Пример №3
При помощи циркуля и линейки построить угол, синус которого равен 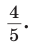
Решение:
Идея решения. Построим прямоугольный треугольник с катетом, равным 4 единицы, и гипотенузой, равной 5 единиц. Синус угла, противолежащего указанному катету, будет равен 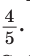
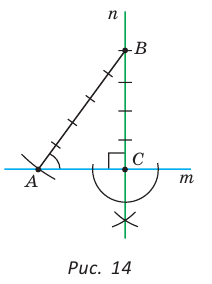
Построение. 1) Строим прямой угол С (рис. 14), для чего проводим произвольную прямую  отмечаем на ней точку С и строим прямую
отмечаем на ней точку С и строим прямую  проходящую через точку С перпендикулярно прямой
проходящую через точку С перпендикулярно прямой  (вспомните по рисунку алгоритм построения). 2) На прямой
(вспомните по рисунку алгоритм построения). 2) На прямой 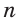 от точки С откладываем последовательно четыре равных отрезка. Получаем отрезок ВС, который содержит 4 единицы. 3) Строим окружность с центром в точке В радиусом, равным пяти единицам. В пересечении этой окружности и прямой
от точки С откладываем последовательно четыре равных отрезка. Получаем отрезок ВС, который содержит 4 единицы. 3) Строим окружность с центром в точке В радиусом, равным пяти единицам. В пересечении этой окружности и прямой 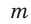 получаем точку А.
получаем точку А.
Угол ВАС — искомый.
Доказательство:
Из 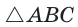 находим
находим 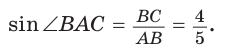
Алгоритм решения прямоугольного треугольника
Под решением прямоугольного треугольника понимают нахождение его неизвестных сторон и углов по некоторым элементам, определяющим этот треугольник. Рассмотрим три задачи:
- нахождение катета по гипотенузе и острому углу;
- нахождение катета по другому катету и острому углу;
- нахождение гипотенузы по катету и острому углу.
Пример №4
Гипотенуза прямоугольного треугольника равна 6, острый угол равен 32° (рис. 23). Найти катет, прилежащий к данному углу. Ответ округлить до 0,1.
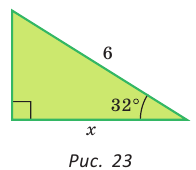
Решение:
Примем длину искомого катета за 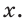


Ответ: 5,1.
Пример №5
Катет прямоугольного треугольника равен 2,5, а прилежащий к нему угол равен 68° (рис. 24). Найти другой катет. Ответ округлить до 0,1.
Решение:
Примем длину неизвестного катета за 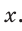
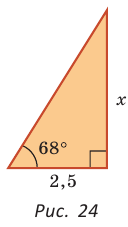
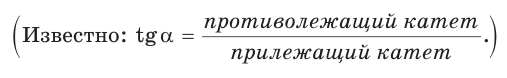
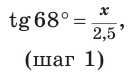
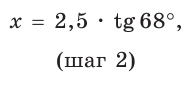

Ответ: 6,2.
Пример №6
Катет прямоугольного треугольника равен 4,2, противолежащий ему угол равен 29° (рис. 25). Найти гипотенузу треугольника. Ответ округлить до 0,1.
Решение:
Примем длину гипотенузы за 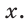
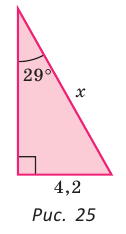
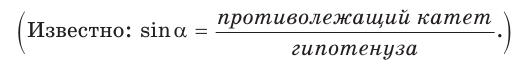
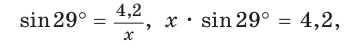
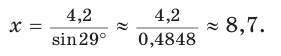
Ответ: 8,7.
Правила решения прямоугольного треугольника
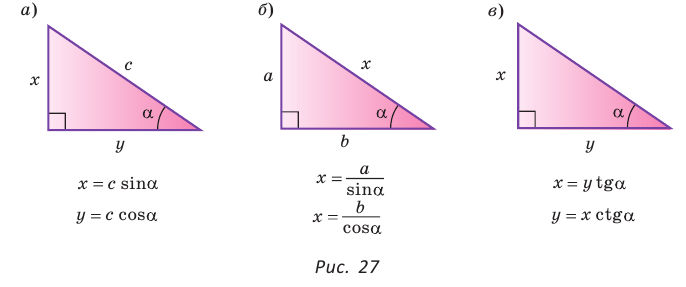
Преобразуем формулы синуса, косинуса, тангенса и котангенса и запишем результаты для треугольника на рисунке 26:
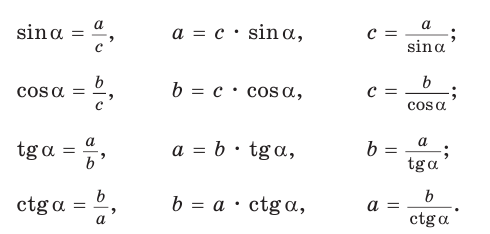
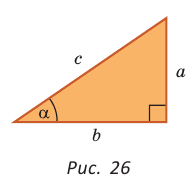
Удобно пользоваться следующими правилами:
- Катет равен гипотенузе, умноженной на синус противолежащего или на косинус прилежащего угла (рис. 27, а).
- Гипотенуза равна катету, деленному на синус противолежащего или на косинус прилежащего угла (рис. 27, б).
- Катет равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к первому катету угла (рис. 27, в).
Пример №7
В 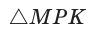 известно:
известно: 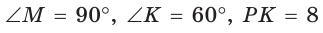 (рис. 28).
(рис. 28).
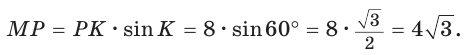
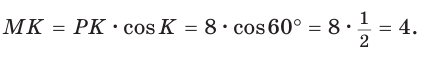
Полезно запомнить!
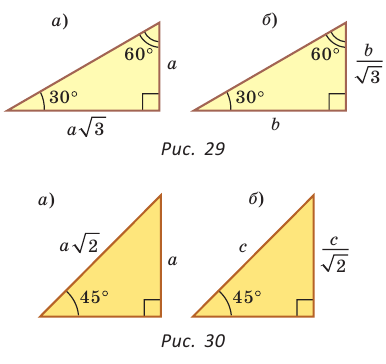
Если в прямоугольном треугольнике с углом 30° (или 60°) дан меньший катет а, то больший
катет 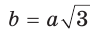 (рис. 29, а). А если дан больший катет
(рис. 29, а). А если дан больший катет 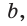 то меньший катет
то меньший катет 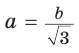 (рис. 29, б).
(рис. 29, б).
Если в прямоугольном треугольнике с углом 45° дан катет а,
то гипотенуза 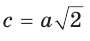 (рис. 30, а), а если дана гипотенуза с, то катет
(рис. 30, а), а если дана гипотенуза с, то катет 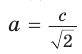 (рис. 30, б).
(рис. 30, б).
Пример №8
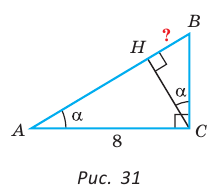
В прямоугольном треугольнике АВС известно: 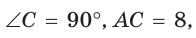
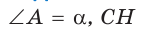 — высота, проведенная к гипотенузе (рис. 31). Найти проекцию НВ катета ВС на гипотенузу.
— высота, проведенная к гипотенузе (рис. 31). Найти проекцию НВ катета ВС на гипотенузу.
Решение:
Заметим, что 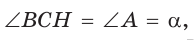 так как эти углы дополняют
так как эти углы дополняют 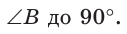 Из
Из 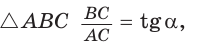
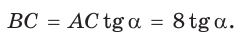 Из
Из 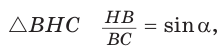
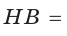
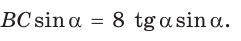
Ответ: 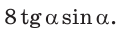
Пример №9
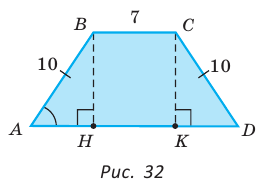
В равнобедренной трапеции ABCD меньшее основание ВС равно 7, боковая сторона АВ равна 10, sinA = 0,8. Найти площадь трапеции.
Решение:
Площадь трапеции находится по формуле 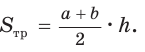 Найдем большее основание и высоту трапеции. Проведем в трапеции высоты ВН и СК (рис. 32). Так как НВСК — прямоугольник (все углы — прямые), то НК = ВС = 7. Из равенства прямоугольных треугольников АНВ и DKC (по катету и гипотенузе) АН = KD. Из прямоугольного треугольника АНВ находим:
Найдем большее основание и высоту трапеции. Проведем в трапеции высоты ВН и СК (рис. 32). Так как НВСК — прямоугольник (все углы — прямые), то НК = ВС = 7. Из равенства прямоугольных треугольников АНВ и DKC (по катету и гипотенузе) АН = KD. Из прямоугольного треугольника АНВ находим: 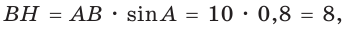 откуда АН = 6 (пифагорова тройка 6, 8, 10). Тогда
откуда АН = 6 (пифагорова тройка 6, 8, 10). Тогда 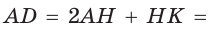
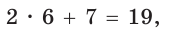
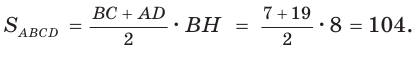
Ответ: 104.
Тригонометрические формулы
Используя формулы 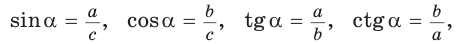 где
где 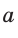 и
и 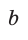 — катеты, с — гипотенуза прямоугольного треугольника, можно получить формулы, связывающие значения тригонометрических функций острого угла.
— катеты, с — гипотенуза прямоугольного треугольника, можно получить формулы, связывающие значения тригонометрических функций острого угла.
1. Основное тригонометрическое тождество
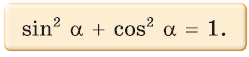
Доказательство:
По теореме Пифагора 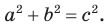
Тогда 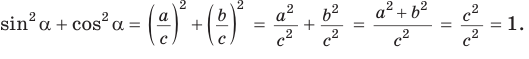
Следствие:
Так как синус и косинус острого угла а положительны, то
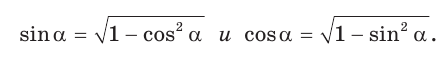
2. Выражение тангенса и котангенса через синус и косинус
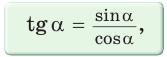
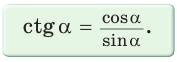
Доказательство:
a)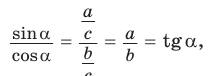 б)
б)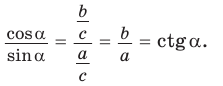
Следствие:
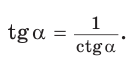
Проверим справедливость основного тригонометрического тождества.
Верно ли, например, что 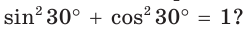 Да, это верно, так как
Да, это верно, так как 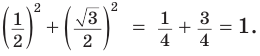
3. Основная задача
Дано: 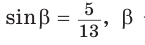 — острый угол.
— острый угол.
Найти: 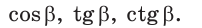
Решение:
Способ 1. Используем основное тригонометрическое тождество: 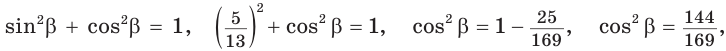
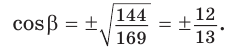 Так как косинус острого угла больше нуля, то
Так как косинус острого угла больше нуля, то 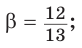 откуда
откуда 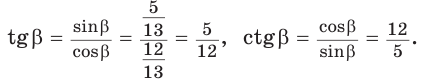
Способ 2. Изобразим прямоугольный треугольник с катетом 5 и гипотенузой 13 (рис. 41). Синус угла, противолежащего данному катету, равен 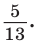 Поэтому этот угол равен
Поэтому этот угол равен 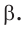 По теореме Пифагора другой катет равен
По теореме Пифагора другой катет равен 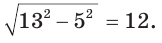 Тогда
Тогда 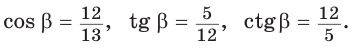
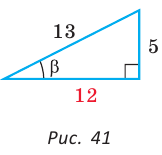
Способ 3. Пусть катет, противолежащий углу 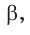 равен 5х, тогда гипотенуза равна
равен 5х, тогда гипотенуза равна 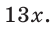 По теореме Пифагора прилежащий катет равен
По теореме Пифагора прилежащий катет равен 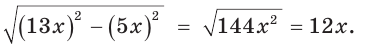 Отсюда
Отсюда 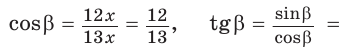
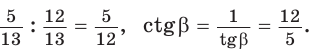
Ответ: 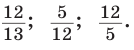
Пример №10
В параллелограмме ABCD (рис. 42) сторона ВС = 50 см, высота ВК = 30 см, 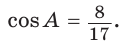 . Найти периметр параллелограмма.
. Найти периметр параллелограмма.
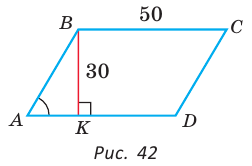
Решение:
Из треугольника АВК находим: 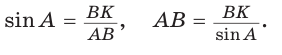 Из основного тригонометрического тождества следует:
Из основного тригонометрического тождества следует: 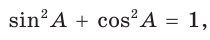
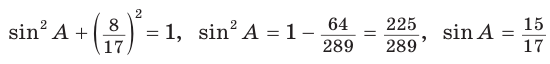 (так как угол А — острый, то sinA > 0). Тогда
(так как угол А — острый, то sinA > 0). Тогда 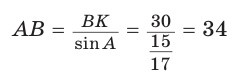 (см )
(см ) 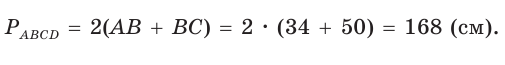
Ответ: 168 см.
Пример №11
Доказать, что при увеличении угла от 0° до 90°:
а) синус угла увеличивается от 0 до 1, а косинус — уменьшается от 1 до 0;
б) тангенс угла увеличивается от О до бесконечности.
Решение:
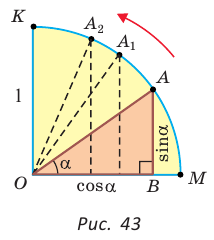
а) Рассмотрим прямоугольные треугольники с гипотенузой, равной 1. Для этого опишем радиусом ОМ, равным 1, четверть окружности — дугу МК (рис. 43). Пусть 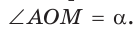 Опустим из точки А перпендикуляр АВ на ОМ. Тогда
Опустим из точки А перпендикуляр АВ на ОМ. Тогда 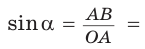
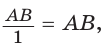
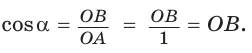 При повороте радиуса ОМ вокруг центра О против часовой стрелки, начиная от ОМ и заканчивая ОК, угол
При повороте радиуса ОМ вокруг центра О против часовой стрелки, начиная от ОМ и заканчивая ОК, угол 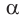 будет увеличиваться от 0° до 90° (образуя указанные на чертеже углы:
будет увеличиваться от 0° до 90° (образуя указанные на чертеже углы: 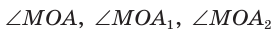 и т. д.). Величина катета АВ, противолежащего углу
и т. д.). Величина катета АВ, противолежащего углу 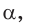 будет увеличиваться от 0 до 1. А величина катета ОВ, наоборот, будет уменьшаться от 1 до 0. Таким образом, при увеличении угла от 0° до 90° его синус увеличивается от 0 до 1, а косинус уменьшается от 1 до 0.
будет увеличиваться от 0 до 1. А величина катета ОВ, наоборот, будет уменьшаться от 1 до 0. Таким образом, при увеличении угла от 0° до 90° его синус увеличивается от 0 до 1, а косинус уменьшается от 1 до 0.
Из формулы 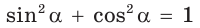 также следует (учитывая положительность синуса и косинуса острого угла), что с увеличением синуса от 0 до 1 косинус уменьшается от 1 до 0.
также следует (учитывая положительность синуса и косинуса острого угла), что с увеличением синуса от 0 до 1 косинус уменьшается от 1 до 0.
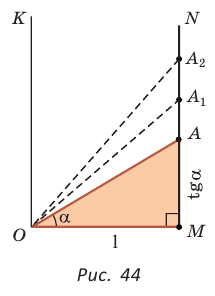
б) Для определения изменения тангенса угла удобно рассматривать треугольники, у которых прилежащий катет не изменяется и остается равным 1, а противолежащий катет изменяется. Рассмотрим прямоугольный треугольник АОМ, у которого отрезок ОМ = 1, 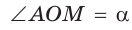 (рис. 44). По определению
(рис. 44). По определению 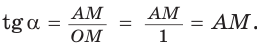 Угол
Угол 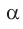 станем изменять, перемещая точку А по прямой MN, начиная от точки М и проходя через точки
станем изменять, перемещая точку А по прямой MN, начиная от точки М и проходя через точки 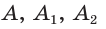 и т. д. При этом угол
и т. д. При этом угол 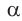 и его тангенс начнут возрастать. Таким образом, когда угол
и его тангенс начнут возрастать. Таким образом, когда угол 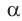 при движении точки А вверх будет стремиться к углу КОМ, равному 90°, то тангенс этого угла будет неограниченно возрастать.
при движении точки А вверх будет стремиться к углу КОМ, равному 90°, то тангенс этого угла будет неограниченно возрастать.
К такому же выводу можно прийти, рассматривая формулу 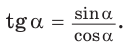 При увеличении угла
При увеличении угла 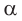 от 0° до 90° числитель дроби будет увеличиваться от 0 до 1, а знаменатель — уменьшаться от 1 до 0, значит, вся дробь будет увеличиваться от 0 до бесконечности. Таким образом, при увеличении угла от 0° до 90° его тангенс увеличивается от 0 до бесконечности.
от 0° до 90° числитель дроби будет увеличиваться от 0 до 1, а знаменатель — уменьшаться от 1 до 0, значит, вся дробь будет увеличиваться от 0 до бесконечности. Таким образом, при увеличении угла от 0° до 90° его тангенс увеличивается от 0 до бесконечности.
Пример №12
В основании прямоугольного параллелепипеда 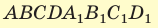 лежит квадрат, диагональ которого
лежит квадрат, диагональ которого 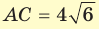 см. Диагональ
см. Диагональ 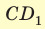 боковой грани составляет с ребром основания
боковой грани составляет с ребром основания 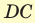 угол
угол  (рис. 46). Найдите объем параллелепипеда.
(рис. 46). Найдите объем параллелепипеда.
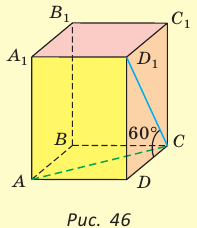
Решение:
Объем прямоугольного параллелепипеда находится по формуле 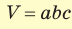 , где а, b и с — его измерения. Так как ABCD — квадрат, то
, где а, b и с — его измерения. Так как ABCD — квадрат, то 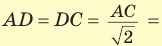
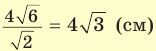 . Из прямоугольного треугольника
. Из прямоугольного треугольника 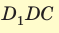 находим
находим 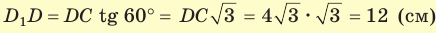 . Искомый объем
. Искомый объем 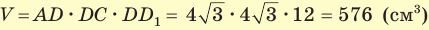 .
.
Ответ: 576 см3.
Синус, косинус, тангенс и котангенс тупого угла
1. Определение значений 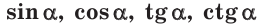 для любого угла а от 0° до 180°
для любого угла а от 0° до 180°
Ранее мы дали определения синуса, косинуса, тангенса и котангенса острого угла через отношение сторон прямоугольного треугольника. Сделаем теперь это для углов от 0° до 180°.
Рассмотрим полуокружность с центром в начале координат и радиусом, равным 1 (рис. 48). От положительной полуоси 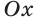 против часовой стрелки отложим острый угол
против часовой стрелки отложим острый угол 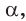 сторона которого пересекает полуокружность в точке
сторона которого пересекает полуокружность в точке 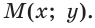 . Из прямоугольного треугольника OMN, где ОМ = 1, ON = х, MN = у, получаем:
. Из прямоугольного треугольника OMN, где ОМ = 1, ON = х, MN = у, получаем: 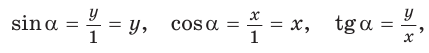
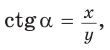 то есть синус, косинус,
то есть синус, косинус,
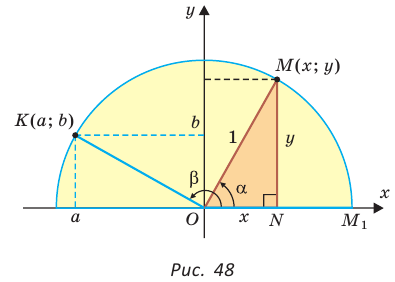
тангенс и котангенс острого угла а выражаются через координаты 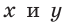 точки
точки 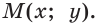 Точно так же определяются значения
Точно так же определяются значения 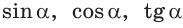 и
и 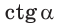 для любого угла а из промежутка
для любого угла а из промежутка 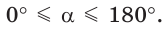 Таким образом, синусом угла а называется ордината
Таким образом, синусом угла а называется ордината 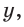 косинусом — абсцисса
косинусом — абсцисса 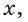 тангенсом — отношение ординаты к абсциссе
тангенсом — отношение ординаты к абсциссе 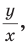 а котангенсом — отношение абсциссы к ординате
а котангенсом — отношение абсциссы к ординате 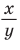 точки М единичной полуокружности.
точки М единичной полуокружности.
Например, для тупого 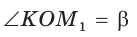 (рис. 48), где
(рис. 48), где 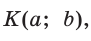 получим:
получим:
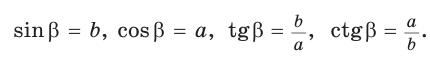
Для любого положения точки 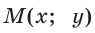 на единичной полуокружности верно равенство
на единичной полуокружности верно равенство 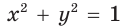 (докажите самостоятельно). Поэтому для углов
(докажите самостоятельно). Поэтому для углов 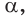 где
где  верно основное тригонометрическое тождество
верно основное тригонометрическое тождество 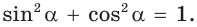
Также верны тождества: 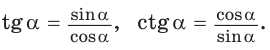
Нахождение синуса, косинуса, тангенса и котангенса тупых углов
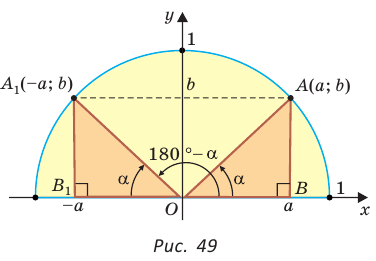
Пусть 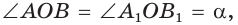 откуда
откуда 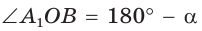 (рис. 49). Так как
(рис. 49). Так как 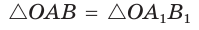 по гипотенузе и острому углу, то
по гипотенузе и острому углу, то 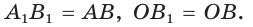 Точки
Точки 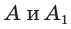 имеют координаты:
имеют координаты: 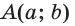 и
и 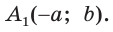 Тогда
Тогда 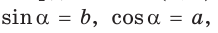
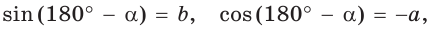 то есть для углов от 0° до 180° справедливы равенства:
то есть для углов от 0° до 180° справедливы равенства:
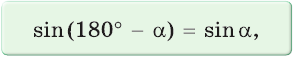
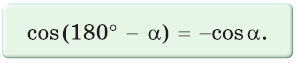
Можно пользоваться следующим правилом:
Синус тупого угла равен синусу смежного с ним острого угла.
Косинус тупого угла равен косинусу смежного с ним острого угла, взятому со знаком «минус».
Пример 1. 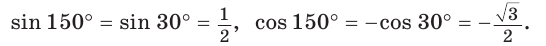
Разделив почленно равенство 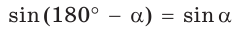 на равенство
на равенство 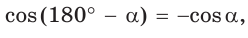 а затем наоборот, получим равенства:
а затем наоборот, получим равенства:
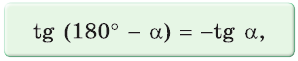
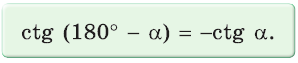
Можно пользоваться следующим правилом:
Тангенс (котангенс) тупого угла равен тангенсу (котангенсу) смежного с ним острого угла, взятому со знаком «минус».
Пример 2. 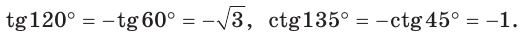
Указанные формулы и правила позволяют находить значения тригонометрических функций тупого угла через значения тригонометрических функций острого угла, который дополняет данный тупой угол до 180°: синусы углов, дополняющих друг друга до 180°, равны между собой, а косинусы, тангенсы и котангенсы — противоположны. Так как синус, косинус, тангенс и котангенс острого угла положительные, то синус тупого угла положительный, а косинус, тангенс и котангенс — отрицательные.
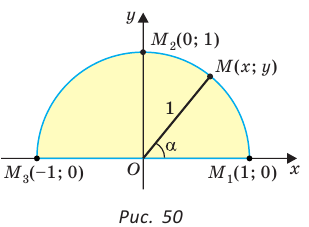
Значения тригонометрических функций для углов 0°, 90°, 180°
Если луч ОМ совпадет с лучом 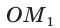 (рис. 50), то будем считать, что
(рис. 50), то будем считать, что 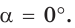 Тогда:
Тогда:
а) 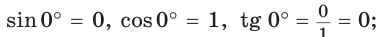 значение
значение 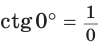 не определено, так как деление на нуль невозможно;
не определено, так как деление на нуль невозможно;
б) 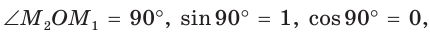
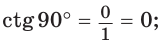 значение
значение 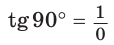 не определено, так как деление на нуль невозможно; в)
не определено, так как деление на нуль невозможно; в) 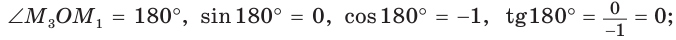 значение
значение 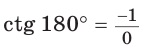 не определено, так как деление на нуль невозможно.
не определено, так как деление на нуль невозможно.
Поскольку проекции радиуса, равного 1, на оси координат меньше либо равны 1, то для углов 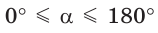 справедливы неравенства:
справедливы неравенства: 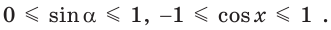
Пример №13
Найти 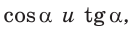 если
если 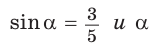 – тупой угол.
– тупой угол.
Решение:
Способ 1. Так как 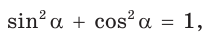 то
то 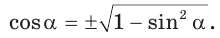 Поскольку угол
Поскольку угол 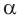 — тупой, то его косинус отрицательный. Поэтому
— тупой, то его косинус отрицательный. Поэтому 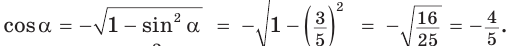 Тогда
Тогда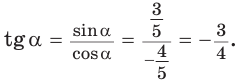
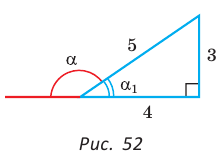
Способ 2. Синус острого угла 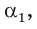 смежного с данным тупым углом
смежного с данным тупым углом 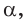 равен также
равен также 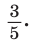 Построим прямоугольный треугольник со сторонами 3, 4 и 5 (рис. 52). В нем
Построим прямоугольный треугольник со сторонами 3, 4 и 5 (рис. 52). В нем 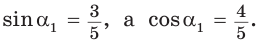 Так как косинусы смежных углов противоположны, то
Так как косинусы смежных углов противоположны, то 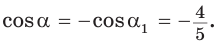 . Аналогично,
. Аналогично, 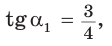
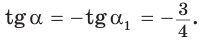
Ответ: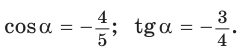
Формулы площади треугольника и площади параллелограмма
Тригонометрические функции позволяют получить формулы для вычисления площади треугольника и площади параллелограмма. Сформулируем их в виде двух теорем.
Теорема. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними, т. е. 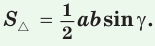
Доказательство:
Пусть в треугольнике 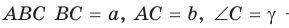 — острый,
— острый, 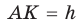 — высота (рис. 56, а).
— высота (рис. 56, а).
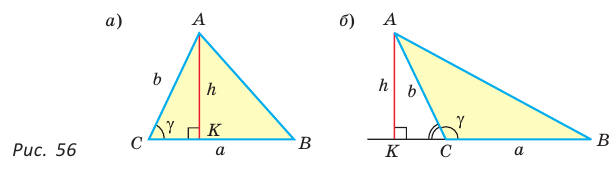
Из прямоугольного треугольника 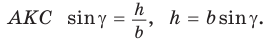 Тогда
Тогда 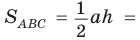
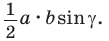
Если угол 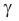 тупой (рис. 56,
тупой (рис. 56, 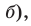 то
то 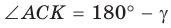 — острый. Из прямоугольного треугольника АКС следует, что
— острый. Из прямоугольного треугольника АКС следует, что 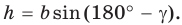 Так как
Так как 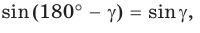 то
то 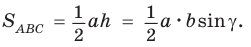
Если 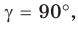 то
то 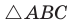 — прямоугольный с катетами
— прямоугольный с катетами 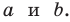 Учитывая, что
Учитывая, что  получим:
получим: 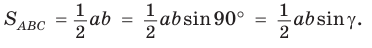
Теорема доказана.
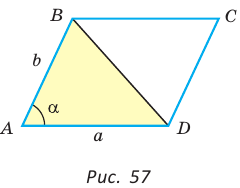
Теорема. Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними, т. е. 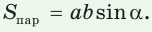
Используя рисунок 57, докажите эту теорему самостоятельно.
Замечание. Если 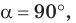 то параллелограмм является прямоугольником. Его площадь
то параллелограмм является прямоугольником. Его площадь 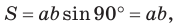 так как
так как  Таким образом, формула площади прямоугольника
Таким образом, формула площади прямоугольника 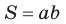 — частный случай формулы площади параллелограмма
— частный случай формулы площади параллелограмма 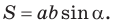

Известно, что слово «синус» в переводе с латинского имеет множество значений: изгиб, дуга, пазуха, бухта, впадина, залив, хорда, забота и нежная любовь. При помощи Интернета выясните:
а) какое из значений подходит к математическому понятию «синуса»;
б) какие из значений относятся к медицине и почему насморк врачи иногда называют синуситом.
Пример №14
Дан параллелограмм ABCD, площадь которого 40 см2, а периметр 36 см. Найти стороны параллелограмма, если его угол D равен 150° (рис. 58).
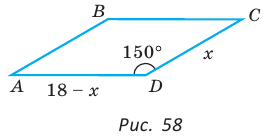
Решение:
Полупериметр параллелограмма равен 18 см. Если 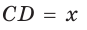 см, то
см, то 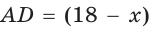 см.
см.
Тогда
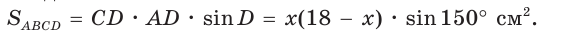
Так как 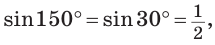 то
то 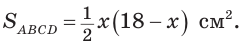
По условию 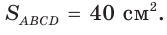 Составим и решим уравнение:
Составим и решим уравнение: 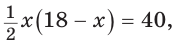
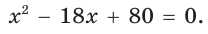 По теореме Виета (обратной)
По теореме Виета (обратной) 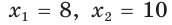 — корни.
— корни.
Если CD = 8 см, то AD = 10 см, если CD = 10 см, то AD = 8 см.
Ответ: 8 см, 10 см.
Пример №15
Доказать, что площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними, т.е. 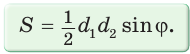
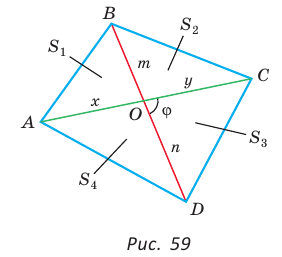
Доказательство:
Пусть диагонали 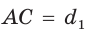 и
и 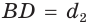 четырехугольника ABCD (рис. 59) пересекаются в точке О,
четырехугольника ABCD (рис. 59) пересекаются в точке О, 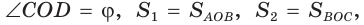
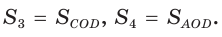 Докажем, что
Докажем, что 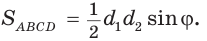
Обозначим 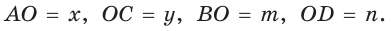 Заметим, что
Заметим, что 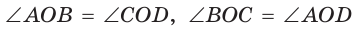 как вертикальные,
как вертикальные, 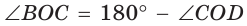 по свойству смежных углов. Поэтому
по свойству смежных углов. Поэтому 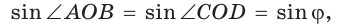
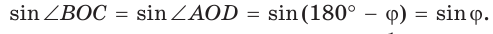 По формуле площади треугольника
По формуле площади треугольника 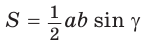 у получим:
у получим:
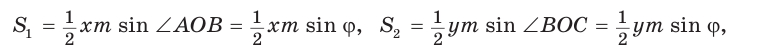
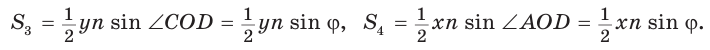
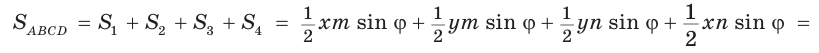
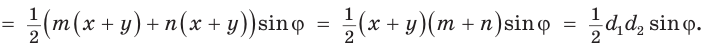
Утверждение доказано
Среднее пропорциональное (среднее геометрическое) в прямоугольном треугольнике
Если для положительных чисел 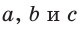 выполняется пропорция
выполняется пропорция 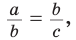 то число
то число 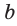 называется средним пропорциональным чисел а и с (между числами а и с). Из указанной пропорции
называется средним пропорциональным чисел а и с (между числами а и с). Из указанной пропорции 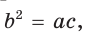 откуда
откуда 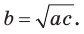 В такой форме записи число
В такой форме записи число 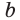 еще называют средним геометрическим чисел а и с.
еще называют средним геометрическим чисел а и с.
Пример №16
Число 4 является средним пропорциональным, или средним геометрическим чисел 2 и 8, так как = 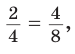 или
или 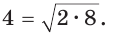
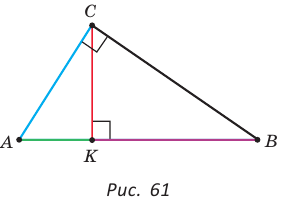
В прямоугольном треугольнике АВС, где 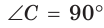 , проведем высоту СК (рис. 61). Отрезок АК является проекцией катета АС на гипотенузу, а отрезок ВК — проекцией катета ВС на гипотенузу. Катеты, гипотенуза, высота и проекции катетов на гипотенузу связаны отношениями, которые мы сформулируем в виде следующей теоремы.
, проведем высоту СК (рис. 61). Отрезок АК является проекцией катета АС на гипотенузу, а отрезок ВК — проекцией катета ВС на гипотенузу. Катеты, гипотенуза, высота и проекции катетов на гипотенузу связаны отношениями, которые мы сформулируем в виде следующей теоремы.
Теорема (о среднем пропорциональном в прямоугольном треугольнике).
а) Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу, т. е. 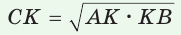 (см. рис. 61).
(см. рис. 61).
б) Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу, т. е. 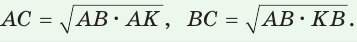
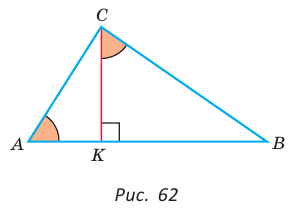
Доказательство:
а)3аметим, что если 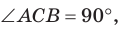
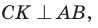 то
то 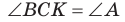 (эти углы дополняют
(эти углы дополняют 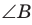 до 90°) (рис. 62). Из
до 90°) (рис. 62). Из 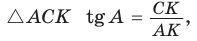 из
из 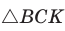
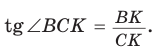 Отсюда
Отсюда 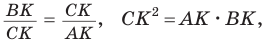
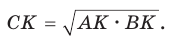
б) Из 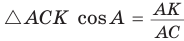 , из
, из 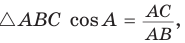 откуда
откуда 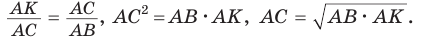
Аналогично доказывается, что 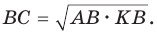 Теорема доказана.
Теорема доказана.
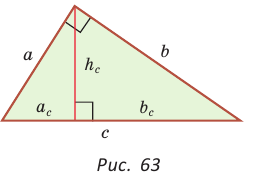
Обозначив катеты 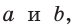 гипотенузу с, высоту
гипотенузу с, высоту 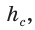 проекции катетов на гипотенузу
проекции катетов на гипотенузу 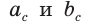 (рис. 63), получим следующие формулы:
(рис. 63), получим следующие формулы:
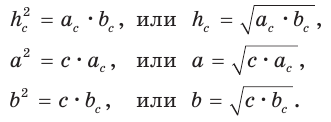
Пример №17
Найти площадь прямоугольного треугольника, если проекции катетов на гипотенузу равны 2 см и 8 см.
Решение:
Пусть СН — высота прямоугольного треугольника АВС 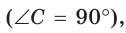 АН = 2 см — проекция катета АС на гипотенузу, НВ = 8 см —
АН = 2 см — проекция катета АС на гипотенузу, НВ = 8 см —
проекция катета СВ на гипотенузу (рис. 64). Так как высота СН есть среднее геометрическое между проекциями катетов на гипотенузу, то 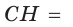
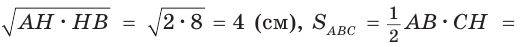
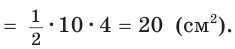
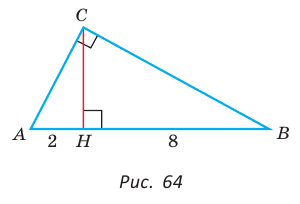
Ответ: 20 см2.
Пример №18
В прямоугольном треугольнике АВС из вершины прямого угла С проведена высота 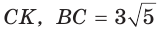 см, АК = 12 см (рис. 65). Найти гипотенузу АВ.
см, АК = 12 см (рис. 65). Найти гипотенузу АВ.
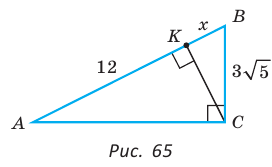
Решение:
Пусть 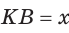 см, тогда
см, тогда 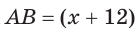 см.
см.
Катет есть среднее пропорциональное между гипотенузой и проекцией катета на гипотенузу. Поэтому 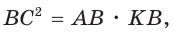 т. е.
т. е. 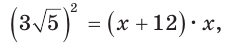
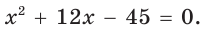 По теореме Виета (обратной)
По теореме Виета (обратной) 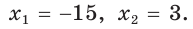 По смыслу задачи
По смыслу задачи 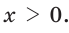 Значит, КВ = 3 см, АВ = 15 см.
Значит, КВ = 3 см, АВ = 15 см.
Ответ: 15 см.
Пример №19
При помощи циркуля и линейки построить отрезок, равный среднему геометрическому отрезков т и п .
Решение:
Пусть даны отрезки т и п . Необходимо построить отрезок 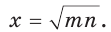
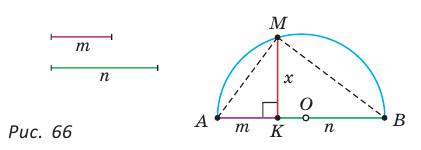
Построение.
1) На произвольной прямой откладываем данные отрезки: 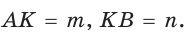
2) На отрезке АВ как на диаметре строим полуокружность, для чего находим середину О отрезка АВ, откуда ОА — радиус данной окружности.
3) Из точки К восстанавливаем перпендикуляр к прямой АВ до пересечения с полуокружностью в точке М (рис. 66).
Отрезок 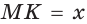 — среднее пропорциональное отрезков
— среднее пропорциональное отрезков 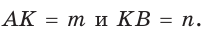
Доказательство:
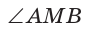 — прямой как вписанный угол, опирающийся на диаметр. В прямоугольном треугольнике АМВ высота МК является средним пропорциональным проекций катетов AM и МВ на гипотенузу
— прямой как вписанный угол, опирающийся на диаметр. В прямоугольном треугольнике АМВ высота МК является средним пропорциональным проекций катетов AM и МВ на гипотенузу 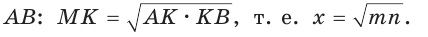
Повторение*
В 8-м классе мы доказали следующую теорему:
Теорема (о касательной и секущей). Если из одной точки к окружности проведены касательная и секущая, то квадрат отрезка касательной, соединяющего данную точку и точку касания, равен произведению отрезков се кущей, соединяющих данную точку и точки пересечения секущей с окружностью, т. е. 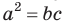 (рис. 70).
(рис. 70).
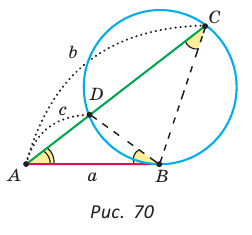
Как видим, отрезок 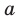 является средним пропорциональным между отрезками
является средним пропорциональным между отрезками 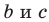 секущей. Глядя на рисунок 70, вспомните идею доказательства теоремы.
секущей. Глядя на рисунок 70, вспомните идею доказательства теоремы.
Теорема о площадях треугольников с общим (равным) углом
Площади треугольников, имеющих общий угол (или равный угол), относятся как произведения сторон, заключающих этот угол (рис. 75),
т.е. 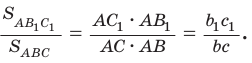
Доказательство:
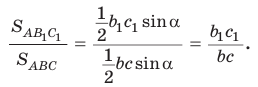
Следствие: Верно:
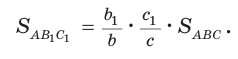
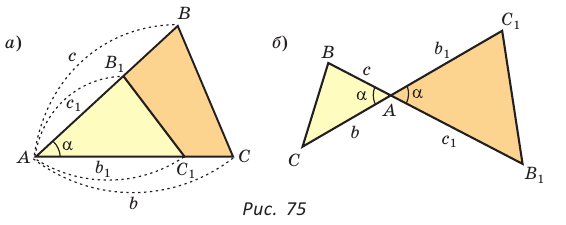
Пример №20
Площадь треугольника АВС равна 16, АК : КС = 3 :1 , AM : МВ = 1 :2 (рис. 76). Найти 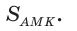
Решение:
Способ 1. По следствию из теоремы о площадях треугольников с общим углом получаем:
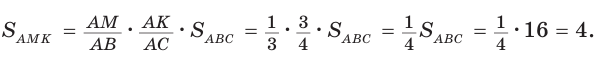
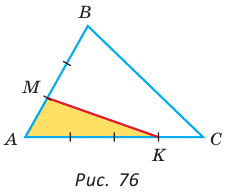
Способ 2. 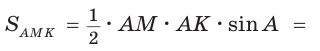
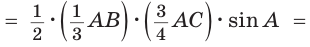
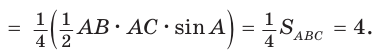
Ответ: 4.
Теорема Менелая
Если дан треугольник АВС и прямая 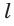 пересекает стороны ВС, АВ и продолжение стороны АС в точках
пересекает стороны ВС, АВ и продолжение стороны АС в точках 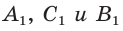 соответственно (рис. 79), то
соответственно (рис. 79), то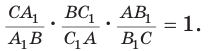
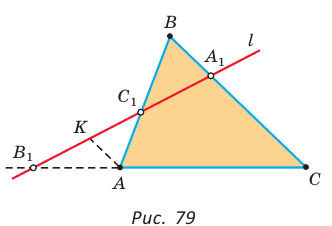
Доказательство:
Проведем отрезок 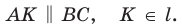 Так как
Так как 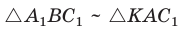 и
и  (по двум углам), то
(по двум углам), то 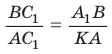 и
и 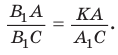 Перемножив почленно указанные пропорции, получим
Перемножив почленно указанные пропорции, получим
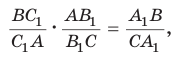 откуда
откуда 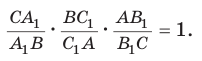
Замечание. При составлении произведения трех отношений теоремы Менелая можно начинать с любой из шести точек (трех вершин треугольника и трех точек пересечения прямой 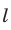 с прямыми, содержащими стороны треугольника) и двигаться по контуру либо по часовой, либо против часовой стрелки. При этом вершины треугольника и точки пересечения должны чередоваться.
с прямыми, содержащими стороны треугольника) и двигаться по контуру либо по часовой, либо против часовой стрелки. При этом вершины треугольника и точки пересечения должны чередоваться.
Пример №21
В треугольнике АВС на сторонах АВ и АС взяты соответственно точки М и К, такие, что AM : МВ = 2 :1 , АК : КС = 3 :2 . Отрезки СМ и ВК пересекаются в точке О. Найти ВО : ОК.
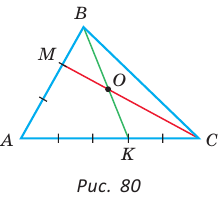
Решение:
Способ 1 (теорема Менелая). Рассмотрим 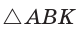 (рис. 80). Прямая
(рис. 80). Прямая 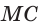 пересекает две его стороны АВ и ВК соответственно в точках М и О и продолжение третьей стороны АК в точке С. По теореме Менелая
пересекает две его стороны АВ и ВК соответственно в точках М и О и продолжение третьей стороны АК в точке С. По теореме Менелая 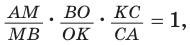 откуда
откуда 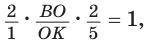
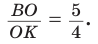
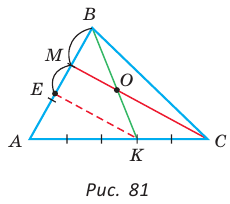
Способ 2 (теорема Фалеса обобщенная). Проведем 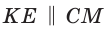 (рис. 81). По теореме Фалеса
(рис. 81). По теореме Фалеса 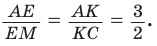 Тогда АЕ — три части, ЕМ — две части, AM — пять частей, откуда
Тогда АЕ — три части, ЕМ — две части, AM — пять частей, откуда 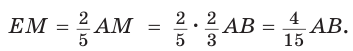
Но 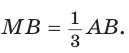 Отсюда
Отсюда 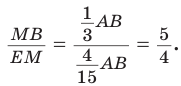 Для
Для 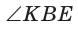
по теореме Фалеса 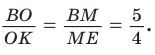
Ответ: 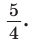
Пример №22
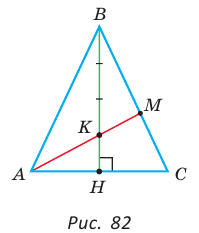
Дан равнобедренный треугольник АВС (АВ = ВС), площадь которого равна 80. Точка К делит высоту ВН в отношении 1 : 3, считая от основания. Прямая АК пересекает сторону ВС в точке М. Найти площадь четырехугольника НКМС (рис. 82).
Решение:
1) 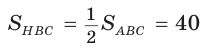 (ВН — высота и медиана треугольника АВС).
(ВН — высота и медиана треугольника АВС).
2) Применим теорему Менелая к треугольнику НВС.
Прямая AM пересекает его стороны ВН и ВС соответственно в точках К и М и продолжение стороны НС в точке 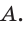 Тогда
Тогда 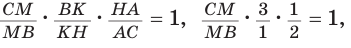
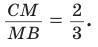 Откуда
Откуда 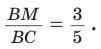
3) 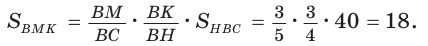
4) 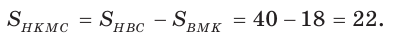
Ответ: 22.
Неравенство Коши
Среднее арифметическое двух неотрицательных чисел больше либо равно их среднему геометрическому, т. е.
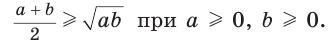
Например, 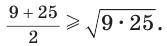 Действительно,
Действительно, 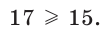
Алгебраическое доказательство указанного неравенства таково. Рассмотрим разность левой и правой частей неравенства 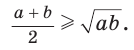 Получим:
Получим: 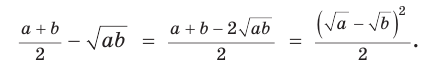 Так как
Так как 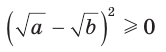 при всех допустимых
при всех допустимых 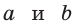 , то
, то 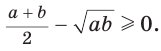 Следовательно, неравенство
Следовательно, неравенство 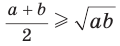 верно.
верно.
Неравенство 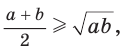 где
где 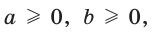 называется неравенством Коши по имени известного французского математика и часто используется при решении олимпиадных задач.
называется неравенством Коши по имени известного французского математика и часто используется при решении олимпиадных задач.
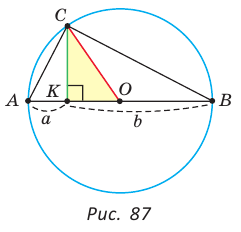
Приведем геометрическое доказательство указанного неравенства. Изобразим окружность с диаметром АВ и центром в точке О (рис. 87). На диаметре возьмем точку К (для определенности левее центра О). Пусть 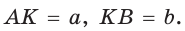 Из точки К восстановим перпендикуляр КС, где точка С принадлежит окружности. Проведем радиус ОС. Так как вписанный угол, опирающийся на диаметр, прямой, то
Из точки К восстановим перпендикуляр КС, где точка С принадлежит окружности. Проведем радиус ОС. Так как вписанный угол, опирающийся на диаметр, прямой, то  прямоугольный, СК — его высота, проведенная к гипотенузе. По теореме о среднем пропорциональном в прямоугольном треугольнике
прямоугольный, СК — его высота, проведенная к гипотенузе. По теореме о среднем пропорциональном в прямоугольном треугольнике 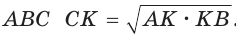 . Но радиус ОС равен половине диаметра АВ, т. е.
. Но радиус ОС равен половине диаметра АВ, т. е. 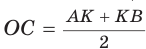 . В
. В 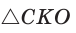 катет меньше гипотенузы, т. е.
катет меньше гипотенузы, т. е. 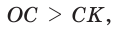 так как катет меньше гипотенузы. Отсюда
так как катет меньше гипотенузы. Отсюда 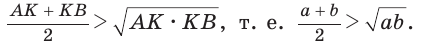
Равенство левой и правой частей неравенства достигается, когда точка К совпадает с точкой О и 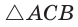 становится равнобедренным и прямоугольным. Поэтому справедливо неравенство
становится равнобедренным и прямоугольным. Поэтому справедливо неравенство 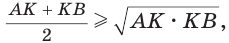 т. е
т. е 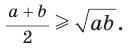
ЗАПОМИНАЕМ
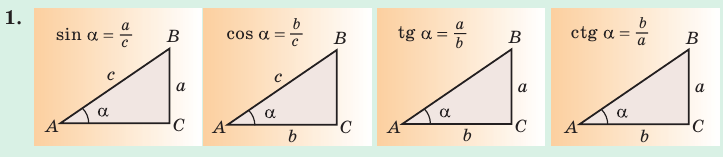
2. Значения тригонометрических функций углов 30 45°, 60°:
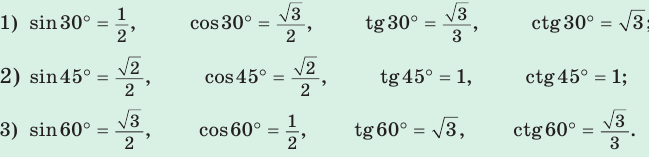
3. Тригонометрические формулы (тождества):
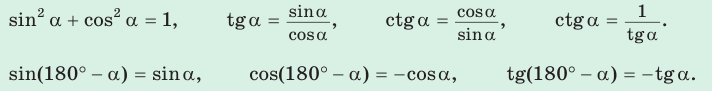
Примеры: 
4. Формулы площади треугольника и параллелограмма:

5. Среднее пропорциональное в прямоугольном треугольнике:
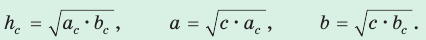
- Сумма углов треугольника
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Угол – определение, виды, как обозначают с примерами
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
