Внешний угол треугольника. Синус и косинус внешнего угла
В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?
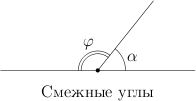
Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна .

Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине — это угол, смежный с углом
. Если угол
острый, то смежный с ним угол — тупой, и наоборот.

Обратите внимание, что:
Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.
Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
1. В треугольнике угол
равен
,
. Найдите тангенс внешнего угла при вершине
.

Пусть — внешний угол при вершине
.
Зная , найдем
по формуле:
Получим:
2. В треугольнике угол
равен
,
. Найдите синус внешнего угла при вершине
.
Задача решается за четыре секунды. Поскольку сумма углов и
равна
,
. Тогда и синус внешнего угла при вершине
также равен
.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Внешний угол треугольника. Синус и косинус внешнего угла» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
07.05.2023
Внешний угол треугольника. Синус и косинус внешнего угла
В некоторых
задачах ЕГЭ требуется найти синус,
косинус или тангенс внешнего
угла
треугольника. А что такое внешний
угол треугольника?
Давайте
вспомним сначала, что такое смежные
углы.
Вот они, на рисунке. У смежных углов
одна сторона общая, а две другие лежат
на одной прямой. Сумма смежных углов
равна
.
Возьмем
треугольник и продолжим одну из его
сторон. Внешний угол
![]()
при
вершине
—
это угол, смежный с углом
. Если
угол
острый, то смежный с ним угол —
тупой, и наоборот.
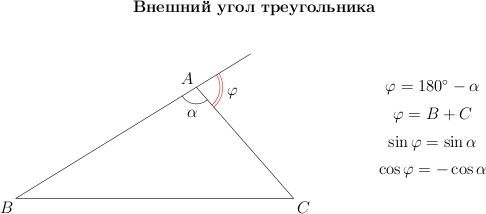
Обратите
внимание, что:
![]()
![]()
![]()
Запомните
эти важные соотношения. Сейчас мы берем
их без доказательств. В разделе
«Тригонометрия», в теме «Тригонометрический
круг»,
мы вернемся к ним.
Легко
доказать, что внешний
угол треугольника равен сумме двух
внутренних углов, не смежных с ним.
1.
В треугольнике
угол
равен
,
![]()
.
Найдите тангенс внешнего угла при
вершине
.
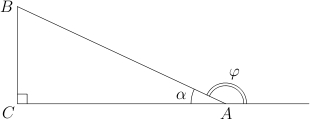
Пусть
—
внешний угол при вершине
.
Имеем:
![]()
Зная
![]()
,
найдем
![]()
по формуле
![]()
Получим:
![]()
2.
В треугольнике
угол
равен
,
![]()
.
Найдите синус внешнего угла при вершине
![]()
.
Задача
решается за четыре секунды. Поскольку
сумма углов
и
равна
,
![]()
.
Тогда и синус внешнего угла при
вершине
также равен
![]()
.
Высота в прямоугольном треугольнике
Вспомним,
что высота
треугольника —
это перпендикуляр, опущенный из его
вершины на противоположную сторону.
В
прямоугольном треугольнике катеты
являются высотами друг к другу. Главный
интерес представляет высота, проведённая
к гипотенузе.
Один
из типов экзаменационных задач В6 в
банке заданий ФИПИ — такие, где
в прямоугольном треугольнике высота
проведена из вершины прямого угла.
Посмотрим, что получается:

Высота
проведена к гипотенузе
![]()
.
Она делит треугольник
на два
прямоугольных треугольника —
![]()
и ![]()
.
Смотрим внимательно на рисунок
и находим на нем равные
углы.
Это и есть ключ к задачам по геометрии,
в которых высота опущена на гипотенузу.
Мы помним,
что сумма двух острых углов прямоугольного
треугольника равна
.
Значит,
![]()
,
то есть угол
равен
углу
.
Аналогично, угол
![]()
.
Иными
словами, каждый из трех углов
треугольника
равен
одному из углов треугольника
и треугольника
.
Треугольники
,
и
называются подобными.
Давайте нарисуем их рядом друг
с другом.
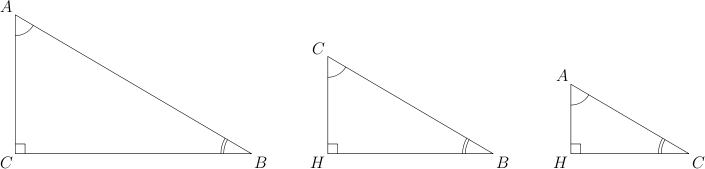
Они
отличаются только размерами. Стороны
подобных треугольников пропорциональны.
Что это значит?
Возьмем
треугольники
и
.
Стороны треугольника
длиннее,
чем стороны треугольника
,
в некоторое число
![]()
раз:
![]()
При
решении задач нам пригодится равенство
углов треугольников
,
и
,
а также пропорциональность их сторон.
Обратите также внимание, что площадь
треугольника
можно
записать двумя разными способами: как
половину произведения катетов и как
половину произведения гипотенузы
на проведенную к ней высоту.
1.
В треугольнике
угол
равен
,
![]()
—
высота,
![]()
,
![]()
.
Найдите
![]()
.
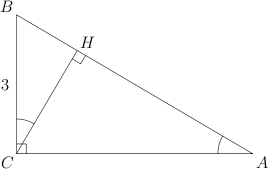
Рассмотрим
треугольник
.
В нем известны косинус угла
и противолежащий катет
![]()
.
Зная синус угла
,
мы могли бы найти гипотенузу
.
Так давайте найдем
![]()
:
![]()
![]()
![]()
![]()
(поскольку
значение синуса острого угла положительно).
Тогда:
![]()
Рассмотрим
прямоугольный треугольник
,
![]()
.
Имеем:
![]()
Отсюда,
поскольку
![]()
:
![]()
и
тогда
![]()
Ответ:
![]()
.
2.
В треугольнике
угол
равен
,
![]()
,
![]()
.
Найдите высоту
.
Сделайте
чертеж и рассмотрите прямоугольный
треугольник
.
Ответ:
![]()
.
3.
В треугольнике
угол
равен
,
![]()
,
![]()
.
К гипотенузе проведена высота
.
Найдите
.
Это
чуть более сложная задача. Ведь вам
неизвестны катеты
и
.
Зато
можно записать теорему Пифагора:
![]()
Нам
известно также, что
![]()
Решая
эту систему из двух уравнений, найдем:
![]()
Запишем
площадь треугольника
двумя
способами:
![]()
и найдем
![]()
.
Найти
высоту, проведенную из вершины прямого
угла, можно было и другим способом.
Мы выбрали самый короткий путь —
составили и решили систему уравнений.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
30.03.201540.15 Mб22спицын мартыненко.djvu
- #
- #
- #
- #
- #
- #
- #
- #
Как найти синус внешнего угла
По определению любой угол составляют два несовпадающих луча, которые выходят из единственной общей точки – вершины. Если один из лучей продолжить за вершину, это продолжение вместе со вторым лучом образует еще один угол – он называется смежным. Смежный угол в вершине любого выпуклого многоугольника называют внешним, так как он лежит вне участка поверхности, ограниченного сторонами этой фигуры.
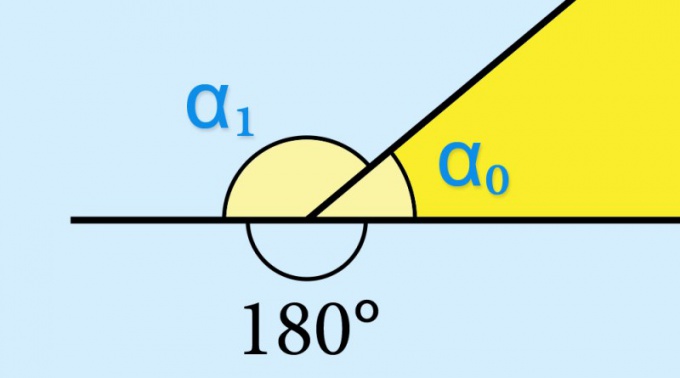
Инструкция
Если вам известно значение синуса внутреннего угла (α₀) геометрической фигуры, вычислять что-либо нет необходимости – синус соответствующего ему внешнего угла (α₁) будет иметь точно такое же значение: sin(α₁) = sin(α₀). Это определяется свойствами тригонометрической функции sin(α₀) = sin(180°-α₀). Если бы требовалось узнать, например, значение косинуса или тангенса внешнего угла, эту величину нужно было бы брать с противоположным знаком.
Существует теорема о том, что в треугольнике сумма величин двух любых внутренних углов равна величине внешнего угла третьей вершины. Используйте ее в том случае, если величина внутреннего угла, соответствующего рассматриваемому внешнему (α₁), неизвестна, а углы (β₀ и γ₀) в двух других вершинах приведены в условиях. Найдите синус от суммы известных углов: sin(α₁) = sin(β₀+γ₀).
Задача с теми же исходными условиями, что и в предыдущем шаге, имеет и другое решение. Оно вытекает из другой теоремы – о сумме внутренних углов треугольника. Так как эта сумма, согласно теореме, должна быть равна 180°, величину неизвестного внутреннего угла можно выразить через два известных (β₀ и γ₀) – она будет равна 180°-β₀-γ₀. Это означает, что вы можете использовать формулу из первого шага, заменив в нем величину внутреннего угла этим выражением: sin(α₁) = sin(180°-β₀-γ₀).
В правильном многоугольнике величина внешнего угла при любой вершине равна величине центрального угла, а значит, может быть рассчитана по той же формуле, что и он. Поэтому, если в условиях задачи дано число сторон (n) многоугольника, при вычислении синуса любого внешнего угла (α₁) исходите из того, что его величина равна полному обороту, поделенному на число сторон. Полный оборот в радианах выражается удвоенным числом Пи, поэтому формула должна иметь такой вид: sin(α₁) = sin(2*π/n). При расчетах в градусах удвоенное Пи замените на 360°: sin(α₁) = sin(360°/n).
Источники:
- найти sin угла
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Внешний угол треугольника
Углы треугольника бывают внутренние и внешние. Что такое внешний угол треугольника? Как его найти?
Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.
Как построить внешний угол треугольника? Нужно продлить сторону треугольника.
∠3 — внешний угол при вершине А,
∠2 — внешний угол при вершине С,
∠1 — внешний угол при вершине В.
Сколько внешних углов у треугольника?
При каждой вершине треугольника есть два внешних угла. Чтобы построить внешний угол при вершине треугольника, можно продлить любую из двух сторон, на которых лежит данная вершина. Таким образом получаем 6 внешних углов.
Внешние углы каждой пары при данной вершины равны между собой (как вертикальные):
Поэтому, когда говорят о внешнем угле треугольника, не важно, какую из сторон треугольника продлили.
Чему равен внешний угол?
Теорема (о внешнем угле треугольника)
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Дано : ∆АВС, ∠1 — внешний угол при вершине С.
∠1 и ∠С (∠АСВ) — смежные, поэтому их сумма равна 180º, значит, ∠1=180º-∠С=180º-(180º-(∠А+∠В))=180º-180º+(∠А+∠В)=∠А+∠В.
Теорема о внешнем угле треугольника: формулировка и задачи
В данной публикации мы рассмотрим одну из основных теорем в геометрии 7 класса – о внешнем угле треугольника. Также разберем примеры решения задач, чтобы закрепить представленный материал.
Определение внешнего угла
Для начала вспомним, что такое внешний угол. Допустим у нас есть треугольник:

Смежный с внутренним углом ( λ ) треугольника угол при той же вершине является внешним. На нашем рисунке он обозначен буквой γ .
-
сумма данных углов равна 180 градусам, т.е. γ + λ = 180° (свойство внешнего угла);
Формулировка теоремы
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Из данной теоремы следует, что внешний угол треугольника больше любого из несмежных с ним внутренних углов.
Примеры задач
Задание 1
Дан треугольник, в котором известны значения двух углов – 45° и 58°. Найдите внешний угол, смежный с неизвестным углом треугольника.
Решение
Воспользовавшись формулой теоремы получаем: 45° + 58° = 103°.
Задание 1
Внешний угол треугольника равен 115°, а один из несмежных с ним внутренних углов – 28°. Вычислите значения оставшихся углов треугольника.
Решение
Для удобства будем использовать обозначения, указанные на рисунках выше. Известный внутренний угол примем за α .
Исходя из теоремы: β = γ – α = 115° – 28° = 87° .
Угол λ является смежным с внешним, а значит вычисляется по следующей формуле (следует из свойства внешнего угла): λ = 180° – γ = 180° – 115° = 65° .
Внешний угол треугольника. Синус и косинус внешнего угла
В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?
Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна .

Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине — это угол, смежный с углом . Если угол острый, то смежный с ним угол — тупой, и наоборот.

Обратите внимание, что:
Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.
Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Ты нашел то, что искал? Поделись с друзьями!
1. В треугольнике угол равен , . Найдите тангенс внешнего угла при вершине .

Пусть — внешний угол при вершине .
Зная , найдем по формуле
2. В треугольнике угол равен , . Найдите синус внешнего угла при вершине .
Задача решается за четыре секунды. Поскольку сумма углов и равна , . Тогда и синус внешнего угла при вершине также равен .
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/vneshnij-ugol-treugolnika/
[/spoiler]
6. Геометрия на плоскости (планиметрия). Часть II
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Работа с внешними углами многоугольника с помощью тригонометрии
Внешний угол многоугольника – угол, смежный с каким-нибудь внутренним углом многоугольника.
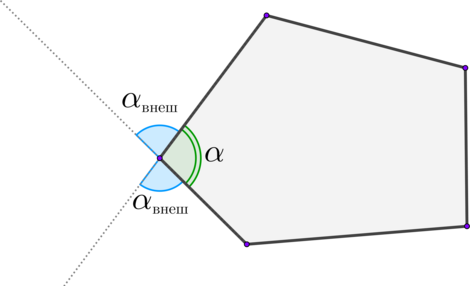
[large{begin{aligned}
&sin alpha_{text{внеш}}=sin
alpha qquad qquad qquad cos alpha_{text{внеш}}=-cos alpha\
&\
&mathrm{tg}, alpha_{text{внеш}}=-, mathrm{tg},alpha qquad
qquad qquad , mathrm{ctg}, alpha_{text{внеш}}= -,
mathrm{ctg},alpha
end{aligned}}]
Замечание: Синус и острого, и тупого угла – положительное число. Косинус, тангенс и котангенс острого угла – положительное число, а тупого угла – отрицательное число.
(острый угол: (0^circ<alpha<90^circ), тупой угол: (90^circ<alpha<180^circ))
Задание
1
#2107
Уровень задания: Сложнее ЕГЭ
Дан выпуклый четырехугольник (GEOM), причем (angle G+angle
E+angle O=330^circ). Найдите синус внешнего угла при вершине (M).
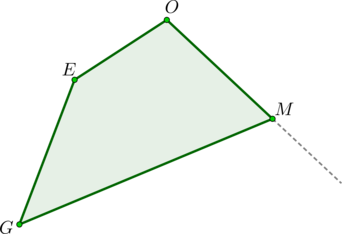
Т.к. сумма углов любого выпуклого четырехугольника равна (360^circ), то (angle M=360^circ – 330^circ =30^circ). Следовательно, (sin angle M=sin 30^circ =0,5). Т.к. синусы смежных углов равны, то (sin M_{text{внеш}}=0,5).
Ответ: 0,5
Задание
2
#2108
Уровень задания: Сложнее ЕГЭ
Дан треугольник (ABC), причем (sin (angle A+angle B)=0,67). Найдите синус угла (ACB).

Т.к. в треугольнике внешний угол при вершине (C) равен сумме углов (A) и (B), то и (sin angle C_{text{внеш}}=sin (angle A+angle
B)=0,67).
Т.к. синусы смежных углов равны, то (sin angle C=sin angle
C_{text{внеш}}=0,67).
Ответ: 0,67
Задание
3
#617
Уровень задания: Сложнее ЕГЭ
В треугольнике (ABC): (angle B < 90^{circ}), (sin {angle ABC} = 0,8). Найдите косинус внешнего угла при вершине (B).
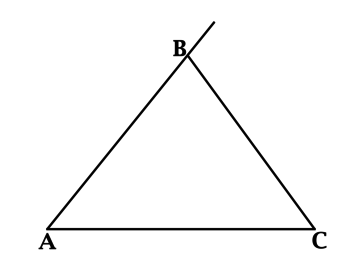
Синусы смежных углов равны: (sin{(180^{circ} – alpha)} = sin{alpha}), тогда синус внешнего угла при вершине (B) равен (0,8).
Используя основное тригонометрическое тождество ((sin^2{alpha} + cos^2{alpha} = 1)), находим, что косинус внешнего угла при вершине (B) равен (pm 0,6).
Так как (angle ABC < 90^{circ}), то внешний угол при вершине (B) – тупой, следовательно, его косинус отрицателен. Косинус внешнего угла при вершине (B) равен (-0,6).
Ответ: -0,6
Задание
4
#2109
Уровень задания: Сложнее ЕГЭ
В треугольнике (ABC) известно, что (cos (angle B+angle C)=0,33). Найдите косинус угла (A).

Т.к. в треугольнике внешний угол при вершине (A) равен сумме углов (B) и (C), то (cos angle A_{text{внеш}}=cos(angle B+angle
C)=0,33).
Т.к. косинусы смежных углов отличаются только знаком, то (cos
angle A=-cos angle A_{text{внеш}}=-0,33).
Ответ: -0,33
Задание
5
#2473
Уровень задания: Сложнее ЕГЭ
Дан выпуклый пятиугольник, причем сумма четырех его внутренних углов равна (420^circ). Найдите квадрат косинуса внешнего угла при вершине оставшегося пятого угла.
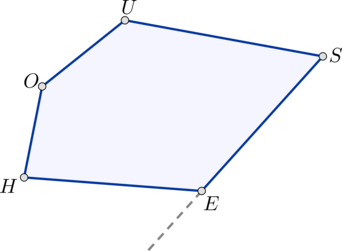
Т.к. сумма внутренних углов выпуклого (n)-угольника вычисляется по формуле (180^circ cdot (n-2)), то сумма внутренних углов нашего пятиугольника равна (540^circ). Следовательно, если (angle
H+angle O+angle U+angle S=420^circ quad Rightarrow quad
angle E=540^circ -420^circ =120^circ).
Следовательно, (angle E_{text{внеш}}=180^circ -angle
E=60^circ). Следовательно, (cosangle E_{text{внеш}}=cos
^260^circ =dfrac14=0,25).
Ответ: 0,25
Задание
6
#618
Уровень задания: Сложнее ЕГЭ
В четырёхугольнике (ABCD) с тупыми углами (C) и (D) продолжение стороны (AD) за точку (D) и продолжение стороны (BC) за точку (C) пересеклись в точке (E) под прямым углом. При этом (sin{angle DCE} = 0,6). Найдите (sin{angle ADC}).
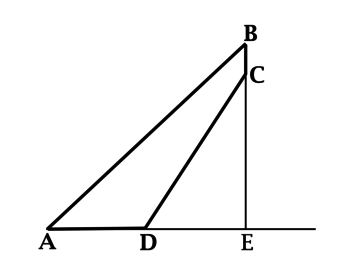
Из основного тригонометрического тождества с учётом того, что (angle DCE) – острый, получаем: (cos{angle DCE} = 0,8).
Из определений синуса и косинуса острого угла в прямоугольном треугольнике получаем, что (sin{angle EDC} = cos{angle DCE} = 0,8).
Так как синусы смежных углов равны, то (sin{angle ADC} = sin{angle EDC} = 0,8).
Ответ: 0,8
Задание
7
#619
Уровень задания: Сложнее ЕГЭ
В невыпуклом четырёхугольнике (ABCD) ((angle C > 180^circ)) сторону (AD) продолжили за точки (A) и (D), получив по одному внешнему углу при вершинах (A) и (D). (angle BAD = 2cdot angle CDA). Найдите косинус внешнего угла при вершине (A), если косинус внешнего угла при вершине (D) получился (-0,9).
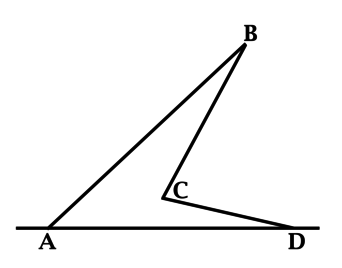
Косинусы смежных углов противоположны: (cos{(180^{circ} – alpha)} = -cos{alpha}).
Косинус внешнего угла при вершине (D) равен ((-1)cdot cos{angle CDA}), откуда (cos{angle CDA} = 0,9).
(angle BAD = 2cdot angle CDA), тогда (cos{angle BAD} = 2cos^2{angle CDA} – 1 = 0,62).
Так как косинус внешнего угла равен минус косинусу угла, смежного с ним, то косинус внешнего угла при вершине (A) равен (-0,62).
Ответ: -0,62
Задания, в которых школьникам необходимо найти внешние углы многоугольника, в ЕГЭ по математике традиционно встречаются из года в год. Правильно решать подобные задачи должны уметь выпускники, сдающие как базовый, так и профильный уровень аттестационного испытания. Школьники, которые освоили задания из раздела «Работа с внешними углами многоугольника», смогут справиться с ЕГЭ и рассчитывать на получение достойных баллов по итогам его прохождения.
Как подготовиться к экзамену?
Перед решением задач на нахождение внешних углов многоугольника в ЕГЭ стоит освежить в памяти определения синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике. Кроме того, для некоторых заданий могут потребоваться формулы основных тригонометрических тождеств.
Восполнить пробелы в знаниях, например, по теме «Вычисление синуса угла треугольника» и лучше усвоить информацию вам поможет образовательный проект «Школково». Для того чтобы выпускники могли успешно справляться с задачами на нахождение внешних углов треугольника в ЕГЭ, мы предоставляем возможность повторить определения и основные правила. Весь необходимый базовый материал вы найдете в разделе «Теоретическая справка». Наши специалисты подобрали соответствующую информацию.
Для закрепления теоретического материала мы предлагаем выполнить упражнения по теме «Работа с внешними углами многоугольника». Подборка простых и сложных заданий представлена в блоке «Каталог». Наши специалисты регулярно обновляют и дополняют упражнения.
Попрактиковаться в решении задач на нахождение внешних углов многоугольника, подобных тем, которые встречаются в ЕГЭ, можно в режиме онлайн, находясь в Москве или любом другом городе России.

УСТАЛ? Просто отдохни
