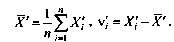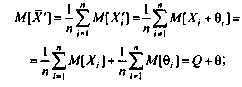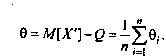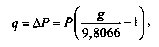Систематической погрешностью называется составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же величины. При этом предполагается, что систематические погрешности представляют собой определенную функцию неслучайных факторов, состав которых зависит от физических, конструкционных и технологических особенностей средств измерений, условий их применения, а также индивидуальных качеств наблюдателя. Сложные детерминированные закономерности, которым подчиняются систематические погрешности, определяются либо при создании средств измерений и комплектации измерительной аппаратуры, либо непосредственно при подготовке измерительного эксперимента и в процессе его проведения. Совершенствование методов измерения, использование высококачественных материалом, прогрессивная технология — все это позволяет на практике устранить систематические погрешности настолько, что при обработке результатов наблюдений с их наличием зачастую не приходится считаться.
Систематические погрешности принято классифицировать в зависимости от причин их возникновения и по характеру их проявления при измерениях.
В зависимости от причин возникновения рассматриваются четыре вида систематических погрешностей.
1. Погрешности метода, или теоретические погрешности, проистекающие от ошибочности или недостаточной разработки принятой теории метода измерений в целом или от допущенных упрощений при проведении измерений.
Погрешности метода возникают также при экстраполяции свойства, измеренного на ограниченной части некоторого объекта, на весь объект, если последний не обладает однородностью измеряемого свойства. Так, считая диаметр цилиндрического вала равным результату, полученному при измерении в одном сечении и в одном направлении, мы допускаем систематическую погрешность, полностью определяемую отклонениями формы исследуемого вала. При определении плотности вещества по измерениям массы и объема некоторой пробы возникает систематическая погрешность, если проба содержала некоторое количество примесей, а результат измерения принимается за характеристику данного вещества -вообще.
К погрешностям метода следует отнести также те погрешности, которые возникают вследствие влияния измерительной аппаратуры на измеряемые свойства объекта. Подобные явления возникают, например, при измерении длин, когда измерительное усилие используемых приборов достаточно велико, при регистрации быстропротекаюших процессов недостаточно быстродействующей аппаратурой, при измерениях температур жидкостными или газовыми термометрами и т.д.
2. Инструментальные погрешности, зависящие от погрешностей применяемых средств измерений.. Среди инструментальных погрешностей в отдельную группу выделяются погрешности схемы, не связанные с неточностью изготовления средств измерения и обязанные своим происхождением самой структурной схеме средств измерений. Исследование инструментальных погрешностей является предметом специальной дисциплины — теории точности измерительных устройств.
3. Погрешности, обусловленные неправильной установкой и взаимным расположением средств измерения, являющихся частью единого комплекса, несогласованностью их характеристик, влиянием внешних температурных, гравитационных, радиационных и других полей, нестабильностью источников питания, несогласованностью входных и выходных параметров электрических цепей приборов и т.д.
4. Личные погрешности, обусловленные индивидуальными особенностями наблюдателя. Такого рода погрешности вызываются, например, запаздыванием или опережением при регистрации сигнала, неправильным отсчетом десятых долей деления шкалы, асимметрией, возникающей при установке штриха посередине между двумя рисками.
По характеру своего поведения в процессе измерения систематические погрешности подразделяются на постоянные и переменные.
Постоянные систематические погрешности возникают, например, при неправильной установке начала отсчета, неправильной градуировке и юстировке средств измерения и остаются постоянными при всех повторных наблюдениях. Поэтому, если уж они возникли, их очень трудно обнаружить в результатах наблюдений.
Среди переменных систематических погрешностей принято выделять прогрессивные и периодические.
Прогрессивная погрешность возникает, например, при взвешивании, когда одно из коромысел весов находится ближе к источнику тепла, чем другое, поэтому быстрее нагревается и
удлиняется. Это приводит к систематическому сдвигу начала отсчета и к монотонному изменению показаний весов.
Периодическая погрешность присуща измерительным приборам с круговой шкалой, если ось вращения указателя не совпадает с осью шкалы.
Все остальные виды систематических погрешностей принято называть погрешностями, изменяющимися по сложному закону.
В тех случаях, когда при создании средств измерений, необходимых для данной измерительной установки, не удается устранить влияние систематических погрешностей, приходится специально организовывать измерительный процесс и осуществлять математическую обработку результатов. Методы борьбы с систематическими погрешностями заключаются в их обнаружении и последующем исключении путем полной или частичной компенсации. Основные трудности, часто непреодолимые, состоят именно в обнаружении систематических погрешностей, поэтому иногда приходится довольствоваться приближенным их анализом.
Способы обнаружения систематических погрешностей. Результаты наблюдений, полученные при наличии систематических погрешностей, будем называть неисправленными и в отличие от исправленных снабжать штрихами их обозначения (например, Х1, Х2 и т.д.). Вычисленные в этих условиях средние арифметические значения и отклонения от результатов наблюдений будем также называть неисправленными и ставить штрихи у символов этих величин. Таким образом,
Поскольку неисправленные результаты наблюдений включают в себя систематические погрешности, сумму которых для каждого /-го наблюдения будем обозначать через 8., то их математическое ожидание не совпадает с истинным значением измеряемой величины и отличается от него на некоторую величину 0, называемую систематической погрешностью неисправленного среднего арифметического. Действительно,
Если систематические погрешности постоянны, т.е. 0/ = 0, /=1,2, …, п, то неисправленные отклонения могут быть непосредственно использованы для оценки рассеивания ряда наблюдений. В противном случае необходимо предварительно исправить отдельные результаты измерений, введя в них так называемые поправки, равные систематическим погрешностям по величине и обратные им по знаку:
q = -Oi.
Таким образом, для нахождения исправленного среднего арифметического и оценки его рассеивания относительно истинного значения измеряемой величины необходимо обнаружить систематические погрешности и исключить их путем введения поправок или соответствующей каждому конкретному случаю организации самого измерения. Остановимся подробнее на некоторых способах обнаружения систематических погрешностей.
Постоянные систематические погрешности не влияют на значения случайных отклонений результатов наблюдений от средних арифметических, поэтому никакая математическая обработка результатов наблюдений не может привести к их обнаружению. Анализ таких погрешностей возможен только на основании некоторых априорных знаний об этих погрешностях, получаемых, например, при поверке средств измерений. Измеряемая величина при поверке обычно воспроизводится образцовой мерой, действительное значение которой известно. Поэтому разность между средним арифметическим результатов наблюдения и значением меры с точностью, определяемой погрешностью аттестации меры и случайными погрешностями измерения, равна искомой систематической погрешности.
Одним из наиболее действенных способов обнаружения систематических погрешностей в ряде результатов наблюдений является построение графика последовательности неисправленных значений случайных отклонений результатов наблюдений от средних арифметических.
Рассматриваемый способ обнаружения постоянных систематических погрешностей можно сформулировать следующим образом: если неисправленные отклонения результатов наблюдений резко изменяются при изменении условий наблюдений, то данные результаты содержат постоянную систематическую погрешность, зависящую от условий наблюдений.
Систематические погрешности являются детерминированными величинами, поэтому в принципе всегда могут быть вычислены и исключены из результатов измерений. После исключения систематических погрешностей получаем исправленные средние арифметические и исправленные отклонения результатов наблюдении, которые позволяют оценить степень рассеивания результатов.
Для исправления результатов наблюдений их складывают с поправками, равными систематическим погрешностям по величине и обратными им по знаку. Поправку определяют экспериментально при поверке приборов или в результате специальных исследований, обыкновенно с некоторой ограниченной точностью.
Поправки могут задаваться также в виде формул, по которым они вычисляются для каждого конкретного случая. Например, при измерениях и поверках с помощью образцовых манометров следует вводить поправки к их показаниям на местное значение ускорения свободного падения
где Р — измеряемое давление.
Введением поправки устраняется влияние только одной вполне определенной систематической погрешности, поэтому в результаты измерения зачастую приходится вводить очень большое число поправок. При этом вследствие ограниченной точности определения поправок накапливаются случайные погрешности и дисперсия результата измерения увеличивается.
Систематическая погрешность, остающаяся после введения поправок на ее наиболее существенные составляющие включает в себя ряд элементарных составляющих, называемых неисключенными остатками систематической погрешности. К их числу относятся погрешности:
• определения поправок;
• зависящие от точности измерения влияющих величин, входящих в формулы для определения поправок;
• связанные с колебаниями влияющих величин (температуры окружающей среды, напряжения питания и т.д.).
Перечисленные погрешности малы, и поправки на них не вводятся.
измеряемой величины динамические погрешности приходится рассматривать как случайные.
Принципы описания и оценивания погрешностей. Оценивание погрешностей производится с целью получения объективных данных о точности результата измерения. Точность результата измерения характеризуется погрешностью. При оценке погрешности надо помнить, что излишняя точность ведет к неоправданному расходу средств и времени, а недостаточная точность в зависимости от цели измерения может привести к признанию годным в действительности негодного изделия, к принятию ошибочного решения и т.п.
Воснове современных подходов к оцениванию погрешностей лежат принципы, обеспечивающие выполнение требований единства измерений.
Систематическая погрешность по определению может быть представлена постоянной величиной либо известной зависимостью (линейная, периодическая
идругие функции от времени или номера наблюдения). Общей моделью случайной погрешности служит случайная величина, обладающая функцией распределения вероятностей.
Характеристики случайной погрешности делятся на точечные и интервальные. К точечным относятся средние квадратические отклонения случайной погрешности, дисперсия; к интервальным – границы неопределенности результата измерения (это означает, что границы, в которых может находиться погрешность, находят как отвечающие некоторой вероятности). Если эти границы определяются как отвечающие некоторой доверительной вероятности, то они называются доверительными интервалами. Если же минимально возможные в конкретном случае границы погрешности оценивают так, что погрешность, выходящую за них, встретить нельзя, то они называются предельными (безусловными) интервалами.
Вцелях единообразия представления результатов и погрешностей измерений показатели точности и формы представления результатов измерений стандартизованы.
Источниками систематических составляющих погрешности измерения могут быть все его компоненты: метод измерения, средства измерения и экспериментатор: Оценивание систематических составляющих представляет достаточно трудную метрологическую задачу. Важность ее определяется тем, что знание систематической погрешности позволяет внести соответствующую поправку в результат измерения и тем самым повысить его точность. Трудность же заключается в сложности обнаружения систематической погрешности, поскольку она не может быть выявлена путем повторных измерений (наблюдений). В самом деле, будучи постоянной по величине для данной группы наблюдений, систематическая погрешность никак визуально не проявится при повторных измерениях одной и той же величины и, следовательно, экспериментатор затруднится ответить на вопрос – имеется ли систематическая погрешность в наблюдаемых результатах.
Постоянные инструментальные систематические погрешности обычно выявляют посредством поверки средства измерения. Поверкой называют определение метрологическим органом погрешностей средства измерения и установление пригодности средства измерения к применению. Поверка производится путем сравнения показаний поверяемого прибора с показаниями более точного (образцового) средства измерения. Ее результаты указываются в свидетельстве о поверке или в паспорте прибора. Обнаруженные таким образом систематические погрешности исключаются из результата измерения путем введения поправки, которая представляет собой погрешность, взятую с противоположным знаком.
ПРИМЕР. При измерении напряжения в сети показания вольтметра 225 В. В свидетельстве о поверке указано, что на этой отметке шкалы систематическая погрешность вольтметра равна +3 В. С учетом поправки напряжение в сети равно 225 – 3 = 222 В.
Систематические составляющие, обусловленные несовершенством методов измерения, ограниченной точностью расчетных формул, положенных в основу измерений, влиянием средств измерений на объект, свойства которого измеряются, относятся к методическим погрешностям. Единых рекомендаций по обнаружению и оцениванию методических составляющих систематической погрешности нет. Поэтому задача решается в каждом конкретном случае индивидуально, на основе анализа примененного метода.
|
ПРИМЕР. |
Оценим |
систематическую |
погрешность |
Ux. |
||
|
измерения напряжения Ux источника, обусловленную наличием |
||||||
|
внутреннего сопротивления |
вольтметра (рис. 10). |
Внутреннее |
Ф |
|||
|
сопротивление источника напряжения R,=50 Ом; сопротивление |
||||||
|
вольтметра Ry = 5 кОм; £/юм=12,2 В. Здесь UmH= – |
р |
|||||
|
-С/ и |
R, |
|||||
|
Ry+R, |
||||||
|
относительная систематическая погрешность, определяемая как |
||||||
|
AС _ |
UЮМ – U X |
р |
||||
|
•100 = ———{——100 составит 0,99 %. Это |
Рис. 10. Измерение |
|||||
|
и. |
и , |
Rl + Ry |
напряжения источника |
|||
|
достаточно ощутимая погрешность и ее следует учесть введением |
вольтметром |
|||||
|
поправки. Поправка V равна погрешности, взятой с обратным |
||||||
|
знаком, или в единицах измеряемой величины |
||||||
|
V = 0,99 • 10’2 • 12,2 = +0,12 В. |
Таким образом, напряжение источника будет 12,2 + 0,12 = 12,32 В.
Полученная оценка систематической погрешности, в свою очередь, имеет некоторую погрешность из-за погрешностей в определении Rvи Rh а также из-за наличия инструментальной погрешности вольтметра. Эта погрешность при введении поправки не исключается и называется неисключенной систематической погрешностью.
Неисключенная систематическая погрешность результата образуется из неисключенных систематических погрешностей метода, средств измерений, погрешностей поправок и др.
При суммировании эти составляющие рассматриваются как случайные величины. При отсутствии данных о виде распределения неисключенных составляющих систематических погрешностей их распределения принимают за равномерные. При равномерном распределении неисключенных
систематических погрешностей границы неисюпоченной систематической погрешности результата измерения 0 вычисляются по формуле
(4)
где 0/ – граница /-й неисюпоченной составляющей систематической погрешности; к – коэффициент, определяемый принятой доверительной вероятностью (при /*=0,95 Л=1,1); т – количество неисюпоченных составляющих.
Личные систематические погрешности связаны с индивидуальными особенностями наблюдателя. Для того чтобы избежать их, необходимо точно соблюдать правила эксплуатации средств измерений и иметь навыки работы с измерительной техникой.
3.3. Компенсация систематической погрешности в процессе измерения
В практике измерений применяется несколько методов, позволяющих за счет некоторого усложнения процедуры измерений получить результат измерения свободным от систематической погрешности. К ним относятся метод замещения, метод противопоставления и метод компенсации погрешности по знаку.
Метод замещения – одна из разновидностей метода сравнения (взвешивание на пружинных весах, у которых имеется постоянная систематическая погрешность, например, из-за смещения шкалы).
Метод противопоставления, являющийся разновидностью метода сравнения, при котором измерение выполняется дважды и проводится так, чтобы в обоих случаях причина постоянной погрешности оказывала разные, но известные по закономерности воздействия на результаты наблюдений.
ПРИМЕР. Измерить сопротивление с помощью одинарного моста методом противопоставления (см. рис. 4, а также п. 4.5).
Сначала измеряемое сопротивление Rx уравновешивают известным сопротивлением R>
£
включенным в плечо сравнения моста. При этом Rx = Я, — , где Ri, Ri – сопротивления плеч
моста. Затем резисторы RK и R меняют местами и вновь уравновешивают мост, регулируя
£
сопротивление резистора R.B этом случае Rx = R[ — .
*з
Из двух последних уравнений исключается отношение Rj/R3‘Тогда Rx =
Метод компенсации погрешности по знаку. Этот метод также предусматривает проведение измерения в два этапа, выполняемых так, чтобы постоянная систематическая погрешность входила в показания средства измерения на каждом этапе с разными знаками. За результат измерения принимают полусумму показаний – систематические погрешности при этом взаимно компенсируются.
Суммирование систематических погрешностей. Поскольку в каждом конкретном случае каждая систематическая составляющая получает конкретную
реализацию (она либо постоянная, либо известен закон ее изменения), то результирующая, суммарная систематическая погрешность представляет собой алгебраическую сумму составляющих
3.4. Случайные погрешности (вероятностное описание)
Каждая случайная погрешность возникает вследствие одновременного воздействия на результат наблюдения многих случайных возмущений, и сама является случайной величиной. В этом случае предсказать результат отдельного наблюдения и исправить его введением поправки невозможно, поэтому используются методы теории вероятностей и математической статистики, которые позволяют установить вероятностные (статистические) закономерности появления случайных погрешностей и на основании этих закономерностей дать количественные оценки результата измерения и его погрешности.
Для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения вероятностей случайной величины и его дифференциальную форму – закон распределения плотности вероятности случайной величины.
Для количественной оценки случайных погрешностей и установления границ случайной погрешности результата измерения могут использоваться: предельная погрешность, интервальная оценка, числовые характеристики закона распределения.
Среднее квадратическое отклонение среднего арифметического значения X вычисляется по формуле
где ф/ = Xf —X ~ это отклонение результата каждого измерения от среднего значения Х ; п – число иизмерений; Х( – результаты отдельных измерений.
Значение <тср характеризует степень разброса X .
Введем понятие доверительной вероятности и доверительного интервала. Пусть Рд есть вероятность того, что X отличается от истинного значения Хис не более чем на А, т.е.
Р(-А<ХНС- X < А) = Рд
Р ( Х – А < Х пс< Х + А) =РД.
Вероятность Рд называется доверительной вероятностью, а интервал значений измеряемой величины о т ! – А д о 1 + А – доверительным интервалом. Приведенные неравенства означают, что с вероятностью РД доверительный интервал заключает в себе истинное значение Хцс.
Требования к характеристикам погрешности и рекомендации по их выбору приведены в нормативном документе МИ 1317-86 «ГСИ. Результаты и характеристики погрешностей измерений. Форма представления. Способы
использования при испытании образцов продукции и контроля их параметров» (ГСИ – Государственная система обеспечения единства измерений).
3.5. Классы точности средств измерений
Характеристики, введенные ГОСТ 8.009-84 (ГСИ. Нормируемые метрологические характеристики средств измерений), наиболее полно описывают метрологические свойства СИ. Учитывать все метрологические характеристики СИ при оценивании погрешности результата измерений – сложная и трудоемкая процедура, оправданная при измерениях повышенной точности. При измерениях на производстве и в обиходе такая точность не всегда нужна. В то же время определенная информация о возможной инструментальной составляющей погрешности измерения необходима. Такая информация дается указанием класса точности СИ. Класс точности – это обобщенная характеристика СИ, выражаемая пределами допускаемых значений его основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность. Класс точности позволяет судить лишь о том, в каких пределах находится погрешность СИ данного типа. Классы точности присваивают СИ при их разработке на основании исследований и испытаний представительной партии средств измерения данного типа. Средство измерений может иметь два и более класса точности (например, при наличии у него двух или более диапазонов измерений одной и той же физической величины; или приборы, предназначенные для измерения нескольких физических величин, также могут иметь различные классы точности для каждой измеряемой величины). Общие положения деления средств измерений по классу точности устанавливает ГОСТ 8.401-80 (ГСИ. Классы точности средств измерений. Общие требования). При этом пределы допускаемых погрешностей нормируют и выражают в форме абсолютных, приведенных или относительных погрешностей, в зависимости от характера изменения погрешностей в пределах диапазона измерений.
Если погрешность результатов измерений в данной области измерений принято выражать в единицах измерений величины или делениях шкалы, то принимается форма абсолютных погрешностей (меры, магазины номинальных ФВ). Если границы абсолютных погрешностей в пределах диапазона измерений практически постоянны, то принимается форма приведенной погрешности, а если эти границы нельзя считать постоянными, то – форма относительной погрешности.
Пределы допускаемой абсолютной погрешности устанавливают по формулам
|
Д = ±д |
(7) |
|
или |
|
|
Д = ± (а + Ьх), |
(8) |
|
где х – значение измеряемой величины; а, b – |
положительные числа, не |
|
зависящие от х. |
Нормирование в соответствии с (7) означает, что в составе погрешности средства измерения присутствует только аддитивная составляющая, а в соответствии с (8) – и аддитивная, и мультипликативная составляющие.
Классы точности СИ, выраженные через абсолютные погрешности, обозначают прописными буквами латинского алфавита или римскими цифрами. При этом чем дальше буква от начала алфавита, тем больше значения допускаемой абсолютной погрешности.
Пределы допускаемой приведенной погрешности определяют по формуле
|
у = — ЛШ ь =±АЛ0″ =±р, |
(9) |
где XN – нормирующее значение, выраженное в тех же единицах, что и х (обычно принимается верхний предел измерения для приборов с односторонней шкалой или сумма пределов для приборов с нулем посередине); р – отвлеченное положительное число, выбираемое из стандартизованного ряда значений (1*10”; 1,5*10”; 2*10”; 2,5*10”; 4*10”; 5*10”; 6*10″, где п = 1,0,-1,-2 ит.д.).
Для измерительных приборов с существенно неравномерной шкалой нормирующее значение устанавливают равным длине шкалы. В этом случае класс точности, например, 1,5 означает, что у=1,5% длины шкалы.
Класс точности через относительную погрешность СИ назначается двумя способами:
• если погрешность СИ имеет в основном мультипликативную составляющую, то пределы допускаемой основной относительной погрешности устанавливают по формуле
8= — •100% = ±Л-10″ =±9, (Ю)
X
где q – отвлеченное положительное число, выбираемое из стандартизованного ряда значений;
• если СИ имеют как мультипликативную, так и аддитивную составляющие, „ то класс точности обозначается двумя Цифрами, соответствующими значениям с и d формулы
где Х%- больший по модулю из пределов измерений (верхний предал измерения, или сумма пределов измерения для приборов с нулем посередине); с> d – положительные числа, выбираемые из стандартизованного ряда. Причем, как правило, c>d. Например, класс точности 0,02/0,01 означает, что с=0,02, а ^=0,01, т.е. приведенное значение относительной погрешности к началу Диапазона измерения у„=Ю,02%, а к концу – ук=0,01%.
Пределы допускаемых дополнительных погрешностей, ^ак правило, устанавливают в виде дольного значения предела допускаемой основной погрешности.
Обозначения классов точности в документах и на приборах приведены в табл. 1.
Таблица 1 Формулы вычисления погрешностей и обозначение классов точности СИ
|
Вид |
Формула по |
Примеры пределов |
Обозначение класса |
СИ, |
||||
|
погреш |
тексту |
допускаемой погрешности |
точно>сти |
рекомендуемые |
||||
|
ности |
вНТД |
на СИ |
к обозначению |
|||||
|
N |
таким способом |
|||||||
|
Д = ± я |
Д = ± ОД А |
Класс |
Меры |
|||||
|
Д = ± (а + Ьх) |
точности |
III |
||||||
|
Абсо |
N или |
Тоже |
||||||
|
лютная |
класс |
|||||||
|
точности |
||||||||
|
(10) |
III |
|||||||
|
8=±0,5 % |
Класс |
© |
Мосты |
|||||
|
точности |
переменного |
|||||||
|
0,5 |
тока, счетчики, |
|||||||
|
Отно- |
делители, |
|||||||
|
измерительные |
||||||||
|
ситель- |
( |
( |
Y |
трансформаторы |
||||
|
ная |
(11) |
д – |
Класс |
0,02/0,01 |
Цифровые СИ, |
|||
|
8 = ± |
0,02 + 0,01 |
К |
-1 |
% точности |
магазины |
|||
|
V |
V |
X |
л / |
0,02/0,01 |
емкостей |
|||
|
(сопротивлений) |
||||||||
|
(9) |
а) при Xtf=XK |
Класс |
1,5 |
Аналоговые СИ; |
||||
|
у=±1,5% |
точности |
если Адг в |
||||||
|
Приве |
1,5 |
единицах |
||||||
|
величины |
||||||||
|
денная |
б) Хы– длина шкалы |
Класс |
Омметры; если |
|||||
|
или се части, мм |
точности |
Хы определяется |
||||||
|
у=±0,5% |
0,5 |
длиной шкалы |
||||||
|
или ее части |
ПРИМЕР. Отсчет по шкале прибора с пределами измерений 0 – 50 А и равномерной шкалой составил 25 А. Пренебрегая другими видами погрешностей измерения, оценить пределы допускаемой абсолютной погрешности этого отсчета при использовании различных СИ класса точности: 0,02/0,01; (од) и 0,5.
|
1. |
Для СИ класса точностии,02/0,01: |
||
|
6= –х |
|||
|
=± c + d |
-1 |
||
|
Так как х=25; ^*=50; с=0,02; *М),01 и 6 – в %, то |
|||
|
Д = ±( 002 + 0,01| — – 1 11— = ±0,008 А. |
|||
|
I |
25 |
JJlOO |
|
|
2. |
Для СИ класса точности (g): |
||
|
6 = ± – ; |
Л ±^ |
=±0,125А. |
х100
3.Для СИ класса точности 0,5:
д
у = ± ——; здесь X^SO, тогда Д = ±5 ° А г „ « ,25д.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для любого прибора характерно отклонение показаний от фактического значения измеряемой величины. Данное диапазон характеризуется приборной погрешностью.
Не известно точно, чему равна приборная погрешность, и как именно она искажает конкретное измерение. Тем самым по своей сути она близка к случайной погрешности, не смотря на то, что является систематической.
Для оценки систематической приборной погрешности также применяют методы математической статистики:
Здесь дельта − приборная погрешность, соответствующая выбранной доверительной вероятности “а”; t – коэффициент Стьюдента при выбранной доверительной вероятности “a” и числе измерений n, стремящемся к бесконечности; б – максимальная приборная погрешность.
Величина максимальной приборной погрешности зависит от прибора.
1. Для стрелочных электроизмерительные приборов, у которых указан класс точности:
где A наибольшее значение, которое может быть измерено по шкале прибора; K – класс точности прибора.
2. Для цифровых приборов максимальная приборная погрешность обычно указывается в паспорте прибора.
3. Если при измерениях используется прибор, у которого класс точности неизвестен или прибор не имеет класса точности (например, измерительная линейка или секундомер), максимальную приборную погрешность принимают равной цене наименьшего деления его шкалы.
В существенном числе лабораторных задач, при величине доверительной вероятности 95%, погрешность измерительного прибора можно принять равной половине цены деления.
Систематические погрешности при повторных измерениях остаются постоянными или изменяются по определенному закону.
Когда судят о погрешности, подразумевают не значение, а интервал значений, в котором с заданной вероятностью находится истинное значение. Поэтому говорят об оценке погрешности. Если бы погрешность оказалась измеренной, т.е. стали бы известны её знак и значение, то её можно было бы исключить из действительного значения измеряемой физической величины и получить истинное значение.
Для получения результатов, минимально отличающихся от истинного значения измеряемой физической величины, проводят многократные наблюдения и проводят математическую обработку полученного массива с целью определения и минимизации случайной составляющей погрешности.
Минимизация систематической погрешности в процессе наблюдений выполняется следующими методами: метод замещения (состоит в замещении измеряемой величины мерой), метод противопоставления (состоит в двух поочерёдных измерениях при замене местами меры и измеряемого объекта), метод компенсации погрешности по знаку (состоит в двух поочерёдных измерениях, при которых влияющая величина становится противоположной).
При многократных наблюдениях возможно апостериорное (после выполнения наблюдений) исключение систематической погрешности в результате анализа рядов наблюдений. Рассмотрим графический анализ. При этом результаты последовательных наблюдений представляются функцией времени либо ранжируются в порядке возрастания погрешности.
Рассмотрим временную зависимость. Будем проводить наблюдения через одинаковые интервалы времени. Результаты последовательных наблюдений являются случайной функцией времени. В серии экспериментов, состоящих из ряда последовательных наблюдений, получаем одну реализацию этой функции. При повторении серии получаем новую реализацию, отличающуюся от первой.
Реализации отличаются преимущественно из-за влияния факторов, определяющих случайную погрешность, а факторы, определяющие систематическую погрешность, одинаково проявляются для соответствующих моментов времени в каждой реализации. Значение, соответствующее каждому моменту времени, называется сечением случайной функции времени. Для каждого сечения можно найти среднее по всем реализациям значение. Очевидно, что эта составляющая и определяет систематическую погрешность. Если через значения систематической погрешности для всех моментов времени провести плавную кривую, то она будет характеризовать временную закономерность изменения погрешности. Зная закономерность изменения, можем определить поправку для исключения систематической погрешности. После исключения систематической погрешности получаем «исправленный ряд результатов наблюдений».
Известен ряд способов исключения систематических погрешностей, которые условно можно разделить па 4 основные группы:
- устранение источников погрешностей до начала измерений;
- исключение почетностей в процессе измерения способами замещения, компенсации погрешностей по знаку, противопоставления, симметричных наблюдений;
- внесение известных поправок в результат измерения (исключение погрешностей начислением);
- оценка границ систематических погрешностей, если их нельзя исключить.
По характеру проявления систематические погрешности подразделяют на постоянные, прогрессивные и периодические.
Постоянные систематические погрешности сохраняют свое значение в течение всего времени измерений (например, погрешность в градуировке шкалы прибора переносится на все результаты измерений).
Прогрессивные погрешности – погрешности, которые в процессе измерении подрастают или убывают (например, погрешности, возникающие вследствие износа контактирующих деталей средств измерения).
И группу систематических погрешностей можно отнести: инструментальные погрешности; погрешности из-за неправильной установки измерительного устройства; погрешности, возникающие вследствие внешних влияний; погрешности метода измерения (теоретические погрешности); субъективные погрешности.