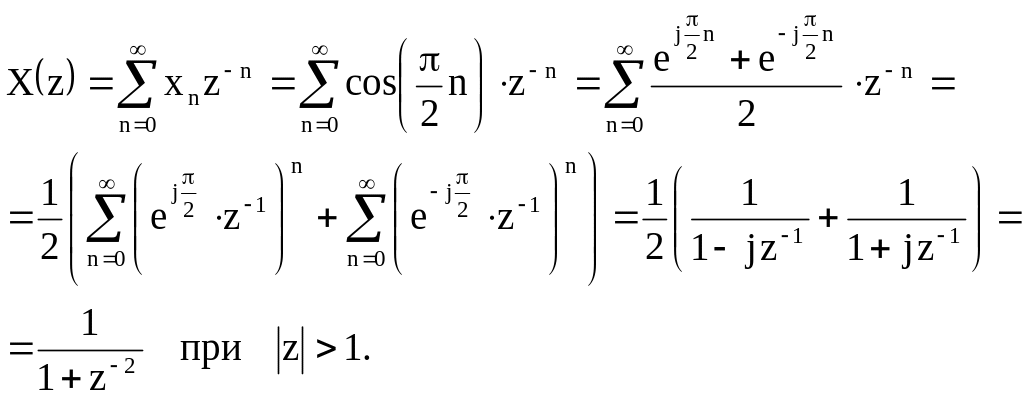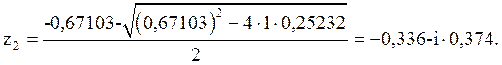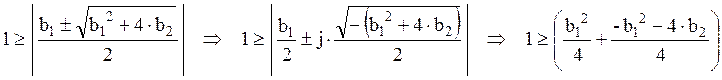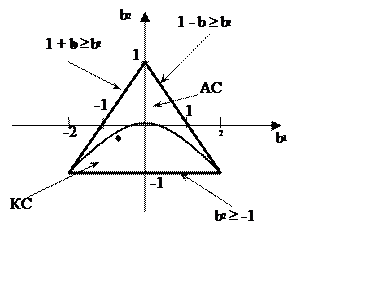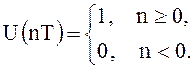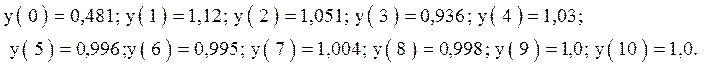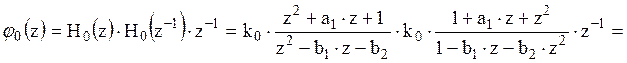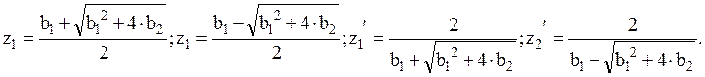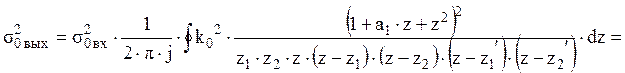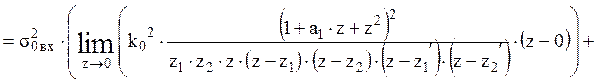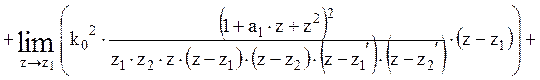Как найти системную функцию

Как найти системную функцию

  1. И мпульсная характеристика и системная

функция цифрового
фильтра

    1. Импульсная
      характеристика фильтра. Понятие о

нерекурсивных и рекурсивных цифровых
фильтрах

Цифровым
фильтром дискретного
сигнала называется линейная
частотно-избирательная система,
реализуемая на основе вычислительного
устройства.

Пусть
при действии на входе цифрового фильтра
последовательности отсчетов xn
на его выходе действует последовательность
yn (рисунок 3.1).

Рисунок 3.1

Если
n-ый отсчет выходного
сигнала фильтра yn
зависит только от отсчетов входного
сигнала в данный и предшествующие
моменты дискретного времени xn,
xn-1,
..и т.д., то такой фильтр называется
нерекурсивным.

Если
n-ый отсчет выходного
сигнала фильтра yn
зависит не только от отсчетов входного
сигнала в данный и предшествующие
моменты дискретного времени xn,
xn-1
..и т.д., но и от отсчетов выходного сигнала
в предшествующие моменты времени yn-1,
yn-2,
..и т.д., то такой фильтр называется
рекурсивным.

Импульсной
характеристикой цифрового фильтра
называется выходной сигнал фильтра при
действии на его входе единичного отсчета
и при нулевых начальных условиях (рисунок
3.2).

Фильтр
с конечной импульсной характеристикой
называется КИХ – фильтром (КИХ – конечная
импульсная характеристика). Фильтр с
бесконечной импульсной характеристикой
называют БИХ – фильтром.

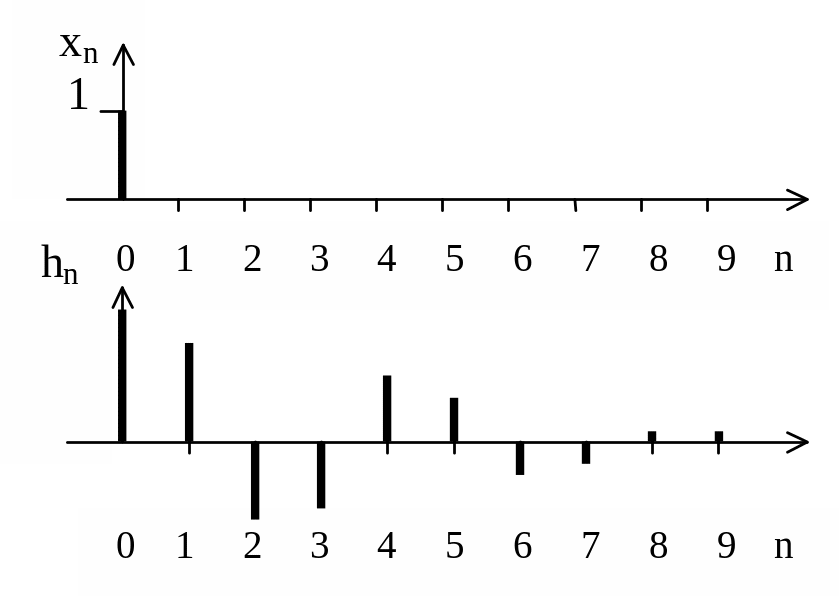
Рисунок
3.2 – Единичный отсчет xn
и импульсная

характеристика hn

3.2.
Определение выходного сигнала фильтра

по
входному сигналу и импульсной
характеристике

Определение
выходного сигнала цифрового фильтра
по входному сигналу и импульсной
характеристике основано на определении
импульсной характеристики и принадлежности
фильтра к линейным системам, для которых
справедлив принцип суперпозиции.

На
рисунке 3.3 приведен пример определения
выходного сигнала фильтра в случае,
когда входной сигнал xn
содержит два отсчета x0
= 2 и x1=
2, а импульсная характеристика 3 отсчета
h0 =
1, h1=0.5,
h2 =
0.25.

Сначала определим реакцию фильтра на
отсчет x0, считая,
что x1=0. Если бы
вместо x0 действовал
единичный отсчет, то выходным сигналом
была бы импульсная характеристика.

Рисунок 3.3 – Определение выходного
сигнала фильтра по входному сигналу и
импульсной характеристике

Так как фильтр линейная система, то при
входном отсчете в x0
раз больше единичного, выходной
сигнал будет представлять собой
импульсную характеристику, все отсчеты
которой умножены на x0,
– x0 hn.

Определим реакцию фильтра на отсчет
сигнала x1 при x0
=0. При x1=1 выходной
сигнал фильтра представлял бы собой
импульсную характеристику, запаздывающую
на один отсчет hn-1.
При отсчете x1,
отличном от единицы, реакцией фильтра
будет запаздывающая на один отсчет
импульсная характеристика, все отсчеты
которой умножены на x1,
– x1 hn-1.

Согласно принципу суперпозиции полученные
реакции суммируются.

В результате

,

,
…..

В общем случае

(3.1)

Согласно последнему соотношению

Однако в рассмотренном примере x2
= 0, поэтому, как видно из рисунка,

В общем случае

В данном примере x2
= x3 = 0, h3
= 0, поэтому

Соотношение 3.1 представляет собой
дискретную свертку последовательностей
xn и
hn,
т.е. выходной сигнал фильтра представляет
собой дискретную свертку входного
сигнала и импульсной характеристики
фильтра.

На рисунке 3.4 дано графическое представление
дискретной свертки при конечной
импульсной характеристике фильтра,
содержащей N+1 отсчет. Из
рисунка видно, что yn
зависит только от отсчетов входного
сигнала xn,
xn-1,
.. xn–N,

следовательно,
данный фильтр является нерекурсивным.

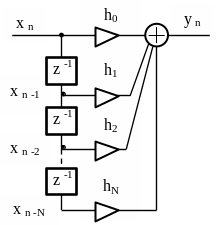
Рисунок 3.4 – Нерекурсивный цифровой
фильтр

Z – преобразование
дискретной свертки (3.1) входного сигнала
xn и
импульсной характеристики hn
равно произведению Z –
преобразований этих последовательностей.

Y(z) = H(z)
X(z),

где

Системной функцией цифрового фильтра
называется отношение Z
– преобразования Y(z)
выходного сигнала фильтра yn
к Z – преобразованию
X(z)
входного сигнала xn.

Из предыдущих соотношений следует, что
системная функция H(z)
представляет собой Z
– преобразование импульсной характеристики
фильтра

(3.2)

Для нерекурсивного фильтра с конечной
импульсной характеристикой имеем

Следовательно, системная функция
нерекурсивного цифрового фильтра
представляет собой полином степени N
комплексной переменной z
-1. Коэффициенты этого полинома
являются отсчетами импульсной
характеристики фильтра.

. В рекурсивном фильтре (рисунок 3.5) n
– ый отсчет выходного сигнала фильтра
yn
связан линейными соотношениями с
отсчетами входного сигнала в данный и
предшествующие моменты дискретного
времени xn,
xn-1,
..xn–N
и отсчетами выходного сигнала в
предшествующие моменты времени yn-1,
yn-2,
.. yn–N.
Соответствующие коэффициенты
пропорциональности B0,
B1, .. BN,
A1, A2,
.. AN
определяют свойства фильтра.

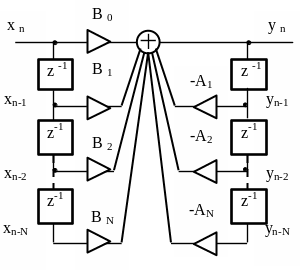
Рисунок
3.5 – Прямая форма программной реализации

рекурсивного фильтра

Согласно схеме

Выразим Z – преобразование
выходного сигнала Y(z)
через Z-преобразование
входного сигнала

Из последнего соотношения получим

Таким образом,
системная функция цифрового фильтра в
общем случае представляет собой
дробно-рациональную функцию. Полином
числителя описывает нерекурсивную
часть фильтра, а полином знаменателя –
рекурсивную.

Нулем системной функции называется
значение комплексной переменной z,
при котором системная функция равна
нулю.

Полюсом системной функции называется
значение комплексной переменной z,
при котором системная функция равна
бесконечности.

Задача №3.1

На входе фильтра действует сигнал

Выходной сигнал фильтра представляет
собой единичный отсчет

Определите системную функцию и импульсную
характеристику фильтра.

Решение задачи №3.1

Для нахождения системной функции
определим Z – преобразования
входного и выходного сигналов


Системная функция определяется
соотношением

Так как коэффициенты системной функции
нерекурсивного фильтра являются
отсчетами его импульсной характеристики,
находим:

Импульсная характеристика фильтра
приведена на рисунке 3.6.

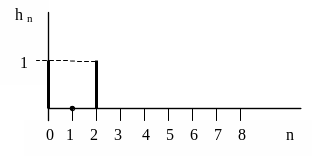
Рисунок 3.6 – Импульсная характеристика
фильтра

Задача №3.2

Определите системную функцию и импульсную
характеристику цифрового фильтра
рисунка 3.7. Определите выходной сигнал
фильтра при действии на входе сигнала

Постройте графики входного сигнала xn,
импульсной характеристики hn,
и выходного сигнала yn.

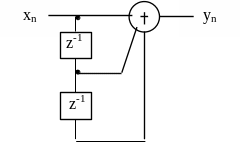
Рисунок 3.7

Решение задачи
№3.2

Из рисунка 3.7 следует, что

Выразим Z – преобразование
выходного сигнала фильтра через Z
– преобразование входного сигнала

Определим системную функцию фильтра

Коэффициенты системной функции
нерекурсивного цифрового фильтра
являются отсчетами его импульсной
характеристики, поэтому

Определим Z – преобразования
входного и выходного сигналов фильтра

Коэффициенты прямого Z –
преобразования выходного сигнала
фильтра являются отсчетами этого
сигнала.

Следовательно,

.

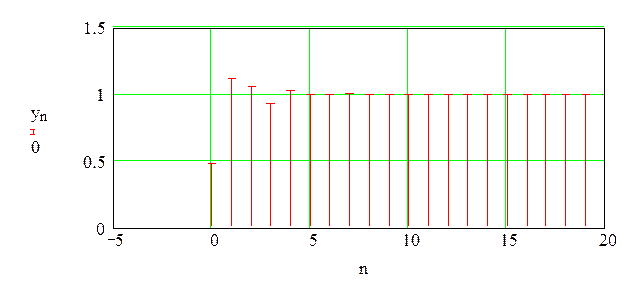
Временные диаграммы импульсной
характеристики, входного и выходного
сигналов приведены на рисунке 3.8.

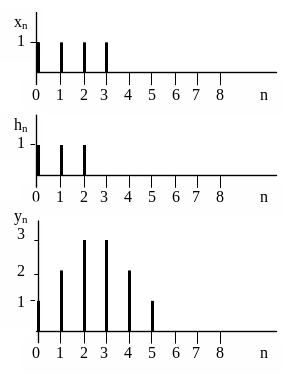
Рисунок 3.8 – Временные диаграммы
импульсной

характеристики, входного и выходного
сигналов

Задача №3.3

Определите системную функцию цифрового
фильтра рисунка 3.9 и найдите полюсы и
нули этой функции при

А = 0.9.

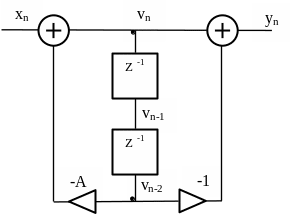
Рисунок 3.9

Решение задачи №3.3

Из схемы следует, что

Данный фильтр является рекурсивным,
так как n -ый отсчет сигнала
на выходе одного из сумматоров vn
зависит не только от отсчета входного
сигнала xn,
но и от задержанного на два интервала
дискретизации отсчета vn-2
этого же сигнала.

Выразим Z – преобразование
выходного сигнала фильтра через Z
– преобразование входного сигнала

Из первого уравнения выразим V(z)
через X(z),
подставим во второе уравнение и получим

Разделив Y(z)
на X(z), найдем
системную функцию

Системная функция H(z)
представляет собой дробно-рациональную
функцию. Знаменатель функции описывает
рекурсивную часть фильтра, а числитель
– нерекурсивную.

Для определения полюсов системной
функции знаменатель приравняем нулю и
найдем корни полученного квадратного
уравнения

Откуда

Для определения нулей системной функции
числитель приравняем нулю

Откуда

Задача №3.4

Определите импульсную характеристику
(с нулевого по третий отсчет) цифрового
фильтра рисунка 3.10 при

A
= – 0.5.

Рисунок 3.10

Решение задачи
№3.4

Учтем, что выходной сигнал фильтра yn
представляет собой импульсную
характеристику hn
при условии, что на входе фильтра
действует единичный отсчет

Заполним таблицу, учитывая, что

и

y-1=
0.

n

xn

yn =
hn

yn-1

0

1

1

0

1

0

0.500

1

2

0

0.250

0.500

3

0

0.125

0.250

Задача №3.5

На рисунке 3.11 приведена импульсная
характеристика цифрового фильтра.

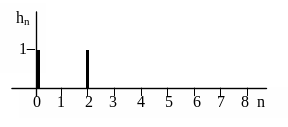
Рисунок 3.11 – Импульсная характеристика
фильтра

На входе фильтра действует сигнал

Определите сигнал на выходе фильтра.

Решение задачи
№3.5

Выходной сигнал фильтра yn
представляет собой дискретную свертку
входного сигнала xn
и импульсной характеристики hn


При n>1

Отсчеты y0 и y1
определяют переходной процесс на выходе
фильтра. В установившемся режиме выходной
сигнал фильтра равен нулю.

Задача №3.6

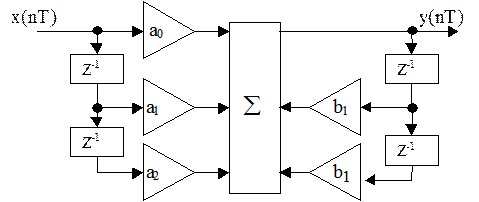
Определите системную функцию цифрового
фильтра рисунка 3.12.

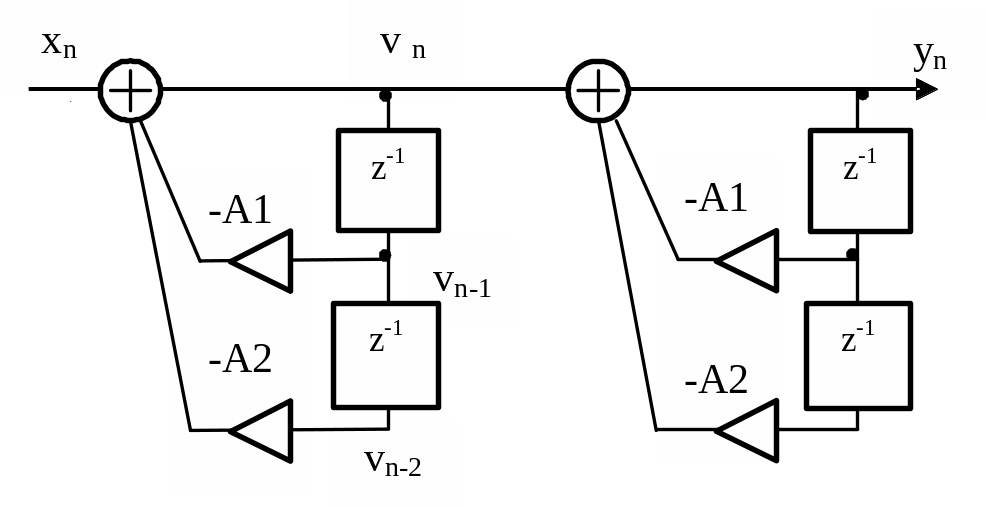
Рисунок 3.12

Решение задачи
№3.6

Согласно определению

где Y(z)
и X(z) – Z
– преобразования сигналов yn
и xn
соответственно.

Преобразуем последнее выражение, умножив
числитель и знаменатель дроби на Z
– преобразование V(z)
сигнала vn

где

– системная функция первого звена
фильтра,

– системная функция второго звена
фильтра.

Из рисунка видно, что звенья фильтра
одинаковы, поэтому H2(z)
= H1(z).

Следовательно,

Для определения системной функции
первого звена запишем выражение для
выходного сигнала фильтра

Воспользовавшись свойствами Z
– преобразования, получим

Обратите внимание на то, что в выражении
для H1(z)
перед коэффициентами A1
и A2 стоит знак «плюс», а
на схеме – «минус».

Системная функция фильтра определяется
соотношением

Задача №3.7

Импульсная характеристика цифрового
фильтра описывается соотношением

где α>0.

Определите системную функцию и приведите
схему фильтра (графическое представление
алгоритма цифровой фильтрации).

Решение задачи №3.7

Системная функция цифрового фильтра
H(z) представляет
собой Z – преобразование
его импульсной характеристики hn

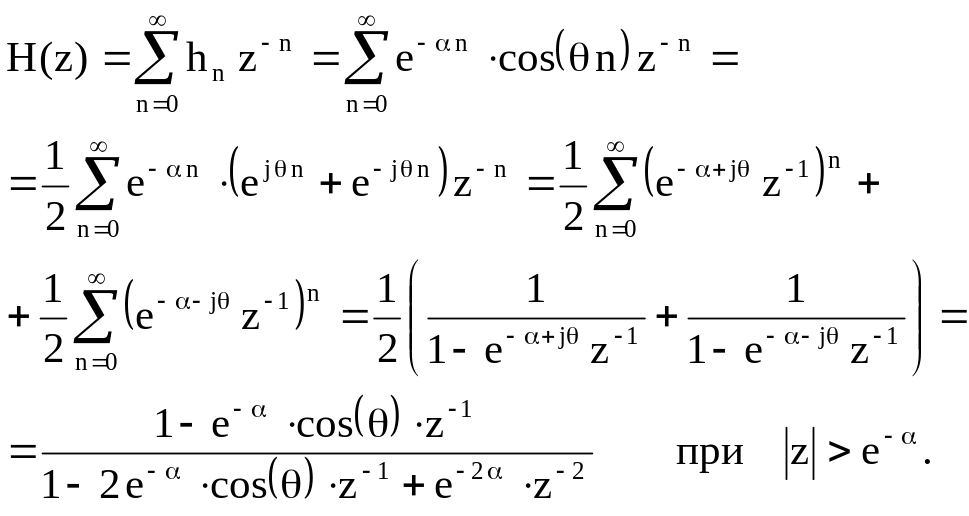
Обозначим

Тогда

Представим H(z)
в виде произведения двух системных
функций:

где

Такое представление системной функции
соответствует последовательному
соединению двух звеньев фильтра:
рекурсивного звена второго порядка с
системной функцией HA(z)
и нерекурсивного звена первого порядка
с системной функцией HB(z)
(рисунок 3.13). Заметим, что если в знаменателе
системной функции перед коэффициентами
A1 и A2 стоит
знак «+», то на схеме ему соответствует
знак «-».

Из рисунка видно, что одна и та же
переменная vn
действует на входе двух элементов
задержки, поэтому один из них можно
исключить и получить каноническую форму
фильтра, приведенную на рисунке 3.14.

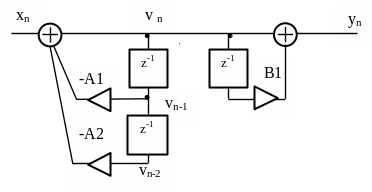
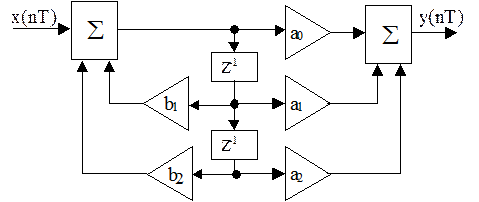
Рисунок 3.13 – Представление цифрового
фильтра

в виде последовательного соединения
двух звеньев

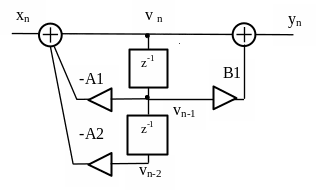
Рисунок 3.14 – Каноническая форма фильтра

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #

    10.06.20155.07 Mб13Методичка_ВТиИТ.rtf

  • #
Источник

Макеты страниц

предыдущие значения входного и выходного сигналов: Сигнал на выходе цифрового фильтра также представляет собой последовательность числовых значений, следующих с интервалом . Этот интервал является единым для всего устройства цифровой обработки сигналов.

Рис. 4.1. Сигнал на входе и на выходе цифрового фильтра

Поэтому если на вход цифрового фильтра подать простейший сигнал в виде единичного импульса (рис. 4.2, а)

то на выходе получим сигнал в виде дискретной последовательности числовых значений, следующих с интервалом

По аналогии с обычными аналоговыми цепями назовем этот ответный сигнал импульсной характеристикой фильтра (рис. 4.2, б). В отличие от импульсной характеристики аналоговой цепи функция является безразмерной.

Рис. 4.2. Единичный импульс и импульсная характеристика цифрового фильтра

Подадим на вход фильтра произвольный дискретный сигнал рис. 4.1, а), представляющий собой набор дискретных значений

Под действием первого элемента на выходе фильтра формируется последовательность умноженная на при действии последовательность умноженная на и сдвинутая вправо на величину и т. д. В результате на выходе получим последовательность причем

Таким образом, выходной сигнал определяется как дискретная свертка входного сигнала и импульсной характеристики. В этом отношении цифровые фильтры аналогичны обычным цепям, где выходной сигнал равен свертке входного сигнала и импульсной характеристики.

Формула (4.1) представляет собой алгоритм цифровой фильтрации. Если импульсная характеристика фильтра описывается последовательностью с конечным числом членов, то фильтр может быть реализован в виде схемы, изображенной на рис. 4.3. Здесь буквой обозначены элементы задержки сигнала на время (на одну ячейку); -элементы, умножающие сигнал на соответствующий коэффициент.

Схема, изображенная на рис. 4.3, не является электрической схемой цифрового фильтра; эта схема представляет собой графическое изображение алгоритма цифровой фильтрации и показывает последовательность арифметических операций, выполняемых при обработке сигнала.

Рис. 4.3. Схема нерекурсивного цифрового фильтра

Для цифровых фильтров, обрабатывающих сигналы в виде абстрактных числовых последовательностей, понятие «задержка на время » является не совсем корректным. Поэтому элементы, задерживающие сигнал на одну ячейку, на схемах цифровых фильтров обычно отмечают символом обозначающим задержку сигнала на языке -преобразований. В дальнейшем будем придерживаться этого обозначения.

Вернемся к схеме цифрового фильтра, изображенной на рис. 4.3, Такие фильтры, где для расчета используются лишь значения входного сигнала, называют простыми или нерекурсивными.

Алгоритм нерекурсивного фильтра легко записать, если известна импульсная характеристика фильтра. Для практической реализации алгоритма необходимо, чтобы импульсная характеристика содержала конечное число членов. Если импульсная характеристика содержит бесконечное число членов, но они быстро убывают по величине, то можно ограничиться конечным числом членов, отбросив те, значения которых малы. В случае, если элементы импульсной характеристики не убывают по величине, алгоритм нерекурсивного фильтра оказывается нереализуемым.

Рис. 4.4. -цепь

В качестве примера рассмотрим простейший цифровой фильтр, аналогичный -цепи (рис. 4.4). Импульсная характеристика -цепи имеет вид

Чтобы записать импульсную характеристику соответствующего цифрового фильтра, в выражении следует заменить на Однако импульсная характеристика -цепи имеет размерность а импульсная характеристика цифрового фильтра должна быть безразмерной. Поэтому опустим множитель в выражении (4.2) и запишем импульсную характеристику цифрового фильтра в виде

Такая импульсная характеристика содержит бесконечно много членов, но их величина убывает по экспоненциальному закону, и можно ограничиться членами, выбирая таким, чтобы

Теперь можно записать выражение для сигнала на выходе фильтра

Это выражение является одновременно алгоритмом цифрового фильтра. Схема этого фильтра представлена на рис. 4.5.

Второй подход к анализу процессов в цифровых фильтрах аналогичен операторному методу анализа обычных аналоговых цепей, только вместо преобразования Лапласа используют -преобразование.

Рис. 4.5. Схема нерекурсивного цифрового фильтра, аналогичного -цепи

Определим параметр цифрового фильтра, аналогичный передаточной функции электрической цепи. Для этого применим -преобразование к импульсной характеристике цифрового фильтра:

Функцию называют системной функцией фильтра.

В соответствии с выражением (4.1) сигнал на выходе цифрового фильтра равен дискретной свертке входного сигнала и импульсной характеристики фильтра. Применяя к этому выражению теорему о -преобразовании свертки, получим, что -преобразование выходного сигнала равно -преобразованию входного сигнала, умноженному на системную функцию фильтра:

Таким образом, системная функция играет роль передаточной функции цифрового фильтра.

В качестве примера найдем системную функцию цифрового фильтра первого порядка, аналогичного -цепи:

Третий метод анализа прохождения сигналов через цифровые фильтры аналогичен классическому методу дифференциальных уравнений. Рассмотрим этот метод на примере цепей порядка.

Простейшей аналоговой цепью 1-го порядка является -цепь (см. рис. 4.4), прохождение сигналов через которую описывается дифференциальным уравнением

Для дискретной цепи вместо дифференциального уравнения (4.8) должно быть записано разностное уравнение, где входной и выходной сигналы задаются для дискретных моментов времени а вместо производной должна фигурировать разность соседних значений сигнала . Для дискретной цепи 1-го порядка разностное уравнение может быть записано в достаточно общем виде

Применим к уравнению -преобразование

откуда найдем системную функцию фильтра

Формула (4.10) является достаточно общим выражением для системной функции цифрового фильтра 1-го порядка. При она совпадает с полученным ранее выражением (4.7) для системной функции цифрового фильтра, эквивалентного -цепи.

Найдем алгоритм цифровой фильтрации, соответствующий системной функции (4.10). Для этого решим уравнение (4.9) относительно

Эквивалентная схема этого алгоритма приведена на рис. 4.6. По сравнению с нерекурсивным фильтром (см. рис. 4.5) здесь добавилась своеобразная «цепь обратной связи», которая означает, что значения выходного сигнала используются в последующих

Рис. 4.6. Схема рекурсивного цифрового фильтра, аналогичного -цепи

расчетах. Фильтры такого типа называют рекурсивными.

Алгоритм (4.11) соответствует фильтру, который полностью эквивалентен рассмотренному ранее нерекурсивному фильтру. Но для определения одного значения выходного сигнала с помощью алгоритма нерекурсивного фильтра (4.4) требуется выполнить операций, а при использовании алгоритма рекурсивного фильтра (4.11) — только две операции. В этом состоит основное преимущество рекурсивных фильтров. Кроме того, рекурсивные фильтры позволяют производить обработку сигнала с более высокой точностью, так как они позволяют более правильно реализовать импульсную характеристику без отбрасывания ее «хвоста». Рекурсивные фильтры позволяют реализовать алгоритмы, вообще нереализуемые с помощью нерекурсивных фильтров. Например, при фильтр, работающий по схеме рис. 4.6, является, по существу, идеальным накопителем-интегратором и имеет импульсную характеристику вида Фильтр с такой характеристикой по нерекурсивной схеме не может быть реализован.

Рассмотренные примеры показывают, что нет смысла применять нерекурсивные алгоритмы для создания цифровых фильтров с импульсной характеристикой большой протяженности. В этих случаях целесообразнее использовать рекурсивные фильтры.

Область применения нерекурсивных алгоритмов — это реализация цифровых фильтров с импульсной характеристикой, содержащей небольшое число членов. Примером может служить простейший дифференциатор, сигнал на выходе которого равен приращению входного сигнала:

Схема такого цифрового фильтра изображена на рис. 4.7.

Рис. 4.7. Схема простейшего цифрового дифференциатора

Рассмотрим теперь цифровой фильтр общего вида, который описывается уравнением

Это уравнение можно рассматривать и как разностное уравнение порядка и как алгоритм цифровой фильтрации, если его переписать иначе, а именно

Рис. 4.8. Схема рекурсивного цифрового фильтра порядка

Алгоритму (4.13) соответствует схема, изображенная на рис. 4.8. Найдем системную функцию такого фильтра. Для этого применим к уравнению -преобразование:

откуда

Выражение (4.14) позволяет установить связь между шачениями элементов схемы фильтра и системной функцией. Коэффициенты в числителе системной функции определяют значения коэффициентов при

Импульсная характеристика колебательного контура имеет

где размерный множитель.

Заменяя на и опуская множитель запишем импульсную характеристику соответствующего цифрового фильтра

Найдем системную функцию этого фильтра как -преобразование от импульсной характеристики:

Таким образом,

Алгоритм данного фильтра запишем в виде

Схема, соответствующая этому алгоритму, приведена на рис. 4.10.

Рис. 4.10 Схема цифрового фильтра 2-го порядка, аналогичного колебательному контуру

Рис. 4.11. Положение нулей и полюсов системной функции цифрового фильтра 2-го порядка, аналогичного колебательному контуру

Анализ выражения для системной функции показывает, что она имеет один нуль при и два полюса: при при Расположение особых точек на плоскости комплексного переменного показано на рис. 4.11. Отметим, что с ростом добротности колебательного контура, соответствующего данному цифровому фильтру, величина коэффициента затухания а уменьшается, стремится к единице и все особые точки приближаются к единичной окружности, что подтверждает сделанный ранее общий вывод.

1

Оглавление

  • ПРЕДИСЛОВИЕ
  • ВВЕДЕНИЕ
  • Глава 1. ОБЩЕЕ ПОНЯТИЕ О ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ
  • § 1.1. Дискретные и цифровые сигналы
  • § 1.2. Дискретные и цифровые фильтры
  • § 1.3. Преимущества и недостатки цифровой обработки сигналов
  • Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
  • § 2.1. Основы дискретизации непрерывных сигналов
  • Спектры дискретизированных сигналов.
  • Восстановление непрерывного сигнала. Погрешности дискретизации и восстановления сигнала.
  • Дискретизация сигналов в спектральной области.
  • Число степеней свободы сигнала.
  • § 2.2. Квантование сигналов
  • Аналого-цифровое преобразование.
  • § 2.3. Устройства для дискретизации, квантования и восстановления непрерывных сигналов
  • Сглаживающие фильтры.
  • Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
  • § 3.2. Дискретное преобразование Фурье
  • § 3.3. Быстрое преобразование Фурье
  • § 3.4. Дискретное преобразование Лапласа
  • § 3.5. z-преобразование
  • § 3.6. Обратное z-преобразование
  • § 3.7. Основные свойства z-преобразования
  • Глава 4. ЦИФРОВЫЕ ФИЛЬТРЫ
  • § 4.2. Важнейшие характеристики цифровых фильтров
  • § 4.3. Частотные характеристики цифровых фильтров
  • § 4.4. Формы реализации цифровых фильтров
  • § 4.5. Основы синтеза цифровых фильтров
  • Прямой синтез цифровых фильтров.
  • Методы синтеза фильтров с конечной импульсной характеристикой.
  • § 4.6. Эффекты квантования в цифровых фильтрах
  • Ошибки, вызываемые неточными значениями постоянных параметров фильтра.
  • Ошибки, вызванные квантованием результатов вычислений.
  • Предельные циклы низкого уровня.
  • § 4.7. Вопросы реализации и применения цифровых фильтров
  • ПРИЛОЖЕНИЯ
  • Приложение 1. Вывод формулы спектральной плотности дискретизированного сигнала
  • Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
  • ЛИТЕРАТУРА
Источник

                              
6. Нахождение нулей и полюсов

Возьмем
системную функцию ЦФ, синтезированного по методу билинейного преобразования:        

, где  ,,,,.

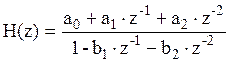
Чтобы
найти значения нулей и полюсов, перейдем к положительным степеням z: .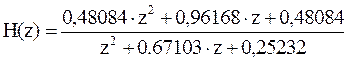

Найдем значения полюсов, для этого приравняем знаменатель
системной функции к нулю, чтобы получить характеристическое уравнение:

, найдем
корни этого уравнения:

,

Значения
полюсов:   и   .

Для
нахождения значения нулей вынесем общий множитель 0,48084  из числителя, чтобы
получить характеристическое уравнение:, корни этого
уравнения:

,
.

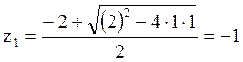
Значения нулей:  и 
.

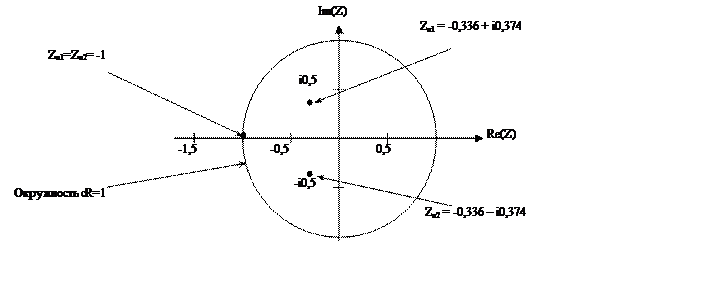
Картина нулей и
полюсов на комплексной Z-плоскости

              7. Проверка условия устойчивости фильтра

Устойчивость
фильтра определяется значениями коэффициентов b1 и b2.

.

Корни
этого уравнения:, .

Фильтр
устойчив, когда ïZï  1.или  , т.е. .

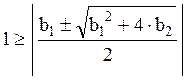
Рассмотрим
два случая:

7.1. 
Когда дискриминант больше либо
равен нулю , отсюда:

в результате решения
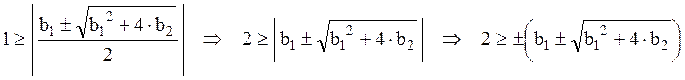
этого неравенства получаем четыре попарно равных неравенства: .

7.2. 
Когда дискриминант меньше нуля , то:

.

По полученным
неравенствам построим треугольник устойчивости:

Треугольник
устойчивости

Так как точка с координатами (b1,b2)
внутри треугольника устойчивости, то ЦФ ФНЧ является устойчивым.

Колебательные
системы (КС): .

Апериодические
системы (АС): .

Судя по
треугольнику устойчивости, данный ЦФ ФНЧ является колебательной системой.

            8. Расчет
первых 10 отсчетов импульсной и переходной                           характеристик, выражение для системной функции и
АЧХ ЦФ

Выражение
для передаточной функции фильтра, рассчитанного  методу билинейного
преобразования:

, где  ,,,,.

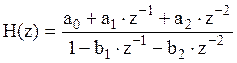
Расчет
АЧХ для фильтра, синтезированного по методу билинейного преобразования:

,

В
системной функции H(z) производится замена z-1 à exp(-jwT):

, разложение
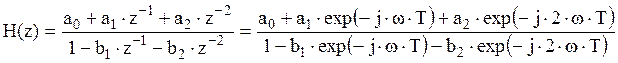
экспоненты через синусы и косинусы:

,
где

,

.

АЧХ:
.

С помощью передаточной функции запишем разностное
уравнение:

, n³0.

Для расчета первых 10 отсчетов импульсной
характеристики производится замена: ,
где ,

.

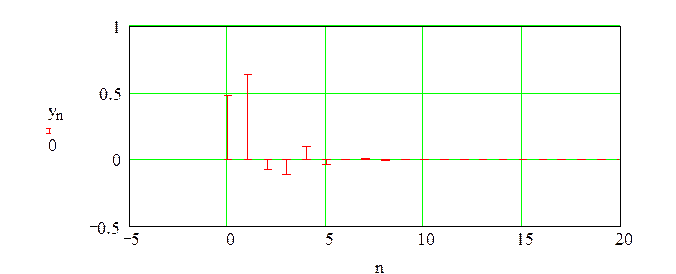
Численные значения первых 10
отсчетов импульсной характеристики:

y(0)=0,481; y(1)=0.639;
y(2)= -0,069; y(3)= – 0,115; y(4)=
0,094;               

y(5)= -0,034;y(6)=
-7,245∙10-4; y(7)= 9,178∙10-3; y(8)= -5,976∙10-3;
                 

y(9)= 1,694∙10-3; 
y(10)= 3,71∙10-4.

График импульсной характеристики

Для расчета первых 10 отсчетов переходной
характеристики в разностном уравнении производится замена: , где

Численные значения первых 10 отсчетов переходной
характеристики:

График
переходной характеристики

9. Структурная схема
фильтра для прямой и канонической форм
реализации

Системная
функция ЦФ ФНЧ, синтезированного в пункте 3:

.

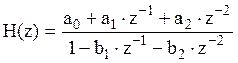
Структурная схема
фильтра для прямой формы реализации

Структурная схема
фильтра для канонической формы реализации

10.
Алгоритм обработки фильтра для прямой и канонической форм реализации и объем
вычислительных операций на один отсчет выходного сигнала

Исходя из структурной схемы фильтра для прямой и канонической
форм реализации запишем разностное уравнение (n≥0):

На рисунке 10.1 проиллюстрирован принцип формирования
выходного сигнала в ЦФ.

 

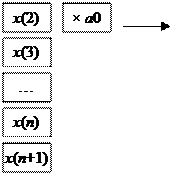Рис. 10.1. –
Формирование выходного сигнала в ЛЦФ

 

 

11.
Расчет среднеквадратического значения шума квантования всех источников

Т.к. , то для уменьшения  схему ЦФ можно
упростить. Эквивалентная шумовая схема фильтра для прямой формы реализации учитывая
то что  т.е. умножения не
происходит, и то что  при
умножении на целое число шумы не вносятся:

Эквивалентная шумовая схема фильтра для прямой формы
реализации

Где –  это
шумы АЦП,  это шумы вносимые
при умножении на коэффициент ,
 и  это шумы вносимые
при умножении на коэффициенты  и
 соответственно.
Нахождение среднеквадратического значения шума АЦП:

.

,

,

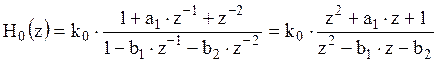
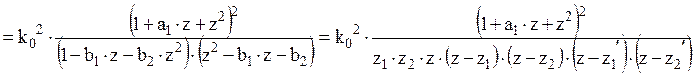
, где  и  корни характеристического
уравнения , а  и  корни
характеристического уравнения .

То есть .

.

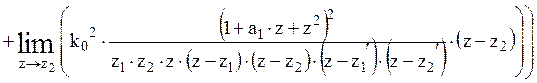
В результате преобразования и подстановки, получаем:

.

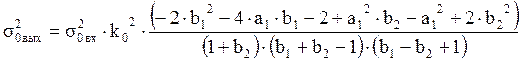
, , где С разрядность
АЦП.

Принимаем
разрядность АЦП равной 8. Тогда:,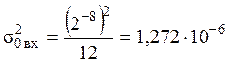
отсюда .

Источник

Расчет важнейшей характеристики ЦФ – частотного коэффициента передачи удобно проводить, используя методы z-преобразований. Сопоставим дискретным сигналам  их z-преобразования  соответственно. Выходной сигнал фильтра  есть свертка входного сигнала и импульсной характеристики. Ввиду свойств z-преобразования, выходному сигналу отвечает функция:

.                                               (3.12)

Системной функцией стационарного линейного ЦФ называют отношение z-преобразования выходного сигнала к z-преобразованию сигнала на входе. Соотношение (3.12) устанавливает, что системная функция фильтра

                                  (3.13)

есть z-преобразование импульсной характеристики.

Сравнивая выражения (3.11) и (3.13), приходим к следующему выводу: чтобы получить частотный коэффициент передачи ЦФ из его системной функции, в последней нужно сделать подстановку .

Пример

Цифровой фильтр имеет импульсную характеристику, состоящую из двух ненулевых отсчетов: . Вычислить частотный коэффициент передачи  фильтра.

Определим системную функцию ЦФ, применив z-преобразование к импульсной характеристике

.

Выполнив подстановку , получим частотный коэффициент передачи:

.

Уравнение АЧХ фильтра имеет вид:

,

в то время как фазо-частотная характеристика (ФЧХ) описывается выражением:

.

Амплитудно-частотная характеристика фильтра является периодической функцией, но практически она имеет смысл лишь в интервале частот от 0 до . На верхней частоте этого интервала каждому периоду дискретизированного гармонического сигнала соответствуют два отсчета. По теореме Котельникова – это есть предельное значение частоты сигнала, который может быть однозначно восстановлен по своим отсчетам. Заметим, что если на вход такого фильтра поступает гармонический сигнал с частотой, значительно более низкой, чем частота дискретизации, такой, что , то

.

Поэтому такая система приближенно выполняет операцию дифференцирования относительно медленных входных сигналов.

Вам также может понравиться

Источник

Добавить комментарий