Как найти систему неравенств по точкам треугольника

Презентация к защите

Задача 1. Даны вершины треугольника А(-3;-2), В(1;8), С(5;3).

Найти: а) уравнения всех трех его сторон;

б) систему неравенств, определяющих множество точек, принадлежащих треугольнику, включая его стороны;

в) внутренний угол А треугольника в градусах и минусах;

г) длину высоты, опущенной из вершины А;

д) площадь треугольника.

а) Уравнения сторон найдем по формуле прямой, проходящей через две данные точки

Уравнение стороны АВ: , или (АВ).

Уравнение стороны АС: или (АС)

б) Каждая из прямых, уравнения которых только это найдены, разделяет плоскость на две полуплоскости, определяемые соответствующими неравенствами.

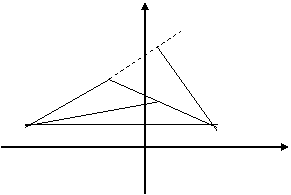
Чтобы определить знаки этих неравенств, возьмем координаты какой-нибудь точки заведомо расположенной внутри треугольника АВС (см. рисунок 1). Такой точкой является, например точка N (0;1) подставляя координаты этой точки в уравнения граничных прямых (сторон) в силу того, что точка N не лежит ни на одной сторон, получим следующую систему неравенств. определяющих множество внутренних точек треугольника.

Система неравенств определяет множество точек, принадлежащих треугольнику АВС, включая его стороны.

в) Внутренний угол треугольника найдем, зная угловые коэффициенты сторон АВ и АС, образующих этот угол, по формуле .

Угловые коэффициенты прямых выложим по формуле .

Получим ; .

Тогда

. Угол определяем с помощью таблицы тангенсов или калькулятора

г) Длину высоты AD ^ BC (рис. 1) найдем как расстояние от данной точки А(-3;-2) до данной прямой ВС: 5х + 4у – 37 = 0 по формуле

, где А, В, С – коэффициенты прямой, – координаты данной точки.

Получим (мин. ед.)

д) Площадь треугольника можно вычислить несколькими способами.

Вычислить ее через координаты вершин треугольника по формуле .

Получим .

Итак, площадь треугольника SABC = 30 кв. ед.

Как задать треугольник системой неравенств

уравнение и длину высоты А D ; уравнение и длину медианы СЕ; внутренний угол В; систему линейных неравенств, определяющую треугольник. Сделать чертеж.

Y

1. Составим уравнения всех сторон треугольника, используя уравнение прямой, проходящей через две данные точки.

.

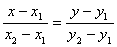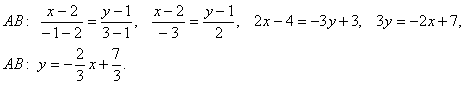
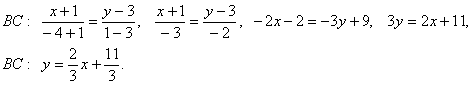
Так как точки А и С имеют одинаковую ординату, используем данное уравнение в преобразованном виде:

.

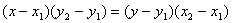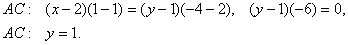
2. Найдем длину высоты А D . Используем формулу расстояния от точки до прямой:

.

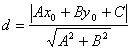Приведем уравнение ВС к общему уравнению прямой.

.

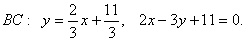
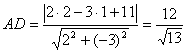3. Составим уравнение высоты А D . Она проходит через точку А(2,1) и перпендикулярна прямой ВС, k _BC =2/3. Из условия перпендикулярности k _AD =-1/ k _BC =-3/2. Воспользуемся уравнением прямой, проходящей через данную точку в данном направлении:

.

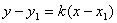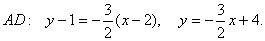
4. Для нахождения длины и уравнения медианы СЕ найдем координаты точки Е как середины отрезка АВ.

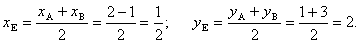Точка Е (1 /2,2).

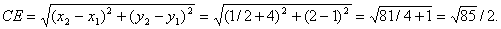
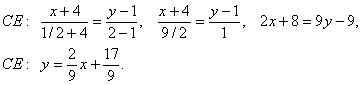
5. Найдем внутренний угол В. Он отсчитывается в положительном направлении от прямой ВС к прямой АВ. k _BC =2/3, k _AB =-2/3.

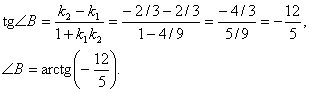
6. Составим систему линейных неравенств, определяющую треугольник. Запишем уравнения сторон в виде

AB : 2 x + 3 y = 7 ,

BC : 2 x – 3 y =- 11 ,

Подставим точку с координатами (-1, 2), лежащую внутри треугольника, в левые части равенств.

2 x – 3 y =- 2-6=-8>-11,

Следовательно, система неравенств, описывающая треугольник, имеет вид

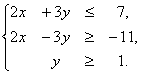
Задача 2. Составить каноническое уравнение гиперболы, если известно, что ее эксцентриситет равен 1,25 и гипербола проходит через точку .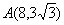

Решение . Каноническое уравнение гиперболы имеет вид 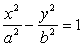. Так как гипербола проходит через точку А (8; 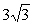), то ее координаты удовлетворяют уравнению гиперболы, т.е. 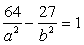. Так, как 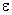= 1,25, то 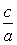= 1,25, но 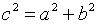, тогда 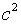= 1,5625 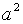или .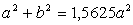

Итак, получаем систему двух уравнений с двумя неизвестными а и b .

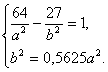
Решая эту систему, находим 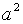= 16 и 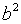= 9, следовательно, каноническое уравнение гиперболы имеет вид .

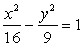Задача 3. Составить уравнение прямой, проходящей через вершину параболы 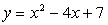и центр окружности .

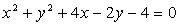Решение . Найдем координаты вершины параболы и координаты центра окружности. Для этого выделим полные квадраты по каждой переменной.

Уравнение параболы: ;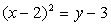

уравнение окружности: .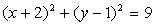

Следовательно, вершина параболы имеет координаты В (2;3), а центр окружности имеет координаты С (-2; 1).

Тогда уравнение искомой прямой составим по формуле

.

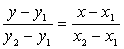Получим 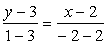, или .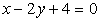

Системы неравенств с двумя переменными

п.1. Алгоритм графического решения системы неравенств с двумя переменными

Найти на координатной плоскости множество решений системы неравенств: $$ left< begin < l >mathrm & \ mathrm & endright. $$ Множество решений – сегмент круга, отсекаемый отрезком AB. Сам отрезок в множество решений не входит.

п.2. Примеры

Пример 1. Найдите на координатной плоскости множество решений системы неравенств.

Выразим y(x) в явном виде

Строим прямые, заштриховываем области над ними, находим пересечение.

Выразим y(x) в явном виде

Заштриховываем область под первой параболой и над второй параболой.

Выразим y(x) в явном виде

Строим гиперболу и прямую. Заштриховываем области под гиперболой и над прямой.

Заштриховываем области вне первой окружности и внутри второй.

Находим пересечение – кольцо.

Пример 2. Задайте системой неравенств треугольник с вершинами
A(2; 3), B(4; 4), C(3; 0)
Уравнения прямых, на которых лежат стороны треугольника:

[spoiler title=”источники:”]

http://lms2.sseu.ru/courses/eresmat/course1/primz1/pr8.htm

http://reshator.com/sprav/algebra/9-klass/sistemy-neravenstv-s-dvumya-peremennymi/

[/spoiler]

A(-3;-1) B(9;8) C(7;-6)
Находим уравнения сторон треугольника
AB: (x – (-3))/(9 – (-3)) = (y – (-1))/(8 – (-1))
(x + 3)/12 = (y + 1)/9 |*36
3 * (x + 3) = 4 * (y + 1)
3x – 4y + 5 = 0
BC: (x – 9)/(7 – 9) = (y – 8)/(-6 – 8)
(x – 9)/(-2) = (y – 8)/(-14) |*(-14)
7 * (x – 9) = y – 8
7x – y – 55 = 0
AC: (x – 7)/(-3 – 7) = (y – (-6))/(-1 – (-6))
(x – 7)/(-10) = (y + 6)/5 |*(-10)
x – 7 = -2 * (y + 6)
x + 2y + 5 = 0

AB: 3x – 4y + 5 = 0, BC: 7x – y – 55 = 0, AC: x + 2y + 5 = 0
Теперь установим, какие неравенства должны получиться.
Относительно прямой AB внутреннее пространство и точка С лежат по одну сторону от прямой.
Подставим координаты точки C в уравнение прямой AB
3 * 7 – 4 * (-6) + 5 = 21 + 24 + 5 > 0
Значит первое неравенство 3x – 4y + 5 > 0
Аналогично для прямой BC и точки A(-3;-1)
7 * (-3) – (-1) – 55 = -21 + 1 – 55 < 0
7x – y – 55 < 0
Для прямой AC и точки B(9;8)
9 + 2 * 8 + 5 > 0
x + 2y + 5 > 0
Ответ:
3x – 4y + 5 > 0, 7x – y – 55 < 0, x + 2y + 5 > 0

Системы неравенств с двумя переменными

1. Алгоритм графического решения системы неравенств с двумя переменными
2. Примеры

п.1. Алгоритм графического решения системы неравенств с двумя переменными

На входе система: (left{ begin{array}{ l } mathrm{F(x,y) lt 0} & \ mathrm{G(x,y gt 0)} & end{array}right. )
Шаг 1. Построить на координатной плоскости кривую F(x, y) = 0. Заштриховать область F(x, y) < 0.
Шаг 2. Построить на координатной плоскости кривую G(x, y) = 0. Заштриховать область G(x, y) > 0.
Шаг 3. Множество решений данной системы – это пересечение двух заштрихованных областей.
Системы с другими знаками сравнения (≤, ≥ и т.д.), а также системы с любым количеством неравенств решаются аналогично.

Например:

Найти на координатной плоскости множество решений системы неравенств: $$ left{ begin{array}{ l } mathrm{x^2+y^2leq 9} & \ mathrm{x+ygt 3} & end{array}right. $$ Множество решений – сегмент круга, отсекаемый отрезком AB. Сам отрезок в множество решений не входит.

п.2. Примеры

Пример 1. Найдите на координатной плоскости множество решений системы неравенств.

a) ( left{ begin{array}{ l } mathrm{x+ygeq 4} & \ mathrm{2x-yleq 2} & end{array}right. )

Выразим y(x) в явном виде

( left{ begin{array}{ l } mathrm{ygeq -x+4} & \ mathrm{ygeq 2x-2} & end{array}right. )

Строим прямые, заштриховываем области над ними, находим пересечение.

б) ( left{ begin{array}{ l } mathrm{y+x^2-6leq 0} & \ mathrm{2y-x^2geq 0} & end{array}right. )

Выразим y(x) в явном виде

( left{ begin{array}{ l } mathrm{yleq -x^2+6} & \ mathrm{ygeq frac{x^2}{2}} & end{array}right. )

Строим параболы.

Заштриховываем область под первой параболой и над второй параболой.

Находим пересечение.

в) ( left{ begin{array}{ l } mathrm{y-frac{6}{x}leq 0} & \ mathrm{3x-2ylt 0} & end{array}right. )

Выразим y(x) в явном виде

( left{ begin{array}{ l } mathrm{yleq frac{6}{x}} & \ mathrm{ygt 1,5x} & end{array}right. )

Строим гиперболу и прямую. Заштриховываем области под гиперболой и над прямой.

Находим пересечение.

г) ( left{ begin{array}{ l } mathrm{x^2+y^2gt 4} & \ mathrm{x^2+y^2leq 9} & end{array}right. )

Строим окружности.

Заштриховываем области вне первой окружности и внутри второй.

Находим пересечение – кольцо.

Пример 2. Задайте системой неравенств треугольник с вершинами
A(2; 3), B(4; 4), C(3; 0)
Уравнения прямых, на которых лежат стороны треугольника:

AB

begin{gather*} mathrm{ frac{x-x_A}{x_B-x_A}=frac{y-y_A}{y_B-y_A}Rightarrowfrac{x-2}{4-2}=frac{y-3}{4-3}Rightarrow x-2=2(y-3) }\ mathrm{ x-2y+4=0} end{gather*}

BC

begin{gather*} mathrm{ frac{x-x_B}{x_C-x_B}=frac{y-y_B}{y_C-y_B}Rightarrowfrac{x-4}{3-4}=frac{y-4}{0-4}Rightarrow -4(x-4)=-(y-4) }\ mathrm{ 4x-y-12=0} end{gather*}

AC

begin{gather*} mathrm{ frac{x-x_A}{x_C-x_A}=frac{y-y_A}{y_C-y_A}Rightarrowfrac{x-2}{3-2}=frac{y-3}{0-3}Rightarrow -2(x-2)=y-3 }\ mathrm{ 3x+y-9=0} end{gather*}

Чтобы расставить знаки ≤, ≥, выбираем произвольную точку внутри треугольника, например D(3; 2), подставляем в полученные уравнения и получаем необходимые знаки:
3 – 2 · 2 + 4 = 3 > 0,   4 · 3 – 2 – 12 = –2 < 0,    3 · 3 + 2 – 9 = 2 > 0

Искомая система неравенств: ( left{ begin{array}{ l } mathrm{x-2y+4geq 0} & \ mathrm{4x-y-12leq 0} & \ mathrm{3x+y-9geq 0} & end{array}right. )

Рейтинг пользователей

Рассмотрим принцип решения задач по теме : “Прямая линия на плоскости, нахождение уравнения прямой, проходящей через заданную точку, нахождение точек пересечения, углов биссектрис и т.д.”.

В качестве примера рассмотрим следующую задачу

Пример: Даны координаты вершин треугольника (ABC)   (A(3; -3); B(-1;-6); C(-6;0))

1. Составьте уравнение сторон треугольника.
2. Найдите уравнение

1. высоты (AD),
2. медианы (BM),
3. биссектрисы (CF).

3. Составьте систему неравенств, областью решения которой является множество всех точек треугольника (ABC).
4. Найдите угол (B) в радианах с точностью до двух знаков.
5. Сделайте чертеж.

Решение:

1. Составьте уравнение сторон треугольника. Для составления уравнения сторон треугольника обратимся к условию задачи. В условии даны координаты трех вершин треугольника, т.е. для составления уравнения прямых (AB,BC,CD) даны по 2 точки, через которые эти прямые проходят. Для решения воспользуемся уравнением прямой, проходящей через две заданные точки $$frac{y-y_1}{y_2-y_1}=frac{x-x_1}{x_2-x_1}$$ где ((x_1;y_1)) – координаты первой известной точки, ((x_2;y_2)) – координаты второй известной точки. Подставим координаты и получим уравнение прямых
   прямая (AB) , проходит через точки (A(3; -3); B(-1;-6)), составим уравнение $$frac{y-(-3)}{(-6)-(-3)}=frac{x-3}{-1-3} =>frac{y+3}{-3}=frac{x-3}{-4} =>y=frac{3}{4}x-frac{21}{4}$$ получили уравнение прямой (AB). В уравнении прямой отметим угловой коэффициент (k_{AB} = frac{3}{4}), который понадобится в следующих задачах.
   прямая (BC), проходит через точки (B(-1;-6);C(-6;0)), составим уравнение $$frac{y-(-6)}{0-(-6)}=frac{x-(-1)}{-6-(-1)} =>frac{y+6}{6}=frac{x+1}{-5} =>y=-frac{6}{5}x-frac{36}{5}$$ получили уравнение прямой (BC). В уравнении прямой отметим угловой коэффициент (k_{BC} = -frac{6}{5}), который понадобится в следующих задачах.
   прямая (AC), проходит через точки (A(3; -3);C(-6;0)), составим уравнение $$frac{y-(-3)}{0-(-3)}=frac{x-3}{-6-3} =>frac{y+3}{3}=frac{x-3}{-9} =>y=-frac{1}{3}x-2$$ получили уравнение прямой (AC). В уравнении прямой отметим угловой коэффициент (k_{AC} = -frac{1}{3}), который понадобится в следующих задачах.
2. Найдите уравнение

1. высоты (AD), в уравнении высоты у нас известна координата только одной точки – (A(3; -3)), поэтому воспользуемся уравнением прямой, проходящей через заданную точку в данном направлении. $$y-y_0=k_{AD}(x-x_0)$$ , где ((x_0;y_0)) – координаты известной точки, а (k_{AD}) – угловой коэффициент. В данном уравнении нам неизвестен только угловой коэффициент. Найдем его, для этого воспользуемся свойство перпендикулярных прямых. Прямая (AD bot BC). Запишем свойство (k_{AD}*k_{BC} = -1 =>k_{AD}*( -frac{6}{5})= -1 =>k_{AD}=frac{5}{6}). Составим уравнение прямой (AD) $$y-(-3)=frac{5}{6}(x-3)=>y = frac{5}{6}x-frac{11}{2}$$
2. медианы (BM), для нахождения уравнения медианы в задаче даны координаты одной точки (B(-1;-6)), а также известно, что медиана делит противоположную сторону пополам. Найдем координаты точки (M).  Для этого воспользуемся формулой координаты точки, которая делит отрезок (AC) в заданном отношении (lambda), где (lambda = frac{AM}{MC}=frac{1}{1}=1), а координаты ((x_1;y_1),(x_2;y_2)) – координаты концов отрезка, который делит точка (M) т.е.точек (A(3; -3); C(-6;0)), подставим и получим $$x = frac{x_1+lambda x_2}{1+lambda}=frac{3+1*(-6)}{1+1}=-frac{3}{2}$$$$y = frac{y_1+lambda y_2}{1+lambda}=frac{-3+1*0}{1+1}=-frac{3}{2}$$получили координаты точки (M(-frac{3}{2};-frac{3}{2})). Получили две точки, через которые проходит прямая, для получения уравнения прямой воспользуемся уравнением прямой, проходящей через заданные две точки (frac{y-y_1}{y_2-y_1}=frac{x-x_1}{x_2-x_1}), подставим координаты точек ( B(-1;-6),M(-frac{3}{2};-frac{3}{2}) ) и получим $$frac{y+6}{-frac{3}{2}+6}=frac{x+1}{-frac{3}{2}+1} =>y=-9x-15$$
3. биссектрисы (CF), для нахождения уравнения биссектрисы воспользуемся свойством биссектрисы угла треугольника: биссектриса внутреннего угла треугольника делит противоположную углу сторону на отрезки, пропорциональные двум другим сторонам (frac{AF}{FB}=frac{AC}{BC}), т.е. таким образом мы найдем коэффициент (lambda), затем воспользуемся формулой координаты точки, которая делит отрезок (AB) в заданном отношении (lambda) и найдем координаты точки (F) и последнее, подставим полученные координаты в уравнение прямой, проходящей через две заданные точки.

   Приступим: найдем длины отрезков (AC), (BC). $$AC = sqrt{(x_c-x_a)^2+(y_b-y_a)^2}=sqrt{(-6-3)^2+(0-(-3))^2} =sqrt{9^2+3^2}=sqrt{90}$$$$BC = sqrt{(x_c-x_b)^2+(y_c-y_b)^2}=sqrt{(-6-(-1))^2+(0-(-6))^2} =sqrt{5^2+6^2}=sqrt{61}$$ теперь найдем коэффициент (lambda=frac{AF}{FB}=frac{AC}{BC}=sqrt{frac{90}{61}}). Найдем координаты точки (F) при известных координатах концов отрезка (AB) (A(3; -3); B(-1;-6)) $$x = frac{x_1+lambda x_2}{1+lambda}=frac{3-sqrt{frac{90}{61}}}{1+sqrt{frac{90}{61}}}$$$$y = frac{y_1+lambda y_2}{1+lambda}=frac{-3-6*sqrt{frac{90}{61}}}{1+sqrt{frac{90}{61}}}$$Получили две точки, через которые проходит прямая (CF), для получения уравнения прямой (CF) воспользуемся уравнением прямой, проходящей через заданные две точки (frac{y-y_1}{y_2-y_1}=frac{x-x_1}{x_2-x_1}), подставим координаты точек ( C(-6;0); F(frac{3-sqrt{frac{90}{61}}}{1+sqrt{frac{90}{61}}};frac{-3-6*sqrt{frac{90}{61}}}{1+sqrt{frac{90}{61}}}) ) и получим $$frac{y-0}{frac{-3-6*sqrt{frac{90}{61}}}{1+sqrt{frac{90}{61}}}-0}=frac{x+6}{frac{3-sqrt{frac{90}{61}}}{1+sqrt{frac{90}{61}}}+6} =>frac{y}{frac{-3-6*sqrt{frac{90}{61}}}{1+sqrt{frac{90}{61}}}}=frac{x+6}{frac{3-sqrt{frac{90}{61}}+6+6*sqrt{frac{90}{61}}}{1+sqrt{frac{90}{61}}}} =>$$$$frac{y}{-3-6*sqrt{frac{90}{61}}}=frac{x+6}{9+5sqrt{frac{90}{61}}}=>$$$$y=frac{x+6}{9+5sqrt{frac{90}{61}}}*(-3-6*sqrt{frac{90}{61}})=>$$$$y=-frac{3+6*sqrt{frac{90}{61}}}{9+5sqrt{frac{90}{61}}}*x-18frac{1+2*sqrt{frac{90}{61}}}{9+5sqrt{frac{90}{61}}}$$

3. Составьте систему неравенств, областью решения которой является множество всех точек треугольника (ABC). Это множество точек, которые лежат ниже прямой (AC), т.е. (y leq -frac{1}{3}x-2), выше прямых (BC) (y geq -frac{6}{5}x-frac{36}{5})  и (AB) (y geq frac{3}{4}x-frac{21}{4}), запишем это $$begin{cases}y leq -frac{1}{3}x-2 \ y geq -frac{6}{5}x-frac{36}{5} \ y geq frac{3}{4}x-frac{21}{4} end{cases}$$
4. Найдите угол (B) в радианах с точностью до двух знаков. Угол между прямыми рассчитывается по формуле $$mbox{tg}a = |frac{k_2-k_1}{1+k_1*k_2}|$$где (k_1=k_{BC}=-frac{6}{5}), (k_2=k_{AB}=frac{3}{4}) подставим в формулу $$mbox{tg}a = |frac{frac{3}{4}+frac{6}{5}}{1-frac{3}{4}*frac{6}{5}}|=19frac{1}{2} => a = 87.06^0$$Данная формула позволяет вычислить острый угол между прямыми. Из рисунка видно, что искомый угол (B) треугольника – тупой угол (ΔADB) – прямоугольный, угол (D=90), остальные два угла в сумме меньше (90^0), т.е. (B = 180^0-a=180^0-87.06^0=92,94^0). В задаче необходимо в ответе указать угол в радианах (B=92,94^0*frac{pi}{180^0}=1,62)
5. Сделайте чертеж.
   
   

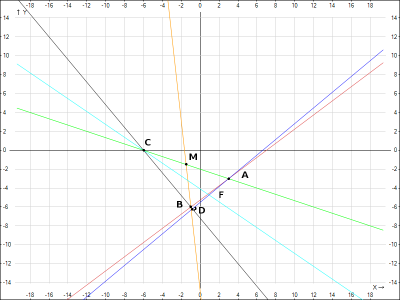
Пример решения
некоторых заданий из типовой работы
«Аналитическая геометрия на плоскости»

Даны вершины
,

,

треугольника АВС. Найти:

1. Уравнения всех
   сторон треугольника;

2. Систему линейных
   неравенств, определяющих треугольник
   АВС;

3. Уравнения высоты,
   медианы и биссектрисы треугольника,
   проведенных из вершины А;

4. Точку пересечения
   высот треугольника;

5. Точку пересечения
   медиан треугольника;

6. Длину высоты,
   опущенной на сторону АВ;

7. Угол А;

8. Сделать чертеж.

Решение:

Пусть вершины
треугольника имеют координаты: А
(1; 4), В
(5; 3), С
(3; 6). Сразу нарисуем чертеж:

1. Чтобы выписать
уравнения всех сторон треугольника,
воспользуемся уравнением прямой,
проходящей через две заданные точки с
координатами (x₀,
y₀)
и (x₁,
y₁):

=

Таким образом,
подставляя вместо (x₀,
y₀)
координаты точки А,
а вместо (x₁,
y₁)
координаты точки В,
мы получим уравнение прямой АВ:

Полученное уравнение
будет уравнением прямой АВ,
записанным в общей форме. Аналогично
находим уравнение прямой АС:

И так же уравнение
прямой ВС:

2. Заметим, что
множество точек треугольника АВС
представляет собой пересечение трех
полуплоскостей, причем каждую полуплоскость
можно задать с помощью линейного
неравенства. Если мы возьмем уравнение
любой из сторон ∆АВС,
например АВ,
тогда неравенства

и

задают точки,
лежащие по разные стороны от прямой АВ.
Нам нужно выбрать ту полуплоскость, где
лежит точка С. Подставим ее координаты
в оба неравенства:

и
.

Правильным будет
второе неравенство, значит, нужные точки
определяются неравенством

.

Аналогично поступаем
с прямой ВС, ее уравнение
.
В качестве пробной используем точку А
(1, 1):

,

значит, нужное
неравенство имеет вид:

.

Если проверим
прямую АС (пробная точка В), то получим:

,

значит, нужное
неравенство будет иметь вид

Окончательно
получаем систему неравенств:

Знаки «≤», «≥»
означают, что точки, лежащие на сторонах
треугольника, тоже включены во множество
точек, составляющих треугольник АВС.

3. а) Для того, чтобы
найти уравнение высоты, опущенной из
вершины А на
сторону ВС,
рассмотрим уравнение стороны ВС:

.
Вектор с координатами

перпендикулярен стороне ВС
и, значит, параллелен высоте. Запишем
уравнение прямой, проходящей через
точку А
параллельно вектору
:

Это уравнение
высоты, опущенной из т. А
на сторону ВС.

б) Найдем координаты
середины стороны ВС
по формулам:

Здесь

– это координаты т. В,
а

– координаты т. С.
Подставим и получим:

Прямая, проходящая
через эту точку и точку А
является искомой медианой:

в) Уравнение
биссектрисы мы будем искать, исходя из
того, что в равнобедренном треугольнике
высота, медиана и биссектриса, опущенные
из одной вершины на основание треугольника,
равны. Найдем два вектора

и

и их длины:

,

Тогда вектор

имеет такое же направление, что и вектор
,
а его длина

Точно так же единичный вектор

совпадает по направлению с вектором

Сумма векторов

есть вектор, который
совпадает по направлению с биссектрисой
угла А.
Таким образом, уравнение искомой
биссектрисы можно записать виде:

4) Уравнение одной
из высот мы уже построили. Построим
уравнение еще одной высоты, например,
из вершины В.
Сторона АС
задается уравнением

Значит, вектор

перпендикулярен АС,
и, тем самым, параллелен искомой высоте.
Тогда уравнение прямой, проходящей
через вершину В
в направлении вектора

(т. е. перпендикулярно АС),
имеет вид:

Известно, что
высоты треугольника пересекаются в
одной точке. В частности, эта точка
является пересечением найденных высот,
т.е. решением системы уравнений:

– координаты этой
точки.

5. Середина АВ
имеет координаты
.
Запишем уравнение медианы к стороне
АВ. Эта
прямая проходит через точки с координатами
(3, 2) и (3, 6), значит, ее уравнение имеет
вид:

Заметим, что ноль
в знаменателе дроби в записи уравнения
прямой означает, что эта прямая проходит
параллельно оси ординат.

Чтобы найти точку
пересечения медиан достаточно решить
систему уравнений:

Точка пересечения
медиан треугольника имеет координаты
.

6. Длина высоты,
опущенной на сторону АВ,
равна расстоянию от точки С
до прямой АВ
с уравнением

и находится по формуле:

7. Косинус угла А
можно найти по формуле косинуса угла
между векторами

и
,
который равен отношению скалярного
произведения этих векторов к произведению
их длин:

:

Соседние файлы в папке Математика

• #
• #
• #
• #
• #
• #
• #