Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву и другим 200 предметам можно здесь всего за 10 минут.
Скалярное произведение векторов
Формула
Пусть даны векторы $ overline{a} = (a_x; a_y) $ и $ overline{b} = (b_x; b_y) $. Как найти скалярное произведение векторов? Для того, чтобы найти скалярное произведение векторов необходимо воспользоваться формулой: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y $$ Стоит заметить, что скалярное произведение записывается в скобках, в которых векторы записываются через запятую. Данное обозначение широко применяется в математике и его нужно запомнить.
Если в задаче векторы заданы тремя координатами (в пространстве), то найти скалярное произведение векторов нужно по другой формуле, основанной на предыдущей. Но с тем же смыслом: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y + a_z cdot b_z $$
По сути скалярное произведение – это сумма произведений соответствующих координат данных векторов. Первая координата умножается на первую, вторая на вторую и затем произведения суммируются.
Примеры решений
| Пример 1 |
| Найти скалярное произведение векторов $ overline{a} = (-1;2) $ и $ overline{b} = (2;1) $ |
| Решение |
|
В данном примере векторы заданы двумя координатами, поэтому применяем первую формулу для плоской задачи. Умножаем соответствующие координаты, а потом складываем их: $$ (overline{a},overline{b}) = -1 cdot 2 + 2 cdot 1 = -2 + 2 = 0 $$ Произведение получилось равным нулю, а это кстати означает, что векторы оказались ортогональными (перпендикулярными) друг к другу. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ (overline{a},overline{b}) = 0 $$ |
| Пример 2 |
|
В пространстве заданы начала и концы векторов: $$ A = (1;3;-2), B = (-1;4;1), C = (2; 1; -2) $$ Требуется найти скалярное произведение векторов $ overline{AB} $ и $ overline{AC} $. |
| Решение |
|
В примеры решения данной задачи даны только точки и сразу вычислить произведение векторов не представляется возможным. Сначала нужно найти сами векторы $ overline{AB} $ и $ overline{AC} $. Вычисляются они с помощью разности соответствующих координат точек (из конца вычитается начало вектора): $$ overline{AB} = (-1 – 1; 4-3; 1-(-2)) = (-2; 1; 3) $$ $$ overline{AC} = (2 – 1; 1 – 3; -2 – (-2)) = (1; -2; 0) $$ Теперь, когда необходимые векторы найдены, то вычисляем их произведение: $$ (overline{AB},overline{AC}) = -2 cdot 1 + 1 cdot (-2) + 3 cdot 0 = -2-2+0 = -4 $$ |
| Ответ |
| $$ (overline{AB},overline{AC}) = -4 $$ |
В статье мы ответили на вопрос: «Как найти скалярное произведение векторов?», а так же привели формулы и примеры решений задач.
Содержание:
- Формула
- Примеры вычисления скалярного произведения векторов
Формула
Для того чтобы найти скалярное произведение двух векторов, заданных своими
координатами, необходимо вычислить сумму произведений
соответствующих координат этих векторов. Для случая, если векторы заданны на плоскости координатами $bar{a}=left(a_{x} ; a_{y}right)$ и $bar{b}=left(b_{x} ; b_{y}right)$, имеет место формула:
$$(bar{a}, bar{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}$$
Если же векторы заданы в пространстве своими координатами: $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$ соответственно, то их скалярное произведение вычисляется по формуле:
$$(bar{a}, bar{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}$$
Примеры вычисления скалярного произведения векторов
Пример
Задание. Найти скалярное произведение векторов $bar{a}=(1 ;-3)$ и $bar{b}=(-2 ;-3)$
Решение. Векторы заданны на плоскости, поэтому для вычисления их скалярного произведения воспользуемся формулой
$$(bar{a}, bar{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}$$
Подставляя координаты заданных векторов, получим
$$(bar{a}, bar{b})=1 cdot(-2)+(-3) cdot(-3)=-2+9=7$$
Ответ. $(bar{a}, bar{b})=7$ lt /$>

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В пространстве заданы точки
$A(-1 ;-2 ; 5), B(-3 ; 2 ; 1)$ и $C(0 ; 1 ;-1)$ . Найти скалярное произведение векторов
$overline{A B}$ и
$overline{A C}$
Решение. Найдем сначала координаты векторов
$overline{A B}$ и
$overline{A C}$ . Для этого из координат конца вычислим соответствующие
координаты начала, получим:
$$overline{A B}=(-3-(-1) ; 2-(-2) ; 1-5)=(-2 ; 4 ;-4)$$
$$overline{A C}=(0-(-1) ; 1-(-2) ;-1-5)=(1 ; 3 ;-6)$$
Далее воспользуемся формулой для вычисления скалярного произведения векторов, заданных в пространстве:
$$(bar{a}, bar{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}$$
Получим
$$(overline{A B}, overline{A C})=(-2) cdot 1+4 cdot 3+(-4)(-6)=-2+12+24=34$$
Ответ. $(overline{A B}, overline{A C})=34$
Читать дальше: как найти векторное произведение векторов.
В данной публикации мы рассмотрим формулы, с помощью которых можно найти скалярное произведение двух векторов, перечислим свойства этого действия, а также разберем примеры решения задач.
- Нахождение скалярного произведения векторов
- Свойства скалярного произведения векторов
- Примеры задач
Нахождение скалярного произведения векторов
Скалярное произведение векторов a и b – это скалярная величина, которая равняется произведению длин этих векторов и косинуса угла между ними.
a · b = |a| · |b| · cos α.
Примечание: скалярной называется величина, значений которой можно выразить одним числом (чаще всего, действительным).
С алгебраической точки зрения, скалярное произведение двух векторов – это сумма попарного произведения соответствующих координат этих векторов.
Формулы скалярного произведения векторов с заданными координатами
| Двухмерное пространство | a · b = ax · bx + ay · by |
| Трехмерное пространство | a · b = ax · bx + ay · by + az · bz |
| n-мерное пространство | a · b = a1 · b1 + a2 · b2 + … + an · bn |
Свойства скалярного произведения векторов
1. Если вектор умножить на себя же, то результат всегда будет больше или равен нулю.
a · a ≥ 0
Примечание: ноль получается исключительно в том случае, когда вектор является нулевым.
a · a = 0, если a = 0
2. При умножении вектора на самого себя получается квадрат его длины (модуля).
a · a = |a|2
3. Для скалярного произведения применим переместительный закон:
a · b = b · a
4. Если два ненулевых вектора ортогональны, их скалярное произведение равняется нулю.
a ⟂ b, a ≠ 0, b ≠ 0 <=> a · b = 0
5. Сочетательный закон:
(α · a) · b = α · (a · b)
6. Дистрибутивность скалярного произведения:
(a + b) · c = a · c + b · c
Примеры задач
Задание 1
Найдем скалярное произведение векторов a = {6; 2} и b = {1; 9}.
Решение:
a · b = 6 · 1 + 2 · 9 = 24
Задание 2
Известны длины векторов (|a| = 5, |b| = 12) и угол между ними (α = 45°). Вычислим их скалярное произведение.
Решение:
a · b = 5 · 12 · cos 45° ≈ 42,4264
В данном
параграфе рассмотрим задачи, связанные
с различными системами координат,
делением отрезка в заданном отношении.
Пример
1.
Даны координаты
точек: А(4;
3), В(7;
6), С(2;
11). Докажем, что треугольник АВС
прямоугольный.
Найдем длины
сторон треугольника
АВС. С этой
целью используем формулу, позволяющую
находить расстояние между двумя точками
на плоскости:
![]() .
.
Длины сторон будут
равны:
![]() ,
,
![]() ,
,
![]() .
.
Учитывая,
что для сторон данного треугольника
выполняется теорема Пифагора
![]() ,
,
то треугольник
АВС
– прямоугольный.
Пример
2.
Даны точки А(2;
1) и В(8;
4). Найдем координаты точки М(х;
у),
которая делит отрезок в отношении 2:1.
Напомним,
что точка М(х;
у)
делит отрезок АВ,
где A(xA,
yA),
B(xB,
yB),
в отношении λ : μ, если ее координаты
удовлетворяют условиям:
![]() ,
,
![]() .
.
Найдем точку М
для данного отрезка
![]() ,
,
![]() .
.
Таким образом,
точка М(6;
3) делит отрезок АВ
в отношении 2:1.
Пример
3.
Найдем прямоугольные
координаты точки А(![]() 3π/4),
3π/4),
если полюс совпадает с началом координат,
а полярная ось направлена по оси абсцисс.
Учитывая
формулы перехода от полярной к
прямоугольной системе координат
x
= r
cosφ, y
= r
sinφ,
получаем
![]() ,
,
![]() .
.
В прямоугольной
декартовой системе координат координаты
точки А(–2;
2).
Пример
4.
Найдем полярные
координаты точек, имеющих следующие
прямоугольные координаты:
А(![]() ;
;
2),В(–4;
4), С(–7;
0).
Используем формулы
перехода от прямоугольных координат к
полярным:
![]()
 ,
,
![]() .
.
Получим координаты
для точки А:
![]() ,
,
![]() ,
,
![]() .
.
Таким образом А(4;
π/6) – полярные координаты (рис. 15).
Для точки В
(рис. 16) имеем
![]() ,
,
![]() ,
,
![]() .
.
Следовательно,
полярные координаты точки В(![]() ,
,
3π/4).
Рассмотрим
точку С(–7;
0) (рис. 17).
В этом случае
![]() ,
,
![]() ,
,
![]() .
.
Можно записать
полярные координаты точки С(7;
π).


Пример
5.
Найдем длину
вектора a
= 20i
+ 30j
– 60k
и его направляющие косинусы.
Напомним,
что направляющие косинусы – это косинусы
углов, которые вектор a(a1,
a2,
a3)
образует с осями координат:
![]() ,
,
![]() ,
,![]() ,
,
где
![]() .
.
Применим эти
формулы к данному вектору, получим
![]() ,
,
![]() ,
,
![]() .
.
Пример
6.
Нормируем вектор
a
= 3i
+ 4j
– 12k.
Нормировать
вектор – это найти вектор единичной
длины а0,
направленный также как и данный вектор.
Для произвольного вектора a(a1,
a2,
a3)
соответствующий вектор единичной длины
можно найти, умножив a
на дробь
![]() .
.
![]() .
.
В нашем случае
![]() и вектор единичной длины:
и вектор единичной длины:
![]() .
.
Пример
7.
Найдем скалярное
произведение векторов
a
= 4i
+ 5j
+ 6k
и b
= 3i
– 4j
+ k.
Для того
чтобы найти скалярное произведение
векторов, нужно умножить соответствующие
координаты и полученные произведения
сложить. Так, для векторов a
= a1i
+ a2j
+ a3k
и b
= b1i
+ b2j
+ b3k
скалярное произведение имеет вид:
(a,
b)
= a1b1
+ a2b2
+ a3b3.
Для данных векторов
получаем
(a,
b)
= 4∙3 + 5∙(–4) +
6∙1 = 12 –
20 + 6 = –2.
Пример
8.
Покажем, что векторы
a
= 2i
– 3j
+ 5k
и b
= i
+ 4j
+ 2k
перпендикулярны.
Два вектора
перпендикулярны, если их скалярное
произведение равно нулю.
Найдем
скалярное произведение:
(a,
b)
= 2∙1 + (–3)∙4 + 5∙2 = 2 – 12 + 10 = 0.
Таким образом,
векторы а
и b
перпендикулярны.
Пример
9.
Выясним, при каком
значении параметра m
векторы a
= 2i
+ 3j
+ mk
и b
= 3i
+ mj
– 2k
перпендикулярны.
Найдем
скалярное произведение векторов а
и b:
(a,
b)
= 2∙3 + 3∙m
– 2∙m
= 6 + m.
Векторы
перпендикулярны, если их скалярное
произведение равно нулю. Приравниваем
к нулю произведение (а,
b):
6 + m
= 0.
При m
= – 6 векторы а
и b
перпендикулярны.
Пример
10.
Найдем скалярное
произведение (3а
+ 4b,
2а
– 3b),
если |a|
= 2, |b|
= 1 и угол φ между а
и b
равен π/3.
Воспользуемся
свойствами скалярного произведения:
(αa,
βb)
= αβ(a,
b),
(a
+ b,
c)
= (a,
c)
+ (b,
c),
(a,
b)
= (b,
a)
(a,
a)
= |a|2,
а также определением
скалярного произведения (a,
b)
= |a|∙|b|∙cosφ.
Перепишем скалярное произведение в
виде
(3a
+ 4b,
2a
– 3b)
= 6(a,
a)
– 9(a,
b)
+ 8(b,
a)
– 12(b,
b)
=
= 6|a|2
– (a,
b)
– 12|b|2
= 6∙22
– 2∙1∙cos(π/3) – 12∙12
= 11.
Пример
11.
Определим угол
между векторами
a
= i
+ 2j
+ 3k
и b
= 6i
+ 4j
– 2k.
Для нахождения
угла воспользуемся определением
скалярного произведения двух векторов
(a,
b)
= |a|∙|b|∙cosφ,
где φ – угол между
векторами а
и b.
Выразим cosφ
из этой формулы
![]() .
.
Учитывая, что (а,
b)
= 1∙6 + 2∙4 + 3∙(–2) = 8,
![]() ,
,![]() ,
,
получаем:
![]() .
.
Следовательно,
![]() .
.
Пример
12.
Найдем векторное
произведение векторов
a
= 5i
– 2j
+ 3k
и b
= i
+ 2j
– 4k.
Известно,
что векторное произведение векторов a
= a1i
+ a2j
+ a3k
и b
= b1i
+ b2j
+ b3k
находится по формуле
 .
.
Следовательно,
для данных векторов

![]()
=
2i
+ 23j
+ 12k.
Рассмотрим
пример, где для нахождения модуля
векторного произведения будет
использоваться определение векторного
произведения, а не выражение его через
координаты сомножителей, как было в
предыдущем примере.
Пример
13.
Найдем модуль
векторного произведения векторов а
+ 2b
и 2а
– 3b,
если |a|
= 1, |b|
= 2 и угол между векторами а
и b
равен 30°.
Из определения
векторного произведения видно, что для
произвольных векторов а
и b
его модуль равен
|[a,
b]
| =
|a|
∙
|b|
∙
sin φ.
Учитывая свойства
векторного произведение
[a,
b]
= – [b,
a],
[a,
a]
= 0,
[αa
+ βb,
c]
= α[a,
c]
+ β[b,
c],
получаем
[a
+ 2b,
2a
– 3b]
= 2[a,
a]
– 3[a,
b]
+ 4[b,
a]
– 6[b,
b]
= –7[a,
b].
Значит, модуль
векторного произведения равен
|[a
+ 2b,
2a
– 3b]|
= |–7[a,
b]|
= 7 ∙ |a|
∙ |b|
∙ sin
30° = 7∙1∙2∙0,5 = 7.
Пример
14.
Вычислим площадь
параллелограмма, построенного на
векторах
a
= 6i
+ 3j
– 2k
и b
= 3i
– 2j
+ 6k.
Известно,
что модуль векторного произведения
двух векторов равен площади параллелограмма,
построенного на этих векторах. Найдем
векторное произведение по формуле:
 ,
,
где
a
= a1i
+ a2j
+ a3k
и
b
= b1i
+ b2j
+ b3k.
Затем
вычислим его модуль.
Для данных
векторов получаем

![]()
= 14i
– 42j
– 21k.
Следовательно,
площадь параллелограмма равна
S
= |[a,
b]|
=
![]()
(кв. ед.).
Пример
15.
Вычислим площадь
треугольника с вершинами А(1;2;1),
В(3;3;4),
С(2;1;3).
Очевидно,
что площадь треугольника АВС
равна половине площади параллелограмма,
построенного на векторах
![]() и
и![]() .
.
В свою очередь,
площадь параллелограмма, построенного
на векторах
![]() и
и![]() ,
,
равна модулю векторного произведения
[![]() ].
].
Таким образом
![]() |[
|[![]() ]|.
]|.
Найдем координаты
векторов
![]() и
и![]() ,
,
вычитая из координат конца вектора
соответствующие координаты начала,
получим
![]() = (3 –
= (3 –
1)i
+ (3 – 2)j
+ (4 – 1)k
= 2i
+ j
+ 3k,
![]() = (2 –
= (2 –
1)i
+ (1 – 2)j
+ (3 – 1)k
= i
– j
+ 2k.
Найдем векторное
произведение:
[![]() ,
,![]() ]
]
=
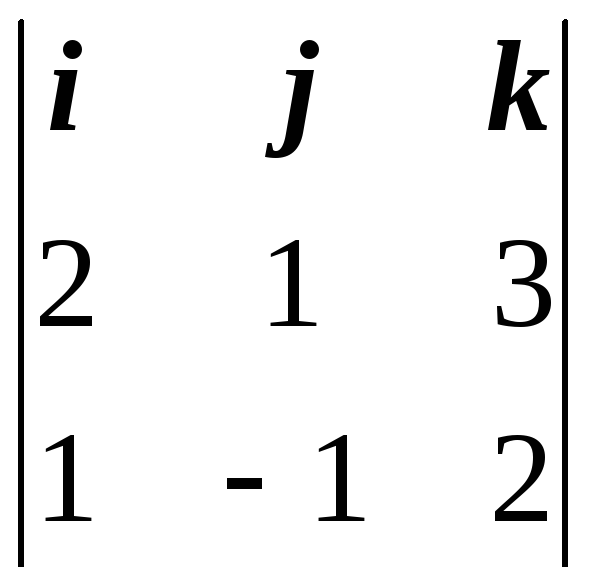
![]()
5i
– j
– 3k.
Найдем модуль
векторного произведения:
|[![]() ]|
]|
=
![]() .
.
Следовательно,
можем получить площадь треугольника:
![]()
![]() (кв. ед.).
(кв. ед.).
Пример
16.
Вычислим площадь
параллелограмма, построенного на
векторах a
+ 3b
и 3a
– b,
если |a|
= 2, |b|
= 1 и угол между а
и b
равен 30°.
Найдем модуль
векторного произведения, используя его
определение и свойства, указанные в
примере 13, получим
[a
+ 3b,
3a
– b]
= 3[a,
a]
– [a,
b]
+ 9[b,
a]
– 3[b,
b]
= –10[a,
b].
Значит,
искомая площадь равна
S
= |[a
+ 3b,
3a
– b]|
= |–10[a,
b]|
= 10 ∙ |a|
∙ |b|
∙ sin 30° =
= 10∙2∙1∙0,5 = 10 (кв.
ед.).
Следующие
примеры будут связаны с использованием
смешанного произведения векторов.
Пример
17.
Показать, что
векторы a
= i
+ 2j
– k,
b
= 3i
+ k
и с
= 5i
+ 4j
– k
компланарны.
Векторы
компланарны, если их смешанное произведение
равно нулю. Для произвольных векторов
a
= a1i
+ a2j
+ a3k,
b
= b1i
+ b2j
+ b3k,
c
= c1i
+ c2j
+ c3k
смешанное
произведение находим по формуле:
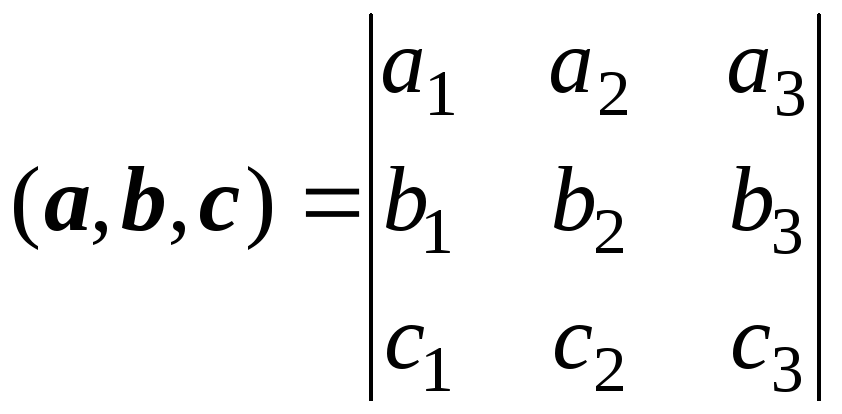 .
.
Для данных
векторов получаем
 .
.
Таким образом,
данные векторы компланарны.
Пример18.
Найдем объем
треугольной пирамиды с вершинами
А(1;1;1),
В(3;2;1),
С(2;4;3),
D(5;2;4).
Найдем
координаты векторов
![]() ,
,![]() и
и![]() ,
,
совпадающих с ребрами пирамиды. Вычитая
из координат конца вектора соответствующие
координаты начала, получаем
![]() = 2i
= 2i
+ 3j,
![]() = i
= i
+ 3j
+ 2k,
![]() = 4i
= 4i
+ j
+ 3k.
Известно, что объем
пирамиды равен 1/6 объема параллелепипеда,
построенного на векторах
![]() ,
,![]() и
и![]() .
.
Таким образом,
![]() .
.
В свою очередь,
объем параллелепипеда равен модулю
смешанного произведения
Vпарал
= |(![]() ,
,![]() ,
,![]() )|.
)|.
Найдем смешанное
произведение
(![]() ,
,![]() ,
,![]() )
)
=
 .
.
Итак, объем пирамиды
равен
![]() (куб. ед.).
(куб. ед.).
В следующих
примерах покажем возможное применение
векторной алгебры.
Пример
19.
Проверим, являются
ли коллинеарными вектора 2а
+ b
и а
– 3b,
где a
= 2i
+ j
– 3k
и b
= i
+ 2j
+ 4k.
Найдем
координаты векторов 2а
+ b
и а
– 3b:
2а
+
b
= 2(2i
+ j
– 3k)
+ i
+ 2j
+ 4k
= 5i
+ 4j
– 2k,
а
– 3b
= 2i
+ j
– 3k
– 3(i
+ 2j
+ 4k)
= –i
– 5j
– 15k.
Известно,
что у коллинеарных векторов пропорциональные
координаты. Учитывая, что
![]() ,
,
получаем, что
вектора 2а
+ b
и а
– 3b
неколлинеарны.
Эту задачу
можно было решить и другим способом.
Критерием коллинеарности векторов
является равенство нулю векторного
произведения:
[2a
+ b,
a
– 3b]
= 2[a,
a]
– 6[a,
b]
+ [b,
a]
– 3[b,
b]
= –7[a,
b].
Найдем векторное
произведение векторов а
и b:

![]()
= 10i
– 11j
+ 3k
≠ 0.
Следовательно,
[2a
+ b,
a
– 3b]
= –7[a,
b]
≠ 0
и векторы 2а
+ b
и а
– 3b
неколлинеарны.
Пример
20.
Найдем работу силы
F(3;
2; 1), когда точка ее приложения А(2;
4;–6), двигаясь прямолинейно, перемещается
в точку В(5;
2; 3).
Известно,
что работа силы – это скалярное
произведение силы F
на вектор перемещения
![]() .
.
Найдем
координаты вектора
![]() :
:
![]() = 3i
= 3i
– 2j
+ 9k.
Следовательно,
работа силы F
по перемещению точки А
в точку В
будет равна скалярному произведению
(F,
![]() )
)
= 3∙3 + 2∙(–2) + 1∙9 = 9 – 4 + 9 = 14.
Пример
21.
Пусть сила F(
2;3;–1) приложена к точке А(4;2;3).
Под действием силы F
точка А
перемещается в точку В(3;1;2).
Найдем модуль момента силы F
относительно точки В.
Известно,
что момент силы равен векторному
произведению силы на перемещение. Найдем
вектор перемещения
![]() :
:
![]() = (3 –
= (3 –
4)i
+
(1 – 2)j
+ (2 – 3)k
= – i
–
j
– k.
Найдем момент силы
как векторное произведение:

![]()
= – 4i
+ 3j
+ k.
Следовательно,
модуль момента силы равен модулю
векторного произведения:
|[F,
![]() ]|
]|
=
![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
