Скалярное произведение и евклидовы пространства
Скалярное произведение
Определение и основные свойства скалярного произведения
Мы рассмотриваем векторное пространство ( mathit{L}).
Определение.
Предположим, что существует числовая функция, которая сопоставляет паре векторов (x,y in mathit{L}) число (его обозначают ((x,y))), причем эта функция имеет следующие свойства. Для любых векторов (x,y,z in mathit{L}) и любого числа (lambda )
1. ((x,y)=(y,x)),
2. ((x+z,y)=(x,y)+(z,y)),
3. ((lambda x,y)=lambda (x,y)),
4. ((x,x) geq 0), причем ((x,x)=0 Leftrightarrow ) (x=0).
Тогда говорят, что на векторном пространстве ( mathit{L}) задано скалярное произведение, и векторное пространство ( mathit{L}) называют евклидовым.
Первое свойство означает симметричность скалярного произведения по сомножителям, из него следует, что оба сомножителя равноправны и скалярное произведение обладает одинаковыми свойствами относительно обоих сомножителей.
Наличие в векторном пространстве скалярного произведения позволяет ввести в векторном пространстве ряд геометрических понятий и объектов, знакомых в “стандартной” трехмерной геометрии. К ним относится длина вектора, угол между векторами, проекция вектора на направление (ось) и т.д.
Стандартное скалярное произведение. Рассмотрим векторное пространство ( mathit{L}) – пространство (n)-столбцов (u=(u_1,u_2,…,u_n)^T). Тогда скалярное произведение для двух таких столбцов можно определить следующим образом:
[
(u,v)=u_1v_1+u_2v_2+…+u_nv_n.
]
Такое скалярное произведение довольно часто употребляется по умолчанию (т.е. если явным образом не введено другое скалярное произведение).
Покажите, что стандартное скалярное произведение обладает всеми перечисленными выше свойствами.
Неравенство Коши-Буняковского
Пусть в векторном пространстве ( mathit{L}) определено скалярное произведение. Тогда из свойств скалярного произведения вытекает следующее неравенство, справедливое для произвольных векторов (u,v in mathit{L}):
[
|(u,v)|^2 leq (u,u)cdot(v,v), quad quad(64)
]
которое называется неравенством Коши-Буняковского .
Возьмем произвольное число (lambda ) и запишем для линейной комбинации (w=u+lambda v) соотношение ((w,w) geq 0):
[
(w,w)=(u+lambda v,u+lambda v)=(u,u)+lambda cdot left ((u,v)+(v,u)right )+lambda ^2cdot (v,v)
]
[
=(u,u)+2lambda cdot (u,v)+lambda ^2cdot (v,v)geq 0.
]
Здесь при раскрытии скобок мы использовали свойства скалярного произведения. Таким образом, наше выражение можно рассматривать как квадратный трехчлен, причем не принимающий отрицательное значепние ни при каких (lambda ). Это означает, что дискриминант этого трехчлена неположителен:
[
D=4(v,u)^2-4(v,v)(u,u) leq 0.
]
Это неравенство эквивалентно неравенству (64).
Длина вектора, углы между векторами, неравенство треугольника
Наличие скалярного произведения позволяет ввести длину вектора (u) согласно соотношению:
[
|u|=sqrt{(u,u)}.
]
При этом неравенство Коши-Буняковского можно переписать в виде
[
|(u,v)| leq |u|cdot |v|.
]
Последнее неравенство позволяет определить угол между векторами . Мы полагаем угол (alpha) между векторами (u,v in mathit{L}) определенным согласно соотношению
[
cos alpha =frac{(u,v)}{|u|cdot |v|}.
]
Правая часть этого соотношения не превосходит по модулю 1, так что для любой пары векторов угол между ними определен.
Определение.
Вектора (u), (v) называются ортогональными , если ((u,v)=0) (так что, согласно предыдущему определению, угол между ними равен (pi /2)).
Далее, из неравенства Коши-Буняковского следует так называемое неравенство треугольника: для любых двух векторов (u,v in mathit{L}) выполняется:
[
|u+v|leq |u|+|v|.
]
Выпишем
[
|u+v|^2=(u+v,u+v)=(u,u)+2(u,v)+(v,v)leq |u|^2+2|u||v|+|v|^2.
]
Извлекая корень, получаем неравенство треугольника.
Проекция на ось
Скалярное произведение позволяет ввести еще один объект, имеющий приложения в геометрии. Пусть (e in mathit{L}) – вектор единичной длины, (|e|=1).
Определение. Проекцией произвольного вектора (u in mathit{L}) на вектор (e) называется вектор ((u,e)e). Его иногда называют также проекцией вектора (u) на ось (имея в виду, что направление оси фиксируется вектором (e)).
Из этого определения следует, что вектор (v=u- (u,e)e) ортогонален вектору (e): ((v,e)=(v,u-(u,e)e)=(v,u)-(v,u)(e,e)=0).
1. Найти скалярное произведение векторов, заданных своими координатами.
а) (u(4, -1)), (v(-1, 7)).
б) (u(2, 1)), (v(1, -37)).
в) (u(1,0, 3)), (v(-4, 15,1)).
г) (u(2,1,1)), (v(-1, 7,9)).
2. Найти угол между векторами, заданными своими координатами.
а) (u(1, -1,1)), (v(5,1, 1)).
б) (u(1,-1, 1)), (v(2, -2,2)).
3. Даны вектора (a=(3;1;2), ,b=(2;7;4),, c=(5;-8;10)). Вычислить вектор ((a,b)c).
4. Вершины четырехугольника (A(2; -3; 1), ,B(-1; 1; 1),, C(-4; 5; 6),, D(2; -3; 6)). Вычислить косинусы его углов.
5. Вычислить внутренний угол при вершине (B) у треугольника (A(-1;-2;4), ,B(-4;-2;0),, C(3;-2;1)).
6. Вычислить угол между диагоналями четырехугольника
a) (A(1;-2;2),, B(1;4;0),,C(-4;1;1),,D(-5;-5;3)).
б) (A(-4; -4; 4), ,B(-3; 2; 3), ,C(2; 5; 1),, D(3; -2; 2)).
7. Даны вектора (a(2; -1; 3),, b(1; -3; 2),, c(3; 2; -4)). Вычислить вектор (x) из условий ((x,a)=10, ,(x,b)=22, , (x,c)=-40).
8. Найти единичный вектор, перпендикулярный векторам (a=3i-j+2k,, b=-i+3j-k).
9. Найти вектор (x), перпендикулярный векторам (a=(2;3;-1), ,b=(1;-2;3)) при условии, что ((x,c)=-6), где (c=(2;-1;1)).
10. Даны два вектора (a(3; -1; 5),, b(1; 2; -3)). Найти вектор (x), перпендикулярный оси (OZ) и удовлетворяющий условиям ((x,a)=9, ,(x,b)=-4).
|
|
Предыдущий раздел |
|
Назад | Далее |
|
Следующий раздел |
|
17 авг. 2022 г.
читать 2 мин
В этом руководстве объясняется, как рассчитать скалярный продукт в Excel.
Что такое скалярный продукт?
Для данного вектора a = [a 1 , a 2 , a 3 ] и вектора b = [b 1 , b 2 , b 3 ] скалярное произведение вектора a и вектора b, обозначаемое как a · b , определяется как:
а · b = а 1 * b 1 + а 2 * b 2 + а 3 * b 3
Например, если a = [2, 5, 6] и b = [4, 3, 2], то скалярное произведение a и b будет равно:
а · б = 2*4 + 5*3 + 6*2
а · б = 8 + 15 + 12
а · б = 35
По сути, скалярное произведение — это сумма произведений соответствующих элементов двух векторов.
Как найти точечный продукт в Excel
Чтобы найти скалярное произведение двух векторов в Excel, мы можем использовать следующие шаги:
1. Введите данные.Введите значения данных для каждого вектора в их собственные столбцы. Например, введите значения данных для вектора a = [2, 5, 6] в столбец A и значения данных для вектора b = [4, 3, 2] в столбец B:

2. Вычислите скалярный продукт. Чтобы вычислить скалярный продукт, мы можем использовать функцию Excel СУММПРОИЗВ() , которая использует следующий синтаксис:
СУММПРОИЗВ(массив1, [массив2], …)
- array — первый массив или диапазон, который необходимо умножить, а затем добавить.
- array2 — второй массив или диапазон для умножения, а затем добавления.
В этом примере мы можем ввести следующее в ячейку D1 , чтобы вычислить скалярное произведение между вектором a и вектором b :
=СУММПРОИЗВ(A1:A3, B1:B3)

Это дает значение 35 , которое соответствует ответу, который мы получили вручную.
Обратите внимание, что мы можем использовать СУММПРОИЗВ() для нахождения скалярного произведения векторов любой длины. Например, предположим, что вектор a и b имеют длину 20. Затем мы можем ввести следующую формулу в ячейку D1 , чтобы вычислить их скалярное произведение:
=СУММПРОИЗВ(A1:A20, B1:B20)

Возможные ошибки при вычислении скалярного произведения
Функция СУММПРОИЗВ() вернет #ЗНАЧ! ошибка, если векторы не имеют одинаковой длины.
Например, если вектор a имеет длину 20, а вектор b имеет длину 19, то формула =СУММПРОИЗВ(A1:A20, B1:B19) вернет ошибку.
Два вектора должны иметь одинаковую длину, чтобы можно было вычислить скалярное произведение.
Дополнительные ресурсы
В следующих руководствах объясняется, как рассчитать скалярный продукт в различных статистических программах:
Как рассчитать скалярный продукт в Google Sheets
Как рассчитать скалярный продукт в R
Как рассчитать скалярный продукт на калькуляторе TI-84
Уважаемые студенты!
Заказать решение задач можно у нас всего за 10 минут.
Скалярное произведение векторов
Формула
Пусть даны векторы $ overline{a} = (a_x; a_y) $ и $ overline{b} = (b_x; b_y) $. Как найти скалярное произведение векторов? Для того, чтобы найти скалярное произведение векторов необходимо воспользоваться формулой: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y $$ Стоит заметить, что скалярное произведение записывается в скобках, в которых векторы записываются через запятую. Данное обозначение широко применяется в математике и его нужно запомнить.
Если в задаче векторы заданы тремя координатами (в пространстве), то найти скалярное произведение векторов нужно по другой формуле, основанной на предыдущей. Но с тем же смыслом: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y + a_z cdot b_z $$
По сути скалярное произведение – это сумма произведений соответствующих координат данных векторов. Первая координата умножается на первую, вторая на вторую и затем произведения суммируются.
Примеры решений
| Пример 1 |
| Найти скалярное произведение векторов $ overline{a} = (-1;2) $ и $ overline{b} = (2;1) $ |
| Решение |
|
В данном примере векторы заданы двумя координатами, поэтому применяем первую формулу для плоской задачи. Умножаем соответствующие координаты, а потом складываем их: $$ (overline{a},overline{b}) = -1 cdot 2 + 2 cdot 1 = -2 + 2 = 0 $$ Произведение получилось равным нулю, а это кстати означает, что векторы оказались ортогональными (перпендикулярными) друг к другу. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ (overline{a},overline{b}) = 0 $$ |
| Пример 2 |
|
В пространстве заданы начала и концы векторов: $$ A = (1;3;-2), B = (-1;4;1), C = (2; 1; -2) $$ Требуется найти скалярное произведение векторов $ overline{AB} $ и $ overline{AC} $. |
| Решение |
|
В примеры решения данной задачи даны только точки и сразу вычислить произведение векторов не представляется возможным. Сначала нужно найти сами векторы $ overline{AB} $ и $ overline{AC} $. Вычисляются они с помощью разности соответствующих координат точек (из конца вычитается начало вектора): $$ overline{AB} = (-1 – 1; 4-3; 1-(-2)) = (-2; 1; 3) $$ $$ overline{AC} = (2 – 1; 1 – 3; -2 – (-2)) = (1; -2; 0) $$ Теперь, когда необходимые векторы найдены, то вычисляем их произведение: $$ (overline{AB},overline{AC}) = -2 cdot 1 + 1 cdot (-2) + 3 cdot 0 = -2-2+0 = -4 $$ |
| Ответ |
| $$ (overline{AB},overline{AC}) = -4 $$ |
В статье мы ответили на вопрос: «Как найти скалярное произведение векторов?», а так же привели формулы и примеры решений задач.
Загрузить PDF
Загрузить PDF
Матрица представляет собой прямоугольное расположение чисел, символов или выражений в строках и столбцах. Чтобы умножить матрицы, вам нужно умножить элементы (или числа) в строках первой матрицы на элементы в столбцах второй матрицы и сложить полученные значения. Для умножения матриц потребуется умножение, сложение и правильная расстановка результатов.
Шаги
-

1
Умножение матриц. В данной статье рассматривается умножение матриц равных размеров, то есть таких, у которых число строк первой матрицы равно числу строк второй матрицы.
- На рисунке: первая матрица А имеет две строки, и вторая матрица B имеет два столбца.
-

2
Обозначьте размеры конечной матрицы. Нарисуйте новую пустую матрицу, которая будет конечной матрицей – результатом произведения первой матрицы на вторую. Конечная матрица имеет столько же строк, как матрица А, и столько же столбцов, как матрица В.
- Матрица А имеет 2 строки, поэтому конечная матрица будет иметь 2 строки.
- Матрица B имеет 2 столбца, поэтому конечная матрица будет иметь 2 столбца.
- Конечная матрица будет иметь 2 строки и 2 столбца.
-

3
Найдите первое скалярное произведение. Для этого умножьте первый элемент первой строки на первый элемент первого столбца, второй элемент первой строки на второй элемент первого столбца, третий элемент первой строки на третий элемент первого столбца. Потом сложите полученные значения. Например, умножим вторую строку на второй столбец (и найдем четвертое скалярное произведение):
- 6 x -5 = -30
- 1 x 0 = 0
- -2 x 2 = -4
- -30 + 0 + (-4) = -34
- Четвертое скалярное произведение равно (-34) и оно записывается в правом нижнем углу конечной матрицы.
- Результат скалярного произведения записывается согласно номерам умножаемой строки и столбца. Например, когда вы нашли скалярное произведение второй строки (матрица А) и второго столбца (матрица B), результат (-34) записывается на пересечении второй строки и второго столбца конечной матрицы.
-

4
Найдите второе скалярное произведение. Для этого умножьте элементы второй строки первой матрицы на элементы первого столбца второй матрицы, а затем сложите результаты.
- 6 x 4 = 24
- 1 x (-3) = -3
- (-2) x 1 = -2
- 24 + (-3) + (-2) = 19
- Второе скалярное произведение равно (-19), и оно записывается на пересечении второй строки и первого столбца конечной матрицы.
-

5
Найдите оставшиеся скалярные произведения. Первое скалярное произведение вычисляется умножением элементов первой строки на элементы первого столбца:
- 2 x 4 = 8
- 3 x (-3) = -9
- (-1) x 1 = -1
- 8 + (-9) + (-1) = -2
- Первое скалярное произведение равно (-2), и оно записывается на пересечении первой строки и первого столбца конечной матрицы.
- Третье скалярное произведение вычисляется умножением элементов первой строки на элементы второго столбца:
- 2 x (-5) = -10
- 3 x 0 = 0
- (-1) x 2 = -2
- -10 + 0 + (-2) = -12
- Третье скалярное произведение равно (-12), и оно записывается на пересечении первой строки и второго столбца конечной матрицы.
-

6
Убедитесь, что результаты всех четырех скалярных произведений правильно расставлены.
Реклама
Советы
- Результат произведения двух матриц имеет столько же строк, как первая матрица, и столько же столбцов, как вторая матрица.
- Записывайте ваши вычисления. Умножение матриц включает много расчетов, в которых легко запутаться.
Реклама
Об этой статье
Эту страницу просматривали 59 654 раза.
Была ли эта статья полезной?
Вычислим скалярное произведение векторов и проверим вектора на ортогональность. Подберем координаты вектора, ортогонального заданному, а также отобразим вектора в прямоугольной системе координат.
Скалярным произведением двух векторов
называется действительное число (скаляр), равное произведению длин умножаемых векторов на косинус угла между ними.
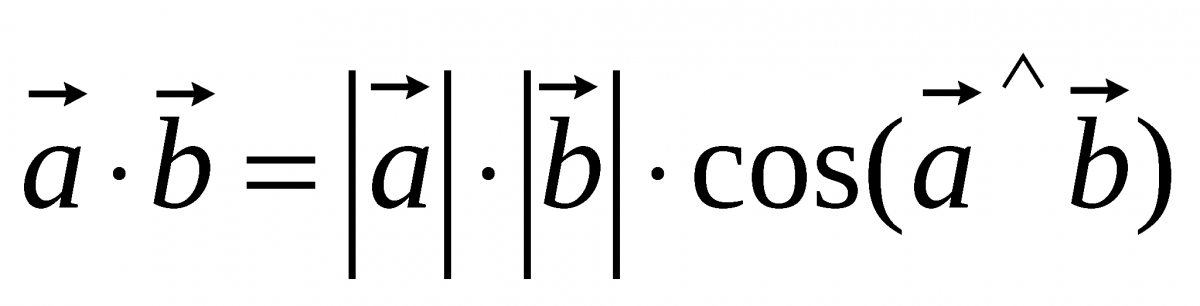
СОВЕТ
: о нахождении длин векторов см. статью
Вычисление длины (модуля) вектора в MS EXCEL
.
В случае двухмерной задачи скалярное произведение векторов
a
= {
a
x
;
a
y
} и
b
= {
b
x
;
b
y
} можно найти воспользовавшись следующей формулой:
a
·
b
=
a
x
·
b
x
+
a
y
·
b
y
Для вычисления скалярного произведения векторов в MS EXCEL идеально подходит функция
СУММПРОИЗВ()
СОВЕТ
: о функции
СУММПРОИЗВ()
см. статью
Функция СУММПРОИЗВ() – Сложение и подсчет с множественными условиями в MS EXCEL
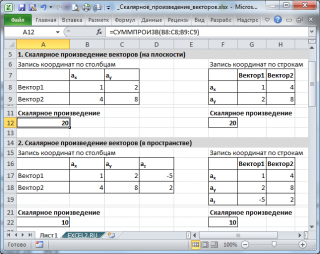
Если координаты 2-х векторов введены в диапазоны
B8:C8
и
B9:C9
соответственно, то формула
=СУММПРОИЗВ(B8:C8;B9:C9)
подсчитает скалярное произведение векторов (см.
файл примера
).
Естественно, для трехмерного случая можно записать аналогичную формулу.
Ортогональность векторов
Два вектора называются ортогональными если угол между ними равен 90 градусов. Т.к. косинус угла 90 градусов равен 0, то и их скалярное произведение равно 0.
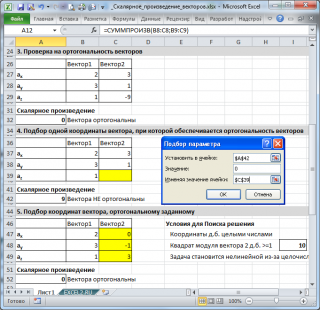
Интерес представляет поиск вектора, ортогонального заданному.
Поиск одной координаты.
Сначала подберем одну из координат трехмерного вектора, так, чтобы он стал ортогональным заданному (2 другие координаты известны). Такая координата всегда существует и решение единственно.
Для нахождения третьей координаты будем использовать инструмент MS EXCEL Подбор параметра (подробнее см.
Подбор параметра в MS EXCEL
).
Пусть координаты заданного вектора равны {2; 3; 1} (и размещены в ячейках
В37:В39
), а известные координаты искомого ортогонального вектора равны {3; 1; ?} (размещены в ячейках
С37:С39
) См. рисунок выше и
файл примера
.
Вычислим в ячейке
А42
скалярное произведение векторов с помощью формулы
=СУММПРОИЗВ(B37:B39;C37:C39)
Вызовем окно
Подбора параметра
для ввода критериев поиска и установим их как показано на рисунке выше. После нажатия кнопки ОК в ячейке
С39
(искомая координата) будет введено значение -9, а скалярное произведение станет равно 0.
Поиск всех координат ортогонального вектора.
Если заданы координаты только исходного вектора и требуется определить все 3 координаты вектора, ортогональному к нему, то, понятно, что решение не единственно.
Например, для двухмерного случая (на плоскости), можно построить 2 разных вектора, которые будут ортогональны заданному (точнее не 2, а бесконечное множество коллинеарных векторов в двух противоположных направлениях).
Так как нам придется одновременно подбирать сразу 3 координаты, то Подбор параметра нам не подходит, нужно использовать
Поиск решения
(См.
файл примера)
.
В качестве ограничений для Поиска решения можно установить: найденные координаты должны быть целыми числами, а квадрат модуля искомого вектора д.б. >1 (иначе 0 вектор будет предложен в качестве решения). Также можно наложить ограничение на максимальную длину вектора.
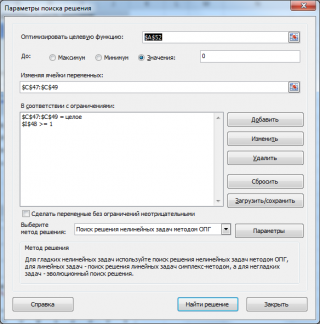
После запуска инструмента Поиск решения будут найдены координаты {0; -1; 3}
Отображение (ортогональных) векторов на плоскости
В двухмерном случае можно отобразить 2 ортогональных вектора.
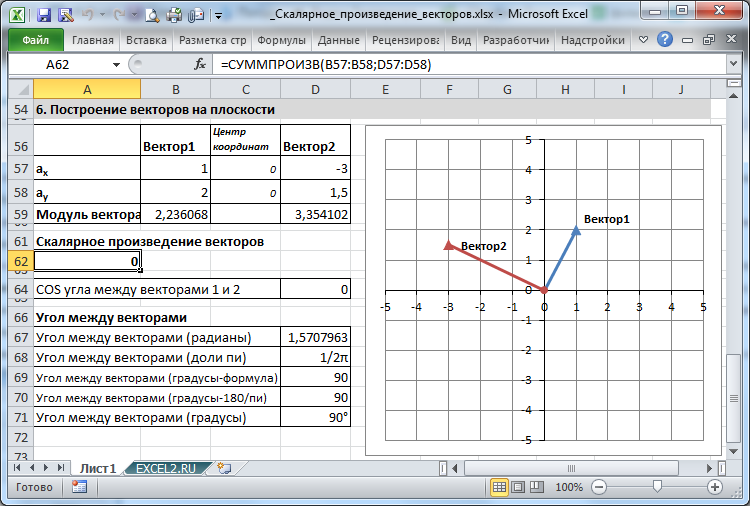
Тип диаграммы установлен График (см.
Основные типы диаграмм в MS EXCEL
, раздел График).
Чтобы вектора выглядели ортогональными, необходимо зафиксировать минимальные и максимальные значения, отображаемые осями (см.
Основы построения диаграмм в MS EXCEL
, раздел 7.Оси), иначе при построении различных пар векторов MS EXCEL будет применять автомасштабирование графика и масштабы осей могут стать не равными (это приведет к тому, что угол 90 градусов не будет выглядеть прямым).

