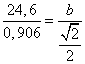Скалярное произведение векторов называют число, равное произведению дин этих векторов на косинус угла между ними.
Обозначение произведения векторов a→ и b→ имеет вид a→,b→. Преобразуем в формулу:
a→,b→=a→·b→·cosa→,b→^. a→ и b→ обозначают длины векторов, a→,b→^ – обозначение угла между заданными векторами. Если хоть один вектор нулевой, то есть имеет значение 0, то и результат будет равен нулю, a→,b→=0
При умножении вектора самого на себя, получим квадрат его дины:
a→,b→=a→·b→·cosa→,a→^=a→2·cos0=a→2
Скалярное умножение вектора самого на себя называют скалярным квадратом.
Вычисляется по формуле:
a→,b→=a→·b→·cosa→,b→^.
Запись a→,b→=a→·b→·cosa→,b→^=a→·npa→b→=b→·npb→a→ показывает, что npb→a→ – это числовая проекция a→ на b→, npa→a→- проекция b→ на a→ соостветсвенно.
Сформулируем определение произведения для двух векторов:
Скалярное произведение двух векторов a→ на b→ называют произведение длины вектора a→ на проекцию b→ на направление a→ или произведение длины b→ на проекцию a→ соответственно.
Скалярное произведение в координатах
Вычисление скалярного произведения можно производить через координаты векторов в заданной плоскости или в пространстве.
Скаларное произведение двух векторов на плоскости, в трехмерном простарнстве называют сумму координат заданных векторов a→ и b→.
При вычислении на плоскости скаларного произведения заданных векторов a→=(ax,ay), b→=(bx,by) в декартовой системе используют:
a→,b→=ax·bx+ay·by,
для трехмерного пространства применимо выражение:
a→,b→=ax·bx+ay·by+az·bz.
Фактически это является третьим определением скалярного произведения.
Докажем это.
Для доказательства используем a→,b→=a→·b→·cosa→,b→^=ax·bx+ay·by для векторов a→=(ax,ay), b→=(bx,by) на декартовой системе.
Следует отложить векторы
OA→=a→=ax,ay и OB→=b→=bx,by.
Тогда длина вектора AB→будет равна AB→=OB→-OA→=b→-a→=(bx-ax,by-ay).
Рассмотрим треугольник OAB.
AB2=OA2+OB2-2·OA·OB·cos(∠AOB) верно , исходя из теоремы косинусов.
По условию видно, что OA=a→, OB=b→, AB=b→-a→, ∠AOB=a→,b→^, значит, формулу нахождения угла между векторами запишем иначе
b→-a→2=a→2+b→2-2·a→·b→·cos(a→,b→^).
Тогда из первого определения следует, что b→-a→2=a→2+b→2-2·(a→,b→), значит (a→,b→)=12·(a→2+b→2-b→-a→2).
Применив формулу вычисления длины векторов, получим:
a→,b→=12·((a2x+ay2)2+(b2x+by2)2-((bx-ax)2+(by-ay)2)2)==12·(a2x+a2y+b2x+b2y-(bx-ax)2-(by-ay)2)==ax·bx+ay·by
Докажем равенства:
(a→,b→)=a→·b→·cos(a→,b→^)==ax·bx+ay·by+az·bz
– соответственно для векторов трехмерного пространства.
Скалярное произведение векторов с координатами говорит о том, что скалярный квадрат вектора равен сумме квадратов его координат в пространстве и на плоскости соответственно. a→=(ax,ay,az), b→=(bx,by,bz) и (a→,a→)=ax2+ay2.
Скалярное произведение и его свойства
Существуют свойства скалярного произведения, которые применимы для a→,b→ и c→:
- коммутативность (a→,b→)=(b→,a→);
- дистрибутивность(a→+b→,c→)=(a→,c→)+(b→,c→), (a→+b→,c→)=(a→,b→)+(a→,c→);
- сочетательное свойство (λ·a→,b→)=λ·(a→,b→),(a→,λ·b→)=λ·(a→,b→), λ – любое число;
- скалярный квадрат всегда больше нуля (a→,a→)≥0, где (a→,a→)=0 в том случае, когда a→ нулевой.
Свойства объяснимы благодаря определению скалярного произведения на плоскости и свойствам при сложении и умножении действительных чисел.
Доказать свойство коммутативности (a→,b→)=(b→,a→). Из определения имеем, что (a→,b→)=ay·by+ay·by и (b→,a→)=bx·ax+by·ay.
По свойству коммутативности равенства ax·bx=bx·ax и ay·by=by·ay верны, значит ax·bx+ay·by=bx·ax+by·ay.
Отсюда следует, что (a→,b→)=(b→,a→). Что и требовалось доказать.
Дистрибутивность справедлива для любых чисел:
(a(1)→+a(2)→+…+a(n)→,b→)=(a(1)→,b→)+(a(2)→,b→)+…+(a(n)→,b→)
и (a→,b(1)→+b(2)→+…+b(n)→)=(a→,b(1)→)+(a→,b(2)→)+…+(a→,b→(n)),
отсюда имеем
(a(1)→+a(2)→+…+a(n)→,b(1)→+b(2)→+…+b(m)→)==(a(1)→,b(1)→)+(a(1)→,b(2)→)+…+(a(1)→,b(m)→)++(a(2)→,b(1)→)+(a(2)→,b(2)→)+…+(a(2)→,b(m)→)+…++(a(n)→,b(1)→)+(a(n)→,b(2)→)+…+(a(n)→,b(m)→)
Скалярное произведение с примерами и решениями
Любая задача такого плана решается с применением свойств и формул, касающихся скалярного произведения:
- (a→,b→)=a→·b→·cos(a→,b→^);
- (a→,b→)=a→·npa→b→=b→·npb→a→;
- (a→,b→)=ax·bx+ay·by или (a→,b→)=ax·bx+ay·by+az·bz;
- (a→,a→)=a→2.
Рассмотрим некоторые примеры решения.
Длина a→ равна 3, длина b→ равна 7. Найти скалярное произведение, если угол имеет 60 градусов.
Решение
По условию имеем все данные, поэтому вычисляем по формуле:
(a→,b→)=a→·b→·cos(a→,b→^)=3·7·cos60°=3·7·12=212
Ответ:(a→,b→)=212.
Заданны векторы a→=(1,-1,2-3), b→=(0,2,2+3). Чему равно скалярной произведение.
Решение
В данном примере рассматривается формула вычисления по координатам, так как они заданы в условии задачи:
(a→,b→)=ax·bx+ay·by+az·bz==1·0+(-1)·2+(2+3)·(2+3)==0-2+(2-9)=-9
Ответ: (a→,b→)=-9
Найти скалярное произведение AB→ и AC→. На координатной плоскости заданы точки A(1,-3), B(5,4), C(1,1).
Решение
Для начала вычисляются координаты векторов, так как по условию даны координаты точек:
AB→=(5-1,4-(-3))=(4,7)AC→=(1-1,1-(-3))=(0,4)
Подставив в формулу с использованием координат, получим:
(AB→,AC→)=4·0+7·4=0+28=28.
Ответ: (AB→,AC→)=28.
Заданы векторы a→=7·m→+3·n→ и b→=5·m→+8·n→, найти их произведение.m→ равен 3 и n→ равен 2 единицам, они перпендикулярные.
Решение
(a→,b→)=(7·m→+3·n→, 5·m→+8·n→). Применив свойство дистрибутивности, получим:
(7·m→+3·n→, 5·m→+8·n→)==(7·m→, 5·m→)+(7·m→, 8·n→)+(3·n→, 5·m→)+(3·n→, 8·n→)
Выносим коэффициент за знак произведения и получим:
(7·m→, 5·m→)+(7·m→, 8·n→)+(3·n→, 5·m→)+(3·n→, 8·n→)==7·5·(m→,m→)+7·8·(m→,n→)+3·5·(n→,m→)+3·8·(n→,n→)==35·(m→,m→)+56·(m→,n→)+15·(n→,m→)+24·(n→,n→)
По свойству коммутативности преобразуем:
35·(m→,m→)+56·(m→,n→)+15·(n→,m→)+24·(n→,n→)==35·(m→,m→)+56·(m→,n→)+15·(m→,n→)+24·(n→,n→)==35·(m→,m→)+71·(m→,n→)+24·(n→,n→)
В итоге получим:
(a→,b→)=35·(m→,m→)+71·(m→,n→)+24·(n→,n→).
Теперь применим формулу для скалярного произведения с заданным по условию углом:
(a→,b→)=35·(m→,m→)+71·(m→,n→)+24·(n→,n→)==35·m→2+71·m→·n→·cos(m→,n→^)+24·n→2==35·32+71·3·2·cosπ2+24·22=411.
Ответ: (a→,b→)=411
Если имеется числовая проекция.
Найти скалярное произведение a→и b→. Вектор a→ имеет координаты a→=(9,3,-3), проекция b→ с координатами (-3,-1,1).
Решение
По условию векторы a→ и проекция b→ противоположно направленные, потому что a→=-13·npa→b→→, значит проекция b→ соответствует длине npa→b→→, при чем со знаком «-»:
npa→b→→=-npa→b→→=-(-3)2+(-1)2+12=-11,
Подставив в формулу, получим выражение:
(a→,b→)=a→·npa→b→→=92+32+(-3)2·(-11)=-33.
Ответ: (a→,b→)=-33.
Задачи при известном скалярном произведении, где необходимо отыскать длину вектора или числовую проекцию.
Какое значение должна принять λ при заданном скалярном произведении a→=(1,0,λ+1) и b→=(λ,1,λ) будет равным -1.
Решение
Из формулы видно, что необходимо найти сумму произведений координат:
(a→,b→)=1·λ+0·1+(λ+1)·λ=λ2+2·λ.
В дано имеем (a→,b→)=-1.
Чтобы найти λ, вычисляем уравнение:
λ2+2·λ=-1, отсюда λ=-1.
Ответ: λ=-1.
Физический смысл скалярного произведения
Механика рассматривает приложение скалярного произведения.
При работе А с постоянной силой F→ перемещаемое тело из точки M в N можно найти произведение длин векторов F→ и MN→ с косинусом угла между ними, значит работа равна произведению векторов силы и перемещения:
A=(F→,MN→).
Перемещение материальной точки на 3 метра под действием силы равной 5 ньтонов направлено под углом 45 градусов относительно оси. Найти A.
Решение
Так как работа – это произведение вектора силы на перемещение, значит, исходя из условия F→=5, S→=3, (F→,S→^)=45°, получим A=(F→,S→)=F→·S→·cos(F→,S→^)=5·3·cos(45°)=1522.
Ответ: A=1522.
Материальная точка, перемещаясь из M(2,-1,-3) в N(5,3λ-2,4) под силой F→=(3,1,2), совершила работа равную 13 Дж. Вычислить длину перемещения.
Решение
При заданных координатах вектора MN→ имеем MN→=(5-2, 3λ-2-(-1), 4-(-3))=(3, 3λ-1,7).
По формуле нахождения работы с векторами F→=(3,1,2) и MN→=(3, 3λ-1,7) получим A=(F⇒, MN→)=3·3+1·(3λ-1)+2·7=22+3λ.
По условию дано, что A=13Дж, значит 22+3λ=13. Отсюда следует λ=-3, значит и MN→=(3,3λ-1,7)=(3,-10,7).
Чтобы найти длину перемещения MN→ , применим формулу и подставим значения:
MN→=32+(-10)2+72=158.
Ответ: 158.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
План урока:
Угол между векторами
Понятие скалярного произведения векторов
Скалярное произведение в координатах
Определение перпендикулярности векторов и прямых
Вычисление угла между векторами
Свойства скалярного произведения
Угол между векторами
Любую пару векторов можно отложить от одной точки. Если при этом вектора не сонаправлены друг с другом, то они образуют некоторый угол. Его и именуют углом между векторами.
Если же пара векторов сонаправлена, то принято считать, что угол между такими векторами составляет 0°.
На рисунке показаны два вектора, a и b. Чтобы определить угол между a и b, надо отложить их от одной и той же точки:
В приведенном примере угол составил 135°. Для обозначения этого угла может быть использована такая запись:
Задание. В квадрате АВСD проведены диагонали, они пересекаются в точке О. Определите, какой угол образуют вектора:
Так как в квадрате диагонали пересекаются под углом 90°, а со сторонами образуют угол 45°, то мы легко определим, что
Здесь нам помог тот факт, что вектора из пунктов а) и б) изначально отложены из одной точки. С пунктом в) ситуация сложнее. Надо отложить от точки А вектор ОА и определить угол, образующийся при этом:
Пусть после откладывания вектора ОА от А получился вектора АА’. Нам надо найти ∠ВАА’. Нам уже известен ∠ОАВ, который является смежным с ∠ВАА’, поэтому можно записать равенство:
Ответ: а) 45°; б) 90°; в) 135°.
Понятие скалярного произведения векторов
Большое распространение в науке получила математическая операция, именуемая скалярным произведением векторов. В геометрии оно помогает находить угол между векторами, а в физике вычислять некоторые физические величины. В рамках школьной программы его используют для нахождения работы, совершенной той или иной силой. В рамках же более сложных дисциплин, с которыми мало кто сталкивается, оно применяется в квантовой механике и специальных разделах математики – тензорной алгебре, теории многообразий и т. п. Ввел его в науку Уильям Гамильтон в 1846 г, который разрабатывал теорию особых чисел – кватерионов. Они, кстати, используются компьютерами для расчетов трехмерной графики в играх и других приложениях.
Прежде, чем мы научимся применять на практике скалярное произведение, сначала сформулируем правило, позволяющее вычислить его.
Например, пусть есть вектора a и b, причем даны их длины:
Угол между a и b тоже известен и составляет 60°, это записывается таким образом:
Задание. Вычислите скалярное произведение векторов d и f, если их длины составляют 6 и 10 соответственно, а угол между векторами равен 45°.
Решение. Просто подставляем числа из условия в формулу:
Задание. АВС – равносторонний треугольник со стороной 4. Каково скалярное произведение векторов АВ и АС?
Решение. Все углы в равностороннем треугольнике равны 60°, поэтому и угол между АВ и АС также составляет 60°.
Ответ: 8.
Напомним, что косинус, взятый от острого угла – это положительная величина, а косинус тупого угла – это отрицательное число. У прямого же угла косинус равен нулю. Это означает, что по знаку скалярного произведения можно определить тип угла между векторами.
Часто скалярное произведение применяется в физике. Например, с его помощью рассчитывается работа, совершаемая силой при перемещении того или иного тела. И сила, и перемещение – это векторные величины. Чтобы найти работу силы, надо скалярно перемножить вектора силы и перемещения:
Эта формула отражает физический смысл скалярного произведения.
Задание. Под воздействием силы 10Н тело переместилось в горизонтальном направлении на 3 метра. При этом сила образует угол 60° с направлением перемещения тела. Какую работу совершила сила?
Решение.
Скалярное произведение в координатах
Оказывается, что для перемножения векторов достаточно знать только их координаты.
Докажем эту формулу. Сначала рассмотрим случай, когда один из перемножаемых векторов, например a, является нулевым. Тогда у него нулевая длина и нулевые координаты:
Теперь рассмотрим случай, когда оба перемножаемых вектора ненулевые. Тогда отложим их от некоторой точки О и, если вектора неколлинеарны, то мы получим ∆ОАВ:
Для частных случаев, когда a и b коллинеарны (то есть либо сонаправлены, либо противоположно направлены), эта формула также справедлива. Если aи b сонаправлены, то угол α принимается равным нулю (и cosα = 1):
Если же a и b направлены противоположно, то α = 180° (и cosα = – 1):
Итак, мы убедились, что в любой ситуации формула (1) справедлива. При этом вектор АВ можно представить как разность a и b:
Если вектор а имеет координаты {x1; у1}, а координаты b– это {x2; у2},то координаты их разности a – b будут записываться в виде {х1 – х2;у1 – у2}. С учетом этого (2) примет вид
В результате нам удалось доказать формулу скалярного произведения через координаты:
Задание. Перемножьте скалярно вектораa и b, если определены их координаты:
Ответ: а) 23; б) 0; в) 5.
Определение перпендикулярности векторов и прямых
Напомним, что скалярное произведение оказывается нулевым исключительно в случае перпендикулярности векторов. Это позволяет использовать его для проверки перпендикулярности векторов.
Задание. Проверьте, являются ли перпендикулярными вектора:
Решение. В каждом случае мы должны скалярно перемножить пару векторов. Если результат окажется нулевым, то можно сделать вывод о перпендикулярности векторов. В противном случае они не перпендикулярны. Первый вектор будет обозначать буквой а, а второй – буквой b:
Ответ: а) да; б) нет; в) да; г) нет.
Задание. При каком значении переменной х вектора а{4; 5} и b{x; – 6} окажутся перпендикулярными?
Решение. Перемножим скалярно вектора и получим некоторое выражение с переменной x:
Найдем, при каком х это выражение обращается в нуль, то есть вектора становятся перпендикулярными:
Задание. Определите, перпендикулярны ли прямые АВ и CD, если даны координаты точек: А(3; 8), В(4; 10), С(7;12) и D(5;13).
Решение. В этой задаче сначала надорассчитать координаты векторов АВ и CD по координатамих начальной и конечной точки:
Мы вычислили координаты векторов: АВ{1; 2} и CD{– 2; 1}. Теперь мы можем проверить их перпендикулярность, скалярно перемножив вектора:
Мы получили ноль. Это означает, что АВ и CD – перпендикулярные вектора. Значит, и прямые, на которых они лежат, также перпендикулярны.
Ответ: перпендикулярны.
Задание. Перпендикулярны ли друг другу прямые, задаваемые уравнениями
Названия точкам в данном примере присвоены произвольно. На следующем шаге по координатам точек мы находим координаты векторов, лежащих на исследуемых прямых:
Полученный ноль показывает, что исходные прямые перпендикулярны.
Ответ: перпендикулярны.
В случае, когда прямые заданы уравнениями, необязательно проделывать столь длительные вычисления для определения их перпендикулярности. Есть теорема, сокращающая объем вычислений.
Докажем это утверждение. Пусть две прямые заданы уравнениями
Найдем какие-нибудь точки этих прямых. Для этого подставим в уравнения значения х = 0 и х = 1:
Прямые окажутся перпендикулярными исключительно в том случае, если это выражение будет нулевым. Это условие перпендикулярности можно записать как уравнение:
В результате мы получили доказываемую нами формулу.
Задание. Проверьте, какие из этих пар прямых перпендикулярны:
Решение. В каждом случае надо просто перемножить угловые коэффициенты прямых, то есть числа, стоящие перед переменной х. Другие числа в этих уравнениях (свободные коэффициенты) никак не влияют на перпендикулярность. Если вычисленное произведение окажется равным (– 1), то из этого будет вытекать перпендикулярность прямых.
Вычисление угла между векторами
Мы научились по координатам векторов определять, перпендикулярны ли они. Однако в более общем случае можно рассчитать угол и между двумя неперпендикулярными векторами.
В самом деле, по известным координатам векторов легко как рассчитать длину каждого из них, так и скалярно перемножить вектора. Тогда из формулы скалярного произведения можно выразить значение косинуса угла между векторами:
Зная же косинус, можно рассчитать и сам угол, используя специальные таблицы либо функцию арккосинуса на калькуляторе.
Задание. Вычислите угол между векторами а{3; 4} и b{8; 15}.
Решение. Сначала рассчитываем длины векторов:
Задание. Точки А(2; 8), В(– 1; 5) и С(3; 1) соединили отрезками и получили ∆АВС. Вычислите угол ∠А в ∆АВС.
Решение.∠А данного треугольника представляет собой угол между двумя векторами АВ и АС. Вычислим координаты этих векторов:
Осталось лишь с помощью калькулятора найти сам ∠А:
Свойства скалярного произведения
Существует несколько важных свойств скалярного произведения. Эти свойства очень схожи с законами алгебры, которые используются при работе с обычными числами.
Переместительный закон легко доказать, опираясь только на определение операции скалярного произведения:
Задание. Известно, что угол между векторами a и с составлет 60°, так же как и угол между векторами b и с. Определены и длины векторов:
Задание. Найдите скалярное произведение векторов p и q, если
Решение. Сначала надо перемножить вектора и раскрыть при этом скобки также, как они раскрываются при перемножении обычных чисел:
Примечание. Иногда скалярное произведение вектора на самого себя именуют скалярным квадратом.
Тогда выражение (1) примет вид:
В сегодняшнем уроке мы узнали, что такое скалярное произведение. Оно имеет много приложений в физике и других науках, в частности, с его помощью вычисляется работа. В геометрии оно помогает вычислять углы между векторами, а значит, и между прямыми. В будущем, при более углубленном изучении геометрии, вы узнаете о существовании других типов произведений векторов – векторном и смешанном.
Содержание:
- Формула
- Примеры вычисления скалярного произведения векторов
Формула
Для того чтобы найти скалярное произведение двух векторов, заданных своими
координатами, необходимо вычислить сумму произведений
соответствующих координат этих векторов. Для случая, если векторы заданны на плоскости координатами $bar{a}=left(a_{x} ; a_{y}right)$ и $bar{b}=left(b_{x} ; b_{y}right)$, имеет место формула:
$$(bar{a}, bar{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}$$
Если же векторы заданы в пространстве своими координатами: $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$ соответственно, то их скалярное произведение вычисляется по формуле:
$$(bar{a}, bar{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}$$
Примеры вычисления скалярного произведения векторов
Пример
Задание. Найти скалярное произведение векторов $bar{a}=(1 ;-3)$ и $bar{b}=(-2 ;-3)$
Решение. Векторы заданны на плоскости, поэтому для вычисления их скалярного произведения воспользуемся формулой
$$(bar{a}, bar{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}$$
Подставляя координаты заданных векторов, получим
$$(bar{a}, bar{b})=1 cdot(-2)+(-3) cdot(-3)=-2+9=7$$
Ответ. $(bar{a}, bar{b})=7$ lt /$>

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В пространстве заданы точки
$A(-1 ;-2 ; 5), B(-3 ; 2 ; 1)$ и $C(0 ; 1 ;-1)$ . Найти скалярное произведение векторов
$overline{A B}$ и
$overline{A C}$
Решение. Найдем сначала координаты векторов
$overline{A B}$ и
$overline{A C}$ . Для этого из координат конца вычислим соответствующие
координаты начала, получим:
$$overline{A B}=(-3-(-1) ; 2-(-2) ; 1-5)=(-2 ; 4 ;-4)$$
$$overline{A C}=(0-(-1) ; 1-(-2) ;-1-5)=(1 ; 3 ;-6)$$
Далее воспользуемся формулой для вычисления скалярного произведения векторов, заданных в пространстве:
$$(bar{a}, bar{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}$$
Получим
$$(overline{A B}, overline{A C})=(-2) cdot 1+4 cdot 3+(-4)(-6)=-2+12+24=34$$
Ответ. $(overline{A B}, overline{A C})=34$
Читать дальше: как найти векторное произведение векторов.
Теоретический урок по предмету математики для решения задач по теме “Векторы”.
Содержание данной страницы электронного справочника для школьников:
- – тема “Свойства векторов” рассматривается на примере решения задачи 86;
- – онлайн задания, как находить угол между векторами, в том числе в координатной форме, как определяется скалярное произведение векторов, скалярный квадрат, представлены в контрольных работах 87 – 107 учебника.
Свойства векторов

1) Вектор коллинеарный с вектором
2) ↑↑
↑↑
3) =

4) =
–
5) Дано: система координат
модуль вектора = 5
= 12
Найдите: OA
Решение:
OA== 13
OA = = 13
Ответ: OA = 13
***

Пусть и
– данные векторы.
1) Отложим от точки O векторы =
и
=
2) Если ↑↓
– противоположно направленные векторы, то лучи OA и OB образуют угол
AOB
3) Если ↑↑
– сонаправленные векторы, то угол между векторами
и
равен 0°.
Угол между двумя векторами и
обозначается так:
Определение:
Два вектора называются перпендикулярными, если угол между ними равен 90°.
***
Задача 86.

Дано:
ABCD – квадрат
AC ∩ BD = O
Найти: углы между векторами BAC,
DAB = ?
Вычисление:
a) Т.к. AC – диагональ квадрата, то она делит угол A пополам. Тогда угол между векторами
= 45°
б) Т.к. ABCD – квадрат, то градусная мера угла между векторами =
= 90°, т.е. прямой угол.
***
Скалярное произведение векторов
Задача 87.

Дано:
ABCD – ромб
BD = AB; AC ∩ BD = 0
Вычислите: угол, образованный векторами
и
,
и
,
и
= ?
Решение:
а) По определению ромба ΔABD – равносторонний (AB = AD = BD).
Значит, все углы в треугольнике равны 60°. Тогда угол между векторами = 60°
б) Т.к. векторы ↑↑
сонаправленные, то угол между векторами
= 0°
в) Т.к. векторы ↑↓
– противоположно направленные, то угол между векторами
= 180°
***
Определение:
Скалярным произведением двух векторов (формула 1) называется произведение длин этих векторов на косинус угла (Cos) между ними.
Обозначение: или
=
*cos (a,b) (1)
Из формулы скалярного произведения векторов через косинус угла (1) следует:
1) скалярное произведение векторов больше нуля, если угол между векторами меньше 90°, т.е.
>0, если
<90°
скалярное произведение векторов меньше нуля, если угол между векторами больше 90°, т.е.
<0, если
>90°
2) Если ↑↑
– сонаправленные векторы, то угол между векторами равен нулю градусов, т.е.
=0°
=
3) Если
– перпендикулярные векторы и
=90°
Cos 90° = 0, то
= 0
Верно и обратное, т.е. если = 0
Вывод: = 0
***
Задача 88.
Дано:
Векторы
=2
=3
Угол α = 90°
Найти: скалярное произведение векторов
Решение:
Используя формулу скалярного произведения векторов через косинус угла, получаем
=
•
• Cos 90° = 2 • 3 • 0 = 0
Ответ: = 0
***
Скалярный квадрат
***
Задача 89.
Дано:
ΔABC – равносторонний

AB = a
Найти: скалярное произведение векторов 1) 2)
Решение: В равностороннем треугольнике все углы равны 60°.
1) =
•Cos (
) =
•
=
2) =
•Cos (120°) = –
***
Задача 90.
Дано:
Векторы
=2;
=3
1) угол α = 45°
2) α = 135°
Найти: скалярное произведение векторов
Решение:
1) =
•Cos 45° = 2 • 3 •
= 3
2) =
•Cos 135° = 2 • 3 •
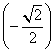
Ответ: 1) 3; 2) -3
***
Задача 91.
Дано:

ΔABC – равносторонний
AB = a
BD – высота
Найти: скалярное произведение векторов
1)
2) 3)
Решение:
1) =
•Cos 120° =
• (-Cos 60°) = –
2) т.к. векторы перпендикулярны BD
AC
= 0
3) =
=
Ответ:1) –; 2) 0 ; 3)
Задача 92.
Дано:

ABCD – ромб
BD ∩ AC = 0
BD = AB
1) ;
2) ;
Найти: величину угла между векторами
1) ; 2)
Решение:
1) Рассмотрим ΔABC – равнобедренный, т.к. AB=BD.
Зная, что в ромбе все стороны равны, получаем ΔABD – равносторонний.
Тогда DAB =
BDA = 60°
По свойству ромба следует, что ADC = 120°
Тогда угол между векторами =120°
2) Т.к. стороны параллельны и векторы сонаправлены:
BA || CD и ↑↑
, тогда векторы параллельны
||
, поэтому векторы равны
=
.
Рассмотрим треугольник ΔCBD – равнобедренный, т.к. две стороны равны: BD=BC.
По определению ромба ΔCBD – равносторонний.
Значит, угол BDC = 60°
По свойству ромба угол ADC = 120°.
Тогда угол между векторами =120°.
Ответ: 1) =120°; 2)
=120°.
***
Скалярное произведение векторов в координатах
Теорема:
Если два вектора имеют координаты {x1; y1};
{ x2; y2}, то скалярным произведением двух векторов (формула 2) называется произведение их координат:
(2)
Доказательство:
1 случай.

Если какой-нибудь вектор – нулевой, то равенство (2) выполняется очевидно.
2 случай.
Если векторы и
– неколлинеарны.
Отложим векторы от произвольной точки O.
Рассмотрим треугольник ΔOBA.
Известно, что формула косинуса
c2 = a2 + b2 – 2ab • Cos α, получаем равенство
AB2 = OB2 + OA2 – 2 • OB • OA • Cos α (3)
Учитывая значения (*) =
;
=
;
=
; а также, что OA = |
|; OB = |
| ; AB = |
|, подставив значения (*) в равенство (3), получаем
||2 = |
|2 + |
|2 – 2
(4)
Используя формулу для вычисления длины вектора по его координатам, получаем
=
;
=
.
Т.к. = {x2 – x1; y2 – y1}, то, используя формулу для вычисления расстояния между двумя точками
, получаем
|| =
.
Тогда из равенства (4) следует
(x2 – x1)2 + (y2 – y1)2 = x22 + y22 + x12 + y12 – 2
x22 -2 x2 x1 + x12 + y22 – 2 y2y1 + y12 = x22 + y22 + x12 + y12 – 2
-2 x2 x1– 2 y2y1 = – 2
= x2 x1 + y2 y1
***
Следствия:
1) Если векторы перпендикулярны, т.е.
{x1; y1}
{ x2; y2}
x1 x2 + y1 y2 = 0
2) По определению скалярного произведения двух векторов (формула 1)
=
•
• Cos α
Cos α =
Формула для нахождения косинуса угла через координаты векторов:

Для вычисления синуса и тангенса угла между векторами через косинус угла используются формулы приведения и тригонометрические функции.
***
Скалярное векторное произведение
Задача 93.
Если {
; -1};
{2; 3}, то
= 0,5 + (-3) = -2,5
***
Задача 94.
Если {x; -1};
{3; 2} и векторы перпендикулярны
, тогда
= 3x – 2
0 = 3x – 2
2 = 3x
x =
***
Задача 95.
Дано:
Координаты точек
A(2;8), B(-1;5), C(3;1)

Найти: косинус угла между векторами Cos A = ?
Решение:
Т.к. каждая координата вектора равна разности соответствующих координат его конца и начала
{b1 – a1; b2 – a2}, тогда
= {
} = {
}
= {
} = {
}
Используя формулу для нахождения углов через координаты векторов
Cos A = , получаем
Cos A = =
=
=
Ответ: Cos A =
***
Длина вектора
Задача 96.
Дано:
угол между векторами равен =
=60° ,
длины векторов || = 1, |
| = |
| = 2
Найти: произведение векторов ()
= ?
Решение:
()
=
+
= |
|•|
|•Cos 60° + |
|•|
|•Cos 60° = 1 + 2 = 3
Ответ: ()
= 3
***
Задача 97.
Дано:
=
,
=
длина векторов ||=|
|=1
– перпендикулярные векторы
Найти: произведение векторов = ?
Решение:
= (
)•(
) = 3
2 + 12
– 2
– 8
2 =
= 32 + 10
– 8
2 = 3|
|2 + 0 – 8|
|2 = -5.
Ответ: = -5.
***
Задача 98.
Дано:
{1,5 ; 2},
{4 ; -0,5}
Найти: произведение векторов = ?
Решение:
= x1 x2 + y1 y2 = 6 + (-1) = 5
Ответ: = 5.
***
Задача 99.
Дано:
{0 ; -3},
{5 ; x}
– перпендикулярные векторы
Найти: произведение векторов = ?
Решение:
= x1 x2 + y1 y2
0 = 0 + (-3x)
3x = 0
x = 0
Ответ: при x=0, .
***
Задача 100.
Дано:
Координаты точек
A(2;8), B(-1;5), C(3;1)
Найти: косинус угла векторов

1) Cos B = ?
2) Cos C = ?
Решение:
1)
Т.к. каждая координата вектора равна разности соответствующих координат его конца и начала
{b1 – a1; b2 – a2}, тогда
= {
} = {
}
= {
} = {
}
Используя формулу для нахождения углов через заданные координаты векторов
Cos B = , получаем
Cos B = =
= 0
2)
= {
} = {
}
= {
} = {
}
Cos C = =
=
=
Ответ: Cos B =0, Cos C =
***
Задача 101.
Дано:
, где i и j – координатные векторы
Найти: длину вектора || = ?
Решение:
Найдем координаты вектора .
{3; -4}
Т.к. длина вектора равна квадратному корню из суммы квадратов его координат || =
, тогда получаем
|| =
=
= 5.
Ответ: || = 5.
***
Задача 102.
Дано:
ABCD – ромб
AB =, AD =

Доказать: диагонали ромба в точке пересечения перпендикулярны
ACBD или
=0
Доказательство:
Т.к. ABCD – ромб – параллелограмм, то векторы параллелограмма ,
=
–
= (
+
) (
–
) =
–
2 +
2 –
=
2 –
2 = =|
|2 -|
|2 = 0. Поэтому угол между векторами
= 90°. Значит, диагонали ромба в точке пересечения перпендикулярны AC
BD.
***
Задача 103.
Дано:
треугольник ΔABC – равнобедренный
AM – медиана
Доказать:
1) 4AM2 = AB2 + AC2 + 2AB • AC • Cos A

2) CH = AM
Доказательство:
1) Т.к. точка M – середина BC, тогда
2=
Значит, (2) • (2
) = (
)(
) =
= AB2 + 2AB + 2AB • AC • Cos A + AC2 = AB2 + AC2 + 2AB • AC • Cos A
Получаем 4AM2 = AB2 + AC2 + 2AB • AC • Cos A
2) По формуле, полученной выше, следует
4CH2 = AC2 + BC2 + 2AC • BC • Cos C
Т.к. треугольник ΔABC – равнобедренный, тогда AB = BC, A =
C
Cos
A = Cos
C
Получим, что 4CH2 = AC2 + BC2(=AB2) + 2AC • BC(=AB) • Cos C (= Cos A)
4CH2 = AC2 + AB2 + 2AC • AB • Cos A
4CH2 = 4AM2
=
2CH = 2AM | : 2
CH = AM
***

Задача 104.
Дано:
ABCD – выпуклый четырехугольник
BD = d1 и AC = d2 – диагонали
d1 ∩ d2 = O – точка пересечения диагоналей
Доказать:
Площадь четырехугольника равна половине произведения диагоналей на синус острого угла между ними
SABCD= d1 • d2 • Sin α
Доказательство:
Площадь четырехугольника – сумма площадей четырех треугольников.
SABCD= S1 + S2 + S3 + S4 , где
S1 = SΔAOB ; S2 = SΔCOB ; S3 = SΔCOD ; S4 = SΔAOD
S1 = BO • OA • Sin α
S2 = BO • OC • Sin (180° – α) =
BO • OC • Sin α
S3 = CO • OD • Sin α
S4 = AO • OD • Sin (180° – α) =
AO • OD • Sin α
Сложив S1 + S2 + S3 + S4, получаем
SABCD= BO • Sin α (OA+OC) +
+ OD • Sin α (CO+OA)
Т.к. OA+OC = AC, CO+OA = AC, BO + OD = BD тогда
SABCD=BO • AC • Sin α +
OD • AC • Sin α =
BD • AC • Sin α
Формула площади выпуклого четырехугольника:
SABCD= d1 • d2 • Sin α
***
Задача 105.
Дано:
два вектора образуют угол α = 150°,
длины векторов || = 2
, |
| = 2

Найти: длину вектора |2–
| = ?
Решение:
BC2 = AB2 + AC2 – 2 AB • AC • Cos 150°
BC2 = 48 + 4 – 2 • 4• 2 • (-
) = 52 + 24 = 76
BC = = 2
Ответ: BC = |2–
| = 2
***
Задача 106.
Дано:

Треугольник ΔABC
Угол B = 45°,
C = 70°
a=24,6
Найти: Угол в градусах A, стороны b, c
Решение:
A = 180° – (45° + 70°) = 75°
Используя теорему синусов
, получаем выражение
b =
≈ 19,2
c =
≈
≈ 25,5
Ответ: A = 75°; b ≈ 19,2; c ≈ 25,5.
***
Задача 107.
Дано:
длины векторов || = 5, |
| = 8,

угол между 2 векторами =60°
Найти: значение векторов
1) ||= ?
2) ||= ?
Решение: По теореме косинусов
1)
AC2 = AB2 + BC2 – 2AB • BC • Cos 120°
AC2 = 25 + 64 – 80 • (- 0,5) = 129

AC = ±, но AC = –
не удовлетворяет решению задачи. Значит, AC =
.
2) BC2 = AB2 + AC2 – 2AB • AC • Cos 60°
BC2 = 89 – 80 • 0,5 = 49
BC = ±, но BC = – 7 не удовлетворяет решению задачи. Значит, BC = 7.
Ответ: || =
; |
| = 7.
***