Выражение скалярного произведения через координаты векторов
Разумеется, что величина скалярного произведения любых векторов и
не зависит от базиса. Однако формулы, выражающие скалярное произведение
через координаты множителей, зависят от базиса, относительно которого определены координаты. Рассмотрим сначала случай стандартного базиса в пространстве, а затем — произвольного.
Скалярное произведение векторов в ортонормированном базисе
Теорема 1.6 (формула вычисления скалярного произведения в ортонормированном базисе). В ортонормированном базисе скалярное произведение векторов равно сумме произведений одноименных координат векторов:
— если векторы и
относительно ортонормированного базиса на плоскости имеют координаты
и
соответственно, то скалярное произведение этих векторов вычисляется по формуле
(1.9)
— если векторы и
относительно ортонормированного базиса в пространстве имеют координаты
и
соответственно, то скалярное произведение этих векторов вычисляется по формуле
(1.10)
Докажем формулу (1.10). Пусть в пространстве задан ортонормированный (стандартный) базис . Скалярные произведения базисных векторов находятся по определению:
(1.11)
Используя линейность скалярного произведения по любому множителю, для векторов и
получаем:
Учитывая (1.11), из девяти слагаемых только три отличны от нуля, поэтому
что и требовалось доказать.
Замечания 1.10
1. Для доказательства формулы (1.9) можно использовать следующее соображение. Множество векторов на плоскости со стандартным базисом можно рассматривать как множество таких векторов в пространстве с базисом
, у которых аппликата равна нулю. Поэтому формулу вычисления скалярного произведения векторов
и
можно получить из (1.10), полагая
.
2. Скалярное произведение можно записать в матричном виде: если и
координатные столбцы векторов
и
в стандартном базисе, то их скалярное произведение находится формуле:
Для векторов на плоскости соответственно получаем
3. Координаты вектора в ортонормированием базисе равны его скалярным произведениям на соответствующие базисные векторы:
В самом деле, подставляя в (1.10) координаты базисного вектора
, приходим к первому равенству (остальные равенства получаются аналогично).
4. Формулы (1.9) и (1.10) совместно с геометрическими свойствами скалярного произведения имеют многочисленные приложения.
Пример 1.15. Даны векторы . Найти скалярные произведения
Решение. По формуле (1.10) вычисляем
Сравнивая вектор со скалярными произведениями
обнаруживаем, что при умножении вектора на базисный вектор получается соответствующая координата данного вектора. Этот результат иллюстрирует пункт 3 замечаний 1.10.
Для нахождения скалярного произведения можно использовать матричную запись (см. пункт 2 замечаний 1.10). Например, векторам соответствуют координатные столбцы
Поэтому
что совпадает с полученными ранее результатами.
Пример 1.16. Прямоугольный параллелепипед построен на векторах
(см. рис. 1.38). Точка
— центр грани
, точка
делит ребро
в отношении
. Требуется найти:
а) величину угла между векторами
и
;
б) длину ортогональной проекции вектора на прямую
.
Решение. Находим координаты векторов в стандартном базисе :
(см. решение примера 1.12)
По формуле (1.10) находим скалярные произведения:
а также длины векторов (см. геометрическое свойство 1 скалярного произведения):
Длина была найдена в примере 1.12.
Теперь по геометрическому свойству 2 находим косинус искомого угла
т.е.
Алгебраическое значение длины ортогональной проекции находим по геометрическомусвойству 3:
Скалярное произведение векторов в произвольном базисе
Пусть — произвольный базис в пространстве. Найдем скалярное произведение векторов
и
:
Запишем полученную формулу в матричном виде. Для этого из чисел , называемых метрическими коэффициентами базиса, составим матрицу Грама системы векторов
:
(1.12)
Координаты каждого из векторов и
представим в виде столбцов
и
соответственно.
Тогда для скалярного произведения получим
или, короче,
(1.13)
Теорема 1.7 (формула вычисления скалярного произведения в произвольном базисе). В произвольном базисе скалярное произведение векторов
и
вычисляется по формуле (1.13), где
— координатные столбцы векторов
и
соответственно, a
—матрица Грама (1.12) базиса
.
Замечания 1.11.
1. Для ортонормированного базиса матрица Грама имеет вид
т.е. является единичной. В этом случае по формуле (1.13) получаем
что совпадает с (1.10).
2. Для произвольного базиса на плоскости скалярное произведение векторов
и
находится по формуле:
где — координатные столбцы векторов
и
соответственно, a
— матрица Грама базиса
.
В частности, для ортонормированного базиса матрица Грама является единичной:
, поэтому скалярное произведение векторов
и
находится по формуле
, что совпадает с (1.9). Заметим, что эта формула также следует из полученной в пункте 1 при
.
Пример 1.17. Найти матрицы Грама для следующих базисов:
а) два единичных вектора , служащие сторонами правильного треугольника
(рис.1.39,а);
б) три единичных вектора , служащие ребрами правильного тетраэдра (рис. 1.39,6).
Найти длины векторов, имеющих в данных базисах следующие разложения: .
Решение. а) Учитывая, что длины базисных векторов равны единице, а угол между ними равен , получаем
Записываем матрицу Грама
Найдем теперь длину вектора . Составляем координатный столбец этого вектора
.
Учитывая формулу (1.13), находим скалярный квадрат: . Следовательно,
.
б) Учитывая, что длины базисных векторов равны единице, а угол между любыми двумя из них равен , получаем
Записываем матрицу Грама: . Найдем теперь длину вектора
. Составляем координатный столбец этого вектора
. Учитывая формулу (1.13), находим скалярный квадрат:
Следовательно,
Скалярное произведение векторов во взаимных базисах
Пусть на плоскости задан базис . Базис
называется взаимным по отношению к базису
, если
Пусть в пространстве задан базис . Базис
называется взаимным по отношению к базису
, если
Взаимные базисы обладают следующими основными свойствами.
1. Свойство взаимности базисов симметричное: если второй базис взаимен по отношению к первому, то первый взаимен ко второму.
2. Для каждого базиса (на плоскости или в пространстве) существует единственный взаимный базис.
3. Пусть векторы и
заданы своими координатами относительно взаимных базисов:
Тогда их скалярное произведение вычисляется по формуле: , т.е. равно сумме произведений одноименных координат векторов, как и в случае ортонормированного базиса.
4. Если и
взаимные базисы, то координаты
любого вектора
относительно базиса
находятся по формулам
Докажем свойство 2. Пусть на плоскости задан базис (рис.1.40,а). Вектор
взаимного базиса перпендикулярен вектору
, так как
(см. второе геометрическое свойство скалярного произведения). Из двух возможных направлений для вектора
выбираем то, которое образует острый угол
с вектором
, так как
. Следовательно, направление вектора
определено однозначно. Осталось выбрать его длину, используя (1.7):
, так как
.
Таким образом, направление и длина первого вектора взаимного базиса определяются однозначно. То же можно сказать и в отношении выбора вектора . Доказательство существования и единственности взаимного базиса в пространстве (рис. 1.40,6) проводится аналогично.
Заметим, что для стандартного базиса на плоскости (или базиса
в пространстве) взаимный базис совпадает с самим базисом
(соответственно
)
Докажем свойство 3. Находим скалярное произведение, используя свойства коммутативности и линейности, а также определение взаимных базисов:
что и требовалось доказать.
Свойство 4 следует из формулы, приведенной в пункте З. В самом деле, . Аналогично доказываются остальные формулы в п.4.
Пример 1.18. а) Найти базис, взаимный базису, заданному в примере 1.17,а (рис.1.39,а).
б) Внутри угла величиной
взята точка
, удаленная от сторон
и
на расстояния 11 и 2 соответственно. Найти длину отрезка
(рис.1.41,б).
Решение. а) Так как базисный вектор единичный, то, учитывая геометрический смысл скалярного произведения (см. разд. 1.4.1), вектор
можно построить следующим образом. Через начало вектора
(точку
) и конец вектора
(точку
) проводим прямые, перпендикулярные векторам
и
соответственно (штриховые линии на рис. 1.41,а). Точка пересечения этих прямых — конец вектора
(его начало совпадает с точкой
). Аналогично строится вектор
(построение изображено штрих- пунктирными линиями на рис. 1.41,а). Тогда по построению справедливо
, а также
. Следовательно, учитывая геометрическое свойство 2 и формулу (1.8):
, т.е. выполняются условия взаимности базисов. Найдем длины векторов взаимного базиса. Поскольку угол между векторами
и
равен
(напомним, что
), то из прямоугольного треугольника с катетом
. Длина вектора
такая же.
б) Зададим на плоскости базис из единичных векторов , который совпадает с базисом, рассмотренным в пункте “а”. По условию задачи известны длины ортогональных проекций вектора
на оси, определяемые векторами взаимного базиса:
. По третьему геометрическому свойству скалярного произведения с учетом свойства 4 взаимных базисов, получаем
где — координаты вектора
в базисе
. Так как
(см. пункт “а”), то
. Длину вектора
вычисляем по формуле, следующей из пункта 2 замечаний 1.10 при
, используя матрицу Грама для базиса
, найденную в примере 1.17 пункт “а”:
Следовательно, .
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Скалярное произведение векторов 
Скаля́рное произведе́ние (иногда называемое внутренним произведением) — результат операции над двумя векторами, являющийся скаляром, то есть числом, не зависящим от выбора системы координат.
Используется в определении длины векторов и угла между ними.
Обычно для скалярного произведения векторов 

или просто
и
второе обозначение применяется в квантовой механике для векторов состояния[1].
В простейшем случае, а именно в случае конечномерного вещественного евклидового пространства, иногда используют «геометрическое» определение скалярного произведения ненулевых векторов 

Равносильное определение: скалярное произведение есть произведение длины проекции первого вектора на второй и длины второго вектора (см. рисунок). Если хотя бы один из векторов нулевой, то произведение считается равным нулю[3].
У понятия скалярного произведения существует также большое количество обобщений для различных векторных пространств, то есть для множеств векторов с операциями сложения и умножения на скаляры[⇨]. Данное выше геометрическое определение скалярного произведения предполагает предварительное определение понятий длины вектора и угла между ними. В современной математике используется обратный подход: аксиоматически определяется скалярное произведение, а уже через него — длины и углы[4]. В частности, скалярное произведение определяется для комплексных векторов, многомерных и бесконечномерных пространств, в тензорной алгебре.
Скалярное произведение и его обобщения играют чрезвычайно большую роль в векторной алгебре, теории многообразий, механике и физике. Например, работа силы при механическом перемещении равна скалярному произведению вектора силы на вектор перемещения[5].
Определение и свойства[править | править код]
Будем говорить, что в вещественном или комплексном векторном пространстве 




- Для любых трёх элементов
пространства
и любых чисел
справедливо равенство:
(линейность скалярного произведения по первому аргументу).
- Для любых
справедливо равенство
, где черта означает комплексное сопряжение.
- Для любого
имеем:
, причём
только при
(положительная определённость и невырожденность скалярного произведения соответственно).
Заметим, что из аксиомы 2 следует, что 
Если 

Из данных аксиом получаются следующие свойства:
- коммутативность для вещественных векторов:

Дистрибутивность скалярного произведения в случае вещественного евклидового пространства
- дистрибутивность относительно сложения:
и
- инволюционная линейность относительно второго аргумента:
(в случае вещественного
— просто линейность по второму аргументу).
(что совпадает с
для вещественного
).
Также есть свойства, связанные не с данными аксиомами:
- неассоциативность относительно умножения на вектор[7]‘:
;
- ортогональность: два ненулевых вектора a и b ортогональны тогда и только тогда, когда (a, b) = 0 (определения ниже).
Замечание. В квантовой физике скалярное произведение (волновых функций, которые комплекснозначны) принято определять как линейное по второму аргументу (а не по первому), соответственно, по первому аргументу оно будет инволюционо линейным. Путаницы обычно не возникает, поскольку традиционное обозначение для скалярного произведения в квантовой физике также отличается: 
Определение и свойства в евклидовом пространстве[править | править код]
Вещественные векторы[править | править код]
В 


Проверка показывает, что все три аксиомы выполнены.
Например, скалярное произведение векторов 

Можно доказать[8], что эта формула равносильна определению через проекции или через косинус: 
Комплексные векторы[править | править код]
Для комплексных векторов 
Пример (для 

Свойства[править | править код]
Помимо общих свойств скалярного произведения, для многомерных евклидовых векторов верно следующее:
- в отличие от обычного умножения скаляров, где если ab = ac и a ≠ 0, то b равняется c, для скалярного умножения векторов это неверно: если a · b = a · c, то есть a · (b − c) = 0, то в общем случае a и b − c лишь ортогональны; но вектор b − c в общем случае не равен 0, то есть b ≠ c;
- правило произведения: для дифференцируемых вектор-функций a(t) и b(t) верно соотношение (a(t), b(t))′ = a′(t) ⋅ b(t) + a(t) ⋅ b′(t)[10];
- оценка угла между векторами:
- в формуле
знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение больше 0, если угол между векторами острый, и меньше 0, если угол между векторами тупой;
- в формуле
- проекция вектора
на направление, определяемое единичным вектором
:
, так как
- площадь параллелограмма, натянутого на два вектора
и
, равна
Теорема косинусов в вещественном пространстве[править | править код]

Теорема косинусов легко выводится с использованием скалярного произведения. Пусть на сторонах треугольника находятся векторы a, b и c, первые два из которых образуют угол θ, как показано в изображении справа. Тогда, следуя свойствам и определению скалярного произведения через косинус:

Связанные определения[править | править код]
В современном аксиоматическом подходе уже на основе понятия скалярного произведения векторов вводятся следующие производные понятия[11]:
Длина вектора, под которой обычно понимается его евклидова норма:
(термин «длина» обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).
Углом 
Данные определения позволяют сохранить формулу: 
Для любых элементов 
В случае, если пространство является псевдоевклидовым, понятие угла определяется лишь для векторов, не содержащих изотропных прямых внутри образованного векторами сектора. Сам угол при этом вводится как число, гиперболический косинус которого равен отношению модуля скалярного произведения этих векторов к произведению их длин (норм):
- Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю. Это определение применимо к любым пространствам с положительно определённым скалярным произведением. Например, ортогональные многочлены на самом деле ортогональны (в смысле этого определения) друг другу в некотором гильбертовом пространстве.
- Пространство (вещественное или комплексное) с положительно определённым скалярным произведением называется предгильбертовым пространством.
- При этом конечномерное вещественное пространство с положительно определённым скалярным произведением называется также евклидовым, а комплексное — эрмитовым или унитарным пространством.
- Случай, когда скалярное произведение не является знакоопределённым, приводит к т. н. пространствам с индефинитной метрикой. Скалярное произведение в таких пространствах уже не порождает нормы (и она обычно вводится дополнительно). Конечномерное вещественное пространство с индефинитной метрикой называется псевдоевклидовым (важнейшим частным случаем такого пространства является пространство Минковского). Среди бесконечномерных пространств с индефинитной метрикой важную роль играют пространства Понтрягина и пространства Крейна.
История[править | править код]
Скалярное произведение было введено У. Гамильтоном в 1846 году[13] одновременно с векторным произведением в связи с кватернионами — соответственно, как скалярная и векторная часть произведения двух кватернионов, скалярная часть которых равна нулю[14].
Вариации и обобщения[править | править код]
В пространстве измеримых интегрируемых с квадратами на некоторой области Ω вещественных или комплексных функций можно ввести положительно определённое скалярное произведение:
При использовании неортонормированных базисов скалярное произведение выражается через компоненты векторов с участием метрического тензора[15] 
При этом сама метрика (говоря точнее, её представление в данном базисе) так связана со скалярными произведениями базисных векторов 
Аналогичные конструкции скалярного произведения можно вводить и на бесконечномерных пространствах, например, на пространствах функций:
где К — положительно определённая, в первом случае симметричная относительно перестановки аргументов (при комплексных x — эрмитова) функция (если нужно иметь обычное симметричное положительно определённое скалярное произведение).
Простейшим обобщением конечномерного скалярного произведения в тензорной алгебре является свёртка по повторяющимся индексам.
См. также[править | править код]
- Гильбертово пространство
- Векторное произведение
- Внешнее произведение
- Псевдоскалярное произведение
- Смешанное произведение
Примечания[править | править код]
- ↑ Hall B. C. Quantum Theory for Mathematicians. — NY: Springer Science & Business Media, 2013. — xvi + 553 p. — (Graduate Texts in Mathematics. Vol. 267). — ISBN 978-1-4614-7115-8. Архивная копия от 31 января 2016 на Wayback Machine — P. 85.
- ↑ Имеется в виду наименьший угол между векторами, не превосходящий
- ↑ Векторная алгебра // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 1. — С. 634.
- ↑ 1 2 Гельфанд, 1971, с. 30—31.
- ↑ Тарг С. М. Работа силы // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193—194. — 704 с. — ISBN 5-85270-087-8.
- ↑ Кудрявцев Л. Д. Математический анализ. II том. — М., Высшая школа, 1970. — с. 316.
- ↑ Weisstein, Eric W. Dot Product Архивная копия от 29 апреля 2021 на Wayback Machine. From MathWorld — A Wolfram Web Resource.
- ↑ Calculus II – Dot Product. tutorial.math.lamar.edu. Дата обращения: 9 мая 2021. Архивировано 9 мая 2021 года.
- ↑ Гельфанд, 1971, с. 86.
- ↑ Stewart, James (2016), Calculus (8 ed.), Cengage, Section 13.2.
- ↑ Гельфанд, 1971, с. 34.
- ↑ §9.5. Линейные пространства со скалярным произведением: евклидовы и унитарные
- ↑ Crowe M. J. A History of Vector Analysis – The Evolution of the Idea of a Vectorial System. — Courier Dover Publications, 1994. — С. 32. — 270 с. — ISBN 0486679101. Архивная копия от 6 марта 2019 на Wayback Machine
- ↑ Hamilton W. R. On Quaternions; or on a New System of Imaginaries in Algebra // Philosophical Magazine. 3rd Series. — London, 1846. — Т. 29. — С. 30.
- ↑ Гельфанд, 1971, с. 240.
Литература[править | править код]
- Гельфанд И. М. Лекции по линейной алгебре. — 4-е изд. — М.: Наука, 1971. — 272 с.
Ссылки[править | править код]
- Емелин А. Скалярное произведение векторов. Дата обращения: 14 ноября 2019.
Скалярное произведение в произвольном базисе
Пусть
![]()
–
базис евклидова пространства
![]()
,
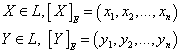
,
рассмотрим скалярное произведение:
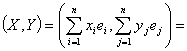
![]()
=
![]()
(*)
Если записать (*) в матричном
виде, то получим:
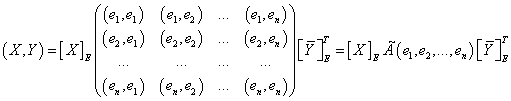
.
Если базис
–
ортонормированный, то
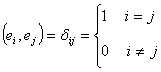
,
то
![]()
.
48B
Ортогональное дополнение подпространства m из l
Пусть
–
евклидово (унитарное) пространство,
подпространство
![]()
.
Вектор
![]()
называется
ортогональным к подпространству
,
если для всех
![]()
![]()
.
Множество всех векторов
![]()
ортогональных
к подпространству
![]()
называется
ортогональным дополнением
и
обозначается
![]()
.
Очевидно, М┴
является подпространством пространства
,
причем для размерности подпространств
![]()
и
размерность пространства
связаны
соотношением
![]()
.
Действительно, выберем
базис ![]()
подпространства
,
дополним его до базиса
,
получим
![]()
.
Ортогонализируем данный базис
методом Грамма-Шмидта, получим:
![]()
–
базис пространства
,
![]()
–
базис подпространства
,
![]()
–
базис подпространства
ортогонального дополнения
.
Говорят, что пространство
является
прямой ортогональной суммой своих
подпространств
и
:
![]()
Ортогональное дополнение подпространства m из l
Пусть
–
евклидово (унитарное) пространство,
подпространство
.
Вектор
называется
ортогональным к подпространству
,
если для всех
.
Множество всех векторов
ортогональных
к подпространству
называется
ортогональным дополнением
и
обозначается
.
Очевидно, М┴
является подпространством пространства
,
причем для размерности подпространств
и
размерность пространства
связаны
соотношением
.
Действительно, выберем
базис
подпространства
,
дополним его до базиса
,
получим
.
Ортогонализируем данный базис
методом Грамма-Шмидта, получим:
–
базис пространства
,
–
базис подпространства
,
–
базис подпространства
ортогонального дополнения
.
Говорят, что пространство
является
прямой ортогональной суммой своих
подпространств
и
:


49/B
Опера́тор (позднелат. operator —
работник, исполнитель, от operor —
работаю, действую) — то же, что
отображение
в математике.
Привычная функция отображает
одно число (аргумент) на другое (значение
функции). Функция нескольких переменных
отображает вектор (ряд чисел) на число.
В случае отображения вектора на вектор,
отображение чаще называют оператором.
А поскольку функции относятся к векторам
(аргумент функции служит индексом, при
этом количество элементов может достигать
континуума для недискретных
функций), операторы часто применяются
к функциям. Таким образом оператор можно
считать обобщением функции: если функция
оперирует числами, возвращая число, то
оператор принимает и возвращает ряд
чисел, то есть оперирует функциями.
Наиболее часто встречающиеся
операторы:
-
Функциональный
анализ: Операторы на пространствах
функций (дифференцирование, интегрирование,
свертка с ядром, преобразование Фурье). -
Линейная
алгебра: Отображения (в
особенности линейные) векторных
пространств (проекторы, повороты
координат, гомотетии, умножения вектора
на матрицу).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Векторная алгебра
Векторная алгебра – это раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства; часть линейной алгебры, занимающаяся векторными пространствами; различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).
Векторы и линейные операции над ними
Займемся теперь таким важным как в самой математике, так и в ее многочисленных приложениях, понятием вектора.
Определение: Вектором, на плоскости или в пространстве называется отрезок прямой с заданным на нем направлением, т. е. одна из его граничных точек считается начальной, а вторая – конечной.
Обозначать векторы мы будем строчными латинскими буквами 
Длина отрезка, изображающего вектор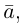 называется его длиной и обозначается через
называется его длиной и обозначается через 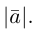 Вектор с совпадающими начальной и конечной точками называется нуль-вектором. Для него используется обозначение
Вектор с совпадающими начальной и конечной точками называется нуль-вектором. Для него используется обозначение 
По определению, два вектора считаются равными, если один из них можно преобразовать в другой с помощью параллельного переноса.
Учитывая приведенное определение, всюду в дальнейшем мы без специальных оговорок будем перемещать вектор параллельным переносом в любую удобную для нас точку.
Два вектора  называются коллинеарными (обозначение
называются коллинеарными (обозначение  ), если отрезки их изображающие параллельны.
), если отрезки их изображающие параллельны.
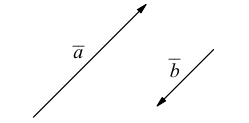
Аналогично, векторы а и b называются ортогональными (обозначение 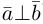 ), если соответствующие отрезки перпендикулярны.
), если соответствующие отрезки перпендикулярны.
Три вектора называются компланарными, если после приведения их общему началу, они будут расположены в одной плоскости.
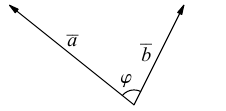
Углом между векторами 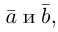 приведенными к общему началу, называется меньший из двух углов между соответствующими отрезками. Обозначать угол мы будем строчными греческими буквами
приведенными к общему началу, называется меньший из двух углов между соответствующими отрезками. Обозначать угол мы будем строчными греческими буквами 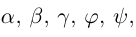 … или через
… или через 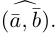
Два ненулевых вектора 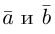 мы будем считать одинаково направленными, если
мы будем считать одинаково направленными, если 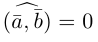 и противоположно направленными, если
и противоположно направленными, если 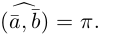
Введем теперь линейные операции над векторами.
а) Умножение числа на вектор.
Произведением действительного числа  на вектор
на вектор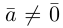 называется вектор
называется вектор 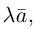 длина которого равна
длина которого равна 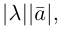 а направление его совпадает с направлением вектора
а направление его совпадает с направлением вектора 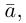 если
если 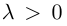 и имеет противоположное с ним направление, если
и имеет противоположное с ним направление, если 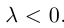 Если
Если 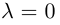 или
или 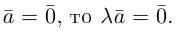
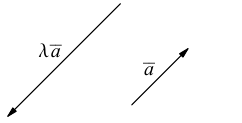
В частности, вектор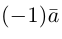 обозначается через
обозначается через 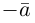 и называется вектором, противоположным вектору
и называется вектором, противоположным вектору 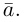
Если 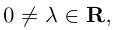 то произведение
то произведение 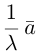 мы будем иногда записывать в виде
мы будем иногда записывать в виде 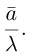
Из приведенного определения сразу же следует, что коллинеарные векторы  линейно связаны, т. е. существует константа
линейно связаны, т. е. существует константа 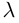 такая,что
такая,что 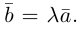 В качестве такой константы следует
В качестве такой константы следует
взять число 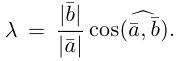 Если
Если 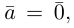 то
то 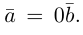 В частности, если
В частности, если 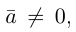 то вектором единичной длины с направлением данного вектора является вектор
то вектором единичной длины с направлением данного вектора является вектор 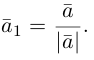
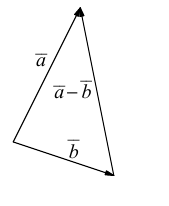
b) Сложение векторов.
Суммой двух векторов  называется вектор
называется вектор 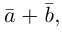 который находится по правилу треугольника
который находится по правилу треугольника
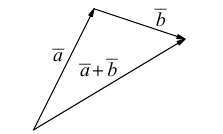
или по равносильному ему правилу параллелограмма
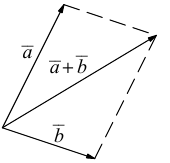
Вектор 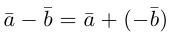 называется разностью векторов
называется разностью векторов 
Свойства линейных операций над векторами аналогичны соответствующим свойствам действительных чисел.
Проекцией вектора  на вектор
на вектор  называется число
называется число
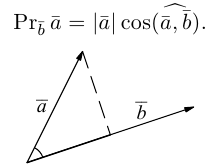
Геометрически очевидны следующие свойства проекции:
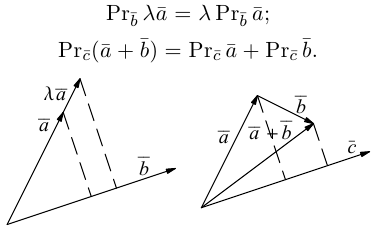
Пример №1
Пусть Е и F – середины сторон AD и ВС соответственно выпуклого четырехугольника ABCD. Доказать, что
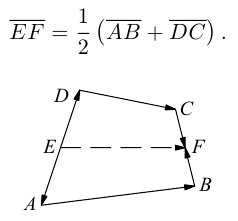
Доказательство. Из четырехугольников EDCF и EABF по правил}’ сложения векторов получим:
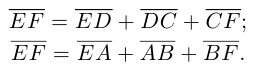
Сложив данные равенства и учитывая, что 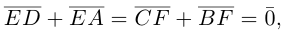 будем иметь:
будем иметь:
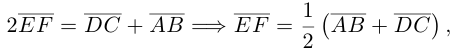
что и требовалось.
Базис и декартова система координат
Определение: Базисом на плоскости называется упорядоченная пара неколлинеарных векторов. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов.
Обозначение: 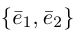 — базис на плоскости,
— базис на плоскости, 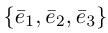 — базис в пространстве. Всюду в дальнейшем, не оговаривая это особо, будем рассматривать только положительно ориентированные базисы, т. е. базисы, у которых кратчайший поворот от вектора
— базис в пространстве. Всюду в дальнейшем, не оговаривая это особо, будем рассматривать только положительно ориентированные базисы, т. е. базисы, у которых кратчайший поворот от вектора 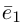 к вектору
к вектору 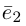 совершается против часовой стрелки, если наблюдение ведется со стороны вектора
совершается против часовой стрелки, если наблюдение ведется со стороны вектора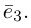 Сформулируем теперь фундаментальное свойство базиса.
Сформулируем теперь фундаментальное свойство базиса.
Теорема. Любой вектор единственным образом разлагается по базису, т. е. представляется в виде 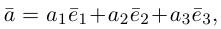 где действительные числа
где действительные числа 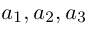 – координаты вектора
– координаты вектора 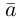 в базисе
в базисе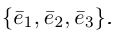
Приведем геометрическое доказательство этого утверждения.
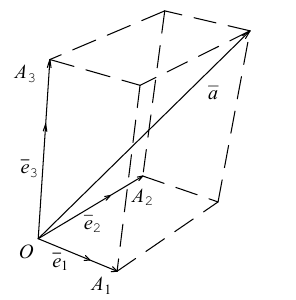
Вектор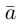 можно единственным образом представить как большую диагональ параллелепипеда, ребра которого, параллельны базисным векторам. Тогда по правилу сложения векторов
можно единственным образом представить как большую диагональ параллелепипеда, ребра которого, параллельны базисным векторам. Тогда по правилу сложения векторов 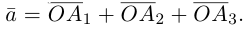 В виду коллинеарности векторов
В виду коллинеарности векторов 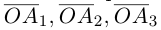 соответствующим базисным векторам, мы можем записать, что
соответствующим базисным векторам, мы можем записать, что 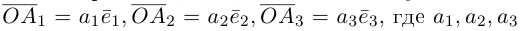 — некоторые действительные числа. Отсюда и следует искомое разложение.
— некоторые действительные числа. Отсюда и следует искомое разложение.
Если базис зафиксирован, то факт, что вектор а в этом базисе имеет координаты 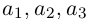 коротко записывается как
коротко записывается как 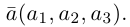
Из доказанной теоремы следует, что при выполнении линейных операций над векторами точно также преобразуются и их координаты, т. е. если 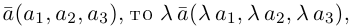 если
если 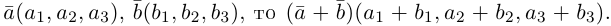 Отсюда, в частности, следует, что два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны, т. е.
Отсюда, в частности, следует, что два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны, т. е.
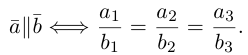
Рассмотрим теперь ортонормированный базис  т.е. базис, в котором все векторы имеют единичную длин}’ и попарно ортогональны. Векторы этого базиса мы будем называть ортами. Пусть в этом базисе
т.е. базис, в котором все векторы имеют единичную длин}’ и попарно ортогональны. Векторы этого базиса мы будем называть ортами. Пусть в этом базисе 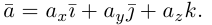
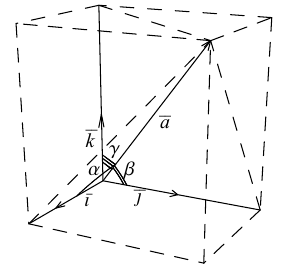
Как видно из чертежа, координаты вектора в ортонормированном базисе представляют собой проекции этого вектора на соответствующие орты. т. е.
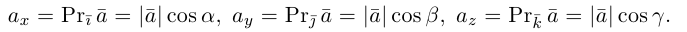
Величины 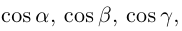 т. е. косинусы углов, которые образует данный вектор с ортами
т. е. косинусы углов, которые образует данный вектор с ортами 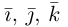 к соответственно, называются направляющими косинусами вектора
к соответственно, называются направляющими косинусами вектора 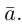 Единичный вектор
Единичный вектор 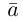 имеет координаты
имеет координаты 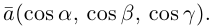
Очевидно также, что
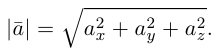
Свяжем теперь с ортонормированным базисом декартову (прямоугольную) систему координат. Для этого поместим начала ортов в некоторую точку О, ось Ох (абсцисс) направим вдоль орта  ось
ось 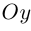 (ординат) — вдоль орта
(ординат) — вдоль орта 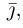 наконец, ось
наконец, ось 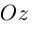 (аппликат) направим вдоль орта
(аппликат) направим вдоль орта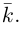

В выбранной системе координат координаты радиуса-вектора 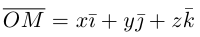 мы будем называть координатами точки М и записывать
мы будем называть координатами точки М и записывать 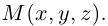
Если известны координаты начальной 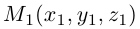 и конечной
и конечной 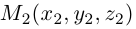 точек вектора, то из равенства
точек вектора, то из равенства 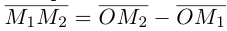 слезет, что его координаты равны
слезет, что его координаты равны
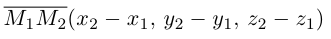 и, значит, расстояние между точками
и, значит, расстояние между точками  вычисляется по формуле
вычисляется по формуле
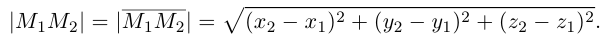
Найдем теперь координаты точки М, делящей отрезок с концами в точках 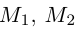 в данном
в данном
отношении 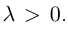 Так как
Так как 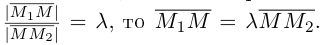 Отсюда, переходя к координатам получим:
Отсюда, переходя к координатам получим:
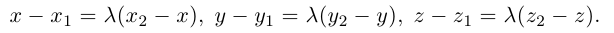
Следовательно, координаты искомой точки вычисляются по формулам:
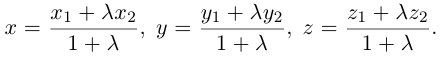
Найдем, в частности, координаты середины отрезка. Здесь А = 1, поэтому
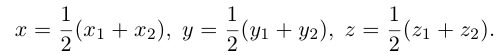
Пример №2
Треугольник задан координатами своих вершин 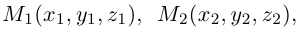
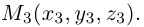 Найти координаты точки пересечения его медиан. Решение.
Найти координаты точки пересечения его медиан. Решение.
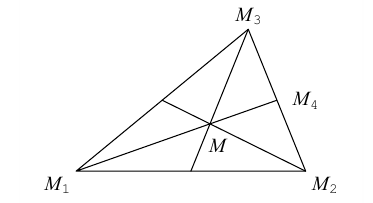
Пусть – середина отрезка
– середина отрезка  – точка пересечения медиан. Тогда
– точка пересечения медиан. Тогда
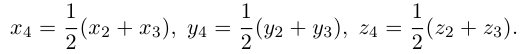
По известному свойству точки пересечения медиан 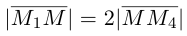 и потому
и потому
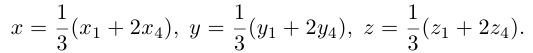
Подставив сюда найденные координаты точки  ползучим:
ползучим:
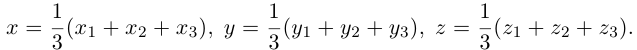
Таким образом, координаты точки пересечения медиан треугольника равны средним арифметическим соответствующих координат его вершин.
Замечание. Базисом n-мерного пространства 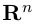 называется упорядоченная совокупность n векторов
называется упорядоченная совокупность n векторов

обладающая тем свойством, что любой вектор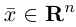 единственным образом представляется в виде линейной комбинации базисных векторов (1), т.е. существуют действительные числа
единственным образом представляется в виде линейной комбинации базисных векторов (1), т.е. существуют действительные числа 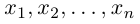 (координаты вектора
(координаты вектора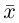 в базисе (1)) такие, что
в базисе (1)) такие, что

В качестве базиса в 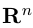 мы можем взять, например, векторы
мы можем взять, например, векторы
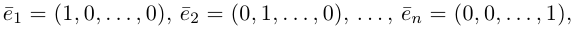
так как, очевидно, любой вектор 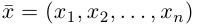 однозначно представляется в виде (2).
однозначно представляется в виде (2).
Скалярное произведение векторов
Определение: Скалярным произведением векторов 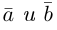 называется число
называется число
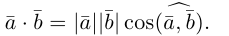
Из этого определения сразу же следует, что
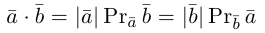
и таким образом, если один из векторов имеет единичную длину, то их скалярное произведение равно проекции второго вектора на единичный.
Отметим основные свойства скалярного произведения.
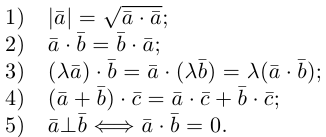
Первые два и последнее свойства немедленно следуют из определения скалярного произведения, а третье и четвертое – из сформулированных в §1 свойств проекции.
Найдем теперь представление скалярного произведения в координатах. Пусть в орто-нормированном базисе  векторы
векторы 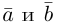 имеют координаты
имеют координаты 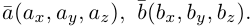 Заметив, что по свойствам 1) и 5) скалярного произведения
Заметив, что по свойствам 1) и 5) скалярного произведения
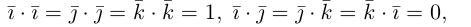
перемножим векторы скалярно, используя свойства 2) – 4):
скалярно, используя свойства 2) – 4):
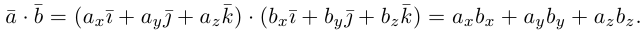
Таким образом, скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат векторов.
Пример №3
Разложить вектор 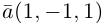 на две ортогональные составляющие, одна из которых коллинеарна вектору
на две ортогональные составляющие, одна из которых коллинеарна вектору 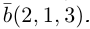
Решение.
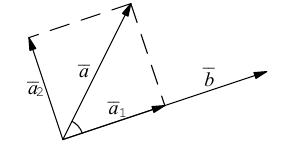
Из чертежа следует, что 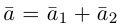 – искомое разложение. Найдем векторы
– искомое разложение. Найдем векторы 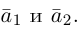 Составляющая
Составляющая 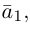 коллинеарная вектору
коллинеарная вектору  равна, очевидно, вектору проекции
равна, очевидно, вектору проекции  и, следовательно,
и, следовательно,
Тогда вторая ортогональная составляющая вектора  равна
равна
В заключение параграфа рассмотрим одно простое приложение скалярного произведения в механике. Пусть под действием постоянной силы 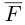 материальная тотп<а переместилась по прямой из положения В в положение С.
материальная тотп<а переместилась по прямой из положения В в положение С.
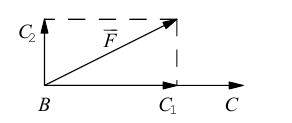
Найдем работу этой силы. Для этого разложим вектор силы 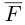 на две ортогональные составляющие. одна из которых коллинеарна вектору перемещения
на две ортогональные составляющие. одна из которых коллинеарна вектору перемещения 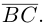 Тогда
Тогда
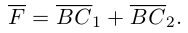
Составляющая 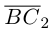 работы не совершает, следовательно, работа силы
работы не совершает, следовательно, работа силы 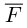 равна работе составляющей
равна работе составляющей 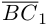 и, таким образом,
и, таким образом,
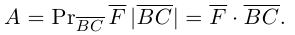
Окончательно, работа силы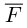 , под действием которой материальная точка перемещается по отрезку прямой из положения В в положение С, вычисляется по формуле:
, под действием которой материальная точка перемещается по отрезку прямой из положения В в положение С, вычисляется по формуле:
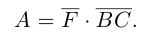
Замечание. Скалярным произведением векторов 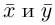 n-мерного пространства
n-мерного пространства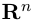 называется число
называется число 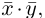 равное произведению первого вектора, записанного строкой, на второй вектор, записанный столбцом. Таким образом, если
равное произведению первого вектора, записанного строкой, на второй вектор, записанный столбцом. Таким образом, если
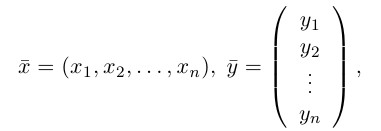
то
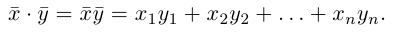
Несложной проверкой мы можем убедиться в том, что таким образом определенное скалярное произведение в 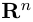 обладает свойствами 2) — 4) скалярного произведения векторов на плоскости или в пространстве.
обладает свойствами 2) — 4) скалярного произведения векторов на плоскости или в пространстве.
Длиной вектора 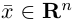 называется число
называется число
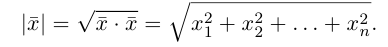
Векторы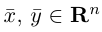 называются ортогональными, если
называются ортогональными, если 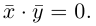 Векторы
Векторы
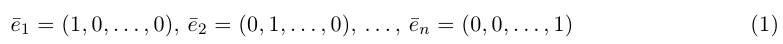
составляют ортонормированный базис пространства 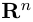 , так как каждый из этих векторов имеет единичную длину и все они попарно ортогональны.
, так как каждый из этих векторов имеет единичную длину и все они попарно ортогональны.
Любой вектор  мы можем рассматривать как точку
мы можем рассматривать как точку
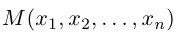
n-мерного пространства с координатами 
Взяв еще одну точку 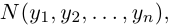 соответствующую вектору
соответствующую вектору 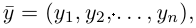 мы под расстоянием между точками М и N будем понимать длину вектора
мы под расстоянием между точками М и N будем понимать длину вектора 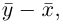 т. е. число
т. е. число
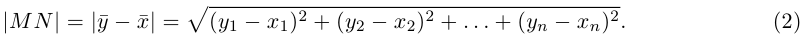
Таким образом переопределенное пространство 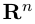 с расстоянием (2) между точками мы будем называть евклидовым пространством, сохранив для него то же обозначение.
с расстоянием (2) между точками мы будем называть евклидовым пространством, сохранив для него то же обозначение.
Совокупность точки О(0.0,…, 0) и ортонормированного базиса (1) называется декартовой системой координат евклидова пространства R”. Точка 0(0,0,… ,0) называется, естественно, началом координат.
Векторное произведение векторов
Определение: Векторным произведением некоялинеарных векторов 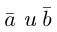 называется вектор
называется вектор  такой, что
такой, что
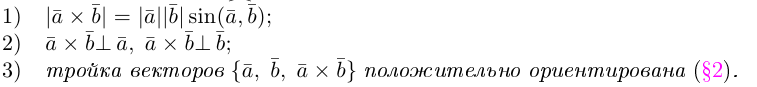
Из этого определения следует, что площадь параллелограмма, построенного на векторах 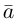 и
и 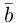 равна длине векторного произведения
равна длине векторного произведения  , т. е.
, т. е.
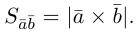
Сформулируем основные свойства векторного произведения.
Первые два свойства очевидным образом следуют из определения векторного произведения. Доказательство третьего ввиду его громоздкости мы приводить не будем.
Найдем формулу для вычисления векторного произведения в координатах. Пусть векторы 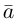 и
и 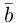 в ортонормированном базисе
в ортонормированном базисе 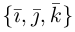 имеют координаты
имеют координаты 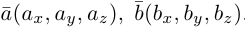 Учитывая, tito по определению векторного произведения
Учитывая, tito по определению векторного произведения
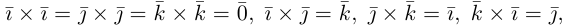
раскроем скобки в векторном произведении 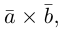 принимая во внимание свойства 1) – 3):
принимая во внимание свойства 1) – 3): 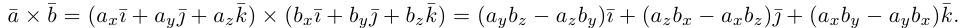
Полученный вектор мы можем записать в виде следующего символического определителя.
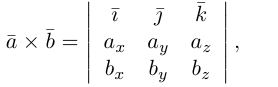
вычислять который удобно разложением по первой строке.
Пример №4
Найти составляющую вектора 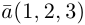 , ортогональную плоскости векторов
, ортогональную плоскости векторов 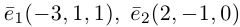 .
.
Решение.
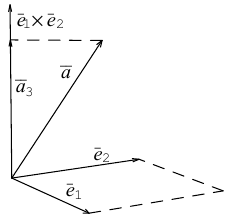
Из чертежа видно, что искомая составляющая представляет собой вектор проекции данного вектора  на векторное произведение
на векторное произведение и, следовательно.
и, следовательно.
Переходим к вычислениям:
Тогда 
Среди многочисленных приложений векторного произведения отметим его применение в механике при вычислении момента силы.
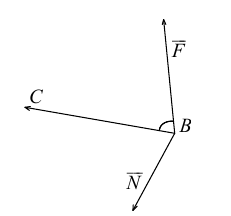
Итак, пусть сила 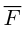 приложена к материальной точке В. Моментом этой силы относительно неподвижной точки С называется вектор
приложена к материальной точке В. Моментом этой силы относительно неподвижной точки С называется вектор
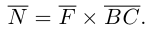
Смешанное произведение векторов
Определение: Смешанным произведением трех векторов 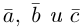 называется число
называется число
Выясним геометрический смысл смешанного произведения для тройки некомпланарных векторов.
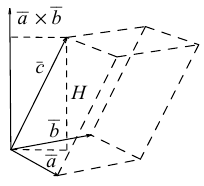
По определению смешанного произведения
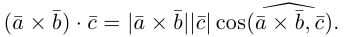
Поскольку 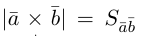 – площадь параллелограмма, построенного на векторах
– площадь параллелограмма, построенного на векторах 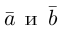 (§4)
(§4)
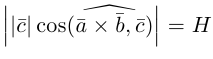 -высота параллелепипеда построенного на векторах
-высота параллелепипеда построенного на векторах 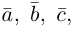 то
то
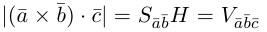
– объем параллелепипеда. Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах.
Если векторы заданы своими координатами в ортонормированном базисе 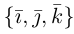 , т.е.
, т.е. 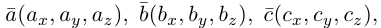 то учитывая формулы для вычисления скалярного и векторного произведений (§3, §4), получим:
то учитывая формулы для вычисления скалярного и векторного произведений (§3, §4), получим:
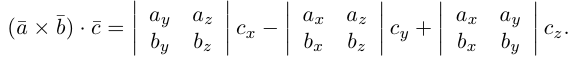
Следовательно (глава I. §2, пункт 3, свойство 7)), в координатах смешанное произведение вычисляется по формуле:
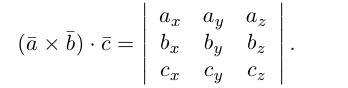
Докажем, пользуясь этой формулой, некоторые свойства смешанного произведения.
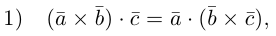
что следует из свойства 4) определителя (глава I. §2, пункт 3). Таким образом, в смешанном произведении можно менять местами знаки скалярного и векторного произведения, и поэтому для него используется более короткое обозначение 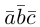 . которым мы и будем пользоваться в дальнейшем.
. которым мы и будем пользоваться в дальнейшем.
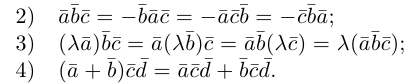
Эти свойства смешанного произведения также являются прямыми следствиями соответствующих свойств определителя.
Докажем еще одно, геометрическое свойство смешанного произведения.
Теорема. Три вектора 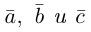 компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
Доказательство. Докажем необходимость условия теоремы. Пусть векторы 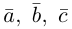 компланарны. Очевидно, что, если хотя бы один из них равен нулю, то и их смешанное произведение равно нулю. Если же все они ненулевые, то, ввиду их компланарности, векторное произведение
компланарны. Очевидно, что, если хотя бы один из них равен нулю, то и их смешанное произведение равно нулю. Если же все они ненулевые, то, ввиду их компланарности, векторное произведение 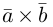 ортогонально вектору с и, следовательно,
ортогонально вектору с и, следовательно, 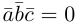 . Аналогично проверяется достаточность условия теоремы.
. Аналогично проверяется достаточность условия теоремы.
Следствие. Три вектора 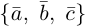 образуют базис в том и только в том случае, когда их смешанное произведение отлично от нуля.
образуют базис в том и только в том случае, когда их смешанное произведение отлично от нуля.
Заметим, кроме того, что, если 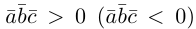 , то угол между векторами
, то угол между векторами 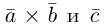 -острый (тупой) и, следовательно, базис
-острый (тупой) и, следовательно, базис 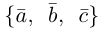 является положительно (отрицательно) ориентированным.
является положительно (отрицательно) ориентированным.
Пример №5
Доказать, что пять точек
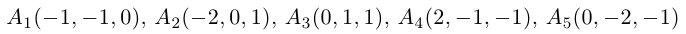
расположены в одной плоскости.
Решение. Рассмотрим векторы 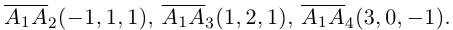 Так как
Так как
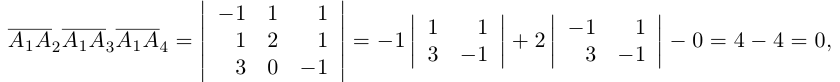
то по доказанной выше теореме эти векторы компланарны и, стало быть. точки  находятся в одной плоскости
находятся в одной плоскости  Аналогично покажем, что и точки
Аналогично покажем, что и точки 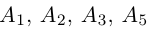 также принадлежат одной плоскости
также принадлежат одной плоскости 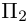 . Действительно,
. Действительно, 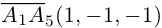
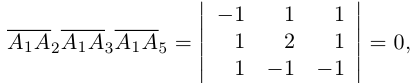
так как первая и третья строки в определителе пропорциональны. Плоскости  имеют три общие точки
имеют три общие точки  , следовательно, они совпадают и, таким образом, все пять точек расположены в одной плоскости.
, следовательно, они совпадают и, таким образом, все пять точек расположены в одной плоскости.
Векторы и линейные операции над ними
Определение: Вектором называется направленный отрезок (рис. 1).
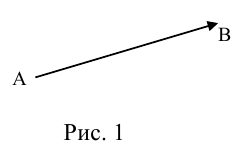 А – начало, В – конец вектора
А – начало, В – конец вектора 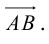
Рис. 1
Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.
Определение: Вектором называется упорядоченная пара точек.
Определение: Длина вектора 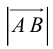 – расстояние между его началом и концом.
– расстояние между его началом и концом.
Определение: Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления.
Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.
Если начало и конец вектора совпадают, он называется нулевым:
 – нулевой вектор: его направление не определено, а длина
– нулевой вектор: его направление не определено, а длина 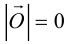 .
.
Определение: Векторы  называются коллинеарными, если они лежат на параллельных прямых:
называются коллинеарными, если они лежат на параллельных прямых: 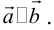
Так как направление нулевого вектора не определено, то он коллинеарен любому другому.
Определение: Векторы называются компланарными, если они параллельны одной плоскости.
Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над векторами
Линейными называются операции сложения векторов и умножения на число.
Сложение
а) Правило параллелограмма (рис.2): начала  совмещаются в одной точке, и
совмещаются в одной точке, и  – диагональ параллелограмма, построенного на
– диагональ параллелограмма, построенного на  .
.
б) Правило треугольника (рис. 3): начало 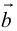 совмещается с концом
совмещается с концом 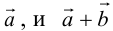 направлен от начала
направлен от начала 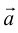 к концу
к концу 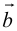 .
.
в) Правило сложения нескольких векторов (рис. 4).
Вектор  замыкает ломаную линию, построенную таким образом: конец предыдущего вектора совмещается с началом последующего и
замыкает ломаную линию, построенную таким образом: конец предыдущего вектора совмещается с началом последующего и  направлен от начала
направлен от начала  к концу
к концу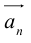 .
.
Умножение на число
Определение: Произведением вектора  на число
на число  называется вектор
называется вектор 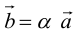 , aудовлетворяющий условиям:
, aудовлетворяющий условиям:
а) 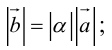
б) 
в)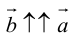 , если
, если 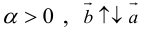 ,a если
,a если 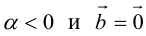 , если
, если 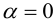 .
.
Произведение 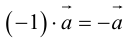 называется вектором, противоположным вектору
называется вектором, противоположным вектору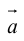 . Очевидно,
. Очевидно, 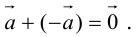 .
.
Определение: Разностью 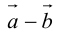 называется сумма вектора
называется сумма вектора 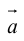 и вектора, противоположного
и вектора, противоположного 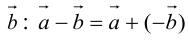 (рис. 5).
(рис. 5).

Начала  совмещаются в одной точке, и
совмещаются в одной точке, и 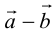 направлен от конца
направлен от конца  к концу
к концу  .
.
Свойства линейных операций
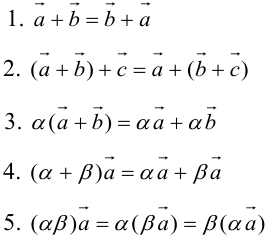
Определение: Результат конечного числа линейных операций над векторами называется их линейной комбинацией: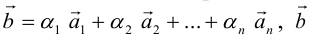 – линейная комбинация векторов
– линейная комбинация векторов 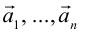 с коэффициентами
с коэффициентами 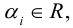
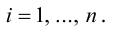
Пример №6
Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить  как линейную комбинацию
как линейную комбинацию
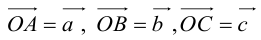 (рис. 6).
(рис. 6).
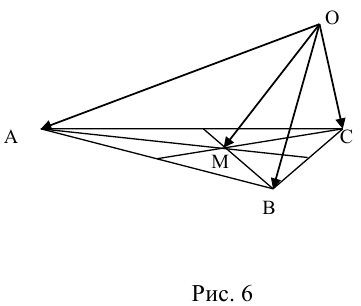
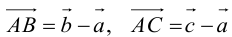 . Так как точка пересечения медиан треугольника делит их в отношении 2:1, считая от вершины, то из правила параллелограмма следует, что
. Так как точка пересечения медиан треугольника делит их в отношении 2:1, считая от вершины, то из правила параллелограмма следует, что 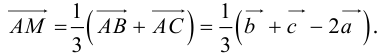
По правилу треугольника 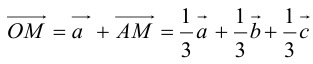 , то есть
, то есть 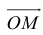 – линейная комбинация
– линейная комбинация 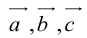 с коэффициентами
с коэффициентами 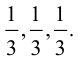
Теорема: Пусть 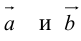 – неколлинеарные векторы. Тогда любой компланарный с ними вектор c может быть представлен в виде
– неколлинеарные векторы. Тогда любой компланарный с ними вектор c может быть представлен в виде
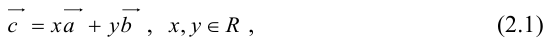
где коэффициенты (2.1) определяются единственным образом.
Представление вектора 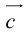 в виде (2.1) называется разложением его по двум неколлинеарным векторам.
в виде (2.1) называется разложением его по двум неколлинеарным векторам.
Доказательство:
- Пусть среди
 есть два коллинеарных, например:
есть два коллинеарных, например: 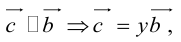
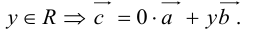
- Пусть среди
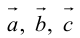 коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с
коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с  , а стороны параллельны прямым, на которых лежат
, а стороны параллельны прямым, на которых лежат  (рис. 7).
(рис. 7).
Тогда c 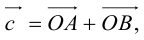 но
но 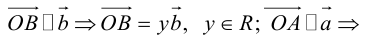
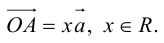 Поэтому
Поэтому 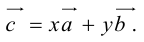
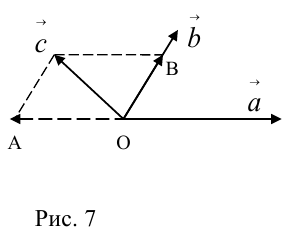
Докажем единственность разложения. Предположим, что 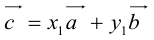 и
и 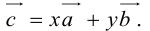 Тогда, вычитая одно равенство из другого, получим:
Тогда, вычитая одно равенство из другого, получим: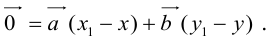
Если 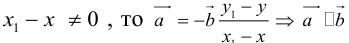 , что противоречит условию. Теорема доказана.
, что противоречит условию. Теорема доказана.
Теорема: Пусть 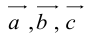 – некомпланарные векторы. Тогда любой вектор
– некомпланарные векторы. Тогда любой вектор 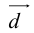 может быть представлен в виде
может быть представлен в виде
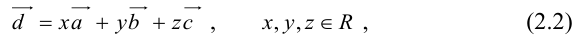
причем единственным образом.
Представление вектора 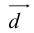 в виде (2.2) называется разложением его по трем некомпланарным.
в виде (2.2) называется разложением его по трем некомпланарным.
Доказать самостоятельно.
Проекция вектора на ось
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
Координаты вектора
Осью называется направленная прямая.
Определение: Ортом оси  называется единичный вектор
называется единичный вектор 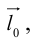
направление которого совпадает с направлением оси.
Определение: Ортогональной проекцией точки М на ось  называется основание
называется основание 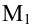 перпендикуляра, опущенного из М на
перпендикуляра, опущенного из М на 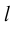 .
.
Определение: Ортогональной проекцией вектора 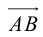 на ось
на ось 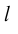 называется длина отрезка
называется длина отрезка  этой оси, заключенного между ортогональными проекциями его начала и конца, взятая со знаком «+», если направление вектора
этой оси, заключенного между ортогональными проекциями его начала и конца, взятая со знаком «+», если направление вектора  совпадает с направлением оси, и со знаком «–», если эти направления противоположны (рис. 8).
совпадает с направлением оси, и со знаком «–», если эти направления противоположны (рис. 8).
Определение: Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).
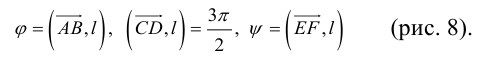
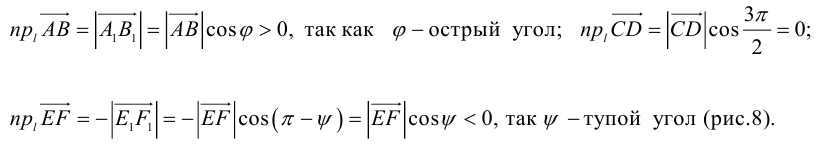
Очевидно, проекцию вектора на ось можно найти по формуле
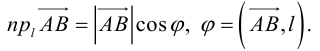
Можно показать, что проекция линейной комбинации векторов равна та-
кой же линейной комбинации их проекций:
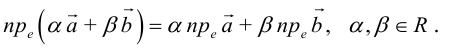
В частности, проекция суммы векторов равна сумме их проекций:
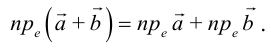
Рассмотрим прямоугольную декартову систему координат ХОY. Обозначим 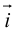 – орт оси ОХ,
– орт оси ОХ, 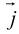 – орт оси OY. Выберем точку A , и пусть x, y – проекции ее на ОХ и OY,то есть координаты этой точки (рис. 9).
– орт оси OY. Выберем точку A , и пусть x, y – проекции ее на ОХ и OY,то есть координаты этой точки (рис. 9).

Аналогично в пространственной системе OXYZ 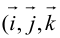 – орты координатных осей) (рис. 10):
– орты координатных осей) (рис. 10):
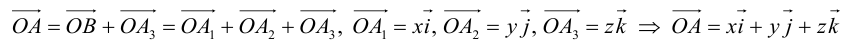
– разложение 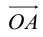 по ортам координатных осей (единственно по теореме 2).
по ортам координатных осей (единственно по теореме 2).
Таким образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором  можно связать три числа x,y,z (или два числа x, y, если вектор плоский), которые являются коэффициентами разложения этого вектора по ортам координатных осей, а также являются проекциями этого вектора на координатные оси.
можно связать три числа x,y,z (или два числа x, y, если вектор плоский), которые являются коэффициентами разложения этого вектора по ортам координатных осей, а также являются проекциями этого вектора на координатные оси.
Определение: Координатами вектора  в любой пдск называются коэффициенты в разложении этого вектора по ортам координатных осей.
в любой пдск называются коэффициенты в разложении этого вектора по ортам координатных осей.
Таким образом, можно дать еще одно определение вектора.
Определение: Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
Пример №7
Если 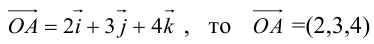 и наоборот, если
и наоборот, если
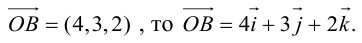
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
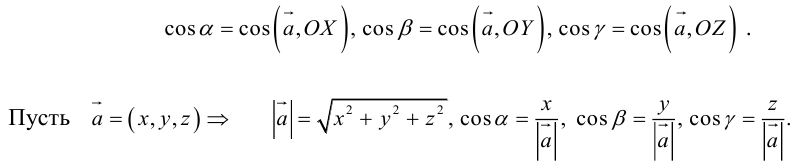
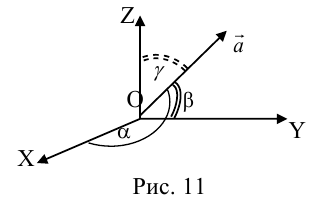
Из этих формул очевидно следует основное свойство направляющих косинусов:
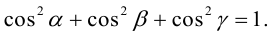
Если известны длина 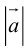 и направляющие косинусы вектора, то его координаты вычисляются по формулам:
и направляющие косинусы вектора, то его координаты вычисляются по формулам:
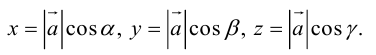
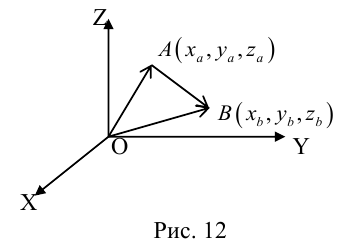
Пусть AB – произвольный вектор в системе OXYZ, OA,OB – радиус-векторы его начала и конца,
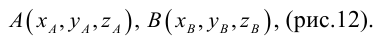
Тогда
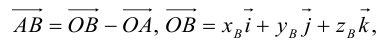
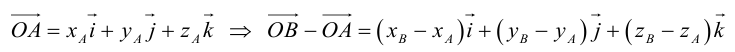 (см. свойства линейных операций над векторами). Таким образом,
(см. свойства линейных операций над векторами). Таким образом,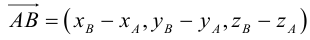 , то есть для определения координат вектора надо из координат его конца вычесть координаты начала.
, то есть для определения координат вектора надо из координат его конца вычесть координаты начала.
Определение: Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
Если  – базис, то
– базис, то  – другой базис, так как изменился порядок следования векторов.
– другой базис, так как изменился порядок следования векторов.
Определение: Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
Такой базис принято обозначать 
Из теоремы 2 следует, что всякий вектор 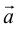 может быть разложен по базису
может быть разложен по базису 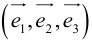 , то есть представлен в виде:
, то есть представлен в виде: 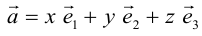 . Числа x,y,z называются координатами
. Числа x,y,z называются координатами 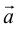 в базисе
в базисе 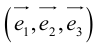 .
.
Определение: Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если 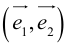 – базис, то представление вектора в виде
– базис, то представление вектора в виде 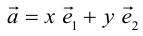 называется разложением
называется разложением 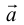 по базису
по базису и x, y – координаты
и x, y – координаты  в этом базисе.
в этом базисе.
Определение: Базисом на прямой называется любой ненулевой вектор этой прямой.
Деление отрезка в данном отношении
Рассмотрим задачу: дан отрезок AB . Найти точку D , которая делит AB в заданном отношении 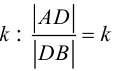 (рис. 14).
(рис. 14).
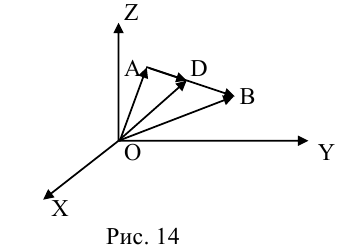
Введем прямоугольную декартову систему координат (пдск) OXYZ, тогда
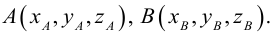
Обозначим
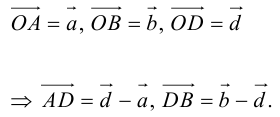
Так как 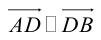 (лежат на одной прямой) и
(лежат на одной прямой) и 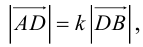 то
то
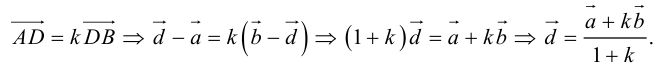
Переходя от этого векторного равенства к равенству соответствующих координат, получим:
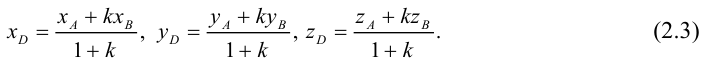
ЗАМЕЧАНИЕ 1. Если D – середина отрезка AB , то k 1, поэтому
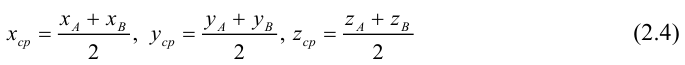
ЗАМЕЧАНИЕ 2. Если k < 0, 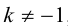 , то точка D лежит за пределами AB : так как
, то точка D лежит за пределами AB : так как 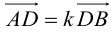 , то при
, то при 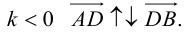
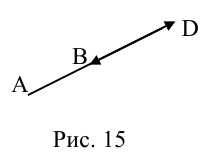
В этом случае 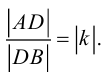
Скалярное произведение векторов
Определение: Скалярным произведением векторов 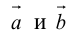 называется скаляр (число), равный
называется скаляр (число), равный 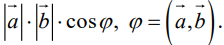
Скалярное произведение обозначается так: 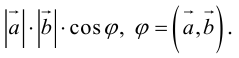 или
или 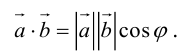
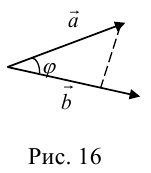
Так как 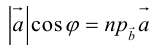 (рис. 16) или
(рис. 16) или 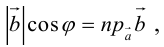 то
то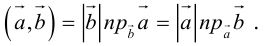
Свойства скалярного произведения
1.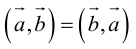 – очевидно из определения.
– очевидно из определения.
2.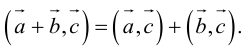
Доказательство:
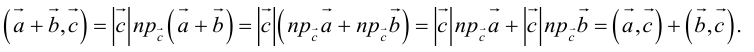
3.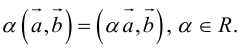
Доказательство:
а) 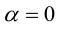 – очевидно.
– очевидно.
б) 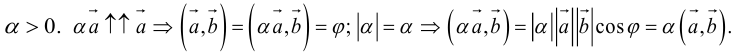
в) 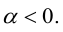 В этом случае
В этом случае
4.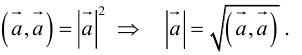
Отсюда следует, что 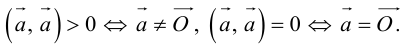
Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:
5.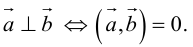
Доказательство:
а) пусть 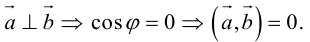
б) пусть 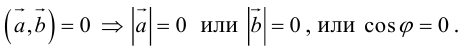
В первом и втором случаях один из сомножителей – нулевой вектор. Его направление не определено, поэтому можно считать, что 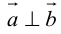 . В третьем случае
. В третьем случае 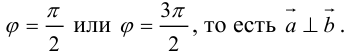
Используя свойства 4 и 5, составим таблицу вычисления скалярного произведения базисных векторов 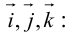
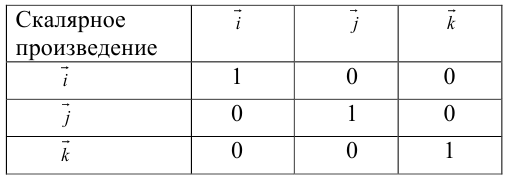
Пусть в некоторой пдск 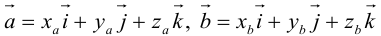 . Найдем скалярное произведение этих векторов:
. Найдем скалярное произведение этих векторов:
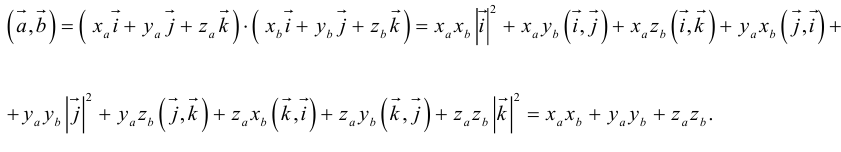
Таким образом, 
Пример №8
Найти, при каком значении x векторы 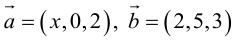 перпендикулярны.
перпендикулярны.
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведение по формуле (2.5): 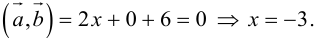
Пример №9
Найти угол между биссектрисой AD и медианой  если
если 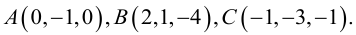
Так как 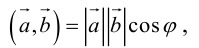
то 
Найдем координаты векторов 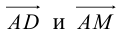 . Точка M – середина BC , поэтому по формулам (2.4)
. Точка M – середина BC , поэтому по формулам (2.4)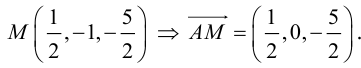
По теореме о биссектрисе внутреннего угла треугольника 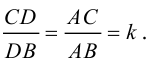
Чтобы найти k , вычислим длины AC и AB :
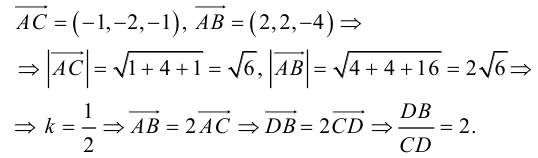
Разделим отрезок CB в данном отношении по формулам (2.3):
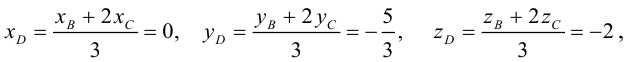
отсюда 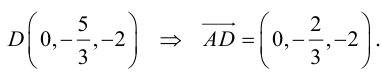
Заметим, что 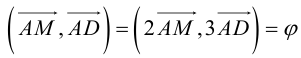 . Это замечание позволит нам не иметь дело с дробями, так как
. Это замечание позволит нам не иметь дело с дробями, так как
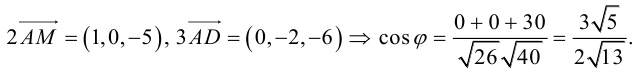
Пример №10
Найти 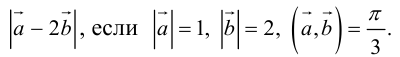
Воспользуемся свойствами 1–4 скалярного произведения:
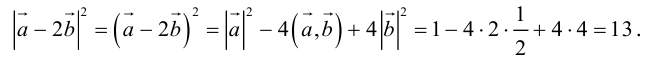
Отсюда 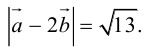
ЗАМЕЧАНИЕ. Так как работа силы  по перемещению материальной точки вдоль вектора
по перемещению материальной точки вдоль вектора 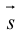 вычисляется по формуле
вычисляется по формуле 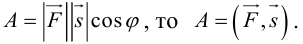
Определение векторного произведения векторов
Определение: Тройка некомпланарных векторов 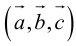 , имеющих общее начало, называется правой (левой), если
, имеющих общее начало, называется правой (левой), если  конца третьего вектора c вращение первого вектора
конца третьего вектора c вращение первого вектора 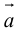 ко второму вектору
ко второму вектору  по кратчайшему пути наблюдается против (по) часовой стрелки (рис. 17).
по кратчайшему пути наблюдается против (по) часовой стрелки (рис. 17).
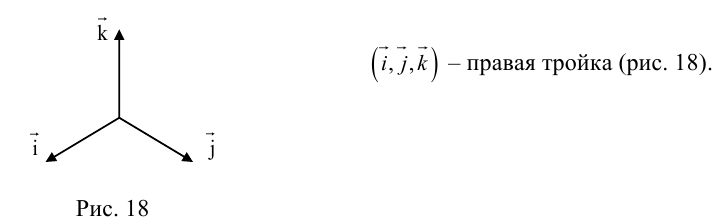
Определение: Векторным произведением вектора 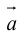 на вектор
на вектор 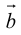 называется вектор
называется вектор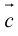 , удовлетворяющий условиям:
, удовлетворяющий условиям:
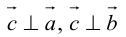 (
(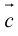 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов 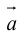 и
и 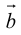 ).
). - Направление
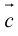 таково, что тройка
таково, что тройка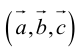 – правая.
– правая. 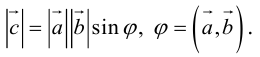
Векторное произведение обозначается так: 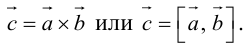
ЗАМЕЧАНИЕ 1. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.
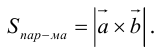
Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.
Заметим, что
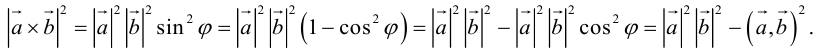
Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле
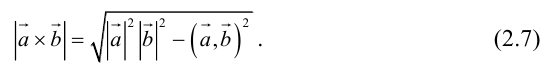
Пример №11
Найти площадь параллелограмма, построенного на векторах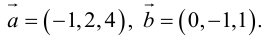
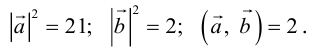
По формуле (2.7): 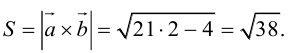
ЗАМЕЧАНИЕ 2. Направление вектора  можно также (кроме п.2) определить по правилу винта: направление вектора
можно также (кроме п.2) определить по правилу винта: направление вектора  совпадает с направлением поступательного движения винта в правой резьбой при вращении его в сторону поворота первого вектора
совпадает с направлением поступательного движения винта в правой резьбой при вращении его в сторону поворота первого вектора  ко второму вектору
ко второму вектору 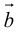 по кратчайшему пути (рис. 19).
по кратчайшему пути (рис. 19).
Свойства векторного произведения
1.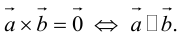
Доказательство:
а)пусть  или
или 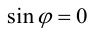 . В первом и втором случаях один из сомножителей – нулевой вектор.
. В первом и втором случаях один из сомножителей – нулевой вектор.
Его направление не определено, поэтому можно считать, что 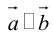 . Если
. Если 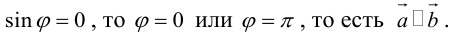
б)пусть 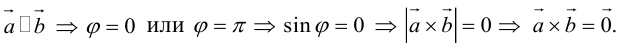
2. 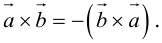
Доказательство: По определению направления векторов 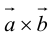 и
и 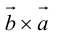 противоположны, а модули равны, значит, векторы отличаются лишь знаком.
противоположны, а модули равны, значит, векторы отличаются лишь знаком.
3.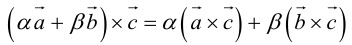 – свойство линейности векторного произведения по первому сомножителю (без доказательства).
– свойство линейности векторного произведения по первому сомножителю (без доказательства).
Векторное произведение также линейно и по второму сомножителю.
Используя определение и свойства 1 и 2, составим таблицу вычисления векторного произведения базисных векторов 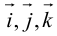 : векторы, стоящие в левом столбце, умножаются на соответствующие векторы верхней строки (рис. 20).
: векторы, стоящие в левом столбце, умножаются на соответствующие векторы верхней строки (рис. 20).
Пусть в некоторой пдск  . Найдем векторное произведение этих векторов:
. Найдем векторное произведение этих векторов:
Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):
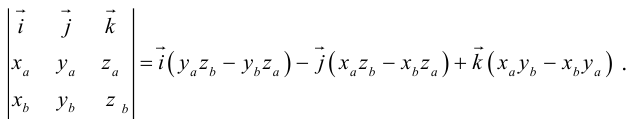
Таким образом,
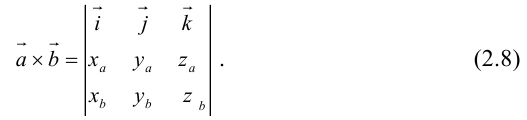
Пример №12
Вычислить векторное произведение векторов 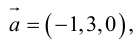
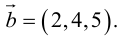
По формуле (2.8): 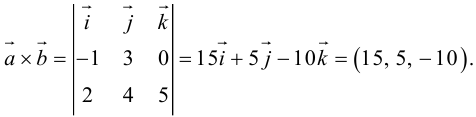
Заметим, что площадь треугольника, построенного на векторах 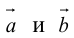 , можно вычислить двумя способами: как половину длины найденного вектора или используя формулу (2.7). Заметим, что
, можно вычислить двумя способами: как половину длины найденного вектора или используя формулу (2.7). Заметим, что 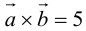
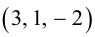
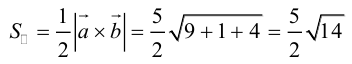
или
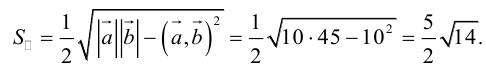
Пример №13
Вычислить площадь параллелограмма, построенного на векторах 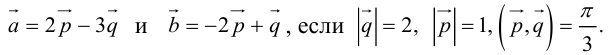
Так как 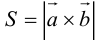 , то вычислим векторное произведение, используя его свойства:
, то вычислим векторное произведение, используя его свойства: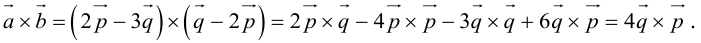
Отсюда 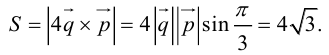
Определение смешанного произведения векторов
Определение: Смешанным произведением векторов  называется число
называется число  – скалярное произведение a на векторное произведение
– скалярное произведение a на векторное произведение 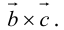
Смешанное произведение обозначается так: 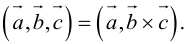
Пусть в некоторой пдск 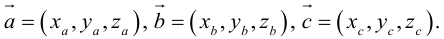
Обозначим
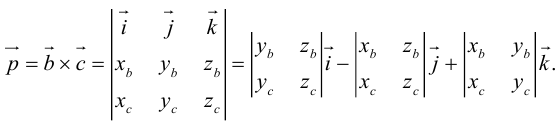
Тогда
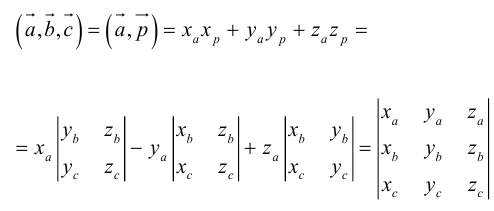
по 7 свойству определителей.
Таким образом,
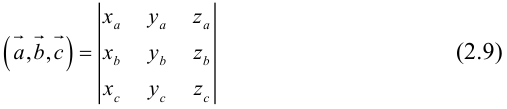
По определению скалярного произведения 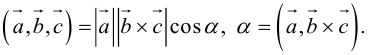
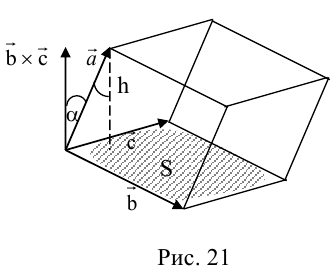
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)
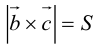 – площадь параллелограмма,
– площадь параллелограмма,
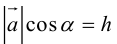 – высота параллелепипеда,
– высота параллелепипеда,
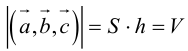 – объем параллелепипеда.
– объем параллелепипеда.
Геометрический смысл смешанного произведения: модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях, при этом 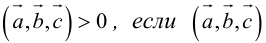 – правая тройка, и
– правая тройка, и 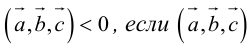 – левая тройка.
– левая тройка.
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения: 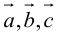 компланарны
компланарны
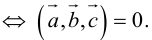
Доказательство: а) 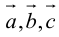 компланарны
компланарны 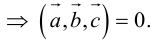
Если 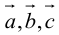 компланарны, то на них нельзя построить параллелепипед, а потому
компланарны, то на них нельзя построить параллелепипед, а потому 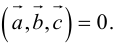
б)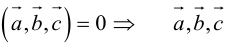 компланарны.
компланарны.
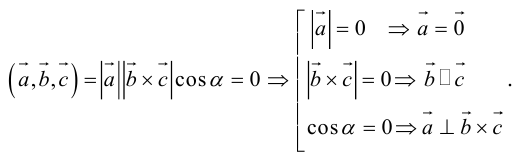
Во всех трех случаях  компланарны: в частности, если
компланарны: в частности, если 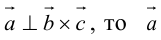 параллелен плоскости векторов
параллелен плоскости векторов  , что означает их компланарность.
, что означает их компланарность.
2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:
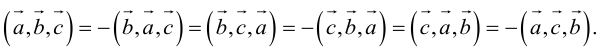
Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.
3. В смешанном произведении векторное и скалярное произведения можно менять местами: 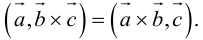
Доказательство: из свойства 2 смешанного произведения и свойства 1 скалярного получим: 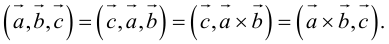
4. Смешанное произведение линейно по каждому из трех сомножителей.
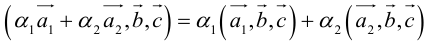 – линейность по первому сомножителю.
– линейность по первому сомножителю.
Доказательство следует из формулы (2.9) и свойств определителей.
Пример №14
Найти объем тетраэдра, построенного на векторах
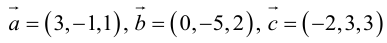 , и его высоту, перпендикулярную плоскости векторов
, и его высоту, перпендикулярную плоскости векторов 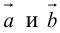 .
.
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому 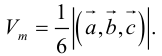
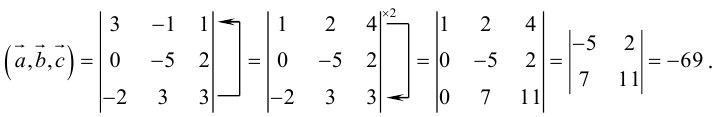
Отсюда 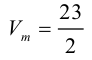 (заметим, что
(заметим, что  – левая тройка, так как смешанное произведение отрицательно).
– левая тройка, так как смешанное произведение отрицательно).
Чтобы найти высоту, воспользуемся формулой
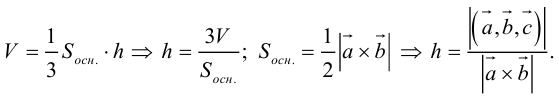
По формуле (2.7) 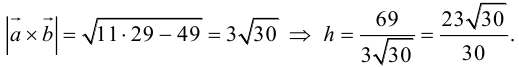
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика
-
Скалярное произведение.
Начать изучение
-
Ориентация прямой, плоскости и пространства.
Начать изучение
-
Площадь ориентированного параллелограмма, объем ориентированного параллелепипеда.
Начать изучение
-
Смешанное произведение.
Начать изучение
-
Выражение векторного и смешанного произведения через компоненты сомножителей.
Начать изучение
-
Детерминанты второго и третьего порядков.
Начать изучение
-
Условия коллинеарности и компланарности.
Начать изучение
-
Площадь параллелограмма.
Начать изучение
-
Двойное векторное произведение.
Начать изучение
-
Биортогональный базис.
Начать изучение
-
О векторных величинах.
Начать изучение
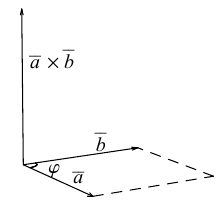
Скалярное произведение.
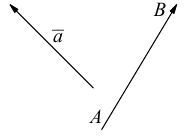
Под углом между векторами мы понимаем угол между векторами, равными данным и имеющими общее начало. В некоторых случаях мы будем указывать, от какого вектора и в каком направлении угол отсчитывается. Если такого указания не сделано, углом между векторами считается тот из углов, который не превосходит (pi). Если угол прямой, то векторы называются ортогональными.
Определение.
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Если хоть один из векторов нулевой, то угол не определен, и скалярное произведение по определению равно нулю.
Скалярное произведение векторов (boldsymbol{a}) и (boldsymbol{b}) обозначается ((boldsymbol{a}), (boldsymbol{b})) или (boldsymbol{ab}). Таким образом, мы можем написать
$$
(boldsymbol{a}, boldsymbol{b}) = |boldsymbol{a}||boldsymbol{b}| cos varphi,nonumber
$$
где (varphi) — угол между векторами (boldsymbol{a}) и (boldsymbol{b}).
Необходимо подчеркнуть следующее принципиальное обстоятельство: скалярное произведение может быть определено только после того, как будет выбрана определенная единица измерения длин векторов. Иначе приведенное выше определение не имеет смысла.
Скалярное умножение имеет следующие очевидные свойства.
- Коммутативность: для любых (boldsymbol{a}) и (boldsymbol{b}) выполнено ((boldsymbol{a, b}) = boldsymbol{b,a})).
- ((boldsymbol{a, a}) = |boldsymbol{a}|^{2}) для любого вектора (boldsymbol{a}).
- Скалярное произведение равно нулю тогда и только тогда, когда сомножители ортогональны или хотя бы один из них равен 0.
- Векторы ортонормированного базиса удовлетворяют равенствам
$$
begin{array}{c}
(boldsymbol{e_{1}}, boldsymbol{e_{1}}) = (boldsymbol{e_{2}}, boldsymbol{e_{2}}) = (boldsymbol{e_{3}}, boldsymbol{e_{3}}) = 1,\
(boldsymbol{e_{1}}, boldsymbol{e_{2}}) = (boldsymbol{e_{2}}, boldsymbol{e_{3}}) = (boldsymbol{e_{3}}, boldsymbol{e_{1}}) = 0.
end{array}nonumber
$$
Утверждение 1.
Если базисные векторы попарно ортогональны, то компоненты любого вектора (boldsymbol{a}) находятся по формулам
$$
alpha_{1} = frac{(boldsymbol{a}, boldsymbol{e_{1}})}{|boldsymbol{e_{1}}|^{2}}, alpha_{2} = frac{(boldsymbol{a}, boldsymbol{e_{2}})}{|boldsymbol{e_{2}}|^{2}}, alpha_{3} = frac{(boldsymbol{a}, boldsymbol{e_{3}})}{|boldsymbol{e_{3}}|^{2}}.nonumber
$$
В частности, если базис ортонормированный
$$
alpha_{1} = (boldsymbol{a}, boldsymbol{e_{1}}), alpha_{2} = (boldsymbol{a}, boldsymbol{e_{2}}), alpha_{3} = (boldsymbol{a}, boldsymbol{e_{3}})label{ref1}
$$
и
$$
boldsymbol{a} = (boldsymbol{a}, boldsymbol{e_{1}})boldsymbol{e_{1}} + (boldsymbol{a}, boldsymbol{e_{2}})boldsymbol{e_{2}} + (boldsymbol{a}, boldsymbol{e_{3}})boldsymbol{e_{3}}.nonumber
$$
Доказательство.
Пусть (boldsymbol{a} = boldsymbol{a_{1}} + boldsymbol{a_{2}} + boldsymbol{a_{3}}), причем каждое слагаемое коллинеарно соответствующему базисному вектору. Мы знаем из доказанного ранее утверждения, что (alpha_{1} = pm |boldsymbol{a_{1}}|/|boldsymbol{e_{1}}|), где выбирается знак + или — в зависимости от того, одинаково или противоположно направлены (boldsymbol{a_{1}}) и (boldsymbol{e_{1}}). Но, как видно из рис. 4.1, (pm |boldsymbol{a_{1}}| = |boldsymbol{a}|cos varphi_{1}), где (varphi_{1}) — угол между векторами (boldsymbol{a}) и (boldsymbol{e_{1}}). Итак, (alpha_{1} = |boldsymbol{a}|cos varphi_{1}/|boldsymbol{e_{1}}| = (boldsymbol{a}, boldsymbol{e_{1}})/|boldsymbol{e_{1}}|^{2}).
Аналогично вычисляются и остальные компоненты.
Определение.
Косинусы углов между вектором (boldsymbol{a}) и базисными векторами декартовой прямоугольной системы координат называются направляющими косинусами этого вектора.
Направляющие косинусы — это компоненты вектора (boldsymbol{a}^{0} = boldsymbol{a}/|boldsymbol{a}|). Их отличительная особенность состоит в том, что сумма их квадратов равна квадрату длины (boldsymbol{a}^{0}), то есть 1 (см. ниже формулу eqref{ref3}).
Утверждение 2.
Для любых векторов (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) и любых чисел (alpha) и (beta) выполнено равенство
$$
(alphaboldsymbol{a} + betaboldsymbol{b}, boldsymbol{c}) = alpha(boldsymbol{a}, boldsymbol{c}) + beta(boldsymbol{b}, boldsymbol{c}).nonumber
$$
В частности, ((alphaboldsymbol{a}, boldsymbol{c}) = alpha(boldsymbol{a}, boldsymbol{c})) и ((boldsymbol{a} + boldsymbol{b}, boldsymbol{c}) = (boldsymbol{a}, boldsymbol{c}) + (boldsymbol{b}, boldsymbol{c})).
Доказательство.
Если (boldsymbol{c} = 0), то утверждение очевидно. Пусть (boldsymbol{c} neq 0). Примем (boldsymbol{c}) за первый вектор базиса, а остальные выберем ортогонально к нему и между собой. Число ((alphaboldsymbol{a} + betaboldsymbol{b}, boldsymbol{c})/|boldsymbol{c}|^{2}) — первая компонента вектора (alphaboldsymbol{a} + betaboldsymbol{b}). Точно так же ((boldsymbol{a}, boldsymbol{c})/|boldsymbol{c}|^{2}) и ((boldsymbol{b}, boldsymbol{c})/|boldsymbol{c}|^{2}) — первые компоненты векторов (boldsymbol{a}) и (boldsymbol{b}). Согласно уже доказанному утверждению
$$
(alphaboldsymbol{a} + betaboldsymbol{b}, boldsymbol{c})/|boldsymbol{c}|^{2} = alpha(boldsymbol{a}, boldsymbol{c})/|boldsymbol{c}|^{2} + beta(boldsymbol{b}, boldsymbol{c})/|boldsymbol{c}|^{2}.nonumber
$$
Отсюда прямо получается доказываемое равенство.
Легко показать, что такая же формула справедлива и для линейной комбинации любого числа векторов. Используя коммутативность скалярного умножения, мы получаем тождество
$$
(boldsymbol{a}, betaboldsymbol{b} + gammaboldsymbol{c}) = beta(boldsymbol{a}, boldsymbol{b}) + gamma(boldsymbol{a}, boldsymbol{c}).nonumber
$$
Теорема 1.
Если базис ортонормированный, то скалярное произведение векторов (boldsymbol{a}) и (boldsymbol{b}) выражается через их компоненты ((alpha_{1}), (alpha_{2}), (alpha_{3})) и ((beta_{1}), (beta_{2}), (beta_{3})) по формуле
$$
(boldsymbol{a}, boldsymbol{b}) = alpha_{1}beta_{1} + alpha_{2}beta_{2} + alpha_{3}beta_{3}label{ref2}
$$
Доказательство.
Действительно, подставим вместо (boldsymbol{a}) его разложение и воспользуемся утверждением 2:
$$
(boldsymbol{a}, boldsymbol{b}) = (alpha_{1}boldsymbol{e_{1}} + alpha_{2}boldsymbol{e_{2}} + alpha_{3}boldsymbol{e_{3}}) = alpha_{1}(boldsymbol{e_{1}}, boldsymbol{b}) + alpha_{2}(boldsymbol{e_{2}}, boldsymbol{b}) + alpha_{3}(boldsymbol{e_{3}}, boldsymbol{b}).nonumber
$$
Теперь доказываемое следует из формулы eqref{ref1}.
Отметим, что требование ортонормированности базиса очень существенно. В произвольном базисе выражение скалярного произведения через компоненты гораздо сложнее. Поэтому в задачах, связанных со скалярным произведением, чаще всего используются ортонормированные базисы.
Если почему-либо все же надо вычислить скалярное произведение в неортонормированном базисе, следует перемножить разложения сомножителей по базису и, раскрыв скобки, подставить в полученное выражение известные скалярные произведения базисных векторов.
Теорема 1 позволяет выписать выражение длины вектора через его компоненты в ортонормированном базисе
$$
|boldsymbol{a}| = sqrt{alpha_{1}^{2} + alpha_{2}^{2} + alpha_{3}^{2}}label{ref3}
$$
а также выражение косинуса угла между векторами
$$
cos varphi = frac{(boldsymbol{a}, boldsymbol{b})}{|boldsymbol{a}||boldsymbol{b}|} = frac{alpha_{1}beta_{1} + alpha_{2}beta_{2} + alpha_{3}beta_{3}}{sqrt{alpha_{1}^{2} + alpha_{2}^{2} + alpha_{3}^{2}}sqrt{beta_{1}^{2} + beta_{2}^{2} + beta_{3}^{2}}}label{ref4}
$$
Используя формулу eqref{ref3}, мы можем вычислить расстояние между точками, если заданы их координаты в декартовой прямоугольной системе координат. В самом деле, пусть точки (A) и (B) имеют координаты ((x, y, z)) и ((x_{1}, y_{1}, z_{1})). Тогда расстояние между ними равно
$$
|overrightarrow{AB}| = sqrt{(x_{1}-x)^{2} + (y_{1}-y)^{2} + (z_{1}-z)^{2}}label{ref5}
$$
Скалярное умножение тесно связано с понятием проекции вектора. Слово “проекция” употребляется в двух смыслах. Введем соответствующие определения.
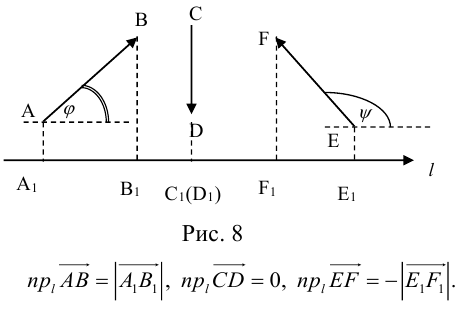
Пусть задан вектор (overrightarrow{AB}) и некоторая прямая (l). Опустим из точек (A) и (B) перпендикуляры на прямую и обозначим их основания (A’) и (B’) (рис. 4.2). Вектор (overrightarrow{A’B’}) называется (ортогональной) векторной проекцией вектора (overrightarrow{AB}) на прямую (l) и обозначается Пр(_{l}overrightarrow{AB}).
Из определения сразу следует, что векторные проекции равных векторов на параллельные прямые равны между собой.
Пусть (boldsymbol{e}) — ненулевой вектор на прямой (l). Тогда (overrightarrow{A’B’} = alphaboldsymbol{e}) при некотором (alpha). Представим (overrightarrow{AB}) в виде (overrightarrow{AB} = overrightarrow{A’B″} = alphaboldsymbol{e} + boldsymbol{b}) и заметим, что вектор (boldsymbol{b} = overrightarrow{B’B″}) ортогонален (boldsymbol{e}). Поэтому после скалярного умножения на (boldsymbol{e}) получаем ((overrightarrow{AB}, boldsymbol{e}) = alpha(boldsymbol{e}, boldsymbol{e})). Находя отсюда (alpha), имеем
$$
mbox{Пр}_{l}overrightarrow{AB} = frac{(overrightarrow{AB}, boldsymbol{e})}{|boldsymbol{e}|^{2}}boldsymbol{e}.label{ref6}
$$
Хотя на вид это выражение зависит от (boldsymbol{e}), фактически оно не меняется при замене (boldsymbol{e}) любым ненулевым вектором (lambdaboldsymbol{e}), коллинеарным (boldsymbol{e}).
Проекцию (overrightarrow{A’B’}) можно представить в виде
$$
frac{(overrightarrow{AB}, boldsymbol{e})}{|boldsymbol{e}|} frac{boldsymbol{e}}{|boldsymbol{e}|}nonumber
$$
и заметить, что ((overrightarrow{AB}, boldsymbol{e})/|boldsymbol{e}|) — это компонента (overrightarrow{A’B’}) по вектору (boldsymbol{e}^{0} = boldsymbol{e}/|boldsymbol{e}|). Так как (|boldsymbol{e}^{0}| = 1), компонента по абсолютной величине равна длине (overrightarrow{A’B’}). Она положительна, если направление (overrightarrow{A’B’}) совпадает с направлением (boldsymbol{e}), и отрицательна в противоположном случае.
Величина ((overrightarrow{AB}, boldsymbol{e})/|boldsymbol{e}|) не меняется при замене (boldsymbol{e}) на сонаправленный вектор (lambdaboldsymbol{e}), (lambda > 0), и меняет знак при замене (boldsymbol{e}) на противоположно направленный вектор.
Прямая линия называется направленной прямой (употребляются также термины ориентированная прямая и ось), если на ней указано определенное направление. Подробнее это определение рассматривается в начале следующего раздела.
Определение.
Число ((overrightarrow{AB}, boldsymbol{e})/|boldsymbol{e}|) называется скалярной проекцией вектора (overrightarrow{AB}) на ось (l), определяемую вектором (boldsymbol{e}) (или на вектор (boldsymbol{e})), и обозначается Пр(_{l}overrightarrow{AB}) или Пр(_{boldsymbol{e}}overrightarrow{AB}).
Из определения следует, что Пр(_{l}overrightarrow{AB} = |overrightarrow{AB}| cos varphi), где (varphi) — угол между (overrightarrow{AB}) и (boldsymbol{e}). Компоненты вектора в ортонормированном базисе равны его скалярным проекциям на оси координат.
Ориентация прямой, плоскости и пространства.
Выше мы дали определение ориентированной прямой (оси). Скажем о нем подробнее, с тем чтобы аналогично ввести определение ориентированной плоскости и ориентированного пространства.
Все базисы (ненулевые векторы) на прямой разделяются на два класса: векторы из одного класса направлены одинаково, а векторы из разных классов направлены противоположно. Говорится, что прямая ориентирована или что на ней задана ориентация, если из двух классов базисов выбран один. Базисы выбранного класса называются положительно ориентированными или положительными.
Задать ориентацию можно, указав какой-либо базис и считая положительно ориентированными все базисы того же класса. Однако то, что прямая ориентирована, не означает, что на ней выбран какой-то определенный базис.
Два базиса на плоскости называются одинаково ориентированными, если в обоих базисах кратчайший поворот от первого вектора ко второму производится в одну сторону, и противоположно ориентированными в противном случае. Например, на рисунке ниже, базисы в левой части ориентированы одинаково, а на правой части — противоположно. Если фиксировать какой-то базис, то любой другой ориентирован с ним либо одинаково, либо противоположно, и, таким образом, все базисы распадаются на два класса: любые два базиса одного класса ориентированы одинаково, базисы разных классов ориентированы противоположно.
Определение.
Плоскость ориентирована, если из двух классов базисов на ней выбран один класс.
Ориентацию можно задать, выбрав базис и считая положительно ориентированными все базисы одного с ним класса. Но, конечно, задание ориентации не предполагает выбор определенного базиса.
В планиметрии часто ориентируют плоскость, считая положительными те базисы, у которых кратчайший поворот от первого вектора ко второму производится против часовой стрелки. Для плоскости в пространстве это соглашение не имеет смысла, так как видимое направление поворота зависит от того, с какой стороны смотреть на плоскость. Но если выбрать одно из полупространств, ограничиваемых плоскостью, и смотреть на повороты именно из него, то класс базиса определяется видимым направлением поворота.
Определение.
Базис в пространстве называется правым, если (считая векторы имеющими общее начало) с конца третьего вектора мы видим кратчайший поворот от первого вектора ко второму направленным против часовой стрелки. В противном случае базис называется левым (рис. 4.3).
Представим себе, что на рис. 4.4 концы векторов лежат в плоскости рисунка, а их общее начало — за плоскостью. Тогда поворот от вектора (boldsymbol{e}_{1}) к вектору (boldsymbol{e}_{2}) и затем к (boldsymbol{e}_{3}) для правого базиса нам виден против часовой стрелки, а для левого — по часовой стрелке.
Определение.
Пространство называется ориентированным, если из двух классов базисов (правых или левых) выбран один. Базисы этого класса называются положительно ориентированными.
Далее мы всегда будем выбирать правую ориентацию пространства, считая положительными правые базисы. Но важно помнить, что выбор ориентации мог бы быть противоположным.
Если пространство ориентировано, то ориентацию любой плоскости в нем можно задать, указав ориентацию прямой, перпендикулярной этой плоскости. При этом положительным базисом (boldsymbol{a}), (boldsymbol{b}) на плоскости считается такой, который вместе с положительным базисом (boldsymbol{n}) на прямой составляет положительный базис пространства (boldsymbol{a}), (boldsymbol{b}), (boldsymbol{n}). Это — внешний способ задания ориентации. Говорится, что ориентация плоскости определяется нормальным вектором (boldsymbol{n}).
Аналогично, в ориентированном пространстве можно внешним образом задать ориентацию прямой линии. Для этого нужно задать ориентацию плоскости, перпендикулярной этой прямой. Положительным базисом на прямой будет такой базис, который вместе с положительным базисом плоскости составляет положительный базис пространства.
Площадь ориентированного параллелограмма, объем ориентированного параллелепипеда.
Если прямая ориентирована, то длине ненулевого вектора на ней можно приписать знак: считать длину положительной, если вектор ориентирован положительно, и отрицательной в противоположном случае. Именно так мы приписываем знак длине векторной проекции, когда определяем скалярную проекцию. Обобщим это определение.
Рассмотрим параллелограмм, построенный на двух векторах так, что две его смежные стороны являются векторами с общим началом. Параллелограмм называется ориентированным, если пара векторов, на которой он построен, упорядочена. На ориентированной плоскости параллелограмм считается положительно или отрицательно ориентированным, смотря по тому, как ориентирована определяющая его пара векторов.
На ориентированной плоскости принято считать площадь ориентированного параллелограмма числом со знаком: она равна площади параллелограмма (положительна), если параллелограмм ориентирован положительно, и равна той же площади со знаком минус, если отрицательно. Мы будем обозначать площадь ориентированного параллелограмма, построенного на векторах (boldsymbol{a}) и (boldsymbol{b}), через (S_{pm}(boldsymbol{a}, boldsymbol{b})).
Рассмотрим теперь параллелепипед, построенный на трех векторах так, что три его ребра, исходящие из одной вершины, являются векторами с общим началом. Параллелепипед называется ориентированным, если эти три ребра упорядочены. В ориентированном пространстве ориентация параллелепипеда положительна или отрицательна смотря по тому, какую тройку образуют векторы, на которых он построен.
В ориентированном пространстве объем ориентированного параллелепипеда — число со знаком: объем положительно ориентированного параллелепипеда считается положительным, а отрицательно ориентированного — отрицательным.
При выбранной нами правой ориентации пространства положительными считаются объемы ориентированных параллелепипедов, построенных на правых тройках векторов.
Смешанное произведение.
Если пространство ориентировано, мы можем ввести следующее определение.
Определение.
Смешанным произведением векторов (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) (в данном порядке) называется число, равное объему ориентированного параллелепипеда, построенного на этих векторах, если они не компланарны, и равное нулю, если компланарны.
Смешанное произведение векторов (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) обозначается ((boldsymbol{a}), (boldsymbol{b}), (boldsymbol{c})).
При перестановке сомножителей в смешанном произведении, самое большее, может измениться только ориентация тройки векторов. Поэтому абсолютная величина смешанного произведения не зависит от порядка сомножителей. Для любых векторов (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) мы получаем, сравнивая ориентации троек векторов (см. рис. 14),
$$
(boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (boldsymbol{c}, boldsymbol{a}, boldsymbol{b}) = (boldsymbol{b}, boldsymbol{c}, boldsymbol{a}) = -(boldsymbol{b}, boldsymbol{a}, boldsymbol{c}) = -(boldsymbol{c}, boldsymbol{b}, boldsymbol{a}) = -(boldsymbol{a}, boldsymbol{c}, boldsymbol{b}).label{ref7}
$$
Следующее предложение устанавливает связь между скалярным произведением и смешанным произведением.
Утверждение 3.
Каковы бы ни были векторы (boldsymbol{b}) и (boldsymbol{c}), найдется единственный (не зависящий от (boldsymbol{a})) вектор (boldsymbol{d}) такой, что при любом (boldsymbol{a}) выполнено равенство
$$
(boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (boldsymbol{a}, boldsymbol{d}).label{ref8}
$$
Доказательство.
Докажем сначала существование вектора (boldsymbol{d}), а потом установим, что такой вектор возможен только один. Пусть векторы (boldsymbol{b}) и (boldsymbol{c}) коллинеарны. Тогда при любом (boldsymbol{a}) векторы (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) компланарны и ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = 0). Поэтому мы можем положить (boldsymbol{d} = 0). Рассмотрим неколлинеарные векторы (boldsymbol{b}) и (boldsymbol{c}) и предположим сначала, что (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) не компланарны. Построим на них ориентированный параллелепипед и примем за его основание параллелограмм, построенный на (boldsymbol{b}) и (boldsymbol{c}) (рис. 4.5). Введем ориентацию на прямой (OH), перпендикулярной основанию. Мы зададим ее с помощью вектора (boldsymbol{n}) длины 1, составляющего с (boldsymbol{b}) и (boldsymbol{c}) правую тройку (boldsymbol{n}), (boldsymbol{b}), (boldsymbol{c}). (Тройка (boldsymbol{b}), (boldsymbol{c}), (boldsymbol{n}) также правая.)
((boldsymbol{a}), (boldsymbol{n})) — скалярная проекция вектора (boldsymbol{a}) на (boldsymbol{n}). По модулю она равна высоте параллелепипеда (OH), а знак ее определяется ориентацией тройки (boldsymbol{a}), (boldsymbol{b}), (boldsymbol{c}). Действительно, ((boldsymbol{a}, boldsymbol{n}) > 0) тогда и только тогда, когда концы векторов (boldsymbol{a}) и (boldsymbol{n}) лежат в одном полупространстве, то есть тройка (boldsymbol{a}), (boldsymbol{b}), (boldsymbol{c}) правая так же, как (boldsymbol{n}), (boldsymbol{b}), (boldsymbol{c}). Таким образом, ((boldsymbol{a}), (boldsymbol{n})) положительно для правой тройки (boldsymbol{a}), (boldsymbol{b}), (boldsymbol{c}) и отрицательно для левой.
Пусть положительное число (S) — площадь основания параллелепипеда. Тогда произведение ((boldsymbol{a}, boldsymbol{n})S) по модулю равно объему параллелепипеда, а знак его совпадает со знаком ((boldsymbol{a}), (boldsymbol{n})). Это значит, что ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = S(boldsymbol{a}, boldsymbol{n})). Полученное равенство совпадает с eqref{ref8}, если
$$
boldsymbol{d} = Sboldsymbol{n}.label{ref9}
$$
Осталось рассмотреть случай, когда (boldsymbol{b}) и (boldsymbol{c}) не коллинеарны, а (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) компланарны. В этом случае (boldsymbol{a}) лежит в плоскости векторов (boldsymbol{b}) и (boldsymbol{c}) и, следовательно, ортогонален вектору (boldsymbol{d}), вычисленному по формуле eqref{ref9}. Поскольку ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = 0) и ((boldsymbol{a}, boldsymbol{n}) = 0), вектор eqref{ref9} удовлетворяет равенству eqref{ref8} и в этом случае. Итак, мы нашли вектор, который удовлетворяет eqref{ref8} при любом (boldsymbol{a}) и определяется только по (boldsymbol{b}) и (boldsymbol{c}).
Допустим, что для фиксированных (boldsymbol{b}) и (boldsymbol{c}) нашлось два вектора (boldsymbol{d_{1}}) и (boldsymbol{d_{2}}) таких, что для любого а выполнено ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (boldsymbol{a}, boldsymbol{d_{1}})) и ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (boldsymbol{a}, boldsymbol{d_{2}})). Отсюда следует, что ((boldsymbol{a}, boldsymbol{d_{1}}) = (boldsymbol{a}, boldsymbol{d_{2}})) или (boldsymbol{a}(boldsymbol{d_{1}}-boldsymbol{d_{2}}) = 0). Поэтому вектор (boldsymbol{d_{1}}-boldsymbol{d_{2}}) ортогонален каждому вектору пространства и, следовательно, равен нулевому вектору. Это доказывает, что вектор (boldsymbol{d}), определяемый формулой eqref{ref8}, может быть только один. Утверждение полностью доказано.
Опишем еще раз, как вектор (boldsymbol{d}) определяется по (boldsymbol{b}) и (boldsymbol{c}).
- Если (boldsymbol{b}) и (boldsymbol{c}) коллинеарны, то (boldsymbol{d} = 0).
- Если (boldsymbol{b}) и (boldsymbol{c}) не коллинеарны, то:
- (|boldsymbol{d}| = S = |boldsymbol{b}||boldsymbol{c}|sin varphi), где (varphi) — угол между (boldsymbol{b}) и (boldsymbol{c});
- вектор (boldsymbol{d}) ортогонален векторам (boldsymbol{b}) и (boldsymbol{c});
- тройка векторов (boldsymbol{b}), (boldsymbol{c}), (boldsymbol{d}) имеет положительную ориентацию.
При нашем выборе ориентации пространства — это правая тройка.
Определение.
Вектор (boldsymbol{d}), определенный перечисленными выше условиями, или, что то же, формулой eqref{ref8}, называется векторным произведением векторов (boldsymbol{b}) и (boldsymbol{c}).
Подчеркнем, что векторное произведение, как и смешанное, определено только для ориентированного пространства. Разумеется, необходим также выбор единицы измерения длин.
Векторное произведение векторов (boldsymbol{b}) и (boldsymbol{c}) обозначают ([boldsymbol{b}, boldsymbol{c}]) или (boldsymbol{b} times boldsymbol{c}). Используя это обозначение, мы можем записать формулу eqref{ref8} в виде
$$
(boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (boldsymbol{a}, [boldsymbol{b}, boldsymbol{c}])label{ref10}
$$
Благодаря этому равенству смешанное произведение и получило свое название.
Пример 1.
Пусть (boldsymbol{e_{1}}), (boldsymbol{e_{2}}), (boldsymbol{e_{3}}) — правый ортонормированный базис. Тогда при выбранной нами правой ориентации пространства
$$
[boldsymbol{e_{2}}, boldsymbol{e_{3}}] = boldsymbol{e_{1}}, [boldsymbol{e_{3}}, boldsymbol{e_{1}}] = boldsymbol{e_{2}}, [boldsymbol{e_{1}}, boldsymbol{e_{2}}] = boldsymbol{e_{3}}.label{ref11}
$$
Если (boldsymbol{f_{1}}), (boldsymbol{f_{2}}), (boldsymbol{f_{3}}) — левый ортонормированный базис, то
$$
[boldsymbol{f_{2}}, boldsymbol{f_{3}}] = -boldsymbol{f_{1}}, [boldsymbol{f_{3}}, boldsymbol{f_{1}}] = -boldsymbol{f_{2}}, [boldsymbol{f_{1}}, boldsymbol{f_{2}}] = -boldsymbol{f_{3}}.nonumber
$$
Утверждение 4.
Векторное умножение антикоммутативно, то есть для любых векторов ([boldsymbol{b}, boldsymbol{c}] = -[boldsymbol{c}, boldsymbol{b}]).
Доказательство.
Действительно, если ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (boldsymbol{a}, boldsymbol{d})), то
$$
(boldsymbol{a}, boldsymbol{c}, boldsymbol{b}) = -(boldsymbol{a}, boldsymbol{d}) = (boldsymbol{a}, (-boldsymbol{d})).nonumber
$$
Получим теперь свойство линейности смешанного и векторного произведений по каждому из сомножителей. Применяя предложение 2 к скалярному произведению ((lambdaboldsymbol{a}_{1} + muboldsymbol{a}_{2}, [boldsymbol{b}, boldsymbol{c}])), мы получим
$$
(lambdaboldsymbol{a}_{1} + muboldsymbol{a}_{2}, boldsymbol{b}, boldsymbol{c}) = lambda (boldsymbol{a}_{1}, boldsymbol{b}, boldsymbol{c}) + mu(boldsymbol{a}_{2}, boldsymbol{b}, boldsymbol{c}).label{ref12}
$$
Из равенств eqref{ref7} следуют аналогичные тождества для остальных сомножителей. Например, для второго сомножителя
$$
(boldsymbol{a}, lambdaboldsymbol{b}_{1} + muboldsymbol{b}_{2}, boldsymbol{c}) = lambda (boldsymbol{a}, boldsymbol{b}_{1}, boldsymbol{c}) + mu(boldsymbol{a}, boldsymbol{b}_{2}, boldsymbol{c}).label{ref13}
$$
Действительно, мы можем переставить интересующий нас сомножитель на первое место, раскрыть скобки, а затем выполнить обратную перестановку.
Утверждение 5.
Для любых векторов (boldsymbol{b}_{1}), (boldsymbol{b}_{2}) и (boldsymbol{c}) и любых чисел (lambda) и (mu) имеет место равенство
$$
[lambdaboldsymbol{b}_{1} + muboldsymbol{b}_{2}, boldsymbol{c}] = lambda[boldsymbol{b}_{1}, boldsymbol{c}] + mu[boldsymbol{b}_{2}, boldsymbol{c}].nonumber
$$
Доказательство.
В самом деле, правой части формулы eqref{ref13} можно придать вид
$$
(boldsymbol{a}, lambda[boldsymbol{b}_{1}, boldsymbol{c}]) + (boldsymbol{a}, mu[boldsymbol{b}_{2}, boldsymbol{c}]).nonumber
$$
Поэтому по утверждению 2 получаем
$$
(boldsymbol{a}, [lambdaboldsymbol{b}_{1} + muboldsymbol{b}_{2}, boldsymbol{c}]) = (boldsymbol{a}, lambda[boldsymbol{b}_{1}, boldsymbol{c}]) + mu[boldsymbol{b}_{2}, boldsymbol{c}]).nonumber
$$
Так как это верно для любого вектора (boldsymbol{a}), мы можем, выбрав ортонормированный базис (boldsymbol{e_{1}}), (boldsymbol{e_{2}}), (boldsymbol{e_{3}}), подставить на место (boldsymbol{a}) последовательно каждый вектор этого базиса. В силу предложения 1 мы получим равенство всех компонент векторов ([lambdaboldsymbol{b}_{1} + muboldsymbol{b}_{2}, boldsymbol{c}]) и (lambda[boldsymbol{b}_{1}, boldsymbol{c}] + mu[boldsymbol{b}_{2}, boldsymbol{c}]), а отсюда и равенство векторов, которое нам нужно было доказать.
Линейность векторного произведения по второму сомножителю можно получить из свойства антикоммутативности.
Выражение векторного и смешанного произведения через компоненты сомножителей.
Если заданы разложения векторов (boldsymbol{a}) и (boldsymbol{b}) по векторам некоторого базиса (boldsymbol{e_{1}}), (boldsymbol{e_{2}}), (boldsymbol{e_{3}}), то мы можем раскрыть скобки:
$$
[boldsymbol{a}, boldsymbol{b}] = [(alpha_{1}boldsymbol{e}_{1} + alpha_{2}boldsymbol{e}_{2} + alpha_{3}boldsymbol{e}_{3}), (beta_{1}boldsymbol{e}_{1} + beta_{2}boldsymbol{e}_{2} + beta_{3}boldsymbol{e}_{3})] =\= (alpha_{1}beta_{2}-alpha_{2}beta_{1})[boldsymbol{e}_{1}, boldsymbol{e}_{2}] + (alpha_{2}beta_{3}-alpha_{3}beta_{2})[boldsymbol{e}_{2}, boldsymbol{e}_{3}] +\+(alpha_{3}beta_{1}-alpha_{1}beta_{3})[boldsymbol{e}_{3}, boldsymbol{e}_{1}].label{ref14}
$$
Здесь использовалась антикоммутативность векторного умножения и то, что векторное произведение двух одинаковых сомножителей — нулевой вектор. В примере 1 были сосчитаны попарные векторные произведения векторов ортонормированного базиса. Поэтому из формулы eqref{ref14} следует следующая теорема.
Теорема 2.
В положительно ориентированном ортонормированном базисе векторное произведение выражается через компоненты сомножителей формулой
$$
[boldsymbol{a}, boldsymbol{b}] = (alpha_{2}beta_{3}-alpha_{3}beta_{2})boldsymbol{e}_{1} + (alpha_{3}beta_{1}-alpha_{1}beta_{3})boldsymbol{e}_{2} + (alpha_{1}beta_{2}-alpha_{2}beta_{1})boldsymbol{e}_{3}.label{ref15}
$$
Если базис ориентирован отрицательно, перед правой частью этой формулы следует поставить знак минус.
Избежать постоянной заботы об ориентации базисов можно двумя способами. Можно договориться при правой ориентации пространства, если не оговорено противное, использовать только правые базисы. Такого соглашения мы и будем придерживаться.
Второй способ состоит в том, чтобы не фиксировать заранее ориентацию пространства, а выбирать ее так, чтобы используемый базис был ориентирован положительно. При таком подходе векторное произведение всегда вычисляется по формуле eqref{ref15}, но приходится следить за тем, как векторное произведение направлено. Этот подход принят, например, в литературе по физике.
Теорема 3.
Смешанное произведение векторов (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) выражается через их компоненты ((alpha_{1}, alpha_{2}, alpha_{3})), ((beta_{1}, beta_{2}, beta_{3})) и ((gamma_{1}, gamma_{2}, gamma_{3})) в произвольном базисе (boldsymbol{e_{1}}), (boldsymbol{e_{2}}), (boldsymbol{e_{3}}) по формуле ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (alpha_{1}beta_{2}gamma_{3} + alpha_{2}beta_{3}gamma_{1} + alpha_{3}beta_{1}gamma_{2}-alpha_{3}beta_{2}gamma_{1}-alpha_{2}beta_{1}gamma_{3}-alpha_{1}beta_{3}gamma_{2}))((boldsymbol{e_{1}}), (boldsymbol{e_{2}}), (boldsymbol{e_{3}})).
Доказательство.
Для доказательства заметим, что ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (boldsymbol{c}, [boldsymbol{a}, boldsymbol{b}])) и умножим скалярно обе части равенства eqref{ref14} на вектор (boldsymbol{c} = gamma_{1}boldsymbol{e_{1}} + gamma_{2}boldsymbol{e_{2}} + gamma_{3}boldsymbol{e_{3}}). Мы получим
$$
(boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = gamma_{1}(alpha_{2}beta_{3}-alpha_{3}beta_{2})(boldsymbol{e_{1}}[boldsymbol{e_{2}}, boldsymbol{e_{3}}]) +\+ gamma_{2}(alpha_{3}beta_{1}-alpha_{1}beta_{3})(boldsymbol{e_{2}}[boldsymbol{e_{3}}, boldsymbol{e_{1}}]) + gamma_{3}(alpha_{1}beta_{2}-alpha_{2}beta_{1})(boldsymbol{e_{3}}[boldsymbol{e_{1}}, boldsymbol{e_{2}}]).nonumber
$$
(Слагаемые, содержащие смешанные произведения с одинаковыми сомножителями, мы не выписываем, так как они равны нулю.) Отсюда, учитывая равенства eqref{ref7} и приводя подобные члены, получаем нужный нам результат.
Детерминанты второго и третьего порядков.
Найденные нами формулы достаточно громоздки. Для их более компактной записи употребляются детерминанты (или определители) второго и третьего порядков.
Рассмотрим четыре числа (alpha_{1}), (alpha_{2}), (beta_{1}), (beta_{2}). Из них можно составить таблицу, называемую матрицей второго порядка:
$$
begin{Vmatrix}
alpha_{1}& alpha_{2}\
beta_{1}& beta_{2}
end{Vmatrix}.nonumber
$$
Определение.
Число (alpha_{1}beta_{2}-alpha_{2}beta_{1}), называется детерминантом этой матрицы или детерминантом второго порядка и обозначается
$$
begin{vmatrix}
alpha_{1}& alpha_{2}\
beta_{1}& beta_{2}
end{vmatrix}.nonumber
$$
Теперь выражение векторного произведения в правом ортонормированном базисе перепишется так:
$$
[boldsymbol{a}, boldsymbol{b}] =
begin{vmatrix}
alpha_{2}& alpha_{3}\
beta_{2}& beta_{3}
end{vmatrix}
boldsymbol{e_{1}} +
begin{vmatrix}
alpha_{3}& alpha_{1}\
beta_{3}& beta_{1}
end{vmatrix}
boldsymbol{e_{2}} +
begin{vmatrix}
alpha_{1}& alpha_{2}\
beta_{1}& beta_{2}
end{vmatrix}
boldsymbol{e_{3}}.nonumber
$$
Из компонент трех векторов можно составить таблицу — матрицу третьего порядка
$$
begin{Vmatrix}
alpha_{1}& alpha_{2}& alpha_{3}\
beta_{1}& beta_{2}& beta_{3}\
gamma_{1}& gamma_{2}& gamma_{3}
end{Vmatrix}.nonumber
$$
Число
$$
alpha_{1}
begin{vmatrix}
beta_{2}& beta_{3}\
gamma_{2}& gamma_{3}
end{vmatrix}
+ alpha_{2}
begin{vmatrix}
beta_{3}& beta_{1}\
gamma_{3}& gamma_{1}
end{vmatrix}
+ alpha_{3}
begin{vmatrix}
beta_{1}& beta_{2}\
gamma_{1}& gamma_{2}
end{vmatrix},
$$
или, что то же самое,
$$
alpha_{1}
begin{vmatrix}
beta_{2}& beta_{3}\
gamma_{2}& gamma_{3}
end{vmatrix}
— alpha_{2}
begin{vmatrix}
beta_{1}& beta_{3}\
gamma_{1}& gamma_{3}
end{vmatrix}
+ alpha_{3}
begin{vmatrix}
beta_{1}& beta_{2}\
gamma_{1}& gamma_{2}
end{vmatrix},nonumber
$$
называется детерминантом этой матрицы или детерминантом третьего порядка и обозначается
$$
begin{vmatrix}
alpha_{1}& alpha_{2}& alpha_{3}\
beta_{1}& beta_{2}& beta_{3}\
gamma_{1}& gamma_{2}& gamma_{3}
end{vmatrix}.nonumber
$$
По теореме 3 в новых обозначениях
$$
(boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) =
begin{vmatrix}
alpha_{1}& alpha_{2}& alpha_{3}\
beta_{1}& beta_{2}& beta_{3}\
gamma_{1}& gamma_{2}& gamma_{3}
end{vmatrix}
(boldsymbol{e_{1}}, boldsymbol{e_{2}}, boldsymbol{e_{3}}).label{ref16}
$$
В частности, в правом ортонормированном базисе
$$
(boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) =
begin{vmatrix}
alpha_{1}& alpha_{2}& alpha_{3}\
beta_{1}& beta_{2}& beta_{3}\
gamma_{1}& gamma_{2}& gamma_{3}
end{vmatrix}.label{ref17}
$$
При помощи теоремы 2 и определения детерминанта можно получить следующее выражение векторного произведения через компоненты сомножителей в правом ортонормированном базисе:
$$
(boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) =
begin{vmatrix}
boldsymbol{e_{1}}& boldsymbol{e_{2}}& boldsymbol{e_{3}}\
alpha_{1}& alpha_{2}& alpha_{3}\
beta_{1}& beta_{2}& beta_{3}
end{vmatrix}.label{ref18}
$$
Детерминанты тесно связаны с системами линейных уравнений, решения которых удобно записывать с их помощью. Дадим этому геометрическую иллюстрацию.
Пусть дана система из трех уравнений
$$
left{
begin{array}{l}
a_{1}x + b_{1}y + c_{1}z = d_{1},\
a_{2}x + b_{2}y + c_{2}z = d_{2},\
a_{3}x + b_{3}y + c_{3}z = d_{3}.
end{array}
right.nonumber
$$
Выберем в пространстве некоторый базис и рассмотрим векторы (boldsymbol{a}(a_{1}, a_{2}, a_{3})), (boldsymbol{b}(b_{1}, b_{2}, b_{3})), (boldsymbol{c}(c_{1}, c_{2}, c_{3})) и (boldsymbol{d}(d_{1}, d_{2}, d_{3})). Тогда система является координатной записью векторного равенства
$$
xboldsymbol{a} + yboldsymbol{b} + zboldsymbol{c} = boldsymbol{d}.label{ref19}
$$
Поэтому решение системы (x,y,z) — коэффициенты разложения (boldsymbol{d}) по (boldsymbol{a}, boldsymbol{b}) и (boldsymbol{c}). Мы можем быть уверены, что система имеет единственное решение, если (boldsymbol{a}), (boldsymbol{b}) и (boldsymbol{c}) не компланарны, то есть ((boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) neq 0). Предположим, что это условие выполнено, и найдем решение. Для этого умножим обе части равенства eqref{ref19} скалярно на векторное произведение ([boldsymbol{b}, boldsymbol{c}]). Мы получим (x(boldsymbol{a}, boldsymbol{b}, boldsymbol{c}) = (boldsymbol{d}, boldsymbol{b}, boldsymbol{c})), и, следовательно, (x) равен отношению детерминантов
$$
begin{vmatrix}
d_{1}& d_{2}& d_{3}\
b_{1}& b_{2}& b_{3}\
c_{1}& c_{2}& c_{3}
end{vmatrix}
mbox{и}
begin{vmatrix}
a_{1}& a_{2}& a_{3}\
b_{1}& b_{2}& b_{3}\
c_{1}& c_{2}& c_{3}
end{vmatrix}.nonumber
$$
Аналогично находятся и остальные неизвестные.
Остановимся на следующих свойствах детерминантов. Из равенств eqref{ref7} следует, что детерминант меняет знак при перестановке каких-либо двух строк матрицы. Формула eqref{ref12} означает, что
$$
begin{vmatrix}
lambda a_{1}’ + mu a_{1}″& lambda a_{2}’ + mu a_{2}″& lambda a_{3}’ + mu a_{3}″\
b_{1}& b_{2}& b_{3}\
c_{1}& c_{2}& c_{3}
end{vmatrix} =\= lambda
begin{vmatrix}
a_{1}’& a_{2}’& a_{3}’\
b_{1}& b_{2}& b_{3}\
c_{1}& c_{2}& c_{3}
end{vmatrix}
+ mu
begin{vmatrix}
a_{1}″& a_{2}″& a_{3}″\
b_{1}& b_{2}& b_{3}\
c_{1}& c_{2}& c_{3}
end{vmatrix}.nonumber
$$
Условия коллинеарности и компланарности.
Утверждение 6.
Каков бы ни был базис ((boldsymbol{e_{1}}, boldsymbol{e_{2}}, boldsymbol{e_{3}})), попарные векторные произведения базисных векторов линейно независимы.
Доказательство.
Докажем это от противного. Рассмотрим равенство
$$
lambda[boldsymbol{e_{2}}, boldsymbol{e_{3}}] + mu[boldsymbol{e_{3}}, boldsymbol{e_{1}}] + nu[boldsymbol{e_{1}}, boldsymbol{e_{2}}] = 0nonumber
$$
и допустим, что какой-нибудь коэффициент, пусть для определенности (lambda), отличен от нуля. Умножив обе части равенства скалярно на (boldsymbol{e_{1}}), мы получим (lambda(boldsymbol{e_{1}}, boldsymbol{e_{2}}, boldsymbol{e_{3}}) = 0). Полученное противоречие доказывает наше предложение.
Следующие предложения дают условия на компоненты векторов в произвольном базисе, необходимые и достаточные для компланарности или коллинеарности векторов.
Утверждение 7.
Равенство нулю детерминанта матрицы из компонент трех векторов необходимо и достаточно для компланарности векторов.
Доказательство.
Это сразу следует из формулы eqref{ref16}, поскольку ((boldsymbol{e_{1}}, boldsymbol{e_{2}}, boldsymbol{e_{3}}) neq 0).
Утверждение 8.
Пусть ((alpha_{1}, alpha_{2}, alpha_{3})) и ((beta_{1}, beta_{2}, beta_{3})) — компоненты векторов (boldsymbol{a}) и (boldsymbol{b}) в некотором базисе. Векторы (boldsymbol{a}) и (boldsymbol{b}) коллинеарны тогда и только тогда, когда
$$
begin{vmatrix}
alpha_{2}& alpha_{3}\
beta_{2}& beta_{3}
end{vmatrix}
=
begin{vmatrix}
alpha_{3}& alpha_{1}\
beta_{3}& beta_{1}
end{vmatrix}
=
begin{vmatrix}
alpha_{1}& alpha_{2}\
beta_{1}& beta_{2}
end{vmatrix}
= 0.label{ref20}
$$
Доказательство.
Достаточность условия очевидна: из равенств eqref{ref20} по формуле eqref{ref14} следует обращение в нуль ([boldsymbol{a}, boldsymbol{b}]), что равносильно коллинеарности векторов. Заметим, что мы пользуемся формулой eqref{ref14}, которая справедлива для произвольного базиса. Наоборот, из обращения в нуль ([boldsymbol{a}, boldsymbol{b}]) и формулы eqref{ref14} мы можем вывести eqref{ref20}, так как в силу предложения 6 векторы ([boldsymbol{e_{2}}, boldsymbol{e_{3}}]), ([boldsymbol{e_{3}}, boldsymbol{e_{1}}]) и ([boldsymbol{e_{1}}, boldsymbol{e_{2}}]) линейно независимы.
Утверждение 9.
Обращение в нуль детерминанта матрицы из компонент двух векторов на плоскости необходимо и достаточно для коллинеарности этих векторов.
Доказательство.
Для доказательства будем считать, что плоскость помещена в пространство и базис в этой плоскости дополнен третьим вектором до базиса в пространстве. Тогда векторы (boldsymbol{a}(alpha_{1}, alpha_{2})) и (boldsymbol{b}(beta_{1}, beta_{2})) на плоскости имеют компоненты ((alpha_{1}, alpha_{2}, 0)) и ((beta_{1}, beta_{2}, 0)) относительно базиса в пространстве. Применяя предложение 8, получаем условие
$$
begin{vmatrix}
alpha_{1}& alpha_{2}\
beta_{1}& beta_{2}
end{vmatrix}
= 0.nonumber
$$
Остальные два детерминанта равны нулю, так как (alpha_{3} = beta_{3} = 0).
Площадь параллелограмма.
Если в пространстве заданы два неколлинеарных вектора, имеющих общее начало, то площадь параллелограмма, построенного на этих векторах, может быть найдена через их компоненты в ортонормированном базисе по формуле
$$
S = |[boldsymbol{a}, boldsymbol{b}]| = sqrt{(alpha_{2}beta_{3}-alpha_{3}beta_{2})^{2} + (alpha_{3}beta_{1}-alpha_{1}beta_{3})^{2} + (alpha_{1}beta_{2}-alpha_{2}beta_{1})^{2}}.label{ref21}
$$
Еще одно выражение для площади параллелограмма мы получим, если заметим, что
$$
|[boldsymbol{a}, boldsymbol{b}]|^{2} = |boldsymbol{a}|^{2}|boldsymbol{b}|^{2} sin^{2} varphi = |boldsymbol{a}|^{2}|boldsymbol{b}|^{2} (1-cos varphi).nonumber
$$
В результате
$$
S^{2} =
begin{vmatrix}
|boldsymbol{a}|^{2}& (boldsymbol{a}, boldsymbol{b})\
(boldsymbol{a}, boldsymbol{b})& |boldsymbol{b}|^{2}
end{vmatrix}.label{ref22}
$$
Найдем теперь площадь ориентированного параллелограмма на ориентированной плоскости. Можно считать, что ориентация плоскости определена вектором (boldsymbol{n}), перпендикулярным плоскости и составляющим правую тройку с положительным базисом на плоскости. Более того, будем предполагать, что (|boldsymbol{n}| = 1).
Пусть дан ориентированный параллелограмм, построенный на векторах (boldsymbol{a}) и (boldsymbol{b}). Рассмотрим скалярную проекцию Пр(_{boldsymbol{n}}[boldsymbol{a}, boldsymbol{b}]). Так как ([boldsymbol{a}, boldsymbol{b}]) и (boldsymbol{n}) коллинеарны, проекция по модулю равна (|[boldsymbol{a}, boldsymbol{b}]|), то есть площади параллелограмма. Она положительна, если ([boldsymbol{a}, boldsymbol{b}]) и (boldsymbol{n}) сонаправлены, и отрицательна в противном случае. Но вектор ([boldsymbol{a}, boldsymbol{b}]) сонаправлен с (boldsymbol{n}), если пара векторов (boldsymbol{a}), (boldsymbol{b}) на плоскости ориентирована положительно. Поэтому Пр(_{n}[boldsymbol{a}, boldsymbol{b}]) равна площади ориентированного параллелограмма, построенного на (boldsymbol{a}) и (boldsymbol{b}). По определению проекции
$$
S_{pm}(boldsymbol{a}, boldsymbol{b}) = (boldsymbol{n}, boldsymbol{a}, boldsymbol{b})nonumber
$$
(напомним, что (|boldsymbol{n}| = 1)). На плоскости выберем произвольный (не обязательно положительный) базис (boldsymbol{e_{1}}), (boldsymbol{e_{2}}). Примем (boldsymbol{n}) за третий базисный вектор и выразим смешанное произведение через координаты сомножителей:
$$
S_{pm}(boldsymbol{a}, boldsymbol{b}) =
begin{vmatrix}
0& 0& 1\
alpha_{1}& alpha_{2}& 0\
beta_{1}& beta_{2}& 0
end{vmatrix}
(boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{n}).nonumber
$$
Вычисляя детерминант, находим, что он равен (alpha_{1}beta_{2}-alpha_{2}beta_{1}), и получаем окончательное выражение
$$
S_{pm}(boldsymbol{a}, boldsymbol{b}) =
begin{vmatrix}
alpha_{1}& alpha_{2}\
beta_{1}& beta_{2}
end{vmatrix}
S_{pm}(boldsymbol{e}_{1}, boldsymbol{e}_{2}).label{ref23}
$$
Эта формула сходна с формулой eqref{ref16}. По существу это та же формула, написанная для двумерного пространства. Если ((boldsymbol{e}_{1}, boldsymbol{e}_{2})) — положительный ортонормированный базис, то
$$
S_{pm}(boldsymbol{a}, boldsymbol{b}) = alpha_{1}beta_{2}-alpha_{2}beta_{1}.label{ref24}
$$
Для площади неориентированного параллелограмма в ортонормированном базисе мы получаем формулу
$$
S = |alpha_{1}beta_{2}-alpha_{2}beta_{1}|.label{ref25}
$$
которая следует и из eqref{ref21}.
Двойное векторное произведение.
Определение.
Выражение ([boldsymbol{a}, [boldsymbol{b}, boldsymbol{c}]]) называется двойным векторным произведением.
Лемма.
$$
[boldsymbol{a} [boldsymbol{b}, boldsymbol{c}]] = (boldsymbol{a}, boldsymbol{c}) boldsymbol{b}-(boldsymbol{a}, boldsymbol{b}) boldsymbol{c}.label{ref26}
$$
Доказательство.
Выберем правый ортонормированный базис ((boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3})) так, чтобы (boldsymbol{e}_{1}) был коллинеарен (boldsymbol{b}), а (boldsymbol{e}_{2}) был компланарен (boldsymbol{b}) и (boldsymbol{c}). Тогда (boldsymbol{b} = beta boldsymbol{e}_{1}), (boldsymbol{c} = gamma_{1} boldsymbol{e}_{1} + gamma_{1} boldsymbol{e}_{2}) и (boldsymbol{a} = alpha_{1} boldsymbol{e}_{1} + alpha_{2} boldsymbol{e}_{2} + alpha_{3} boldsymbol{e}_{3}). Отсюда получаем ([boldsymbol{b}, boldsymbol{c}] = betagamma_{2}boldsymbol{e}_{3}) и
$$
[boldsymbol{a} [boldsymbol{b}, boldsymbol{c}]] = -alpha_{1}betagamma_{2}boldsymbol{e}_{2} + alpha_{2}betagamma_{2}boldsymbol{e}_{1}.nonumber
$$
С другой стороны,
$$
(boldsymbol{a}, boldsymbol{c}) boldsymbol{b} = (alpha_{1}gamma_{1} + alpha_{2}gamma_{2})betaboldsymbol{e}_{1}, (boldsymbol{a}, boldsymbol{b}) boldsymbol{c} = alpha_{1}beta(gamma_{1}boldsymbol{e}_{1} + gamma_{2}boldsymbol{e}_{2}).nonumber
$$
Разность правых частей двух последних равенств совпадает с найденным выше двойным векторным произведением. Это заканчивает доказательство.
Биортогональный базис.
Определение.
Базис, составленный из векторов
$$
boldsymbol{e^{*}}_{1} = frac{[boldsymbol{e}_{2}, boldsymbol{e}_{3}]}{(boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3})}, boldsymbol{e^{*}}_{2} = frac{[boldsymbol{e}_{3}, boldsymbol{e}_{1}]}{(boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3})}, boldsymbol{e^{*}}_{3} = frac{[boldsymbol{e}_{1}, boldsymbol{e}_{2}]}{(boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3})}
$$
называется взаимным или биортогональным для базиса (boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}).
Из утверждения 6 вытекает, что (boldsymbol{e^{*}}_{1}, boldsymbol{e^{*}}_{2}, boldsymbol{e^{*}}_{3}), не компланарны и действительно образуют базис. Название “биортогональный” связано с тем, что векторы обоих базисов, имеющие разные номера, ортогональны: ((boldsymbol{e}_{i}, boldsymbol{e^{*}}_{j}) = 0) при (i neq j). Кроме того, ((boldsymbol{e}_{i}, boldsymbol{e^{*}}_{i}) = 1) для всех (i).
Нетрудно проверить, что ортонормированный базис совпадает со своим взаимным.
Утверждение 10.
Если (boldsymbol{e^{*}}_{1}, boldsymbol{e^{*}}_{2}, boldsymbol{e^{*}}_{3}) — базис, взаимный с (boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}), то произвольный вектор (boldsymbol{a}) раскладывается по этим базисам так:
$$
boldsymbol{a} = (boldsymbol{a}, boldsymbol{e^{*}}_{1}) boldsymbol{e}_{1} + (boldsymbol{a}, boldsymbol{e^{*}}_{2}) boldsymbol{e}_{2} + (boldsymbol{a}, boldsymbol{e^{*}}_{3}) boldsymbol{e}_{3},label{ref27}
$$
$$
boldsymbol{a} = (boldsymbol{a}, boldsymbol{e}_{1}) boldsymbol{e^{*}}_{1} + (boldsymbol{a}, boldsymbol{e}_{2}) boldsymbol{e^{*}}_{2} + (boldsymbol{a}, boldsymbol{e}_{3}) boldsymbol{e^{*}}_{3}.label{ref28}
$$
Доказательство.
Чтобы доказать eqref{ref27}, умножим равенство (boldsymbol{a} = alpha_{1}boldsymbol{e}_{1} + alpha_{2}boldsymbol{e}_{2} + alpha_{3}boldsymbol{e}_{3}) скалярно сначала на (boldsymbol{e^{*}}_{1}), затем на (boldsymbol{e^{*}}_{2}) и на (boldsymbol{e^{*}}_{3}). Мы получим (alpha_{1} = (boldsymbol{a}, boldsymbol{e^{*}}_{1})), (alpha_{2} = (boldsymbol{a}, boldsymbol{e^{*}}_{2})), (alpha_{3} = (boldsymbol{a}, boldsymbol{e}_{3})). Аналогично доказывается равенство eqref{ref28}.
Утверждение 11.
Если (boldsymbol{e^{*}}_{1}, boldsymbol{e^{*}}_{2}, boldsymbol{e^{*}}_{3}) — базис, взаимный с (boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}), то базис (boldsymbol{e^{**}}_{1}, boldsymbol{e^{**}}_{2}, boldsymbol{e^{**}}_{3}), взаимный с (boldsymbol{e^{*}}_{1}, boldsymbol{e^{*}}_{2}, boldsymbol{e^{*}}_{3}), совпадает с (boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}).
Доказательство.
Действительно, равенство eqref{ref28}, написанное для базиса (boldsymbol{e^{*}}_{1}, boldsymbol{e^{*}}_{2}, boldsymbol{e^{*}}_{3}), имеет вид
$$
boldsymbol{a} = (boldsymbol{a}, boldsymbol{e_{1}^{*}}) boldsymbol{e_{1}^{**}} + (boldsymbol{a}, boldsymbol{e_{2}^{*}}) boldsymbol{e_{2}^{**}} + (boldsymbol{a}, boldsymbol{e_{3}^{*}}) boldsymbol{e_{3}^{**}}.nonumber
$$
Подставляя сюда вместо а последовательно ((boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3})) и учитывая, что ((boldsymbol{e}_{i}, boldsymbol{e^{*}}_{j}) = 0) при (i neq j), а ((boldsymbol{e}_{i}, boldsymbol{e^{*}}_{i}) = 1), получаем (boldsymbol{e}_{1} = boldsymbol{e^{**}}_{1}), (boldsymbol{e}_{2} = boldsymbol{e^{**}}_{2}) и (boldsymbol{e}_{3} = boldsymbol{e^{**}}_{3}).
Числа ((boldsymbol{a}, boldsymbol{e}_{1})), ((boldsymbol{a}, boldsymbol{e}_{2})) и ((boldsymbol{a}, boldsymbol{e}_{3})) однозначно определяют вектор а с помощью векторов базиса (boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}). Они называются ковариантными координатами вектора а в базисе (boldsymbol{e}_{1}, boldsymbol{e}_{2}, boldsymbol{e}_{3}). По отношению к базису (boldsymbol{e^{*}}_{1}, boldsymbol{e^{*}}_{2}, boldsymbol{e^{*}}_{3}) — это обычные координаты вектора. Обычные координаты, чтобы подчеркнуть их отличие от ковариантных координат, называют контрвариантными координатами.
О векторных величинах.
В приложениях математики часто рассматриваются величины, изображаемые векторами: силы, скорости, моменты сил и так далее. Векторам, изображающим такие величины, приписывается размерность. Не вдаваясь в существо дела, мы ограничимся изложением формальных правил действий с размерностями.
С формальной точки зрения, размерность — это одночлен, составленный из какого-то набора символов. Такие одночлены перемножаются и делятся, как обычные одночлены. Имеют место следующие правила действий с векторными величинами:
- Модуль векторной величины имеет ту же размерность, что и сама величина.
- Складывать векторные величины можно только в том случае, когда их размерности совпадают. При этом размерность суммы та же, что и у слагаемых.
- При умножении векторной величины на скалярную их размерности перемножаются.
- Скалярное, векторное и смешанное произведения имеют размерность, равную произведению размерностей сомножителей. Это легко следует из первого правила, определений скалярного и векторного произведений и формулы eqref{ref10}.
Для того чтобы изобразить векторную величину на чертеже, мы должны условиться о масштабе: сколькими единицами длины (например, см) мы будем изображать одну единицу данной размерности (например, км, м/с, Н).
Если в векторном произведении сомножители имеют размерность длины, то произведение имеет размерность площади. Масштаб для изображения единиц площади выбирается так, чтобы одна единица площади изображалась одной линейной единицей. При этом длина векторного произведения будет численно равна площади параллелограмма, построенного на сомножителях.
Поскольку единица длины у нас выбрана и не меняется, указанное соглашение ни к каким противоречиям привести не может. Однако оно не так безобидно, как может показаться. Именно, два математика, пользующиеся этим соглашением, но разными единицами длины (например, француз, пользующийся сантиметрами, и англичанин — дюймами), для одних и тех же векторов нарисуют несовпадающие векторные произведения. Как связаны длины этих произведений, если дюйм равен примерно 2,5 см?



















