Как найти скалярное произведение векторов в пространстве

Как найти скалярное произведение векторов в пространстве

Скалярное произведение векторов {displaystyle (mathbf {a} ,mathbf {b} )} равно произведению {displaystyle |mathbf {a} ||mathbf {b} |cos(theta )}

Скаля́рное произведе́ние (иногда называемое внутренним произведением) — результат операции над двумя векторами, являющийся скаляром, то есть числом, не зависящим от выбора системы координат.
Используется в определении длины векторов и угла между ними.

Обычно для скалярного произведения векторов mathbf {a} и mathbf {b} используется одно из следующих обозначений.

{displaystyle (mathbf {a} ,mathbf {b} )}
{displaystyle mathbf {a} cdot mathbf {b} , {vec {a}}cdot {vec {b}}} или просто {displaystyle mathbf {a} mathbf {b} }
langle mathbf {a} ,mathbf {b} rangle и {displaystyle langle a|brangle ;} второе обозначение применяется в квантовой механике для векторов состояния[1].

В простейшем случае, а именно в случае конечномерного вещественного евклидового пространства, иногда используют «геометрическое» определение скалярного произведения ненулевых векторов mathbf {a} и mathbf {b} как произведения длин этих векторов на косинус угла между ними[2]:

{displaystyle (mathbf {a} ,mathbf {b} )=|mathbf {a} ||mathbf {b} |cos(theta ).}

Равносильное определение: скалярное произведение есть произведение длины проекции первого вектора на второй и длины второго вектора (см. рисунок). Если хотя бы один из векторов нулевой, то произведение считается равным нулю[3].

У понятия скалярного произведения существует также большое количество обобщений для различных векторных пространств, то есть для множеств векторов с операциями сложения и умножения на скаляры[⇨]. Данное выше геометрическое определение скалярного произведения предполагает предварительное определение понятий длины вектора и угла между ними. В современной математике используется обратный подход: аксиоматически определяется скалярное произведение, а уже через него — длины и углы[4]. В частности, скалярное произведение определяется для комплексных векторов, многомерных и бесконечномерных пространств, в тензорной алгебре.

Скалярное произведение и его обобщения играют чрезвычайно большую роль в векторной алгебре, теории многообразий, механике и физике. Например, работа силы при механическом перемещении равна скалярному произведению вектора силы на вектор перемещения[5].

Определение и свойства[править | править код]

Будем говорить, что в вещественном или комплексном векторном пространстве L определено скалярное произведение, если каждой паре векторов {displaystyle mathbf {a} ,mathbf {b} } из L поставлено в соответствие число {displaystyle (mathbf {a} ,mathbf {b} )} из того числового поля, над которым задано {displaystyle L,} удовлетворяющее следующим аксиомам.

  1. Для любых трёх элементов {displaystyle mathbf {a} _{1},mathbf {a} _{2},mathbf {b} } пространства mathbb {L} и любых чисел alpha ,beta справедливо равенство: {displaystyle (alpha mathbf {a} _{1}+beta mathbf {a} _{2},mathbf {b} )=alpha (mathbf {a} _{1},mathbf {b} )+beta (mathbf {a} _{2},mathbf {b} )} (линейность скалярного произведения по первому аргументу).
  2. Для любых {displaystyle mathbf {a} ,mathbf {b} } справедливо равенство {displaystyle (mathbf {a} ,mathbf {b} )={overline {(mathbf {b} ,mathbf {a} )}}}, где черта означает комплексное сопряжение.
  3. Для любого {displaystyle mathbf {a} } имеем: {displaystyle (mathbf {a} ,mathbf {a} )geqslant 0}, причём {displaystyle (mathbf {a} ,mathbf {a} )=0} только при {displaystyle mathbf {a} =0} (положительная определённость и невырожденность скалярного произведения соответственно).

Заметим, что из аксиомы 2 следует, что {displaystyle (mathbf {a} ,mathbf {a} )} — вещественное число. Поэтому аксиома 3 имеет смысл, несмотря на комплексные (в общем случае) значения скалярного произведения. Если аксиома 3 не выполняется, то произведение называется индефинитным или неопределённым.

Если {displaystyle (mathbf {a} ,mathbf {a} )=0} не только при {displaystyle mathbf {a} =0}, то произведение называется квазискалярным[6].

Из данных аксиом получаются следующие свойства:

  1. коммутативность для вещественных векторов: {displaystyle (mathbf {a} ,mathbf {b} )=(mathbf {b} ,mathbf {a} );}

    Дистрибутивность скалярного произведения в случае вещественного евклидового пространства

  2. дистрибутивность относительно сложения: {displaystyle (mathbf {a} +mathbf {b} ,mathbf {c} )=(mathbf {a} ,mathbf {c} )+(mathbf {b} ,mathbf {c} )} и {displaystyle (mathbf {c} ,mathbf {a} +mathbf {b} )=(mathbf {c} ,mathbf {a} )+(mathbf {c} ,mathbf {b} );}
  3. инволюционная линейность относительно второго аргумента: {displaystyle (mathbf {a} ,(alpha _{1}mathbf {b} _{1}+alpha _{2}mathbf {b} _{2}))={overline {alpha _{1}}}(mathbf {a} ,mathbf {b} _{1})+{overline {alpha _{2}}}(mathbf {a} ,mathbf {b} _{2});} (в случае вещественного L — просто линейность по второму аргументу).
  4. {displaystyle (alpha mathbf {a} ,beta mathbf {b} )=alpha {overline {beta }}(mathbf {a} ,mathbf {b} )} (что совпадает с {displaystyle alpha beta (mathbf {a} ,mathbf {b} )} для вещественного L).

Также есть свойства, связанные не с данными аксиомами:

  1. неассоциативность относительно умножения на вектор[7]‘: {displaystyle (mathbf {a} ,mathbf {b} )mathbf {c} neq mathbf {a} (mathbf {b} ,mathbf {c} )};
  2. ортогональность: два ненулевых вектора a и b ортогональны тогда и только тогда, когда (a, b) = 0 (определения ниже).

Замечание. В квантовой физике скалярное произведение (волновых функций, которые комплекснозначны) принято определять как линейное по второму аргументу (а не по первому), соответственно, по первому аргументу оно будет инволюционо линейным. Путаницы обычно не возникает, поскольку традиционное обозначение для скалярного произведения в квантовой физике также отличается: {displaystyle langle phi |psi rangle }, т.е. аргументы отделяются вертикальной чертой, а не запятой, и скобки всегда угловые.

Определение и свойства в евклидовом пространстве[править | править код]

Вещественные векторы[править | править код]

В n-мерном вещественном евклидовом пространстве векторы определяются своими координатами — наборами n вещественных чисел в ортонормированном базисе. Определить скалярное произведение векторов {displaystyle mathbf {a} =(a_{1},a_{2}dots a_{n}),mathbf {b} =(b_{1},b_{2}dots b_{n})} можно так[4]:

{displaystyle langle mathbf {a} ,mathbf {b} rangle =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}+dots +a_{n}b_{n}.}

Проверка показывает, что все три аксиомы выполнены.

Например, скалярное произведение векторов {displaystyle (1,3,-5)} и {displaystyle (4,-2,-1)} будет вычислено так:

{displaystyle {begin{aligned} (1,3,-5)cdot (4,-2,-1)&=1cdot 4+3cdot (-2)+(-5)cdot (-1)\&=4-6+5\&=3.end{aligned}}}

Можно доказать[8], что эта формула равносильна определению через проекции или через косинус: {displaystyle (mathbf {a} ,mathbf {b} )=|mathbf {a} ||mathbf {b} |cos(theta ).}

Комплексные векторы[править | править код]

Для комплексных векторов {displaystyle mathbf {a} =(a_{1},a_{2}dots a_{n}),mathbf {b} =(b_{1},b_{2}dots b_{n})} определим аналогично[9]:

{displaystyle langle mathbf {a} ,mathbf {b} rangle =sum _{k=1}^{n}a_{k}{overline {b_{k}}}=a_{1}{overline {b_{1}}}+a_{2}{overline {b_{2}}}+cdots +a_{n}{overline {b_{n}}}.}

Пример (для n=2): {displaystyle (1+i,2)cdot (2+i,i)=(1+i)cdot ({overline {2+i}})+2cdot {overline {i}}=(1+i)cdot (2-i)+2cdot (-i)=3-i.}

Свойства[править | править код]

Помимо общих свойств скалярного произведения, для многомерных евклидовых векторов верно следующее:

  1. в отличие от обычного умножения скаляров, где если ab = ac и a ≠ 0, то b равняется c, для скалярного умножения векторов это неверно: если a · b = a · c, то есть a · (b − c) = 0, то в общем случае a и b − c лишь ортогональны; но вектор b − c в общем случае не равен 0, то есть b ≠ c;
  2. правило произведения: для дифференцируемых вектор-функций a(t) и b(t) верно соотношение (a(t), b(t))′ = a′(t) ⋅ b(t) + a(t) ⋅ b′(t)[10];
  3. оценка угла между векторами:
    в формуле {displaystyle (mathbf {mathbf {a} } ,mathbf {b} )=|mathbf {a} |cdot |mathbf {b} |cdot cos angle {(mathbf {a} ,mathbf {b} )}} знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение больше 0, если угол между векторами острый, и меньше 0, если угол между векторами тупой;
  4. проекция вектора mathbf {a} на направление, определяемое единичным вектором mathbf {e} :
    {displaystyle a_{e}=(mathbf {a} ,mathbf {e} )=|mathbf {a} ||mathbf {e} |cos angle {(mathbf {a} ,mathbf {e} )}=|mathbf {a} |cos angle {(mathbf {a} ,mathbf {e} )}}, так как {displaystyle |mathbf {e} |=1;}
  5. площадь параллелограмма, натянутого на два вектора {displaystyle mathbf {a} } и {displaystyle mathbf {b} }, равна {displaystyle {sqrt {(mathbf {a} ,mathbf {a} )(mathbf {b} ,mathbf {b} )-(mathbf {a} ,mathbf {b} )^{2}}}.}

Теорема косинусов в вещественном пространстве[править | править код]

Dot product cosine rule.svg

Теорема косинусов легко выводится с использованием скалярного произведения. Пусть на сторонах треугольника находятся векторы a, b и c, первые два из которых образуют угол θ, как показано в изображении справа. Тогда, следуя свойствам и определению скалярного произведения через косинус:

{displaystyle {begin{aligned}mathbf {color {orange}c} cdot mathbf {color {orange}c} &=(mathbf {color {red}a} -mathbf {color {blue}b} )cdot (mathbf {color {red}a} -mathbf {color {blue}b} )\&=mathbf {color {red}a} cdot mathbf {color {red}a} -mathbf {color {red}a} cdot mathbf {color {blue}b} -mathbf {color {blue}b} cdot mathbf {color {red}a} +mathbf {color {blue}b} cdot mathbf {color {blue}b} \&=|mathbf {color {red}a} |^{2}-mathbf {color {red}a} cdot mathbf {color {blue}b} -mathbf {color {red}a} cdot mathbf {color {blue}b} +|mathbf {color {blue}b} |^{2}\&=|mathbf {color {red}a} |^{2}-2mathbf {color {red}a} cdot mathbf {color {blue}b} +|mathbf {color {blue}b} |^{2}\&=|mathbf {color {red}a} |^{2}+|mathbf {color {blue}b} |^{2}-2|mathbf {color {red}a} |{cdot }|mathbf {color {blue}b} |cos mathbf {color {purple}theta } .\end{aligned}}}

Связанные определения[править | править код]

В современном аксиоматическом подходе уже на основе понятия скалярного произведения векторов вводятся следующие производные понятия[11]:

Длина вектора, под которой обычно понимается его евклидова норма:

{displaystyle |mathbf {a} |={sqrt {(mathbf {a} ,mathbf {a} )}}}

(термин «длина» обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).

Углом varphi между двумя ненулевыми векторами евклидова пространства (в частности, евклидовой плоскости) называется число, косинус которого равен отношению скалярного произведения этих векторов к произведению их длин (норм):

{displaystyle cos varphi ={frac {(mathbf {a} ,mathbf {b} )}{|mathbf {a} ||mathbf {b} |}} (0leqslant varphi leqslant pi ).}

Данные определения позволяют сохранить формулу: {displaystyle (mathbf {a} ,mathbf {b} )=|mathbf {a} ||mathbf {b} |cos(varphi )} и в общем случае. Корректность формулы для косинуса гарантирует неравенство Коши — Буняковского[12]:

Для любых элементов {displaystyle mathbf {a} ,mathbf {b} } векторного пространства со скалярным произведением выполняется неравенство:

{displaystyle vert (mathbf {a} ,mathbf {b} )vert ^{2}leqslant (mathbf {a} ,mathbf {a} )(mathbf {b} ,mathbf {b} )}

В случае, если пространство является псевдоевклидовым, понятие угла определяется лишь для векторов, не содержащих изотропных прямых внутри образованного векторами сектора. Сам угол при этом вводится как число, гиперболический косинус которого равен отношению модуля скалярного произведения этих векторов к произведению их длин (норм):

{displaystyle |(mathbf {a} ,mathbf {b} )|=|mathbf {a} ||mathbf {b} |operatorname {ch} varphi .}
  • Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю. Это определение применимо к любым пространствам с положительно определённым скалярным произведением. Например, ортогональные многочлены на самом деле ортогональны (в смысле этого определения) друг другу в некотором гильбертовом пространстве.
  • Пространство (вещественное или комплексное) с положительно определённым скалярным произведением называется предгильбертовым пространством.
    • При этом конечномерное вещественное пространство с положительно определённым скалярным произведением называется также евклидовым, а комплексное — эрмитовым или унитарным пространством.
  • Случай, когда скалярное произведение не является знакоопределённым, приводит к т. н. пространствам с индефинитной метрикой. Скалярное произведение в таких пространствах уже не порождает нормы (и она обычно вводится дополнительно). Конечномерное вещественное пространство с индефинитной метрикой называется псевдоевклидовым (важнейшим частным случаем такого пространства является пространство Минковского). Среди бесконечномерных пространств с индефинитной метрикой важную роль играют пространства Понтрягина и пространства Крейна.

История[править | править код]

Скалярное произведение было введено У. Гамильтоном в 1846 году[13] одновременно с векторным произведением в связи с кватернионами — соответственно, как скалярная и векторная часть произведения двух кватернионов, скалярная часть которых равна нулю[14].

Вариации и обобщения[править | править код]

В пространстве измеримых интегрируемых с квадратами на некоторой области Ω вещественных или комплексных функций можно ввести положительно определённое скалярное произведение:

{displaystyle (mathbf {f} ,mathbf {g} )=int limits _{Omega }f(x){overline {g(x)}}dOmega }

При использовании неортонормированных базисов скалярное произведение выражается через компоненты векторов с участием метрического тензора[15] g_{ij}:

{displaystyle (mathbf {a} ,mathbf {b} )=g_{ij}a^{i}b^{j}}

При этом сама метрика (говоря точнее, её представление в данном базисе) так связана со скалярными произведениями базисных векторов f_{i} :

{displaystyle g_{ij}=(mathbf {f} _{i},mathbf {f} _{j})}

Аналогичные конструкции скалярного произведения можно вводить и на бесконечномерных пространствах, например, на пространствах функций:

{displaystyle (mathbf {f} ,mathbf {g} )=int limits _{(Omega _{1}times Omega _{2})}K(x_{1},x_{2})f(x_{1})g(x_{2})d(Omega _{1}times Omega _{2})}
{displaystyle (mathbf {f} ,mathbf {g} )=int limits _{Omega }K(x)f(x)g(x)dOmega }

где К — положительно определённая, в первом случае симметричная относительно перестановки аргументов (при комплексных x — эрмитова) функция (если нужно иметь обычное симметричное положительно определённое скалярное произведение).

Простейшим обобщением конечномерного скалярного произведения в тензорной алгебре является свёртка по повторяющимся индексам.

См. также[править | править код]

  • Гильбертово пространство
  • Векторное произведение
  • Внешнее произведение
  • Псевдоскалярное произведение
  • Смешанное произведение

Примечания[править | править код]

  1. ↑ Hall B. C. Quantum Theory for Mathematicians. — NY: Springer Science & Business Media, 2013. — xvi + 553 p. — (Graduate Texts in Mathematics. Vol. 267). — ISBN 978-1-4614-7115-8. Архивная копия от 31 января 2016 на Wayback Machine — P. 85.
  2. ↑ Имеется в виду наименьший угол между векторами, не превосходящий pi.
  3. ↑ Векторная алгебра // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 1. — С. 634.
  4. ↑ 1 2 Гельфанд, 1971, с. 30—31.
  5. ↑ Тарг С. М. Работа силы // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193—194. — 704 с. — ISBN 5-85270-087-8.
  6. ↑ Кудрявцев Л. Д. Математический анализ. II том. — М., Высшая школа, 1970. — с. 316.
  7. ↑ Weisstein, Eric W. Dot Product Архивная копия от 29 апреля 2021 на Wayback Machine. From MathWorld — A Wolfram Web Resource.
  8. ↑ Calculus II – Dot Product. tutorial.math.lamar.edu. Дата обращения: 9 мая 2021. Архивировано 9 мая 2021 года.
  9. ↑ Гельфанд, 1971, с. 86.
  10. ↑ Stewart, James (2016), Calculus (8 ed.), Cengage, Section 13.2.
  11. ↑ Гельфанд, 1971, с. 34.
  12. ↑ §9.5. Линейные пространства со скалярным произведением: евклидовы и унитарные
  13. ↑ Crowe M. J. A History of Vector Analysis – The Evolution of the Idea of a Vectorial System. — Courier Dover Publications, 1994. — С. 32. — 270 с. — ISBN 0486679101. Архивная копия от 6 марта 2019 на Wayback Machine
  14. ↑ Hamilton W. R. On Quaternions; or on a New System of Imaginaries in Algebra // Philosophical Magazine. 3rd Series. — London, 1846. — Т. 29. — С. 30.
  15. ↑ Гельфанд, 1971, с. 240.

Литература[править | править код]

  • Гельфанд И. М. Лекции по линейной алгебре. — 4-е изд. — М.: Наука, 1971. — 272 с.

Ссылки[править | править код]

  • Емелин А. Скалярное произведение векторов. Дата обращения: 14 ноября 2019.
Источник

Скалярное произведение векторов

Формула

Пусть даны векторы $ overline{a} = (a_x; a_y) $ и $ overline{b} = (b_x; b_y) $. Как найти скалярное произведение векторов? Для того, чтобы найти скалярное произведение векторов необходимо воспользоваться формулой: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y $$ Стоит заметить, что скалярное произведение записывается в скобках, в которых векторы записываются через запятую. Данное обозначение широко применяется в математике и его нужно запомнить.

Если в задаче векторы заданы тремя координатами (в пространстве), то найти скалярное произведение векторов нужно по другой формуле, основанной на предыдущей. Но с тем же смыслом: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y + a_z cdot b_z $$

По сути скалярное произведение – это сумма произведений соответствующих координат данных векторов. Первая координата умножается на первую, вторая на вторую и затем произведения суммируются.

Примеры решений

Пример 1
Найти скалярное произведение векторов $ overline{a} = (-1;2) $ и $ overline{b} = (2;1) $
Решение

В данном примере векторы заданы двумя координатами, поэтому применяем первую формулу для плоской задачи. Умножаем соответствующие координаты, а потом складываем их:

$$ (overline{a},overline{b}) = -1 cdot 2 + 2 cdot 1 = -2 + 2 = 0 $$

Произведение получилось равным нулю, а это кстати означает, что векторы оказались ортогональными (перпендикулярными) друг к другу.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Ответ
$$ (overline{a},overline{b}) = 0 $$
Пример 2

В пространстве заданы начала и концы векторов: $$ A = (1;3;-2), B = (-1;4;1), C = (2; 1; -2) $$ Требуется найти скалярное произведение векторов $ overline{AB} $ и $ overline{AC} $.
Решение

В примеры решения данной задачи даны только точки и сразу вычислить произведение векторов не представляется возможным. Сначала нужно найти сами векторы $ overline{AB} $ и $ overline{AC} $. Вычисляются они с помощью разности соответствующих координат точек (из конца вычитается начало вектора):

$$ overline{AB} = (-1 – 1; 4-3; 1-(-2)) = (-2; 1; 3) $$

$$ overline{AC} = (2 – 1; 1 – 3; -2 – (-2)) = (1; -2; 0) $$

Теперь, когда необходимые векторы найдены, то вычисляем их произведение:

$$ (overline{AB},overline{AC}) = -2 cdot 1 + 1 cdot (-2) + 3 cdot 0 = -2-2+0 = -4 $$
Ответ
$$ (overline{AB},overline{AC}) = -4 $$

В статье мы ответили на вопрос: «Как найти скалярное произведение векторов?», а так же привели формулы и примеры решений задач.

Источник

Содержание:

  • Формула
  • Примеры вычисления скалярного произведения векторов

Формула

Для того чтобы найти скалярное произведение двух векторов, заданных своими
координатами, необходимо вычислить сумму произведений
соответствующих координат этих векторов. Для случая, если векторы заданны на плоскости координатами $bar{a}=left(a_{x} ; a_{y}right)$ и $bar{b}=left(b_{x} ; b_{y}right)$, имеет место формула:

$$(bar{a}, bar{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}$$

Если же векторы заданы в пространстве своими координатами: $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$ соответственно, то их скалярное произведение вычисляется по формуле:

$$(bar{a}, bar{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}$$

Примеры вычисления скалярного произведения векторов

Пример

Задание. Найти скалярное произведение векторов $bar{a}=(1 ;-3)$ и $bar{b}=(-2 ;-3)$

Решение. Векторы заданны на плоскости, поэтому для вычисления их скалярного произведения воспользуемся формулой

$$(bar{a}, bar{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}$$

Подставляя координаты заданных векторов, получим

$$(bar{a}, bar{b})=1 cdot(-2)+(-3) cdot(-3)=-2+9=7$$

Ответ. $(bar{a}, bar{b})=7$ lt /$>

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. В пространстве заданы точки
$A(-1 ;-2 ; 5), B(-3 ; 2 ; 1)$ и $C(0 ; 1 ;-1)$ . Найти скалярное произведение векторов
$overline{A B}$ и
$overline{A C}$

Решение. Найдем сначала координаты векторов
$overline{A B}$ и
$overline{A C}$ . Для этого из координат конца вычислим соответствующие
координаты начала, получим:

$$overline{A B}=(-3-(-1) ; 2-(-2) ; 1-5)=(-2 ; 4 ;-4)$$
$$overline{A C}=(0-(-1) ; 1-(-2) ;-1-5)=(1 ; 3 ;-6)$$

Далее воспользуемся формулой для вычисления скалярного произведения векторов, заданных в пространстве:

$$(bar{a}, bar{b})=a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}$$

Получим

$$(overline{A B}, overline{A C})=(-2) cdot 1+4 cdot 3+(-4)(-6)=-2+12+24=34$$

Ответ. $(overline{A B}, overline{A C})=34$

Читать дальше: как найти векторное произведение векторов.

Источник

Пусть
– ортогональный базис евклидова
пространстваЕ.
Найдем, как выражается скалярное
произведение двух векторов через их
координаты в этом базисе.

Пусть
–
координаты вектора,
а–
координаты векторав этом базисе, то есть:

Тогда:

(16)

Если базис
является ортонормированным, то есть

,
(17)

то выражение (16) в
таком базисе примет вид

).
(18)

Таким образом, в
нормированном ортогональном базисе
скалярное произведение двух векторов
равно сумме произведений их соответствующих
координат.

    1. Изоморфизм евклидовых пространств

Если рассмотреть
ряд n-мерных
евклидовых пространств, то эти пространства
могут отличаться одно от другого во
всяком случае способом задания векторов
базиса. Возникает вопрос: какие из этих
пространств действительно различны и
какие различия являются лишь чисто
внешними?

Для того, чтобы
вопрос был точно поставлен, нужно
определить, какие два

евклидова
пространства будем считать несущественно
различающимися (изоморфными).

ОПРЕДЕЛЕНИЕ
7. Два евклидовых пространства

и

называются изоморфными,
если между их элементами можно установить
взаимно однозначное соответствие
так, что:

1.
Еслии,
то.

2.
Если,
то.

3.
Еслии,
то.

Таким образом, два
евклидовых пространства

и
изоморфны,
если они изоморфны как линейные
пространства. И этот изоморфизм таков,
что он сохраняет скалярное произведение
соответствующих векторов.

§ 3. Билинейные квадратичные формы

4.1. Линейная функция

Рассмотрим
простейшие числовые функции, аргументами
которых являются вектора. Простейшей
числовой функцией в пространстве L
является линейная функция.

ОПРЕДЕЛЕНИЕ 1.
Функция
называетсялинейной,
если
ставит в соответствие число и при этом
выполнены условия:

.

.

Выберем в n-мерном
линейном пространстве
базис.
Так как каждый векторможно представить в виде:

,

то в силу свойства
линейной функции имеем:

.

Итак, в линейном
n-мерном
пространстве
с заданным базисом линейная функция
может быть представлена в виде

,
(1)

где
постоянные, зависящие лишь от выбора
базиса, а– координаты векторав этом базисе.

Выясним, как
меняются коэффициенты линейной функции
при замене одного базиса другим.

Пусть
и– два базиса в.
Предположим, что векторывыражаются через векторы базисаследующим образом:

,

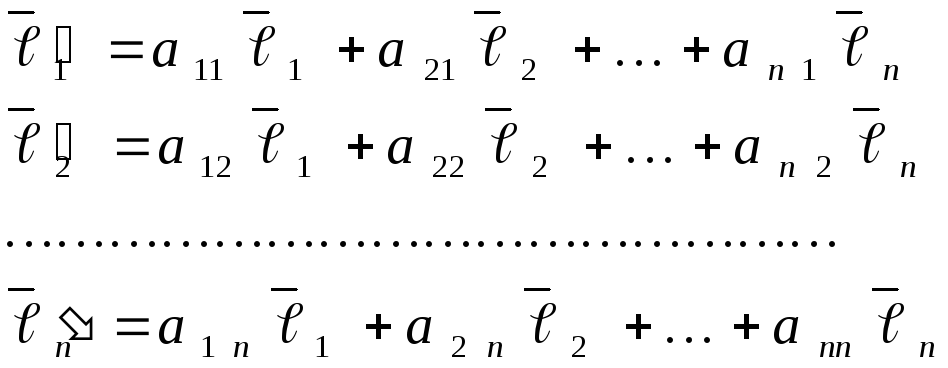В базисе
линейная функцияопределяется выражением

,
(2)

а в базисе
– выражением

.
(3)

Так как

то

Следовательно,
коэффициенты
линейной формы
преобразуются при переходе к другому
базису так же, как векторы базиса этого
пространства.

4.2. Билинейные формы

ОПРЕДЕЛЕНИЕ
2. Выражение

называется билинейной
функцией (билинейной формой) от векторов

и
,если:

.
При фиксированном

есть линейная функция от
,
то есть:

а)
,

б)
.

.
При фиксированном

есть линейная функция от
,
то есть:

а)
,

б)
.

ОПРЕДЕЛЕНИЕ 3.
Билинейная
функция (форма) называется симметричной,
если для всех векторов
и
имеет место равенство:

(4)

В частности, из
определения скалярного произведения


в евклидовом пространстве Е
 следует,
что это произведение является симметричной
билинейной формой.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.


Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Сумма векторов:

Разность векторов:

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1.  В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2.  В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и :

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму.

3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

Для точки M:

То есть A + C + D = 0.

Для точки N:

Аналогично для точки K:

Получили систему из трех уравнений:

.

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

;

.

Выразим C и B через A и подставим в третье уравнение:

.

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.

Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.

Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Упростим систему:

.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать “параллелепипед”.

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.

Итак, AA1 = √3

Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор  или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D

  

Решим эту систему. Выберем

Тогда

Уравнение плоскости A1DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A1DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Векторы в пространстве и метод координат» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Добавить комментарий