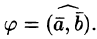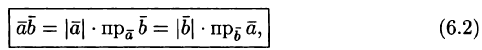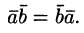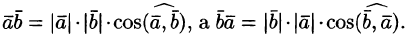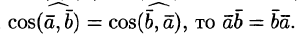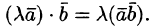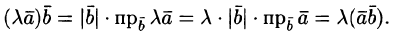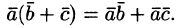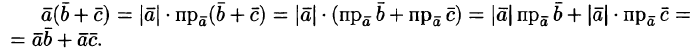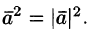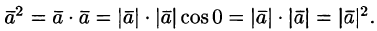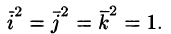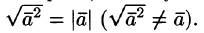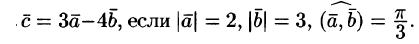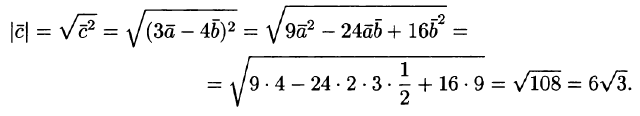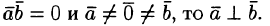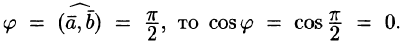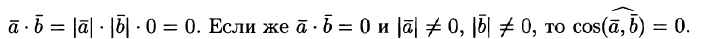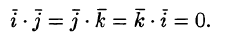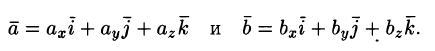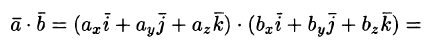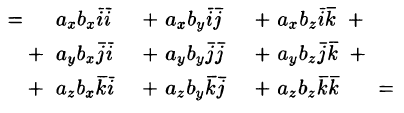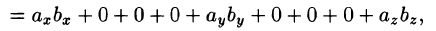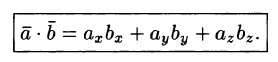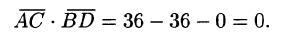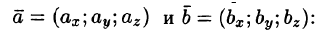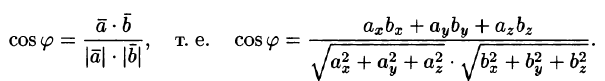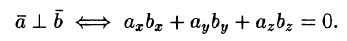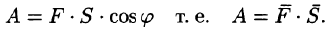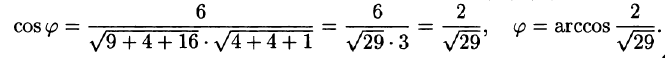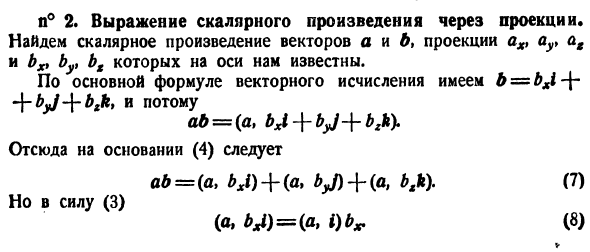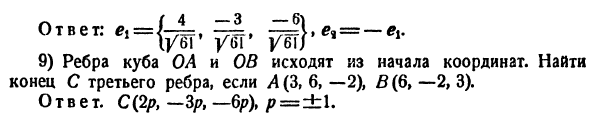Скалярное произведение векторов 
равно произведению 
Скаля́рное произведе́ние (иногда называемое внутренним произведением) — результат операции над двумя векторами, являющийся скаляром, то есть числом, не зависящим от выбора системы координат.
Используется в определении длины векторов и угла между ними.
Обычно для скалярного произведения векторов 
и 
используется одно из следующих обозначений.
- или просто
- и второе обозначение применяется в квантовой механике для векторов состояния[1].
В простейшем случае, а именно в случае конечномерного вещественного евклидового пространства, иногда используют «геометрическое» определение скалярного произведения ненулевых векторов и как произведения длин этих векторов на косинус угла между ними[2]:
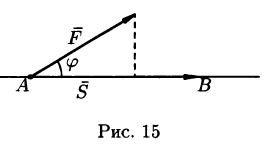
Равносильное определение: скалярное произведение есть произведение длины проекции первого вектора на второй и длины второго вектора (см. рисунок). Если хотя бы один из векторов нулевой, то произведение считается равным нулю[3].
У понятия скалярного произведения существует также большое количество обобщений для различных векторных пространств, то есть для множеств векторов с операциями сложения и умножения на скаляры[⇨]. Данное выше геометрическое определение скалярного произведения предполагает предварительное определение понятий длины вектора и угла между ними. В современной математике используется обратный подход: аксиоматически определяется скалярное произведение, а уже через него — длины и углы[4]. В частности, скалярное произведение определяется для комплексных векторов, многомерных и бесконечномерных пространств, в тензорной алгебре.
Скалярное произведение и его обобщения играют чрезвычайно большую роль в векторной алгебре, теории многообразий, механике и физике. Например, работа силы при механическом перемещении равна скалярному произведению вектора силы на вектор перемещения[5].
Определение и свойства[править | править код]
Будем говорить, что в вещественном или комплексном векторном пространстве 
определено скалярное произведение, если каждой паре векторов 
из поставлено в соответствие число из того числового поля, над которым задано 
удовлетворяющее следующим аксиомам.
- Для любых трёх элементов пространства и любых чисел справедливо равенство: (линейность скалярного произведения по первому аргументу).
- Для любых справедливо равенство , где черта означает комплексное сопряжение.
- Для любого имеем: , причём только при (положительная определённость и невырожденность скалярного произведения соответственно).
Заметим, что из аксиомы 2 следует, что 
— вещественное число. Поэтому аксиома 3 имеет смысл, несмотря на комплексные (в общем случае) значения скалярного произведения. Если аксиома 3 не выполняется, то произведение называется индефинитным или неопределённым.
Если 
не только при 
, то произведение называется квазискалярным[6].
Из данных аксиом получаются следующие свойства:
- коммутативность для вещественных векторов:
Дистрибутивность скалярного произведения в случае вещественного евклидового пространства
- дистрибутивность относительно сложения: и
- инволюционная линейность относительно второго аргумента: (в случае вещественного — просто линейность по второму аргументу).
- (что совпадает с для вещественного ).
Также есть свойства, связанные не с данными аксиомами:
- неассоциативность относительно умножения на вектор[7]‘: ;
- ортогональность: два ненулевых вектора a и b ортогональны тогда и только тогда, когда (a, b) = 0 (определения ниже).
Замечание. В квантовой физике скалярное произведение (волновых функций, которые комплекснозначны) принято определять как линейное по второму аргументу (а не по первому), соответственно, по первому аргументу оно будет инволюционо линейным. Путаницы обычно не возникает, поскольку традиционное обозначение для скалярного произведения в квантовой физике также отличается: 
, т.е. аргументы отделяются вертикальной чертой, а не запятой, и скобки всегда угловые.
Определение и свойства в евклидовом пространстве[править | править код]
Вещественные векторы[править | править код]
В 
-мерном вещественном евклидовом пространстве векторы определяются своими координатами — наборами вещественных чисел в ортонормированном базисе. Определить скалярное произведение векторов 
можно так[4]:
Проверка показывает, что все три аксиомы выполнены.
Например, скалярное произведение векторов 
и 
будет вычислено так:
Можно доказать[8], что эта формула равносильна определению через проекции или через косинус: 
Комплексные векторы[править | править код]
Для комплексных векторов определим аналогично[9]:
Пример (для 
): 
Свойства[править | править код]
Помимо общих свойств скалярного произведения, для многомерных евклидовых векторов верно следующее:
- в отличие от обычного умножения скаляров, где если ab = ac и a ≠ 0, то b равняется c, для скалярного умножения векторов это неверно: если a · b = a · c, то есть a · (b − c) = 0, то в общем случае a и b − c лишь ортогональны; но вектор b − c в общем случае не равен 0, то есть b ≠ c;
- правило произведения: для дифференцируемых вектор-функций a(t) и b(t) верно соотношение (a(t), b(t))′ = a′(t) ⋅ b(t) + a(t) ⋅ b′(t)[10];
- оценка угла между векторами:
- в формуле знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение больше 0, если угол между векторами острый, и меньше 0, если угол между векторами тупой;
- в формуле
- проекция вектора на направление, определяемое единичным вектором :
- , так как
- площадь параллелограмма, натянутого на два вектора и , равна
Теорема косинусов в вещественном пространстве[править | править код]
Теорема косинусов легко выводится с использованием скалярного произведения. Пусть на сторонах треугольника находятся векторы a, b и c, первые два из которых образуют угол θ, как показано в изображении справа. Тогда, следуя свойствам и определению скалярного произведения через косинус:
Связанные определения[править | править код]
В современном аксиоматическом подходе уже на основе понятия скалярного произведения векторов вводятся следующие производные понятия[11]:
Длина вектора, под которой обычно понимается его евклидова норма:
(термин «длина» обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).
Углом 
между двумя ненулевыми векторами евклидова пространства (в частности, евклидовой плоскости) называется число, косинус которого равен отношению скалярного произведения этих векторов к произведению их длин (норм):
Данные определения позволяют сохранить формулу: 
и в общем случае. Корректность формулы для косинуса гарантирует неравенство Коши — Буняковского[12]:
Для любых элементов векторного пространства со скалярным произведением выполняется неравенство:
В случае, если пространство является псевдоевклидовым, понятие угла определяется лишь для векторов, не содержащих изотропных прямых внутри образованного векторами сектора. Сам угол при этом вводится как число, гиперболический косинус которого равен отношению модуля скалярного произведения этих векторов к произведению их длин (норм):
- Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю. Это определение применимо к любым пространствам с положительно определённым скалярным произведением. Например, ортогональные многочлены на самом деле ортогональны (в смысле этого определения) друг другу в некотором гильбертовом пространстве.
- Пространство (вещественное или комплексное) с положительно определённым скалярным произведением называется предгильбертовым пространством.
- При этом конечномерное вещественное пространство с положительно определённым скалярным произведением называется также евклидовым, а комплексное — эрмитовым или унитарным пространством.
- Случай, когда скалярное произведение не является знакоопределённым, приводит к т. н. пространствам с индефинитной метрикой. Скалярное произведение в таких пространствах уже не порождает нормы (и она обычно вводится дополнительно). Конечномерное вещественное пространство с индефинитной метрикой называется псевдоевклидовым (важнейшим частным случаем такого пространства является пространство Минковского). Среди бесконечномерных пространств с индефинитной метрикой важную роль играют пространства Понтрягина и пространства Крейна.
История[править | править код]
Скалярное произведение было введено У. Гамильтоном в 1846 году[13] одновременно с векторным произведением в связи с кватернионами — соответственно, как скалярная и векторная часть произведения двух кватернионов, скалярная часть которых равна нулю[14].
Вариации и обобщения[править | править код]
В пространстве измеримых интегрируемых с квадратами на некоторой области Ω вещественных или комплексных функций можно ввести положительно определённое скалярное произведение:
При использовании неортонормированных базисов скалярное произведение выражается через компоненты векторов с участием метрического тензора[15] 
:
При этом сама метрика (говоря точнее, её представление в данном базисе) так связана со скалярными произведениями базисных векторов 
:
Аналогичные конструкции скалярного произведения можно вводить и на бесконечномерных пространствах, например, на пространствах функций:
где К — положительно определённая, в первом случае симметричная относительно перестановки аргументов (при комплексных x — эрмитова) функция (если нужно иметь обычное симметричное положительно определённое скалярное произведение).
Простейшим обобщением конечномерного скалярного произведения в тензорной алгебре является свёртка по повторяющимся индексам.
См. также[править | править код]
- Гильбертово пространство
- Векторное произведение
- Внешнее произведение
- Псевдоскалярное произведение
- Смешанное произведение
Примечания[править | править код]
- ↑ Hall B. C. Quantum Theory for Mathematicians. — NY: Springer Science & Business Media, 2013. — xvi + 553 p. — (Graduate Texts in Mathematics. Vol. 267). — ISBN 978-1-4614-7115-8. Архивная копия от 31 января 2016 на Wayback Machine — P. 85.
- ↑ Имеется в виду наименьший угол между векторами, не превосходящий
- ↑ Векторная алгебра // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 1. — С. 634.
- ↑ 1 2 Гельфанд, 1971, с. 30—31.
- ↑ Тарг С. М. Работа силы // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193—194. — 704 с. — ISBN 5-85270-087-8.
- ↑ Кудрявцев Л. Д. Математический анализ. II том. — М., Высшая школа, 1970. — с. 316.
- ↑ Weisstein, Eric W. Dot Product Архивная копия от 29 апреля 2021 на Wayback Machine. From MathWorld — A Wolfram Web Resource.
- ↑ Calculus II – Dot Product. tutorial.math.lamar.edu. Дата обращения: 9 мая 2021. Архивировано 9 мая 2021 года.
- ↑ Гельфанд, 1971, с. 86.
- ↑ Stewart, James (2016), Calculus (8 ed.), Cengage, Section 13.2.
- ↑ Гельфанд, 1971, с. 34.
- ↑ §9.5. Линейные пространства со скалярным произведением: евклидовы и унитарные
- ↑ Crowe M. J. A History of Vector Analysis – The Evolution of the Idea of a Vectorial System. — Courier Dover Publications, 1994. — С. 32. — 270 с. — ISBN 0486679101. Архивная копия от 6 марта 2019 на Wayback Machine
- ↑ Hamilton W. R. On Quaternions; or on a New System of Imaginaries in Algebra // Philosophical Magazine. 3rd Series. — London, 1846. — Т. 29. — С. 30.
- ↑ Гельфанд, 1971, с. 240.
Литература[править | править код]
- Гельфанд И. М. Лекции по линейной алгебре. — 4-е изд. — М.: Наука, 1971. — 272 с.
Ссылки[править | править код]
- Емелин А. Скалярное произведение векторов. Дата обращения: 14 ноября 2019.
Скалярное произведение векторов
Формула
Пусть даны векторы $ overline{a} = (a_x; a_y) $ и $ overline{b} = (b_x; b_y) $. Как найти скалярное произведение векторов? Для того, чтобы найти скалярное произведение векторов необходимо воспользоваться формулой: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y $$ Стоит заметить, что скалярное произведение записывается в скобках, в которых векторы записываются через запятую. Данное обозначение широко применяется в математике и его нужно запомнить.
Если в задаче векторы заданы тремя координатами (в пространстве), то найти скалярное произведение векторов нужно по другой формуле, основанной на предыдущей. Но с тем же смыслом: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y + a_z cdot b_z $$
По сути скалярное произведение – это сумма произведений соответствующих координат данных векторов. Первая координата умножается на первую, вторая на вторую и затем произведения суммируются.
Примеры решений
| Пример 1 |
| Найти скалярное произведение векторов $ overline{a} = (-1;2) $ и $ overline{b} = (2;1) $ |
| Решение |
|
В данном примере векторы заданы двумя координатами, поэтому применяем первую формулу для плоской задачи. Умножаем соответствующие координаты, а потом складываем их: $$ (overline{a},overline{b}) = -1 cdot 2 + 2 cdot 1 = -2 + 2 = 0 $$ Произведение получилось равным нулю, а это кстати означает, что векторы оказались ортогональными (перпендикулярными) друг к другу. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ (overline{a},overline{b}) = 0 $$ |
| Пример 2 |
|
В пространстве заданы начала и концы векторов: $$ A = (1;3;-2), B = (-1;4;1), C = (2; 1; -2) $$ Требуется найти скалярное произведение векторов $ overline{AB} $ и $ overline{AC} $. |
| Решение |
|
В примеры решения данной задачи даны только точки и сразу вычислить произведение векторов не представляется возможным. Сначала нужно найти сами векторы $ overline{AB} $ и $ overline{AC} $. Вычисляются они с помощью разности соответствующих координат точек (из конца вычитается начало вектора): $$ overline{AB} = (-1 – 1; 4-3; 1-(-2)) = (-2; 1; 3) $$ $$ overline{AC} = (2 – 1; 1 – 3; -2 – (-2)) = (1; -2; 0) $$ Теперь, когда необходимые векторы найдены, то вычисляем их произведение: $$ (overline{AB},overline{AC}) = -2 cdot 1 + 1 cdot (-2) + 3 cdot 0 = -2-2+0 = -4 $$ |
| Ответ |
| $$ (overline{AB},overline{AC}) = -4 $$ |
В статье мы ответили на вопрос: «Как найти скалярное произведение векторов?», а так же привели формулы и примеры решений задач.
Скалярное произведение векторов называют число, равное произведению дин этих векторов на косинус угла между ними.
Обозначение произведения векторов a→ и b→ имеет вид a→,b→. Преобразуем в формулу:
a→,b→=a→·b→·cosa→,b→^. a→ и b→ обозначают длины векторов, a→,b→^ – обозначение угла между заданными векторами. Если хоть один вектор нулевой, то есть имеет значение 0, то и результат будет равен нулю, a→,b→=0
При умножении вектора самого на себя, получим квадрат его дины:
a→,b→=a→·b→·cosa→,a→^=a→2·cos0=a→2
Скалярное умножение вектора самого на себя называют скалярным квадратом.
Вычисляется по формуле:
a→,b→=a→·b→·cosa→,b→^.
Запись a→,b→=a→·b→·cosa→,b→^=a→·npa→b→=b→·npb→a→ показывает, что npb→a→ – это числовая проекция a→ на b→, npa→a→- проекция b→ на a→ соостветсвенно.
Сформулируем определение произведения для двух векторов:
Скалярное произведение двух векторов a→ на b→ называют произведение длины вектора a→ на проекцию b→ на направление a→ или произведение длины b→ на проекцию a→ соответственно.
Скалярное произведение в координатах
Вычисление скалярного произведения можно производить через координаты векторов в заданной плоскости или в пространстве.
Скаларное произведение двух векторов на плоскости, в трехмерном простарнстве называют сумму координат заданных векторов a→ и b→.
При вычислении на плоскости скаларного произведения заданных векторов a→=(ax,ay), b→=(bx,by) в декартовой системе используют:
a→,b→=ax·bx+ay·by,
для трехмерного пространства применимо выражение:
a→,b→=ax·bx+ay·by+az·bz.
Фактически это является третьим определением скалярного произведения.
Докажем это.
Для доказательства используем a→,b→=a→·b→·cosa→,b→^=ax·bx+ay·by для векторов a→=(ax,ay), b→=(bx,by) на декартовой системе.
Следует отложить векторы
OA→=a→=ax,ay и OB→=b→=bx,by.
Тогда длина вектора AB→будет равна AB→=OB→-OA→=b→-a→=(bx-ax,by-ay).
Рассмотрим треугольник OAB.
AB2=OA2+OB2-2·OA·OB·cos(∠AOB) верно , исходя из теоремы косинусов.
По условию видно, что OA=a→, OB=b→, AB=b→-a→, ∠AOB=a→,b→^, значит, формулу нахождения угла между векторами запишем иначе
b→-a→2=a→2+b→2-2·a→·b→·cos(a→,b→^).
Тогда из первого определения следует, что b→-a→2=a→2+b→2-2·(a→,b→), значит (a→,b→)=12·(a→2+b→2-b→-a→2).
Применив формулу вычисления длины векторов, получим:
a→,b→=12·((a2x+ay2)2+(b2x+by2)2-((bx-ax)2+(by-ay)2)2)==12·(a2x+a2y+b2x+b2y-(bx-ax)2-(by-ay)2)==ax·bx+ay·by
Докажем равенства:
(a→,b→)=a→·b→·cos(a→,b→^)==ax·bx+ay·by+az·bz
– соответственно для векторов трехмерного пространства.
Скалярное произведение векторов с координатами говорит о том, что скалярный квадрат вектора равен сумме квадратов его координат в пространстве и на плоскости соответственно. a→=(ax,ay,az), b→=(bx,by,bz) и (a→,a→)=ax2+ay2.
Скалярное произведение и его свойства
Существуют свойства скалярного произведения, которые применимы для a→,b→ и c→:
- коммутативность (a→,b→)=(b→,a→);
- дистрибутивность(a→+b→,c→)=(a→,c→)+(b→,c→), (a→+b→,c→)=(a→,b→)+(a→,c→);
- сочетательное свойство (λ·a→,b→)=λ·(a→,b→),(a→,λ·b→)=λ·(a→,b→), λ – любое число;
- скалярный квадрат всегда больше нуля (a→,a→)≥0, где (a→,a→)=0 в том случае, когда a→ нулевой.
Свойства объяснимы благодаря определению скалярного произведения на плоскости и свойствам при сложении и умножении действительных чисел.
Доказать свойство коммутативности (a→,b→)=(b→,a→). Из определения имеем, что (a→,b→)=ay·by+ay·by и (b→,a→)=bx·ax+by·ay.
По свойству коммутативности равенства ax·bx=bx·ax и ay·by=by·ay верны, значит ax·bx+ay·by=bx·ax+by·ay.
Отсюда следует, что (a→,b→)=(b→,a→). Что и требовалось доказать.
Дистрибутивность справедлива для любых чисел:
(a(1)→+a(2)→+…+a(n)→,b→)=(a(1)→,b→)+(a(2)→,b→)+…+(a(n)→,b→)
и (a→,b(1)→+b(2)→+…+b(n)→)=(a→,b(1)→)+(a→,b(2)→)+…+(a→,b→(n)),
отсюда имеем
(a(1)→+a(2)→+…+a(n)→,b(1)→+b(2)→+…+b(m)→)==(a(1)→,b(1)→)+(a(1)→,b(2)→)+…+(a(1)→,b(m)→)++(a(2)→,b(1)→)+(a(2)→,b(2)→)+…+(a(2)→,b(m)→)+…++(a(n)→,b(1)→)+(a(n)→,b(2)→)+…+(a(n)→,b(m)→)
Скалярное произведение с примерами и решениями
Любая задача такого плана решается с применением свойств и формул, касающихся скалярного произведения:
- (a→,b→)=a→·b→·cos(a→,b→^);
- (a→,b→)=a→·npa→b→=b→·npb→a→;
- (a→,b→)=ax·bx+ay·by или (a→,b→)=ax·bx+ay·by+az·bz;
- (a→,a→)=a→2.
Рассмотрим некоторые примеры решения.
Длина a→ равна 3, длина b→ равна 7. Найти скалярное произведение, если угол имеет 60 градусов.
Решение
По условию имеем все данные, поэтому вычисляем по формуле:
(a→,b→)=a→·b→·cos(a→,b→^)=3·7·cos60°=3·7·12=212
Ответ:(a→,b→)=212.
Заданны векторы a→=(1,-1,2-3), b→=(0,2,2+3). Чему равно скалярной произведение.
Решение
В данном примере рассматривается формула вычисления по координатам, так как они заданы в условии задачи:
(a→,b→)=ax·bx+ay·by+az·bz==1·0+(-1)·2+(2+3)·(2+3)==0-2+(2-9)=-9
Ответ: (a→,b→)=-9
Найти скалярное произведение AB→ и AC→. На координатной плоскости заданы точки A(1,-3), B(5,4), C(1,1).
Решение
Для начала вычисляются координаты векторов, так как по условию даны координаты точек:
AB→=(5-1,4-(-3))=(4,7)AC→=(1-1,1-(-3))=(0,4)
Подставив в формулу с использованием координат, получим:
(AB→,AC→)=4·0+7·4=0+28=28.
Ответ: (AB→,AC→)=28.
Заданы векторы a→=7·m→+3·n→ и b→=5·m→+8·n→, найти их произведение.m→ равен 3 и n→ равен 2 единицам, они перпендикулярные.
Решение
(a→,b→)=(7·m→+3·n→, 5·m→+8·n→). Применив свойство дистрибутивности, получим:
(7·m→+3·n→, 5·m→+8·n→)==(7·m→, 5·m→)+(7·m→, 8·n→)+(3·n→, 5·m→)+(3·n→, 8·n→)
Выносим коэффициент за знак произведения и получим:
(7·m→, 5·m→)+(7·m→, 8·n→)+(3·n→, 5·m→)+(3·n→, 8·n→)==7·5·(m→,m→)+7·8·(m→,n→)+3·5·(n→,m→)+3·8·(n→,n→)==35·(m→,m→)+56·(m→,n→)+15·(n→,m→)+24·(n→,n→)
По свойству коммутативности преобразуем:
35·(m→,m→)+56·(m→,n→)+15·(n→,m→)+24·(n→,n→)==35·(m→,m→)+56·(m→,n→)+15·(m→,n→)+24·(n→,n→)==35·(m→,m→)+71·(m→,n→)+24·(n→,n→)
В итоге получим:
(a→,b→)=35·(m→,m→)+71·(m→,n→)+24·(n→,n→).
Теперь применим формулу для скалярного произведения с заданным по условию углом:
(a→,b→)=35·(m→,m→)+71·(m→,n→)+24·(n→,n→)==35·m→2+71·m→·n→·cos(m→,n→^)+24·n→2==35·32+71·3·2·cosπ2+24·22=411.
Ответ: (a→,b→)=411
Если имеется числовая проекция.
Найти скалярное произведение a→и b→. Вектор a→ имеет координаты a→=(9,3,-3), проекция b→ с координатами (-3,-1,1).
Решение
По условию векторы a→ и проекция b→ противоположно направленные, потому что a→=-13·npa→b→→, значит проекция b→ соответствует длине npa→b→→, при чем со знаком «-»:
npa→b→→=-npa→b→→=-(-3)2+(-1)2+12=-11,
Подставив в формулу, получим выражение:
(a→,b→)=a→·npa→b→→=92+32+(-3)2·(-11)=-33.
Ответ: (a→,b→)=-33.
Задачи при известном скалярном произведении, где необходимо отыскать длину вектора или числовую проекцию.
Какое значение должна принять λ при заданном скалярном произведении a→=(1,0,λ+1) и b→=(λ,1,λ) будет равным -1.
Решение
Из формулы видно, что необходимо найти сумму произведений координат:
(a→,b→)=1·λ+0·1+(λ+1)·λ=λ2+2·λ.
В дано имеем (a→,b→)=-1.
Чтобы найти λ, вычисляем уравнение:
λ2+2·λ=-1, отсюда λ=-1.
Ответ: λ=-1.
Физический смысл скалярного произведения
Механика рассматривает приложение скалярного произведения.
При работе А с постоянной силой F→ перемещаемое тело из точки M в N можно найти произведение длин векторов F→ и MN→ с косинусом угла между ними, значит работа равна произведению векторов силы и перемещения:
A=(F→,MN→).
Перемещение материальной точки на 3 метра под действием силы равной 5 ньтонов направлено под углом 45 градусов относительно оси. Найти A.
Решение
Так как работа – это произведение вектора силы на перемещение, значит, исходя из условия F→=5, S→=3, (F→,S→^)=45°, получим A=(F→,S→)=F→·S→·cos(F→,S→^)=5·3·cos(45°)=1522.
Ответ: A=1522.
Материальная точка, перемещаясь из M(2,-1,-3) в N(5,3λ-2,4) под силой F→=(3,1,2), совершила работа равную 13 Дж. Вычислить длину перемещения.
Решение
При заданных координатах вектора MN→ имеем MN→=(5-2, 3λ-2-(-1), 4-(-3))=(3, 3λ-1,7).
По формуле нахождения работы с векторами F→=(3,1,2) и MN→=(3, 3λ-1,7) получим A=(F⇒, MN→)=3·3+1·(3λ-1)+2·7=22+3λ.
По условию дано, что A=13Дж, значит 22+3λ=13. Отсюда следует λ=-3, значит и MN→=(3,3λ-1,7)=(3,-10,7).
Чтобы найти длину перемещения MN→ , применим формулу и подставим значения:
MN→=32+(-10)2+72=158.
Ответ: 158.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Определение скалярного произведения:
Скалярным произведением двух ненулевых векторов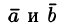 
называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначается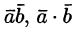 
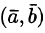
(или 
). Итак, по определению,
где 
Формуле (6.1) можно придать иной вид. Так как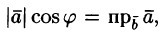 
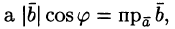
(см. рис. 14), 
то получаем:
т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.
Свойства скалярного произведения
1.Скалярное произведение обладает переместительным свойством: 
И так как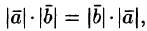 
как произведение чисел и 
2.Скалярное произведение обладает сочетательным свойством относительно скалярного множителя: 
3.Скалярное произведение обладает распределительным свойством: 
4.Скалярный квадрат вектора равен квадрату его длины: 
В частности: 
Если вектор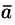 
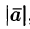
возвести скалярно в квадрат и затем извлечь корень, то получим не первоначальный вектор, а его модуль 
, т. е. 
Пример:
Найти длину вектора
Решение:
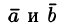
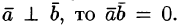
5.Если векторы (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если 
Справедливо и обратное утверждение: если 
Так как
Следовательно,
Отсюда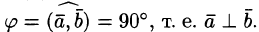 
В частности:
Выражение скалярного произведения через координаты
Пусть заданы два вектора
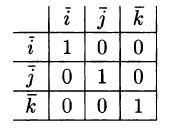
Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов i, j, k:
т. e.
Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.
Пример:
Доказать, что диагонали четырехугольника, заданного координатами вершин A(-4;- 4; 4), В(-3;2;2), С(2;5;1), D(3; -2; 2), взаимно перпендикулярны.
Решение:
Составим вектора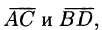 
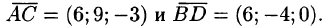
лежащие на диагоналях данного четырехугольника. Имеем: 
Найдем скалярное произведение этих векторов:
Отсюда следует, что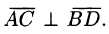 
Диагонали четырехугольника ABCD взаимно перпендикулярны.
Некоторые приложения скалярного произведения
Угол между векторами
Определение угла (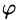
между ненулевыми векторами 
Отсюда следует условие перпендикулярности ненулевых векторов
Проекция вектора на заданное направление
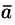
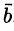
Нахождение проекции вектора на направление, заданное вектором 
, может осуществляться по формуле
Работа постоянной силы
Пусть материальная точка перемещается прямолинейно из положения А в положение В под действием постоянной силы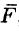 
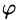
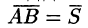
, образующей угол с перемещением 
(см. рис. 15).
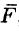
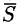
Из физики известно, что работа силы при перемещении 
равна
Таким образом, работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения.
Пример:
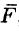
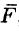
Вычислить работу, произведенную силой =(3; 2; 4), если точка ее приложения перемещается прямолинейно из положения A(2; 4; 6) в положение В (4; 2; 7). Под каким углом к АВ направлена сила ?
Решение: Находим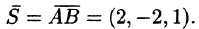 
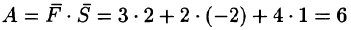
Стало быть,
(ед. работы).
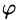
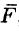
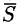
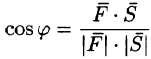
Угол между и находим по формуле 
т. е.
Скалярное произведение векторов
Смотрите также:
Предмет высшая математика
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
План урока:
Угол между векторами
Понятие скалярного произведения векторов
Скалярное произведение в координатах
Определение перпендикулярности векторов и прямых
Вычисление угла между векторами
Свойства скалярного произведения
Угол между векторами
Любую пару векторов можно отложить от одной точки. Если при этом вектора не сонаправлены друг с другом, то они образуют некоторый угол. Его и именуют углом между векторами.
Если же пара векторов сонаправлена, то принято считать, что угол между такими векторами составляет 0°.
На рисунке показаны два вектора, a и b. Чтобы определить угол между a и b, надо отложить их от одной и той же точки:
В приведенном примере угол составил 135°. Для обозначения этого угла может быть использована такая запись:
Задание. В квадрате АВСD проведены диагонали, они пересекаются в точке О. Определите, какой угол образуют вектора:
Так как в квадрате диагонали пересекаются под углом 90°, а со сторонами образуют угол 45°, то мы легко определим, что
Здесь нам помог тот факт, что вектора из пунктов а) и б) изначально отложены из одной точки. С пунктом в) ситуация сложнее. Надо отложить от точки А вектор ОА и определить угол, образующийся при этом:
Пусть после откладывания вектора ОА от А получился вектора АА’. Нам надо найти ∠ВАА’. Нам уже известен ∠ОАВ, который является смежным с ∠ВАА’, поэтому можно записать равенство:
Ответ: а) 45°; б) 90°; в) 135°.
Понятие скалярного произведения векторов
Большое распространение в науке получила математическая операция, именуемая скалярным произведением векторов. В геометрии оно помогает находить угол между векторами, а в физике вычислять некоторые физические величины. В рамках школьной программы его используют для нахождения работы, совершенной той или иной силой. В рамках же более сложных дисциплин, с которыми мало кто сталкивается, оно применяется в квантовой механике и специальных разделах математики – тензорной алгебре, теории многообразий и т. п. Ввел его в науку Уильям Гамильтон в 1846 г, который разрабатывал теорию особых чисел – кватерионов. Они, кстати, используются компьютерами для расчетов трехмерной графики в играх и других приложениях.
Прежде, чем мы научимся применять на практике скалярное произведение, сначала сформулируем правило, позволяющее вычислить его.
Например, пусть есть вектора a и b, причем даны их длины:
Угол между a и b тоже известен и составляет 60°, это записывается таким образом:
Задание. Вычислите скалярное произведение векторов d и f, если их длины составляют 6 и 10 соответственно, а угол между векторами равен 45°.
Решение. Просто подставляем числа из условия в формулу:
Задание. АВС – равносторонний треугольник со стороной 4. Каково скалярное произведение векторов АВ и АС?
Решение. Все углы в равностороннем треугольнике равны 60°, поэтому и угол между АВ и АС также составляет 60°.
Ответ: 8.
Напомним, что косинус, взятый от острого угла – это положительная величина, а косинус тупого угла – это отрицательное число. У прямого же угла косинус равен нулю. Это означает, что по знаку скалярного произведения можно определить тип угла между векторами.
Часто скалярное произведение применяется в физике. Например, с его помощью рассчитывается работа, совершаемая силой при перемещении того или иного тела. И сила, и перемещение – это векторные величины. Чтобы найти работу силы, надо скалярно перемножить вектора силы и перемещения:
Эта формула отражает физический смысл скалярного произведения.
Задание. Под воздействием силы 10Н тело переместилось в горизонтальном направлении на 3 метра. При этом сила образует угол 60° с направлением перемещения тела. Какую работу совершила сила?
Решение.
Скалярное произведение в координатах
Оказывается, что для перемножения векторов достаточно знать только их координаты.
Докажем эту формулу. Сначала рассмотрим случай, когда один из перемножаемых векторов, например a, является нулевым. Тогда у него нулевая длина и нулевые координаты:
Теперь рассмотрим случай, когда оба перемножаемых вектора ненулевые. Тогда отложим их от некоторой точки О и, если вектора неколлинеарны, то мы получим ∆ОАВ:
Для частных случаев, когда a и b коллинеарны (то есть либо сонаправлены, либо противоположно направлены), эта формула также справедлива. Если aи b сонаправлены, то угол α принимается равным нулю (и cosα = 1):
Если же a и b направлены противоположно, то α = 180° (и cosα = – 1):
Итак, мы убедились, что в любой ситуации формула (1) справедлива. При этом вектор АВ можно представить как разность a и b:
Если вектор а имеет координаты {x1; у1}, а координаты b– это {x2; у2},то координаты их разности a – b будут записываться в виде {х1 – х2;у1 – у2}. С учетом этого (2) примет вид
В результате нам удалось доказать формулу скалярного произведения через координаты:
Задание. Перемножьте скалярно вектораa и b, если определены их координаты:
Ответ: а) 23; б) 0; в) 5.
Определение перпендикулярности векторов и прямых
Напомним, что скалярное произведение оказывается нулевым исключительно в случае перпендикулярности векторов. Это позволяет использовать его для проверки перпендикулярности векторов.
Задание. Проверьте, являются ли перпендикулярными вектора:
Решение. В каждом случае мы должны скалярно перемножить пару векторов. Если результат окажется нулевым, то можно сделать вывод о перпендикулярности векторов. В противном случае они не перпендикулярны. Первый вектор будет обозначать буквой а, а второй – буквой b:
Ответ: а) да; б) нет; в) да; г) нет.
Задание. При каком значении переменной х вектора а{4; 5} и b{x; – 6} окажутся перпендикулярными?
Решение. Перемножим скалярно вектора и получим некоторое выражение с переменной x:
Найдем, при каком х это выражение обращается в нуль, то есть вектора становятся перпендикулярными:
Задание. Определите, перпендикулярны ли прямые АВ и CD, если даны координаты точек: А(3; 8), В(4; 10), С(7;12) и D(5;13).
Решение. В этой задаче сначала надорассчитать координаты векторов АВ и CD по координатамих начальной и конечной точки:
Мы вычислили координаты векторов: АВ{1; 2} и CD{– 2; 1}. Теперь мы можем проверить их перпендикулярность, скалярно перемножив вектора:
Мы получили ноль. Это означает, что АВ и CD – перпендикулярные вектора. Значит, и прямые, на которых они лежат, также перпендикулярны.
Ответ: перпендикулярны.
Задание. Перпендикулярны ли друг другу прямые, задаваемые уравнениями
Названия точкам в данном примере присвоены произвольно. На следующем шаге по координатам точек мы находим координаты векторов, лежащих на исследуемых прямых:
Полученный ноль показывает, что исходные прямые перпендикулярны.
Ответ: перпендикулярны.
В случае, когда прямые заданы уравнениями, необязательно проделывать столь длительные вычисления для определения их перпендикулярности. Есть теорема, сокращающая объем вычислений.
Докажем это утверждение. Пусть две прямые заданы уравнениями
Найдем какие-нибудь точки этих прямых. Для этого подставим в уравнения значения х = 0 и х = 1:
Прямые окажутся перпендикулярными исключительно в том случае, если это выражение будет нулевым. Это условие перпендикулярности можно записать как уравнение:
В результате мы получили доказываемую нами формулу.
Задание. Проверьте, какие из этих пар прямых перпендикулярны:
Решение. В каждом случае надо просто перемножить угловые коэффициенты прямых, то есть числа, стоящие перед переменной х. Другие числа в этих уравнениях (свободные коэффициенты) никак не влияют на перпендикулярность. Если вычисленное произведение окажется равным (– 1), то из этого будет вытекать перпендикулярность прямых.
Вычисление угла между векторами
Мы научились по координатам векторов определять, перпендикулярны ли они. Однако в более общем случае можно рассчитать угол и между двумя неперпендикулярными векторами.
В самом деле, по известным координатам векторов легко как рассчитать длину каждого из них, так и скалярно перемножить вектора. Тогда из формулы скалярного произведения можно выразить значение косинуса угла между векторами:
Зная же косинус, можно рассчитать и сам угол, используя специальные таблицы либо функцию арккосинуса на калькуляторе.
Задание. Вычислите угол между векторами а{3; 4} и b{8; 15}.
Решение. Сначала рассчитываем длины векторов:
Задание. Точки А(2; 8), В(– 1; 5) и С(3; 1) соединили отрезками и получили ∆АВС. Вычислите угол ∠А в ∆АВС.
Решение.∠А данного треугольника представляет собой угол между двумя векторами АВ и АС. Вычислим координаты этих векторов:
Осталось лишь с помощью калькулятора найти сам ∠А:
Свойства скалярного произведения
Существует несколько важных свойств скалярного произведения. Эти свойства очень схожи с законами алгебры, которые используются при работе с обычными числами.
Переместительный закон легко доказать, опираясь только на определение операции скалярного произведения:
Задание. Известно, что угол между векторами a и с составлет 60°, так же как и угол между векторами b и с. Определены и длины векторов:
Задание. Найдите скалярное произведение векторов p и q, если
Решение. Сначала надо перемножить вектора и раскрыть при этом скобки также, как они раскрываются при перемножении обычных чисел:
Примечание. Иногда скалярное произведение вектора на самого себя именуют скалярным квадратом.
Тогда выражение (1) примет вид:
В сегодняшнем уроке мы узнали, что такое скалярное произведение. Оно имеет много приложений в физике и других науках, в частности, с его помощью вычисляется работа. В геометрии оно помогает вычислять углы между векторами, а значит, и между прямыми. В будущем, при более углубленном изучении геометрии, вы узнаете о существовании других типов произведений векторов – векторном и смешанном.
