Как найти скалярный квадрат вектора по координатам

Как найти скалярный квадрат вектора по координатам

Определение 1

Скалярное произведение векторов называют число, равное произведению дин этих векторов на косинус угла между ними.

Обозначение произведения векторов a→ и b→ имеет вид a→,b→. Преобразуем в формулу:

a→,b→=a→·b→·cosa→,b→^. a→ и b→ обозначают длины векторов, a→,b→^ – обозначение угла между заданными векторами. Если хоть один вектор нулевой, то есть имеет значение 0, то и результат будет равен нулю, a→,b→=0

При умножении вектора самого на себя, получим квадрат его дины:

a→,b→=a→·b→·cosa→,a→^=a→2·cos0=a→2

Определение 2

Скалярное умножение вектора самого на себя называют скалярным квадратом.

Вычисляется по формуле:

a→,b→=a→·b→·cosa→,b→^.

Запись a→,b→=a→·b→·cosa→,b→^=a→·npa→b→=b→·npb→a→ показывает, что npb→a→ – это числовая проекция a→ на b→, npa→a→- проекция b→ на a→ соостветсвенно.

Сформулируем определение произведения для двух векторов:

Скалярное произведение двух векторов a→ на b→ называют произведение длины вектора a→ на проекцию b→ на направление a→ или произведение длины b→ на проекцию a→ соответственно.

Скалярное произведение в координатах

Вычисление скалярного произведения можно производить через координаты векторов в заданной плоскости или в пространстве.

Скаларное произведение двух векторов на плоскости, в трехмерном простарнстве называют сумму координат заданных векторов a→ и b→.

При вычислении на плоскости скаларного произведения заданных векторов a→=(ax,ay), b→=(bx,by) в декартовой системе используют:

a→,b→=ax·bx+ay·by,

для трехмерного пространства применимо выражение:

a→,b→=ax·bx+ay·by+az·bz.

Фактически это является третьим определением скалярного произведения.

Докажем это.

Доказательство 1

Для доказательства используем a→,b→=a→·b→·cosa→,b→^=ax·bx+ay·by для векторов a→=(ax,ay), b→=(bx,by) на декартовой системе.

Следует отложить векторы

OA→=a→=ax,ay и OB→=b→=bx,by.

Тогда длина вектора AB→будет равна AB→=OB→-OA→=b→-a→=(bx-ax,by-ay).

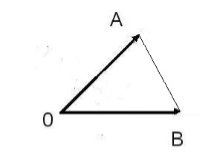
Рассмотрим треугольник OAB.

AB2=OA2+OB2-2·OA·OB·cos(∠AOB) верно , исходя из теоремы косинусов.

По условию видно, что OA=a→, OB=b→, AB=b→-a→, ∠AOB=a→,b→^, значит, формулу нахождения угла между векторами запишем иначе

b→-a→2=a→2+b→2-2·a→·b→·cos(a→,b→^).

Тогда из первого определения следует, что b→-a→2=a→2+b→2-2·(a→,b→), значит (a→,b→)=12·(a→2+b→2-b→-a→2).

Применив формулу вычисления длины векторов, получим:
a→,b→=12·((a2x+ay2)2+(b2x+by2)2-((bx-ax)2+(by-ay)2)2)==12·(a2x+a2y+b2x+b2y-(bx-ax)2-(by-ay)2)==ax·bx+ay·by

Докажем равенства:

(a→,b→)=a→·b→·cos(a→,b→^)==ax·bx+ay·by+az·bz

– соответственно для векторов трехмерного пространства.

Скалярное произведение векторов с координатами говорит о том, что скалярный квадрат вектора равен сумме квадратов его координат в пространстве и на плоскости соответственно. a→=(ax,ay,az), b→=(bx,by,bz) и (a→,a→)=ax2+ay2.

Скалярное произведение и его свойства

Существуют свойства скалярного произведения, которые применимы для a→,b→ и c→:

  1. коммутативность (a→,b→)=(b→,a→);
  2. дистрибутивность(a→+b→,c→)=(a→,c→)+(b→,c→), (a→+b→,c→)=(a→,b→)+(a→,c→);
  3. сочетательное свойство (λ·a→,b→)=λ·(a→,b→),(a→,λ·b→)=λ·(a→,b→), λ – любое число;
  4. скалярный квадрат всегда больше нуля (a→,a→)≥0, где (a→,a→)=0 в том случае, когда a→ нулевой.
Пример 1

Свойства объяснимы благодаря определению скалярного произведения на плоскости и свойствам при сложении и умножении действительных чисел.

Доказать свойство коммутативности (a→,b→)=(b→,a→). Из определения имеем, что (a→,b→)=ay·by+ay·by и (b→,a→)=bx·ax+by·ay.

По свойству коммутативности равенства ax·bx=bx·ax и ay·by=by·ay верны, значит ax·bx+ay·by=bx·ax+by·ay.

Отсюда следует, что (a→,b→)=(b→,a→). Что и требовалось доказать.

Дистрибутивность справедлива для любых чисел:

(a(1)→+a(2)→+…+a(n)→,b→)=(a(1)→,b→)+(a(2)→,b→)+…+(a(n)→,b→)

и (a→,b(1)→+b(2)→+…+b(n)→)=(a→,b(1)→)+(a→,b(2)→)+…+(a→,b→(n)),

отсюда имеем

(a(1)→+a(2)→+…+a(n)→,b(1)→+b(2)→+…+b(m)→)==(a(1)→,b(1)→)+(a(1)→,b(2)→)+…+(a(1)→,b(m)→)++(a(2)→,b(1)→)+(a(2)→,b(2)→)+…+(a(2)→,b(m)→)+…++(a(n)→,b(1)→)+(a(n)→,b(2)→)+…+(a(n)→,b(m)→)

Скалярное произведение с примерами и решениями

Любая задача такого плана решается с применением свойств и формул, касающихся скалярного произведения:

  1. (a→,b→)=a→·b→·cos(a→,b→^);
  2. (a→,b→)=a→·npa→b→=b→·npb→a→;
  3. (a→,b→)=ax·bx+ay·by или (a→,b→)=ax·bx+ay·by+az·bz;
  4. (a→,a→)=a→2.

Рассмотрим некоторые примеры решения.

Пример 2

Длина a→ равна 3, длина b→ равна 7. Найти скалярное произведение, если угол имеет 60 градусов.

Решение

По условию имеем все данные, поэтому вычисляем по формуле:

(a→,b→)=a→·b→·cos(a→,b→^)=3·7·cos60°=3·7·12=212

Ответ:(a→,b→)=212.

Пример 3

Заданны векторы a→=(1,-1,2-3), b→=(0,2,2+3). Чему равно скалярной произведение.

Решение

В данном примере рассматривается формула вычисления по координатам, так как они заданы в условии задачи:

(a→,b→)=ax·bx+ay·by+az·bz==1·0+(-1)·2+(2+3)·(2+3)==0-2+(2-9)=-9

Ответ: (a→,b→)=-9

Пример 4

Найти скалярное произведение AB→ и AC→. На координатной плоскости заданы точки A(1,-3), B(5,4), C(1,1).

Решение

Для начала вычисляются координаты векторов, так как по условию даны координаты точек:

AB→=(5-1,4-(-3))=(4,7)AC→=(1-1,1-(-3))=(0,4)

Подставив в формулу с использованием координат, получим:

(AB→,AC→)=4·0+7·4=0+28=28.

Ответ: (AB→,AC→)=28.

Пример 5

Заданы векторы a→=7·m→+3·n→ и b→=5·m→+8·n→, найти их произведение.m→ равен 3 и n→ равен 2 единицам, они перпендикулярные.

Решение

(a→,b→)=(7·m→+3·n→, 5·m→+8·n→). Применив свойство дистрибутивности, получим:

(7·m→+3·n→, 5·m→+8·n→)==(7·m→, 5·m→)+(7·m→, 8·n→)+(3·n→, 5·m→)+(3·n→, 8·n→)

Выносим коэффициент за знак произведения и получим:

(7·m→, 5·m→)+(7·m→, 8·n→)+(3·n→, 5·m→)+(3·n→, 8·n→)==7·5·(m→,m→)+7·8·(m→,n→)+3·5·(n→,m→)+3·8·(n→,n→)==35·(m→,m→)+56·(m→,n→)+15·(n→,m→)+24·(n→,n→)

По свойству коммутативности преобразуем:

35·(m→,m→)+56·(m→,n→)+15·(n→,m→)+24·(n→,n→)==35·(m→,m→)+56·(m→,n→)+15·(m→,n→)+24·(n→,n→)==35·(m→,m→)+71·(m→,n→)+24·(n→,n→)

В итоге получим:

(a→,b→)=35·(m→,m→)+71·(m→,n→)+24·(n→,n→).

Теперь применим формулу для скалярного произведения с заданным по условию углом:

(a→,b→)=35·(m→,m→)+71·(m→,n→)+24·(n→,n→)==35·m→2+71·m→·n→·cos(m→,n→^)+24·n→2==35·32+71·3·2·cosπ2+24·22=411.

Ответ: (a→,b→)=411

Если имеется числовая проекция.

Пример 6

Найти скалярное произведение a→и b→. Вектор a→ имеет координаты a→=(9,3,-3), проекция b→ с координатами (-3,-1,1).

Решение

По условию векторы a→ и проекция b→ противоположно направленные, потому что a→=-13·npa→b→→, значит проекция b→ соответствует длине npa→b→→, при чем со знаком «-»:

npa→b→→=-npa→b→→=-(-3)2+(-1)2+12=-11,

Подставив в формулу, получим выражение:

(a→,b→)=a→·npa→b→→=92+32+(-3)2·(-11)=-33.

Ответ: (a→,b→)=-33.

Задачи при известном скалярном произведении, где необходимо отыскать длину вектора или числовую проекцию.

Пример 7

Какое значение должна принять λ при заданном скалярном произведении a→=(1,0,λ+1) и b→=(λ,1,λ) будет равным -1.

Решение

Из формулы видно, что необходимо найти сумму произведений координат:

(a→,b→)=1·λ+0·1+(λ+1)·λ=λ2+2·λ.

В дано имеем (a→,b→)=-1.

Чтобы найти λ, вычисляем уравнение:

λ2+2·λ=-1, отсюда λ=-1.

Ответ: λ=-1.

Физический смысл скалярного произведения

Механика рассматривает приложение скалярного произведения.

При работе А с постоянной силой F→ перемещаемое тело из точки M в N можно найти произведение длин векторов F→ и MN→ с косинусом угла между ними, значит работа равна произведению векторов силы и перемещения:

A=(F→,MN→).

Пример 8

Перемещение материальной точки на 3 метра под действием силы равной 5 ньтонов направлено под углом 45 градусов относительно оси. Найти A.

Решение

Так как работа – это произведение вектора силы на перемещение, значит, исходя из условия F→=5, S→=3, (F→,S→^)=45°, получим A=(F→,S→)=F→·S→·cos(F→,S→^)=5·3·cos(45°)=1522.

Ответ: A=1522.

Пример 9

Материальная точка, перемещаясь из M(2,-1,-3) в N(5,3λ-2,4) под силой F→=(3,1,2), совершила работа равную 13 Дж. Вычислить длину перемещения.

Решение

При заданных координатах вектора MN→ имеем MN→=(5-2, 3λ-2-(-1), 4-(-3))=(3, 3λ-1,7).

По формуле нахождения работы с векторами F→=(3,1,2) и MN→=(3, 3λ-1,7) получим A=(F⇒, MN→)=3·3+1·(3λ-1)+2·7=22+3λ.

По условию дано, что A=13Дж, значит 22+3λ=13. Отсюда следует λ=-3, значит и MN→=(3,3λ-1,7)=(3,-10,7).

Чтобы найти длину перемещения MN→ , применим формулу и подставим значения:

MN→=32+(-10)2+72=158.

Ответ: 158.

Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Скалярное произведение векторов {displaystyle (mathbf {a} ,mathbf {b} )} равно произведению {displaystyle |mathbf {a} ||mathbf {b} |cos(theta )}

Скаля́рное произведе́ние (иногда называемое внутренним произведением) — результат операции над двумя векторами, являющийся скаляром, то есть числом, не зависящим от выбора системы координат.
Используется в определении длины векторов и угла между ними.

Обычно для скалярного произведения векторов mathbf {a} и mathbf {b} используется одно из следующих обозначений.

{displaystyle (mathbf {a} ,mathbf {b} )}
{displaystyle mathbf {a} cdot mathbf {b} , {vec {a}}cdot {vec {b}}} или просто {displaystyle mathbf {a} mathbf {b} }
langle mathbf {a} ,mathbf {b} rangle и {displaystyle langle a|brangle ;} второе обозначение применяется в квантовой механике для векторов состояния[1].

В простейшем случае, а именно в случае конечномерного вещественного евклидового пространства, иногда используют «геометрическое» определение скалярного произведения ненулевых векторов mathbf {a} и mathbf {b} как произведения длин этих векторов на косинус угла между ними[2]:

{displaystyle (mathbf {a} ,mathbf {b} )=|mathbf {a} ||mathbf {b} |cos(theta ).}

Равносильное определение: скалярное произведение есть произведение длины проекции первого вектора на второй и длины второго вектора (см. рисунок). Если хотя бы один из векторов нулевой, то произведение считается равным нулю[3].

У понятия скалярного произведения существует также большое количество обобщений для различных векторных пространств, то есть для множеств векторов с операциями сложения и умножения на скаляры[⇨]. Данное выше геометрическое определение скалярного произведения предполагает предварительное определение понятий длины вектора и угла между ними. В современной математике используется обратный подход: аксиоматически определяется скалярное произведение, а уже через него — длины и углы[4]. В частности, скалярное произведение определяется для комплексных векторов, многомерных и бесконечномерных пространств, в тензорной алгебре.

Скалярное произведение и его обобщения играют чрезвычайно большую роль в векторной алгебре, теории многообразий, механике и физике. Например, работа силы при механическом перемещении равна скалярному произведению вектора силы на вектор перемещения[5].

Определение и свойства[править | править код]

Будем говорить, что в вещественном или комплексном векторном пространстве L определено скалярное произведение, если каждой паре векторов {displaystyle mathbf {a} ,mathbf {b} } из L поставлено в соответствие число {displaystyle (mathbf {a} ,mathbf {b} )} из того числового поля, над которым задано {displaystyle L,} удовлетворяющее следующим аксиомам.

  1. Для любых трёх элементов {displaystyle mathbf {a} _{1},mathbf {a} _{2},mathbf {b} } пространства mathbb {L} и любых чисел alpha ,beta справедливо равенство: {displaystyle (alpha mathbf {a} _{1}+beta mathbf {a} _{2},mathbf {b} )=alpha (mathbf {a} _{1},mathbf {b} )+beta (mathbf {a} _{2},mathbf {b} )} (линейность скалярного произведения по первому аргументу).
  2. Для любых {displaystyle mathbf {a} ,mathbf {b} } справедливо равенство {displaystyle (mathbf {a} ,mathbf {b} )={overline {(mathbf {b} ,mathbf {a} )}}}, где черта означает комплексное сопряжение.
  3. Для любого {displaystyle mathbf {a} } имеем: {displaystyle (mathbf {a} ,mathbf {a} )geqslant 0}, причём {displaystyle (mathbf {a} ,mathbf {a} )=0} только при {displaystyle mathbf {a} =0} (положительная определённость и невырожденность скалярного произведения соответственно).

Заметим, что из аксиомы 2 следует, что {displaystyle (mathbf {a} ,mathbf {a} )} — вещественное число. Поэтому аксиома 3 имеет смысл, несмотря на комплексные (в общем случае) значения скалярного произведения. Если аксиома 3 не выполняется, то произведение называется индефинитным или неопределённым.

Если {displaystyle (mathbf {a} ,mathbf {a} )=0} не только при {displaystyle mathbf {a} =0}, то произведение называется квазискалярным[6].

Из данных аксиом получаются следующие свойства:

  1. коммутативность для вещественных векторов: {displaystyle (mathbf {a} ,mathbf {b} )=(mathbf {b} ,mathbf {a} );}

    Дистрибутивность скалярного произведения в случае вещественного евклидового пространства

  2. дистрибутивность относительно сложения: {displaystyle (mathbf {a} +mathbf {b} ,mathbf {c} )=(mathbf {a} ,mathbf {c} )+(mathbf {b} ,mathbf {c} )} и {displaystyle (mathbf {c} ,mathbf {a} +mathbf {b} )=(mathbf {c} ,mathbf {a} )+(mathbf {c} ,mathbf {b} );}
  3. инволюционная линейность относительно второго аргумента: {displaystyle (mathbf {a} ,(alpha _{1}mathbf {b} _{1}+alpha _{2}mathbf {b} _{2}))={overline {alpha _{1}}}(mathbf {a} ,mathbf {b} _{1})+{overline {alpha _{2}}}(mathbf {a} ,mathbf {b} _{2});} (в случае вещественного L — просто линейность по второму аргументу).
  4. {displaystyle (alpha mathbf {a} ,beta mathbf {b} )=alpha {overline {beta }}(mathbf {a} ,mathbf {b} )} (что совпадает с {displaystyle alpha beta (mathbf {a} ,mathbf {b} )} для вещественного L).

Также есть свойства, связанные не с данными аксиомами:

  1. неассоциативность относительно умножения на вектор[7]‘: {displaystyle (mathbf {a} ,mathbf {b} )mathbf {c} neq mathbf {a} (mathbf {b} ,mathbf {c} )};
  2. ортогональность: два ненулевых вектора a и b ортогональны тогда и только тогда, когда (a, b) = 0 (определения ниже).

Замечание. В квантовой физике скалярное произведение (волновых функций, которые комплекснозначны) принято определять как линейное по второму аргументу (а не по первому), соответственно, по первому аргументу оно будет инволюционо линейным. Путаницы обычно не возникает, поскольку традиционное обозначение для скалярного произведения в квантовой физике также отличается: {displaystyle langle phi |psi rangle }, т.е. аргументы отделяются вертикальной чертой, а не запятой, и скобки всегда угловые.

Определение и свойства в евклидовом пространстве[править | править код]

Вещественные векторы[править | править код]

В n-мерном вещественном евклидовом пространстве векторы определяются своими координатами — наборами n вещественных чисел в ортонормированном базисе. Определить скалярное произведение векторов {displaystyle mathbf {a} =(a_{1},a_{2}dots a_{n}),mathbf {b} =(b_{1},b_{2}dots b_{n})} можно так[4]:

{displaystyle langle mathbf {a} ,mathbf {b} rangle =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}+dots +a_{n}b_{n}.}

Проверка показывает, что все три аксиомы выполнены.

Например, скалярное произведение векторов {displaystyle (1,3,-5)} и {displaystyle (4,-2,-1)} будет вычислено так:

{displaystyle {begin{aligned} (1,3,-5)cdot (4,-2,-1)&=1cdot 4+3cdot (-2)+(-5)cdot (-1)\&=4-6+5\&=3.end{aligned}}}

Можно доказать[8], что эта формула равносильна определению через проекции или через косинус: {displaystyle (mathbf {a} ,mathbf {b} )=|mathbf {a} ||mathbf {b} |cos(theta ).}

Комплексные векторы[править | править код]

Для комплексных векторов {displaystyle mathbf {a} =(a_{1},a_{2}dots a_{n}),mathbf {b} =(b_{1},b_{2}dots b_{n})} определим аналогично[9]:

{displaystyle langle mathbf {a} ,mathbf {b} rangle =sum _{k=1}^{n}a_{k}{overline {b_{k}}}=a_{1}{overline {b_{1}}}+a_{2}{overline {b_{2}}}+cdots +a_{n}{overline {b_{n}}}.}

Пример (для n=2): {displaystyle (1+i,2)cdot (2+i,i)=(1+i)cdot ({overline {2+i}})+2cdot {overline {i}}=(1+i)cdot (2-i)+2cdot (-i)=3-i.}

Свойства[править | править код]

Помимо общих свойств скалярного произведения, для многомерных евклидовых векторов верно следующее:

  1. в отличие от обычного умножения скаляров, где если ab = ac и a ≠ 0, то b равняется c, для скалярного умножения векторов это неверно: если a · b = a · c, то есть a · (b − c) = 0, то в общем случае a и b − c лишь ортогональны; но вектор b − c в общем случае не равен 0, то есть b ≠ c;
  2. правило произведения: для дифференцируемых вектор-функций a(t) и b(t) верно соотношение (a(t), b(t))′ = a′(t) ⋅ b(t) + a(t) ⋅ b′(t)[10];
  3. оценка угла между векторами:
    в формуле {displaystyle (mathbf {mathbf {a} } ,mathbf {b} )=|mathbf {a} |cdot |mathbf {b} |cdot cos angle {(mathbf {a} ,mathbf {b} )}} знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение больше 0, если угол между векторами острый, и меньше 0, если угол между векторами тупой;
  4. проекция вектора mathbf {a} на направление, определяемое единичным вектором mathbf {e} :
    {displaystyle a_{e}=(mathbf {a} ,mathbf {e} )=|mathbf {a} ||mathbf {e} |cos angle {(mathbf {a} ,mathbf {e} )}=|mathbf {a} |cos angle {(mathbf {a} ,mathbf {e} )}}, так как {displaystyle |mathbf {e} |=1;}
  5. площадь параллелограмма, натянутого на два вектора {displaystyle mathbf {a} } и {displaystyle mathbf {b} }, равна {displaystyle {sqrt {(mathbf {a} ,mathbf {a} )(mathbf {b} ,mathbf {b} )-(mathbf {a} ,mathbf {b} )^{2}}}.}

Теорема косинусов в вещественном пространстве[править | править код]

Dot product cosine rule.svg

Теорема косинусов легко выводится с использованием скалярного произведения. Пусть на сторонах треугольника находятся векторы a, b и c, первые два из которых образуют угол θ, как показано в изображении справа. Тогда, следуя свойствам и определению скалярного произведения через косинус:

{displaystyle {begin{aligned}mathbf {color {orange}c} cdot mathbf {color {orange}c} &=(mathbf {color {red}a} -mathbf {color {blue}b} )cdot (mathbf {color {red}a} -mathbf {color {blue}b} )\&=mathbf {color {red}a} cdot mathbf {color {red}a} -mathbf {color {red}a} cdot mathbf {color {blue}b} -mathbf {color {blue}b} cdot mathbf {color {red}a} +mathbf {color {blue}b} cdot mathbf {color {blue}b} \&=|mathbf {color {red}a} |^{2}-mathbf {color {red}a} cdot mathbf {color {blue}b} -mathbf {color {red}a} cdot mathbf {color {blue}b} +|mathbf {color {blue}b} |^{2}\&=|mathbf {color {red}a} |^{2}-2mathbf {color {red}a} cdot mathbf {color {blue}b} +|mathbf {color {blue}b} |^{2}\&=|mathbf {color {red}a} |^{2}+|mathbf {color {blue}b} |^{2}-2|mathbf {color {red}a} |{cdot }|mathbf {color {blue}b} |cos mathbf {color {purple}theta } .\end{aligned}}}

Связанные определения[править | править код]

В современном аксиоматическом подходе уже на основе понятия скалярного произведения векторов вводятся следующие производные понятия[11]:

Длина вектора, под которой обычно понимается его евклидова норма:

{displaystyle |mathbf {a} |={sqrt {(mathbf {a} ,mathbf {a} )}}}

(термин «длина» обычно применяется к конечномерным векторам, однако в случае вычисления длины криволинейного пути часто используется и в случае бесконечномерных пространств).

Углом varphi между двумя ненулевыми векторами евклидова пространства (в частности, евклидовой плоскости) называется число, косинус которого равен отношению скалярного произведения этих векторов к произведению их длин (норм):

{displaystyle cos varphi ={frac {(mathbf {a} ,mathbf {b} )}{|mathbf {a} ||mathbf {b} |}} (0leqslant varphi leqslant pi ).}

Данные определения позволяют сохранить формулу: {displaystyle (mathbf {a} ,mathbf {b} )=|mathbf {a} ||mathbf {b} |cos(varphi )} и в общем случае. Корректность формулы для косинуса гарантирует неравенство Коши — Буняковского[12]:

Для любых элементов {displaystyle mathbf {a} ,mathbf {b} } векторного пространства со скалярным произведением выполняется неравенство:

{displaystyle vert (mathbf {a} ,mathbf {b} )vert ^{2}leqslant (mathbf {a} ,mathbf {a} )(mathbf {b} ,mathbf {b} )}

В случае, если пространство является псевдоевклидовым, понятие угла определяется лишь для векторов, не содержащих изотропных прямых внутри образованного векторами сектора. Сам угол при этом вводится как число, гиперболический косинус которого равен отношению модуля скалярного произведения этих векторов к произведению их длин (норм):

{displaystyle |(mathbf {a} ,mathbf {b} )|=|mathbf {a} ||mathbf {b} |operatorname {ch} varphi .}
  • Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю. Это определение применимо к любым пространствам с положительно определённым скалярным произведением. Например, ортогональные многочлены на самом деле ортогональны (в смысле этого определения) друг другу в некотором гильбертовом пространстве.
  • Пространство (вещественное или комплексное) с положительно определённым скалярным произведением называется предгильбертовым пространством.
    • При этом конечномерное вещественное пространство с положительно определённым скалярным произведением называется также евклидовым, а комплексное — эрмитовым или унитарным пространством.
  • Случай, когда скалярное произведение не является знакоопределённым, приводит к т. н. пространствам с индефинитной метрикой. Скалярное произведение в таких пространствах уже не порождает нормы (и она обычно вводится дополнительно). Конечномерное вещественное пространство с индефинитной метрикой называется псевдоевклидовым (важнейшим частным случаем такого пространства является пространство Минковского). Среди бесконечномерных пространств с индефинитной метрикой важную роль играют пространства Понтрягина и пространства Крейна.

История[править | править код]

Скалярное произведение было введено У. Гамильтоном в 1846 году[13] одновременно с векторным произведением в связи с кватернионами — соответственно, как скалярная и векторная часть произведения двух кватернионов, скалярная часть которых равна нулю[14].

Вариации и обобщения[править | править код]

В пространстве измеримых интегрируемых с квадратами на некоторой области Ω вещественных или комплексных функций можно ввести положительно определённое скалярное произведение:

{displaystyle (mathbf {f} ,mathbf {g} )=int limits _{Omega }f(x){overline {g(x)}}dOmega }

При использовании неортонормированных базисов скалярное произведение выражается через компоненты векторов с участием метрического тензора[15] g_{ij}:

{displaystyle (mathbf {a} ,mathbf {b} )=g_{ij}a^{i}b^{j}}

При этом сама метрика (говоря точнее, её представление в данном базисе) так связана со скалярными произведениями базисных векторов f_{i} :

{displaystyle g_{ij}=(mathbf {f} _{i},mathbf {f} _{j})}

Аналогичные конструкции скалярного произведения можно вводить и на бесконечномерных пространствах, например, на пространствах функций:

{displaystyle (mathbf {f} ,mathbf {g} )=int limits _{(Omega _{1}times Omega _{2})}K(x_{1},x_{2})f(x_{1})g(x_{2})d(Omega _{1}times Omega _{2})}
{displaystyle (mathbf {f} ,mathbf {g} )=int limits _{Omega }K(x)f(x)g(x)dOmega }

где К — положительно определённая, в первом случае симметричная относительно перестановки аргументов (при комплексных x — эрмитова) функция (если нужно иметь обычное симметричное положительно определённое скалярное произведение).

Простейшим обобщением конечномерного скалярного произведения в тензорной алгебре является свёртка по повторяющимся индексам.

См. также[править | править код]

  • Гильбертово пространство
  • Векторное произведение
  • Внешнее произведение
  • Псевдоскалярное произведение
  • Смешанное произведение

Примечания[править | править код]

  1. ↑ Hall B. C. Quantum Theory for Mathematicians. — NY: Springer Science & Business Media, 2013. — xvi + 553 p. — (Graduate Texts in Mathematics. Vol. 267). — ISBN 978-1-4614-7115-8. Архивная копия от 31 января 2016 на Wayback Machine — P. 85.
  2. ↑ Имеется в виду наименьший угол между векторами, не превосходящий pi.
  3. ↑ Векторная алгебра // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 1. — С. 634.
  4. ↑ 1 2 Гельфанд, 1971, с. 30—31.
  5. ↑ Тарг С. М. Работа силы // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 193—194. — 704 с. — ISBN 5-85270-087-8.
  6. ↑ Кудрявцев Л. Д. Математический анализ. II том. — М., Высшая школа, 1970. — с. 316.
  7. ↑ Weisstein, Eric W. Dot Product Архивная копия от 29 апреля 2021 на Wayback Machine. From MathWorld — A Wolfram Web Resource.
  8. ↑ Calculus II – Dot Product. tutorial.math.lamar.edu. Дата обращения: 9 мая 2021. Архивировано 9 мая 2021 года.
  9. ↑ Гельфанд, 1971, с. 86.
  10. ↑ Stewart, James (2016), Calculus (8 ed.), Cengage, Section 13.2.
  11. ↑ Гельфанд, 1971, с. 34.
  12. ↑ §9.5. Линейные пространства со скалярным произведением: евклидовы и унитарные
  13. ↑ Crowe M. J. A History of Vector Analysis – The Evolution of the Idea of a Vectorial System. — Courier Dover Publications, 1994. — С. 32. — 270 с. — ISBN 0486679101. Архивная копия от 6 марта 2019 на Wayback Machine
  14. ↑ Hamilton W. R. On Quaternions; or on a New System of Imaginaries in Algebra // Philosophical Magazine. 3rd Series. — London, 1846. — Т. 29. — С. 30.
  15. ↑ Гельфанд, 1971, с. 240.

Литература[править | править код]

  • Гельфанд И. М. Лекции по линейной алгебре. — 4-е изд. — М.: Наука, 1971. — 272 с.

Ссылки[править | править код]

  • Емелин А. Скалярное произведение векторов. Дата обращения: 14 ноября 2019.
Источник

Уважаемые студенты!
Заказать решение задач можно у нас всего за 10 минут.

Скалярное произведение векторов

Формула

Пусть даны векторы $ overline{a} = (a_x; a_y) $ и $ overline{b} = (b_x; b_y) $. Как найти скалярное произведение векторов? Для того, чтобы найти скалярное произведение векторов необходимо воспользоваться формулой: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y $$ Стоит заметить, что скалярное произведение записывается в скобках, в которых векторы записываются через запятую. Данное обозначение широко применяется в математике и его нужно запомнить.

Если в задаче векторы заданы тремя координатами (в пространстве), то найти скалярное произведение векторов нужно по другой формуле, основанной на предыдущей. Но с тем же смыслом: $$ (overline{a},overline{b}) = a_x cdot b_x + a_y cdot b_y + a_z cdot b_z $$

По сути скалярное произведение – это сумма произведений соответствующих координат данных векторов. Первая координата умножается на первую, вторая на вторую и затем произведения суммируются.

Примеры решений

Пример 1
Найти скалярное произведение векторов $ overline{a} = (-1;2) $ и $ overline{b} = (2;1) $
Решение

В данном примере векторы заданы двумя координатами, поэтому применяем первую формулу для плоской задачи. Умножаем соответствующие координаты, а потом складываем их:

$$ (overline{a},overline{b}) = -1 cdot 2 + 2 cdot 1 = -2 + 2 = 0 $$

Произведение получилось равным нулю, а это кстати означает, что векторы оказались ортогональными (перпендикулярными) друг к другу.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Ответ
$$ (overline{a},overline{b}) = 0 $$
Пример 2

В пространстве заданы начала и концы векторов: $$ A = (1;3;-2), B = (-1;4;1), C = (2; 1; -2) $$ Требуется найти скалярное произведение векторов $ overline{AB} $ и $ overline{AC} $.
Решение

В примеры решения данной задачи даны только точки и сразу вычислить произведение векторов не представляется возможным. Сначала нужно найти сами векторы $ overline{AB} $ и $ overline{AC} $. Вычисляются они с помощью разности соответствующих координат точек (из конца вычитается начало вектора):

$$ overline{AB} = (-1 – 1; 4-3; 1-(-2)) = (-2; 1; 3) $$

$$ overline{AC} = (2 – 1; 1 – 3; -2 – (-2)) = (1; -2; 0) $$

Теперь, когда необходимые векторы найдены, то вычисляем их произведение:

$$ (overline{AB},overline{AC}) = -2 cdot 1 + 1 cdot (-2) + 3 cdot 0 = -2-2+0 = -4 $$
Ответ
$$ (overline{AB},overline{AC}) = -4 $$

В статье мы ответили на вопрос: «Как найти скалярное произведение векторов?», а так же привели формулы и примеры решений задач.

Источник

Скалярное произведение векторов

Угол
между векторами 
 может
принимать значения от 0 до 180 градусов
(от 0 до 
 радиан)
включительно. Аналитически данный факт
записывается в виде двойного
неравенства: 
 либо 
 (в
радианах).

В
литературе значок угла 
 часто
пропускают и пишут просто 
.

Определение: Скалярным
произведением двух векторов 
 и 
 называется
ЧИСЛО, равное произведению длин этих
векторов на косинус угла между ними:

Обозначение: скалярное
произведение обозначается через 
 или
просто 
.

Результат
операции является ЧИСЛОМ:
Умножается вектор на вектор, а получается
число. Действительно, если длины
векторов 
 –
это числа, косинус угла – число, то их
произведение 
 тоже
будет числом.

Пример

Найти
скалярное произведение векторов 
 и 
,
если 

Решение: 

Ответ: 

Угол между векторами и значение скалярного произведения

Длины
ненулевых векторов всегда положительны: 
,
поэтому знак может зависеть только от
значения косинуса.

1)
Если угол между
векторами острый: 
  (от
0 до 90 градусов), то 
,
и скалярное
произведение будет положительным: 
.
Особый случай: если векторы сонаправлены,
то угол между ними считается нулевым 
,
и скалярное произведение также будет
положительным. Поскольку 
,
то формула упрощается: 
.

2)
Если угол между
векторами тупой: 
  (от
90 до 180 градусов), то 
,
и, соответственно, скалярное
произведение отрицательно: 
.
Особый случай: если векторы направлены
противоположно, то
угол между ними считается развёрнутым: 
 (180
градусов). Скалярное произведение тоже
отрицательно, так как 

3)
Если угол между
векторами прямой: 
 (90
градусов), то 
 и скалярное
произведение равно нулю: 
.

Скалярное
произведение двух векторов равно нулю
тогда и только тогда, когда данные
векторы ортогональны.
Короткая математическая запись: 

Третий
случай имеет большую практическую
значимость, поскольку
позволяет проверить, ортогональны
векторы или нет.

Скалярный квадрат вектора Что будет, если вектор умножить на самого себя?

Или: 

Число 
 называется скалярным
квадратом вектора 
,
и обозначатся как 
.

Таким
образом, скалярный
квадрат вектора 
 равен
квадрату длины данного вектора:

Из
данного равенства можно получить формулу
для вычисления длины вектора:

Свойства
скалярного произведения.

Для
произвольных векторов 
 и
любого числа 
 справедливы
следующие свойства:

1) 
 –
переместительный или коммутативный закон
скалярного произведения.

2) 
 –
распределительный или дистрибутивный закон
скалярного произведения. Попросту,
можно раскрывать скобки.

3) 
 –
сочетательный или ассоциативный закон
скалярного произведения. Константу
можно вынести из скалярного произведения.

Пример

Найти
скалярное произведение векторов 
 и 
,
если известно, что 
.

Решение: 

(1)
Подставляем выражения векторов 
.

(2)
Раскрываем скобки по правилу умножения
многочленов. Раскрыть скобки нам
позволяет дистрибутивное свойство
скалярного произведения.

(3)
В первом и последнем слагаемом компактно
записываем скалярные квадраты векторов: 
.
Во втором слагаемом используем
перестановочность скалярного
произведения: 
.

(4)
Приводим подобные слагаемые: 
.

(5)
В первом слагаемом используем формулу
скалярного квадрата 
,
о которой не так давно упоминалось. В
последнем слагаемом, соответственно,
работает та же штука: 
.
Второе слагаемое раскладываем по
стандартной формуле 
.

(6)
Подставляем данные условия 
,
и ВНИМАТЕЛЬНО проводим окончательные
вычисления.

Ответ: 

Пример

Найти
длину вектора 
,
если 
.

Решение:

 

(1)
Поставляем выражение вектора 
.

(2)
Используем формулу длины: 
,
при этом в качестве вектора «вэ» у нас
выступает целое выражение 
.

(3)
Используем школьную формулу квадрата
суммы 
.

(4)
Дальнейшее аналогично действиям из
двух предыдущих задач.

Ответ: 

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник
Автор статьи

Наталья Игоревна Восковская

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Угол между векторами

Рассмотрим два данных вектора $overrightarrow{a}$ и $overrightarrow{b}$. Отложим от произвольно выбранной точки $O$ векторы $overrightarrow{a}=overrightarrow{OA}$ и $overrightarrow{b}=overrightarrow{OB}$, тогда угол $AOB$ называется углом между векторами $overrightarrow{a}$ и $overrightarrow{b}$ (рис. 1).

Рисунок 1.

Отметим здесь, что если векторы $overrightarrow{a}$ и $overrightarrow{b}$ сонаправлены или один из них является нулевым вектором, тогда угол между векторами равен $0^0$.

Логотип iqutor

Сделаем домашку
с вашим ребенком за 380 ₽

Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online

Бесплатное пробное занятие

*количество мест ограничено

Обозначение: $widehat{overrightarrow{a},overrightarrow{b}}$

Понятие скалярного произведения векторов

Определение 1

Скалярное произведение двух векторов – это скаляр (число), равный произведению длин двух векторов на косинус угла между этими векторами.

Математически это определение можно записать следующим образом:

Скалярное произведение может равняться нулю в двух случаях:

  1. Если один из векторов будет нулевым вектором (Так как тогда его длина равна нулю).

  2. Если векторы будут взаимно перпендикулярны (то есть $cos{90}^0=0$).

Отметим также, что скалярное произведение больше нуля, если угол между этими векторами острый (так как ${cos left(widehat{overrightarrow{a},overrightarrow{b}}right) } >0$), и меньше нуля, если угол между этими векторами тупой (так как ${cos left(widehat{overrightarrow{a},overrightarrow{b}}right) }

С понятием скалярного произведения связано понятие скалярного квадрата.

«Как найти скалярное произведение векторов» 👇

Определение 2

Скалярным квадратом вектора $overrightarrow{a}$ называется скалярное произведение этого вектора самого на себя.

Получаем, что скалярный квадрат равен

[overrightarrow{a}overrightarrow{a}=left|overrightarrow{a}right|left|overrightarrow{a}right|{cos 0^0 }=left|overrightarrow{a}right|left|overrightarrow{a}right|={left|overrightarrow{a}right|}^2]

Вычисление скалярного произведения по координатам векторов

Помимо стандартного способа нахождения значения скалярного произведения, который вытекает из определения, существует еще один способ.

Рассмотрим его.

Пусть векторы $overrightarrow{a}$ и $overrightarrow{b}$ имеют координаты $left(a_1,b_1right)$ и $left(a_2,b_2right)$, соответственно.

Скалярное произведение векторов $overrightarrow{a}$ и $overrightarrow{b}$ равно сумме произведений соответствующих координат.

Математически это можно записать следующим образом

[overrightarrow{a}overrightarrow{b}=a_1a_2+b_1b_2]

Доказательство.

  1. Пусть один из векторов будет нулевым вектором. К примеру, $overrightarrow{a}=(0,0)$.

    Тогда $overrightarrow{a}overrightarrow{b}=0$. С другой стороны $a_1a_2+b_1b_2=0cdot a_2+0cdot b_2=0$, значит

    [overrightarrow{a}overrightarrow{b}=a_1a_2+b_1b_2]

  2. Оба вектора не будут нулевыми векторами.

    Отложим от произвольной точки $O$ векторы $overrightarrow{OA}$ и $overrightarrow{OB}$ (рис. 2).

    Иллюстрация теоремы 1

    Рисунок 2. Иллюстрация теоремы 1

    По теореме косинусов, получим:

    [{AB}^2={OA}^2+{OB}^2-2OAcdot OBcosO]

    Так как $overrightarrow{AB}=overrightarrow{OB}-overrightarrow{OA}$, получим

    [{|overrightarrow{OB}-overrightarrow{OA}|}^2={|overrightarrow{OA}|}^2+{|overrightarrow{OB}|}^2-2left|overrightarrow{OA}right||overrightarrow{OB}|] [overrightarrow{OA}overrightarrow{OB}=frac{1}{2}left({|overrightarrow{OA}|}^2+{|overrightarrow{OB}|}^2-{|overrightarrow{OB}-overrightarrow{OA}|}^2right)]

    Так как векторы $overrightarrow{OA}$ и $overrightarrow{OB}$ имеют координаты $left(a_1,b_1right)$ и $left(a_2,b_2right)$, соответственно, то $overrightarrow{OB}-overrightarrow{OA}=left(a_2-a_1,b_2-b_1right)$. Тогда равенство примет вид

    [overrightarrow{OA}overrightarrow{OB}=frac{1}{2}left(a^2_1+b^2_1+a^2_2+b^2_2-{(a_2-a_1)}^2-{(b_2-b_1)}^2right)=a_1a_2+b_1b_2]

Теорема доказана.

Эта теорема имеет несколько следствий:

Следствие 1: Векторы $overrightarrow{a}$ и $overrightarrow{b}$ перпендикулярны тогда и только тогда, когда $a_1a_2+b_1b_2=0$

Следствие 2: Косинус угла между векторами равен $cosalpha =frac{a_1a_2+b_1b_2}{sqrt{a^2_1+b^2_1}cdot sqrt{a^2_2+b^2_2}}$

Свойства скалярного произведения векторов

Для любых трех векторов и действительного числа $k$ справедливо:

  1. ${overrightarrow{a}}^2ge 0$

    Данное свойство следует из определения скалярного квадрата (определение 2).

  2. Переместительный закон: $overrightarrow{a}overrightarrow{b}=overrightarrow{b}overrightarrow{a}$.

    Данное свойство следует из определения скалярного произведения (определение 1).

  3. Распределительный закон:

    $left(overrightarrow{a}+overrightarrow{b}right)overrightarrow{c}=overrightarrow{a}overrightarrow{c}+overrightarrow{b}overrightarrow{c}$.
    end{enumerate}

    По теореме 1, имеем:

    [left(overrightarrow{a}+overrightarrow{b}right)overrightarrow{c}=left(a_1+a_2right)a_3+left(b_1+b_2right)b_3=a_1a_3+a_2a_3+b_1b_3+b_2b_3==overrightarrow{a}overrightarrow{c}+overrightarrow{b}overrightarrow{c}]

  4. Сочетательный закон: $left(koverrightarrow{a}right)overrightarrow{b}=k(overrightarrow{a}overrightarrow{b})$.
    end{enumerate}

    По теореме 1, имеем:

    [left(koverrightarrow{a}right)overrightarrow{b}=ka_1a_2+kb_1b_2=kleft(a_1a_2+b_1b_2right)=k(overrightarrow{a}overrightarrow{b})]

Пример задачи на вычисление скалярного произведения векторов

Пример 1

Найти скалярное произведение векторов $overrightarrow{a}$ и $overrightarrow{b}$, если $left|overrightarrow{a}right|=3$ и $left|overrightarrow{b}right|=2$, а угол между ними равен ${{30}^0, 45}^0, {90}^0, {135}^0$.

Решение.

Используя определение 1, получаем

Для ${30}^0:$

[overrightarrow{a}overrightarrow{b}=6{cos left({30}^0right) }=6cdot frac{sqrt{3}}{2}=3sqrt{3}]

Для ${45}^0:$

[overrightarrow{a}overrightarrow{b}=6{cos left({45}^0right) }=6cdot frac{sqrt{2}}{2}=3sqrt{2}]

Для ${90}^0:$

[overrightarrow{a}overrightarrow{b}=6{cos left({90}^0right) }=6cdot 0=0]

Для ${135}^0:$

[overrightarrow{a}overrightarrow{b}=6{cos left({135}^0right) }=6cdot left(-frac{sqrt{2}}{2}right)=-3sqrt{2}]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Добавить комментарий