Как найти скалярный потенциал поля

У этого термина существуют и другие значения, см. Потенциал.

Скаля́рный потенциа́л векторного поля (чаще просто потенциал векторного поля) — это скалярная функция phi такая, что во всех точках области определения поля

где обозначает градиент phi . В физике обычно потенциалом называют величину, противоположную по знаку (потенциал силы, потенциал электрического поля).

Потенциальные поля[править | править код]

Сечение двумерной плоскостью гравитационного потенциала создаваемого однородной сферой. Окружность образованная совокупностью точек перегиба одновременно соответствует кривой пересечения сферы и секущей плоскости.

Поле называется потенциальным, если для него существует скалярный потенциал. Для потенциального поля криволинейный интеграл между двумя точками:

$phi ({mathbf r})=int limits _{C}{mathbf {A}}({mathbf {r}})cdot ,d{mathbf {r}}=int limits _{a}^{b}{mathbf {A}}({mathbf {r}}(t))cdot {mathbf {{dot r}}}(t),dt$

не зависит от пути интегрирования , соединяющего эти точки. Это равносильно тому, что интеграл по любому замкнутому контуру равен нулю:

$oint limits _{C}{mathbf {A}}({mathbf {r}})cdot ,{mathbf {dr}}=0$

В физических терминах это означает, что механическая работа по перемещению пробного тела в силовом потенциальном поле не зависит от траектории перемещения, а только от положения начальной и конечной точек траектории.

Непрерывное векторное поле в односвязной области трёхмерного пространства потенциально тогда и только тогда, когда оно безвихревое:

{mathbf {A}}=operatorname {grad},phi Leftrightarrow operatorname {rot},{mathbf {A}}=0

Обобщением этой теоремы на случай произвольного конечномерного пространства является лемма Пуанкаре. Для таких пространств существует изоморфизм между векторными полями и 1-формами $omega _{{{mathbf {A}}}}$ , при этом вопрос о существовании потенциала сводится к вопросу об обращении внешнего дифференцирования. Лемма Пуанкаре утверждает, что любая замкнутая форма в односвязной области конечномерного пространства точна.

Заметим, что в общем случае неодносвязного пространства условия замкнутости недостаточно. Легко проверить, что поле на плоскости

${mathbf {A}}=left({frac {-y}{x^{2}+y^{2}}},{frac {x}{x^{2}+y^{2}}}right)$

является безвихревым в любой односвязной области, не содержащей точку (0,0) , однако

$int limits _{C}{mathbf {A}}({mathbf {r}})cdot ,{mathbf {dr}}=2pi$

для любого контура , один раз обходящего вокруг начала координат против часовой стрелки.

Ньютонов потенциал[править | править код]

Из любого векторного поля в $mathbb {R} ^{3}$ можно выделить его потенциальную составляющую. Соответствующий ей потенциал можно записать в явном виде, не производя разложение самого поля. Он определяется интегралом, называющимся ньютоновым потенциалом:

$phi ({mathbf {r}}_{0})={frac {1}{4pi }}int limits _{{{mathbb {R}}^{3}}}{frac {operatorname {div},{mathbf {A}}}{left|{mathbf {r}}-{mathbf {r}}_{0}right|}}dV$

При этом дивергенция поля должна убывать на бесконечности быстрее, чем ${frac {1}{r^{2}}}$ . В случае безвихревого поля этот интеграл даёт скалярный потенциал поля.

Дивергенцию можно отождествить с плотностью зарядов . В частности, для поля

${mathbf {A}}=-{frac {{mathbf {r}}}{r^{3}}}$

получаем обычную формулу для ньютонова гравитационного потенциала точечной массы, расположенной в начале координат:

$phi ({mathbf {r}}_{0})=int limits _{{{mathbb {R}}^{3}}}{frac {delta ({mathbf {r}})}{left|{mathbf {r}}-{mathbf {r}}_{0}right|}}dV={frac {1}{r}}$

где — трёхмерная дельта-функция Дирака.

См. также[править | править код]

Векторный потенциал
Теорема разложения Гельмгольца

Источник

Записав систему уравнений Максвелла,
теперь следует найти способ их решения.
Для стационарных полей эта задача
существенно облегчается введением
вспомогательных величин – потенциалов
и.
Оказывается, что, видоизменив надлежащим
образом определение скалярного и
векторного потенциалов, можно
воспользоваться ими и для решения
уравнений Максвелла в общем случае,
когда векторы электромагнитного поля
зависят от времени.

Будем считать, что диэлектрическая
и магнитнаяпроницаемости одинаковы на всем
протяжении поля и поверхностных зарядов
и токов в поле нет. При этих условиях
векторыии их первые производные всюду остаются
непрерывными, что существенно упрощает
решение поставленной задачи.

Далее полученные результаты могут
быть достаточно легко обобщены на случай
наличия скачкообразного изменения
ина отдельных поверхностях раздела
различных сред, в то время как задача
решения уравнений Максвелла при
произвольной зависимостииот координат точки чрезвычайно
усложняется.

В электростатике

,
гдескалярный
потенциал и,

т.е. поле вектора
потенциально.

Изменяющееся во времени магнитное поле
создает вихревое электрическое поле

т.е. полное электрическое поле приобретает
непотенциальную составляющую.

Поскольку магнитных зарядов пока
нет, то

и, как и раньше,,

где
векторный
потенциал.

Теперь, в общем случае, поля
изависят от времени. Поэтому и потенциалыибудут зависеть от координат и от времени.

Выразим вихревое электрическое поле
через векторный потенциал, воспользовавшись
уравнениями

и:

,
или,

откуда следует, что вектор
–потенциальный, поэтому именно этот
вектор может быть представлен в виде
градиента скалярного потенциала:

.
(7.1)

Итак, в общем случае вектор электрического
поля выражается через векторный и
скалярный потенциалы:

,
(7.2)

где
– поле электромагнитной индукции;– поле электрических зарядов.

Магнитное поле, по-прежнему описывается
выражением

(7.3)

Неоднозначность определения потенциалов.
Калибровочное преобразование.

Как и в случае стационарных полей
скалярный
и векторныйпотенциалы определены неоднозначно,
т.е. одно и то же электромагнитное поле
может быть представлено различными
значениями потенциалов.

Это связано с тем, что скалярный и
векторный потенциалы поля являются
лишь вспомогательными функциями, а
непосредственный физический смысл
имеют только напряженность
электрического и индукциямагнитного полей. Именно эти характеристики
поля однозначно определяют энергию
поля, силы, действующие со стороны поля
на заряженные частицы, плотность токов
и т.д. Поэтому любые два поля, описываемые
одними и теми же значениямии,
но разными значениями потенциалови,
физически тождественны.

Каков же произвол в определении
потенциалов
ипри заданных значениях векторови?

Пусть потенциалы электромагнитного
поля связаны с силовыми характеристиками
иуравнениями

Так как ротор градиента тождественно
равен нулю, то если мы прибавим к вектору
градиент произвольной скалярной функции

(7.4)

то новому значению векторного потенциала
будет соответствовать прежнее значение
магнитной индукции

.
(7.5)

Если
не зависит от времени, то и значение
напряженности электрического поляне изменится при заменена.
Если же,
т.е. является функцией времени, то
значение векторасохранится неизменным, если одновременно
с заменойбудет выполнена замена,
причем

(7.6)

Действительно,

.
(7.7)

Т.о., напряженность и индукция
электромагнитного поля остаются
неизменными при одновременном прибавлении
к векторному потенциалу градиента
произвольной скалярной функции и
вычитании из скалярного потенциала
умноженной на коэффициент
производной по времени от той же скалярной
функции.

Преобразования

и(7.8)

носят название калибровочных
преобразований.

Инвариантность поля по отношению к
этому классу преобразований потенциалов
называется калибровочной илиградиентнойинвариантностью.

Требование калибровочной инвариантности
уравнений теоретической физики, т.е.
требование, чтобы физическое содержание
этих уравнений зависело только от
напряженности и индукции электромагнитного
поля и оставалось неизменным при всех
преобразованиях потенциалов поля,
играет важную роль в физических теориях.
Решение отдельных конкретных задач
часто облегчается специальной,
целесообразной для данной задачи,
калибровкой потенциалов.

Дифференциальные уравнения для
потенциалов электромагнитного поля.

Пусть
,ина всем протяжении поля.

,
(7.9)

(7.10)

Подставим выражения
ив уравнение (7.10):

;
(7.11)

из векторной алгебры известно

.
(7.12)

Тогда

,
(7.13)

или

.
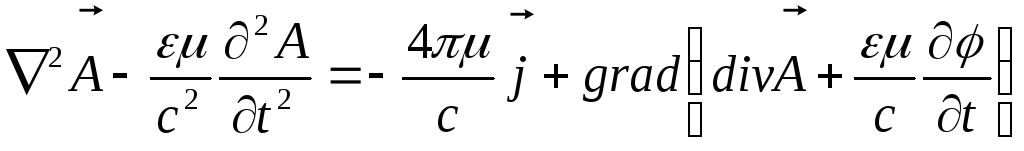(7.14)

Воспользовавшись неоднозначностью
определения потенциалов
и,
можем наложить некоторое условие,
определяющее их взаимосвязь, в частности,
так называемое, условие Лоренца:

(7.15)

Тогда уравнение (7.14) для векторного
потенциала
в калибровке Лоренца приобретает вид:

.
(7.16)

Вводя условие Лоренца, которое должно
сохраняться при калибровочных
преобразованиях, мы, т.о., накладываем
ограничения на вид скалярной функции
:

,
(7.17)

т.е. условие Лоренца оказывается
инвариантным лишь при калибровочных
преобразованиях с функцией
,
удовлетворяющей уравнению:

(7.18)

Воспользовавшись уравнением Максвелла

найдем теперь дифференциальное уравнение
для скалярного потенциала
,
имея в виду уравнение (7.2)

или

.
(7.19)

Из условия Лоренца (7.15)

(7.20)

поэтому

или

.
(7.21)

Т.о., мы получили дифференциальные
уравнения (7.16) и (7.21) для векторного и
скалярного потенциалов, соответственно.
Эти уравнения носят название уравнений
Даламбера. Вместе сусловием Лоренцаони позволяют определить значения
потенциалов электромагнитного поля по
заданному распределению зарядов и токов
проводимости.

Зная
и,
можно с помощью уравнений

найти векторы
и.

Отметим, что хотя скалярный потенциал
,
как и в случае стационарных полей,
зависит лишь от распределения зарядов,
а векторный– от распределения токов проводимости,
напряженность же электрического поля
зависит не только от градиента скалярного
потенциала, но и от производной по
времени векторного потенциала. В этом
обстоятельстве проявляется закон
электромагнитной индукции.

Для стационарных полей все производные
по времени обращаются в нуль, и все
уравнения, как и следовало ожидать,
сводятся к полученным ранее уравнениям,
описывающим стационарные поля.

Пока остается открытым вопрос о
физическом смысле коэффициента
.
Ответ на него мы получим чуть позже.

Соседние файлы в папке ЭЛЕКТРОМАГНЕТИЗМ1

Источник

Потенциальное и соленоидальное поле

Краткая теория

Векторное поле

называется потенциальным векторным полем если
оно является градиентом некоторого скалярного поля

.
Это скалярное поле

называется соответственно потенциалом векторного
поля

.
Векторное поле называется вихревым или соленоидальным векторным полем, если
через любую замкнутую поверхность S его поток равен нулю.

Пример решения задачи

Задача

Проверить,
является ли векторное поле

потенциальным и соленоидальным. В случае
потенциальности поля

найти его потенциал.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Проверка на потенциальность

Для потенциальности поля необходимо
и достаточно, чтобы

Таким образом, поле является
потенциальным.

Проверка на соленоидальность

Для соленоидальности поля:

Таким образом, поле не является
соленоидальным.

Вычисление потенциала

Потенциал можно вычислить по
формуле:

Выберем в качестве точки

точку

Источник

From Wikipedia, the free encyclopedia

This article is about a general description of a function used in mathematics and physics to describe conservative fields. For the scalar potential of electromagnetism, see electric potential. For all other uses, see potential.

In mathematical physics, scalar potential, simply stated, describes the situation where the difference in the potential energies of an object in two different positions depends only on the positions, not upon the path taken by the object in traveling from one position to the other. It is a scalar field in three-space: a directionless value (scalar) that depends only on its location. A familiar example is potential energy due to gravity.

Vector field (right) and corresponding scalar potential (left).

A scalar potential is a fundamental concept in vector analysis and physics (the adjective scalar is frequently omitted if there is no danger of confusion with vector potential). The scalar potential is an example of a scalar field. Given a vector field F, the scalar potential P is defined such that:

$mathbf {F} =-nabla P=-left({frac {partial P}{partial x}},{frac {partial P}{partial y}},{frac {partial P}{partial z}}right),$

^[1]

where ∇P is the gradient of P and the second part of the equation is minus the gradient for a function of the Cartesian coordinates x, y, z.^[a] In some cases, mathematicians may use a positive sign in front of the gradient to define the potential.^[2] Because of this definition of P in terms of the gradient, the direction of F at any point is the direction of the steepest decrease of P at that point, its magnitude is the rate of that decrease per unit length.

In order for F to be described in terms of a scalar potential only, any of the following equivalent statements have to be true:

${displaystyle -int _{a}^{b}mathbf {F} cdot dmathbf {l} =P(mathbf {b} )-P(mathbf {a} ),}$ where the integration is over a Jordan arc passing from location a to location b and P(b) is P evaluated at location b.
where the integral is over any simple closed path, otherwise known as a Jordan curve.

The first of these conditions represents the fundamental theorem of the gradient and is true for any vector field that is a gradient of a differentiable single valued scalar field P. The second condition is a requirement of F so that it can be expressed as the gradient of a scalar function. The third condition re-expresses the second condition in terms of the curl of F using the fundamental theorem of the curl. A vector field F that satisfies these conditions is said to be irrotational (conservative).

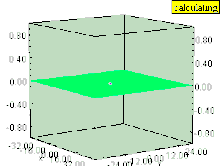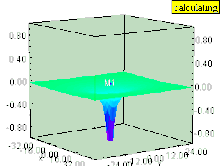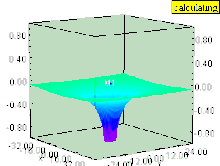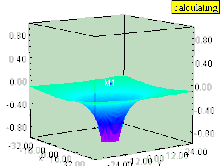
Gravitational potential well of an increasing mass where F = –∇P

Scalar potentials play a prominent role in many areas of physics and engineering. The gravity potential is the scalar potential associated with the gravity per unit mass, i.e., the acceleration due to the field, as a function of position. The gravity potential is the gravitational potential energy per unit mass. In electrostatics the electric potential is the scalar potential associated with the electric field, i.e., with the electrostatic force per unit charge. The electric potential is in this case the electrostatic potential energy per unit charge. In fluid dynamics, irrotational lamellar fields have a scalar potential only in the special case when it is a Laplacian field. Certain aspects of the nuclear force can be described by a Yukawa potential. The potential play a prominent role in the Lagrangian and Hamiltonian formulations of classical mechanics. Further, the scalar potential is the fundamental quantity in quantum mechanics.

Not every vector field has a scalar potential. Those that do are called conservative, corresponding to the notion of conservative force in physics. Examples of non-conservative forces include frictional forces, magnetic forces, and in fluid mechanics a solenoidal field velocity field. By the Helmholtz decomposition theorem however, all vector fields can be describable in terms of a scalar potential and corresponding vector potential. In electrodynamics, the electromagnetic scalar and vector potentials are known together as the electromagnetic four-potential.

Integrability conditions[edit]

If F is a conservative vector field (also called irrotational, curl-free, or potential), and its components have continuous partial derivatives, the potential of F with respect to a reference point r₀ is defined in terms of the line integral:

$V(mathbf {r} )=-int _{C}mathbf {F} (mathbf {r} )cdot ,dmathbf {r} =-int _{a}^{b}mathbf {F} (mathbf {r} (t))cdot mathbf {r} '(t),dt,$

where C is a parametrized path from r₀ to r,

$mathbf {r} (t),aleq tleq b,mathbf {r} (a)=mathbf {r_{0}} ,mathbf {r} (b)=mathbf {r} .$

The fact that the line integral depends on the path C only through its terminal points r₀ and r is, in essence, the path independence property of a conservative vector field. The fundamental theorem of line integrals implies that if V is defined in this way, then F = –∇V, so that V is a scalar potential of the conservative vector field F. Scalar potential is not determined by the vector field alone: indeed, the gradient of a function is unaffected if a constant is added to it. If V is defined in terms of the line integral, the ambiguity of V reflects the freedom in the choice of the reference point r₀.

Altitude as gravitational potential energy[edit]

uniform gravitational field near the Earth’s surface

Plot of a two-dimensional slice of the gravitational potential in and around a uniform spherical body. The inflection points of the cross-section are at the surface of the body.

An example is the (nearly) uniform gravitational field near the Earth’s surface. It has a potential energy

where U is the gravitational potential energy and h is the height above the surface. This means that gravitational potential energy on a contour map is proportional to altitude. On a contour map, the two-dimensional negative gradient of the altitude is a two-dimensional vector field, whose vectors are always perpendicular to the contours and also perpendicular to the direction of gravity. But on the hilly region represented by the contour map, the three-dimensional negative gradient of U always points straight downwards in the direction of gravity; F. However, a ball rolling down a hill cannot move directly downwards due to the normal force of the hill’s surface, which cancels out the component of gravity perpendicular to the hill’s surface. The component of gravity that remains to move the ball is parallel to the surface:

${displaystyle mathbf {F} _{mathrm {S} }=-mg sin theta }$

where θ is the angle of inclination, and the component of F_S perpendicular to gravity is

${displaystyle mathbf {F} _{mathrm {P} }=-mg sin theta cos theta =-{1 over 2}mgsin 2theta .}$

This force F_P, parallel to the ground, is greatest when θ is 45 degrees.

Let Δh be the uniform interval of altitude between contours on the contour map, and let Δx be the distance between two contours. Then

${displaystyle theta =tan ^{-1}{frac {Delta h}{Delta x}}}$

so that

${displaystyle F_{P}=-mg{Delta x,Delta h over Delta x^{2}+Delta h^{2}}.}$

However, on a contour map, the gradient is inversely proportional to Δx, which is not similar to force F_P: altitude on a contour map is not exactly a two-dimensional potential field. The magnitudes of forces are different, but the directions of the forces are the same on a contour map as well as on the hilly region of the Earth’s surface represented by the contour map.

Pressure as buoyant potential[edit]

In fluid mechanics, a fluid in equilibrium, but in the presence of a uniform gravitational field is permeated by a uniform buoyant force that cancels out the gravitational force: that is how the fluid maintains its equilibrium. This buoyant force is the negative gradient of pressure:

$mathbf {f_{B}} =-nabla p.,$

Since buoyant force points upwards, in the direction opposite to gravity, then pressure in the fluid increases downwards. Pressure in a static body of water increases proportionally to the depth below the surface of the water. The surfaces of constant pressure are planes parallel to the surface, which can be characterized as the plane of zero pressure.

If the liquid has a vertical vortex (whose axis of rotation is perpendicular to the surface), then the vortex causes a depression in the pressure field. The surface of the liquid inside the vortex is pulled downwards as are any surfaces of equal pressure, which still remain parallel to the liquids surface. The effect is strongest inside the vortex and decreases rapidly with the distance from the vortex axis.

The buoyant force due to a fluid on a solid object immersed and surrounded by that fluid can be obtained by integrating the negative pressure gradient along the surface of the object:

$F_{B}=-oint _{S}nabla pcdot ,dmathbf {S} .$

Scalar potential in Euclidean space[edit]

In 3-dimensional Euclidean space $mathbb {R} ^{3}$ , the scalar potential of an irrotational vector field E is given by

${displaystyle Phi (mathbf {r} )={1 over 4pi }int _{mathbb {R} ^{3}}{frac {operatorname {div} mathbf {E} (mathbf {r} ')}{|mathbf {r} -mathbf {r} '|}},dV(mathbf {r} ')}$

where dV(r’) is an infinitesimal volume element with respect to r’. Then

${displaystyle mathbf {E} =-mathbf {nabla } Phi =-{1 over 4pi }mathbf {nabla } int _{mathbb {R} ^{3}}{frac {operatorname {div} mathbf {E} (mathbf {r} ')}{|mathbf {r} -mathbf {r} '|}},dV(mathbf {r} ')}$

This holds provided E is continuous and vanishes asymptotically to zero towards infinity, decaying faster than 1/r and if the divergence of E likewise vanishes towards infinity, decaying faster than 1/r².

Written another way, let

${displaystyle Gamma (mathbf {r} )={frac {1}{4pi }}{frac {1}{|mathbf {r} |}}}$

be the Newtonian potential. This is the fundamental solution of the Laplace equation, meaning that the Laplacian of Γ is equal to the negative of the Dirac delta function:

${displaystyle nabla ^{2}Gamma (mathbf {r} )+delta (mathbf {r} )=0.}$

Then the scalar potential is the divergence of the convolution of E with Γ:

{displaystyle Phi =operatorname {div} (mathbf {E} *Gamma ).}

Indeed, convolution of an irrotational vector field with a rotationally invariant potential is also irrotational. For an irrotational vector field G, it can be shown that

${displaystyle nabla ^{2}mathbf {G} =mathbf {nabla } (mathbf {nabla } cdot {}mathbf {G} ).}$

Hence

${displaystyle nabla operatorname {div} (mathbf {E} *Gamma )=nabla ^{2}(mathbf {E} *Gamma )=mathbf {E} *nabla ^{2}Gamma =-mathbf {E} *delta =-mathbf {E} }$

as required.

More generally, the formula

holds in n-dimensional Euclidean space (n > 2) with the Newtonian potential given then by

${displaystyle Gamma (mathbf {r} )={frac {1}{n(n-2)omega _{n}|mathbf {r} |^{n-2}}}}$

where ω_n is the volume of the unit n-ball. The proof is identical. Alternatively, integration by parts (or, more rigorously, the properties of convolution) gives

${displaystyle Phi (mathbf {r} )=-{frac {1}{nomega _{n}}}int _{mathbb {R} ^{n}}{frac {mathbf {E} (mathbf {r} ')cdot (mathbf {r} -mathbf {r} ')}{|mathbf {r} -mathbf {r} '|^{n}}},dV(mathbf {r} ').}$

Notes[edit]

^ The second part of this equation is only valid for Cartesian coordinates, other coordinate systems such as cylindrical or spherical coordinates will have more complicated representations, derived from the fundamental theorem of the gradient.

References[edit]

^ Herbert Goldstein. Classical Mechanics (2 ed.). pp. 3–4. ISBN 978-0-201-02918-5.
^ See [1] for an example where the potential is defined without a negative. Other references such as Louis Leithold, The Calculus with Analytic Geometry (5 ed.), p. 1199 avoid using the term potential when solving for a function from its gradient.

Источник

Потенциальные поля[править | править код]

Ньютонов потенциал[править | править код]

См. также[править | править код]

Потенциальное и соленоидальное поле