Содержание
- Как найти склонение солнца формула
- Методы определения склонения солнца
- Формула для расчета склонения солнца
- Пример расчета склонения солнца
- Заключение
- Как найти склонение солнца формула
- Что такое склонение солнца?
- Формула для расчета склонения солнца
- Как определить значения компонентов?
- Итог
- Как найти склонение солнца формула
- Что такое склонение солнца?
- Как вычислить склонение солнца?
- Заключение
Как найти склонение солнца формула
Склонение направления на солнце – это важная характеристика, которая используется в астрономических расчетах и навигации. Оно указывает направление на солнце относительно точки наблюдения и может изменяться в зависимости от времени года и часа дня. Но как найти склонение солнца формула? В этой статье мы рассмотрим несколько подходов к решению этой задачи.
Методы определения склонения солнца
Существует несколько методов определения склонения солнца, в том числе:
- Метод на основе спектрального анализа
- Метод геометрической оптики
- Метод на основе действительной геодезии
Каждый из этих методов имеет свои преимущества и ограничения, и выбор нужного зависит от конкретной задачи и условий ее выполнения.
Формула для расчета склонения солнца
Одним из наиболее простых и эффективных способов расчета склонения солнца является использование следующей формулы:
sin φ = sin δ sin H / cos h
Здесь φ – широта точки наблюдения, δ – деклинация солнца, H – часовой угол солнца и h – высота солнца над горизонтом.
Эта формула позволяет определить угол между локальным меридианом и направлением на солнце в ортодромических координатах. Для ее использования необходимо знать координаты и время наблюдения, а также деклинацию и часовой угол солнца для данной даты и места наблюдения.
Пример расчета склонения солнца
Допустим, мы хотим определить склонение солнца для места наблюдения с координатами 55°55’N и 37°37’E в 12:00 по местному времени 21 июня.
Сначала находим деклинацию солнца для данной даты. Для этого воспользуемся следующей формулой:
δ = 23.45° sin [360 / 365 (284 + n)]
Здесь n – номер дня года, начиная с 1 января.
Подставляя значения для 21 июня, получаем:
δ = 23.45° sin [360 / 365 (284 + 172)] = 23.44°
Затем находим часовой угол солнца для данного места и времени. Для этого воспользуемся формулой:
H = 15 (t — 12) + L
Здесь t – время в часах и долях часа с начала суток в местном времени, а L – долгота места наблюдения.
Подставляя значения, получаем:
H = 15 (12 — 12) + 37°37’E = 564°
И, наконец, находим высоту солнца над горизонтом:
h = arcsin[sinφ sinδ + cosφ cosδ cosH]
Здесь φ – широта места наблюдения.
Подставляя значения, получаем:
h = arcsin[sin 55.92° sin 23.44° + cos 55.92° cos 23.44° cos 168°] = 66.66°
Таким образом, склонение солнца для данного места и времени равно:
sinφ = sin δ sin H / cos h = sin 23.44° sin 168° / cos 66.66° = 0.637
Заключение
Как мы видим, формула для определения склонения солнца довольно проста и позволяет быстро получить необходимую информацию для астрономических расчетов и навигации. Однако для ее использования необходимо иметь достоверные данные о координатах и времени наблюдения, а также деклинации и часовом угле солнца для заданной даты и места наблюдения.
Надеемся, что данная статья помогла вам понять, как найти склонение солнца формула, и что она будет полезна в вашей работе.
Как найти склонение солнца формула
Солнце – невероятно важный источник света и тепла для нашей планеты. Его расположение и склонение имеют несомненное влияние на нашу жизнь, поэтому знание формулы для определения его склонения – очень важно.
Что такое склонение солнца?
Склонение солнца – это угол между направлением на точку весеннего равноденствия и точкой пересечения эклиптики и созвездий. Эта точка называется точкой осеннего равноденствия.
Географическое положение и склонение солнца имеют важное значение для тех, кто занимается астрономией или навигацией. Например, они используются для определения грузоподъемности кораблей, расчетов площадей сельскохозяйственных угодий, и многих других задач.
Формула для расчета склонения солнца
Существует специальная формула, которая позволяет рассчитать склонение солнца. Представим ее ниже:
sin δ = sin ε sin λ
В этой формуле:
- δ – склонение солнца
- ε – наклон эклиптики к экватору
- λ – долгота
Формула использует три компонента: синус склонения, синус наклона и синус долготы. Для того, чтобы рассчитать склонение солнца, вы должны знать значение каждого из этих компонентов.
Как определить значения компонентов?
Если у вас нет комплексных инструментов для расчета, то вы можете использовать таблицы географических координат, чтобы определить значения компонентов для заданной даты и места их наблюдения.
Если вы знаете значения для заданной даты, то вы можете использовать их для расчета склонения солнца, используя формулу, которую мы представили выше.
Итог
Определение склонения солнца – очень важный процесс для многих профессиональных областей, таких как астрономия и навигация. Зная формулу для расчета склонения солнца, вы можете найти его склонение в любой день и месте, где бы вы ни находились. Надеемся, что эта статья помогла вам понять, как найти склонение солнца формула.
Как найти склонение солнца формула
Солнце — это одно из наиболее ярких и стабильных небесных тел в нашей солнечной системе. Оно является главным источником света и тепла для нашей Земли и других планет в системе. Изучение его положения и движения важно для многих научных и практических задач, включая астрономию и навигацию.
Что такое склонение солнца?
Склонение солнца — это угол между лучом солнечного света, проходящего через зенит, и плоскостью экватора нашей планеты. Он может изменяться в зависимости от времени года и широты проживания.
Найти склонение солнца может быть полезно во многих ситуациях. Например, для настройки солнечных батарей, для корректировки часов и календарей, для астрономических наблюдений и т.д.
Как вычислить склонение солнца?
Существует несколько способов вычисления склонения солнца, одним из наиболее простых и универсальных является использование специальных таблиц и формул.
Значение склонения солнца может быть вычислено по следующей формуле:
sin δ = sin ε sin φ + cos ε cos φ cos H
где δ — склонение, ε — наклон эклиптики, φ — широта местности, H — местный часовой угол.
В этой формуле sin, cos — тригонометрические функции, которые могут быть вычислены с помощью специальных таблиц или калькуляторов.
Кроме того, для определения местного часового угла может потребоваться знание географической долготы и времени местного меридиана.
Заключение
Таким образом, вычисление склонения солнца может быть произведено с помощью специальной формулы, которая учитывает широту местности и местное время. Знание склонения может быть полезно для разных целей, от корректировки солнечных часов до настройки астрономических телескопов.
- склонение солнца
- вычисление склонения
- формула для склонения солнца
- Печать
Страницы: [1] Вниз
A A A A

Тема: кто знает как найти склонение солнца в конкретный день и час? (Прочитано 8186 раз)
0 Пользователей и 1 Гость просматривают эту тему.
akram80
суть в следующем: для расчета интенсивности потока прямой солнечной радиации необходимо знать высоту солнца h.
sin(h) = sin(j)*cos(d) + cos(j)*cos(d)*cos(t)
где d – склонение
t – часовой угол
j – географическая широта
с j и t вопросов нет.
а склонение? его по таблицам, что ли брать? а если мне необходимо проследить изменение его при разной величине часового угла в течение суток?
есть конечно выражения связывающие экваториальные и горизонтальные координаты:
sin(d) = sin(j)*cos(z) – cos(j)*sin(z)*cos(A)
sin(A)=cos(d)sin(t)/cos(h)
z+h=90 град
z – зенитное расстояние
A – азимут
но я сомневаюсь, что склонение считается по ним. так как в них не наблюдается изменение склонения в зависимости от времени года. а, насколько я понимаю, она – зависимость – должна быть.
в общем как-то неясен этот вопрос…
thank
Записан
Берешь любую нормальную программу планетарий: Cart du Ciel, а лучше RedShift4 или 5 версию – там хоть на любую секунду. Или астрономический Ежегодник – там тоже есть таблицы.
Могут быть и сайты “он-лайн”, где это можно просчитать…
Записан
Записан
We must hang together or we all shall hang separately
Записан
akram80
Это конечно все здорово: программы и таблицы. Особенно благодарен за ссылки на англоязычный сайт (сложновато для меня, а ошибиться не хочется) 
смысл в том чтобы используя формулы получить значения склонения, которые в свою очередь используются для расчета интенсивности солнечной радиации. И это все в динамике на протяжении суток и всего лета.
Естественно это не конечная цель. полученные данные применяются в дальнейших расчетах.
поэтому: как найти эти самые исходные формулы?
Записан
Это конечно все здорово: программы и таблицы. Особенно благодарен за ссылки на англоязычный сайт (сложновато для меня, а ошибиться не хочется)
. НО
смысл в том чтобы используя формулы получить значения склонения, которые в свою очередь используются для расчета интенсивности солнечной радиации. И это все в динамике на протяжении суток и всего лета.
Естественно это не конечная цель. полученные данные применяются в дальнейших расчетах.поэтому: как найти эти самые исходные формулы?
Яндексом по ключевым словам “перевод из эклиптических координат в экваториальные”. Третья ссылка – http://hea.iki.rssi.ru/~nick/astro/scecl.htm. Надеюсь, это статья вам поможет.
Записан
…смысл в том чтобы используя формулы получить значения склонения, которые в свою очередь используются для …
поэтому: как найти эти самые исходные формулы?
Смотря какая точность требуется. Если пренебречь эллиптичностью земной орбиты (а она невелика), то формула зависимости склонения от порядкового дня в году будет элементарной: delta = eps*sin((D-D0)/365.25), где eps – угол наклона эклиптики к экватору (~ 23°26′), D – порядковый номер текущего (т.е. для которого ищется склонение Солнца) дня в году, D0 – порядковый номер дня весеннего равноденствия (примерно 81 – это можно уточнить). С порядковыми днями удобно работать через юлианские, но если особой точности не требуется, то есть разные пути радикального упрощения таких вычислений.
А для большей точности уже придётся учитывать неравномерность орбитального движения Земли – в первом приближении движущееся во эклиптике Солнце заставить двигаться с переменной скорость (на среднюю скорость наложить соответствующую синусоиду), а затем эклиптические координаты перевести в экваториальные. И тогда, уже после перевода в горизонтальные, не забыть ещё и рефракцию учесть…
Записан
Александрович Николай, Москва – юг Подмосковья, АстроТоп России, 300-мм F/6 Ньютон + Celestron Advanced C8-SGT в обсерватории под Москвой, ТАЛ-1, DeepSky 25×100, SW1201+Coronado PST, Canon EOS 6D
AN1440
В ветке “Электронная астрономия” где-то далеко есть тема “Как рассчитываются…” – там настолько подробно, что хуже некуда!
Записан
- Печать
Страницы: [1] Вверх
У этого термина существуют и другие значения, см. Склонение.
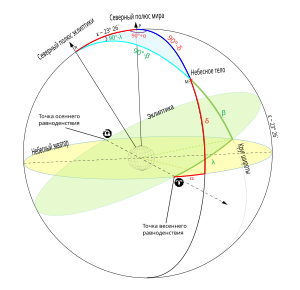
Экваториальные и эклиптические координаты небесных тел. Склонение обозначено
Склонение в астрономии (обозначается 
Описание[править | править код]
В экваториальной системе небесных координат одной из двух координат является склонение. Склонение светила — дуга круга склонений между ним и плоскостью экватора[1][2], или, проще говоря, угловое расстояние между светилом и небесным экватором. Склонение считается положительным, если светило находится в северном полушарии небесной сферы, и отрицательным — если в южном. Таким образом, склонение может находиться в диапазоне от −90° до +90°[3][4], причём эти значения достигаются, соответственно, на южном и на северном полюсах мира, а на небесном экваторе склонение равно нулю[5].
Склонение принято обозначать 


В первой экваториальной системе координат дополнительно к склонению используется часовой угол светила 

Суточное движение светил[править | править код]
Склонение светила связано с высотами его верхней и нижней кульминации 





- если
, то
и верхняя кульминация происходит к югу от зенита;
- если
, то
и верхняя кульминация происходит к северу от зенита;
- если
, то верхняя кульминация происходит точно в зените, на высоте
.
Высота нижней кульминации определяется формулой 
Если 




Положения восхода и захода светил, если они возможны, также зависят от склонения. Светила с нулевым склонением восходят на востоке и заходят на западе, тогда как при 

Со склонением светила и широтой места наблюдения можно также связать часовой угол 

Если данное уравнение не имеет решений, то светило является незаходящим или невосходящим; если решение только одно, то светило касается горизонта в верхней либо в нижней кульминации, что возможно при 







Склонение Солнца[править | править код]
Склонение и прямое восхождение Солнца меняются в течение года из-за вращения Земли вокруг Солнца. В момент весеннего равноденствия Солнце находится в точке весеннего равноденствия, и его склонение и прямое восхождение равны нулю. После этого склонение Солнца начинает увеличиваться и доходит до максимального значения — 23°26′ — в момент летнего солнцестояния, и в этот момент его прямое восхождение равняется 6h. После этого оно начинает уменьшаться: в момент осеннего равноденствия склонение снова равняется нулю, а прямое восхождение — 12h. В момент зимнего солнцестояния склонение достигает своего минимума — −23°26′ (прямое восхождение равно 18h), после чего снова начинает расти и доходит до нуля в момент весеннего равноденствия. Таким образом, в разные сезоны световой день длится по-разному, а в приполярных областях бывают полярные дни и полярные ночи[14].
Влияние прецессии[править | править код]
Из-за прецессии оси Земли меняется положение полюсов мира и небесного экватора с периодом в 26000 лет, следовательно, даже у неподвижных объектов меняется склонение и прямое восхождение. Для точной записи координат необходимо учитывать момент времени, в который они были измерены, называемый эпохой. Координаты также можно пересчитать для другой эпохи, и в данный момент в основном используется эпоха J2000.0, которой соответствует момент полудня 1 января 2000 года[15].
Примечания[править | править код]
- ↑ 1 2 Жаров, 2006, с. 75—76.
- ↑ Склонение. Большая российская энциклопедия. Дата обращения: 25 января 2023.
- ↑ 1 2 Karttunen et al., 2016, p. 17.
- ↑ Кононович, Мороз, 2004, с. 20—21.
- ↑ Declination (англ.). Encyclopedia Britannica. Дата обращения: 27 января 2023.
- ↑ Celestial Coordinates. spiff.rit.edu. Дата обращения: 25 января 2023.
- ↑ Кононович, Мороз, 2004, с. 21—22.
- ↑ Кононович, Мороз, 2004, с. 17, 25.
- ↑ Жаров, 2006, с. 94—95.
- ↑ Кононович, Мороз, 2004, с. 25.
- ↑ 1 2 Кононович, Мороз, 2004, с. 23.
- ↑ Karttunen et al., 2016, pp. 19—20.
- ↑ 1 2 Жаров, 2006, с. 96—97.
- ↑ Кононович, Мороз, 2004, с. 27—28.
- ↑ Karttunen et al., 2016, pp. 22—23.
Литература[править | править код]
- Кононович Э. В., Мороз В. И. Общий курс астрономии. — 2-е, исправленное. — М.: УРСС, 2004. — 544 с. — ISBN 5-354-00866-2.
- Жаров В. Е. Сферическая астрономия. — Фрязино: Век 2, 2006. — 480 с. — (Монографии и учебники). — 500 экз. — ISBN 5-85099-168-9.
- Karttunen H., Kroger P., Oja H., Poutanen M., Donner K. J. Fundamental Astronomy. — 6th Edition. — Berlin; Heidelberg; N. Y.: Springer, 2016. — 550 p. — ISBN 978-3-662-53045-0.
Положение Солнца в небе является функцией как времени и географического расположения наблюдений на земной поверхности «s. Как околоземные орбиты на Солнце на протяжении более года , Солнце , кажется, двигаться по отношению к неподвижным звездам на небесной сфере , по круговой траектории , называемой эклиптикой .
Вращение Земли вокруг своей оси вызывает суточное движение , так что кажется, что Солнце движется по небу по пути Солнца, который зависит от географической широты наблюдателя . Время, когда Солнце проходит через меридиан наблюдателя, зависит от географической долготы .
Следовательно, чтобы найти положение Солнца в заданном месте в заданное время, можно проделать следующие три шага:
- вычислить положение Солнца в эклиптической системе координат ,
- преобразовать в экваториальную систему координат , и
- преобразовать в горизонтальную систему координат для местного времени и местоположения наблюдателя. Это система координат , как правило , используется для вычисления положения Солнца с точки зрения солнечного зенитного угла и угла солнечного азимута , и оба параметра могут быть использованы , чтобы изобразить путь Солнца .
Этот расчет полезен в астрономии , навигации , геодезии , метеорологии , климатологии , солнечной энергии и дизайне солнечных часов .
Примерное положение
Эклиптические координаты
Эти уравнения из Астрономического альманаха можно использовать для расчета видимых координат Солнца , среднего равноденствия и эклиптики даты с точностью около 0 ° 0,01 (36 дюймов) для дат между 1950 и 2050 годами. закодированы в подпрограмму Fortran 90 в Ref. и используются для расчета зенитного угла Солнца и солнечного азимута в наблюдаемом с поверхности Земли.
Начните с вычисления n – количества дней (положительных или отрицательных, включая дробные дни) с полудня по Гринвичу по земному времени 1 января 2000 года ( J2000.0 ). Если известна юлианская дата желаемого времени, то
Средняя долгота Солнца, с поправкой на аберрации света , является:
Средняя аномалия Солнца ( на самом деле, Земли по своей орбите вокруг Солнца, но это удобно делать вид Солнца вокруг Земли), является:
Задайте и в диапазоне от 0 ° до 360 °, добавляя или вычитая кратные 360 ° по мере необходимости.
Наконец, эклиптическая долгота Солнца:
Эклиптики широта Солнца почти:
-
,
поскольку эклиптическая широта Солнца никогда не превышает 0,00033 °,
а расстояние от Солнца до Земли в астрономических единицах равно:
-
.
Наклон эклиптики
Если угол наклона эклиптики нигде не получен, его можно приблизительно определить:
Экваториальные координаты

Прямое восхождение ,
-
, где находится в том же квадранте, что и ,
Чтобы получить RA в правом квадранте в компьютерных программах, используйте функцию Arctan с двойным аргументом, такую как ATAN2 (y, x)
и склонение ,
-
.
Прямоугольные экваториальные координаты
Правосторонние прямоугольные экваториальные координаты в астрономических единицах равны:
- Где ось находится в направлении мартовского равноденствия , ось – в сторону июньского солнцестояния , а ось – в направлении северного полюса мира .
Горизонтальные координаты
Склонение Солнца при взгляде с Земли
Путь Солнца над небесной сферой в течение дня для наблюдателя на 56 ° северной широты. Путь Солнца меняется в зависимости от его склонения в течение года. Пересечения кривых с горизонтальной осью показывают азимуты в градусах от севера, где Солнце восходит и заходит.
Обзор
Солнце, кажется, движется на север во время северной весны , пересекая небесный экватор в мартовское равноденствие . Его склонение достигает максимума, равного углу наклона оси Земли (23,44 °) во время июньского солнцестояния , затем уменьшается до минимума (-23,44 °) во время декабрьского солнцестояния , когда его значение является отрицательным по отношению к наклону оси. Эта вариация порождает времена года .
Линейный график склонения Солнца в течение года напоминает синусоиду с амплитудой от 23,44 °, а одна лопасти волны на несколько дней дольше , чем другие, среди других отличий.
Следующие явления произошли бы, если бы Земля была идеальной сферой , вращающейся по круговой орбите вокруг Солнца, и если бы ее ось была наклонена на 90 °, так что сама ось находилась в плоскости орбиты (аналогично Урану ). На одну дату в год, Солнце будет прямо над головой на Северный полюс , поэтому его склонение будет + 90 °. В течение следующих нескольких месяцев подсолнечная точка будет двигаться к Южному полюсу с постоянной скоростью, пересекая круги широты с постоянной скоростью, так что склонение Солнца будет линейно уменьшаться со временем. В конце концов, Солнце окажется прямо над Южным полюсом со склонением -90 °; затем он начнёт двигаться на север с постоянной скоростью. Таким образом, график солнечного склонения, если смотреть с этой сильно наклоненной Земли, будет напоминать треугольную волну, а не синусоидальную волну, зигзагообразную между плюсами и минус 90 °, с линейными сегментами между максимумами и минимумами.
Если осевой наклон на 90 ° уменьшается, то абсолютные максимальное и минимальное значения наклона уменьшатся, чтобы равняться осевому наклону. Кроме того, формы максимумов и минимумов на графике станут менее острыми, изогнувшись, чтобы напоминать максимумы и минимумы синусоидальной волны. Однако даже когда осевой наклон равен наклону реальной Земли, максимумы и минимумы остаются более острыми, чем у синусоидальной волны.
На самом деле, орбита Земли является эллиптической . Земля движется вокруг Солнца около перигелия в начале января быстрее , чем около афелия в начале июля. Это заставляет процессы, подобные изменению солнечного склонения, происходить в январе быстрее, чем в июле. На графике это делает минимумы более острыми, чем максимумы. Кроме того, поскольку перигелий и афелий не происходят в точные даты солнцестояний, максимумы и минимумы слегка асимметричны. Темпы изменений до и после не совсем равны.
Поэтому график видимого склонения Солнца по-разному отличается от синусоидальной волны. Как показано ниже, его точный расчет сопряжен с некоторыми трудностями.
Расчеты
Наклонение Солнца , δ ☉ , – это угол между лучами Солнца и плоскостью экватора Земли. Наклон оси Земли ( астрономы называют ее наклоном эклиптики ) – это угол между осью Земли и линией, перпендикулярной орбите Земли. Наклон оси Земли медленно меняется в течение тысяч лет, но его текущее значение около ε = 23 ° 26 ‘почти постоянно, поэтому изменение солнечного склонения в течение одного года почти такое же, как и в течение следующего года.
Во время солнцестояний угол между лучами Солнца и плоскостью экватора Земли достигает максимального значения 23 ° 26 ‘. Следовательно, δ ☉ = + 23 ° 26 ‘в день северного летнего солнцестояния и δ ☉ = -23 ° 26′ в период южного летнего солнцестояния.
В момент каждого равноденствия центр Солнца, кажется, проходит через небесный экватор , а δ ☉ равно 0 °.
Склонение Солнца в любой момент рассчитывается по формуле:
где EL – долгота эклиптики (по сути, положение Земли на ее орбите). Поскольку эксцентриситет земной орбиты невелик, ее орбиту можно аппроксимировать как круг, что вызывает ошибку до 1 °. Приближение круга означает, что EL будет на 90 ° впереди солнцестояний на орбите Земли (в дни равноденствия), так что sin (EL) можно записать как sin (90 + NDS) = cos (NDS), где NDS – количество дни после декабрьского солнцестояния. Также используя приближение, что arcsin [sin (d) · cos (NDS)] близко к d · cos (NDS), получается следующая часто используемая формула:
где N – день года, начинающийся с N = 0 в полночь по всемирному времени (UT), когда начинается 1 января (т.е. часть дней в порядковой дате -1). Число 10 в (N + 10) – это приблизительное количество дней после декабрьского солнцестояния до 1 января. Это уравнение переоценивает склонение около сентябрьского равноденствия до + 1,5 °. Аппроксимация синусоидальной функции сама по себе приводит к ошибке до 0,26 ° и не рекомендуется для использования в приложениях солнечной энергии. Формула Спенсера 1971 года (основанная на ряде Фурье ) также не рекомендуется из-за ошибки до 0,28 °. Дополнительная ошибка до 0,5 ° может возникнуть во всех уравнениях для равноденствий, если не использовать десятичный разряд при выборе N для корректировки времени после полуночи UT для начала этого дня. Таким образом, приведенное выше уравнение может иметь погрешность до 2,0 °, что примерно в четыре раза больше угловой ширины Солнца, в зависимости от того, как оно используется.
Склонение можно более точно рассчитать, если не делать двух приближений, используя параметры орбиты Земли для более точной оценки EL:
который можно упростить, оценив константы до:
N – количество дней с полуночи UT, когда начинается 1 января (т. Е. Часть дней в порядковой дате -1) и может включать десятичные дроби для корректировки на местное время позже или раньше в течение дня. Число 2 в (N-2) – это приблизительное количество дней до перигелия Земли после 1 января . Число 0,0167 – текущее значение эксцентриситета орбиты Земли. Эксцентриситет очень медленно меняется со временем, но для дат, довольно близких к настоящему, его можно считать постоянным. Наибольшие ошибки в этом уравнении составляют менее ± 0,2 °, но менее ± 0,03 ° для данного года, если число 10 корректируется в большую или меньшую сторону в дробных днях, в зависимости от того, насколько далеко декабрьское солнцестояние предыдущего года произошло до или после. полдень 22 декабря. Эти точности сравниваются с продвинутыми расчетами NOAA, которые основаны на алгоритме Жана Мееуса 1999 года с точностью до 0,01 °.
(Приведенная выше формула связана с достаточно простым и точным вычислением уравнения времени , которое описано здесь .)
Более сложные алгоритмы корректируют изменения эклиптической долготы, используя термины в дополнение к поправке на эксцентриситет 1-го порядка, описанной выше. Они также исправляют наклон 23,44 °, который очень незначительно меняется со временем. Поправки также могут включать влияние Луны на смещение положения Земли от центра орбиты пары вокруг Солнца. После определения склонения относительно центра Земли применяется дополнительная поправка на параллакс , которая зависит от расстояния наблюдателя от центра Земли. Эта поправка меньше 0,0025 °. Погрешность вычисления положения центра Солнца может быть менее 0,00015 °. Для сравнения, ширина Солнца около 0,5 °.
Атмосферная рефракция
Вышеописанные расчеты склонения не включают эффекты преломления света в атмосфере, из-за которых видимый угол возвышения Солнца, видимый наблюдателем, оказывается выше фактического угла возвышения, особенно при малых возвышениях Солнца. Например, когда Солнце находится на высоте 10 °, кажется, что оно находится под углом 10,1 °. Наклонение Солнца может использоваться вместе с его прямым восхождением для расчета его азимута, а также его истинного возвышения, которое затем может быть скорректировано на преломление, чтобы определить его видимое положение.
Уравнение времени
Уравнение времени – над осью солнечные часы будут отображаться быстрее по сравнению с часами, показывающими среднее местное время, а под осью солнечные часы будут отображаться медленными.
В дополнение к ежегодному колебанию видимого положения Солнца с севера на юг, соответствующему описанному выше изменению его склонения, существует также меньшее, но более сложное колебание в направлении восток-запад. Это вызвано наклоном оси Земли, а также изменениями скорости ее орбитального движения вокруг Солнца, вызванными эллиптической формой орбиты. Основными эффектами этого колебания с востока на запад являются изменения во времени таких событий, как восход и закат, а также в показаниях солнечных часов по сравнению с часами, показывающими местное среднее время . Как показано на графике, солнечные часы могут быть быстрее или медленнее примерно на 16 минут по сравнению с часами. Поскольку Земля вращается со средней скоростью в один градус каждые четыре минуты относительно Солнца, это 16-минутное смещение соответствует смещению на восток или запад примерно на четыре градуса видимого положения Солнца по сравнению с его средним положением. Смещение на запад заставляет солнечные часы опережать время.
Поскольку основной эффект этого колебания касается времени, его называют уравнением времени , используя слово «уравнение» в несколько архаичном смысле, означающем «исправление». Колебания измеряются в единицах времени, минутах и секундах, что соответствует количеству, на которое солнечные часы опережают часы. Уравнение времени может быть положительным или отрицательным.
Аналемма
Аналемма представляет собой диаграмма , которая показывает годовые изменения положения Солнца на небесной сфере , относительно среднего положения, как видно из фиксированного места на Земле. (Слово аналемма также иногда, но редко, используется в других контекстах.) Его можно рассматривать как изображение видимого движения Солнца в течение года , которое напоминает восьмерку. Аналемму можно изобразить, наложив фотографии, сделанные в одно и то же время дня с разницей в несколько дней в течение года .
Аналемму также можно рассматривать как график склонения Солнца , обычно отображаемый вертикально, против уравнения времени , нанесенного горизонтально. Обычно масштабы выбираются таким образом, чтобы равные расстояния на диаграмме представляли равные углы в обоих направлениях на небесной сфере. Таким образом, 4 минуты (точнее 3 минуты 56 секунд) в уравнении времени представлены таким же расстоянием, как 1 ° в склонении , поскольку Земля вращается со средней скоростью 1 ° каждые 4 минуты относительно Солнца. .
Аналемма нарисована так, как если бы наблюдатель смотрел вверх на небе. Если вверху показан север , то справа – запад . Обычно это делается даже тогда, когда аналемма отмечена на географическом глобусе , на котором континенты и т. Д. Показаны с запада влево.
Некоторые аналеммы отмечены, чтобы показать положение Солнца на графике в разные даты с интервалом в несколько дней в течение года. Это позволяет аналемме , которые будут использоваться , чтобы сделать простые аналоговые вычисления величин , такими как время и азимуты от восхода и захода солнца . Аналеммы без даты используются для корректировки времени, показываемого солнечными часами .
Смотрите также
- Эклиптика
- Влияние солнечного угла на климат
- Таблицы Солнца Ньюкомба
- Угол солнечного азимута
- Угол возвышения Солнца
- Солнечное излучение
- Солнечное время
- Путь солнца
- Уравнение восхода солнца
использованная литература
внешние ссылки
- Алгоритм положения Солнца , на веб-сайте Центра данных по возобновляемым ресурсам Национальной лаборатории возобновляемых источников энергии .
- Калькулятор положения Солнца , на pveducation.org . Интерактивный калькулятор, показывающий путь Солнца в небе.
- NOAA Solar Calculator , на веб-сайте отдела глобального мониторинга NOAA Earth System Research Laboratory .
- Калькулятор склонения и положения солнца NOAA
- Система HORIZONS на сайте JPL . Очень точное положение объектов Солнечной системы на основе эфемерид серии JPL DE .
- Общие эфемериды тел Солнечной системы , на сайте IMCCE . Положение объектов Солнечной системы на основе эфемерид серии INPOP.
- Положение Солнца в пакете R. Insol.
Макеты страниц
В практике широко применяется упрощенный способ определения экваториальных координат Солнца, позволяющий определять их при отсутствии ААЕ. В основу этого способа положены
закономерности годового движения среднего Солнца и истинного, Гринвичский часовой угол истинного Солнца определяется по формуле:

Из приведенной формулы следует, что для определения гринвичского часового угла истинного Солнца необходимо найти часовой угол среднего Солнца и затем учесть поправку к полученному часовому углу на дату полета на величину уравнения времени.
Чтобы упростить указанный расчет, пользуются заранее составленной таблицей (см. приложение 13), в которой для соответствующих часов и минут московского времени указаны гринвичские часовые углы среднего Солнца. Поправки к часовым углам на дату полета определяют по специальному графику (см. рисунок в приложении 13), в котором дано также склонение Солнца. Величина склонения Солнца может быть рассчитана также по формуле

где 23,5° — максимальная величина склонения Солнца; п — количество дней, прошедших после равноденствия или предшествующих равноденствию.
Количество дней, прошедших после равноденствия, берется перед солнцестоянием, а количество дней, предшествующих равноденствию, берется после солнцестояния.
Обычно указанную формулу решают с помощью навигационной линейки. Для этого необходимо треугольный индекс шкалы 4 установить на число 23,5, взятое по шкале 5. Затем против количества дней я, взятого по шкале 3, прочитать по шкале 5 склонение Солнца. Знак склонения определяется в зависимости от положения Солнца на эклиптике.
Рассмотрим на примере порядок определения экваториальных координат Солнца упрощенным способом.
Пример. Дата полета 20 августа. Определить гринвичский часовой угол и склонение Солнца для московского времени 
Решение. 1. Определяем по таблице (см. приложение 13) гринвичский часовой угол среднего Солнца для заданного момента времени:

2. Находим по графику (см. рисунок в приложении 13) поправку к гринвичскому часовому углу на дату полета: 
3. Определяем гринвичский – часовой угол истинного Солнца:

4. Определяем склонение Солнца по графику (см. приложение 13): 
Для расчета склонения Солнца на НЛ находим количество дней, предшествующих равноденствию. От 20 августа до 23 сентября осталось 34 дня. Затем производим действия на НЛ, как это было указано выше, и получаем, что 20 августа склонение Солнца 









































![delta _ { odot} = arcsin left [ sin left (-23,44 ^ { circ} right) cdot sin left (EL right) right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/88a08dc771b0aad640193a7c3ef372bb8f41140d)
![delta _ { odot} = - 23,44 ^ { circ} cdot cos left [{ frac {360 ^ { circ}} {365}} cdot left (N + 10 right) right ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/eae7c990d26a9bb3d2f5a7a88768d28be0628fc2)
![delta _ { odot} = arcsin left [ sin left (-23,44 ^ { circ} right) cdot cos left ({ frac {360 ^ { circ}} {365.24}} left (N + 10 right) + { frac {360 ^ { circ}} { pi}} cdot 0.0167 sin left ({ frac {360 ^ { circ}} {365.24}} влево (N-2 вправо) вправо) вправо) вправо]](https://wikimedia.org/api/rest_v1/media/math/render/svg/11d079f081b428348b4a17de9515fdc031088d48)
![{ displaystyle delta _ { odot} = - arcsin left [0,39779 cos left (0,98565 ^ { circ} left (N + 10 right) +1,914 ^ { circ} sin left ( 0,98565 ^ { circ} left (N-2 right) right) right) right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/583fa421f34aaf0bc31729bebc784ed8d17d9742)


