Как найти склонение солнца по широте

Как найти склонение солнца по широте

Содержание

  1. Как найти склонение солнца по широте?
  2. Шаг 1: Определение широты
  3. Шаг 2: Определение времени года
  4. Шаг 3: Используйте таблицу
  5. Итог
  6. Как найти склонение солнца по широте
  7. Что такое склонение солнца по широте
  8. Как найти склонение солнца по широте
  9. С использованием таблицы склонений солнца
  10. С помощью специальных программ и приложений
  11. С помощью математических формул и таблиц
  12. Общий итог
  13. Как найти склонение солнца по широте
  14. Шаг 1:Определить широту места
  15. Шаг 2: Определить временную зону места
  16. Шаг 3: Рассчитать деклинацию солнца
  17. Шаг 4: Рассчитать высоту солнца
  18. Шаг 5: Определить азимут солнца
  19. Итого

Как найти склонение солнца по широте?

Солнечное склонение — это угол между плоскостью экватора и плоскостью солнечного диска. Как найти склонение солнца по широте? Чтобы определить это, вам потребуется знание текущей географической широты, и времени года.

Шаг 1: Определение широты

Первым шагом является определение географической широты. Этот параметр указывает на расположение точки на поверхности земли на северном или южном полушарии. Широта измеряется в градусах, минутах и секундах, и может быть найдена с помощью карты мира или программы геолокации на вашем смартфоне.

Например:

Москва, Россия — 55.7558° N, 37.6173° E

Сидней, Австралия — 33.8651° S, 151.2093° E

Кейптаун, Южная Африка — 33.9249° S, 18.4241° E

Шаг 2: Определение времени года

Вторым шагом является определение времени года. Солнечное склонение меняется в зависимости от времени года, так как земля вращается вокруг солнца и находится в разных положениях в разные времена года.

Зимой солнечное склонение находится на южном полушарии, а летом на северном. Таким образом, если вы находитесь на северном полушарии и это лето, то склонение солнца будет находиться выше горизонта, в то время как зимой, когда солнечное склонение находится ниже, солнце будет ниже горизонта.

Шаг 3: Используйте таблицу

Как определить склонение солнца на определенный день и время? Для этого используются таблицы солнечного склонения.

Получив значения для широты и времени года, в таблице можно найти текущее солнечное склонение.

Например, при широте 55.7558° N в Москве, склонение солнца в мае составляет около 18 градусов, в июне — около 22 градусов, в сентябре — около 12 градусов, а в декабре — около -16 градусов.

Итог

Как найти склонение солнца по широте? Определите географическую широту, определите временное положение и используйте таблицы солнечного склонения. Это простой и быстрый способ узнать склонение солнца в любой точке мира в любое время года.

Как найти склонение солнца по широте

Знание склонения солнца по широте может быть полезно не только мореплавателям, но и любому, кто хочет точно определить время восхода и заката, а также продолжительность дня и ночи в конкретной точке земного шара. Ниже будет рассмотрен способ нахождения склонения солнца по широте.

Что такое склонение солнца по широте

Склонение солнца по широте — это угол между плоскостью Гринвича (плоскостью меридиана, проходящего через Гринвич в Лондоне, Англия) и плоскостью меридиана точки, в которой происходит наблюдение, на момент восхода или заката солнца.

Найдя значение склонения солнца по широте, можно рассчитать время восхода и заката солнца, а также продолжительность дня и ночи в данной точке земного шара.

Как найти склонение солнца по широте

Существует несколько способов нахождения склонения солнца по широте:

  • С использованием таблицы склонений солнца.
  • С помощью специальных программ и приложений.
  • С помощью математических формул и таблиц.

Рассмотрим основные методы.

С использованием таблицы склонений солнца

Склонение солнца по широте определяется по таблице склонений солнца, которую можно найти в специальных справочниках. В таблице указаны значение склонения солнца по широтам для каждого дня года.

Чтобы найти значение склонения солнца по широте для конкретной даты, необходимо найти в таблице соответствующую строку с нужной датой и столбец с нужной широтой. В пересечении этой строки и столбца будет находиться значение склонения солнца для данной точки земного шара.

С помощью специальных программ и приложений

Существуют специальные программы и приложения, которые могут помочь в нахождении склонения солнца по широте. Такие программы учитывают множество факторов, таких как время года, широта, долгота, временная зона, высота горизонта и т.д.

Для этого необходимо ввести данные о местоположении наблюдателя и дату, на которую нужно найти склонение солнца. Программа сама вычислит значение склонения солнца по широте.

С помощью математических формул и таблиц

Если у вас нет доступа к таблицам склонений солнца и вы не можете воспользоваться специальными программами, вы можете найти значение склонения солнца по широте с помощью математических формул и таблиц.

Для этого необходимо знать долготу точки наблюдения, а также время восхода или заката солнца на эту дату. На основе этих данных можно рассчитать значение склонения солнца по широте с помощью математических формул и таблиц.

Общий итог

Найдя значение склонения солнца по широте, вы сможете точно рассчитать время восхода и заката солнца, а также продолжительность дня и ночи в данной точке земного шара. Существует несколько способов нахождения склонения солнца по широте, таких как использование таблиц склонений солнца, специальных программ и приложений, а также математических формул и таблиц.

Надеемся, что данная статья помогла вам разобраться в данной теме.

Напоминаем, что знание склонения солнца по широте может быть полезно не только мореплавателям, но и любому, кто хочет точно определить время восхода и заката, а также продолжительность дня и ночи в конкретной точке земного шара.

Как найти склонение солнца по широте

Каждый день мы встаем и ложимся в зависимости от положения солнца. Помимо этого, положение солнца имеет огромное значение для многих процессов в природе, а также для людей, которые занимаются сельским хозяйством или ориентируются в местности. Чтобы узнать склонение солнца по широте, нужно провести несколько простых расчетов. В этой статье мы расскажем, как это сделать.

Шаг 1:Определить широту места

Первый шаг к определению склонения солнца — определить широту места. Чтобы это сделать, можно воспользоваться картами или GPS-навигатором. Для тех, кто находится в помещении, можно воспользоваться интернет-сервисами, которые показывают координаты местности.

Шаг 2: Определить временную зону места

Второй шаг — определить временную зону места. Это важно, потому что время в разных частях мира может отличаться. Чтобы определить временную зону, можно воспользоваться интернетом или спросить у местных жителей.

Шаг 3: Рассчитать деклинацию солнца

Третий шаг — рассчитать деклинацию солнца. Деклинация — это угол между экватором и точкой, где находится солнце на небесной сфере. В августе деклинация равняется примерно 15 градусам. В январе деклинация примерно -15 градусов. Остальные месяцы лежат между этими значениями.

Шаг 4: Рассчитать высоту солнца

Четвертый шаг — рассчитать высоту солнца от горизонта. Высота солнца зависит от времени года, широты, даты и времени. Путем проведения простых расчетов можно определить высоту солнца в любое время года и в любом месте на земле.

Шаг 5: Определить азимут солнца

Азимут солнца — это угол между направлением на север и направлением на солнце. Для того чтобы определить азимут солнца, нужно знать текущее время и местоположение. Также обычно необходима специальная формула расчета.

Эти шаги помогут определить склонение солнца по широте и времени. Результаты расчета будут полезны при планировании работ на природе, а также во многих других сферах.

Итого

Определение склонения солнца по широте и времени может показаться сложным заданием, но на самом деле это простой процесс, который легко освоить. Зная текущую широту и временную зону, а также проведя несколько простых расчетов, можно определить высоту и азимут солнца. Эти данные могут быть полезными во многих сферах, от фермерства до ориентирования на местности.

  • Склонение солнца — это важный параметр для многих сфер деятельности.
  • Определение склонения солнца по широте и времени — процесс, который можно освоить.
  • Несмотря на узкую специализацию, эти знания могут пригодиться во многих ситуациях на природе.
Источник

У этого термина существуют и другие значения, см. Склонение.

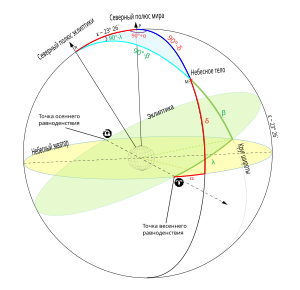
Экваториальные и эклиптические координаты небесных тел. Склонение обозначено delta

Склонение в астрономии (обозначается delta или dec — от англ. declination) — координата объекта на небесной сфере, которая не меняется при суточном вращении Земли. Склонение равно угловому расстоянию на небесной сфере от плоскости небесного экватора до светила, оно положительно для объектов в северном полушарии и отрицательно — в южном.

Описание[править | править код]

В экваториальной системе небесных координат одной из двух координат является склонение. Склонение светила — дуга круга склонений между ним и плоскостью экватора[1][2], или, проще говоря, угловое расстояние между светилом и небесным экватором. Склонение считается положительным, если светило находится в северном полушарии небесной сферы, и отрицательным — если в южном. Таким образом, склонение может находиться в диапазоне от −90° до +90°[3][4], причём эти значения достигаются, соответственно, на южном и на северном полюсах мира, а на небесном экваторе склонение равно нулю[5].

Склонение принято обозначать delta или dec (от англ. declination)[3][6]. В редких случаях его могут заменять полярным расстоянием p, которое равно угловому расстоянию между светилом и северным полюсом мира, таким образом, {displaystyle p=90^{circ }-delta } и эта величина меняется от 0 до 180°[1].

В первой экваториальной системе координат дополнительно к склонению используется часовой угол светила t, а во второй экваториальной — прямое восхождение alpha . Склонение, как и прямое восхождение не меняются из-за суточного вращения Земли, поэтому вторая экваториальная система используется наиболее широко[7].

Суточное движение светил[править | править код]

Склонение светила связано с высотами его верхней и нижней кульминации {displaystyle h_{text{в}}} и {displaystyle h_{text{н}}} посредством географической широты места наблюдения varphi , причём широты в южном полушарии считаются отрицательными. Формулы для {displaystyle h_{text{в}}} примут разный вид в зависимости от соотношения между varphi и delta [8][9]:

если {displaystyle delta <varphi }, то {displaystyle h_{text{в}}=90^{circ }-varphi +delta } и верхняя кульминация происходит к югу от зенита;
если {displaystyle delta >varphi }, то {displaystyle h_{text{в}}=90^{circ }+varphi -delta } и верхняя кульминация происходит к северу от зенита;
если {displaystyle delta =varphi }, то верхняя кульминация происходит точно в зените, на высоте {displaystyle h_{text{в}}=90^{circ }}.

Высота нижней кульминации определяется формулой {displaystyle h_{text{н}}=varphi +delta -90^{circ }}[10].

Если {displaystyle h_{text{н}}>0}, то светило никогда не заходит под горизонт и называется незаходящим; если {displaystyle h_{text{в}}<0}, то светило никогда не восходит из-за горизонта и называется невосходящим. Таким образом, если {displaystyle |delta |<90^{circ }-|varphi |}, то в ходе суточного движения светило восходит и заходит. Для северного полушария, если {displaystyle delta >90^{circ }-varphi }, то светило является незаходящим, если {displaystyle delta <varphi -90^{circ }} — невосходящим[11][12].

Положения восхода и захода светил, если они возможны, также зависят от склонения. Светила с нулевым склонением восходят на востоке и заходят на западе, тогда как при delta >0 восход и заход происходят на северо-востоке и северо-западе соответственно, а при {displaystyle delta <0} — на юго-востоке и на юго-западе[11].

Со склонением светила и широтой места наблюдения можно также связать часовой угол t и азимут точки A, где происходит его восход и заход[13]:

{displaystyle cos t=-tan delta tan varphi }

Если данное уравнение не имеет решений, то светило является незаходящим или невосходящим; если решение только одно, то светило касается горизонта в верхней либо в нижней кульминации, что возможно при {displaystyle varphi -delta =90^{circ }} или {displaystyle varphi +delta =90^{circ }}. В остальных случаях уравнение имеет два решения, t_{r} и t_{s}, причём {displaystyle 180^{circ }<t_{r}<360^{circ }} и t_{r} соответствует восходу, а {displaystyle 0^{circ }<t_{s}<180^{circ }} и t_{s} соответствует заходу. Азимут точек восхода и захода определяется из системы уравнений[13]:

{displaystyle sin A=cos delta sin t}
{displaystyle cos A=-sin delta cos varphi +cos delta sin varphi cos t}

Склонение Солнца[править | править код]

Склонение и прямое восхождение Солнца меняются в течение года из-за вращения Земли вокруг Солнца. В момент весеннего равноденствия Солнце находится в точке весеннего равноденствия, и его склонение и прямое восхождение равны нулю. После этого склонение Солнца начинает увеличиваться и доходит до максимального значения — 23°26′ — в момент летнего солнцестояния, и в этот момент его прямое восхождение равняется 6h. После этого оно начинает уменьшаться: в момент осеннего равноденствия склонение снова равняется нулю, а прямое восхождение — 12h. В момент зимнего солнцестояния склонение достигает своего минимума — −23°26′ (прямое восхождение равно 18h), после чего снова начинает расти и доходит до нуля в момент весеннего равноденствия. Таким образом, в разные сезоны световой день длится по-разному, а в приполярных областях бывают полярные дни и полярные ночи[14].

Влияние прецессии[править | править код]

Из-за прецессии оси Земли меняется положение полюсов мира и небесного экватора с периодом в 26000 лет, следовательно, даже у неподвижных объектов меняется склонение и прямое восхождение. Для точной записи координат необходимо учитывать момент времени, в который они были измерены, называемый эпохой. Координаты также можно пересчитать для другой эпохи, и в данный момент в основном используется эпоха J2000.0, которой соответствует момент полудня 1 января 2000 года[15].

Примечания[править | править код]

  1. ↑ 1 2 Жаров, 2006, с. 75—76.
  2. ↑ Склонение. Большая российская энциклопедия. Дата обращения: 25 января 2023.
  3. ↑ 1 2 Karttunen et al., 2016, p. 17.
  4. ↑ Кононович, Мороз, 2004, с. 20—21.
  5. ↑ Declination (англ.). Encyclopedia Britannica. Дата обращения: 27 января 2023.
  6. ↑ Celestial Coordinates. spiff.rit.edu. Дата обращения: 25 января 2023.
  7. ↑ Кононович, Мороз, 2004, с. 21—22.
  8. ↑ Кононович, Мороз, 2004, с. 17, 25.
  9. ↑ Жаров, 2006, с. 94—95.
  10. ↑ Кононович, Мороз, 2004, с. 25.
  11. ↑ 1 2 Кононович, Мороз, 2004, с. 23.
  12. ↑ Karttunen et al., 2016, pp. 19—20.
  13. ↑ 1 2 Жаров, 2006, с. 96—97.
  14. ↑ Кононович, Мороз, 2004, с. 27—28.
  15. ↑ Karttunen et al., 2016, pp. 22—23.

Литература[править | править код]

  • Кононович Э. В., Мороз В. И. Общий курс астрономии. — 2-е, исправленное. — М.: УРСС, 2004. — 544 с. — ISBN 5-354-00866-2.
  • Жаров В. Е. Сферическая астрономия. — Фрязино: Век 2, 2006. — 480 с. — (Монографии и учебники). — 500 экз. — ISBN 5-85099-168-9.
  • Karttunen H., Kroger P., Oja H., Poutanen M., Donner K. J. Fundamental Astronomy. — 6th Edition. — Berlin; Heidelberg; N. Y.: Springer, 2016. — 550 p. — ISBN 978-3-662-53045-0.
Источник

Склонение (астрономия)

  • Склонение (δ) в астрономии — одна из двух координат экваториальной системы координат. Равняется угловому расстоянию на небесной сфере от плоскости небесного экватора до светила и обычно выражается в градусах, минутах и секундах дуги. Склонение положительно к северу от небесного экватора и отрицательно к югу от него.

    * Объект на небесном экваторе имеет склонение 0°

    * Склонение северного полюса небесной сферы равно +90°

    Склонение южного полюса равно −90°У склонения всегда указывается знак, даже если оно положительно.

    Склонение небесного объекта, проходящего через зенит, равно широте наблюдателя (если считать северную широту со знаком +, а южную со знаком −).

    В северном полушарии Земли для заданной широты φ небесные объекты со склонением δ > 90° − φ не заходят за горизонт, поэтому называются незаходящими. Если же склонение объекта δ < −90° + φ, то объект называется невосходящим, то есть он не наблюдаем на широте φ. В южном полушарии Земли незаходящими являются небесные объекты со склонением δ < −90° − φ, а невосходящими — со склонением δ > 90° + φ (φ для южного полушария берётся со знаком минус).

Источник: Википедия

Связанные понятия

Прямое восхождение (α, R. A. — от англ. right ascension) — длина дуги небесного экватора от точки весеннего равноденствия до круга склонения светила. Прямое восхождение — одна из координат второй экваториальной системы (есть ещё и первая, в которой используется часовой угол). Вторая координата — склонение.

Небе́сный эква́тор — большой круг небесной сферы, плоскость которого перпендикулярна оси мира и совпадает с плоскостью земного экватора. Небесный экватор делит небесную сферу на два полушария: северное полушарие, с вершиной в северном полюсе мира, и южное полушарие, с вершиной в южном полюсе мира. Созвездия, через которые проходит небесный экватор, называют экваториальными.

Небе́сная сфе́ра — воображаемая сфера произвольного радиуса, на которую проецируются небесные тела: служит для решения различных астрометрических задач. За центр небесной сферы принимают глаз наблюдателя; при этом наблюдатель может находиться как на поверхности Земли, так и в других точках пространства (например, он может быть отнесён к центру Земли). Для наземного наблюдателя вращение небесной сферы воспроизводит суточное движение светил на небе.

Эпоха в астрономии (от греч. έποχή — «остановка») — момент времени, для которого определены астрономические координаты или элементы орбиты. Астрономические координаты могут быть пересчитаны из одной эпохи в другую с учётом прецессии, а также собственного движения.

Полюс мира — точка на небесной сфере, вокруг которой происходит видимое суточное движение звёзд из-за вращения Земли вокруг своей оси. Направление на Северный полюс мира совпадает с направлением на географический север, а на Южный полюс мира — с направлением на географический юг. Северный полюс мира находится в созвездии Малой Медведицы с поляриссимой — Полярной звездой, южный — в созвездии Октант. В результате прецессии земной оси полюса мира смещаются примерно на 20 ” в год.

Упоминания в литературе

Экваториальную систему координат, которая строится на небесном экваторе, астрологи тоже применяют. Прямое восхождение (ά) и склонение (δ) – это две координаты, которые в данной системе определяют местонахождение небесного тела.

Вообще собственные движения звезд хоть и малы, но для ближайших звезд весьма заметны на больших промежутках времени. Например, нынешнее угловое склонение той же Альфы Центавра равно примерно минус 60°, то есть увидеть ее невозможно не только из средних, но и из субтропических северных широт. Однако древним египтянам эта звезда была хорошо знакома: в IV тысячелетии до н. э. она располагалась на небе всего в 30° южнее небесного экватора. Небесные объекты с таким склонением можно прекрасно наблюдать даже Крыму, не то что в Египте.

Локьер оставил достаточно практических советов для будущих астроархеологов. Он составил целый набор четких графиков для определения склонения звезды (для широт от 49° до 59°) от определенного азимута (рис. 11). Он справедливо отметил, какое значение имеет линия горизонта и как рефракция влияет на расчеты. По его мнению, линию горизонта можно примерно определить по контурным линиям на 1-дюймовых военно-топографических картах или их эквивалентах. Другими полезными цифрами являются изменения склонений самых ярких звезд, встречающиеся в расчетах древних жрецов-астрономов. Они показывают изменения склонения звезд (связанные с прецессией), рассчитанные на период от –2150 до –150. Изучение этих цифр подчеркивает одну из проблем, о которой уже упоминалось ранее (выше), то есть предварительно необходимо знать приблизительную дату(ы), когда именно проводилось какое-либо наблюдение за звездами. Например, если звезда № 26 (Спика, альфа Девы) и звезда № 25 (Бетельгейзе, альфа Ориона) находились на значительном расстоянии друг от друга в своем склонении в –2000, то примерно в –650 значения их склонения были такими же.

Чтобы пользоваться чертежом, надо знать, как велико угловое расстояние («склонение») Солнца от экватора в ту или иную сторону для различных дней года. Соответствующие данные указаны в табличке на стр. 23.

Чтобы пользоваться чертежом, надо знать, как велико угловое расстояние («склонение») Солнца от экватора в ту или иную сторону для различных дней года. Соответствующие данные указаны в табличке на стр. 28.

Связанные понятия (продолжение)

Галактическая система координат — это система небесных координат, имеющая начало отсчёта в Солнце и направление отсчёта от центра галактики Млечный Путь. Плоскость галактической системы координат совпадает с плоскостью галактического диска. Подобно географическим, галактические координаты имеют широту и долготу.

Экли́птика (от лат. (linea) ecliptica, от др.-греч. ἔκλειψις — затмение) — большой круг небесной сферы, по которому происходит видимое годичное движение Солнца. Соответственно плоскость эклиптики — плоскость обращения Земли вокруг Солнца (земной орбиты). Современное, более точное определение эклиптики — сечение небесной сферы плоскостью орбиты барицентра системы Земля — Луна.

Эклиптическая система координат, или эклиптикальные координаты:49 — это система небесных координат, в которой основной плоскостью является плоскость эклиптики, а полюсом — полюс эклиптики. Она применяется при наблюдениях за движением небесных тел Солнечной системы, плоскости орбит многих из которых, как известно, близки к плоскости эклиптики, а также при наблюдениях за видимым перемещением Солнца по небу за год:30.

Система небесных координат используется в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение объектов на небесной сфере. Таким образом, система небесных координат является сферической системой координат, в которой третья координата — расстояние — часто неизвестна и не играет роли.

Астрономи́ческая едини́ца (русское обозначение: а.е.; международное: с 2012 года — au; ранее использовалось обозначение ua) — исторически сложившаяся единица измерения расстояний в астрономии. Исходно принималась равной большой полуоси орбиты Земли, которая в астрономии считается средним расстоянием от Земли до Солнца:126.

Пятьдесят восемь навигационных звёзд имеют особый статус в области астрономической навигации. Из приблизительно 6000 звёзд, видимых невооруженным глазом в оптимальных условиях, выбранные звёзды являются одними из самых ярких и охватывают 38 созвездий на небесной сфере от склонения -70° до +89 °. Многие из навигационных звёзд были названы в древности вавилонянами, греками, римлянами и арабами.

Сидери́ческий пери́од обраще́ния (от лат. sidus, звезда; род. падеж sideris) — промежуток времени, в течение которого какое-либо небесное тело-спутник совершает вокруг главного тела полный оборот относительно звёзд. Понятие «сидерический период обращения» применяется к обращающимся вокруг Земли телам — Луне (сидерический месяц) и искусственным спутникам, а также к обращающимся вокруг Солнца планетам, кометам и др.

Галактическая плоскость — плоскость, в которой расположена большая часть массы дисковой галактики. Перпендикулярные к галактической плоскости направления указывают на полюса галактики. Наиболее часто термины «галактическая плоскость» и «полюса галактики» применяются для обозначения плоскости и полюсов Млечного Пути.

Угловой размер (иногда также угол зрения) — это угол между прямыми линиями, соединяющими диаметрально противоположные крайние точки измеряемого (наблюдаемого) объекта и глаз наблюдателя.

Окта́нт (лат. Octans) — маленькое и очень тусклое созвездие южного полушария неба, включающее Южный полюс мира.

Предварение равноденствий (лат. praecessio aequinoctiorum) — историческое название для постепенного смещения точек весеннего и осеннего равноденствий (то есть точек пересечения небесного экватора с эклиптикой) навстречу видимому годичному движению Солнца. Другими словами, каждый год весеннее равноденствие наступает немного раньше, чем в предыдущем году — примерно на 20 минут 24 секунды. В угловых единицах смещение составляет сейчас примерно 50,3″ в год, или 1 градус каждые 71,6 года. Это смещение…

Радиа́нт (лат. radians, род. п. лат. radiantis — излучающий) — область небесной сферы, кажущаяся источником метеоров, которые наблюдаются при встрече Земли с роем метеорных тел, движущихся вокруг Солнца по общей орбите.

Преце́ссия — явление, при котором момент импульса тела меняет своё направление в пространстве.

Покры́тие — это астрономическое явление, во время которого, с точки зрения наблюдателя из определённой точки, одно небесное тело проходит перед другим небесным телом, заслоняя его часть.

Кульминация (астрономия) — прохождение центра светила через небесный меридиан в процессе его суточного движения. Иначе — прохождение центром светила точки пересечения суточной параллели светила и небесного меридиана.

В списке приведены самые яркие звёзды, наблюдаемые с Земли, в оптическом диапазоне по видимой звёздной величине. Для кратных звёзд приведена суммарная звёздная величина.

Подробнее: Список самых ярких звёзд

Звёздная величина́ (блеск) — безразмерная числовая характеристика яркости объекта, обозначаемая буквой m (от лат. magnitudo «величина, размер»). Обычно понятие применяется к небесным светилам. Звёздная величина характеризует поток энергии от рассматриваемого светила (энергию всех фотонов в секунду) на единицу площади. Таким образом, видимая звёздная величина зависит и от физических характеристик самого объекта (то есть светимости), и от расстояния до него. Чем меньше значение звёздной величины, тем…

Зодиакальные созвездия (от греч. ζωδιακός, «звериный») — 13 созвездий, расположенных вдоль эклиптики, видимого годового пути Солнца среди звёзд. Название связано с тем, что большинство зодиакальных созвездий с древних времён носит названия животных.

Ма́сса Земли́ (в астрономии обозначается M⊕, где ⊕ — символ Земли) — масса планеты Земля, в астрономии используется как внесистемная единица массы. 1 M⊕ = (5,9722 ± 0,0006) × 1024 кг.

Фе́никс (лат. Phoenix, Phe) — созвездие южного полушария неба. Занимает на небе площадь в 469,3 квадратного градуса, содержит 68 звёзд, видимых невооружённым глазом.

Спектрально-двойной — называют систему двойных звёзд, если двойственность обнаруживается при помощи спектральных наблюдений. Обычно это системы, у которых скорости компонентов достаточно велики, а расположены они настолько близко, что увидеть их раздельно с использованием современных телескопов невозможно. В результате орбитального движения звёзд вокруг центра масс одна из них приближается к нам, а другая от нас удаляется, их лучевые скорости (вдоль направления на наблюдателя) неодинаковы и, как…

Подробнее: Спектрально-двойные звёзды

Науго́льник (лат. Norma) — созвездие южного полушария неба, лежит к юго-западу от Скорпиона, севернее Южного Треугольника, в контакте с Циркулем. Через него проходят обе ветви Млечного Пути, но эта область неба бедна яркими звёздами. Созвездие не содержит звёзд ярче 4,0 визуальной звёздной величины, 42 звезды, видимые невооружённым глазом, площадь на небе 165,3 квадратного градуса. Наилучшие условия для наблюдений в мае — июне, частично наблюдается в южных районах России (к югу от 48 С.Ш). В созвездии…

Же́ртвенник (лат. Ara) — созвездие южного полушария неба. Площадь 237,0 кв. градуса, 60 звёзд, видимых невооружённым глазом. На юге России (южнее широты 44° 30′) небольшая часть созвездия (но без ярких звёзд) восходит совсем низко над горизонтом в мае-июне. Звезда α Жертвенника (звёздная величина 2,95) в России не наблюдается, но при благоприятных условиях заметна вблизи линии горизонта в южных городах постсоветского пространства, расположенных южнее широты 40° 08′ (Бухаре, Самарканде, Нахичевани…

Золота́я Ры́ба (порт. Dorado от лат. Doradus) — созвездие южного полушария неба. Занимает на небе площадь в 179,2 квадратного градуса. Содержит 32 звезды, видимых невооружённым глазом.

В этот список ближайших к Земле звёзд, отсортированный в порядке увеличения расстояния, вошли звёзды, расположенные в радиусе 5 пк (16,308 св. года) от Земли. Включая Солнце, в настоящее время известны 57 звёздных систем, которые могут находиться в пределах этого расстояния. Эти системы содержат в общей сложности 64 звезды и 13 коричневых карликов.

Прохожде́ние, или астрономи́ческий транзи́т — это астрономическое явление, во время которого с точки зрения наблюдателя из определённой точки одно небесное тело проходит перед другим небесным телом, заслоняя его часть.

Противостояние (оппозиция) — такое положение небесного тела Солнечной системы, в котором разница эклиптических долгот его и Солнца равна 180°. Таким образом, это тело находится примерно на продолжении линии «Солнце — Земля» и видно с Земли примерно в противоположном Солнцу направлении. Противостояние возможно только для верхних планет и других тел, находящихся дальше от Солнца, чем Земля.

Возни́чий (лат. Auriga) — созвездие северного полушария неба. Самая яркая звезда — Капелла, 0,1 визуальной звёздной величины. Наиболее благоприятные условия видимости в декабре — январе. Видно на всей территории России.

Синоди́ческий пери́од обраще́ния (от греч. σύνοδος — соединение) — промежуток времени между двумя последовательными соединениями Луны или какой-нибудь планеты Солнечной системы с Солнцем при наблюдении за ними с Земли. При этом соединения планет с Солнцем должны происходить в фиксированном линейном порядке, что существенно для внутренних планет: например, это будут последовательные верхние соединения, когда планета проходит за Солнцем.

Микроско́п (лат. Microscopium) — небольшое созвездие южного полушария неба. Лежит к югу от Козерога, к северу от Индейца, восточнее Стрельца и западнее Южной Рыбы и Журавля.

Орёл (лат. Aquila) — экваториальное созвездие. Западная его часть лежит в восточной ветви Млечного Пути, южнее Стрелы. Площадь созвездия — 652,5 квадратного градуса, число звёзд ярче 6m — 70.

Кассиопе́я (лат. Cassiopeia) — созвездие Северного полушария неба. Ярчайшие звёзды Кассиопеи (от 2,2 до 3,4 звёздной величины) образуют фигуру, похожую на буквы «М» или «W». Созвездие занимает на небе площадь в 598,4 квадратного градуса и содержит около 90 звёзд ярче 6m (то есть видимых невооружённым глазом). Большая часть созвездия лежит в полосе Млечного Пути и содержит много рассеянных звёздных скоплений.

Переменные звезды имеют специальные обозначения, если они ещё не были обозначены буквой греческого алфавита, в формате обозначения Байера, в сочетании с именем созвездия в родительном падеже, в котором эта звезда находится. (см. Список созвездий и их латинское название (родительный падеж)).

Подробнее: Обозначения переменных звёзд

Большая полуось — один из основных геометрических параметров объектов, образованных посредством конического сечения.

Ове́н (лат. Aries) — одно из наиболее известных зодиакальных созвездий, хотя в нём нет звёзд ярче второй величины. Три главные звезды — Хамаль («голова барана»), Шератан («след» или «знак») и Мезартим (соответственно α, β, и γ Овна) легко найти: они лежат к югу от Треугольника. Звезда четвёртой величины Мезартим стала одной из первых двойных звезд, открытых при помощи телескопа (Робертом Гуком в 1664 году).

Астрономический объект или Небесное тело — естественное физическое тело, ассоциация, или структура, которую современная наука определяет как расположенную в наблюдаемой Вселенной. Термин «астрономический объект» нередко используется наравне с термином «тело». Как правило, «небесное тело» представляет собой обособленную, единую, связанную гравитацией (а иногда и электромагнетизмом) структуру. Например: астероиды, спутники, планеты и звёзды. «Астрономические объекты» — гравитационно связанные структуры…

Звёздные су́тки — период вращения какого-либо небесного тела вокруг собственной оси в инерциальной системе отсчёта, за которую обычно принимается система отсчёта, связанная с удалёнными звёздами. Для Земли это время, за которое Земля совершает один оборот вокруг своей оси по отношению к далёким звёздам.

Абсолютная звёздная величина — физическая величина, характеризующая светимость астрономического объекта. Для разных типов объектов используются разные определения абсолютной величины.

Живопи́сец (лат. Pictor) — маленькое созвездие южного полушария неба. Занимает на небе площадь в 247,7 квадратного градуса, содержит 49 звёзд, видимых невооружённым глазом. На юге России (южнее широты +47°) восходит небольшая часть созвездия (но без ярких звёзд). Первая относительно яркая звезда созвездия – β Живописца (её звёздная величина 3,85) восходит южнее широты +38°56′ (в пределах территории бывшего СССР она восходит в Душанбе, Астаре, Ашхабаде, Кушке). В созвездии Живописца находится звезда…

Се́тка (лат. Reticulum, Ret) — созвездие южного полушария неба. Занимает на небе площадь в 113,9 квадратного градуса, содержит 22 звезды, видимые невооружённым глазом.

Компас (лат. Pyxis, Pyx) — созвездие южного полушария неба. Занимает на небе площадь в 220,8 квадратного градуса, содержит 43 звёзды, видимые невооружённым глазом. На территории России полностью наблюдается в южных районах, а также на юге центральных. Лучшее время года для наблюдения — февраль-март.

Единоро́г (лат. Monoceros от греч. μονόκερως), экваториальное созвездие. Занимает на небе площадь в 481,6 квадратного градуса и содержит 146 звёзд, видимых невооружённым глазом. Лежит в Млечном пути, однако ярких звёзд не содержит. Местонахождение созвездия — внутри зимнего треугольника, образованного яркими звёздами — Сириусом, Проционом и Бетельгейзе, по которым его легко найти. Единорог — одно из 15 созвездий, через которые проходит линия небесного экватора. Видно в центральных и южных районах…

Тука́н (лат. Tucana, Tuc) — созвездие южного полушария неба. Занимает на небе площадь в 294,6 квадратного градуса, содержит 44 звезды, видимые невооружённым глазом.

Накло́н о́си враще́ния — угол отклонения оси вращения небесного тела от перпендикуляра к плоскости его орбиты. Другими словами — угол между плоскостями экватора небесного тела и его орбиты.

Упоминания в литературе (продолжение)

Для удобства описания границ созвездий их решено было проводить в виде ломаных линий, проходящих точно по сетке постоянных небесных координат – склонений и прямых восхождений. При этом созвездия стали напоминать некоторые африканские страны и американские штаты, границы которых проведены по параллелям и меридианам. Ну что же, это вполне рациональный способ, позволяющий легко закрепить границы в математической форме. Однако со временем в этой изящной идее стал проявляться один мелкий недостаток.

Земного экватора на небесной сфере) полосой ? 30°, звезды бога Ану (бог Неба) – по склонению от + 30° до + 60° и звезды бога Энлиля (бог Земли) – околополярные звезды со склонениями больше + 60°. Астрологический сборник «Энума, Ану, Энлиль» был самым основным и важным руководством для практического применения.

Род определяется по окончаниям им. п. ед. ч., свойственным определенному роду в пределах данного склонения. Следовательно, для того чтобы определить род любого существительного III склонения, надо учитывать три момента:

Существительные III склонения встречались крайне редко, например: os, corpus, caput, foramen, dens. Такой методический подход был абсолютно оправдан. III склонение – самое трудное для усвоения и имеет ряд особенностей, отличающих его от остальных склонений.

Часы, изготовленные человеком, измеряют пренебрежимо малые с эволюционной точки зрения доли – часы, минуты, секунды – и поэтому основаны на быстрых динамических процессах: качании маятника, раскручивании пружины, колебаниях кристаллов, горении свечи, вытекании воды из сосуда или высыпании песка, вращении Земли (определяемом по движению солнечной тени). Эти процессы протекают с известной постоянной скоростью. Маятник качается с известной частотой, определяемой, по крайней мере в теории, только его длиной, но не амплитудой колебаний и не массой груза на его конце. Напольные часы работают благодаря присоединению маятника к анкеру, передающему движение зубчатому колесу, которое при помощи системы шестеренок обеспечивает ход секундной, минутной и часовой стрелок. Пружинные часы работают почти так же. Кварцевые часы работают при помощи эквивалента маятника – колебаний кристаллов определенного вида под воздействием энергии, поставляемой батарейкой. Водяные и огненные часы обладают куда меньшей точностью, но ими широко пользовались до изобретения часов, основанных на постоянстве хода. Они основаны не на подсчете отрезков времени, как маятниковые или цифровые часы, а на измерении объема. Солнечные часы – неточный способ измерения времени. Однако вращение Земли позволяет создать более точные, хотя и медленные часы, которые мы называем календарем. Это происходит именно потому, что при таком масштабе часы становятся не измеряющими (как солнечные часы, измеряющие постоянно меняющееся склонение солнца), а счетными (подсчитывающими число циклов день/ночь).

Группа артиклевых слов выделяется также и авторами коллективного труда «Grundzüge einer deutschen Grammatik», однако это не означает отказа от местоимения как части речи. Они отмечают, что артиклевые слова (местоимения) характеризуются тем, что они влияют на флексию последующего прилагательного: следующее за ними прилагательное изменяется по слабому склонению. К подобного рода словам они относят: diese, alle, jede, welche и другие. Они ведут себя так же, как и определенный артикль. Как видно, критерии выделения артиклевых слов разные: у Фатера Г., Гримма Г. – невозможность перестановки артикля без существительного, невозможность употребления другого слова перед артиклем, а у авторов «Grundzüge einer deutschen Grammatik» – влияние артикля на следующее за ним прилагательное.

Источник
  • Печать

Страницы: [1]   Вниз

A A A A

Тема: кто знает как найти склонение солнца в конкретный день и час?  (Прочитано 8192 раз)

0 Пользователей и 1 Гость просматривают эту тему.

akram80

суть в следующем: для расчета интенсивности потока прямой солнечной радиации необходимо знать высоту солнца h.
sin(h) = sin(j)*cos(d) + cos(j)*cos(d)*cos(t)
где d – склонение
t – часовой угол
j – географическая широта
с j и t вопросов нет.
а склонение? его по таблицам, что ли брать? а если мне необходимо проследить изменение его при разной величине часового угла в течение суток?
есть конечно выражения связывающие экваториальные и горизонтальные координаты:
sin(d) = sin(j)*cos(z) – cos(j)*sin(z)*cos(A)
sin(A)=cos(d)sin(t)/cos(h)
z+h=90 град
z – зенитное расстояние
A  – азимут
но я сомневаюсь, что склонение считается по ним. так как в них не наблюдается изменение склонения в зависимости от времени года. а, насколько я понимаю,  она – зависимость – должна быть.
в общем как-то неясен этот вопрос…
thank


Записан

 Берешь любую нормальную программу планетарий: Cart du Ciel, а лучше RedShift4 или 5 версию – там хоть на любую секунду. Или астрономический Ежегодник – там тоже есть таблицы.
 Могут быть и сайты “он-лайн”, где это можно просчитать…


Записан


Записан

We must hang together or we all shall hang separately


Записан

akram80

Это конечно все здорово: программы и таблицы. Особенно благодарен за ссылки на англоязычный сайт (сложновато для меня, а ошибиться не хочется) :). НО
смысл в том чтобы используя формулы получить значения склонения, которые в свою очередь используются для расчета интенсивности солнечной радиации. И это все в динамике на протяжении суток и всего лета.
Естественно это не конечная цель. полученные данные применяются  в дальнейших расчетах.

поэтому: как найти эти самые исходные формулы?


Записан

Это конечно все здорово: программы и таблицы. Особенно благодарен за ссылки на англоязычный сайт (сложновато для меня, а ошибиться не хочется) :). НО
смысл в том чтобы используя формулы получить значения склонения, которые в свою очередь используются для расчета интенсивности солнечной радиации. И это все в динамике на протяжении суток и всего лета.
Естественно это не конечная цель. полученные данные применяются  в дальнейших расчетах.

поэтому: как найти эти самые исходные формулы?

Яндексом по ключевым словам “перевод из эклиптических координат в экваториальные”. Третья ссылка – http://hea.iki.rssi.ru/~nick/astro/scecl.htm. Надеюсь, это статья вам поможет.


Записан

…смысл в том чтобы используя формулы получить значения склонения, которые в свою очередь используются для …
поэтому: как найти эти самые исходные формулы?

Смотря какая точность требуется. Если пренебречь эллиптичностью земной орбиты (а она невелика), то формула зависимости склонения от порядкового дня в году будет элементарной: delta = eps*sin((D-D0)/365.25), где  eps – угол наклона эклиптики к экватору (~ 23°26′), D – порядковый номер текущего (т.е. для которого ищется склонение Солнца) дня в году,  D0 – порядковый номер дня весеннего равноденствия (примерно 81 – это можно уточнить). С порядковыми днями удобно работать через юлианские, но если особой точности не требуется, то есть разные пути радикального упрощения таких вычислений.

А для большей точности уже придётся учитывать неравномерность орбитального движения Земли – в первом приближении движущееся во эклиптике Солнце заставить двигаться с переменной скорость (на среднюю скорость наложить соответствующую синусоиду), а затем эклиптические координаты перевести в экваториальные. И тогда, уже после перевода в горизонтальные, не забыть ещё и рефракцию учесть…


Записан

Александрович Николай, Москва – юг Подмосковья, АстроТоп России, 300-мм F/6 Ньютон + Celestron Advanced C8-SGT в обсерватории под Москвой, ТАЛ-1, DeepSky 25×100, SW1201+Coronado PST, Canon EOS 6D

AN1440

В ветке “Электронная астрономия” где-то далеко есть тема “Как рассчитываются…” – там настолько подробно, что хуже некуда!


Записан

  • Печать

Страницы: [1]   Вверх

Источник

The position of the Sun in the sky is a function of both the time and the geographic location of observation on Earth’s surface. As Earth orbits the Sun over the course of a year, the Sun appears to move with respect to the fixed stars on the celestial sphere, along a circular path called the ecliptic.

Earth’s rotation about its axis causes diurnal motion, so that the Sun appears to move across the sky in a Sun path that depends on the observer’s geographic latitude. The time when the Sun transits the observer’s meridian depends on the geographic longitude.

To find the Sun’s position for a given location at a given time, one may therefore proceed in three steps as follows:[1][2]

  1. calculate the Sun’s position in the ecliptic coordinate system,
  2. convert to the equatorial coordinate system, and
  3. convert to the horizontal coordinate system, for the observer’s local time and location. This is the coordinate system normally used to calculate the position of the Sun in terms of solar zenith angle and solar azimuth angle, and the two parameters can be used to depict the Sun path.[3]

This calculation is useful in astronomy, navigation, surveying, meteorology, climatology, solar energy, and sundial design.

Approximate position[edit]

Ecliptic coordinates[edit]

These equations, from the Astronomical Almanac,[4][5]
can be used to calculate the apparent coordinates of the Sun, mean equinox and ecliptic of date, to a precision of about 0°.01 (36″), for dates between 1950 and 2050. These equations are coded into a Fortran 90 routine in Ref.[3] and are used to calculate the solar zenith angle and solar azimuth angle as observed from the surface of the Earth.

Start by calculating n, the number of days (positive or negative, including fractional days) since Greenwich noon, Terrestrial Time, on 1 January 2000 (J2000.0). If the Julian date for the desired time is known, then

n={mathrm {JD}}-2451545.0

The mean longitude of the Sun, corrected for the aberration of light, is:

L=280.460^{circ }+0.9856474^{circ }n

The mean anomaly of the Sun (actually, of the Earth in its orbit around the Sun, but it is convenient to pretend the Sun orbits the Earth), is:

g=357.528^{circ }+0.9856003^{circ }n

Put L and g in the range 0° to 360° by adding or subtracting multiples of 360° as needed.

Finally, the ecliptic longitude of the Sun is:

lambda =L+1.915^{circ }sin g+0.020^{circ }sin 2g

The ecliptic latitude of the Sun is nearly:

beta =0,

as the ecliptic latitude of the Sun never exceeds 0.00033°,[6]

and the distance of the Sun from the Earth, in astronomical units, is:

R=1.00014-0.01671cos g-0.00014cos 2g.

Obliquity of the ecliptic[edit]

Where the obliquity of the ecliptic is not obtained elsewhere, it can be approximated:

epsilon =23.439^{circ }-0.0000004^{circ }n

Equatorial coordinates[edit]

lambda , beta and R form a complete position of the Sun in the ecliptic coordinate system. This can be converted to the equatorial coordinate system by calculating the obliquity of the ecliptic, epsilon , and continuing:

Right ascension,

alpha =arctan(cos epsilon tan lambda ), where alpha is in the same quadrant as lambda ,

To get RA at the right quadrant on computer programs use double argument Arctan function such as ATAN2(y,x)

{displaystyle alpha =arctan 2(cos epsilon sin lambda ,cos lambda )}

and declination,

delta =arcsin(sin epsilon sin lambda ).

Rectangular equatorial coordinates[edit]

Right-handed rectangular equatorial coordinates in astronomical units are:

X=Rcos lambda
Y=Rcos epsilon sin lambda
Z=Rsin epsilon sin lambda
Where X axis is in the direction of the March equinox, the Y axis towards June Solstice, and the Z axis towards the North celestial pole.[7]

Horizontal coordinates[edit]

Declination of the Sun as seen from Earth [edit]

The path of the Sun over the celestial sphere through the course of the day for an observer at 56°N latitude. The Sun’s path changes with its declination during the year. The intersections of the curves with the horizontal axis show azimuths in degrees from North where the Sun rises and sets.

The Sun appears to move northward during the northern spring, crossing the celestial equator on the March equinox. Its declination reaches a maximum equal to the angle of Earth’s axial tilt (23.44°)[8][9] on the June solstice, then decreases until reaching its minimum (−23.44°) on the December solstice, when its value is the negative of the axial tilt. This variation produces the seasons.

A line graph of the Sun’s declination during a year resembles a sine wave with an amplitude of 23.44°, but one lobe of the wave is several days longer than the other, among other differences.

The following phenomena would occur if Earth were a perfect sphere, in a circular orbit around the Sun, and if its axis is tilted 90°, so that the axis itself is on the orbital plane (similar to Uranus). At one date in the year, the Sun would be directly overhead at the North Pole, so its declination would be +90°. For the next few months, the subsolar point would move toward the South Pole at constant speed, crossing the circles of latitude at a constant rate, so that the solar declination would decrease linearly with time. Eventually, the Sun would be directly above the South Pole, with a declination of −90°; then it would start to move northward at a constant speed. Thus, the graph of solar declination, as seen from this highly tilted Earth, would resemble a triangle wave rather than a sine wave, zigzagging between plus and minus 90°, with linear segments between the maxima and minima.

If the 90° axial tilt is decreased, then the absolute maximum and minimum values of the declination would decrease, to equal the axial tilt. Also, the shapes of the maxima and minima on the graph would become less acute, being curved to resemble the maxima and minima of a sine wave. However, even when the axial tilt equals that of the actual Earth, the maxima and minima remain more acute than those of a sine wave.

In reality, Earth’s orbit is elliptical. Earth moves more rapidly around the Sun near perihelion, in early January, than near aphelion, in early July. This makes processes like the variation of the solar declination happen faster in January than in July. On the graph, this makes the minima more acute than the maxima. Also, since perihelion and aphelion do not happen on the exact dates as the solstices, the maxima and minima are slightly asymmetrical. The rates of change before and after are not quite equal.

The graph of apparent solar declination is therefore different in several ways from a sine wave. Calculating it accurately involves some complexity, as shown below.

Calculations[edit]

The declination of the Sun, δ☉, is the angle between the rays of the Sun and the plane of the Earth’s equator. The Earth’s axial tilt (called the obliquity of the ecliptic by astronomers) is the angle between the Earth’s axis and a line perpendicular to the Earth’s orbit. The Earth’s axial tilt changes slowly over thousands of years but its current value of about ε = 23°26′ is nearly constant, so the change in solar declination during one year is nearly the same as during the next year.

At the solstices, the angle between the rays of the Sun and the plane of the Earth’s equator reaches its maximum value of 23°26′. Therefore, δ☉ = +23°26′ at the northern summer solstice and δ☉ = −23°26′ at the southern summer solstice.

At the moment of each equinox, the center of the Sun appears to pass through the celestial equator, and δ☉ is 0°.

The Sun’s declination at any given moment is calculated by:

delta _{odot }=arcsin left[sin left(-23.44^{circ }right)cdot sin left(ELright)right]

where EL is the ecliptic longitude (essentially, the Earth’s position in its orbit). Since the Earth’s orbital eccentricity is small, its orbit can be approximated as a circle which causes up to 1° of error. The circle approximation means the EL would be 90° ahead of the solstices in Earth’s orbit (at the equinoxes), so that sin(EL) can be written as sin(90+NDS)=cos(NDS) where NDS is the number of days after the December solstice. By also using the approximation that arcsin[sin(d)·cos(NDS)] is close to d·cos(NDS), the following frequently used formula is obtained:

delta _{odot }=-23.44^{circ }cdot cos left[{frac {360^{circ }}{365}}cdot left(N+10right)right]

where N is the day of the year beginning with N=0 at midnight Universal Time (UT) as January 1 begins (i.e. the days part of the ordinal date −1). The number 10, in (N+10), is the approximate number of days after the December solstice to January 1. This equation overestimates the declination near the September equinox by up to +1.5°. The sine function approximation by itself leads to an error of up to 0.26° and has been discouraged for use in solar energy applications.[2] The 1971 Spencer formula[10] (based on a Fourier series) is also discouraged for having an error of up to 0.28°.[11] An additional error of up to 0.5° can occur in all equations around the equinoxes if not using a decimal place when selecting N to adjust for the time after UT midnight for the beginning of that day. So the above equation can have up to 2.0° of error, about four times the Sun’s angular width, depending on how it is used.

The declination can be more accurately calculated by not making the two approximations, using the parameters of the Earth’s orbit to more accurately estimate EL:[12]

delta _{odot }=arcsin left[sin left(-23.44^{circ }right)cdot cos left({frac {360^{circ }}{365.24}}left(N+10right)+{frac {360^{circ }}{pi }}cdot 0.0167sin left({frac {360^{circ }}{365.24}}left(N-2right)right)right)right]

which can be simplified by evaluating constants to:

{displaystyle delta _{odot }=-arcsin left[0.39779cos left(0.98565^{circ }left(N+10right)+1.914^{circ }sin left(0.98565^{circ }left(N-2right)right)right)right]}

N is the number of days since midnight UT as January 1 begins (i.e. the days part of the ordinal date −1) and can include decimals to adjust for local times later or earlier in the day. The number 2, in (N-2), is the approximate number of days after January 1 to the Earth’s perihelion. The number 0.0167 is the current value of the eccentricity of the Earth’s orbit. The eccentricity varies very slowly over time, but for dates fairly close to the present, it can be considered to be constant. The largest errors in this equation are less than ± 0.2°, but are less than ± 0.03° for a given year if the number 10 is adjusted up or down in fractional days as determined by how far the previous year’s December solstice occurred before or after noon on December 22. These accuracies are compared to NOAA’s advanced calculations[13][14] which are based on the 1999 Jean Meeus algorithm that is accurate to within 0.01°.[15]

(The above formula is related to a reasonably simple and accurate calculation of the Equation of Time, which is described here.)

More complicated algorithms[16][17] correct for changes to the ecliptic longitude by using terms in addition to the 1st-order eccentricity correction above. They also correct the 23.44° obliquity which changes very slightly with time. Corrections may also include the effects of the moon in offsetting the Earth’s position from the center of the pair’s orbit around the Sun. After obtaining the declination relative to the center of the Earth, a further correction for parallax is applied, which depends on the observer’s distance away from the center of the Earth. This correction is less than 0.0025°. The error in calculating the position of the center of the Sun can be less than 0.00015°. For comparison, the Sun’s width is about 0.5°.

Atmospheric refraction[edit]

The declination calculations described above do not include the effects of the refraction of light in the atmosphere, which causes the apparent angle of elevation of the Sun as seen by an observer to be higher than the actual angle of elevation, especially at low Sun elevations.[2] For example, when the Sun is at an elevation of 10°, it appears to be at 10.1°. The Sun’s declination can be used, along with its right ascension, to calculate its azimuth and also its true elevation, which can then be corrected for refraction to give its apparent position.[2][14][18]

Equation of time[edit]

The equation of time — above the axis a sundial will appear fast relative to a clock showing local mean time, and below the axis a sundial will appear slow.

In addition to the annual north–south oscillation of the Sun’s apparent position, corresponding to the variation of its declination described above, there is also a smaller but more complex oscillation in the east–west direction. This is caused by the tilt of the Earth’s axis, and also by changes in the speed of its orbital motion around the Sun produced by the elliptical shape of the orbit.[2] The principal effects of this east–west oscillation are variations in the timing of events such as sunrise and sunset, and in the reading of a sundial compared with a clock showing local mean time. As the graph shows, a sundial can be up to about 16 minutes fast or slow, compared with a clock. Since the Earth rotates at a mean speed of one degree every four minutes, relative to the Sun, this 16-minute displacement corresponds to a shift eastward or westward of about four degrees in the apparent position of the Sun, compared with its mean position. A westward shift causes the sundial to be ahead of the clock.

Since the main effect of this oscillation concerns time, it is called the equation of time, using the word “equation” in a somewhat archaic sense meaning “correction”. The oscillation is measured in units of time, minutes and seconds, corresponding to the amount that a sundial would be ahead of a clock. The equation of time can be positive or negative.

Analemma[edit]

An analemma is a diagram that shows the annual variation of the Sun’s position on the celestial sphere, relative to its mean position, as seen from a fixed location on Earth. (The word analemma is also occasionally, but rarely, used in other contexts.) It can be considered as an image of the Sun’s apparent motion during a year, which resembles a figure-8. An analemma can be pictured by superimposing photographs taken at the same time of day, a few days apart for a year.

An analemma can also be considered as a graph of the Sun’s declination, usually plotted vertically, against the equation of time, plotted horizontally. Usually, the scales are chosen so that equal distances on the diagram represent equal angles in both directions on the celestial sphere. Thus 4 minutes (more precisely 3 minutes, 56 seconds), in the equation of time, are represented by the same distance as 1° in the declination, since Earth rotates at a mean speed of 1° every 4 minutes, relative to the Sun.

An analemma is drawn as it would be seen in the sky by an observer looking upward. If north is shown at the top, then west is to the right. This is usually done even when the analemma is marked on a geographical globe, on which the continents, etc., are shown with west to the left.

Some analemmas are marked to show the position of the Sun on the graph on various dates, a few days apart, throughout the year. This enables the analemma to be used to make simple analog computations of quantities such as the times and azimuths of sunrise and sunset. Analemmas without date markings are used to correct the time indicated by sundials.[19]

Light-time effects[edit]

We see light from the Sun about 20 angle seconds from where the Sun is when the light is seen. See Solar annual aberration.

See also[edit]

  • Solar annual aberration
  • Ecliptic
  • Effect of Sun angle on climate
  • Newcomb’s Tables of the Sun
  • Solar azimuth angle
  • Solar elevation angle
  • Solar irradiance
  • Solar time
  • Sun path
  • Sunrise equation

References[edit]

  1. ^ Meeus, Jean (1991). “Chapter 12: Transformation of Coordinates”. Astronomical Algorithms. Richmond, VA: Willmann Bell, Inc. ISBN 0-943396-35-2.
  2. ^ a b c d e Jenkins, Alejandro (2013). “The Sun’s position in the sky”. European Journal of Physics. 34 (3): 633–652. arXiv:1208.1043. Bibcode:2013EJPh…34..633J. doi:10.1088/0143-0807/34/3/633. S2CID 119282288.
  3. ^ a b Zhang, T., Stackhouse, P.W., Macpherson, B., and Mikovitz, J.C., 2021. A solar azimuth formula that renders circumstantial treatment unnecessary without compromising mathematical rigor: Mathematical setup, application and extension of a formula based on the subsolar point and atan2 function. Renewable Energy, 172, 1333-1340. DOI: https://doi.org/10.1016/j.renene.2021.03.047
  4. ^
    U.S. Naval Observatory; U.K. Hydrographic Office, H.M. Nautical Almanac Office (2008). The Astronomical Almanac for the Year 2010. U.S. Govt. Printing Office. p. C5. ISBN 978-0-7077-4082-9.
  5. ^
    Much the same set of equations, covering the years 1800 to 2200, can be found at Approximate Solar Coordinates, at the U.S. Naval Observatory website Archived 2016-01-31 at the Wayback Machine. Graphs of the error of these equations, compared to an accurate ephemeris, can also be viewed.
  6. ^
    Meeus (1991), p. 152
  7. ^
    U.S. Naval Observatory Nautical Almanac Office (1992). P. Kenneth Seidelmann (ed.). Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley, CA. p. 12. ISBN 0-935702-68-7.
  8. ^ “Selected Astronomical Constants, 2015 (PDF)” (PDF). US Naval Observatory. 2014. p. K6–K7.
  9. ^ “Selected Astronomical Constants, 2015 (TXT)”. US Naval Observatory. 2014. p. K6–K7.
  10. ^ J. W. Spencer (1971). “Fourier series representation of the position of the sun”.
  11. ^ Sproul, Alistair B. (2007). “Derivation of the solar geometric relationships using vector analysis”. Renewable Energy. 32 (7): 1187–1205. doi:10.1016/j.renene.2006.05.001.
  12. ^ “SunAlign”. Archived from the original on 9 March 2012. Retrieved 28 February 2012.
  13. ^ “NOAA Solar Calculator”. Earth System Research Laboratory. Retrieved 28 February 2012.
  14. ^ a b “Solar Calculation Details”. Earth System Research Laboratory. Retrieved 28 February 2012.
  15. ^ “Astronomical Algorithms”. Retrieved 28 February 2012.
  16. ^ Blanco-Muriel, Manuel; Alarcón-Padilla, Diego C; López-Moratalla, Teodoro; Lara-Coira, Martín (2001). “Computing the Solar Vector” (PDF). Solar Energy. 70 (5): 431–441. Bibcode:2001SoEn…70..431B. doi:10.1016/s0038-092x(00)00156-0.
  17. ^ Ibrahim Reda & Afshin Andreas. “Solar Position Algorithm for Solar Radiation Applications” (PDF). Retrieved 28 February 2012.
  18. ^ “Atmospheric Refraction Approximation”. National Oceanic and Atmospheric Administration. Retrieved 28 February 2012.
  19. ^ Sundial#Noon marks

External links[edit]

  • Solar Position Algorithm, at National Renewable Energy Laboratory’s Renewable Resource Data Center website.
  • Sun Position Calculator, at pveducation.org. An interactive calculator showing the Sun’s path in the sky.
  • NOAA Solar Calculator, at the NOAA Earth System Research Laboratory’s Global Monitoring Division website.
  • NOAA’s declination and sun position calculator
  • HORIZONS System, at the JPL website. Very accurate positions of Solar System objects based on the JPL DE series ephemerides.
  • General ephemerides of the solar system bodies, at the IMCCE website. Positions of Solar System objects based on the INPOP series ephemerides.
  • Solar position in R. Insol package.
Источник

Добавить комментарий