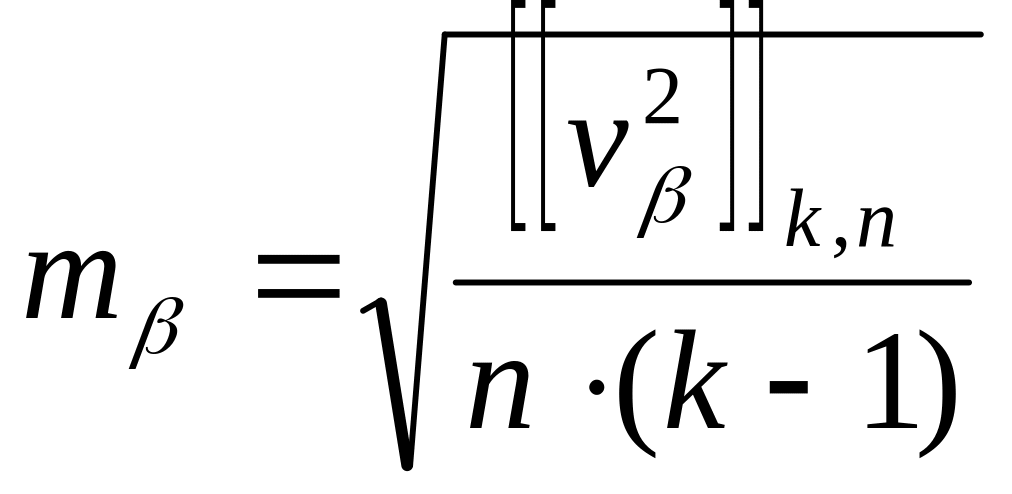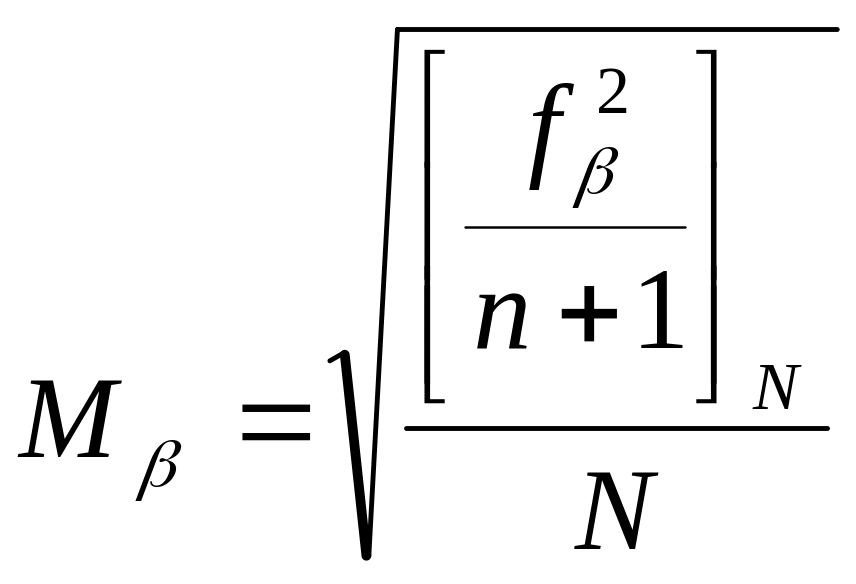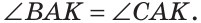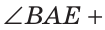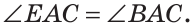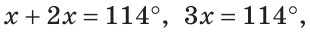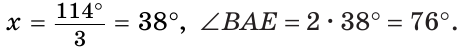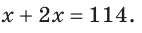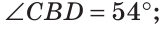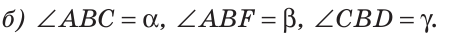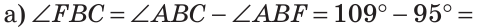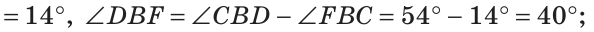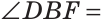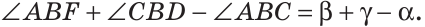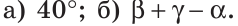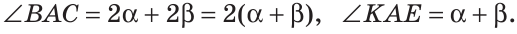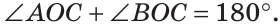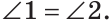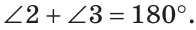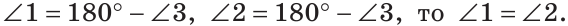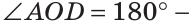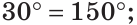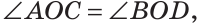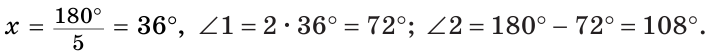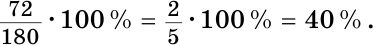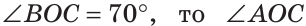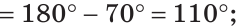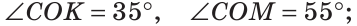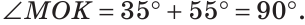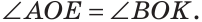Перед
уравниванием всей системы полигонометрических
ходов на объекте необходимо оценить
реальную точность измерений углов и
сторон в ходах. Правильно подсчитанные
СКО измерения углов и сторон
позволяют правильно назначить веса
угловых и линейных измерений и,
следовательно, обеспечить оптимальные
условия для уравнивания отдельных ходов
и систем ходов.
Оценка точности
измерения углов может выполняться:
-
по уклонениям от
среднего в приёмах; -
по разностям двойных
измерений; -
по значениям угловых
невязок в отдельных полигонометрических
ходах.
Соответственно
есть и три разных набора формул для
вычисления СКО измерения углов
.
Для
одного приёма измерения угла
,
где
–
количество приёмов,
–
уклонение угла в каждом приёме от
среднего из всех приёмов. На пункте
число приёмов бывает от 2 до 6, поэтому
надёжность такого подсчёта
невелика, тем более, что на разных пунктах
значение
может получиться разным. При использовании
результатов измерений на
пунктах хода СКО измерения угла одним
приёмом вычисляют по формуле
,
а
СКО среднего значения угла из
приёмов – по формуле
.
Набор формул для
оценки точности измерения углов по
разностям двойных измерений мы приводить
не будем.
СКО измерений углов
по значениям невязок в отдельных ходах
(полигонах) вычисляется по формуле
;
здесь:
–
угловая невязка в ходе,
–
количество сторон в ходе,
–
количество ходов (полигонов).
3.3.5. Уравнивание полигонометрического хода коррелатным способом мнк
В
полигонометрическом ходе, как и в любом
построении, выделяют три типа данных:
исходные данные (это – координаты
первого и последнего пунктов хода и
дирекционные углы примычных направлений
в начале и в конце хода); измеренные
данные (это – горизонтальные углы, их
количество равно
,
и длины сторон хода, их количество равно
);
определяемые данные (это – координаты
определяемых пунктов, их количество
равно
).
Метод наименьших
квадратов имеет две модификации:
параметрический и коррелатный способы
уравнивания. В первом из них количество
нормальных уравнений равно количеству
определяемых неизвестных, во втором –
количеству избыточных измерений; при
ручном счёте тот или иной способ выбирали
в зависимости от соотношения этих чисел;
уравнивание полигонометрического хода,
как правило, выполнялось коррелатным
способом. При машинной обработке на
персональном компьютере количество
нормальных уравнений большого значения
не имеет, и на первый план выступает
простота алгоритма того или иного
способа. По этому показателю параметрический
способ уравнивания оказался предпочтительнее
коррелатного, и в настоящее время
большинство программ уравнивания
геодезических построений составлены
в соответствии с алгоритмом параметрического
уравнивания. Коррелатный способ мы
рассматриваем в историческом и
теоретическом аспектах проблемы
уравнивания.
Как отмечалось в
главе 2, в матричной записи теория
коррелатного способа МНК-уравнивания
имеет следующий вид. Система уравнений
поправок записывается в виде матричного
уравнения
;
здесь
–
матрица коэффициентов уравнений поправок
размером
(
строк и
столбцов);
–
вектор поправок размером
(
строк,
1 столбец);
-вектор
невязок размером
(
строк,
1 столбец);
–
количество измерений,
–
количество определяемых неизвестных,
–
количество избыточных измерений, равное
количеству условий
.
Условие
минимума суммы квадратов поправок
записывается так
.
Система нормальных
уравнений коррелат имеет вид
,
где
–
матрица коэффициентов нормальных
уравнений коррелат,
;
–
матрица обратных весов измеренных
элементов,
;
–
вектор коррелат размером
.
Поправки в измерения выражаются через
коррелаты по формуле
.
В отдельном
полигонометрическом ходе три избыточных
измерения и три условных уравнения
связи.
Первое уравнение –
условное уравнение дирекционных углов
,
где
–
угловая невязка хода; для левых углов
;
–
количество сторон в ходе;
–
поправки в измеренные значения углов.
Ещё
два уравнения – это условные уравнения
координат (X
и
Y):
;
.
Здесь
и
–
координатные невязки;
,
.
Поправки
и
– это поправки к вычисленным значениям
приращений координат, которые являются
зависимыми величинами; по теории МНК в
уравнениях должны стоять поправки к
измеренным элементам
и
.
Преобразование условных уравнений
координат выполняется с помощью
дифференциальных формул приращений
координат
;
.
В
этих формулах через
и
обозначены приращения координат по
сторонам хода;
и
– поправки в дирекционные углы и длины
сторон хода. Если выразить
в километрах, поправки в углы – в
секундах, поправки в длины сторон – в
сантиметрах, то значение
.
Условные уравнения
координат запишутся в виде
,
.
Эти уравнения ещё
не являются окончательными, так как
поправки в дирекционные углы нужно
выразить через поправки в измеренные
углы. Выразив каждый дирекционный угол
через измеренные углы, получим
,
.
Таким образом, все
условные уравнения получены.
Нормальные уравнения
коррелат имеют вид
,
,
.
В
этих уравнениях через
обозначен обратный вес измеренных
величин
.
Приведём полную
запись нормальных уравнений коррелат:
,
Из
решения нормальных уравнений коррелат
находят значения трёх коррелат
.
Поправки в измеренные
значения углов и сторон хода вычисляют
по формулам
,
.
Поправки
в дирекционные углы получают по поправкам
.
Уравненные
углы, дирекционные углы и длины сторон
находят путём введения поправок
.
Уравненные значения приращений координат
находят по уравненным длинам и дирекционным
углам сторон хода. Заключительным
контролем вычислений являются равенства
,
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Добро пожаловать!
Войдите или зарегистрируйтесь сейчас!
Войти
Страница 1 из 5
-
Форумчанин
- Регистрация:
- 3 ноя 2021
- Сообщения:
- 28
- Симпатии:
- 2
Как найти допустимую угловую невязку разомкнутого полигонометрического хода, если стандартное отклонение измерения одного угла =3”, а число вершин=10, а исходные углы(нач. и кон.)безошибочны?
#1
-
Команда форума
Форумчанин- Регистрация:
- 10 дек 2008
- Сообщения:
- 16.919
- Симпатии:
- 4.788
А что сказано об в этом в учебнике/методичке/Интернете?
#2
-
Форумчанин
- Регистрация:
- 1 июн 2019
- Сообщения:
- 3.904
- Симпатии:
- 1.282
- Адрес:
-
Пермь
Если не указана доверительная вероятность или доверительный коэффициент, то задача решения не имеет. Недостаточно исходных данных.
#3
-
Форумчанин
- Регистрация:
- 3 ноя 2021
- Сообщения:
- 28
- Симпатии:
- 2
Он вроде равен 2
— Сообщения объединены, 3 ноя 2021, Оригинальное время сообщения: 3 ноя 2021 —
Не нашел, наверное плохо искал
#4
-
Форумчанин
- Регистрация:
- 1 июн 2019
- Сообщения:
- 3.904
- Симпатии:
- 1.282
- Адрес:
-
Пермь
Приведу пример. Допустимая СКО измерения углов в теодолитном ходе 30″ (30″ = 0.5′). Допустимая невязка равна 1′ ⋅ √n при доверительном коэффициенте равном 2; n – число углов в ходе. Например, при числе углов n = 9 допустимая невязка равняется 3′. Сможете решить свою задачу по аналогии?
#5
-
Форумчанин
- Регистрация:
- 3 ноя 2021
- Сообщения:
- 28
- Симпатии:
- 2
То есть у меня допустимая невязка будет равна 1’√10=3.162′?
#6
-
Форумчанин
- Регистрация:
- 1 июн 2019
- Сообщения:
- 3.904
- Симпатии:
- 1.282
- Адрес:
-
Пермь
Ответ неправильный. У вас другая величина СКО, она равняется 3″. Соответственно, величина перед корнем будет не 1′, а другая. Какая? Вспоминаем про доверительный коэффициент равный 2 и смотрим на пример выше.
#7
-
Форумчанин
- Регистрация:
- 27 июн 2014
- Сообщения:
- 5.650
- Симпатии:
- 1.964
- Адрес:
-
г. Москва
То есть тнбе “это” ненужно. Иди лучше водки жахни.
#8
-
Форумчанин
- Регистрация:
- 3 ноя 2021
- Сообщения:
- 28
- Симпатии:
- 2
Тогда 0.316?
— Сообщения объединены, 3 ноя 2021, Оригинальное время сообщения: 3 ноя 2021 —
Не, ну я же пытаюсь разобраться
#9
-
Форумчанин
- Регистрация:
- 27 июн 2014
- Сообщения:
- 5.650
- Симпатии:
- 1.964
- Адрес:
-
г. Москва
-
Форумчанин
- Регистрация:
- 1 июн 2019
- Сообщения:
- 3.904
- Симпатии:
- 1.282
- Адрес:
-
Пермь
0.316 чего? Дайте ответ в секундах, пожалуйста.
Всему своё время. Сначала учёба, потом приём “вакцины”.
#11
-
Форумчанин
- Регистрация:
- 3 ноя 2021
- Сообщения:
- 28
- Симпатии:
- 2
-
Форумчанин
- Регистрация:
- 27 июн 2014
- Сообщения:
- 5.650
- Симпатии:
- 1.964
- Адрес:
-
г. Москва
Всё “это” бесполезно. Пока напрямую ответ не на пишешь, толку 0. Может так и поступать?!!
#13
-
Форумчанин
- Регистрация:
- 1 июн 2019
- Сообщения:
- 3.904
- Симпатии:
- 1.282
- Адрес:
-
Пермь
Не торопитесь с ответом. Распишите полное решение.
— Сообщения объединены, 3 ноя 2021, Оригинальное время сообщения: 3 ноя 2021 —
А если написать ответ – толк будет? Нет. Главное – мыслительный процесс запустить. А сейчас это сделать не так то просто. Мы – поколение ЕГЭ. Со всеми вытекающими.
#14
-
Форумчанин
- Регистрация:
- 3 ноя 2021
- Сообщения:
- 28
- Симпатии:
- 2
Ну 3”= 0.05′, потом 0.05 умножаем на коэфицент, и число вершин равно 10, значит 0.1’*√10, а ну минут, а не секунд получается?
#15
-
Форумчанин
- Регистрация:
- 27 июн 2014
- Сообщения:
- 5.650
- Симпатии:
- 1.964
- Адрес:
-
г. Москва
Хоть какой то будет: ТС отвяжется. Иначе никакого.
#16
-
Форумчанин
- Регистрация:
- 1 июн 2019
- Сообщения:
- 3.904
- Симпатии:
- 1.282
- Адрес:
-
Пермь
Конечно. Если вы секунды переводите в минуты, то и единицы измерения у вас в итоге – минуты. И никак иначе быть не может. А если не переводить минуты в секунды, какой будет ответ?
— Сообщения объединены, 3 ноя 2021, Оригинальное время сообщения: 3 ноя 2021 —
А он к вам лично и не привязывался. Просто создал тему на форуме.
#17
-
Форумчанин
- Регистрация:
- 3 ноя 2021
- Сообщения:
- 28
- Симпатии:
- 2
Тогда (3”*2)*√10,=18.972′?
— Сообщения объединены, 3 ноя 2021 —
Спасибо большое, хоть разобрался.
#18
-
Форумчанин
- Регистрация:
- 27 июн 2014
- Сообщения:
- 5.650
- Симпатии:
- 1.964
- Адрес:
-
г. Москва
А я не про себя и про него беспокоюсь. А про тебя, “великий учитель”. Чушь всё “это” собачья!
#19
-
Форумчанин
- Регистрация:
- 1 июн 2019
- Сообщения:
- 3.904
- Симпатии:
- 1.282
- Адрес:
-
Пермь
Верно. Только ответ нужно округлить до десятых или сотых долей секунд. Тысячные доли секунд – числа в данном случае абсолютно не значащие. Округление допусков всегда выполняется в меньшую сторону (в сторону “ужесточения” допуска). Например, 18.9″ при округлении до десятых долей секунд. Вопрос для закрепления – если доверительный коэффициент принять равным 3, а СКО измерения угла принять равной 15″ – какая допустимая угловая невязка будет в ходе? Число измеренных углов принять равным 16.
#20
Страница 1 из 5
Поделиться этой страницей
Содержание:
Определение: Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, и частью плоскости, которую они ограничивают.
Два угла называются равными, если их можно совместить наложением.
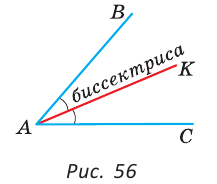
Биссектрисой угла называется луч, который выходит из вершины угла и делит его на два равных угла.
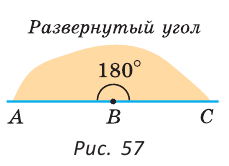
Определение. Развернутым углом называется угол, стороны которого являются дополнительными лучами.
На рисунке 56 луч АК — биссектриса угла ВАС и
На рисунке 57 угол ABC — развернутый, лучи ВА и ВС — дополнительные. Другая (незакрашенная) полуплоскость относительно прямой АС также задает развернутый угол ABC.
Углы измеряются в градусах, минутах, секундах.
Развернутый угол равен 180°; 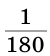
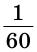
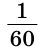
Угол, равный 5 градусов 20 минут и 35 секунд, записывается так: 5°20’35”.
Вместо «градусная мера угла равна 20°» часто говорят «угол равен 20°», вместо найти «градусную меру угла» говорят «найти угол».
Определения
Определение: Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, и частью плоскости, которую они ограничивают.
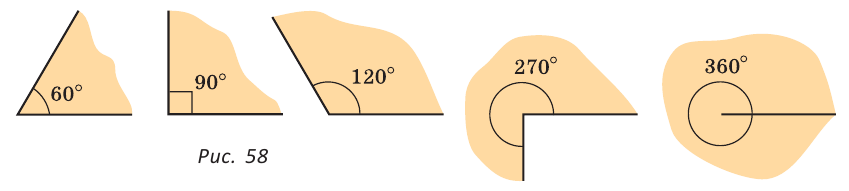
Определение: Угол, равный 90°, называется прямым; угол, меньший 90°, — острым; угол, больший 90°, но меньший 180°, — тупым; угол, равный 360°, называется полным (его стороны совпадают).
На рисунке 58 последовательно изображены: острый угол, равный 60°; прямой угол, равный 90°; тупой угол, равный 120°; угол, равный 270°; и полный угол, равный 360°.
Градусная мера угла является его важной характеристикой. Свойства градусной меры угла: любой угол имеет градусную меру, выраженную некоторым положительным числом; равным углам соответствуют равные градусные меры, а большему углу — большая градусная мера. И наоборот.
Аксиомы
Аксиома измерения углов. Если внутри угла из его вершины провести луч, то он разобьет данный угол на два угла, сумма градусных мер которых равна градусной мере данного угла.
Аксиома откладывания углов. От любого луча в данную полуплоскость можно отложить угол данной градусной меры, и притом только один.
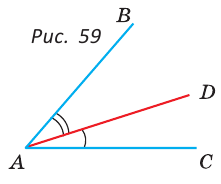
На рисунке 59 луч AD проходит внутри угла ВАС. По аксиоме измерения углов 
Два луча с общим началом задают на плоскости два угла. В дальнейшем будем рассматривать меньший из этих двух углов (если они неразвернутые). Такой угол меньше 180°.
Пример №1
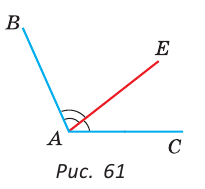
Внутри угла ВАС, равного 114°, из его вершины проведен луч АЕ. Угол ВАЕ в 2 раза больше угла ЕАС. Найти величину угла ВАЕ.
Решение:
Пусть 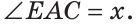
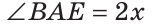
По аксиоме измерения углов
Тогда
Ответ: 76о
Замечания. 1. Возможен другой способ записи решения, когда рядом с буквой 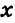
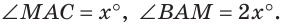
2. В дальнейшем при решении задач не будем ссылаться на аксиому измерения углов.
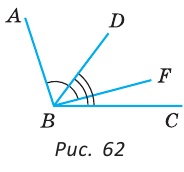
Пример №2
Внутри угла проведены лучи BD и BF (рис. 62).
Найти величину угла DBF, если:
Решение:
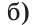
Отсюда
Ответ:
Пример №3
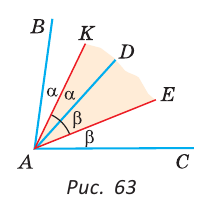
Луч AD делит угол ВАС на два угла BAD и CAD. Доказать, что угол между биссектрисами АК и АЕ углов BAD и CAD равен половине угла ВАС (рис. 63).
Доказательство:
Так как АК иАЕ — биссектрисы, то 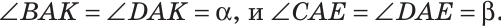
Следовательно, 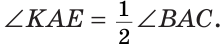
Замечание. В данной задаче мы доказали свойство: «Если внутри угла из его вершины провести луч, то угол между биссектрисами полученных углов равен половине данного угла».
Геометрия 3D
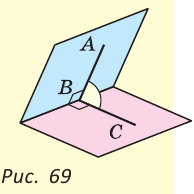
В пространстве при пересечении двух плоскостей образуются двугранные углы. Две полуплоскости с общей границей являются гранями такого двугранного угла, а их граница — его ребром. Измеряется двугранный угол величиной линейного угла, образованного двумя лучами, проведенными в каждой из полуплоскостей из точки на ребре двугранного угла перпендикулярно этому ребру. На рисунке 69 ZABC — линейный угол изображенного двугранного угла.
Геометрия 3D
В пространстве при пересечении двух плоскостей образуются двугранные углы. Две полуплоскости с общей границей являются гранями такого двугранного угла, а их граница — его ребром. Измеряется двугранный угол величиной линейного угла, образованного двумя лучами, проведенными в каждой из полуплоскостей из точки на ребре двугранного угла перпендикулярно этому ребру. На рисунке 69 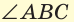
Смежные углы. Вертикальные углы
Определение. Два угла называются смежными, если у них одна сторона общая, а две другие являются дополнительными лучами.
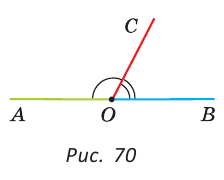
Если на рисунке 70 лучи OA и ОВ дополнительные, то углы АОС и ВОС — смежные.
Теорема (свойство смежных углов). Сумма смежных углов равна 180°.
Дано: 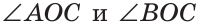
Доказать:
Доказательство:
Из определения смежных углов следует, что лучи OA и ОВ являются дополнительными и поэтому образуют развернутый угол АОВ, равный 180°. Луч ОС проходит между сторонами этого угла, и по аксиоме измерения углов 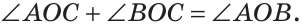
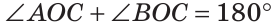
Следствия.
- Если смежные углы равны, то каждый из них прямой.
- Если два угла равны, то равны и смежные с ними углы.
Замечание. Все теоремы курса геометрии 7—9 классов описывают свойства фигур на плоскости.
Определение. Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами к сторонам другого.
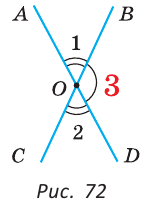
При пересечении двух прямых АС и DB в точке О (рис. 71) получим, что лучи OA и ОС, О В и OD — дополнительные. Поэтому углы AOD и BОС — вертикальные. Углы АОВ и DOC также вертикальные.
Теорема (свойство вертикальных углов). Вертикальные углы равны.
Дано: 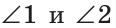
Доказать:
Доказательство:
Углы 1 и 3 смежные, так как лучи OA и OD — дополнительные по определению вертикальных углов. По свойству смежных углов 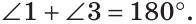
Так как
Теорема доказана.
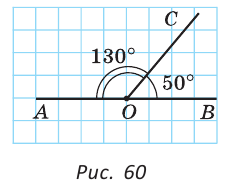
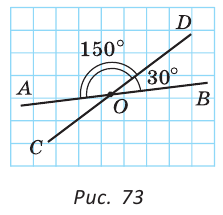
Углом между двумя пересекающимися прямыми называется меньший из образованных ими углов. Если при пересечении прямых АВ и CD (рис. 73) 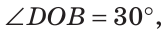
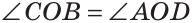
При пересечении двух прямых образуются четыре угла (не считая развернутых). Если один из них 90°, то и остальные по 90° (докажите самостоятельно). Говорят, что прямые пересекаются под прямым углом.
Угол между параллельными прямыми считается равным 0°.
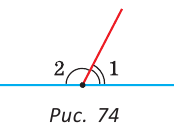
Пример №4
Смежные углы относятся как 2:3. а) Найти величину каждого из углов, б) Определить, сколько процентов развернутого угла составляет меньший угол.
Решение:
а) Пусть 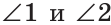
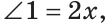
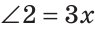
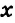
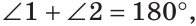
б) Меньшим является 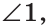
Ответ: 72°, 108°; 40 %.
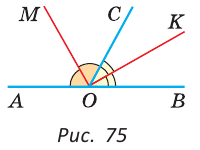
Пример №5
а) Найти угол между биссектрисами ОК и ОМ смежных углов ВОС и АОС (рис. 75), если 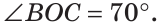
Решение:
а) Если
б) Так как ОМ и ОК — биссектрисы, то
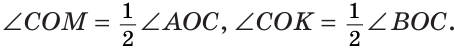
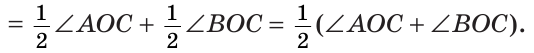
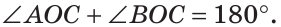
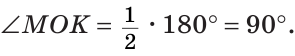
Замечание. Можно было сослаться на ключевую задачу 3* к § 5.
Пример №6
Доказать, что биссектрисы вертикальных углов образуют развернутый угол.
Решение:
а) Пусть ОЕ и ОК — биссектрисы вертикальных углов АОС и BOD (рис. 76). Докажем, что 
б) 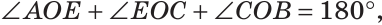
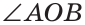
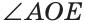
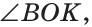
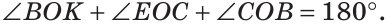

Замечание. Из решения задачи следует свойство: если 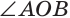
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
- Свойства прямоугольного треугольника
- Расстояние между параллельными прямыми
- Задачи на построение циркулем и линейкой
- Задачи на построение по геометрии