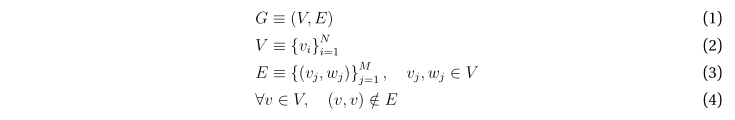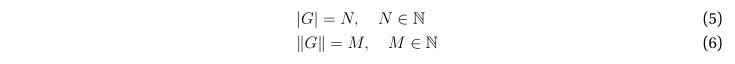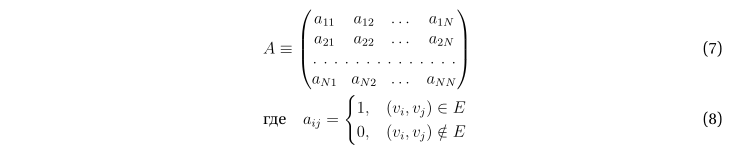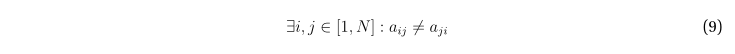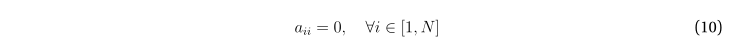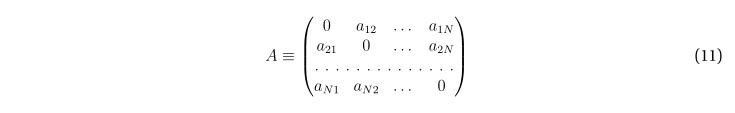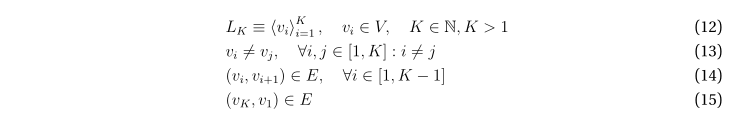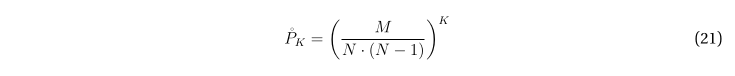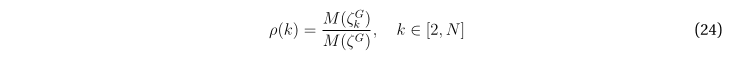Как найти сколько циклов в графе

Оценка количества простых циклов на графе

Введение

В ряде практических приложений возникает необходимость поиска простых циклов на графах, в связи с чем встаёт вопрос об оценке количества вычислительных операций, необходимых для этого, т.е. вычислительной сложности задачи.

Сама по себе задача перебора циклов на конкретном графе не является особенно сложной и легко реализуется средствами практически любого языка программирования, поддерживающего рекурсивные вычисления. Однако поиск методов априорной оценки вычислительных затрат переборного алгоритма, к моему удивлению, не дал вменяемых результатов. Тем не менее, достаточно простые рассуждения позволяют получить требуемую оценку, неплохо согласующуюся с тестовыми данными и позволяющую, помимо прочего, получить некоторую дополнительную информацию о структуре результатов перебора.

Формализация задачи

Итак, для определенности будем рассматривать граф G – ориентированный, без петель.

При этом порядок графа равен, очевидно, N, а количество рёбер – M.

Графу можно взаимно однозначно сопоставить матрицу смежности A.

Вследствие ориентированности графа G соответствующая матрица смежности в общем случае асимметрична:

Условие (4) отсутствия петель в графе приводит к тому, что на главной диагонали матрицы смежности допустимы только нулевые элементы

и матрица, таким образом, имеет вид

Под простым циклом L длины K на графе G будем понимать такую последовательность K неповторяющихся вершин графа, что каждые две последовательные вершины в последовательности, а также последняя и первая вершины в ней, смежны. Далее речь будет идти только о простых циклах; будем, для краткости, называть их просто циклами.

Будем далее обозначать

Оценка количества циклов

Для построения оценочной формулы примем следующее допущение: для графа G нам известны только порядок графа и количество рёбер в нём; точный вид матрицы смежности, какие-либо закономерности её формирования и т.п. нам неизвестны. Другими словами, мы будем считать, что наш конкретный граф был сконструирован в результате стохастического процесса такого рода:

• Были зафиксированы N вершин графа, т.е. множество V.

• Матрица смежности размером N x N была заполнена нулевыми значениями.

• В матрице смежности совершенно случайным образом были выбраны ровно M элементов, не лежащих на главной диагонали, и им были присвоены единичные значения.

• На указанных вершинах в соответствии с матрицей смежности были построены ребра графа E.

С учётом изложенного и (11), вероятность того, что произвольный элемент матрицы смежности вне главной диагонали равен единице, очевидно, равна

Легко увидеть, что выражения (12), (13) определяют циклическое размещение без повторений длины K из генеральной совокупности V размером в N элементов; из комбинаторики известно, что количество различных размещений при этом составляет

Для того, чтобы циклическое размещение из (12), (13) соответствовало циклу на графе G, необходимо, чтобы выполнялись условия (14), (15), т.е. чтобы существовали соответствующие рёбра, или, другими словами, K соответствующих элементов матрицы смежности были равны единице. С учётом (18), вероятность этого составляет

Таким образом, исходя из выбранной модели формирования графа G, произвольное циклическое размещение без повторений, состоящее из K вершин графа, формирует цикл на этом графе с вероятностью (21).

Заметим, что теперь количество циклов длины K на графе можно рассматривать как случайную величину, математическое ожидание которой из (19) и (21) составляет

И, наконец, математическое ожидание количества циклов на графе G с учётом (17) равно

Это и есть искомая оценка.

Замечания и обсуждение

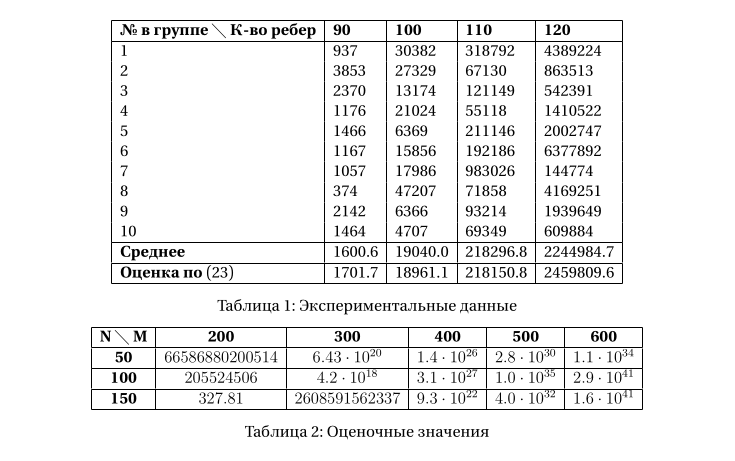
Прежде всего, заметим, что указанная оценка довольно неплохо согласуется с экспериментальными данными. В таблице 1 приведены данные о количестве циклов в графах, полученные переборным методом. Эксперимент охватывал 4 группы графов, в каждой группе содержалось по 10 графов с 50-ю вершинами каждый и количеством рёбер 90, 100, 110 и 120 для каждой из групп соответственно. Несмотря на то, что для каждого конкретного графа количество циклов может заметно отличаться от оценочного, среднее по группе значение достаточно близко к нему.

Далее, стоит отметить, что даже для сравнительно небольших графов оценка (23) предсказывает наличие весьма значительного количества циклов на них; ряд оценочных значений приведен в таблице 2. Это стоит учитывать при планировании вычислений, связанных с перебором циклов на графе: они могут занять несколько больше времени и ресурсов, чем кажется!

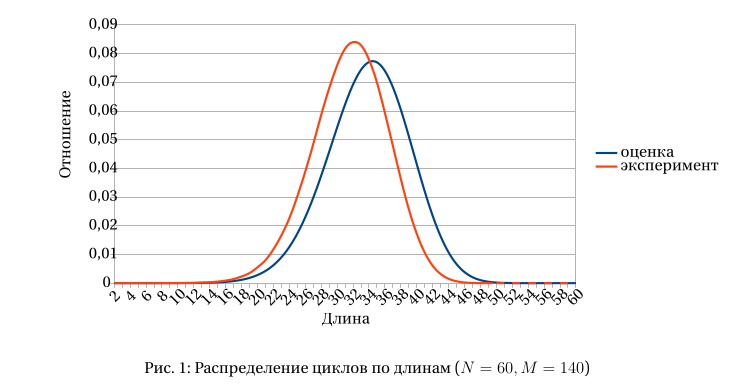
Ещё одним интересным моментом является то, что формула (23) позволяет легко построить функцию, которую можно интерпретировать как оценку плотности распределения циклов по длинам:

На рис. 1 изображены графики оценочной и экспериментальной плотности распределения циклов по длинам на графе с 60 вершинами и 140 рёбрами. Как видно, они довольно неплохо согласуются между собой. При этом под экспериментальной плотностью понимается

где количества циклов в отношении получены прямым подсчётом.

Таким образом, оценка (24) позволяет сделать вполне обоснованное предсказание о характерных длинах циклов на графе.

Остаётся заметить, что хотя рассуждения в статье относятся к случаю простых циклов на ориентированных графах без петель, подобные результаты могут быть получены для прочих типов графов и циклов путём аналогичных рассуждений.

Заключение

Я надеюсь, что полученные результаты заинтересуют читателя, будут кому-то полезны в его практической деятельности и, быть может, послужат толчком к дальнейшим исследованиям в этой области.

The following is a demo implementation in C# (and Java, see end of answer) based on depth first search.

An outer loop scans all nodes of the graph and starts a search from every node. Node neighbours (according to the list of edges) are added to the cycle path. Recursion ends if no more non-visited neighbours can be added. A new cycle is found if the path is longer than two nodes and the next neighbour is the start of the path. To avoid duplicate cycles, the cycles are normalized by rotating the smallest node to the start. Cycles in inverted ordering are also taken into account.

This is just a naive implementation.
The classical paper is: Donald B. Johnson. Finding all the elementary circuits of a directed graph. SIAM J. Comput., 4(1):77–84, 1975.

A recent survey of modern algorithms can be found here

using System;
using System.Collections.Generic;

namespace akCyclesInUndirectedGraphs
{
    class Program
    {
        //  Graph modelled as list of edges
        static int[,] graph =
            {
                {1, 2}, {1, 3}, {1, 4}, {2, 3},
                {3, 4}, {2, 6}, {4, 6}, {7, 8},
                {8, 9}, {9, 7}
            };

        static List<int[]> cycles = new List<int[]>();

        static void Main(string[] args)
        {
            for (int i = 0; i < graph.GetLength(0); i++)
                for (int j = 0; j < graph.GetLength(1); j++)
                {
                    findNewCycles(new int[] {graph[i, j]});
                }

            foreach (int[] cy in cycles)
            {
                string s = "" + cy[0];

                for (int i = 1; i < cy.Length; i++)
                    s += "," + cy[i];

                Console.WriteLine(s);
            }
        }

        static void findNewCycles(int[] path)
        {
                int n = path[0];
                int x;
                int[] sub = new int[path.Length + 1];

                for (int i = 0; i < graph.GetLength(0); i++)
                    for (int y = 0; y <= 1; y++)
                        if (graph[i, y] == n)
                        //  edge referes to our current node
                        {
                            x = graph[i, (y + 1) % 2];
                            if (!visited(x, path))
                            //  neighbor node not on path yet
                            {
                                sub[0] = x;
                                Array.Copy(path, 0, sub, 1, path.Length);
                                //  explore extended path
                                findNewCycles(sub);
                            }
                            else if ((path.Length > 2) && (x == path[path.Length - 1]))
                            //  cycle found
                            {
                                int[] p = normalize(path);
                                int[] inv = invert(p);
                                if (isNew(p) && isNew(inv))
                                    cycles.Add(p);
                            }
                        }
        }

        static bool equals(int[] a, int[] b)
        {
            bool ret = (a[0] == b[0]) && (a.Length == b.Length);

            for (int i = 1; ret && (i < a.Length); i++)
                if (a[i] != b[i])
                {
                    ret = false;
                }

            return ret;
        }

        static int[] invert(int[] path)
        {
            int[] p = new int[path.Length];

            for (int i = 0; i < path.Length; i++)
                p[i] = path[path.Length - 1 - i];

            return normalize(p);
        }

        //  rotate cycle path such that it begins with the smallest node
        static int[] normalize(int[] path)
        {
            int[] p = new int[path.Length];
            int x = smallest(path);
            int n;

            Array.Copy(path, 0, p, 0, path.Length);

            while (p[0] != x)
            {
                n = p[0];
                Array.Copy(p, 1, p, 0, p.Length - 1);
                p[p.Length - 1] = n;
            }

            return p;
        }

        static bool isNew(int[] path)
        {
            bool ret = true;

            foreach(int[] p in cycles)
                if (equals(p, path))
                {
                    ret = false;
                    break;
                }

            return ret;
        }

        static int smallest(int[] path)
        {
            int min = path[0];

            foreach (int p in path)
                if (p < min)
                    min = p;

            return min;
        }

        static bool visited(int n, int[] path)
        {
            bool ret = false;

            foreach (int p in path)
                if (p == n)
                {
                    ret = true;
                    break;
                }

            return ret;
        }
    }
}

The cycles for the demo graph:

1,3,2
1,4,3,2
1,4,6,2
1,3,4,6,2
1,4,6,2,3
1,4,3
2,6,4,3
7,9,8

The algorithm coded in Java:

import java.util.ArrayList;
import java.util.List;

public class GraphCycleFinder {

    //  Graph modeled as list of edges
    static int[][] graph =
        {
            {1, 2}, {1, 3}, {1, 4}, {2, 3},
            {3, 4}, {2, 6}, {4, 6}, {7, 8},
            {8, 9}, {9, 7}
        };

    static List<int[]> cycles = new ArrayList<int[]>();

    /**
     * @param args
     */
    public static void main(String[] args) {

        for (int i = 0; i < graph.length; i++)
            for (int j = 0; j < graph[i].length; j++)
            {
                findNewCycles(new int[] {graph[i][j]});
            }

        for (int[] cy : cycles)
        {
            String s = "" + cy[0];

            for (int i = 1; i < cy.length; i++)
            {
                s += "," + cy[i];
            }

            o(s);
        }

    }

    static void findNewCycles(int[] path)
    {
            int n = path[0];
            int x;
            int[] sub = new int[path.length + 1];

            for (int i = 0; i < graph.length; i++)
                for (int y = 0; y <= 1; y++)
                    if (graph[i][y] == n)
                    //  edge refers to our current node
                    {
                        x = graph[i][(y + 1) % 2];
                        if (!visited(x, path))
                        //  neighbor node not on path yet
                        {
                            sub[0] = x;
                            System.arraycopy(path, 0, sub, 1, path.length);
                            //  explore extended path
                            findNewCycles(sub);
                        }
                        else if ((path.length > 2) && (x == path[path.length - 1]))
                        //  cycle found
                        {
                            int[] p = normalize(path);
                            int[] inv = invert(p);
                            if (isNew(p) && isNew(inv))
                            {
                                cycles.add(p);
                            }
                        }
                    }
    }

    //  check of both arrays have same lengths and contents
    static Boolean equals(int[] a, int[] b)
    {
        Boolean ret = (a[0] == b[0]) && (a.length == b.length);

        for (int i = 1; ret && (i < a.length); i++)
        {
            if (a[i] != b[i])
            {
                ret = false;
            }
        }

        return ret;
    }

    //  create a path array with reversed order
    static int[] invert(int[] path)
    {
        int[] p = new int[path.length];

        for (int i = 0; i < path.length; i++)
        {
            p[i] = path[path.length - 1 - i];
        }

        return normalize(p);
    }

    //  rotate cycle path such that it begins with the smallest node
    static int[] normalize(int[] path)
    {
        int[] p = new int[path.length];
        int x = smallest(path);
        int n;

        System.arraycopy(path, 0, p, 0, path.length);

        while (p[0] != x)
        {
            n = p[0];
            System.arraycopy(p, 1, p, 0, p.length - 1);
            p[p.length - 1] = n;
        }

        return p;
    }

    //  compare path against known cycles
    //  return true, iff path is not a known cycle
    static Boolean isNew(int[] path)
    {
        Boolean ret = true;

        for(int[] p : cycles)
        {
            if (equals(p, path))
            {
                ret = false;
                break;
            }
        }

        return ret;
    }

    static void o(String s)
    {
        System.out.println(s);
    }

    //  return the int of the array which is the smallest
    static int smallest(int[] path)
    {
        int min = path[0];

        for (int p : path)
        {
            if (p < min)
            {
                min = p;
            }
        }

        return min;
    }

    //  check if vertex n is contained in path
    static Boolean visited(int n, int[] path)
    {
        Boolean ret = false;

        for (int p : path)
        {
            if (p == n)
            {
                ret = true;
                break;
            }
        }

        return ret;
    }

}

Совет: уточните формулировку

К сожалению, без точной формулировки задачи ответить на ваш вопрос очень сложно. Для начала, что вы ищете? Простые циклы? Элементы циклического пространства? Обычные циклы? Понимаете ли вы, что для полного графа с n вершинами размер ответа в любой из вышеперечисленных задач не меньше n!? Такой огромный размер ответа (а, значит, и время работы) говорит о том, что с практической точки зрения задача мало полезна (для полного графа с 14 вершинами это порядка 100 миллиардов циклов). Поэтому я крайне рекомендую уточнить постановку/необходимость задачи.

Если всё же нужно решить именно эту задачу

Например, с помощью алгоритмов поиска MST можно найти все фундаментальные циклы графа. Каждый цикл в графе является линейной комбинацией (коэффициенты берутся 0 или 1, сложение — исключающее или циклов) фундаментальных циклов, поэтому, перебрав эти комбинации, и взяв только нужные вам (только связные, или только простые), вы найдёте ответ. Это далеко не самый оптимальный алгоритм (O(2^m), где m — число рёбер), и я не сомневаюсь, что его можно немного улучшить, если уточнить постановку задачи.