Загрузить PDF
Загрузить PDF
Определить площадь плоских фигур в квадратных сантиметрах (также обозначаемых как см2) достаточно просто. В самом легком случае, когда требуется рассчитать площадь квадрата или прямоугольника, она вычисляется произведением длины и ширины. Площадь других фигур (кругов, треугольников и так далее) можно определить с помощью целого ряда специальных математических формул. Также, если потребуется, можно без труда перевести площадь в квадратные сантиметры из других единиц измерения.
-
1
Определите длину измеряемой площади. У квадратов и прямоугольников по четыре стороны, расположенных под прямыми углами относительно друг друга. В случае с прямоугольниками, их противоположные стороны равны между собой, тогда как у квадратов равны все стороны. Измерьте одну из сторон квадрата или большую из сторон прямоугольника, чтобы определить ее длину в сантиметрах.[1]
-
2
Определите ширину измеряемой площади. Далее измерьте в сантиметрах любую из сторон, смежных с той, которую вы измерили в первую очередь. Эта сторона будет находиться под углом в 90 градусов к первой. Вторая мерка будет обозначать ширину квадрата или прямоугольника.[2]
- Так как у квадрата все стороны одинаковы, его длина будет равна ширине. Поэтому у квадрата можно изначально измерить только одну сторону.
-
3
Умножьте длину на ширину. Просто перемножьте длину и ширину фигуры, чтобы определить площадь квадрата или прямоугольника в квадратных сантиматрах.[3]
- Например, допустим, что длина прямоугольника составляет 4 см, а ширина – 3 см. В таком случае площадь фигуры рассчитывается следующим образом: 4 × 3 = 12 квадратных сантиметров.
- В случае с квадратом (по причине равных сторон) можно просто умножить саму на себя длину одной из его сторон (другими словами, возвести ее “в квадрат” или “во вторую степень”), чтобы определить площадь фигуры в квадратных сантиметрах.
Реклама
-
1
Найдите площадь круга по формуле: S = π × r2. Чтобы найти площадь круга в квадратных сантиметрах, необходимо знать расстояние в сантиметрах от центра круга до линии его окружности. Это расстояние называется радиусом окружности. Как только радиус будет известен, обозначьте его буквой r из вышеупомянутой формулы. Умножьте значение радиуса само на себя и на число π (3,1415926…), чтобы узнать площадь круга в квадратных сантиметрах.[4]
- Например, площадь круга с радиусом 4 см составит 50,27 квадратных сантиметра в результате перемножения 3,14 и 16.
-
2
Вычислите площадь треугольника по формуле: S = 1/2 b × h. Площадь треугольника в квадратных сантиметрах вычисляется умножением половины длины его основания b (в сантиметрах) на его высоту h (в сантиметрах). Основанием треугольника выбирается одна из его сторон, тогда как высота треугольника – это перпендикуляр, опущенный к основанию треугольника из противоположной к нему вершины. Площадь треугольника можно вычислить через длину основания и высоту по любой из сторон треугольника и противоположной к ней вершине.[5]
- Например, если длина основания треугольника составляет 4 см, а высота, проведенная к основанию – 3 см, площадь составит: 2 x 3 = 6 квадратных сантиметра.
-
3
Найдите площадь параллелограмма по формуле: S = b × h. Параллелограммы подобны прямоугольникам за одним исключением – их углы не обязательно равны 90 градусам. Соответственно, расчет площади параллелограмма производится аналогичным для прямоугольника способом: длина стороны основания в сантиметрах умножается на высоту параллелограмма в сантиметрах. За основание берут любую из сторон, а высота определяется длиной перпендикуляра к ней из противоположного тупого угла фигуры.[6]
- Например, если длина основания параллелограмма составляет 5 см, а его высота – 4 см, его площадь составит: 5 x 4 = 20 квадратных сантиметров.
-
4
Вычислите площадь трапеции по формуле: S = 1/2 × h × (B+b). Трапеция – это четырехугольник две стороны которого параллельны между собой, а остальные две – нет. Чтобы определить площадь трапеции в квадратных сантиметрах, необходимо знать три мерки (в сантиметрах): длину более длинной параллельной стороны B, длину более короткой параллельной стороны b и высоту трапеции h (определяемую как кратчайшее расстояние между ее параллельными сторонами по перпендикулярному к ним отрезку). Сложите между собой длины двух параллельных сторон, поделите сумму пополам и умножьте на высоту, чтобы получить площадь трапеции в квадратных сантиметрах.[7]
- Например, если более длинная из параллельных сторон трапеции равна 6 см, более короткая – 4 см, а высота – 5 см, площадь фигуры составит: ½ x (6+4) х 5 = 25 квадратных сантиметров.
-
5
Найдите площадь правильного шестиугольника: S = ½ × P × a. Приведенная формула верна только для правильного шестиугольника с шестью равными сторонами и шестью одинаковыми углами. Буквой P обозначается периметр фигуры (или произведение длины одной стороны на шесть, что справедливо для правильного шестиугольника). Буквой a обозначается длина апофемы – расстояние от центра шестиугольника до середины одной из его сторон (точки, расположенной посередине между двумя соседними вершинами фигуры). Перемножьте периметр и апофему в сантиметрах и поделите результат на два, чтобы найти площадь правильного шестиугольника.[8]
- Например, если у правильного шестиугольника шесть равных сторон по 4 см (то есть его периметр P = 6 x 4 = 24 см), а длина апофемы равна 3,5 см, то его площадь составит: ½ x 24 x 3,5 = 42 квадратных сантиметра.
-
6
Вычислите площадь правильного восьмиугольника по формуле: S = 2a² × (1 + √2). Для расчета площади правильного восьмиугольника (с восемью равными сторонами и восемью одинаковыми углами) нужно знать только длину одной из сторон фигуры в сантиметрах (обозначенной в формуле буквой “a”). Подставьте соответствующее значение в формулу и вычислите результат.[9]
- Например, если длина стороны правильного восьмиугольника равна 4 см, то площадь этой фигуры составляет: 2 х 16 x (1 + 1,4) = 32 x 2,4 = 76,8 квадратных сантиметров.
Реклама
-
1
Переведите все мерки в сантиметры, прежде чем производить расчет площади. Чтобы сразу рассчитать площадь в квадратных сантиметрах, необходимо подставлять все параметры в формулу расчета площади также в сантиметрах (это касается, длины, высоты, апофемы и так далее). Поэтому, если ваши исходные данные выражены в других единицах измерения (например, в метрах), сначала их следует перевести в сантиметры. Ниже приведены соотношения наиболее популярных единиц измерения.
- 1 метр = 100 сантиметров
- 1 сантиметр = 10 миллиметров
- 1 дюйм = 2,54 сантиметра
- 1 фут = 30,48 сантиметра
- 1 сантиметр = 0,3937 дюйма
-
2
Чтобы перевести площадь из квадратных метров в квадратные сантиметры, ее следует умножить на 10000 (то есть площадь одного квадратного метра в сантиметрах), или на произведение 100 см на 100 см. Если вы знаете площадь фигуры в квадратных метрах, ее можно перевести в квадратные сантиметры умножением на 10000.[10]
- Например, 0,5 квадратного метра = 0,5 x 10000 = 5000 квадратных сантиметров.
-
3
Чтобы перевести в квадратные сантиметры площадь, выраженную в квадратных дюймах, умножьте ее на 6,4516. Как уже упоминалось, 1 дюйм равен 2,54 сантиметра, тогда как квадратный дюйм составляет 6,4516 квадратных сантиметров (или 2,54 x 2,54). Таким образом, если вам необходимо конвертировать в квадратные сантиметры площадь, равную 10 квадратным дюймам, следует умножить 10 на 6,4516, и у вас получится 64,5 квадратных сантиметров.[11]
- Также следует упомянуть, что в одном гектаре содержится 10000 квадратных метров, тогда как каждый квадратный метр равен 10000 квадратных сантиметров. Поэтому, чтобы выразить один гектар в сантиметрах, следует умножить 10000 на 10000 и получится 100 миллионов квадратных сантиметров.
Реклама
Об этой статье
Эту страницу просматривали 153 706 раз.
Была ли эта статья полезной?
Как найти квадратный сантиметр
Квадратные сантиметры обычно используются для измерения небольших площадей. Это может быть книга, лист бумаги или экран монитора. Найти количество квадратных сантиметров можно как непосредственным измерением, так и с помощью соответствующих геометрических формул.

Вам понадобится
- – калькулятор;
- – линейка.
Инструкция
Чтобы найти количество квадратных сантиметров (площадь) в прямоугольнике, умножьте длину прямоугольника на его ширину. То есть воспользуйтесь формулой:
Ккс = Д * Ш,
где:
Д – длина прямоугольника,
Ш – его ширина, а
Ккс – количество квадратных сантиметров (площадь).
Чтобы площадь получилась в квадратных сантиметрах (см²), длину и ширину прямоугольника предварительно переведите в сантиметры.
Пример: прямоугольник имеет длину 2 см и ширину 15 мм.
Вопрос: скольким квадратным сантиметрам равняется площадь прямоугольника?
Решение:
15 мм = 1,5 см.
2 (см) * 1,5 (см) = 3 (см²).
Ответ: площадь прямоугольника равняется 3 см².
Для нахождения площади прямоугольного треугольника перемножьте длины его катетов и разделите полученное произведение на 2.
Чтобы найти количество квадратных сантиметров в произвольном треугольнике, перемножьте высоту и основание треугольника, затем поделите полученное значение пополам.
Если известны длины сторон треугольника, то для вычисления его площади воспользуйтесь формулой Герона:
Ккс = √(p * (p-а) * (p-b) * (p-с)),
где p – полупериметр треугольника, то есть p=(а+b+с)/2,
где а, b, с – длины сторон треугольника.
Для расчета площади круга воспользуйтесь классической формулой (пи эр квадрат). Если круг неполный (сектор), умножьте площадь соответствующего круга на количество градусов в секторе, а затем разделите на 360.
Длины сторон треугольника и его высота, а также радиус круга должны быть выражены в сантиметрах.
Пример: длина диагонали экрана стандартного монитора составляет 17 дюймов.
Вопрос: сколько квадратных сантиметров занимает экран монитора?
Решение: так как в одном дюйме содержится 2,54 см, то длина диагонали экрана монитора будет равняться 2,54 * 17 = 43,18 см.
Обозначим через a, b, d длину, ширину и величину диагонали экрана, соответственно. Тогда по теореме Пифагора:
d² = a²+b².
Так как соотношение сторон в стандартном (не широкоформатном) дисплее составляет 3:4, то получается: a = 4/3 * b, откуда:
a²+b²=(4/3 * b)² + b²=7/3 * b².
Подставляя значение d=43,18, получаем:
(43,18)² = 7/3 * b².
Следовательно, b=28,268, а=37,691.
Значит площадь экрана равняется: 1065,438 (см²)
Ответ: площадь экрана семнадцатидюймового стандартного монитора составляет 1065,44 см².
Источники:
- 5730 кв дм перевести в кв м и кв см
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Математика
5 класс
Урок №30
Площадь прямоугольника. Единицы площади
Перечень рассматриваемых вопросов:
– понятие площади фигуры;
-единицы измерения площади;
– площадь прямоугольника, квадрата;
– приближенное измерение площади фигуры на клетчатой бумаге.
Тезаурус
Прямоугольник – четырёхугольник, у которого все углы прямые (равны 90 градусам).
Квадрат – прямоугольник, у которого все стороны равны.
Площадь прямоугольника– число, которое показывает, сколько квадратных единиц содержится в прямоугольнике.
Основная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений.// С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Сегодня мы начнём занятие с задачи. Представим, что две девочки пришли в магазин, чтобы купить в подарок подруге на день рождения коробку конфет. На витрине были разложены самые разные наборы сладостей. Девочки решили купить ту коробку, которая больше. А какая из них больше? Как это измерить? Можно сравнить коробки по длине и ширине или просто положить их друг на друга. Но одна коробка оказалась длиннее, а другая – шире. Какая же из них больше? Как это узнать?
Чтобы ответить на эти вопросы, мы поговорим о вычислении площади прямоугольника.
Для начала введём понятие площади фигуры.
Если какую-нибудь площадь можно разбить на n квадратов со стороной, например, 1 см, то получится, что площадь фигуры равна n см2.
За единицу измерения площадей принимают не только квадратный сантиметр, но и квадратный миллиметр, квадратный дециметр, квадратный метр.
Это площади квадратов, длины сторон которых равны одному миллиметру, одному дециметру и одному метру соответственно.
Далее покажем, что подразумевается под площадью прямоугольника.
Площадью прямоугольника называют число, которое показывает, сколько квадратных единиц содержится в прямоугольнике.
Называя величину площади, необходимо указывать единицу измерения.
Например, прямоугольник состоит из пятнадцати квадратов; площадь каждого квадрата составляет 1 см2. Следовательно, площадь всего прямоугольника равна 15 см2.
S = 15 см2
Решим задачу.
Найдём площадь прямоугольника ABCD, который имеет длину АВ = 6 см и ширину ВС = 7 см. Для этого разделим его на квадратные сантиметры. Сосчитаем, сколько квадратных сантиметров в нём содержится.
В прямоугольнике ABCD квадратный сантиметр содержится сорок два раза – значит, его площадь равна: S = 42 см2 = 6 см · 7 см = АВ · ВС.
Поэтому можно ввести формулу для нахождения площади прямоугольника.
Чтобы найти площадь прямоугольника S, нужно умножить его длину a на ширину b.
S = а · b
Так как квадрат является прямоугольником, у которого все стороны равны, то его площадь можно вычислить как квадрат его стороны а.
S = а · а = а2
Далее найдём соотношение между единицами измерения площадей.
Так как 1 см = 10 мм, следовательно, 1 см2 = 102 мм2 = 100 мм2.
Соответственно, 1 дм2 = 102 см2 = 100 см2
1 м2 = 102 дм2 = 100 дм2
1 км2 = 10002 м2 = 1000000 м2.
Для измерения небольших площадей земельных участков используют специальную единицу измерения– ар, которая равна площади квадрата со стороной десять метров. В обиходе ар называют соткой, так как один ар– это сто квадратных метров.
1 ар = 102 м2 = 100 м2
Для обмера больших земельных территорий ввели единицу один гектар, которая соответствует площади квадрата со стороной сто метров.
1 га = 1002 м2 = 10000 м2 = 100 а
Решим задачу.
Найдём площадь прямоугольника.
При измерении окажется, что стороны с недостатком приближенно равны трём и пяти сантиметрам. Значит, площадь прямоугольника больше, чем произведение этих сторон, то есть пятнадцати квадратных сантиметров.
S (с недостатком) = 3 · 5 = 15 см2
Если взять стороны в приближении с избытком, то есть четыре и шесть сантиметров, то площадь будет меньше произведения сторон, а именно равна двадцати четырём квадратным сантиметрам.
S (с избытком) = 4 · 6 = 24 см2
Таким образом, площадь этого прямоугольника варьируется от пятнадцати до двадцати четырёх квадратных сантиметров.
15 см2 < S < 24 см2
Отметим, что равные прямоугольники имеют равную площадь.
Сравним площади закрашенных квадратов, изображённых на рисунке.
Решение: если посмотреть внимательно на рисунок, то можно заметить, что все фигуры расположены в одинаковых квадратах со стороной 9 клеток, следовательно, площади этих квадратов одинаковы. На верхнем рисунке шесть фигур – два квадрата и четыре треугольника. На нижнем рисунке пять фигур – квадрат и четыре треугольника.
Далее внимательно посмотрим на треугольники – все они одинаковы, следовательно, их площади одинаковы. И, если из больших квадратов, в которых расположены наши фигуры, мы отнимем сумму площадей равных треугольников, получится, что площади оставшихся фигур (квадратов) верхней и нижней части равны.
Примеры заданий из Тренировочного модуля
№ 1. В квадрате все стороны равны 5 см. Чему равна площадь квадрата?
Решение: Для нахождения площади квадрата воспользуемся следующей формулой:
S = а2 = 5см · 5 см = 25 см2
№ 2. Найдите площадь фигуры.
Решение: сначала следует разделить фигуру на три прямоугольника, далее найти площадь каждого по формулеS=а · b, а затем сложить площади трёх фигур. Или можно найти площадь прямоугольника со сторонами 10 см и 3 см, она равна 30 см2. Далее вычислить площадь вырезанной фигуры со сторонами 2см на 1 см, она составляет 2см2. И вычесть 2 см2 из 30см2.
Ответ: 28 см2.
Калькулятор для расчета площади
Данный онлайн-калькулятор позволяет рассчитать площадь различных геометрических фигур, таких как:
|
|
Для удобства расчетов вы можете выбрать единицу измерения (миллиметр, сантиметр, метр, километр, фут, ярд, дюйм, миля). Также полученный результат можно конвертировать в другую единицу измерения путем выбора её из выпадающего списка.
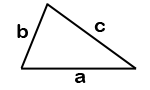
Способ нахождения площади треугольника:
| a= |
|
| b= | |
|
c= |
Вычислить
Рассчитать площадь круга, если известен:
| r= |

|
Вычислить
Способ нахождения площади параллелограмма:
| a= |

|
| h= | |
Вычислить
Рассчитать площадь сектора круга, если известен:
|
r= |

|
|
θ= |
Вычислить
Способ нахождения площади трапеции:
Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры.
| Метрические единицы измерения площади: | |
| Квадратный метр, производная единица системы СИ 1 м2 = | 1 са (сантиар) |
| Квадратный километр – 1 км2 = | 1 000 000 м2 |
| Гектар – 1 га = | 10 000 м2 |
| Ар (сотка) – 1 а = | 100 м2 (сотка как правило применяется для измерения земельных участков и равна 100 м2 или 10м х 10м) |
| Квадратный дециметр, 100 дм2 = | 1 м2; |
| Квадратный сантиметр, 10 000 см2 = | 1 м2; |
| Квадратный миллиметр, 1 000 000 мм2 = | 1 м2. |
Данный онлайн-калькулятор удобен при расчете площадей помещений и земельных участков.
Как рассчитать площадь прямоугольника
На данной странице калькулятор поможет рассчитать площадь прямоугольника онлайн. Для расчета задайте длину сторон или длины диагоналей и угол между ними.
Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам).
Через стороны
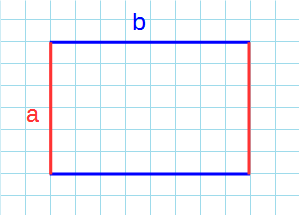
Формула для нахождения площади прямоугольника через стороны:
a, b – стороны прямоугольника.
Через диагонали и угол между ними
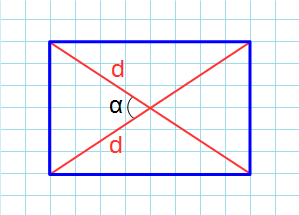
Формула для нахождения площади прямоугольника через диагонали и угол между ними:
d – диагональ; α – угол между диагоналями.

















