Задание
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объем жидкости равен 190 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
Решение
- Объем конуса равен 1/3 произведения его высоты на площадь основания, а площадь основания — это площадь круга:
V = 1/3*h*Socн = 1/3*h*π*(D/2)2.
- Для решения данной задачи будем рассматривать объемы двух конусов:
- объем конуса, у которого уровень жидкости равен 1/2 высоты – Vмен
- объем конуса, наполненный доверху – Vбол
- Нам известно, что высота большего конуса в два раза больше высоты меньшего.
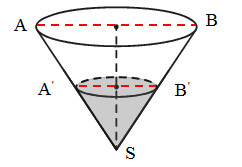
- Определим во сколько раз основание меньшего конуса меньше большего. Для удобства введем буквенные обозначения, как показано на рисунке, и рассмотрим треугольники АSВ и А‘SВ‘. Данные треугольники подобны. Из этого делаем вывод, что основание АВ больше основания А‘В‘ в два раза, так как высота треугольника АSВ в два раза больше высоты треугольника А‘SВ‘.
- АВ и А‘В‘ являются диаметрами оснований конусов. Запишем, чему равен объем большего конуса в буквенном виде:
Vбол = 1/3*h*π*(D/2)2
- Теперь запишем, чему равен объем меньшего конуса и преобразуем получившееся выражение:
Vмен = 1/3*h/2*π*(D/2/2)2 = (1/3*h*π*(D/2)2)/(2*4) = Vбол/8 = 190 мл
- Найдем объем заполненного цилиндра, то есть объем большего конуса:
Vбол/8 = 190 мл
Vбол = 190*8 = 1520 мл
- Осталось вычислить, сколько жидкости необходимо долить, чтобы заполнить сосуд доверху:
Vбол–Vмен = 1520–190 = 1330 мл необходимо долить.
Ответ: 1330
Казак
Мыслитель
(6510)
7 лет назад
Данные исчерпывающие.
Объём конуса равен 1/3 h * Pi * r^2
h – высота конуса, r – радиус основания
Стакан состоит из большого конуса, положительного, радиусом основания 3 см и высотой 30 см, и отрицательного малого, радиусом 2 см и высотой 20 см.
V = Pi/3 * (30*9 – 20*4) = Pi/3*190 = 198,97 см^3
Мистер Х
Просветленный
(24021)
7 лет назад
Не нужна высота.
Задача решается составлением уравнения.
Мне лень его писать.
Сам пиши.
Простая задача.
И интегралы тут не нужны, как пишут ёбнутые.
Huge WorldМыслитель (5739)
7 лет назад
а если стакан 50 см высотой – то диаметр на высоте воды будет почти такой же как и внизу (то есть ближе к 4 см). так что надо…
Виктор —-
Ученик
(246)
7 лет назад
Взять мерную колбу и налить полный стакан. среднюю лини получившейся трапеции прими за диаметр и посчитай объем цилиндра. по моему все известно
nmjdt nfuie
Гуру
(4779)
7 лет назад
Объём усечённого конуса равен
V=(1/3)*pi*h*(R^2+R*r+r^2)
pi-число пи
R-больший радиус
r-меньший радиус
h-высота
^-возведение в степень
Дано:
R = 6/2 = 3 см
r = 4/2 = 2см
h = 10 см
Решение:
V=(1/3)*pi*h*(R^2+R*r+r^2)=(1/3)*pi*10*(3^2+3*2+2^2)=
=(1/3)*pi*10*(9+6+4)=(1/3)*pi*10*19=(1/3)*190*pi= 198,967 см^3
1л=1дм^3
1дм^3=1000см^3
1л=1000мл=1000см^3
Ответ: 199 мл
Huge WorldМыслитель (5739)
7 лет назад
но я не понял, если стакан высотой 50 см – то там меньше воды налито на 10 см ( тк диаметр воды вверху постепенно растет и на 10 см он маленький), а если стакан 12 см – то вверху диаметр воды почти 6(значит больше налито)
© 2007 – 2023 Сообщество учителей-предметников “Учительский портал”
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены

В сосуд в виде конуса налита жидкость до 1/3 высоты. Объем налитой жидкости 4 мл. Сколько миллилитров жидкости нужно долить ,чтобы заполнить сосуд доверху. как решить???
Светило науки – 11974 ответа – 404277 раз оказано помощи
Отношение высоты заполненного жидкостью конуса к высоте всего конуса равно 1:3 (1/3).
Тогда отношение объёма конуса, заполненного жидкостью, к объёму всего конуса составит: 1:3³ или 1:27.
Объём с жидкостью (1 часть) равна 4 мл, тогда объём всего конуса равен:
4*27=108 (мл)
4 мл жидкости уже налиты, значит осталось долить:
108-4=104 (мл)
Ответ: 104 мл жидкости нужно долить ,чтобы заполнить сосуд доверху .

Конус — тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной
точки (вершины конуса) и проходящих через плоскую поверхность.
Иногда конусом называют часть такого тела, имеющую ограниченный объём и полученную объединением
всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае
называют основанием конуса, а конус называют опирающимся на данное основание).
Воспользуйтесь онлайн калькулятором для расчета объема пирамиды: объем конуса, онлайн расчет.
Для расчета объемов других тел воспользуйтесь этим калькулятором: калькулятор объемов фигур.
- Отрезок, соединяющий вершину и границу основания, называется образующей конуса.
- Объединение образующих конуса называется образующей (или боковой) поверхностью конуса.
Образующая поверхность конуса является конической поверхностью.
- Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого
отрезка), называется высотой конуса.
- Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине
конуса, внутри конуса).
- Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и
ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром, то
конус называется прямым. При этом прямая, соединяющая вершину и центр основания, называется
осью конуса.
- Косой (наклонный) конус — конус, у которого ортогональная проекция вершины на основание не
совпадает с его центром симметрии.
- Круговой конус — конус, основание которого является кругом.
- Прямой круговой конус (часто его называют просто конусом) можно получить вращением
прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось
- Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно
эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный
- Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся
между вершиной и основанием, называется усечённым конусом, или коническим слоем.
Объем конуса вычисляется по формуле:
где R — радиус основания конуса,
Усеченный конус.
Усеченный конус получится, если в конусе провести сечение, параллельное основанию. Тело
ограниченное этим сечением, основанием и боковой поверхностью конуса называется усеченным конусом.
Объем усеченного конуса вычисляется по формуле:
h — высота конуса
r — радиус верхнего основания
R — радиус нижнего основания
или по формуле объема усечённого конуса (не обязательно прямого и кругового):
S1 и S2 — площади соответственно верхнего (ближнего к вершине) и нижнего оснований,
h и H — расстояния от плоскости соответственно верхнего и нижнего основания до вершины.
УСЛОВИЕ:
В сосуд в виде конуса налита жидкость до 1/3 высоты. Объём налитой жидкости 16 мл. Сколько миллилитров жидкости нужно долить, чтобы наполнить со суд доверху?
РЕШЕНИЕ:
записываешь формулу нахождения объема для полного конуса V=1/3*пи*Н*R^2
теперь пишешь формулу для конуса, объем жидкости которого нам известен
V = 1/3* Pi * (Н/3) * (R/3)^2 = 1/3*1/27*Pi*H*R^2 = 16
Дальше 16 делить на 1/27, чтобы привести к объему полного конуса получаешь 432
и 432 — 16 = 416 мл нужно долить чтобы заполнить весь объем
ремонт своими руками
Данный калькулятор рассчитывает массу, объём усеченного конуса, а так же объём жидкости находящейся в усеченном конусе.
Выберите материал из которого сделано изделие:
Вид материала







