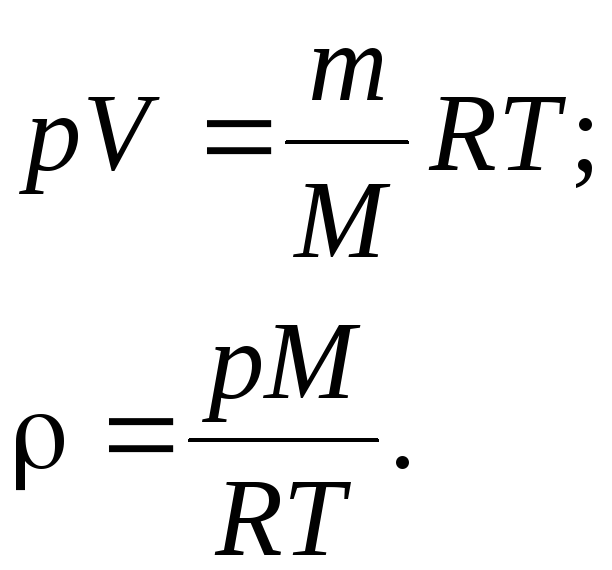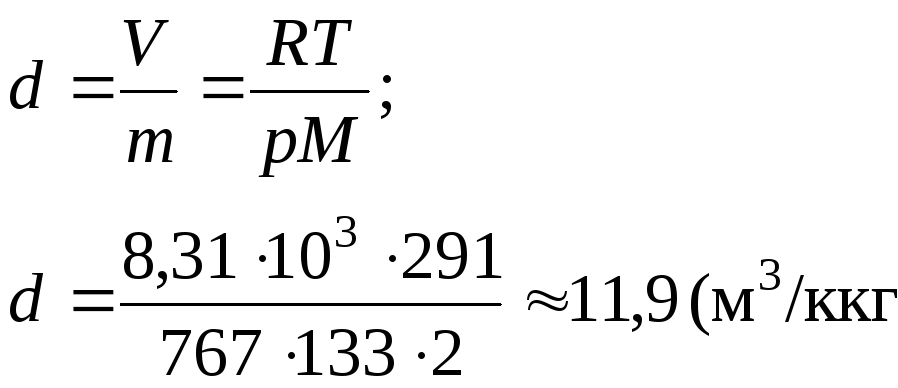Как найти сколько молей в сосуде - Сайт, где вы сможете решить свои вопросы

Задача. Определите число молей идеального газа, находящегося в сосуде вместимостью displaystyle V=540 см³ при нормальных условиях.

Дано:

displaystyle V=540 см³

Найти:
displaystyle nu — ?

Решение

Думаем: фраза «при нормальных условиях» говорит о ещё нескольких добавочных дано (нормальное давление — Па, нормальная температура — displaystyle T=273 К). При заданных условиях (давление, объём и температура), химическое количество вещества может быть найдено исходя из уравнения Менделеева-Клапейрона:

displaystyle PV=nu RT (1)

Решаем: выразим из (1) искомое химическое количество

$displaystyle nu =frac{PV}{RT}$ (2)

Считаем: учитывая $displaystyle ^{2}$ м $displaystyle ^{-2}$ *кг*с $displaystyle ^{-1}$ *К $displaystyle ^{-1}$ *Моль $displaystyle ^{-1}$ и переведя объём в единицы СИ $displaystyle ^{3}$ см $displaystyle =540*{{10}^{-6}}$ $displaystyle ^{3}$ м $displaystyle ^{3}$ , получим

$displaystyle nu =frac{1*{{10}^{5}}*540*{{10}^{-6}}}{8,31*273}approx 23,8*{{10}^{-3}}$ моль

Ответ: $displaystyle nu approx 23,8*{{10}^{-3}}$ моль.

Ещё задачи на тему «Химическое количество вещества«.

Источник

Demon …

Знаток

(357),
закрыт

11 лет назад

Лучший ответ

Nighthawk

Высший разум

(118781)

11 лет назад

У меня два варианта. Либо в большинстве школ в восьмом классе учитель не может написать на доске формулу вычисления количества вещества:

n = m/M = V/Vm = N/Na

и объяснить, как делать перерасчет между массой, объемом и количеством частиц вещества, или ученики не в состоянии воспринять действия сложнее сложения.
_______________
Подставь в формулу и реши:
M(O2) = 32 г/моль
Na (число Авогадро) = 6.02*10^23

Остальные ответы

Похожие вопросы

Источник

Как найти количество молекул в молях

Молекула обладает настолько мизерными размерами, что количество молекул даже в крохотной крупинке или капле какого-либо вещества будет просто грандиозным. Оно не поддается измерению с помощью обычных методов исчисления.

Для определения, сколько молекул находится в том или ином количестве вещества, используется понятие «моль». Моль – это такое количество вещества, в котором находится 6,022*10^23 его молекул (или атомов, или ионов). Эта громадная величина носит название «постоянная Авогадро», она названа в честь знаменитого итальянского ученого. Величина обозначается NA. С помощью постоянной Авогадро можно очень легко определить, сколько молекул содержится в любом количестве молей любого вещества. Например, в 1,5 молях содержится 1,5*NA = 9,033*10^23 молекул. В тех случаях, когда требуется очень высокая точность измерения, необходимо использовать значение числа Авогадро с большим количеством знаков после запятой. Наиболее полная его величина составляет: 6,022 141 29(27)*10^23.

Определить, сколько молей содержится в каком-то количестве вещества, очень просто. Для этого нужно только иметь точную формулу вещества и таблицу Менделеева под рукой. Предположим, у вас есть 116 граммов обыкновенной поваренной соли. Вам нужно определить, сколько молей содержится в таком количестве (и, соответственно, сколько там молекул)?

Прежде всего вспомните химическую формулу поваренной соли. Она выглядит следующим образом: NaCl. Молекула этого вещества состоит из двух атомов (точнее, ионов): натрия и хлора. Какова ее молекулярная масса? Она складывается из атомных масс элементов. С помощью таблицы Менделеева вы знаете, что атомная масса натрия приблизительно равна 23, а атомная масса хлора – 35. Следовательно, молекулярная масса этого вещества составляет 23 + 35 = 58. Масса измеряется в атомных единицах массы, где за эталон принят самый легкий атом – водорода.

А зная молекулярную массу вещества, вы тут же сможете определить и ее молярную массу (то есть массу одного моля). Дело в том, что численно молекулярная и молярная масса полностью совпадают, у них только разные единицы измерения. Если молекулярная масса измеряется в атомных единицах, то молярная – в граммах. Следовательно, 1 моль поваренной соли весит приблизительно 58 граммов. А у вас, по условиям задачи, 116 граммов поваренной соли, то есть 116/58 = 2 моля. Умножив 2 на постоянную Авогадро, вы определите, что в 116 граммах хлорида натрия находится примерно 12,044*10^23 молекул, или примерно 1,2044*10^24.

Источник

Вода в сосуде занимает объем 10 см3 при температуре 4°C. Какое число молекул воды содержится в сосуде? Найти массу молекулы и оценить ее размер.

Оцените сложность задачи:

0 голосов, средняя сложность: 0.0000

Решения задачи

Данные задачи: Вода в сосуде

Объем воды	V	$10^{-5}$	м3
Температура воды	t	4	°C
Число молекул	N	?
Масса молекулы	$m_{0}$	?
Размер молекулы	d	?

Число молекул можно найти, если определить число молей воды в занимаемом ею объеме

$ N = N_{A}ν $

Зная химическую формулу воды

$ H_{2}O $

с помощью периодической системы элементов Д.И. Менделеева находим ее молярную массу

$ μ = (1×2+16)×10^{-3}=18×10^{-3}frac{кг}{моль} $

Число молей

$ ν = frac{m}{μ} $

Массу вещества находим

$ m = ρV $

$ρ – плотность воды$

узнаем из таблиц физических величин, ее значение заданное при определенной температуре

Откуда находим число молекул

$ N = N_{A}frac{ρV}{μ}=6,02×10^{23}frac{1000×10^{-5}}{18×10^{-3}}=3,34×10^{23} молекул $

Масса одной молекулы

$ m_{0} = frac{μ}{N_{A}}=frac{18×10^{-3}}{6,02×10^{23}}=2,99×10^{-26} кг $

Чтобы оценить размер молекулы d, сделаем допущение: молекулы плотно прилегают друг к другу и образуют кубическую ячейку. Тогда объем молекулы

$ V_{0} = d^{3} $,

$ d = sqrt{V_{0}} $

С другой стороны, объем занимаемый одной молекулой, можно найти зная объем воды и число молекул в этом объеме

$ V_{0} = frac{V}{N}=frac{μ}{ρN_{A}} $

И тогда находим

$ d = sqrt{frac{V}{N}}=sqrt{frac{10^{-5}}{3,34×10^{23}}}=sqrt{frac{μ}{ρN_{A}}}=3,11×10^{-10} м $

Ответ:

$ 3,34×10^{23} – число молекул; $

$ 2,99×10^{-26} кг – масса молекулы $

$ размер молекулы 3,11×10^{-10} м $

Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь

Источник

Примеры решения задач

1. Молекулярно-кинетическая теория идеальных газов

Задача
1. Определить,
сколько киломолей и молекул водорода
содержится в объеме 50 м³
под давлением 767 мм рт. ст. при температуре
18°С. Какова плотность и удельный объем
газа?

Дано:

V = 50 м³

Ρ = 767
мм. рт. ст.  767·133 Па

Т = 291 К

М = 2
кг/моль

Решение:

На основании уравнения
Менделеева – Клайперона:

устанавливаем
число киломолей ν,
содержащихся в заданном объеме V.
Зная р –
давление,
V
– объем, Т
– температуру газа, R
– молярную газовую постоянную

ν
– ?

N
– ?

ρ
– ?

d
– ?

можно
определить
ν:

Число
молекул N,
содержащихся
в данном объеме, находим, используя
число Авогадро N_А
(которое определяет какое количество
молекул содержится в одном киломоле).
Общее количество молекул, находящихся
в массе m
данного
газа, может быть установлено, так как
известно число молей ν.

Подставляя
в формулу число киломолей, устанавливаем
число молекул, содержащихся в объеме
V:

Плотность
газа ρ = m/V
определяем
из уравнения Менделеева – Клайперона:

Подставляя
числовые значения в единицах СИ в
формулу, определим плотность газа:

Удельный
объем газа d
определяем из уравнения Менделеева –
Клайперона:

(м³/кг).

Ответ:
11,9 м³/кг.

Задача
2. В сосуде
объемом 2 м³
находится смесь 4 кг гелия и 2 кг
водорода при температуре 27°С. Определить
давление и молярную массу смеси газов.

Дано:

V = 2 м³

m₁= 4 кг

М₁= 4·10^-3кг/кмоль

m₂= 2 кг

М₂= 2·10^-3кг/кмоль

Т₁= 300 К

Решение:

Воспользуемся
уравнением Менделеева – Клайперона,
применив его к гелию и водороду:

(1)

(2)

где
р₁
– парциальное
давление гелия; m₁–
масса
гелия;

р
– ?

М
– ?

М₁
– его молярная
масса; V
– объем
сосуда; Т
– температура газа;
R = 8,31 Дж/(моль·К)
–молярная газовая постоянная; р₂–парциальное
давление водорода; m₂– масса
водорода; М₂
– его молярная масса.

По
закону Дальтона:
(3)

Из
уравнений (1) и (2) выразим р₁и р₂
и подставим
в уравнение (3):

(4)

С
другой стороны, уравнение Менделеева
– Клайперона для смеси газов имеет вид:

(5)

Сравнивая
(4) и (5) найдем молярную массу смеси газов
по формуле:

,
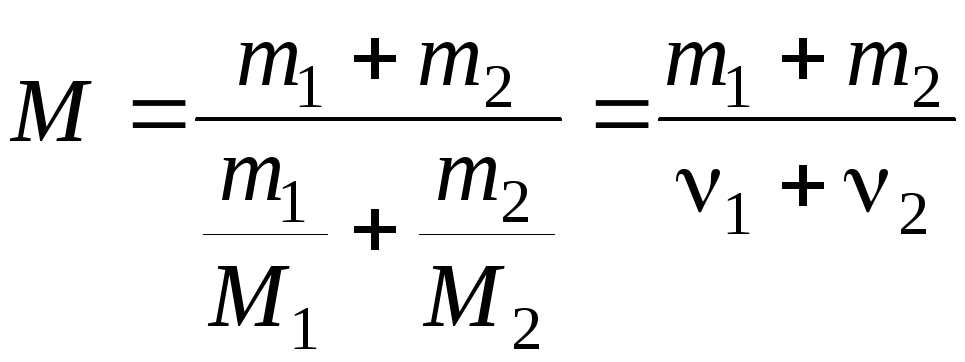
(6)

где
ν₁
и ν₂
– число молей гелия и водорода
соответственно.

(кг/моль).

Ответ:
3·10^-3 кг/моль.

Задача
3. При каком
давлении средняя длина свободного
пробега молекул водорода <λ> = 2,5
см при температуре 68°С? Диаметр молекул
водорода принять равным d = 2,3·10
^–10м.

Дано:

<λ>= 2,5·10^-2
м

Т= 341 К

d= 2,3·10^-10м

N_A= 6,02·10²⁶кмоль^-1

Решение:

Давление
водорода при температуре Т
можно найти по уравнению Менделеева-
Клайперона, в котором удобно ввести
число молекул n₀
в 1 м³.

р
– ?

Это
проводится следующим образом:

;

;

;

где
N_A
– число
Авогадро и k
– постоянная Больцмана.

Следовательно,
Так как,
имеем.

Число
молекул в 1 м³
выразим через среднюю длину свободного
пробега. Из формулы
,
находим
Таким
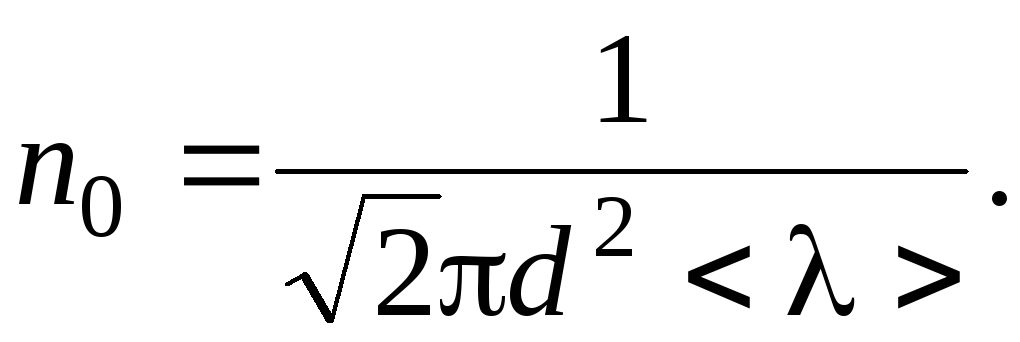
образом:

(Па).

Ответ:
0,8 Па.

Задача
4. Определить
плотность разреженного азота, если
средняя длина свободного пробега молекул
10 см. Какова концентрация молекул?

Дано:

< λ > = 10
см = 0,1
м

Решение:

Средняя
длина пробега молекулы определяется
формулой:

р
– ?

n₀
– ?

,
(1)

где
d
– эффективный
диаметр молекул (для азота d = 0,31·10
^–9м).

Концентрацию
молекул найдем из равенства:

, (2)

где
N_A
– число
Авогадро; М = 28·10
^–3кг/моль
– молярная масса азота.

Решая
совместно уравнения (1) и (2), находим:

(кг/м³).

Ответ:
1,09·10^-6 кг/м³.

Задача 5.
Вычислить
коэффициент внутреннего трения и
коэффициент диффузии кислорода,
находящегося при давлении 0,2 МПа и
температуре 280 К.

Дано:

p = 2·10⁵Па

d = 2,9·10^-10м

М = 32·10^-3кг/моль

Т = 280 К

Решение:

На
основании представлений молекулярно
– кинетической теории газов коэффициент
внутреннего трения идеального газа
(динамическая вязкость) и коэффициент
диффузии определяются по формулам:

η
– ?

D
– ?

(1);

(2),

где
ρ –
плотность газа; < λ >
– средняя длина свободного пробега
молекул; <υ_ар>
– средняя арифметическая скорость
молекул.

Из
(1) и (2) следует (3)

Среднюю
арифметическую скорость и среднюю длину
свободного пробега молекул находим по
формулам:

(4)

,
(5)

где
R = 8,31 Дж/(моль·К) – молярная
газовая постоянная; Т – термодинамическая
температура;
d = 2,9·10 ^–10м – эффективный
диаметр молекулы кислорода; n₀ – число
молекул в 1 м³(концентрация).

Из
уравнения Менделеева – Клайперона
определяем n₀

(см. задачу
3):
(6)

где
р
– давление; k
= 1,38·10 ^–23Дж/К –
постоянная Больцмана.

Подставляя
(6) в уравнение (5), получаем:. (7)

Окончательный
вид расчетной формулы для коэффициента
диффузии найдем, подставляя выражения
(4) и (7) в уравнение (2):

.
(8)

Плотность
кислорода определяется по формуле:.
С учетом (6) имеем:. (9)

Подставляя
(9) и (8) в (3), получаем расчетную формулу
для коэффициента внутреннего трения:

Вычисляем:

Ответ:
.

Задача
6. Наружная
поверхность кирпичной стены площадью
25 м²
и толщиной 37 см имеет температуру
259 К, а внутренняя поверхность–293 К.
Помещение отапливается электроплитой.
Определить ее мощность, если температура
в помещении поддерживается постоянной.
Теплопроводность кирпича 0,4 Вт/(м·К).