|
Произвольный прямоугольник имеет всего две оси симметрии, то есть в его плоскости мы можем найти только две прямых, при обороте вокруг которых, одна часть прямоугольника совпадет со второй частью. Эти прямые проходят через центр пересечения диагоналей прямоугольника и параллельны его сторонам. Иначе говоря проходят через средины противоположных сторон. Вот как это смотрится в рисунке по клеткам, оси симметрии m и l:
В частном случае, если стороны прямоугольника равны, то есть он является квадратом, то у него появляются две дополнительные оси симметрии – те самые диагонали квадрата, на рисунке прямые s и k:
автор вопроса выбрал этот ответ лучшим Геометрическая фигура прямоугольник относится к самым простым и в то же время является одной из основных фигур в геометрии. Если в прямоугольнике провести диагонали, то их точке пересечения будет и центром фигуры, и центром симметрии. Через центр симметрии можно провести очень много прямых но только две, которые будут параллельны сторонам, будут осями симметрии. В случае, когда прямоугольник является одновременно ромбом, параллелограммом и квадратом, его диагонали (их две) – также будут осями симметрии. Если диагонали прямоугольника пересекаются под прямым углом, то он имеет четыре оси симметрии, в остальных случаях – две оси.
РУДЬКО 5 лет назад Совершенно естественно, что прямоугольник имеет две оси симметрии.Каждая из них проходит через середины противоположных сторон. Есть одно исключение для прямоугольников.Это квадрат.Как известно, квадрат- это прямоугольник , у которого все стороны равны между собой. Так вот, у квадрата будет четыре оси симметрии. Это две линии, соединяющие середины противоположных сторон, а также диагонали квадрата.
На картинке также изображён ромб, но его можно принимать во внимание только в том случае, если ромб является квадратом.В остальных случаях ромб прямоугольником не является. Потому как прямоугольник- это четырёхугольник, у которого все углы прямые.
Nelli4ka 5 лет назад Тут нужно сразу заметить: квадрат тоже можно назвать прямоугольником, у которого, правда, все стороны равны. Потому сделаем поправочку и найдем оси симметрии для прямоугольника, который не является квадратом. Для этого нам нужно разделить пополам сначала две его более короткие стороны и соединить линией – так мы получим первую ось, а потом – разделить пополам более длинные, тогда мы получим вторую ось симметрии, вот так:
А вот в квадрате, кстати, осей симметрии уже больше – не две, а целых четыре (две еще проходят по диагоналям, из угла в угол). У ромба, также как и у прямоугольника, осей симметрии две.
Alexgroovy 5 лет назад Чтобы ответить на вопрос, нужно знать, что из себя представляет ось симметрии прямоугольника. Таким термином обозначается любая прямая, которая проходит через точку пересечения диагоналей и при этом сохраняется параллельность сторонам. Прямоугольник имеет 2 оси симметрии и это доказывается в курсах математики и геометрии.
На рисунке видно как проходят оси симметрии прямоугольника. У квадрата таких осей больше (4), а у равностороннего треугольника – 3. Если это именно прямоугольник, то он имеет две оси симметрии. Из середин горизонтальных и вертикальных сторон. Если же этот прямоугольник является ещё и квадратом, то тогда у него имеется четыре оси симметрии. Две как у прямоугольника, а две другие являются диагоналями квадрата. Вот рисунок, на котором можно посмотреть где проходят эти оси симметрии в прямоугольнике и в квадрате:
KillNUR 5 лет назад Прямоугольник – плоская фигура у которой противоположные стороны равны и параллельны. Осей симметрии у прямоугольнике две. Каждая из них проходит через середины противоположных сторон. Линии проходящие через противоположные углы прямоугольника не будут осями симметрии, так как при вращении фигуры по таким осям половинки не будут совпадать. дольфаника 5 лет назад Чтобы убедиться, сколько прямоугольник имеет осей симметрии на самом деле, начертим прямоугольник и отметим центр фигуры, который находится на пересечении прямых, проходящих через середины сторон фигуры. Выходит две оси симметрии, как показано на таблице. Симметричные фигуры равны по всем сторонам и величинам углов.
Rafail 8 лет назад Прямоугольник имеет три оси симметрии второго порядка. Две из них лежат в плоскости прямоугольника и проходят через середины противоположных сторон. Третья ось симметрии перпендикулярна плоскости прямоугольника и проходит через его центр (точку пересечения диагоналей). PRAVDA911 5 лет назад Из школьного курса геометрии нам известно, что у прямоугольника имеется две оси симметрии и это мы можем проверить на рисунке, начертив оси симметрии.
А вот если взять квадрат – то у него уже мы можем наблюдать все четыре оси симметрии.
alexm12 8 лет назад Обычный прямоугольник имеет две оси симметрии проходяших через середины противоположных сторон. Частный случай прямоугольника – квадрат имеет четыре оси симметрии, две добавочные проходят через противоположные углы. Знаете ответ? |
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Прямоугольник – это четырехугольник, у которого все углы прямые.
На рис. 1 изображен прямоугольник АВСD.
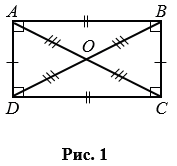
Отрезки АВ и СD, АD и ВС – противолежащие стороны прямоугольника. Противолежащие стороны прямоугольника не имеют общих точек. В прямоугольнике противолежащие стороны равны, тогда на рис. 1 в прямоугольнике АВСD: АВ = DС, АD = ВС.
Отрезки АВ и АD, АD и DC, DC и ВС, АВ и ВС – соседние или смежные стороны. Смежные стороны – стороны, которые имеют общую вершину. Смежные стороны прямоугольника имеют специальные названия: длина и ширина.
Отрезки АС и ВD – диагонали прямоугольника. Диагонали прямоугольника соединяют противолежащие вершины. Диагонали прямоугольника равны и точкой пересечения делятся пополам. Так на рис. 1 АС = ВD и ОА = ОВ = ОС = ОD.
Периметр – это сумма длин всех сторон многоугольника. Обозначается периметр буквой 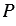 .
.
Учитывая, что в прямоугольнике противоположные стороны равны, его периметр вычисляется по формуле: 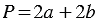 или
или 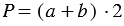 , где
, где 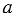 и
и 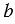 смежные стороны прямоугольника (длина и ширина).
смежные стороны прямоугольника (длина и ширина).
Площадь прямоугольника обозначается буквой 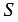 . Площадь прямоугольника равна произведению его смежных сторон, т.е. если
. Площадь прямоугольника равна произведению его смежных сторон, т.е. если 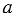 и
и 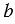 смежные стороны прямоугольника, то его площадь
смежные стороны прямоугольника, то его площадь 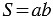 .
.
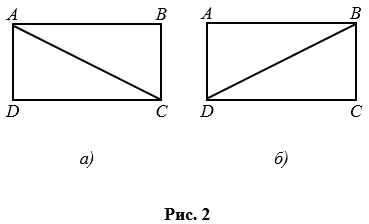
Каждая диагональ прямоугольника делит его на два равных треугольника. На рис. 2, 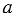 диагональ АС делит прямоугольник АВСD на два равных треугольника АВС и АDС, т.е.
диагональ АС делит прямоугольник АВСD на два равных треугольника АВС и АDС, т.е. 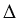 АВС =
АВС = 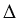 АDС, а на рис. 2, б диагональ ВD делит прямоугольник АВСD на два равных треугольника ВАD и ВСD, т.е.
АDС, а на рис. 2, б диагональ ВD делит прямоугольник АВСD на два равных треугольника ВАD и ВСD, т.е.
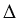 ВАD =
ВАD = 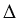 ВСD.
ВСD.
Прямоугольник, у которого все стороны равны, называют квадратом.
Ось симметрии
Прямоугольник имеет ось симметрии. Ось симметрии прямоугольника – это прямая, проходящая через средины противоположных сторон прямоугольника. У прямоугольника две оси симметрии, на рис. 3 прямые 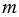 и
и 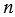 оси симметрии прямоугольника АВСD.
оси симметрии прямоугольника АВСD.
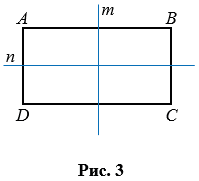
Если лист бумаги перегнуть по прямым 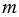 (или
(или 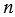 ), то две части прямоугольника, лежащие по разные стороны от прямой
), то две части прямоугольника, лежащие по разные стороны от прямой 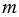 (или
(или 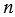 ), совпадут.
), совпадут.
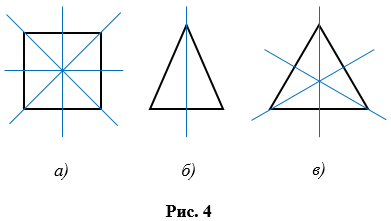
Существуют и другие фигуры, которые имеют ось симметрии, такие фигуры называют симметричными относительно прямой. Так, например, квадрат имеет четыре оси симметрии (рис. 4, 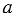 ), равнобедренный треугольник одну ось симметрии (рис. 4, б), а равносторонний треугольник – три оси симметрии (рис.4, в).
), равнобедренный треугольник одну ось симметрии (рис. 4, б), а равносторонний треугольник – три оси симметрии (рис.4, в).
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Плоскость
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Угол. Обозначение углов
Прямой и развернутый угол
Чертежный треугольник
Измерение углов. Транспортир. Виды углов
Треугольник и его виды
Окружность, круг, шар
Цилиндр, конус
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 677,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 938,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1342,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 363,
Мерзляк, Полонский, Якир, Учебник
Номер 366,
Мерзляк, Полонский, Якир, Учебник
Номер 371,
Мерзляк, Полонский, Якир, Учебник
Номер 567,
Мерзляк, Полонский, Якир, Учебник
Номер 921,
Мерзляк, Полонский, Якир, Учебник
Номер 1080,
Мерзляк, Полонский, Якир, Учебник
Номер 1118,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 327,
Мерзляк, Полонский, Якир, Учебник
Номер 667,
Мерзляк, Полонский, Якир, Учебник
Номер 776,
Мерзляк, Полонский, Якир, Учебник
Номер 1179,
Мерзляк, Полонский, Якир, Учебник
Номер 1180,
Мерзляк, Полонский, Якир, Учебник
Номер 1308,
Мерзляк, Полонский, Якир, Учебник
Задание 127,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 191,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 721,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 916,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 81,
Мерзляк, Полонский, Якир, Учебник
Номер 82,
Мерзляк, Полонский, Якир, Учебник
Номер 378,
Мерзляк, Полонский, Якир, Учебник
Номер 409,
Мерзляк, Полонский, Якир, Учебник
Номер 411,
Мерзляк, Полонский, Якир, Учебник
Номер 892,
Мерзляк, Полонский, Якир, Учебник
Номер 1111,
Мерзляк, Полонский, Якир, Учебник
Номер 1112,
Мерзляк, Полонский, Якир, Учебник
Задание 401,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 502,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8 класс
Номер 67,
Мерзляк, Полонский, Якир, Учебник
Номер 313,
Мерзляк, Полонский, Якир, Учебник
Номер 450,
Мерзляк, Полонский, Якир, Учебник
Если в четырехугольнике все углы прямые, то его называют прямоугольником.
На рисунке 125 изображен прямоугольник ABCD.
Стороны AB и BC имеют общую вершину B. Их называют соседними сторонами прямоугольника ABCD. Также соседними являются, например, стороны BC и CD.
Соседние стороны прямоугольника называют его длиной и шириной.
Стороны AB и CD не имеют общих вершин. Их называют противоположными сторонами прямоугольника ABCD. Также противолежащими являются стороны BC и AD.
Противолежащие стороны прямоугольника равны.
На рисунке 125 AB = CD, BC = AD. Если длина прямоугольника равна a, а ширина − b, то его периметр вычисляют по уже знакомой тебе формуле:
P = 2a + 2b
Прямоугольник, у которого все стороны равны, называют квадратом (рис. 126).
Проведем прямую l, проходящую через середины двух противолежащих сторон прямоугольника (рис. 127). Если лист бумаги перегнуть по прямой l, то две части прямоугольника, лежащие по разные стороны от прямой l, совпадут.
Аналогичным свойством обладают фигуры, изображенные на рисунке 128. Такие фигуры называют симметричными относительно прямой. Прямую l называют осью симметрии фигуры.
Итак, прямоугольник − это фигура, имеющая ось симметрии. Также ось симметрии имеет равнобедренный треугольник (рис. 129).
Фигура может иметь более одной оси симметрии. Например, прямоугольник, отличный от квадрата, имеет две оси симметрии (рис. 130), а квадрат − четыре оси симметрии (рис. 131). Равносторонний треугольник имеет три оси симметрии (рис. 132).
Изучая окружающий мир, мы часто встречаемся с симметрией. Примеры симметрии в природе показаны на рисунке 133.
Объекты, имеющие ось симметрии, легко воспринимаются и приятные для глаза. Недаром в Древней Греции слово “симметрия” служило синонимом слов “гармония”, “красота”.
Идея симметрии широко используется в изобразительном искусстве, архитектуре (рис. 134).
Какова симметрия прямоугольника? Есть ли у прямоугольника ось симметрии и центр симметрии?
Утверждение
 Прямоугольник имеет две оси симметрии.
Прямоугольник имеет две оси симметрии.
Осями симметрии прямоугольника являются прямые, проходящие через точку пересечения диагоналей параллельно сторонам.
Доказательство:
 Пусть O — точка пересечения диагоналей прямоугольника ABCD, K и F — точки пересечения прямой, проходящей через точку O параллельно стороне AB, со сторонами AD и BC. Тогда
Пусть O — точка пересечения диагоналей прямоугольника ABCD, K и F — точки пересечения прямой, проходящей через точку O параллельно стороне AB, со сторонами AD и BC. Тогда
![]()
Прямоугольные треугольники AOK и DOK равны по катету и гипотенузе (OK- общий катет, OA=OD по свойству диагоналей параллелограмма). Следовательно, AK=DK, то есть прямая FK проходит через середину стороны AD.
Отметим на стороне AB произвольную точку X. Проведём прямую через точку X прямую, перпендикулярную прямой FK. Точки пересечения этой прямой с прямыми FK и CD обозначим через P и X1.
Четырёхугольники AXPK и KPX1D — прямоугольники (так как у них все углы прямые). Следовательно, XP=AK, PX1=KD. А так как AK=DK, то и XP=PX1. Значит, X1 — точка, симметричная точке X относительно прямой FK.
Имеем: точка, симметричная относительно прямой FK произвольной точке прямоугольника, также принадлежит прямоугольнику.
Точки F и K симметричны сами себе относительно прямой FK.
Таким образом, FK — ось симметрии прямоугольника.
Аналогично доказывается, что прямая, проходящая через точку O параллельно AD является осью симметрии ABCD.
Что и требовалось доказать.
Утверждение.
Прямоугольник — центрально симметричная фигура.
Центром симметрии параллелограмма является точка пересечения его диагоналей.
Так как параллелограмм — центрально-симметричная фигура с центром симметрии в точке пересечения диагоналей, то это верно и для частного случая параллелограмма — прямоугольника.
Давайте представим себе такую историю.
– Саша, чем ты занимаешься? – поинтересовался
у друга Паша.
– Папа научил меня делать самолётик оригами!
– восхищался Саша. – Посмотри, как круто летает такой самолётик!
– Да… его полёт завораживает! – наблюдал за
самолётиком Паша. – Только вот я бы уточнил, что искусство создания бумажных
самолётиков называется аэрогами или бумажная
авиация. Это одна из техник оригами, при которой необходимо не только
сложить красивую фигурку, похожую на оригинал, но и предусмотреть её лётные
характеристики. Самолёты из бумаги были известны более 2000 лет назад. Однако
тогда это были не самолётики, а птички.
Датой создания бумажного самолётика считается
1909 год, но более популярной датой является 1930 год. Тогда основатель
известной компании по аэродинамике Lockheed
Corporation Джек Нортроп
заинтересовался, как из бумаги сделать самолёт.
– А зачем этому человеку нужны были бумажные
самолётики? – поинтересовался Паша.
– Изобретатель хотел протестировать на
бумажных самолётах свои новые идеи, – продолжил Паша. – Использование бумажной
подделки в воздухе помогало правильно подбирать форму для будущих летательных
аппаратов.
– Как же это интересно! – с восторгом сказал
Саша.
– И это ещё не всё! – продолжил Паша. – В
наши дни бумажная авиация, или аэрогами, получила
мировую известность. Каждый человек знает, как сложить элементарный самолётик и
запустить его. Но на сегодняшний день это уже не просто забава, а серьёзное
увлечение, по которому проводят соревнования по всему миру.
– Вот бы
мне побывать на таких соревнованиях, – сказал Саша.
– Обязательно побываешь! – подбодрил друга
Паша. – Главное верить в свою мечту! Ну и, конечно же, тебе ещё будет полезным
познакомиться с условиями создания и схемами бумажных самолётиков. Одними из
главных условий создания самолётика являются использование бумаги прямоугольной
или квадратной формы и чёткое соблюдение симметрии.
– Ого! – задумался Саша. – Вот про
прямоугольные и квадратные формы я всё знаю, а про симметрию совсем ничего, –
расстроился он.
– А давай спросим у Электроши,
– предложил Паша. – Он точно всё знает!
– Ребята, прежде чем я вам расскажу о
прямоугольниках и симметрии, давайте немного разомнёмся и выполним устные задания,
– предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас
должно было получиться!
– А теперь поговорим о прямоугольниках, –
предложил Электроша. – И сразу начнём с вопроса: как
вы понимаете, что такое прямоугольник?
– Прямоугольник – это
четырёхугольник, у которого все углы прямые, – ответил Паша.
– Молодец! – похвалил Пашу Электроша. – Посмотрите: на листе изображён прямоугольник ABCD. Вы уже знакомы с элементами
многоугольников. Назовите элементы нашего прямоугольника.
– Прямоугольник ABCD имеет 4 вершины: А, B, C и D, 4 одноимённых
угла и 4 стороны: AB, BC, CD и DA – ответил Саша.
– Всё верно! – подтвердил Электроша.
– Посмотрите: стороны AB и BC
имеют общую вершину B.
Такие стороны называют соседними сторонами прямоугольника ABCD. Также соседними сторонами
будут стороны BC и CD с общей вершиной C, CD и DA с общей вершиной D, DA и AB с общей вершиной А.
Соседние стороны прямоугольника являются его
измерениями, и их называют длиной и шириной.
– А что вы можете сказать о сторонах,
например, AB и CD нашего прямоугольника ABCD? – спросил у ребят Электроша.
– Стороны AB и CD не имеют общих вершин, – ответили мальчишки.
– Молодцы! – похвалил ребят Электроша. – Такие стороны называют противолежащими
сторонами прямоугольника ABCD. Также противолежащими будут стороны BC и AD. Запомните! Противолежащие стороны прямоугольника
равны.
– А теперь посмотрите: на листке изображён
прямоугольник ABCD,
его противолежащие стороны равны. Если длину прямоугольника обозначить буквой а, а ширину – буквой b, то его периметр можно вычислить по формуле:
P = 2a + 2b.
– Среди прямоугольников есть особые, –
продолжил Электроша, – у которых все стороны имеют
одну и ту же длину. Вы, конечно, помните, что такие прямоугольники называют квадратами.
Если длину стороны квадрата обозначить буквой а, то
его периметр можно вычислить по формуле: P = 4a.
– А теперь давайте проведём небольшой
эксперимент. Возьмите лист бумаги прямоугольной формы и сложите его пополам
так, чтобы противолежащие стороны совпали. Затем разверните этот лист. Что вы
можете сказать о двух частях, получившихся в результате сгиба листа? – спросил
у ребят Электроша.
– Видно, что две части нашего прямоугольного
листа, лежащие по разные стороны от линии сгиба, совпадают.
– Молодцы! – похвалил ребят Электроша. – Прямую, которую мы получили в результате сгибания
листа, называют осью симметрии.
Запомните! Ось симметрии – это прямая (или
воображаемая линия), которая делит геометрическую фигуру на две зеркально
одинаковые фигуры. Фигуру, которая имеет ось симметрии, называют симметричной
относительно прямой.
– Скажите, сколько осей симметрии имеет
прямоугольник? – спросил Электроша.
– Так как
у прямоугольника 2 пары противолежащих сторон, то через их середины можно
провести 2 оси симметрии, –
сказал Паша.
– Правильно! А, может, вы ещё сможете
привести примеры симметричных фигур в геометрии?
– Например, квадрат, – начал Саша. – У
квадрата тоже 2 пары противолежащих сторон, значит, через их середины можно
провести 2 оси симметрии.
– Саша, ты чуть-чуть не досчитался! – сказал Электроша. – Вы уже знакомы с таким понятием, как
диагональ. Напомню, что диагональ – это отрезок, соединяющий
любые две несоседние вершины.
Если лист квадратной формы сложить пополам по
диагоналям, то заметим, что и эти пары частей совпадут относительно линий
сгиба.
– Значит, у квадрата 4 оси симметрии? –
уточнил Саша.
– Верно! – ответил Электроша
– Квадрат имеет 4 оси симметрии: 2 оси симметрии проходят через середины
противолежащих сторон и 2 – через диагонали квадрата.
Также осями симметрии обладают и некоторые
треугольники. Так, например, в равнобедренном треугольнике можно провести 1 ось
симметрии, а в равностороннем – 3.
– С симметрией вы очень часто встречаетесь и
в жизни. Люди с давних времён используют симметрию в рисунках, орнаментах,
предметах быта, архитектуре, искусстве.
Даже многие буквы нашего алфавита обладают
симметрией.
Однако больше всего восхищает симметрия в
природе, где не было вмешательства человеческой руки. Её можно наблюдать в
форме листьев и цветов растений, окраске и расположении различных органов
животных, в форме кристаллических тел.
В порхающей бабочке и сказочной зимней
снежинке.
Объекты, которые обладают осью симметрии,
всегда легко воспринимаются и приятны для глаза. Недаром в Древней Греции слово
«симметрия» служило синонимом слов «гармония», «красота». Симметрия
означает соразмерность, наличие определённого порядка в расположении частей.
– А теперь, ребята, давайте посмотрим, как вы
всё поняли, и выполним несколько заданий.
Задание первое: боксёрский ринг – это
площадка квадратной формы со стороной 7 м. Ринг огорожен тройным канатом.
Сколько метров каната нужно для одного ринга?
Решение: чтобы узнать, сколько понадобится
метров каната для ринга, нужно знать периметр ринга. Мы знаем, что ринг имеет
форму квадрата со стороной 7 м. Применяя формулу для вычисления периметра
квадрата, получаем, что наш ринг имеет периметр 28 м. Так как ринг огорожен
тройным канатом, то для одного ринга понадобится 84 метра каната.
Следующее задание: сколько осей симметрии
имеет шестиугольник с равными сторонами?
Решение: так как, по условию, шестиугольник
имеет равные стороны, а их 6, значит, можно провести 3 оси симметрии через
середины противолежащих сторон. Также можно провести ещё 3 оси симметрии через
диагонали шестиугольника. Тогда всего получим 6 осей симметрии.
Ось симметрии – это прямая (или воображаемая линия), которая
делит геометрическую фигуру на две зеркально одинаковые фигуры.
Фигуру, которая имеет ось симметрии, называют
симметричной относительно прямой.
У прямоугольника 2 оси симметрии, у квадрата
– 4, у равнобедренного треугольника – 1, а у равностороннего – 3.









