Как найти сколько ребер у многогранника

План урока:

Понятие многогранника

Теорема Эйлера

Призма

Типичные задачи на призмы

Понятие многогранника

Ранее мы уже познакомились с тетраэдром и параллелепипедом. Поверхность тетраэдра состоит из 4 треугольников, а параллелепипеда – из 6 параллелограммов. Они являются частными случаями такой фигуры, как многогранник.

Надо понимать, что под многогранником понимают одновременно как поверхность, составленную из многоуг-ков, так и тот объем, который эта поверхность ограничивает. Иногда, чтобы отличать два этих понятия, используют термин «поверхность многогранника».

Каждый многоугольник, образующий поверхность многогранника, именуется гранью многогранника. При этом предполагается, что любые две соседние грани находятся в разных плос-тях.

Многоугольники, образующие поверхность многогранника, имеют свои стороны,которые именуют ребрами многогранника. Вершины же этих многоуг-ков именуют вершинами многогранников. Можно утверждать, что ребра – это отрезки, по которым пересекаются соседние грани. В свою очередь вершины – это точки, где пересекаются соседние ребра. Отрезок, соединяющий две вершины, которые не принадлежат одной грани, именуется диагональю многогранника. Важно отметить, что каждое ребро принадлежит ровно 2 граням. Вершина принадлежит как минимум трем граням, однако может принадлежать и большему их числу.

Если все точки многогранника находятся по одну сторону от любой плос-ти, проходящей через какую-либо грань многогранника, то он называется выпуклым. В противном случае, если через одну из граней проходит плос-ть, «разрезающая» многогранник на две других фигуры, многогранник именуют невыпуклым. На бытовом уровне это означает, что выпуклый многогранник можно поставить на ровную поверхность (например, стол) на любую грань. А вот у невыпуклого многогранника найдется такая грань, на которую его поставить нельзя. Покажем несколько примеров:

На рисунке у невыпуклых многогранников красным цветом показаны плос-ти, которые рассекают многогранник. На эти грани не получится «поставить» многогранник – будет мешать выступающая часть. Заметим, что в выпуклом многограннике всякая диагональ лежит внутри фигуры. А вот у невыпуклого многогранника можно соединить вершины отрезком, лежащим вне объема фигуры. Добавим, что у выпуклого многогранника каждая грань обязательно является выпуклым многоугольником.

Теорема Эйлера

У каждого многогранника можно подсчитать количество граней, вершин и ребер. Например, у тетраэдра 4 грани, 4 вершины и 6 ребер. В свою очередь у параллелепипеда уже 6 граней, 8 вершин и 12 граней. Есть ли какая-то взаимосвязь между этими числами?

Можно заметить, что если у тетраэдра сложить число вершин и граней, а далее вычесть из суммы количество ребер, то получится число 2:

4 + 4 – 6 = 2

Если выполнить такие же действия для параллелепипеда, то снова получится двойка:

6 + 8 – 12 = 2

Оказывается, это не просто совпадение. Для любого выпуклого многогранника справедлива теорема Эйлера:

Мы не будем доказывать эту теорему, так как ее доказательство достаточно сложное. Отдельно отметим, что для невыпуклых многогранников эта теорема может и не выполняться.

Задание. Известно, что некоторый выпуклый многогранник состоит из 20 граней и имеет 30 ребер. Сколько у него вершин?

Решение. Запишем теорему Эйлера:

Задание. Поверхность выпуклого многогранника составлена из 12 пятиугольников. Сколько у такого многогранника ребер и вершин?

Решение. У многогранника будет ровно 12 граней. Попробуем подсчитать количество ребер. Так как каждая представляет собой пятиугольник, то все вместе они имеют 12•5 = 60 ребер. Однако при этом мы каждое ребро подсчитали дважды, ведь любое ребро принадлежит строго 2 граням. То есть на самом деле есть только 60:2 = 30 ребер. По теореме Эйлера легко подсчитаем и количество вершин:

Задание. Выпуклый многогранник имеет 8 граней, из них 4 – это четырехугольники, а ещё 4 – пятиугольники. Сколько у него ребер и вершин?

Решение. Как и в предыдущей задаче, снова сложим количество сторон всех граней:

Задание. Существует ли выпуклый многогранник, каждая грань которого является шестиугольником?

Предположим, что такой многогранник существует, и у него Г граней. Тогда его грани имеют в сумме 6Г сторон. Но каждая из этих сторон будет ребром ровно для 2 граней, поэтому всего будет 3Г ребер:

Теперь вспомним, что в каждой вершине сходятся не менее трех ребер. Значит, если мы посчитаем все ребра, выходящие из каждого ребра, то получим величину, не меньшую 3В. Но, так как каждое ребро проходит строго через 2 вершины, мы снова подсчитали ребра дважды. То есть количество ребер будет не меньше 3/2В, или 1,5В:

Это неравенство противоречит полученному ранее равенству Р = 3Г. Противоречие показывает, что на самом деле не может существовать выпуклый многогранник, каждая грань которого – шестиугольник, ч. т. д.

Примечание. Аналогично можно продемонстрировать, что не может существовать и выпуклый многогранник, поверхность которого состоит из многоуг-ков, каждый из которых имеет не менее 6 сторон. Другими словами, любой выпуклый многогранник имеет хотя бы одну грань, которая является треугольником, четырехугольником или пятиугольником.

Призма

Пусть в некоторой плос-ти α есть n-угольник с вершинами А₁, А₂, А₃,…, А_n. Пусть в другой плос-ти β, которая параллельна α, есть равный ему многоуг-к В₁В₂В₃…В_n, причем отрезки А₁В₁, А₂В₂, А₃В₃…, А_nВ_n параллельны друг другу:

В результате мы получили геометрическую фигуру, которую именуют призмой. Многоуг-ки А₁А₂А₃…А_n и В₁В₂В₃…В_n именуются основаниями призмы, а все остальные грани – это боковые грани призмы. Можно доказать, что боковые грани – это параллелограммы. Действительно, в четырехуг-ке А₁А₂В₂В₁ стороны А₁В₁ и А₂В₂ параллельны по условию. Также они равны по теореме 12 из этого урока. Это и значит, что А₁А₂В₂В₁ – это параллелограмм (по одному из его признаков). Тоже самое можно доказать и для остальных боковых граней. Теперь мы можем сформулировать определение призмы:

Ребра призмы, не принадлежащие основанию, именуются боковыми ребрами призмы. Ясно, что любые два соседних ребра параллельны, ведь они являются сторонами параллелограммами. Но тогда по свойству транзитивности параллельности получается, что вообще любые два боковых ребра параллельны. Если из какой-нибудь точки основания построен перпендикуляр к противоположному основанию, то он именуется высотой призмы:

Естественно, что высота перпендикулярна обоим основаниям. Возможна ситуация, когда высота падает не на основание, а на какую-нибудь точку плос-ти основания, не находящуюся внутри него. Ясно, что все высоты призмы имеют одинаковую длину независимо от того, через какие точки они проведены, ведь высота по своей сути – это расстояние между плос-тями оснований.

Особый интерес вызывают призмы, где боковые ребра и основания перпендикулярны друг другу. Такие призмы именуются прямыми. Ясно, что у них боковые грани оказываются уже не просто параллелограммами, а уже прямоуг-ками. При этом любое боковое ребро одновременно является и высотой. Все остальные призмы именуют наклонными.

Если в основании призмы находится n-угольник, то призму называют n-угольной. В частности, в основании треугольной призмы лежит треуг-к, в основании десятиугольной призмы находится десятиугольник и т. д. Наконец, в особую группу выделяют прямые призмы, основаниями которых представляют собой правильные многоуг-ки. Их так и именуют – правильные призмы.

Если сложить площадь всех граней призмы, то получится сумма, которую именуют площадью полной поверхности призмы. Обычно ее обозначают как S_полн. Если же складываются только площади боковых граней, то в сумме получается площадь боковой поверхности призмы, обозначаемая как S_бок. Если площадь основания призмы обозначить как S_осн., то справедлива будет очевидная формула:

Действительно, пусть есть прямая призма с основаниями А₁А₂…А_n и B₁B₂…B_n:

Так как ее боковые ребра перпендикулярны основаниям, то они должны быть перпендикулярны и тем ребрам, которые образуют основания. Это значит, каждая боковая грань – это прямоуг-к. При этом боковые ребра – это одновременно и высоты призмы. Тогда площадь боковых граней вычисляется так:

Отметим наконец, что параллелепипед можно считать частным случаем призмы, а прямоугольный параллелепипед – частным случаем прямой призмы.

Типичные задачи на призмы

Призмы нередко встречаются в заданиях ЕГЭ, поэтому важно уметь решать задачи, в которых используются эти фигуры.

Задание. Сколько диагоналей имеет n-угольная призма?

Решение. В любом многограннике диагональ соединяет точки, не лежащие на одной грани. Каждая вершина призмы принадлежит одному из оснований, причем в n-угольной призме каждому основанию принадлежат n вершин.

Возьмем произвольную вершину на одном из оснований и посчитаем, сколько диагоналей из нее можно провести. Если соединять ее отрезками с другими вершинами, принадлежащему тому же основанию, то получатся диагонали грани, но не диагонали призмы (зеленые линии на рисунке):

Значит, остается только провести прямые к тем вершинами, которые лежат в другом основании. Так как в другом основании находятся n вершин, то и отрезков будет ровно n. Однако три из них не будут диагоналями (показаны на рисунке синим цветом), так как будут либо являться одним из ребер призмы либо одной из диагоналей. Получается, что из вершины можно провести (n – 3) диагоналей. Так как в основании находятся n вершин, то всего можно построить n•(n– 3) диагоналей.

Ответ: n•(n – 3) диагоналей.

Задание. Длина стороны правильной треугольной призмы составляет 8 см, а ее боковое ребро имеет длину 6 см. Через сторону основания проведено сечение, которое пересекает другое основание в противолежащей вершине. Какова площадь этого сечения?

Решение. Выполним построение по условию задачи:

Здесь сечение проведено через ребро В₁С₁ и противолежащую ей вершину А. Призма правильная, поэтому ее основания ∆АВС и ∆А₁В₁С₁ – это равносторонние треуг-ки, и все их стороны равны 8 см. По определению правильная призма обязательно ещё и прямая. Тогда боковые грани – прямоуг-ки.

∆АВВ₁ – прямоугольный, с помощью теоремы Пифагора мы можем вычислить его гипотенузу АВ₁:

Аналогично можно вычислить, что и диагональ АС₁ также равна 10 см. Вообще в правильных призмах все грани – это равные друг другу прямоуг-ки, поэтому и диагонали у них одинаковы.

Длина ребра В₁С₁ составляет 8 см. Получается, нам надо вычислить площадь равнобедренного ∆АВ₁С₁ с основанием 8 см и боковыми сторонами 10 см. Это можно сделать множеством способов. Самый простой из них заключается в использовании формулы Герона. Для ее применения сначала вычислим полупериметр ∆АВ₁С₁:

Задание. В основании призмы находится равносторонний ∆АВС. Ребро АА₁ образует одинаковые углы с ребрами АС и АВ. Докажите, что ребра АА₁ и ВС перпендикулярны и что СС₁В₁В – прямоуг-к.

Решение. Выполняем построение:

По условию ∠А₁АВ и ∠А₁АС одинаковы. Проведем диагонали А₁В и А₁С. В итоге мы получим ∆А₁АВ и А₁АС. У них есть АА₁ – общая сторона, стороны АВ и АС одинаковы (ведь ∆АВС – равносторонний), а углы между ними одинаковы. Значит, ∆А₁АВ и А₁АС равны, и тогда диагонали А₁В и А₁С одинаковы.

Получается, что точка А₁ равноудалена вершин В и С. Аналогично и точка А равноудалена от В и С, ведь АВ и АС одинаковы. Это значит, что и А₁, и А лежат на серединных перпендикулярах, проведенных к отрезку ВС:

Обозначим середину ВС как Н, тогда НА₁ и НА – серединные перпендикулярны. То есть ВС⊥АН и ВС⊥А₁Н. Но это значит (по признаку перпендикулярности прямой и плос-ти), что ВС перпендикулярен всей плос-ти АНА₁. Из этого вытекает, что ВС⊥АА₁, ч. т. д.

Осталось показать, что грань СС₁В₁В – это прямоуг-к. Так как ВВ₁||АА₁, и ВС⊥АА₁, то и ВС⊥ВВ₁. Значит в параллелограмме СС₁В₁В (напомним, что в призме все боковые грани – параллелограммы) есть прямой угол. Это значит, что он является прямоуг-ком, ч. т. д.

Задание. Призма АВСА₁В₁С₁ – наклонная. Известно, что АС = АВ = 13 и ВС = 10. Боковые ребра призмы образуют с основанием АВС угол 45°. Проекция точки А₁ на плос-ть АВС совпадает с точкой пересечения медиан в ∆АВС. Какова площадь грани СС₁В₁В?

Решение. Снова выполняем построение:

Здесь О – это проекция точки А₁ и одновременно точка пересечения медиан. H– середина отрезка ВС, то есть АН – как раз одна из медиан. Заметим, что так как ∆АВС равнобедренный, и ВС – это его основание, то АН одновременно является и высотой, то есть ∠ВНА = 90°. Раз Н – середина ВС, то ВН будет вдвое короче ВС:

Напомним, точка пересечения медиан делит их в отношении 2:1, поэтому мы можем найти ОА:

Понятно, что ОА – это проекция прямой ОА на плос-ть АВС. Тогда угол между ребром АА₁ и плос-тью АВС, по условию равный 45° – это ∠ОАА₁.

Из прямоугольного ∆АОА₁ с помощью тригонометрии мы найдем длину ребра АА₁:

Теперь покажем, что грань СС₁В₁В – прямоуг-к. Ясно, что ОА₁⊥ВН, ведь ОА₁ – перпендикуляр ко всей плос-ти АВС. Но также ВН⊥АН. Значит, ВН перпендикулярен плос-ти АОА₁, и, в частности, перпендикулярен ребру АА₁. Но тогда и ВВ₁⊥ВН, ведь ВВ₁||АА₁. Значит, грань СС₁В₁В – прямоуг-к, ведь в ней есть прямой угол. Для нахождения площади прямоуг-ка надо перемножить две его смежные стороны:

Задание. Ребро при основании правильной 6-угольной призмы имеет длину 23, а боковое ребро равно 50. Вычислите площадь поверхности призмы (и полную, и боковую).

Решение.

Сначала найдем площадь и периметр основания. Формулы для правильных многоуг-ков мы уже изучали:

Здесь а – сторона шестиугольника, R и r – радиусы описанной и вписанной окружности, n– число сторон шестиугольника. Во второй формуле мы использовали известный факт, что длина стороны правильного 6-угольника совпадает с радиусом описанной около него окружности.

Далее вычисляем площадь боковой поверхности:

Добавив к этому значению удвоенную площадь поверхности основания, найдем и полную площадь призмы:

Задание. В правильной треугольной призме АВСА₁В₁С₁, у которой все ребра одинаковы и равны единице, вычислите угол между гранью АВС и сечением АСВ₁:

Решение. Вспомним, что для нахождения угла между плос-тями необходимо построить в этих плос-тях перпендикуляры к линии их пересечения, причем эти перпендикуляры должны падать на одну и ту же точку.

Пересекаются плос-ти АВС и АСВ₁ по грани АС. Заметим, что и ∆АВС, и ∆АСВ₁ – равнобедренные, причем у них общее основание АС. Действительно, АВ = ВС, так как в основании правильной призмы лежит равносторонний треуг-к, а АВ₁ = СВ₁, так как это диагонали равных граней АВВ₁А₁ и ВСС₁В₁.

Если мы отметим середину отрезка АС (например, точкой Н) и соединим ее с В и В₁, то мы получим две медианы НВ и НВ₁, которые одновременно будут и высотой. Это значит, что именно ∠ВНВ₁ и будет искомым углом между плос-тями:

Осталось найти ∠ВНВ₁. Длину ВВ₁ мы уже знаем, она составляет 1.

АН вдвое короче АС:

Теперь заметим, что ∆НВВ₁ – прямоугольный, поэтому для него можно использовать тригонометрию:

Задание. Найдите угол между прямыми А₁D и СD₁ в правильной призме, показанной на рисунке:

Все ребра этой призмы равны единице.

Решение. Сначала внимательно рассмотрим верхнее основание призмы. Так как оно представляет собой правильный многоуг-к, то вокруг него можно описать окружность. Обозначим центр этой окружности как О и проведем радиусы к вершинам:

Так как в правильном шестиуг-ке радиус описанной окружности равен стороне шестиугольника, то получается, что ∆А₁ОВ₁, ∆В₁ОС₁ и ∆С₁ОD₁ – равносторонние. Тогда ∠А₁ОВ₁, ∠B₁OC₁ и ∠С₁ОD₁ составляют по 60°. Тогда ∠А₁ОD₁ равен 180°, то есть точки А₁, О и D₁ находятся на одной прямой А₁D₁. Также заметим, что эта прямая параллельна ребру В₁С₁, ведь ∠D₁OC₁и ∠ОС₁B₁ являются накрест лежащими для этих прямых (при секущей ОС₁) и при том они одинаковы. Так как отрезки А₁О и D₁O как стороны равносторонних треуг-ков равны 1, то

Теперь вернемся к призме:

Так как А₁D₁||В₁С₁ и В₁С₁||ВС, то и А₁D₁||ВС. Это значит, что через А₁D₁ и ВС можно провести плос-ть, в которой будут лежать и интересующие нас прямые А₁В и СD₁. Для нахождения угла между ними надо рассмотреть четырехуг-к А₁D₁CB. Раз А₁D₁||ВС, то этот четырехуг-к является трапецией.

Далее найдем длину А₁В. Для этого используем ∆АВА₁:

Аналогично из ∆СDD₁ можно определить, что СD₁ имеет такую же длину. Это значит, что А₁D₁CB – равнобедренная трапеция.

Теперь рассмотрим отдельно эту трапецию, чтобы найти искомый угол:

Опустим из вершин трапеции В и С перпендикуляры на А₁D₁. В итоге получим прямоуг-к ВСРН, где

Сегодня мы более детально изучили понятие многогранника и познакомились с новой геометрической фигурой – призмой. Призма довольно часто встречается в задаче С2 на ЕГЭ. Также мы узнали о теореме Эйлера, из которой вытекают некоторые важные факты. Один из них заключается в том, что не бывает выпуклых многогранников, у которых ни одна грань не является треуг-ком, четырехуг-ком или пятиуг-ком.

Подсчитаем количество вершин и граней куба до отпиливания.

У куба (displaystyle 8) вершин и (displaystyle 12) рёбер.

Посмотрим, как изменится количество рёбер, если отпилить одну вершину так, как это показано на рисунке в условии.  

Количество рёбер увеличится на (displaystyle 3) ребра новой треугольной грани.

При отпиливании всех (displaystyle 8) вершин количество рёбер увеличится на (displaystyle 3 cdot 8=24{small.}) 

То есть:

(displaystyle left.begin{aligned}&text{small к 12 старым рёбрам}\&text{small добавятся 24 новых ребра}end{aligned}right} text{small всего 36 рёбер})

Итак, если отпилить у куба все вершины, то у получившегося многогранника будет (displaystyle 36) рёбер.

Ответ: (displaystyle 36{small.})

 «Вершины,
ребра, грани многогранника»

Теоретическая
часть:

Многогранник
(многогранная поверхность) – это поверхность,
составленная из многоугольников, ограничивающая некоторое геометрическое тело.
Примером многогранника является куб, параллелепипед, призма и т.д.

Грани многогранника –
это многоугольники, из которых составлен многогранник. Например, гранями
параллелепипеда являются параллелограммы.

Стороны граней называются
ребрами, а концы ребер – вершинами многогранника.

Отрезок, соединяющий две
вершины, не принадлежащие одной грани, называется диагональю
многогранника.

Плоскость, по обе стороны
от которой имеются точки многогранника, называется секущей плоскостью, а
общая часть многогранника и секущей плоскости – сечением многогранника.

Многогранники бывают выпуклые
и невыпуклые.

Многогранник называется выпуклым,
если он расположен по одну сторону от плоскости каждой его грани. Все грани
выпуклого многогранника являются выпуклыми многоугольниками.

В выпуклом многограннике
сумма всех плоских углов при каждой его меньше 360⁰.

Теорема Эйлера: в любом
выпуклом многограннике сумма числа граней и числа вершин больше числа ребер на
2.

f
+ e – k
= 2, где f
– число граней, e – число вершин, k – число ребер.

Леонардо Эйлер (1707 –
1783) – швейцарец по происхождению, выдающийся математик. Большую часть жизни
работал в России.

Практическая часть:

Домашнее
задание

№
1

Составить
конспект

№
2

№
3

Решить задачу: Начертите
произвольный прямоугольный параллелепипед, укажите все его вершины, ребра и
грани. Проверьте выполнимость формулы Эйлера.

Эталоны
ответов:

№
2

Выпуклые
многогранники: а, б, д

Невыпуклые
многогранники: в, г

№3

8
вершин, 12 ребер, 6 граней

Формула
Эйлера: 6 + 8 – 12 = 2

Математика 5 класс Дорофеев. 10. Чему вы научились. Обязательные умения. Номер №1

Решение

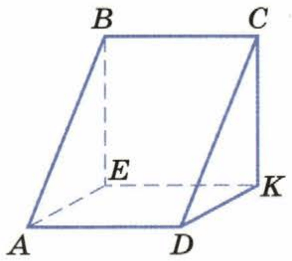
6 вершин: A, B, E, C, D, K.
9 ребер: AB, BE, AE, DC, CK, DK, AD, BC, EK.
5 граней всего, из них:
треугольники: ABE, CDK;
четырехугольники: ABCD, BCKE, AEKD.

По каким формулам можно определить, какое количество граней, ребер и вершин имеет призма? Например, сколько граней, ребер и вершин у треугольной или шестиугольной призмы? Общее количество граней, ребер и вершин призмы будет зависеть от ее формы. Так количество граней равняется количеству боковых граней + количество оснований равняется 2n, где n есть количество ребер в основании. Количество ребер равняется n x 3, где n есть количество ребер в основании. Количество вершин равняется (n + 2) x 2, где n есть количество ребер в основании. Таким образом к примеру, для треугольной призмы (треугольник в основании) количество граней будет равняться 5, количество ребер – 9 и, наконец, количество вершин – 6. Если взять шестиугольную призму (шестиугольник в основании), то количество граней будет равняться 8, количество ребер – 18, ну а количество вершин – 12. система выбрала этот ответ лучшим Ксарф­акс [156K] 5 лет назад  Призма Это многогранник, у которой основания являются равными многоугольниками (они находятся в параллельных плоскостях), а боковые грани – параллелограммами. Так как в качестве основания призмы выступает многоугольник (например, четырехугольник или шестиугольник), то количество граней, ребер и вершин будет зависеть от вида данного многоугольника. Узнать, сколько граней, ребер и вершин у призмы, можно с помощью формул (n – число сторон у многогранника): 1) Количество граней = n + 2. n – боковые грани, 2 – основания призмы. 2) Количество ребер = 3n. Если посмотреть на любую призму, то сразу видно, что из любой вершины выходит по 3 ребра – 1 боковое и 2 в основании. 3) Количество вершин = 2n. У каждого основания будет n вершин (например, у шестиугольника их 6), а всего оснований у нас 2. Например: Треугольная призма имеет 3 + 2 = 5 граней, 3 * 3 = 9 ребер и 2 * 3 = 6 вершин. Четырехугольная призма имеет 4 + 2 = 6 граней, 3 * 4 = 12 ребер и 2 * 4 = 8 вершин. Шестиугольная призма имеет 6 + 2 = 8 граней, 3 * 6 = 18 ребер и 2 * 6 = 12 вершин. VVlad­anS [2K] 5 лет назад  Мне очень понравился ответ Грустного Роджера, но ведь наименьшее число граней 5 у треугольной пирамиды, вершин 6 тоже у нее и ребер 9, как верно заметил Дмитро Вахмиянин. Действительно, для любого натурального числа n>2 существует в евклидовом трехмерном пространстве призма с числом сторон многоугольника в основании, равном числу n, и для нее будет верно, что Количество граней = n+3 (6 для треугольной и 8 для шестиугольной). Количество ребер = 3n (9 для треугольной и 18 для шестиугольной). Количество вершин = 2n (6 для треугольной и 12 для шестиугольной). Лично для меня всегда удивительно, что вершин меньше, чем ребер. Я себя заставил поверить и выучить, что у любого выпуклого многогранника меньше всего количество граней, потом по возрастающей идет количество вершин и больше всего количество ребер. В общем случае, если у выпук. многогранника в каждой вершине пересекается k ребер, то число ребер должно превышать число вершин в k/2 раз. Н Например, для призмы k=3, поэтому неудивительно, что для n-угольной призмы число ребер в {k/2=}полтора раза больше числа вершин. Так уж устроен этот мир. Груст­ный Родже­р [395K] 5 лет назад  Целиком определяется тем, какой многоугольник лежит в основании призмы. Ясное дело, что количество боковых граней равно числу сторон этого многоугольника, плюс у нас два основания, поэтому общее число граней равно n+2 (n – число сторон многоугольника). Столь же очевидно, что на каждую вершину многоугольника приходится три ребра – одно боковое и по одному в каждом основании. Поэтому общее число рёбер равно 3n. Лара Степа­нова [3.5K] более месяца назад  В некоторых заданиях по математике действительно нужно ответить на вопрос сколько граней или сколько ребер или сколько вершин у многогранника. Если дан рисунок, обладая пространственным мышлением нетрудно посчитать количество ребер, граней и вершин. Если в основании лежит треугольник, то вот они три вершины внизу и три вверху. Если четырехугольник , то вверху 4 и внизу четыре. То есть тогда можно догадаться, что вершин в два раза больше, чем вершин в многоугольнике, являющемся основанием. получается формула 2n Далее смотрим сколько ребер: у треугольной призмы – три ребра в нижнем основании, три в верхнем и еще три ребра соединяющие вершины верхнего и нижнего основания. У четырехугольной 4 внизу, 4 вверху и 4 боковых. Получается тоже в три раза больше, чем количество вершин многоугольника, являющегося основанием. Итак получается формула 3n И наконец количество граней. У треугольной призмы 1 грань вверху, 1 внизу и три боковых – всего 5, У 4-угольной – 1 внизу, 1 вверху и 4 боковых. Получается формула n+2 Лара Изюми­нка [59.6K] 3 года назад  В принципе можно нарисовать призму, а потом просто аккуратно посчитать требуемое, но существуют и формулы, позволяющиеся не запутаться, если это будет призма с большим количеством граней. Приведем эти формулы: Количество граней – это n + 2, где n – количество сторон многоугольника, лежащего в основании. Понятно как возникла эта формула. У нас будет n боковых граней и 2 основания призмы. Количество ребер будем считать по формуле 3n. Тоже понятно, как возникла эта формула. Ведь из любой вершины выходит по 3 ребра. Количество вершин можно найти по формуле 2n. Что тоже очевидно. Ведь у нас вершины – это вершины 2 многоугольников, лежащих в основаниях. Vodil­a [16.6K] более года назад  Ответить на этот вопрос несложно. Если призма четырехугольная, треугольная ( то есть в основании лежит треугольник, четырехугольник) , то можно итак посчитать, но если в ней больше граней, то можно воспользоваться специальными формулами для расчета. В формулах у нас будет к – количество сторон 1 многоугольника, который лежит в основании (по факту их два). Итак, для подсчета количества граней можно воспользоваться формулой к + 2, Далее посчитаем количество ребер по формуле 3к. Ну, а количество вершин поможет найти формула 2к. Для примера, ести у нас 6-угольная призма, то в ней будет 8 граней, 24 ребра, 16 вершин. Optor­ius [13.8K] 6 месяцев назад  Существуют такие формулы определения числа вершин, ребер и граней призмы. Для n-угольной призмы: Число вершин(В) = 2*n. Число ребер(Р) = 3*n. Число граней(Г) = n + 2. К примеру, для 6-угольной призмы будет такой расклад: В = 12, Р = 18, Г = 8. Если говорить о треугольной призмы, то сложив 3+2 получим 5 граней. Так 3 умножим на 3 получим 9 ребер и если умножим 2 на 3 = 6 вершин. Если говорить о призме у которой четыре угла, то к 4 прибавим 2 и получим 6 граней. 3 помножим на 4 получим = 12 ребер. 2 умножим на 4 получим 8 вершин. Если говорить о шестиугольной призме, то сложив 6 и 2 получим 8 граней. Так 3 помножим на 6 получим 18 ребер и при умножении 2 на 6 будет 12 вершин. Dmitr­o Vahmy­anin [8] 5 лет назад  Треугольная: вершин 2*3=6 граней 2+3=5 ребер 3*3=9 Шестиугольная: вершин 2*6=12 граней 2+6=8 ребер 3*6=18 Восьмиугольная: вершин 2*8=16 граней 2+8=10 ребер 3*8=24 Знаете ответ?