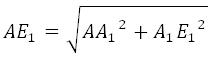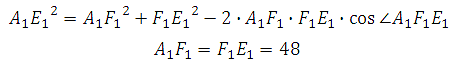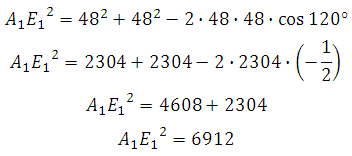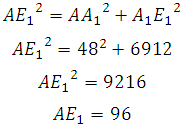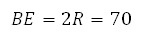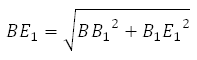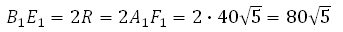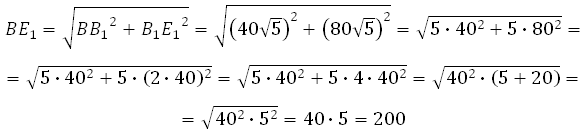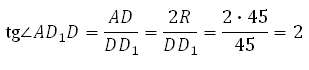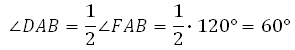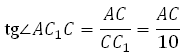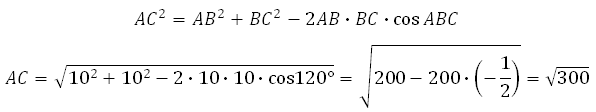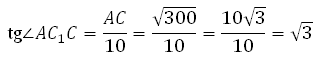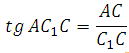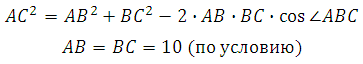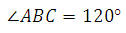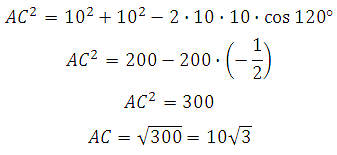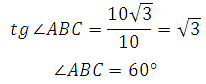|
По каким формулам можно определить, какое количество граней, ребер и вершин имеет призма? Например, сколько граней, ребер и вершин у треугольной или шестиугольной призмы? Общее количество граней, ребер и вершин призмы будет зависеть от ее формы. Так количество граней равняется количеству боковых граней + количество оснований равняется 2n, где n есть количество ребер в основании. Количество ребер равняется n x 3, где n есть количество ребер в основании. Количество вершин равняется (n + 2) x 2, где n есть количество ребер в основании. Таким образом к примеру, для треугольной призмы (треугольник в основании) количество граней будет равняться 5, количество ребер – 9 и, наконец, количество вершин – 6. Если взять шестиугольную призму (шестиугольник в основании), то количество граней будет равняться 8, количество ребер – 18, ну а количество вершин – 12. система выбрала этот ответ лучшим Ксарфакс 5 лет назад Призма Это многогранник, у которой основания являются равными многоугольниками (они находятся в параллельных плоскостях), а боковые грани – параллелограммами. Так как в качестве основания призмы выступает многоугольник (например, четырехугольник или шестиугольник), то количество граней, ребер и вершин будет зависеть от вида данного многоугольника. Узнать, сколько граней, ребер и вершин у призмы, можно с помощью формул (n – число сторон у многогранника): 1) Количество граней = n + 2. n – боковые грани, 2 – основания призмы. 2) Количество ребер = 3n. Если посмотреть на любую призму, то сразу видно, что из любой вершины выходит по 3 ребра – 1 боковое и 2 в основании. 3) Количество вершин = 2n. У каждого основания будет n вершин (например, у шестиугольника их 6), а всего оснований у нас 2. Например: Треугольная призма имеет 3 + 2 = 5 граней, 3 * 3 = 9 ребер и 2 * 3 = 6 вершин. Четырехугольная призма имеет 4 + 2 = 6 граней, 3 * 4 = 12 ребер и 2 * 4 = 8 вершин. Шестиугольная призма имеет 6 + 2 = 8 граней, 3 * 6 = 18 ребер и 2 * 6 = 12 вершин. VVladanS 5 лет назад Мне очень понравился ответ Грустного Роджера, но ведь наименьшее число граней 5 у треугольной пирамиды, вершин 6 тоже у нее и ребер 9, как верно заметил Дмитро Вахмиянин. Действительно, для любого натурального числа n>2 существует в евклидовом трехмерном пространстве призма с числом сторон многоугольника в основании, равном числу n, и для нее будет верно, что Количество граней = n+3 (6 для треугольной и 8 для шестиугольной). Количество ребер = 3n (9 для треугольной и 18 для шестиугольной). Количество вершин = 2n (6 для треугольной и 12 для шестиугольной). Лично для меня всегда удивительно, что вершин меньше, чем ребер. Я себя заставил поверить и выучить, что у любого выпуклого многогранника меньше всего количество граней, потом по возрастающей идет количество вершин и больше всего количество ребер. В общем случае, если у выпук. многогранника в каждой вершине пересекается k ребер, то число ребер должно превышать число вершин в k/2 раз. Н Например, для призмы k=3, поэтому неудивительно, что для n-угольной призмы число ребер в {k/2=}полтора раза больше числа вершин. Так уж устроен этот мир. Грустный Роджер 5 лет назад Целиком определяется тем, какой многоугольник лежит в основании призмы. Ясное дело, что количество боковых граней равно числу сторон этого многоугольника, плюс у нас два основания, поэтому общее число граней равно n+2 (n – число сторон многоугольника). Столь же очевидно, что на каждую вершину многоугольника приходится три ребра – одно боковое и по одному в каждом основании. Поэтому общее число рёбер равно 3n. Лара Степанова более месяца назад В некоторых заданиях по математике действительно нужно ответить на вопрос сколько граней или сколько ребер или сколько вершин у многогранника. Если дан рисунок, обладая пространственным мышлением нетрудно посчитать количество ребер, граней и вершин. Если в основании лежит треугольник, то вот они три вершины внизу и три вверху. Если четырехугольник , то вверху 4 и внизу четыре. То есть тогда можно догадаться, что вершин в два раза больше, чем вершин в многоугольнике, являющемся основанием. получается формула 2n Далее смотрим сколько ребер: у треугольной призмы – три ребра в нижнем основании, три в верхнем и еще три ребра соединяющие вершины верхнего и нижнего основания. У четырехугольной 4 внизу, 4 вверху и 4 боковых. Получается тоже в три раза больше, чем количество вершин многоугольника, являющегося основанием. Итак получается формула 3n И наконец количество граней. У треугольной призмы 1 грань вверху, 1 внизу и три боковых – всего 5, У 4-угольной – 1 внизу, 1 вверху и 4 боковых. Получается формула n+2 Лара Изюминка 3 года назад В принципе можно нарисовать призму, а потом просто аккуратно посчитать требуемое, но существуют и формулы, позволяющиеся не запутаться, если это будет призма с большим количеством граней. Приведем эти формулы: Количество граней – это n + 2, где n – количество сторон многоугольника, лежащего в основании. Понятно как возникла эта формула. У нас будет n боковых граней и 2 основания призмы. Количество ребер будем считать по формуле 3n. Тоже понятно, как возникла эта формула. Ведь из любой вершины выходит по 3 ребра. Количество вершин можно найти по формуле 2n. Что тоже очевидно. Ведь у нас вершины – это вершины 2 многоугольников, лежащих в основаниях. Vodila более года назад Ответить на этот вопрос несложно. Если призма четырехугольная, треугольная ( то есть в основании лежит треугольник, четырехугольник) , то можно итак посчитать, но если в ней больше граней, то можно воспользоваться специальными формулами для расчета. В формулах у нас будет к – количество сторон 1 многоугольника, который лежит в основании (по факту их два). Итак, для подсчета количества граней можно воспользоваться формулой к + 2, Далее посчитаем количество ребер по формуле 3к. Ну, а количество вершин поможет найти формула 2к. Для примера, ести у нас 6-угольная призма, то в ней будет 8 граней, 24 ребра, 16 вершин. Optorius 6 месяцев назад Существуют такие формулы определения числа вершин, ребер и граней призмы. Для n-угольной призмы: Число вершин(В) = 2*n. Число ребер(Р) = 3*n. Число граней(Г) = n + 2. К примеру, для 6-угольной призмы будет такой расклад: В = 12, Р = 18, Г = 8. Если говорить о треугольной призмы, то сложив 3+2 получим 5 граней. Так 3 умножим на 3 получим 9 ребер и если умножим 2 на 3 = 6 вершин. Если говорить о призме у которой четыре угла, то к 4 прибавим 2 и получим 6 граней. 3 помножим на 4 получим = 12 ребер. 2 умножим на 4 получим 8 вершин. Если говорить о шестиугольной призме, то сложив 6 и 2 получим 8 граней. Так 3 помножим на 6 получим 18 ребер и при умножении 2 на 6 будет 12 вершин. Dmitro Vahmyanin 5 лет назад Треугольная: вершин 2*3=6 граней 2+3=5 ребер 3*3=9 Шестиугольная: вершин 2*6=12 граней 2+6=8 ребер 3*6=18 Восьмиугольная: вершин 2*8=16 граней 2+8=10 ребер 3*8=24 Знаете ответ? |
Люди,а как найти количество ребер призмы,если знаем только количество граней призмы?
Наталья Николаенко
Мастер
(1706),
закрыт
12 лет назад
Завада
Гений
(88938)
12 лет назад
Вычти 2 и утрой результат.
soloПросветленный (24873)
12 лет назад
я понимаю, что 120 это правильно, но если следовать логике, то 40 граней, у каждой по 4 ребра, тогда должно быть 160, где логическая ошибка, подскажите пожалуйста
soloПросветленный (24873)
12 лет назад
сама и нашла, т.к. ребра один раз уже принадлежат смежной грани
Наталья Николаенко
Мастер
(1706)
А почему -2 а потом умножить на 3?
На этой странице вы узнаете
- Чем упаковка стикеров похожа на призму?
- Как можно попасть в призму в реальной жизни?
- Как сложить игральные кости из листа бумаги?
- Как найти объем воды в аквариуме?
Слышали такое выражение «смотреть сквозь призму чего-либо»? Оно значит ситуацию, в которой мы воспринимаем что-либо под влиянием каких-то убеждений или представлений. Замысловато, конечно… Возможно, потому что и сама призма — непростое понятие. Давайте разберемся с ней с точки зрения математики.
Определение призмы
Многие из нас пользуются стикерами. Для записи своих дел, для закладок, для пометок при ведении конспектов. Даже если мы ими не пользуемся, то наверняка видели их в магазинах или у родственников и друзей.

Один такой стикер можно принять за плоскость. Теперь вспомним, как выглядит упаковка с ними. Много-много стикеров накладываются друг на друга и получается небольшая объемная фигура, сверху и снизу которой лежат два абсолютно одинаковых листа. При этом сразу заметим, что нижний и верхний стикеры будут параллельны друг другу.

На самом деле, упаковка со стикерами является не чем иным, как призмой!
Призма — это многогранник, в котором две грани являются равными многоугольниками и лежат в параллельных плоскостях, а все остальные — параллелограммами.
Упаковка стикеров является объемной фигурой, в основаниях которой лежат равные прямоугольники. А боковые стороны упаковки являются параллелограммом. Таким образом, упаковка стикеров полностью соответствует определению призмы.
Определение может показаться немного запутанным, но в нем нет ничего страшного. Разберемся, поближе взглянув на составные призмы.
Строение призмы
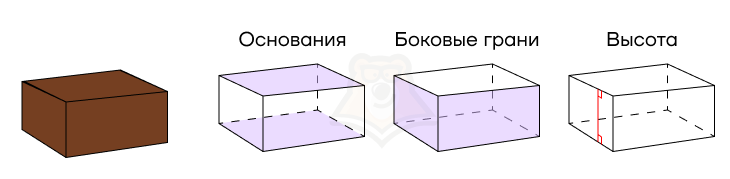
Представим себе обычную коробку. Ее дно и крышка равны между собой и лежат в параллельных плоскостях. Это и есть равные многоугольники. Также их называют основаниями призмы.
Посмотрим на стенки коробки. Они являются параллелограммами, просто с прямыми углами. Подробнее про параллелограммы можно прочитать в статье «Параллелограмм». Эти параллелограммы называются боковыми гранями призмы.
Возьмем линейку и измерим расстояние между основаниями призмы. Для этого из любой точки одного основания проведем перпендикуляр к другому.
Подробнее про расстояния между плоскостями можно узнать в статьях «Углы в пространстве» и «Расстояния между фигурами».
Может возникнуть вопрос, что мы сейчас нашли? Мы нашли высоту призмы.
Высота призмы — перпендикуляр, опущенный из любой точки одного основания на другое основание призмы.
В задачах намного удобнее опускать перпендикуляр не из произвольной точки, а из вершины призмы.
Рассмотрим элементы призмы.
Ребро — это линия пересечения двух плоскостей.
Представим, что вместо картонных стенок в нашей коробке ткань, которую нам нужно натянуть на каркас так, чтобы коробка не изменилась. В этом случае все прямые этого каркаса и будут ребрами.
Ребра бывают двух видов:
- ребра оснований,
- боковые ребра.
Отличить их также легко: ребра основания являются стороной многоугольника, который в нем лежит, в то время как боковые ребра не принадлежат основаниям.
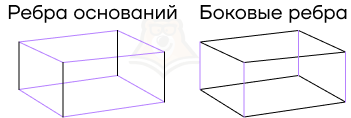
У боковых ребер есть одно очень важное свойство: они равны между собой и параллельны.
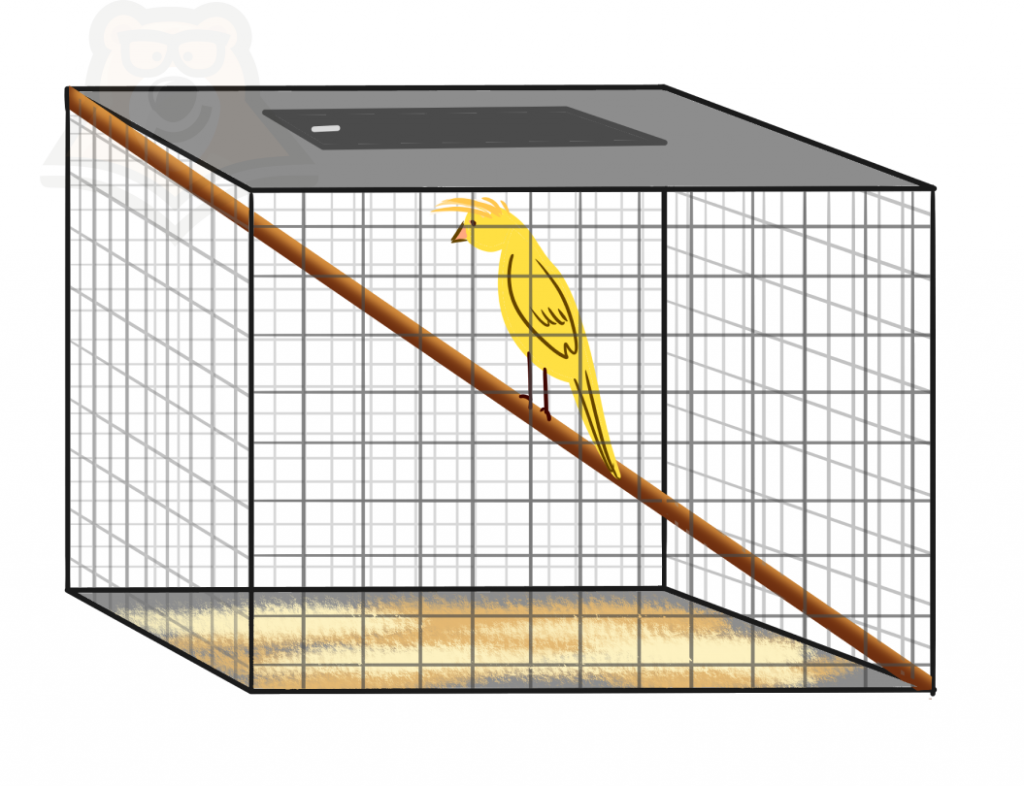
Диагональ призмы — отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.
Например, мы можем взять клетку попугая и от угла до угла сделать ему жердочку, чтобы птичке было весело жить. Эта жердочка и будет диагональю призмы.
Виды призм
Вернемся к рассуждениям о том, чем упаковка стикеров похожа на призму. Например, куб и параллелепипед будут отличаться. А если в основании призмы будет лежать треугольник или шестиугольник? Или двадцатиугольник? Разделим призмы на несколько видов.
Мы рассмотрим две классификации.
В первом случае будем рассматривать призмы по фигурам, которые лежат в основании. В многоугольнике может быть множество сторон, а значит, и в основании призмы может быть треугольник, четырехугольник, шестиугольник, десятиугольник и так далее.
В зависимости от фигуры в основании призмы могут называться по-разному. Вот три основных, которые чаще всего встречаются при решении заданий:
- треугольная призма,
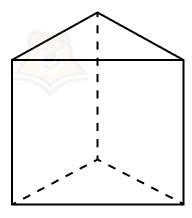
- четырехугольная призма,
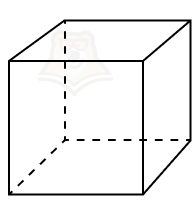
- шестиугольная призма.
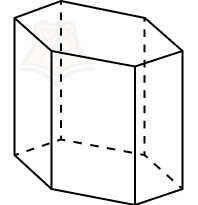
Аналогичным образом можно дать название любой призме, например, десятиугольная призма или стоугольная призма.
В определении призмы сказано, что в боковых гранях лежат параллелограммы. До этого мы чертили только прямоугольники, но в боковых гранях могут лежать не только они.
С этим связана вторая классификация призм. По этому признаку призмы делятся всего на два вида:
- прямые,
- наклонные.
Разберемся в них чуть подробнее.
Прямая призма — призма, боковые ребра которой перпендикулярны основаниям.
В этом случае боковые ребра и ребра оснований действительно образовывают прямоугольник.
Наклонная призма — призма, боковые ребра которой находятся под углом к основаниям.
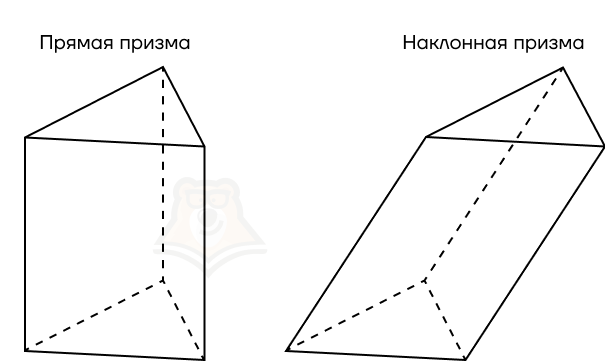
Где мы можем найти прямые и наклонные призмы? Оказывается, в архитектуре. Обычный жилой дом типовой застройки будет прямой призмой. А вот примером наклонной призмы может служить комплекс зданий “Ворота Европы” в Мадриде.

Чуть подробнее остановимся на прямых призмах. Они встречаются достаточно часто и обладают несколькими важными свойствами.
Посмотрите на свою комнату. Если по плану квартиры она будет многоугольником, то вы как бы сидите в призме. Теперь ответим на вопрос: как найти высоту комнаты?
Простой ответ: померить по стене. А если посмотреть на угол, то можно заметить, что ребро призмы совпадает с высотой. Таким образом, мы получаем первое свойство прямых призм.
Свойство 1. Высота прямой призмы совпадает с её боковым ребром.
Посмотрим на стены комнаты, на их форму. Они все являются прямоугольниками, верно?
Свойство 2. Все боковые грани прямой призмы — прямоугольники.
Многие комнаты и помещения, особенно в типовой застройке, обладают формой призмы. Сидя в комнате, в классе, в столовой, даже в автобусе — мы как бы находимся внутри большой призмы.
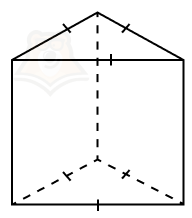
Если мы в основании прямой призмы разместим правильный многоугольник, у нас получится правильная призма.
Правильная призма — прямая призма, в основании которой лежит правильный многоугольник.
Например, в правильной треугольной призме будет лежать равносторонний треугольник, а в правильной шестиугольной призме — правильный шестиугольник.
Определение параллелепипеда
Еще одной разновидностью прямоугольной призмы является параллелепипед.
Параллелепипед — это четырехугольная призма, все грани которой являются параллелограммами.
Параллелепипеды встречаются повсюду: коробки, мебель, комнаты, здания, склады, магазины. Поэтому изучить их не составит труда.
Свойство параллелепипеда, видимое невооруженным глазом: противоположные грани параллелепипеда равны. Как пример, вспомним ту же комнату: потолок и пол равны, так же как и стены, находящиеся напротив друг друга.
Нельзя не упомянуть про одно очень важное свойство параллелепипеда:
- Все его диагонали пересекаются в одной точке и этой точкой делятся пополам. Это свойство справедливо для всех видов параллелепипеда.
Какие бывают параллелепипеды?
Параллелепипеды также бывают прямыми и наклонными. В этих случаях все определения такие же, как и для всех остальных призм.
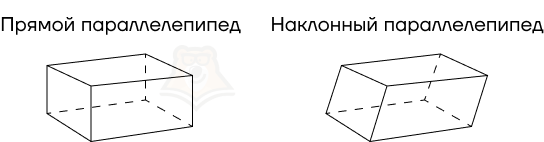
Прямой параллелепипед
Рассмотрим несколько интересных свойств прямого параллелепипеда.
1 свойство. Боковые ребра прямого параллелепипеда перпендикулярны основаниям.
2 свойство. Высота прямоугольного параллелепипеда равна длине его бокового ребра.
3 свойство. Боковые грани, которые лежат напротив друг друга, равны между собой и являются прямоугольниками.
Прямые параллелепипеды можно разделить еще на два вида:
- Прямой параллелепипед: в основании лежит параллелограмм;
- Прямоугольный параллелепипед: в основании лежит прямоугольник.
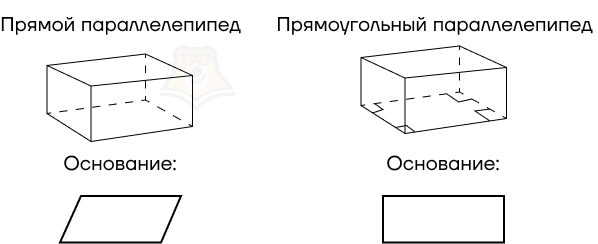
Рассмотрим свойства прямоугольного параллелепипеда.
1 свойство. Все грани прямоугольного параллелепипеда являются прямоугольниками.
2 свойство. Все углы в прямоугольном параллелепипеде, образованные двумя гранями, равны 90°.
3 свойство. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин его ширины, длины и высоты.
Таким образом, мы получаем важную формулу для параллелепипеда.
d2 = a2 + b2 + c2
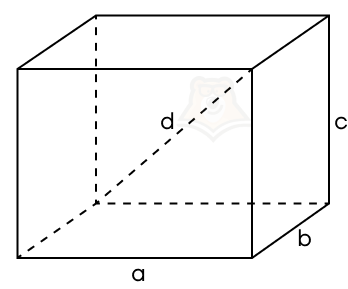
Пример 1. Дан прямоугольный параллелепипед. Два ребра, выходящие из одной его вершины, равны (sqrt{35}) и (sqrt{46}). Диагональ параллелепипеда равна 15. Найдите третье ребро параллелепипеда.
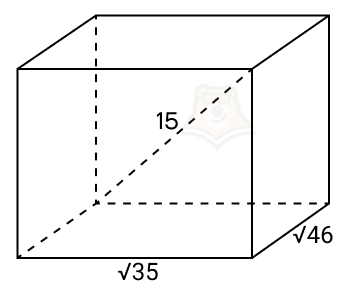
Решение. Пусть третье ребро параллелепипеда равняется х. Получаем уравнение:
(15^2 = (sqrt{35})^2 + (sqrt{46})^2 + x^2)
225 = 35 + 46 + x2
x2 = 144
x = 12
Ответ: 12.
У прямоугольного параллелепипеда существует еще несколько видов. Прямоугольные параллелепипеды делятся на:
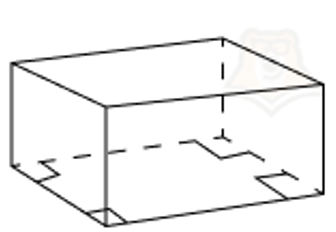
- Произвольный прямоугольный параллелепипед. В основании может лежать прямоугольник.
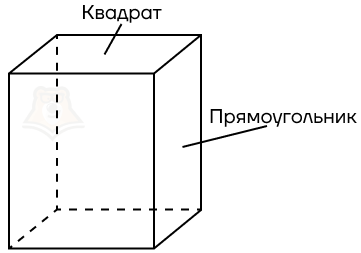
- Правильный прямоугольный параллелепипед. В основании лежит правильный четырехугольник, то есть квадрат.
При этом боковые ребра не равны ребрам основания. Следовательно, в основаниях будут лежать квадраты, а в боковых гранях прямоугольники.
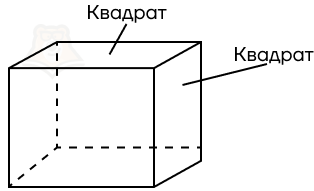
- Куб. В основании лежит квадрат, а боковые ребра равны ребрам основания.
В кубе все ребра равны, а все его грани будут квадратом.
Таким образом, мы рассмотрели все виды параллелепипеда.

Формулы для призмы
Однако ни одна задача не может быть решена без формул. Поэтому необходимо рассмотреть несколько основных формул, которые могут встретиться не только в задачах, но и в жизни.
Немного вспомним моделирование, а именно развертку кубика. Мы знаем, что из листа бумаги без труда можно сложить кубик, если правильно его вычертить.
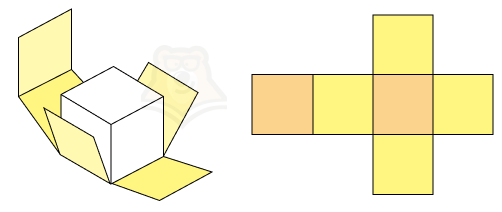
Задумали вы вечером сыграть с семьей или друзьями в настольную игру. Но вот незадача: игральные кости опять куда-то запропастились. Не беда.Достаточно вычертить на листе бумаги несколько квадратов, вырезать получившуюся фигуру, согнуть по ребрам и склеить между собой с помощью клея. В итоге получатся кубики для игры.
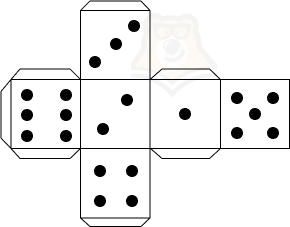
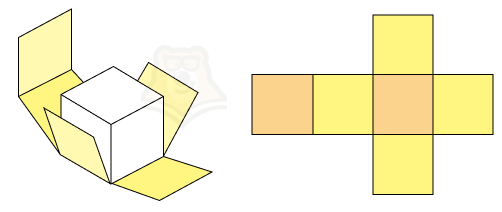
На рисунке оранжевым показаны основания, а желтым боковые грани нашего будущего кубика. А теперь представим, что нам нужно найти площадь боковой поверхности. Как это сделать?
Нужно найти площади желтых квадратиков и сложить их.
Площадь боковой поверхности призмы — сумма площадей всех боковых ее граней.
Единой формулы тут нет, поскольку призмы могут очень сильно отличаться друг от друга. В произвольных призмах придется считать площадь каждой боковой грани, а уже после их складывать.
Но есть один фокус! Правда, он работает только для прямой призмы. Если по условию дана прямая призма, то можно воспользоваться формулой
Sбок. = P * h
В этой формуле Р — периметр основания, h — высота призмы, которая совпадает с высотой боковой грани.
Пример 1. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равняется 2, а высота 10.
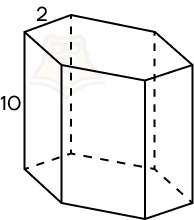
Решение.
Шаг 1. Поскольку правильная призма по определению прямая, мы можем воспользоваться формулой S = Ph.
Шаг 2. В основании правильной призмы лежит правильный шестиугольник, следовательно, периметр основания будет равен 6 * 2 = 12.
Шаг 3. Осталось найти только площадь боковой поверхности. Подставляем данные в формулу и получаем: S = 12 * 10 = 120.
Ответ: 120.
Пример 2. Дана прямая треугольная призма, в основании которой лежит прямоугольный треугольник с катетами 12 и 5. Высота призмы равна 13. Найдите площадь ее боковой поверхности.
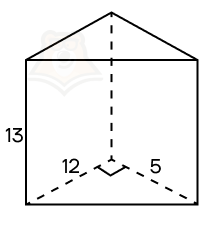
Решение.
Шаг 1. Поскольку призма прямая, можно воспользоваться формулой S = Ph.
Шаг 2. Найдем периметр основания. Для этого необходимо найти гипотенузу треугольника. Воспользуемся теоремой Пифагора: (sqrt{12^2 + 5^2} = sqrt{144 + 25} = sqrt{169} = 13).
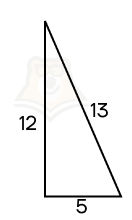
Шаг 3. Найдем периметр основания: P = 12 + 5 + 13 = 30.
Шаг 4. Осталось найти только площадь боковой поверхности. Подставляем данные в формулу и получаем: S = 30 * 13 = 390.
Ответ: 390.
Мы научились находить площадь боковой поверхности. А как найти всю площадь призмы? Вспомним нашу развертку с кубиком. Чтобы найти всю площадь кубика, нужно найти площадь всех квадратов, из которых он состоит. То есть и площадь боковой поверхности, и площадь оснований.
Площадь полной поверхности призмы — сумма площадей всех граней.
Следовательно, нам нужно сложить площади всех боковых граней и дважды площадь основания. Получаем следующую формулу.
S = Sбок + 2Sосн
Вспомним обычный хлеб, черный или белый. Его форма очень приближена к параллелепипеду. Тогда его корочка будет площадью полной поверхности параллелепипеда. А все что внутри, то есть мякиш, можно принять за объем.
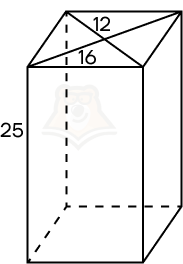
Пример 3. Дана прямая призма, в основании которой лежит ромб с диагоналями 12 и 16. Боковое ребро призмы равно 25. Найдите площадь поверхности призмы.
Решение.
Шаг 1. Найдем площадь основания. Площадь ромба можно найти по формуле (frac{1}{2} * D_1 * D_2). Следовательно, площадь ромба равна (frac{1}{2} * 12 * 16 = 96).
Шаг 2. Заметим, что диагонали ромба образуют четыре равных прямоугольных треугольника. Следовательно, чтобы найти сторону ромба, достаточно рассмотреть прямоугольный треугольник с катетами 6 и 8. По теореме Пифагора сторона ромба будет равна (sqrt{6^2 + 8^2} = sqrt{36 + 64} = sqrt{100} = 10).
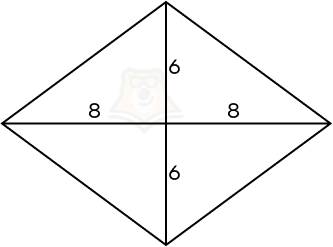
Шаг 3. Периметр ромба будет равен 4 * 10 = 40. Тогда площадь боковой поверхности равна 40 * 25 = 1000.
Шаг 4. Площадь полной поверхности будет равняться 1000 + 2 * 96 = 1000 + 192 = 1192.
Ответ: 1192
Пример 4. Площадь поверхности правильной четырехугольной призмы равняется 1980. Сторона основания равна 5. Найдите боковое ребро этой призмы.
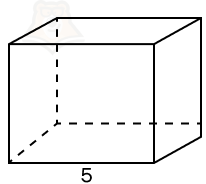
Решение.
Шаг 1. Воспользуемся формулой S = Sбок + 2Sосн. Площадь основания будет равняться площади квадрата, то есть 5 * 5 = 25.
Шаг 2. Подставим известные величины в формулу:
1980 = Sбок + 2 * 25
Sбок = 1930
Шаг 3. Площадь боковой поверхности равна произведению периметра основания на высоту призмы. Периметр равен 5 * 4 = 20. Тогда получаем уравнение:
20h = 1930
h = 96,5
Шаг 4. Поскольку по условию дана правильная призма, то высота совпадает с боковым ребром. Следовательно, боковое ребро равняется 96,5.
Ответ: 96,5.
Теперь рассмотрим, как найти объем призмы. Допустим, мы налили в прямоугольный аквариум немного воды. Как определить, сколько воды мы налили?
Для этого достаточно воспользоваться формулой объема призмы.
V = Sосн. * h
Эта формула общая, однако для каждой призмы она может принять свой вид в зависимости от того, какую формулу нужно использовать для поиска площади основания или высоты.
Например, чтобы найти объем воды в аквариуме, необходимо длину умножить на ширину и на высоту, а значит формула принимает вид V = abh.
Для этого достаточно перемножить ширину, длину аквариума и высоту воды. Тем самым мы найдем объем призмы, форму которой принимает вода в аквариуме.
Пример 5. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 12 и 15. Боковое ребро призмы равно 4. Найдите объем этой призмы.
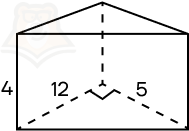
Решение.
Шаг 1. Для начала найдем площадь основания. В этом случае мы можем воспользоваться формулой (frac{1}{2}ab). Площадь равна (frac{1}{2} * 12 * 15 = 90).
Шаг 2. Воспользуемся формулой объема призмы и подставим известные величины:
V = 90 * 4 = 360.
Ответ: 360.
Пример 6. Дан сосуд, в основании которого лежит правильный треугольник. В этот сосуд налили 3000 см3 воды. Высота жидкости оказалась равной 10 см. После этого в сосуд опустили шарик и высота изменилась с 10 см на 14 см. Найдите объем шарика.
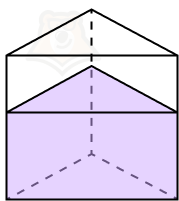
Решение. Немного вспомним физику, а именно тот факт, что объем вытесненной жидкости равен объему тела. Значит, чтобы найти объем шарика, необходимо найти насколько изменился объем воды.
Шаг 1. Найдем площадь основания сосуда. Для этого немного преобразуем формулу объема:
(S = frac{V}{h})
Тогда:
(S = frac{3000}{10} = 300)
Шаг 2. А теперь найдем объем после того, как в воду погрузили шарик. Он будет равен 300 * 14 = 4200.
Шаг 3. Объем вытесненной жидкости равен 4200 — 3000 = 1200.
Ответ: 1200.
Мы рассмотрели основные формулы, которые применяются для решения задач. Стоит заметить, что они универсальны, и в каждой задаче их рационально преобразовывать под ситуацию.
Фактчек
- Призма — это многогранник, в котором две грани являются равными многоугольниками и лежат в параллельных плоскостях, а все остальные — параллелограммами. Равные многоугольники называются основаниями призмы, а остальные стороны — боковыми гранями. В призме есть ребра — линии пересечения двух ее граней. Ребра как бы образуют каркас призмы.
- Призмы можно разделить на несколько видов по тому, какая фигура лежит в основании: треугольник, четырехугольник, шестиугольник или любой другой многоугольник. Призмы бывают прямые и наклонные. В прямых призмах боковые ребра перпендикулярны основанию, а в наклонных — нет. Правильная призма — прямая призма, в основании которой лежит правильный многоугольник.
- Параллелепипед — это четырехугольная призма, все грани которой являются параллелограммами. Параллелепипеды бывают наклонными и прямыми. Прямые параллелепипеды включают в себя прямоугольные параллелепипеды, которые, в свою очередь, делятся на произвольные, правильные и кубы.
- В призме можно найти площадь боковой поверхности, площадь полной поверхности и объем. Для каждого из этих случаев необходимо пользоваться формулами.
Проверь себя
Задание 1.
Что такое диагональ призмы?
- Отрезок, соединяющий две соседние вершины в призме.
- Отрезок, соединяющий противоположные углы в боковой грани призмы.
- Отрезок, соединяющий противоположные углы в основании призмы.
- Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.
Задание 2.
Что такое прямая призма?
- Призма, боковые ребра которой перпендикулярны основаниям.
- Призма, боковые ребра которой расположены под острым углом относительно основания.
- Призма, боковые ребра которой расположены под тупым углом относительно основания.
- Призма, в основании которой лежит прямоугольник.
Задание 3.
Как найти высоту прямой призмы?
- Высоту нужно найти с помощью оснований.
- Высота совпадает с боковым ребром.
- Необходимо найти расстояние между двумя вершинами, не принадлежащими одной грани.
- В прямой призме невозможно найти высоту.
Задание 4.
Какая фигура лежит в основании прямоугольного параллелепипеда?
- Параллелограмм с острыми углами.
- Ромб с острыми углами.
- Трапеция.
- Прямоугольник.
Задание 5.
Как найти площадь полной поверхности призмы?
- Нужно найти сумму площадей всех боковых граней.
- Нужно сложить площадь боковой поверхности и площадь основания.
- Нужно сложить площадь боковой поверхности и удвоенную площадь основания.
- Нужно сложить площади оснований.
Ответы: 1. — 4 2. — 1 3. — 2 4. — 4 5. — 3
Автор:
Louise Ward
Дата создания:
5 Февраль 2021
Дата обновления:
18 Май 2023
Геометрические призмы – это трехмерные фигуры, определяемые наличием вершины и низа, который представляет собой правильный многоугольник, такой как квадрат или треугольник, и прямых сторон или краев, которые соединяют верх и низ. Призмы состоят из оснований, граней, ребер и вершин. Геометрические призмы используются для обучения математическим понятиям, таким как объем и емкость, а также используются в строительстве. Пентагон в Вашингтоне, округ Колумбия, вероятно, самая известная пятиугольная призма в мире.
Подсчитайте количество граней в призме. Так как края определены как стороны, где грани встречаются, это поможет вам понять, сколько ребер у вас будет.
Отметьте стороны, где встречаются две стороны. Это твои края.
Подсчитайте все отметки, которые вы сделали, и это будет общее количество ребер. Для некоторых геометрических призм просто посчитайте количество граней и умножьте, сложите или вычтите число, чтобы найти число ребер. Например, для прямоугольных кубов и призм подсчитайте количество граней и умножьте на два, чтобы получить количество ребер. Для треугольных призм подсчитайте количество граней и вычтите одну, чтобы получить количество ребер.
Содержание
- Сколько краев у гексагональной призмы?
- Как посчитать края шестиугольной призмы?
- 1- Разложить призму
- заключение
- Шестиугольная призма и ее основные характеристики
- О какой призме пойдет речь?
- Элементы
- Диагонали призмы
- Площадь поверхности
- Объем призмы
- Правильная шестиугольная призма
Сколько краев у гексагональной призмы?
Знать сколько ребер имеет шестиугольная призма значение «край», «призма» и «шестиугольник» должны быть известны. Первые два понятия являются общими определениями, а третье понятие связано с формой геометрической фигуры..
Когда речь идет о шестиугольнике, упоминается шестиугольник (многоугольник). Приставка «гекса» указывает на то, что многоугольник имеет шесть сторон.
Ребро — это ребро объекта. Геометрически это линия, соединяющая две последовательные вершины геометрической фигуры.
Призма — это геометрическая фигура, ограниченная двумя параллельными и равными основаниями, а их боковые грани являются параллелограммами..
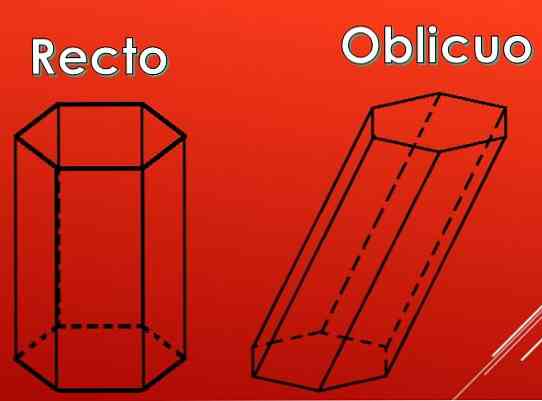
На следующем изображении видно, что боковые грани шестиугольной призмы могут быть прямоугольниками, но они также могут быть параллелограммами..
По типу параллелограммов премии могут быть классифицированы на два типа: прямые и косые.
Как посчитать края шестиугольной призмы?
Число ребер, которые будет иметь шестиугольная призма, не изменится, если это прямая или наклонная призма. Кроме того, количество ребер также не зависит от длины сторон.
Подсчет граней шестиугольной призмы можно выполнить несколькими способами. Вот два способа:
1- Разложить призму
Один из способов подсчета ребер состоит в разложении шестиугольной призмы на двух ее основаниях и боковых гранях. Таким образом, вы получите два шестиугольника и параллелограмм с пятью внутренними линиями.
Каждый шестиугольник имеет шесть ребер, поэтому призма будет иметь более 12 ребер.
На первый взгляд считается, что параллелограмм содержит девять ребер (семь вертикальных и два горизонтальных). Но удобно остановиться, чтобы проанализировать этот случай.
Когда параллелограмм согнут для образования призмы, видно, что первая строка слева соединится с последней строкой справа, с которой обе линии представляют одно ребро.
Но как насчет двух горизонтальных линий?
Когда все части снова собраны вместе, горизонтальные линии будут соединены, каждая, с шестью краями каждого шестиугольника. По этой причине считать их отдельно было бы ошибкой.
Таким образом, параллелограмм содержит шесть ребер призмы, которые вместе с 12 ребрами, подсчитанными в начале, дают в общей сложности 18 ребер.
2.- Проектирование каждого края
Другой способ, намного проще сосчитать ребра, это использование факта, что основания шестиугольных призм являются шестиугольниками, тогда каждое основание имеет шесть ребер.
С другой стороны, из каждой вершины шестиугольника одно ребро проецируется на соответствующую вершину другого шестиугольника; то есть есть шесть ребер, которые соединяют одну базу с другой.
Добавив все ребра, вы получите в общей сложности 18 ребер.
заключение
Можно показать, что число ребер призмы в три раза больше количества ребер, которые имеет многоугольник, который образует ее.
Следовательно, пятиугольная призма будет иметь 3 * 5 = 15 ребер, семиугольная призма будет иметь 3 * 7 = 21 ребро, и, таким образом, она может быть применена к любой призме..
Источник
Шестиугольная призма и ее основные характеристики
Изучением призм занимается пространственная геометрия. Важными их характеристиками являются заключенный в них объем, площадь поверхности и число составляющих элементов. В статье рассмотрим все эти свойства для шестиугольной призмы.
О какой призме пойдет речь?
Призма шестиугольная — это фигура, образованная двумя многоугольниками, имеющими шесть сторон и шесть углов, и шестью параллелограммами, соединяющими отмеченные шестиугольники в единое геометрическое образование.
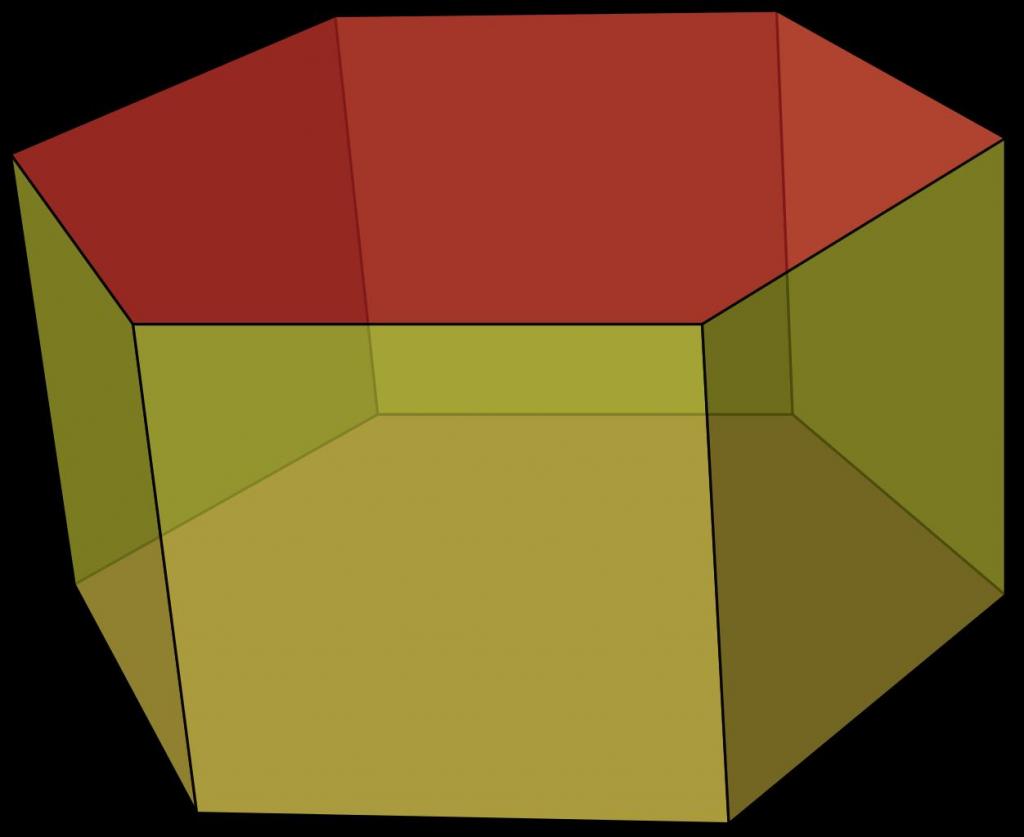
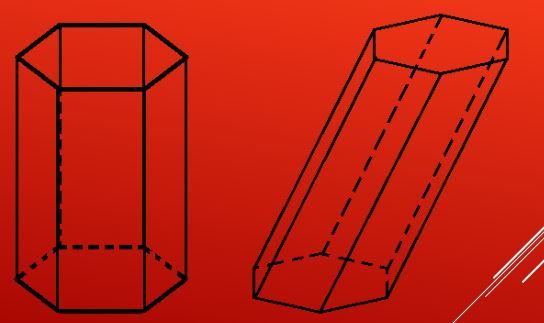
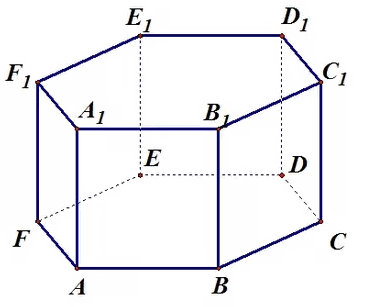
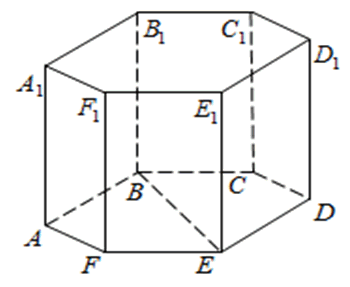
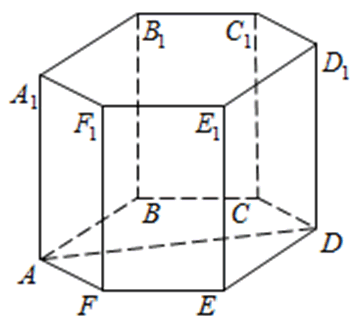
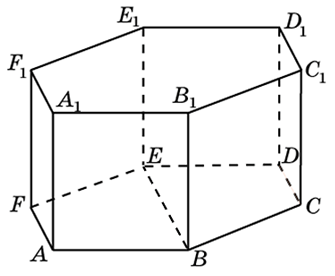
На рисунке изображен пример этой призмы.
Отмеченный красным цветом шестиугольник называется основанием фигуры. Очевидно, что число ее оснований равно двум, причем оба они идентичны. Желто-зеленоватые грани призмы называются ее боковыми сторонами. На рисунке они представлены квадратами, но в общем случае они являются параллелограммами.
Шестиугольная призма может быть наклонной и прямой. В первом случае углы между основанием и боковыми сторонами не являются прямыми, во втором они равны 90 o . Также эта призма может быть правильной и неправильной. Правильная шестиугольная призма обязательно должна быть прямой и иметь правильный шестиугольник в основании. Приведенная выше призма на рисунке этим требованиям удовлетворяет, поэтому она называется правильной. Далее в статье будем изучать только ее свойства, как общий случай.
Элементы
Для любой призмы главными ее элементами являются ребра, грани и вершины. Шестиугольная призма не является исключением. Приведенный выше рисунок позволяет посчитать количество этих элементов. Так, граней или сторон мы получаем 8 (два основания и шесть боковых параллелограммов), число вершин составляет 12 (по 6 вершин для каждого основания), количество ребер шестиугольной призмы равно 18 (шесть боковых и 12 для оснований).
В 1750-е годы Леонард Эйлер (швейцарский математик) установил для всех полиэдров, к которым относится призма, математическую связь между числами указанных элементов. Эта связь имеет вид:
число ребер = число граней + число вершин — 2.
Указанные выше цифры удовлетворяют этой формуле.
Диагонали призмы
Все диагонали шестиугольной призмы можно разделить на два типа:
- те, которые лежат в плоскостях ее граней;
- те, которые принадлежат всему объему фигуры.
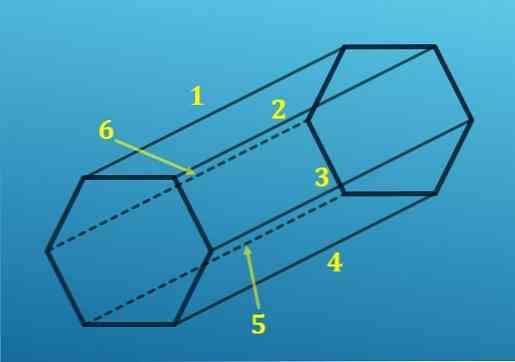
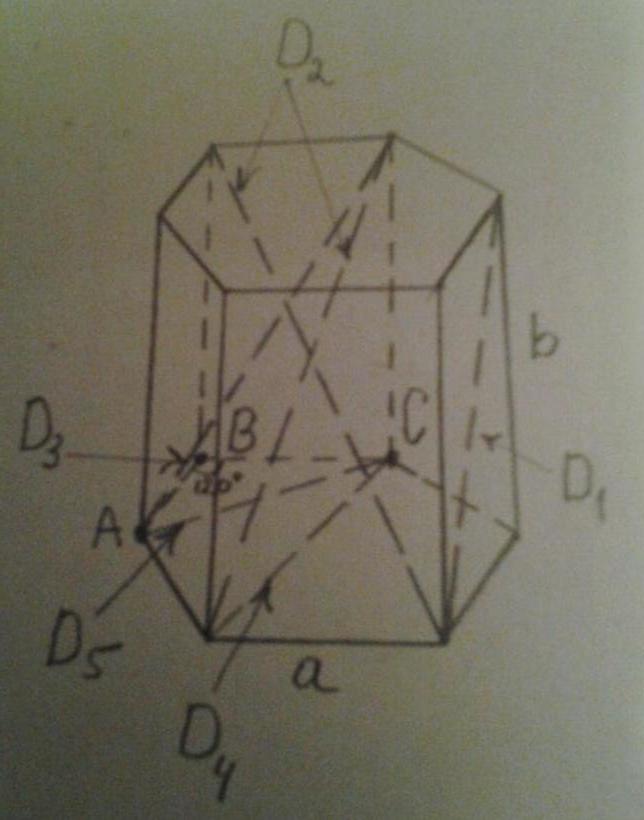
Рисунок ниже показывает все эти диагонали.
Видно, что D1 — это диагональ боковой стороны, D2 и D3 — диагонали всей призмы, D4 и D5 — диагонали основания.
Длины диагоналей боковых сторон между собой равны. Вычислить их легко, используя всем известную теорему Пифагора. Обозначим символом a длину стороны шестиугольника, символом b — длину бокового ребра. Тогда диагональ имеет длину:
Диагональ D4 также легко определяется. Если вспомнить, что правильный шестиугольник вписывается в окружность радиусом a, то D4 является диаметром этой окружности, то есть получим следующую формулу:
Диагональ D5 основания найти несколько сложнее. Для этого следует рассмотреть равносторонний треугольник ABC (см. рис.). Для него AB = BC = a, угол ABC равен 120 o . Если из этого угла опустить высоту (она же будет биссектрисой и медианой), тогда половина основания AC будет равно:
Сторона AC является диагональю D5, поэтому получаем:
Теперь остается найти диагонали D2 и D3 правильной шестиугольной призмы. Для этого нужно увидеть, что они являются гипотенузами соответствующих прямоугольных треугольников. Воспользовавшись теоремой Пифагора, получаем:
Таким образом, самой большой диагональю для любых значений a и b является D2.
Площадь поверхности
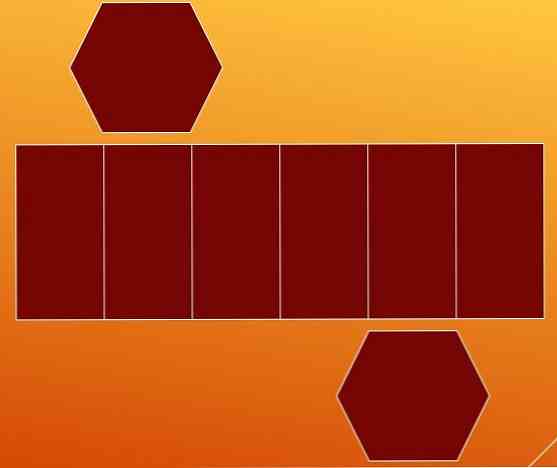
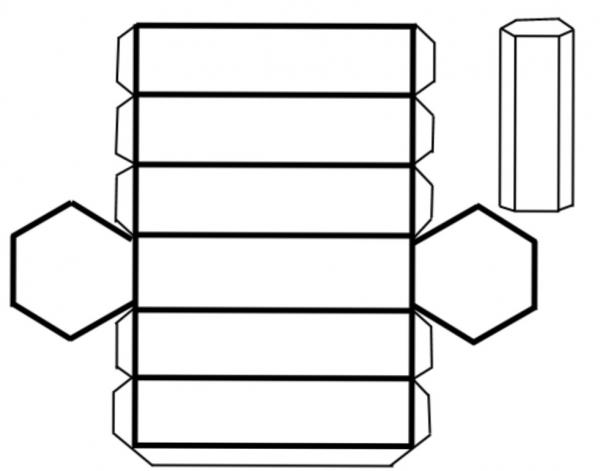
Чтобы понять, о чем идет речь, проще всего рассмотреть развертку этой призмы. Она показана на рисунке.
Видно, что для определения площади всех сторон рассматриваемой фигуры необходимо рассчитать отдельно площадь четырехугольника и площадь шестиугольника, затем умножить их на соответствующие целые числа, равные количеству каждого n-угольника в призме, и сложить полученные результаты. Шестиугольников 2, прямоугольников 6.
Для площади прямоугольника получаем:
Тогда площадь боковой поверхности равна:
Для определения площади шестиугольника проще всего воспользоваться соответствующей формулой, которая имеет вид:
Подставляя в это выражение число n равное 6, получаем площадь одного шестиугольника:
Это выражение следует умножить на два, чтобы получить площадь оснований призмы:
Остается сложить Sos и S2, чтобы получить полную площадь поверхности фигуры:
Объем призмы
После того как была получена формула для площади шестиугольного основания, вычислить объем, заключенный в рассматриваемую призму, проще простого. Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:
Отметим, что произведение основания на высоту дает значение объема абсолютно любой призмы, включая наклонную. Однако в последнем случае расчет высоты осложняется, поскольку она уже не будет равна длине бокового ребра. Что касается шестиугольной правильной призмы, то значение ее объема является функцией двух переменных: сторон a и b.
Источник
Правильная шестиугольная призма
На сайте уже были рассмотрены некоторые типы задач по стереометрии, которые входят в единый банк заданий экзамена по математике. Например, задания про составные многогранники .
Призма называется правильной если её боковые перпендикулярны основаниям и в основаниях лежит правильный многоугольник. То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.
Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.
В этой статье для вас задачи на решение призмы, в основании которой лежит правильный шестиугольник . Особенностей и сложностей в решении нет никаких. В чём суть? Дана правильная шестиугольная призма, требуется вычислить расстояние между двумя вершинами или найти заданный угол. Задачи на самом деле простые, в итоге решение сводится к нахождению элемента в прямоугольном треугольнике.
Используется теорема Пифагора и теорема косинусов . Необходимо знание определений тригонометрических функций в прямоугольном треугольнике.
Обязательно посмотрите информацию о правильном шестиугольнике в этой статье (пункт 6) . Ещё вам пригодится навык извлечения квадратного корня их большого числа. Можете посмотреть статью на решение многогранников, там тоже вычисляли расстояние между вершинами и углы.
Кратко: что представляет собой правильный шестиугольник?
Известно, что в правильном шестиугольнике стороны равны. Кроме этого, углы между сторонами тоже равны .
*Противолежащие стороны параллельны.
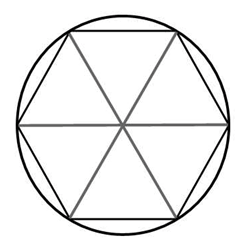
Радиус окружности описанной около правильного шестиугольника равен его стороне. *Это подтверждается очень просто: если мы соединим противоположные вершины шестиугольника, то получим шесть равных равносторонних треугольников. Почему равносторонних?
У каждого треугольника угол при его вершине лежащей в центре равен 60 0 (360:6=60). Так как у треугольника две стороны имеющие общую вершину в центре равны (это радиусы описанной окружности), то каждый угол при основании такого равнобедренного треугольника так же равен 60 градусам.
То есть правильный шестиугольник, образно говоря, состоит как бы из шести равных равносторонних треугольников.
Какой полезный для решения задач факт ещё следует отметить? Угол при вершине шестиугольника (угол между его соседними сторонами) равен 120 градусам.
*Умышленно не коснулись формул правильного N-угольника. Данные формулы мы подробно рассмотрим в будущем, здесь они просто не нужны.
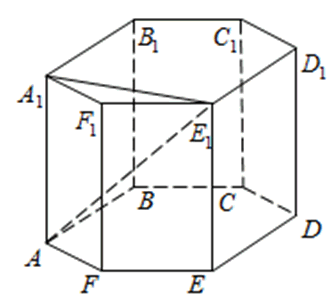
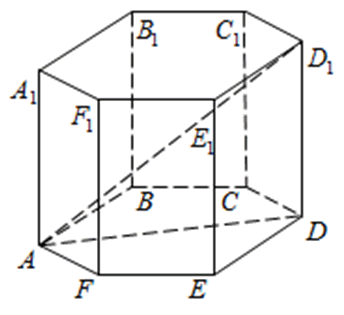
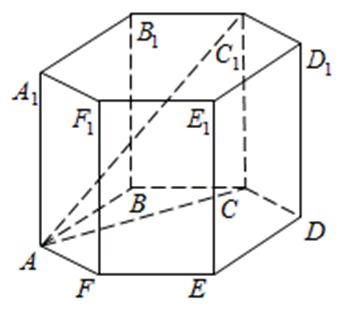
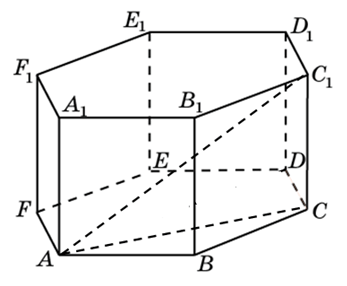
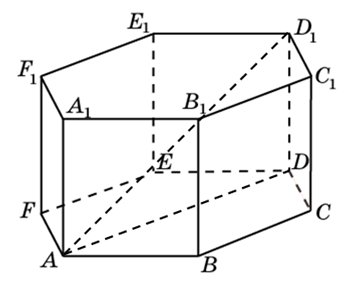
272533. В правильной шестиугольной призме ABCDEFA 1B 1C 1D 1E 1F 1 все ребра равны 48. Найдите расстояние между точками A и E1.
Рассмотрим прямоугольный треугольник AA 1 E 1 . По теореме Пифагора:
*Угол между сторонами правильного шестиугольника равен 120 градусам.
Отрезок АЕ 1 является гипотенузой, АА 1 и А 1 Е 1 катеты. Ребро АА 1 нам известно. Катет А 1 Е 1 мы можем найти используя используя теорему косинусов.
Теорема: Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.
*Обратите внимание, что 48 возводить в квадрат совсем не обязательно.
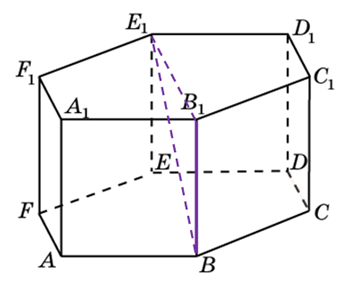
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 35. Найдите расстояние между точками B и E.
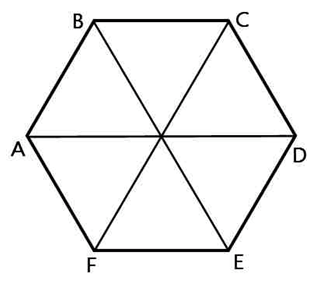
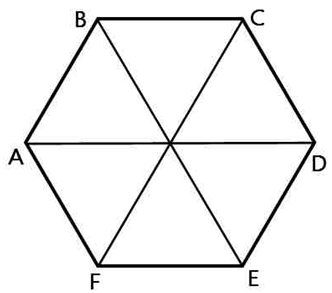
Рассмотрим правильный шестиугольник:
Сказано, что все рёбра равны 35, то есть сторона шестиугольника лежащего в основании равна 35. А так же, как уже сказано, радиус описанной около него окружности равен этому же числу.
273353. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны сорока корням из пяти. Найдите расстояние между точками B и E1.
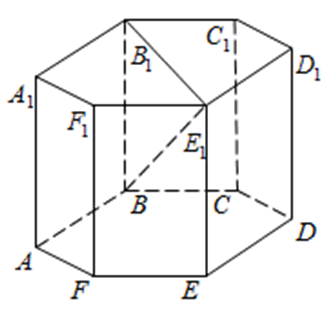
Рассмотрим прямоугольный треугольник BB 1 E 1 . По теореме Пифагора:
Отрезок B 1 E 1 равен двум радиусам описанной около правильного шестиугольника окружности, а её радиус равен стороне шестиугольника, то есть
273683. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 45. Найдите тангенс угла AD1D.
Рассмотрим прямоугольный треугольник ADD1, в котором AD равно диаметру окружности, описанной вокруг основания. Известно, что радиус окружности, описанной вокруг правильного шестиугольника равен его стороне.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 23. Найдите угол DAB. Ответ дайте в градусах.
Рассмотрим правильный шестиугольник:
В нём углы между сторонами равны 120°. Значит,
Сама длина ребра не имеет значения, на величину угла она не влияет.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах.
Рассмотрим прямоугольный треугольник AC1C:
Найдём AC . В правильном шестиугольнике углы между его сторонами равны 120 градусам, тогда по теореме косинусов для треугольника АВС :
Значит, угол AC 1 C равен 60 градусам.
274453. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах.
Рассмотрим треугольник AС 1 С, он прямоугольный. Вычислим тангенс указанного в условии угла и определим угол. Известно, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то есть
Катет С1С = 10. Отрезок АС вычислим по теореме косинусов (это мы уже делали в первой задаче, запишем ещё раз):
В правильном шестиугольнике углы при вершинах равны 120 градусам, то есть
245364. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками А и Е1.
245365. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками В и Е.
245366. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1все ребра равны корню из пяти. Найдите расстояние между точками В и Е1.
245367. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите тангенс угла AD1D.
245368. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол DAB. Ответ дайте в градусах.
245369. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол AC1C. Ответ дайте в градусах.
В состав ЕГЭ включены и другие задачи по стереометрии, и они довольно разнообразны. Обязательно будем их рассматривать, не пропустите! Успехов вам!
Источник