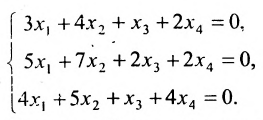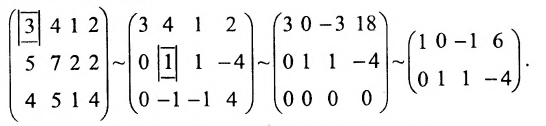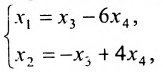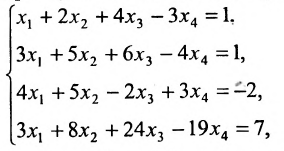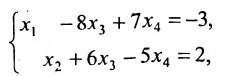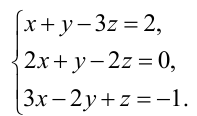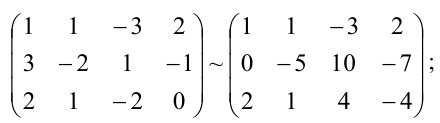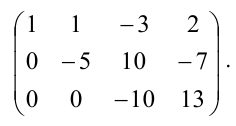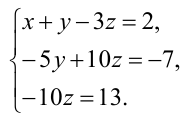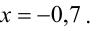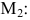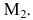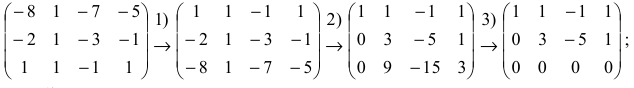3. Выяснить сколько решений имеет система линейных уравнений, заданная расширенной матрицей

при различных значениях параметра a.
Решение. Если 
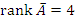
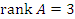
Если a = 0, то 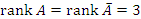
Следовательно, система имеет бесконечное множество решений.
Исследование СЛАУ. Общие сведения
В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.
Общие сведения (определения, условия, методы, виды)
Системы линейных алгебраических уравнений с n неизвестными могут иметь:
- единственное решение;
- бесконечное множество решение (неопределенные СЛАУ);
- ни одного решения (несовместные СЛАУ).
Пример 1
Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.
Система x + y = 1 2 x + 7 y = – 3 имеет единственное решение x = 2 ; y = 1 .
Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 – t при – ∞ t ∞ .
Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:
- Совместна ли система?
- Если система совместна, то, какое количество решений она имеет — одно или несколько?
- Как найти все решения?
Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:
- если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
- если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
- если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.
Ранг матрицы и его свойства
Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.
Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда
В математике выделяют следующие подходы к определению ранга матрицы:
- при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
- при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
- при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.
Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .
Свойства ранга матрицы:
- квадратная невырожденная матрица обладает рангом, который отличается от нуля;
- если транспонировать матрицу, то ранг матрицы не изменяется;
- если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
- при удалении нулевого столбца или строки ранг матрицы не изменяется;
- ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
- при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
- ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
- когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .
Пример 2
А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0
r ( A 1 ) = 1 , r ( B 1 ) = 1
А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6
Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Первая часть.
Исследовать систему линейных агебраических уравнений (СЛАУ) на совместность означает выяснить, есть у этой системы решения, или же их нет. Ну и если решения есть, то указать сколько их.
Нам понадобятся сведения из темы “Система линейных алгебраических уравнений. Основные термины. Матричная форма записи”. В частности, нужны такие понятия, как матрица системы и расширенная матрица системы, поскольку именно на них опирается формулировка теоремы Кронекера-Капелли. Как обычно, матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde$.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. $rang A=rangwidetilde$.
Следствие из теоремы Кронекера-Капелли
Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения или нет, а если существуют – то сколько.
Исследовать СЛАУ $ left <begin& -3x_1+9x_2-7x_3=17;\ & -x_1+2x_2-4x_3=9;\ & 4x_1-2x_2+19x_3=-42. endright.$ на совместность. Если СЛАУ совместна, указать количество решений.
Чтобы выяснить наличие решений заданной СЛАУ, используем теорему Кронекера-Капелли. Нам понадобятся матрица системы $A$ и расширенная матрица системы $widetilde$, запишем их:
Способ №1. Вычисление рангов по определению.
Согласно определению, ранг – это наивысший порядок миноров матрицы, среди которых есть хоть один, отличный от нуля. Обычно исследование начинают с миноров первого порядка, но здесь удобнее приступить сразу к вычислению минора третьего порядка матрицы $A$. Элементы минора третьего порядка находятся на пересечении трёх строк и трёх столбцов рассматриваемой матрицы. Так как матрица $A$ содержит всего 3 строки и 3 столбца, то минор третьего порядка матрицы $A$ – это определитель матрицы $A$, т.е. $Delta A$. Для вычисления определителя применим формулу №2 из темы “Формулы для вычисления определителей второго и третьего порядков”:
$$ Delta A=left| begin -3 & 9 & -7 \ -1 & 2 & -4 \ 4 & -2 & 19 end right|=-21. $$
Итак, есть минор третьего порядка матрицы $A$, который не равен нулю. Минор четвёртого порядка составить невозможно, так как для него требуется 4 строки и 4 столбца, а в матрице $A$ всего 3 строки и 3 столбца. Итак, наивысший порядок миноров матрицы $A$, среди которых есть хотя бы один не равный нулю, равен 3. Следовательно, $rang A=3$.
Задача решена. Какие недостатки и преимущества имеет данный способ? Для начала поговорим о плюсах. Во-первых, нам понадобилось найти всего один определитель. После этого мы сразу сделали вывод о количестве решений. Обычно в стандартных типовых расчётах даются системы уравнений, которые содержат три неизвестных и имеют единственное решение. Для таких систем данный метод очень даже удобен, ибо мы заранее знаем, что решение есть (иначе примера не было бы в типовом расчёте). Т.е. нам остаётся только показать наличие решения наиболее быстрым способом. Во-вторых, вычисленное значение определителя матрицы системы (т.е. $Delta A$) пригодится после: когда станем решать заданную систему методом Крамера или с помощью обратной матрицы.
Однако метод вычисления ранга по определению нежелательно применять, если матрица системы $A$ является прямоугольной. В этом случае лучше применить второй метод, о котором пойдёт речь ниже. Кроме того, если $Delta A=0$, то мы ничего не сможем сказать о количестве решений заданной неоднородной СЛАУ. Может, СЛАУ имеет бесконечное количество решений, а может – ни одного. Если $Delta A=0$, то требуется дополнительное исследование, которое зачастую является громоздким.
Подводя итог сказанному, отмечу, что первый способ хорош для тех СЛАУ, у которых матрица системы квадратна. При этом сама СЛАУ содержит три или четыре неизвестных и взята из стандартных типовых расчетов или контрольных работ.
Способ №2. Вычисление ранга методом элементарных преобразований.
Какие преимущества второго способа? Главное преимущество – это его универсальность. Нам совершенно неважно, является ли матрица системы квадратной или нет. Кроме того, мы фактически провели преобразования прямого хода метода Гаусса. Осталось лишь пару действий, и мы смогли бы получить решение данной СЛАУ. Честно говоря, второй способ нравится мне более первого, но выбор – это дело вкуса.
Ответ: Заданная СЛАУ совместна и определена.
$$ left( begin 1 & -1 & 2 & -1\ -1 & 2 & -3 & 3 \ 2 & -3 & 5 & -4 \ 3 & -2 & 5 & 1 \ 2 & -1 & 3 & 2 end right) begin phantom<0>\r_2+r_1\r_3-2r_1\ r_4-3r_1\r_5-2r_1endrightarrow left( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & -1 & 1 & -2 \ 0 & 1 & -1 & 4 \ 0 & 1 & -1 & 4 end right) begin phantom<0>\phantom<0>\r_3-r_2\ r_4-r_2\r_5+r_2endrightarrow\ $$ $$ rightarrowleft( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 0 end right) begin phantom<0>\phantom<0>\phantom<0>\ r_4-r_3\phantom<0>endrightarrow left( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 end right) $$
Расширенная матрица системы приведена к ступенчатому виду. Ранг ступенчатой матрицы равен количеству её ненулевых строк, поэтому $rangwidetilde=3$. Матрица $A$ (до черты) тоже приведена к ступенчатому виду, и ранг её равен 2, $rang=2$.
Ответ: система несовместна.
Приводим расширенную матрицу системы к ступенчатому виду:
$$ left( begin 2 & 0 & 7 & -5 & 11 & 42\ 1 & -2 & 3 & 0 & 2 & 17 \ -3 & 9 & -11 & 0 & -7 & -64 \ -5 & 17 & -16 & -5 & -4 & -90 \ 7 & -17 & 23 & 0 & 15 & 132 end right) overset> <rightarrow>$$ $$ rightarrowleft( begin 1 & -2 & 3 & 0 & 2 & 17\ 2 & 0 & 7 & -5 & 11 & 42\ -3 & 9 & -11 & 0 & -7 & -64\ -5 & 17 & -16 & -5 & -4 & -90 \ 7 & -17 & 23 & 0 & 15 & 132 end right) begin phantom<0>\ r_2-2r_1 \r_3+3r_1 \ r_4+5r_1 \ r_5-7r_1 end rightarrow left( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 3 & -2 & 0 & -1 & -13\ 0 & 7 & -1 & -5 & 6 & -5 \ 0 & -3 & 2 & 0 & 1 & 13 end right) begin phantom<0>\ phantom<0>\4r_3+3r_2 \ 4r_4-7r_2 \ 4r_5+3r_2 end rightarrow $$ $$ rightarrowleft( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 0 & -11 & 15 & -25 & -76\ 0 & 0 & -11 & 15 & -25 & -76 \ 0 & 0 & 11 & -15 & 25 & 76 end right) begin phantom<0>\ phantom<0>\phantom <0>\ r_4-r_3 \ r_5+r_2 end rightarrow left( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 0 & -11 & 15 & -25 & -76\ 0 & 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 & 0 end right) $$
Мы привели расширенную матрицу системы и саму матрицу системы к ступенчатому виду. Ранг расширенной матрицы системы равен трём, ранг матрицы системы также равен трём. Так как система содержит $n=5$ неизвестных, т.е. $rangwidetilde=ranglt$, то согласно пункту №2 следствия из теоремы Кронекера-Капелли данная система является неопределённой, т.е. имеет бесконечное количество решений.
Ответ: система является неопределённой.
Во второй части мы разберём примеры, которые нередко включают в типовые расчёты или контрольные работы по высшей математике: исследование на совместность и решение СЛАУ в зависимости от значений параметров, входящих в неё.
Решение систем линейных алгебраических уравнений, методы решения, примеры.
Решение систем линейных алгебраических уравнений (СЛАУ), несомненно, является важнейшей темой курса линейной алгебры. Огромное количество задач из всех разделов математики сводится к решению систем линейных уравнений. Этими факторами объясняется причина создания данной статьи. Материал статьи подобран и структурирован так, что с его помощью Вы сможете
- подобрать оптимальный метод решения Вашей системы линейных алгебраических уравнений,
- изучить теорию выбранного метода,
- решить Вашу систему линейных уравнений, рассмотрев подробно разобранные решения характерных примеров и задач.
Краткое описание материала статьи.
Сначала дадим все необходимые определения, понятия и введем обозначения.
Далее рассмотрим методы решения систем линейных алгебраических уравнений, в которых число уравнений равно числу неизвестных переменных и которые имеют единственное решение. Во-первых, остановимся на методе Крамера, во-вторых, покажем матричный метод решения таких систем уравнений, в-третьих, разберем метод Гаусса (метод последовательного исключения неизвестных переменных). Для закрепления теории обязательно решим несколько СЛАУ различными способами.
После этого перейдем к решению систем линейных алгебраических уравнений общего вида, в которых число уравнений не совпадает с числом неизвестных переменных или основная матрица системы является вырожденной. Сформулируем теорему Кронекера – Капелли, которая позволяет установить совместность СЛАУ. Разберем решение систем (в случае их совместности) с помощью понятия базисного минора матрицы. Также рассмотрим метод Гаусса и подробно опишем решения примеров.
Обязательно остановимся на структуре общего решения однородных и неоднородных систем линейных алгебраических уравнений. Дадим понятие фундаментальной системы решений и покажем, как записывается общее решение СЛАУ с помощью векторов фундаментальной системы решений. Для лучшего понимания разберем несколько примеров.
В заключении рассмотрим системы уравнений, сводящиеся к линейным, а также различные задачи, при решении которых возникают СЛАУ.
Навигация по странице.
Определения, понятия, обозначения.
Будем рассматривать системы из p линейных алгебраических уравнений с n неизвестными переменными ( p может быть равно n ) вида
– неизвестные переменные, – коэффициенты (некоторые действительные или комплексные числа), – свободные члены (также действительные или комплексные числа).
Такую форму записи СЛАУ называют координатной.
В матричной форме записи эта система уравнений имеет вид ,
где – основная матрица системы, – матрица-столбец неизвестных переменных, – матрица-столбец свободных членов.
Если к матрице А добавить в качестве (n+1)-ого столбца матрицу-столбец свободных членов, то получим так называемую расширенную матрицу системы линейных уравнений. Обычно расширенную матрицу обозначают буквой Т , а столбец свободных членов отделяют вертикальной линией от остальных столбцов, то есть,
Решением системы линейных алгебраических уравнений называют набор значений неизвестных переменных , обращающий все уравнения системы в тождества. Матричное уравнение при данных значениях неизвестных переменных также обращается в тождество .
Если система уравнений имеет хотя бы одно решение, то она называется совместной.
Если система уравнений решений не имеет, то она называется несовместной.
Если СЛАУ имеет единственное решение, то ее называют определенной; если решений больше одного, то – неопределенной.
Если свободные члены всех уравнений системы равны нулю , то система называется однородной, в противном случае – неоднородной.
Решение элементарных систем линейных алгебраических уравнений.
Если число уравнений системы равно числу неизвестных переменных и определитель ее основной матрицы не равен нулю, то такие СЛАУ будем называть элементарными. Такие системы уравнений имеют единственное решение, причем в случае однородной системы все неизвестные переменные равны нулю.
Такие СЛАУ мы начинали изучать в средней школе. При их решении мы брали какое-нибудь одно уравнение, выражали одну неизвестную переменную через другие и подставляли ее в оставшиеся уравнения, следом брали следующее уравнение, выражали следующую неизвестную переменную и подставляли в другие уравнения и так далее. Или пользовались методом сложения, то есть, складывали два или более уравнений, чтобы исключить некоторые неизвестные переменные. Не будем подробно останавливаться на этих методах, так как они по сути являются модификациями метода Гаусса.
Основными методами решения элементарных систем линейных уравнений являются метод Крамера, матричный метод и метод Гаусса. Разберем их.
Решение систем линейных уравнений методом Крамера.
Пусть нам требуется решить систему линейных алгебраических уравнений
в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля, то есть, .
Пусть – определитель основной матрицы системы, а – определители матриц, которые получаются из А заменой 1-ого, 2-ого, …, n-ого столбца соответственно на столбец свободных членов:
При таких обозначениях неизвестные переменные вычисляются по формулам метода Крамера как . Так находится решение системы линейных алгебраических уравнений методом Крамера.
Решите систему линейных уравнений методом Крамера .
Основная матрица системы имеет вид . Вычислим ее определитель (при необходимости смотрите статью определитель матрицы: определение, методы вычисления, примеры, решения):
Так как определитель основной матрицы системы отличен от нуля, то система имеет единственное решение, которое может быть найдено методом Крамера.
Составим и вычислим необходимые определители (определитель получаем, заменив в матрице А первый столбец на столбец свободных членов , определитель – заменив второй столбец на столбец свободных членов, – заменив третий столбец матрицы А на столбец свободных членов):
Находим неизвестные переменные по формулам :
Основным недостатком метода Крамера (если это можно назвать недостатком) является трудоемкость вычисления определителей, когда число уравнений системы больше трех.
Для более детальной информации смотрите раздел метод Крамера: вывод формул, примеры, решения.
Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
Пусть система линейных алгебраических уравнений задана в матричной форме , где матрица A имеет размерность n на n и ее определитель отличен от нуля.
Так как , то матрица А – обратима, то есть, существует обратная матрица . Если умножить обе части равенства на слева, то получим формулу для нахождения матрицы-столбца неизвестных переменных . Так мы получили решение системы линейных алгебраических уравнений матричным методом.
Решите систему линейных уравнений матричным методом.
Перепишем систему уравнений в матричной форме:
Так как
то СЛАУ можно решать матричным методом. С помощью обратной матрицы решение этой системы может быть найдено как .
Построим обратную матрицу с помощью матрицы из алгебраических дополнений элементов матрицы А (при необходимости смотрите статью методы нахождения обратной матрицы):
Осталось вычислить – матрицу неизвестных переменных, умножив обратную матрицу на матрицу-столбец свободных членов (при необходимости смотрите статью операции над матрицами):
или в другой записи x1 = 4, x2 = 0, x3 = -1 .
Основная проблема при нахождении решения систем линейных алгебраических уравнений матричным методом заключается в трудоемкости нахождения обратной матрицы, особенно для квадратных матриц порядка выше третьего.
Более подробное описание теории и дополнительные примеры смотрите в статье матричный метод решения систем линейных уравнений.
Решение систем линейных уравнений методом Гаусса.
Пусть нам требуется найти решение системы из n линейных уравнений с n неизвестными переменными
определитель основной матрицы которой отличен от нуля.
Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключается x1 из всех уравнений системы, начиная со второго, далее исключается x2 из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменная xn . Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется прямым ходом метода Гаусса. После завершения прямого хода метода Гаусса из последнего уравнения находится xn , с помощью этого значения из предпоследнего уравнения вычисляется xn-1 , и так далее, из первого уравнения находится x1 . Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется обратным ходом метода Гаусса.
Кратко опишем алгоритм исключения неизвестных переменных.
Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменную x1 из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на , и так далее, к n-ому уравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет вид
где , а .
К такому же результату мы бы пришли, если бы выразили x1 через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x1 исключена из всех уравнений, начиная со второго.
Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке
Будем считать, что (в противном случае мы переставим местами вторую строку с k-ой , где ). Приступаем к исключению неизвестной переменной x2 из всех уравнений, начиная с третьего.
Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на , и так далее, к n-ому уравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет вид
где , а . Таким образом, переменная x2 исключена из всех уравнений, начиная с третьего.
Далее приступаем к исключению неизвестной x3 , при этом действуем аналогично с отмеченной на рисунке частью системы
Так продолжаем прямой ход метода Гаусса пока система не примет вид
С этого момента начинаем обратный ход метода Гаусса: вычисляем xn из последнего уравнения как , с помощью полученного значения xn находим xn-1 из предпоследнего уравнения, и так далее, находим x1 из первого уравнения.
Решите систему линейных уравнений методом Гаусса.
Исключим неизвестную переменную x1 из второго и третьего уравнения системы. Для этого к обеим частям второго и третьего уравнений прибавим соответствующие части первого уравнения, умноженные на и на соответственно:
Теперь из третьего уравнения исключим x2 , прибавив к его левой и правой частям левую и правую части второго уравнения, умноженные на :
На этом прямой ход метода Гаусса закончен, начинаем обратный ход.
Из последнего уравнения полученной системы уравнений находим x3 :
Из второго уравнения получаем .
Из первого уравнения находим оставшуюся неизвестную переменную и этим завершаем обратный ход метода Гаусса .
Более детальную информацию и дополнительные примеры смотрите в разделе решение элементарных систем линейных алгебраических уравнений методом Гаусса.
Решение систем линейных алгебраических уравнений общего вида.
В общем случае число уравнений системы p не совпадает с числом неизвестных переменных n :
Такие СЛАУ могут не иметь решений, иметь единственное решение или иметь бесконечно много решений. Это утверждение относится также к системам уравнений, основная матрица которых квадратная и вырожденная.
Далее нам потребуется понятие минора матрицы и ранга матрицы, которые даны в статье ранг матрицы: определение, методы нахождения, примеры, решения.
Теорема Кронекера – Капелли.
Прежде чем находить решение системы линейных уравнений необходимо установить ее совместность. Ответ на вопрос когда СЛАУ совместна, а когда несовместна, дает теорема Кронекера – Капелли:
для того, чтобы система из p уравнений с n неизвестными ( p может быть равно n ) была совместна необходимо и достаточно, чтобы ранг основной матрицы системы был равен рангу расширенной матрицы, то есть, Rank(A)=Rank(T) .
Рассмотрим на примере применение теоремы Кронекера – Капелли для определения совместности системы линейных уравнений.
Выясните, имеет ли система линейных уравнений решения.
Найдем ранг основной матрицы системы . Воспользуемся методом окаймляющих миноров. Минор второго порядка отличен от нуля. Переберем окаймляющие его миноры третьего порядка:
Так как все окаймляющие миноры третьего порядка равны нулю, то ранг основной матрицы равен двум.
В свою очередь ранг расширенной матрицы равен трем, так как минор третьего порядка
отличен от нуля.
Таким образом, , следовательно, по теореме Кронекера – Капелли можно сделать вывод, что исходная система линейных уравнений несовместна.
система решений не имеет.
Итак, мы научились устанавливать несовместность системы с помощью теоремы Кронекера – Капелли.
А как же находить решение СЛАУ, если установлена ее совместность?
Для этого нам потребуется понятие базисного минора матрицы и теорема о ранге матрицы.
Минор наивысшего порядка матрицы А , отличный от нуля, называется базисным.
Из определения базисного минора следует, что его порядок равен рангу матрицы. Для ненулевой матрицы А базисных миноров может быть несколько, один базисный минор есть всегда.
Для примера рассмотрим матрицу .
Все миноры третьего порядка этой матрицы равны нулю, так как элементы третьей строки этой матрицы представляют собой сумму соответствующих элементов первой и второй строк.
Базисными являются следующие миноры второго порядка, так как они отличны от нуля
Миноры базисными не являются, так как равны нулю.
Теорема о ранге матрицы.
Если ранг матрицы порядка p на n равен r , то все элементы строк (и столбцов) матрицы, не образующие выбранный базисный минор, линейно выражаются через соответствующие элементы строк (и столбцов), образующих базисный минор.
Что нам дает теорема о ранге матрицы?
Если по теореме Кронекера – Капелли мы установили совместность системы, то выбираем любой базисный минор основной матрицы системы (его порядок равен r ), и исключаем из системы все уравнения, которые не образуют выбранный базисный минор. Полученная таким образом СЛАУ будет эквивалентна исходной, так как отброшенные уравнения все равно излишни (они согласно теореме о ранге матрицы являются линейной комбинацией оставшихся уравнений).
В итоге, после отбрасывания излишних уравнений системы, возможны два случая.
Если число уравнений r в полученной системе будет равно числу неизвестных переменных, то она будет определенной и единственное решение можно будет найти методом Крамера, матричным методом или методом Гаусса.
Решите систему линейных алгебраических уравнений .
Ранг основной матрицы системы равен двум, так как минор второго порядка отличен от нуля. Ранг расширенной матрицы также равен двум, так как единственный минор третьего порядка равен нулю
а рассмотренный выше минор второго порядка отличен от нуля. На основании теоремы Кронекера – Капелли можно утверждать совместность исходной системы линейных уравнений, так как Rank(A)=Rank(T)=2 .
В качестве базисного минора возьмем . Его образуют коэффициенты первого и второго уравнений:
Третье уравнение системы не участвует в образовании базисного минора, поэтому исключим его из системы на основании теоремы о ранге матрицы:
Так мы получили элементарную систему линейных алгебраических уравнений. Решим ее методом Крамера:
Если число уравнений r в полученной СЛАУ меньше числа неизвестных переменных n , то в левых частях уравнений оставляем слагаемые, образующие базисный минор, остальные слагаемые переносим в правые части уравнений системы с противоположным знаком.
Неизвестные переменные (их r штук), оставшиеся в левых частях уравнений, называются основными.
Неизвестные переменные (их штук), которые оказались в правых частях, называются свободными.
Теперь считаем, что свободные неизвестные переменные могут принимать произвольные значения, при этом r основных неизвестных переменных будут выражаться через свободные неизвестные переменные единственным образом. Их выражение можно найти решая полученную СЛАУ методом Крамера, матричным методом или методом Гаусса.
Разберем на примере.
Решите систему линейных алгебраических уравнений .
Найдем ранг основной матрицы системы методом окаймляющих миноров. В качестве ненулевого минора первого порядка возьмем . Начнем поиск ненулевого минора второго порядка, окаймляющего данный минор:
Так мы нашли ненулевой минор второго порядка. Начнем поиск ненулевого окаймляющего минора третьего порядка:
Таким образом, ранг основной матрицы равен трем. Ранг расширенной матрицы также равен трем, то есть, система совместна.
Найденный ненулевой минор третьего порядка возьмем в качестве базисного.
Для наглядности покажем элементы, образующие базисный минор:
Оставляем в левой части уравнений системы слагаемые, участвующие в базисном миноре, остальные переносим с противоположными знаками в правые части:
Придадим свободным неизвестным переменным x2 и x5 произвольные значения, то есть, примем , где – произвольные числа. При этом СЛАУ примет вид
Полученную элементарную систему линейных алгебраических уравнений решим методом Крамера:
Следовательно, .
В ответе не забываем указать свободные неизвестные переменные.
, где – произвольные числа.
Чтобы решить систему линейных алгебраических уравнений общего вида, сначала выясняем ее совместность, используя теорему Кронекера – Капелли. Если ранг основной матрицы не равен рангу расширенной матрицы, то делаем вывод о несовместности системы.
Если ранг основной матрицы равен рангу расширенной матрицы, то выбираем базисный минор и отбрасываем уравнения системы, которые не участвуют в образовании выбранного базисного минора.
Если порядок базисного минора равен числу неизвестных переменных, то СЛАУ имеет единственное решение, которое находим любым известным нам методом.
Если порядок базисного минора меньше числа неизвестных переменных, то в левой части уравнений системы оставляем слагаемые с основными неизвестными переменными, остальные слагаемые переносим в правые части и придаем свободным неизвестным переменным произвольные значения. Из полученной системы линейных уравнений находим основные неизвестные переменные методом Крамера, матричным методом или методом Гаусса.
Метод Гаусса для решения систем линейных алгебраических уравнений общего вида.
Методом Гаусса можно решать системы линейных алгебраических уравнений любого вида без предварительного их исследования на совместность. Процесс последовательного исключения неизвестных переменных позволяет сделать вывод как о совместности, так и о несовместности СЛАУ, а в случае существования решения дает возможность отыскать его.
С точки зрения вычислительной работы метод Гаусса является предпочтительным.
Запись общего решения однородных и неоднородных систем линейных алгебраических с помощью векторов фундаментальной системы решений.
В этом разделе речь пойдет о совместных однородных и неоднородных системах линейных алгебраических уравнений, имеющих бесконечное множество решений.
Разберемся сначала с однородными системами.
Фундаментальной системой решений однородной системы из p линейных алгебраических уравнений с n неизвестными переменными называют совокупность линейно независимых решений этой системы, где r – порядок базисного минора основной матрицы системы.
Если обозначить линейно независимые решения однородной СЛАУ как ( – это матрицы столбцы размерности n на 1 ), то общее решение этой однородной системы представляется в виде линейной комбинации векторов фундаментальной системы решений с произвольными постоянными коэффициентами , то есть, .
Что обозначает термин общее решение однородной системы линейных алгебраических уравнений (орослау)?
Смысл прост: формула задает все возможные решения исходной СЛАУ, другими словами, взяв любой набор значений произвольных постоянных , по формуле мы получим одно из решений исходной однородной СЛАУ.
Таким образом, если мы найдем фундаментальную систему решений, то мы сможем задать все решения этой однородной СЛАУ как .
Покажем процесс построения фундаментальной системы решений однородной СЛАУ.
Выбираем базисный минор исходной системы линейных уравнений, исключаем все остальные уравнения из системы и переносим в правые части уравнений системы с противоположными знаками все слагаемые, содержащие свободные неизвестные переменные. Придадим свободным неизвестным переменным значения 1,0,0,…,0 и вычислим основные неизвестные, решив полученную элементарную систему линейных уравнений любым способом, например, методом Крамера. Так будет получено X (1) – первое решение фундаментальной системы. Если придать свободным неизвестным значения 0,1,0,0,…,0 и вычислить при этом основные неизвестные, то получим X (2) . И так далее. Если свободным неизвестным переменным придадим значения 0,0,…,0,1 и вычислим основные неизвестные, то получим X (n-r) . Так будет построена фундаментальная система решений однородной СЛАУ и может быть записано ее общее решение в виде .
Для неоднородных систем линейных алгебраических уравнений общее решение представляется в виде , где – общее решение соответствующей однородной системы, а – частное решение исходной неоднородной СЛАУ, которое мы получаем, придав свободным неизвестным значения 0,0,…,0 и вычислив значения основных неизвестных.
Разберем на примерах.
Найдите фундаментальную систему решений и общее решение однородной системы линейных алгебраических уравнений .
Ранг основной матрицы однородных систем линейных уравнений всегда равен рангу расширенной матрицы. Найдем ранг основной матрицы методом окаймляющих миноров. В качестве ненулевого минора первого порядка возьмем элемент основной матрицы системы. Найдем окаймляющий ненулевой минор второго порядка:
Минор второго порядка, отличный от нуля, найден. Переберем окаймляющие его миноры третьего порядка в поисках ненулевого:
Все окаймляющие миноры третьего порядка равны нулю, следовательно, ранг основной и расширенной матрицы равен двум. Базисным минором возьмем . Отметим для наглядности элементы системы, которые его образуют:
Третье уравнение исходной СЛАУ не участвует в образовании базисного минора, поэтому, может быть исключено:
Оставляем в правых частях уравнений слагаемые, содержащие основные неизвестные, а в правые части переносим слагаемые со свободными неизвестными:
Построим фундаментальную систему решений исходной однородной системы линейных уравнений. Фундаментальная система решений данной СЛАУ состоит из двух решений, так как исходная СЛАУ содержит четыре неизвестных переменных, а порядок ее базисного минора равен двум. Для нахождения X (1) придадим свободным неизвестным переменным значения , тогда основные неизвестные найдем из системы уравнений
.
Решим ее методом Крамера:
Таким образом, .
Теперь построим X (2) . Для этого придадим свободным неизвестным переменным значения , тогда основные неизвестные найдем из системы линейных уравнений
.
Опять воспользуемся методом Крамера:
Получаем .
Так мы получили два вектора фундаментальной системы решений и , теперь мы можем записать общее решение однородной системы линейных алгебраических уравнений:
, где C1 и C2 – произвольные числа.
Найдите общее решение неоднородной системы линейных алгебраических уравнений .
Общее решение этой системы уравнений будем искать в виде .
Исходной неоднородной СЛАУ соответствует однородная система
общее решение которой мы нашли в предыдущем примере
.
Следовательно, нам осталось найти частное решение неоднородной системы линейных алгебраических уравнений .
Ранг основной матрицы системы равен двум, ранг расширенной матрицы системы также равен двум, так как все миноры третьего порядка, окаймляющие минор , равны нулю. Также примем минор в качестве базисного, исключим третье уравнение из системы и перенесем слагаемые со свободными неизвестными в правые части уравнений системы:
Для нахождения придадим свободным неизвестным переменным значения , тогда система уравнений примет вид , откуда методом Крамера найдем основные неизвестные переменные:
Имеем , следовательно,
где C1 и C2 – произвольные числа.
Следует заметить, что решения неопределенной однородной системы линейных алгебраических уравнений порождают линейное пространство размерности , базисом которого является фундаментальная система решений.
Решение систем уравнений, сводящихся к СЛАУ.
Некоторые системы уравнений с помощью замены переменных можно свести к линейным. Рассмотрим несколько примеров.
[spoiler title=”источники:”]
http://math1.ru/education/sys_lin_eq/kapelli.html
http://www.cleverstudents.ru/systems/solving_systems_of_linear_equations.html
[/spoiler]
В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.
Общие сведения (определения, условия, методы, виды)
Системы линейных алгебраических уравнений с n неизвестными могут иметь:
- единственное решение;
- бесконечное множество решение (неопределенные СЛАУ);
- ни одного решения (несовместные СЛАУ).
Система x+y+z=12x+2y+2z=3не имеет решений, поэтому она несовместна.
Система x+y=12x+7y=-3имеет единственное решение x=2; y=1.
Система x+y=12x+2y=23x+3y=3имеет бесконечное множество решений x=ty=1-tпри -∞<t<∞.
Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:
- Совместна ли система?
- Если система совместна, то, какое количество решений она имеет — одно или несколько?
- Как найти все решения?
Если система малоразмерна при m=n, то ответить на поставленные вопросы можно при помощи метода Крамера:
- если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
- если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
- если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.
Ранг матрицы и его свойства
Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.
Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда
В математике выделяют следующие подходы к определению ранга матрицы:
- при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
- при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
- при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.
Обозначение ранга матрицы: r(A), rg(A), rA.
Свойства ранга матрицы:
- квадратная невырожденная матрица обладает рангом, который отличается от нуля;
- если транспонировать матрицу, то ранг матрицы не изменяется;
- если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
- при удалении нулевого столбца или строки ранг матрицы не изменяется;
- ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
- при умножении все элементов строки/столбца на число k не равно нулю ранг матрицы не изменяется;
- ранг матрицы не больше меньшего из ее размеров: r(А)≤min (m; n) ;
- когда все элементы матрицы равны нулю, то только тогда r(A)=0 .
А1=111222333, B1=100000
r(A1)=1, r(B1)=1
А2=123405670000; В2=11312143125054136
r(A2)=2; r(B2)=2
А3=111123149
r(A3)=3
Ранг матрицы А1 вычислен на основании свойства определителя, который содержит строки с пропорциональными элементами, поскольку любой минор второго или третьего порядка матрицы А1 равняется нулю.
Ранги матриц В1, А2 вычислены при помощи вычеркивания нулевых строк, поскольку в матрице А2 минор отличается от нуля на пересечении 2-х первых строк и 2-х первых столбцов.
Матрица А3 — невырожденная, поскольку ее ранг равняется 3. (Можно проверить условие ∆=А3 не равно нулю).
Теперь вычислим ранг матрицы В2 при помощи элементарных преобразований:
- элементы 1-ой строки умножим на (-2) и прибавим к соответствующим элементам 2-ой строки;
- элементы 1-ой строки умножим на (-1) и прибавим к соответствующим элементам 3-ей строки;
- элементы 1-ой строки умножим на (-5) и прибавим к соответствующим элементам 4-ой строки:
В2=11312143125054136 (-2)(-1)(-5)+++⇒11310-1-21012-10-1-21⇒
3-ю строку прибавим ко 2-ой и 4-ой строкам:
⇒11310000012-10000⇒1131012-1
Таким образом, число ненулевых строк равно 2 или минор 2-го порядка в левом углу матрицы:
М(2)=1101=10 не равно нулю⇒r(B2)=2
ч.т.д.
Теорема Кронеккера-Капелли (о разрешимости СЛАУ)
Теорема Кронеккера-Капелли — теорема, которая доказывает: чтобы СЛАУ была совместной, необходимым и достаточным условием является равенство ранга r матрицы рангу расширенной матрицы.
Для совместных СЛАУ справедливой считается следующая теорема.
Пусть ранг матрицы, которая составлена из коэффициентов СЛАУ, равен рангу расширенной матрицы. В таком случае, если r=n (где n — число неизвестных системы), то система имеет единственное решение, если r<n, то система имеет бесконечное множество решений.
Если система определена, то для ее решения подходят методы Крамера, Гаусса и матричный метод.
Если система не определена, то некоторым (n-r) неизвестным (свободным) можно давать произвольные значения, а r неизвестных (базисных) определяются через свободные единственным способом.
При этом базисными становятся те, чей определитель, который составлен из коэффициентов при них и отличен от нуля. Выражения главных переменных, которые получены через свободные, объявляются решением системы.
Исследуем и решаем матрицу:
x -2x -x + 2x =12x – x + 4x +4x =5 +4x -2x +x =54x +x +4x +9x =2
Составляем расширенную матрицу системы и приводим ее к ступенчатому виду методом Гаусса.
Определяем ее ранг, а ранг основной матрицы определяем закрытием столбца правых частей.
1-2-1212-144504-21541492(-2)(-4)++⇒1-2-1210360304-2150981-2÷(3)⇒
⇒1-2-121012010-2-2150881-2(-4)(-9)++1-2-1210120100-101100-101-11(-1)+⇒
⇒0-2-1210120100-10110000-12⇒r(A)=31(Ap)=41r(A) не равно r(Ap).
Ответ: система не совместна.
Рассматриваем систему линейных уравнений и находим ранг матрицы:
n=4, m=3:x1-3×2+4×3-x4=13×1+7×2-10×3+5×4=52×1+2x-3x32x4=3
A=1-34-137-10522-32(-3)(-2)++⇒1-34-1016-22808-11412+⇒
⇒1-34-1016-2280000⇒r(A)=2
Составляем расширенную матрицу системы и находим ее ранг:
Ap=1-34-137-10522-32153(-3)(-2)++⇒1-34-1016-22808-11412112+⇒
⇒1-34-1016-2280000120⇒r(Ap)=2
r(A)=r(Ap)=2 — система совместная, r=2<n=4 ⇒ — система неопределенная.
Решаем систему методом Гаусса: преобразования расширенной матрицы системы приводят к системе уравнений вида:
x1-3×2+4×3-x4=116×2-22×3+8×4=2; ∆=1-3016=16 не равно нулю.
Главные переменные — x1 и x2. Свободные переменные — неизвестные x3 и x4. Записываем систему уравнений в виде:
x1-3×2=1-4×3+x48x2=1+11×3-4×4
С помощью обратного хода находим:
x=118x-12x+18.
Из 1-го уравнения:
x1=3×2-4×3+x4+1=338×3-32×4+38-4×3+x4+1=18×3-12×4+118
Ответ: система неопределенная.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Первая часть.
Исследовать систему линейных агебраических уравнений (СЛАУ) на совместность означает выяснить, есть у этой системы решения, или же их нет. Ну и если решения есть, то указать сколько их.
Нам понадобятся сведения из темы “Система линейных алгебраических уравнений. Основные термины. Матричная форма записи”. В частности, нужны такие понятия, как матрица системы и расширенная матрица системы, поскольку именно на них опирается формулировка теоремы Кронекера-Капелли. Как обычно, матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde{A}$.
Теорема Кронекера-Капелли
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. $rang A=rangwidetilde{A}$.
Напомню, что система называется совместной, если она имеет хоть одно решение. Теорема Кронекера-Капелли говорит вот о чём: если $rang A=rangwidetilde{A}$, то решение есть; если $rang Aneqrangwidetilde{A}$, то данная СЛАУ не имеет решений (несовместна). Ответ на вопрос о количестве этих решений даёт следствие из теоремы Кронекера-Капелли. В формулировке следствия использована буква $n$, которая равна количеству переменных заданной СЛАУ.
Следствие из теоремы Кронекера-Капелли
- Если $rang Aneqrangwidetilde{A}$, то СЛАУ несовместна (не имеет решений).
- Если $rang A=rangwidetilde{A} < n$, то СЛАУ является неопределённой (имеет бесконечное количество решений).
- Если $rang A=rangwidetilde{A} = n$, то СЛАУ является определённой (имеет ровно одно решение).
Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения или нет, а если существуют – то сколько.
Пример №1
Исследовать СЛАУ $
left {begin{aligned}
& -3x_1+9x_2-7x_3=17;\
& -x_1+2x_2-4x_3=9;\
& 4x_1-2x_2+19x_3=-42.
end{aligned}right.$ на совместность. Если СЛАУ совместна, указать количество решений.
Решение
Чтобы выяснить наличие решений заданной СЛАУ, используем теорему Кронекера-Капелли. Нам понадобятся матрица системы $A$ и расширенная матрица системы $widetilde{A}$, запишем их:
$$
A=left( begin{array} {ccc}
-3 & 9 & -7 \ -1 & 2 & -4 \ 4 & -2 & 19
end{array} right);;
widetilde{A}=left( begin{array} {ccc|c}
-3 & 9 &-7 & 17 \ -1 & 2 & -4 & 9\ 4 & -2 & 19 & -42
end{array} right).
$$
Нужно найти $rang A$ и $rangwidetilde{A}$. Для этого есть много способов, некоторые из которых перечислены в разделе “Ранг матрицы”. Обычно для исследования таких систем применяют два метода: “Вычисление ранга матрицы по определению” или “Вычисление ранга матрицы методом элементарных преобразований”.
Способ №1. Вычисление рангов по определению.
Согласно определению, ранг – это наивысший порядок миноров матрицы, среди которых есть хоть один, отличный от нуля. Обычно исследование начинают с миноров первого порядка, но здесь удобнее приступить сразу к вычислению минора третьего порядка матрицы $A$. Элементы минора третьего порядка находятся на пересечении трёх строк и трёх столбцов рассматриваемой матрицы. Так как матрица $A$ содержит всего 3 строки и 3 столбца, то минор третьего порядка матрицы $A$ – это определитель матрицы $A$, т.е. $Delta A$. Для вычисления определителя применим формулу №2 из темы “Формулы для вычисления определителей второго и третьего порядков”:
$$
Delta A=left| begin{array} {ccc}
-3 & 9 & -7 \ -1 & 2 & -4 \ 4 & -2 & 19
end{array} right|=-21.
$$
Итак, есть минор третьего порядка матрицы $A$, который не равен нулю. Минор четвёртого порядка составить невозможно, так как для него требуется 4 строки и 4 столбца, а в матрице $A$ всего 3 строки и 3 столбца. Итак, наивысший порядок миноров матрицы $A$, среди которых есть хотя бы один не равный нулю, равен 3. Следовательно, $rang A=3$.
Нам требуется найти также и $rangwidetilde{A}$. Давайте посмотрим на структуру матрицы $widetilde{A}$. До черты в матрице $widetilde{A}$ находятся элементы матрицы $A$, причём мы выяснили, что $Delta Aneq 0$. Следовательно, у матрицы $widetilde{A}$ есть минор третьего порядка, который не равен нулю. Миноров четвёртого порядка матрицы $widetilde{A}$ составить мы не можем, поэтому делаем вывод: $rangwidetilde{A}=3$.
Так как $rang A=rangwidetilde{A}$, то согласно теореме Кронекера-Капелли система совместна, т.е. имеет решение (хотя бы одно). Чтобы указать количество решений, учтём, что наша СЛАУ содержит 3 неизвестных: $x_1$, $x_2$ и $x_3$. Так как количество неизвестных $n=3$, то делаем вывод: $rang A=rangwidetilde{A}=n$, поэтому согласно пункту №3 следствия из теоремы Кронекера-Капелли, система является определённой, т.е. имеет единственное решение.
Задача решена. Какие недостатки и преимущества имеет данный способ? Для начала поговорим о плюсах. Во-первых, нам понадобилось найти всего один определитель. После этого мы сразу сделали вывод о количестве решений. Обычно в стандартных типовых расчётах даются системы уравнений, которые содержат три неизвестных и имеют единственное решение. Для таких систем данный метод очень даже удобен, ибо мы заранее знаем, что решение есть (иначе примера не было бы в типовом расчёте). Т.е. нам остаётся только показать наличие решения наиболее быстрым способом. Во-вторых, вычисленное значение определителя матрицы системы (т.е. $Delta A$) пригодится после: когда станем решать заданную систему методом Крамера или с помощью обратной матрицы.
Однако метод вычисления ранга по определению нежелательно применять, если матрица системы $A$ является прямоугольной. В этом случае лучше применить второй метод, о котором пойдёт речь ниже. Кроме того, если $Delta A=0$, то мы ничего не сможем сказать о количестве решений заданной неоднородной СЛАУ. Может, СЛАУ имеет бесконечное количество решений, а может – ни одного. Если $Delta A=0$, то требуется дополнительное исследование, которое зачастую является громоздким.
Подводя итог сказанному, отмечу, что первый способ хорош для тех СЛАУ, у которых матрица системы квадратна. При этом сама СЛАУ содержит три или четыре неизвестных и взята из стандартных типовых расчетов или контрольных работ.
Способ №2. Вычисление ранга методом элементарных преобразований.
Подробно это метод описан в соответствующей теме. Мы станем вычислять ранг матрицы $widetilde{A}$. Почему именно матрицы $widetilde{A}$, а не $A$? Дело в том, что матрица $A$ является частью матрицы $widetilde{A}$, поэтому вычисляя ранг матрицы $widetilde{A}$ мы одновременно найдем и ранг матрицы $A$.
begin{aligned}
&widetilde{A} =left( begin{array} {ccc|c}
-3 & 9 &-7 & 17 \ -1 & 2 & -4 & 9\ 4 & -2 & 19 & -42
end{array} right) rightarrow left|text{меняем местами первую и вторую строки}right| rightarrow \
&rightarrow left( begin{array} {ccc|c}
-1 & 2 & -4 & 9 \
-3 & 9 &-7 & 17\
4 & -2 & 19 & -42
end{array} right)
begin{array} {l} phantom{0} \ r_2-3r_1\ r_3+4r_1 end{array} rightarrow
left( begin{array} {ccc|c}
-1 & 2 & -4 & 9 \
0 & 3 &5 & -10\
0 & 6 & 3 & -6
end{array} right)
begin{array} {l} phantom{0} \ phantom{0}\ r_3-2r_2 end{array}rightarrow\
&rightarrow left( begin{array} {ccc|c}
-1 & 2 & -4 & 9 \
0 & 3 &5 & -10\
0 & 0 & -7 & 14
end{array} right)
end{aligned}
Мы привели матрицу $widetilde{A}$ к ступенчатому виду. Полученная ступенчатая матрица имеет три ненулевых строки, поэтому её ранг равен 3. Следовательно, и ранг матрицы $widetilde{A}$ равен 3, т.е. $rangwidetilde{A}=3$. Делая преобразования с элементами матрицы $widetilde{A}$ мы одновременно преобразовывали и элементы матрицы $A$, расположенные до черты. Матрица $A$ также приведена к ступенчатому виду: $left( begin{array} {ccc}
-1 & 2 & -4 \
0 & 3 &5 \
0 & 0 & -7
end{array} right)$. Вывод: ранг матрицы $A$ также равен 3, т.е. $rang A=3$.
Так как $rang A=rangwidetilde{A}$, то согласно теореме Кронекера-Капелли система совместна, т.е. имеет решение. Чтобы указать количество решений, учтём, что наша СЛАУ содержит 3 неизвестных: $x_1$, $x_2$ и $x_3$. Так как количество неизвестных $n=3$, то делаем вывод: $rang A=rangwidetilde{A}=n$, поэтому согласно пункту №3 следствия из теоремы Кронекера-Капелли, система определена, т.е. имеет единственное решение.
Какие преимущества второго способа? Главное преимущество – это его универсальность. Нам совершенно неважно, является ли матрица системы квадратной или нет. Кроме того, мы фактически провели преобразования прямого хода метода Гаусса. Осталось лишь пару действий, и мы смогли бы получить решение данной СЛАУ. Честно говоря, второй способ нравится мне более первого, но выбор – это дело вкуса.
Ответ: Заданная СЛАУ совместна и определена.
Пример №2
Исследовать СЛАУ
$ left{ begin{aligned}
& x_1-x_2+2x_3=-1;\
& -x_1+2x_2-3x_3=3;\
& 2x_1-x_2+3x_3=2;\
& 3x_1-2x_2+5x_3=1;\
& 2x_1-3x_2+5x_3=-4.
end{aligned} right.$
на совместность.
Решение
Находить ранги матрицы системы и расширенной матрицы системы будем методом элементарных преобразований. Расширенная матрица системы: $widetilde{A}=left( begin{array} {ccc|c} 1 & -1 & 2 & -1\ -1 & 2 & -3 & 3 \ 2 & -1 & 3 & 2 \ 3 & -2 & 5 & 1 \ 2 & -3 & 5 & -4 end{array} right)$. Найдём требуемые ранги, преобразовывая расширенную матрицу системы:
$$
left( begin{array} {ccc|c}
1 & -1 & 2 & -1\
-1 & 2 & -3 & 3 \
2 & -3 & 5 & -4 \
3 & -2 & 5 & 1 \
2 & -1 & 3 & 2 end{array} right)
begin{array} {l} phantom{0}\r_2+r_1\r_3-2r_1\ r_4-3r_1\r_5-2r_1end{array}rightarrow
left( begin{array} {ccc|c}
1 & -1 & 2 & -1\
0 & 1 & -1 & 2 \
0 & -1 & 1 & -2 \
0 & 1 & -1 & 4 \
0 & 1 & -1 & 4 end{array} right)
begin{array} {l} phantom{0}\phantom{0}\r_3-r_2\ r_4-r_2\r_5+r_2end{array}rightarrow\
$$
$$
rightarrowleft( begin{array} {ccc|c}
1 & -1 & 2 & -1\
0 & 1 & -1 & 2 \
0 & 0 & 0 & 2 \
0 & 0 & 0 & 2 \
0 & 0 & 0 & 0 end{array} right)
begin{array} {l} phantom{0}\phantom{0}\phantom{0}\ r_4-r_3\phantom{0}end{array}rightarrow
left( begin{array} {ccc|c}
1 & -1 & 2 & -1\
0 & 1 & -1 & 2 \
0 & 0 & 0 & 2 \
0 & 0 & 0 & 0 \
0 & 0 & 0 & 0 end{array} right)
$$
Расширенная матрица системы приведена к ступенчатому виду. Ранг ступенчатой матрицы равен количеству её ненулевых строк, поэтому $rangwidetilde{A}=3$. Матрица $A$ (до черты) тоже приведена к ступенчатому виду, и ранг её равен 2, $rang{A}=2$.
Так как $rang Aneqrangwidetilde{A}$, то согласно теореме Кронекера-Капелли система несовместна (т.е. не имеет решений).
Ответ: система несовместна.
Пример №3
Исследовать СЛАУ
$$left{ begin{aligned}
& 2x_1+7x_3-5x_4+11x_5=42;\
& x_1-2x_2+3x_3+2x_5=17;\
& -3x_1+9x_2-11x_3-7x_5=-64;\
& -5x_1+17x_2-16x_3-5x_4-4x_5=-90;\
& 7x_1-17x_2+23x_3+15x_5=132.
end{aligned} right.$$
на совместность.
Решение
Приводим расширенную матрицу системы к ступенчатому виду:
$$
left( begin{array}{ccccc|c}
2 & 0 & 7 & -5 & 11 & 42\
1 & -2 & 3 & 0 & 2 & 17 \
-3 & 9 & -11 & 0 & -7 & -64 \
-5 & 17 & -16 & -5 & -4 & -90 \
7 & -17 & 23 & 0 & 15 & 132 end{array} right)
overset{r_1leftrightarrow{r_3}}{rightarrow}
$$
$$
rightarrowleft( begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 2 & 17\
2 & 0 & 7 & -5 & 11 & 42\
-3 & 9 & -11 & 0 & -7 & -64\
-5 & 17 & -16 & -5 & -4 & -90 \
7 & -17 & 23 & 0 & 15 & 132 end{array} right)
begin{array} {l} phantom{0}\ r_2-2r_1 \r_3+3r_1 \ r_4+5r_1 \ r_5-7r_1 end{array} rightarrow
left( begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 2 & 17\
0 & 4 & 1 & -5 & 7 & 8\
0 & 3 & -2 & 0 & -1 & -13\
0 & 7 & -1 & -5 & 6 & -5 \
0 & -3 & 2 & 0 & 1 & 13 end{array} right)
begin{array} {l} phantom{0}\ phantom{0}\4r_3+3r_2 \ 4r_4-7r_2 \ 4r_5+3r_2 end{array} rightarrow
$$
$$
rightarrowleft( begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 2 & 17\
0 & 4 & 1 & -5 & 7 & 8\
0 & 0 & -11 & 15 & -25 & -76\
0 & 0 & -11 & 15 & -25 & -76 \
0 & 0 & 11 & -15 & 25 & 76 end{array} right)
begin{array} {l} phantom{0}\ phantom{0}\phantom{0} \ r_4-r_3 \ r_5+r_2 end{array} rightarrow
left( begin{array}{ccccc|c}
1 & -2 & 3 & 0 & 2 & 17\
0 & 4 & 1 & -5 & 7 & 8\
0 & 0 & -11 & 15 & -25 & -76\
0 & 0 & 0 & 0 & 0 & 0 \
0 & 0 & 0 & 0 & 0 & 0 end{array} right)
$$
Мы привели расширенную матрицу системы и саму матрицу системы к ступенчатому виду. Ранг расширенной матрицы системы равен трём, ранг матрицы системы также равен трём. Так как система содержит $n=5$ неизвестных, т.е. $rangwidetilde{A}=rang{A}lt{n}$, то согласно пункту №2 следствия из теоремы Кронекера-Капелли данная система является неопределённой, т.е. имеет бесконечное количество решений.
Ответ: система является неопределённой.
Во второй части мы разберём примеры, которые нередко включают в типовые расчёты или контрольные работы по высшей математике: исследование на совместность и решение СЛАУ в зависимости от значений параметров, входящих в неё.
Содержание:
Базисные и свободные переменные:
Пусть задана система
Элементарными преобразованиями системы линейных уравнений называются следующие преобразования:
- исключение из системы уравнения вида
- умножение обеих частей одного из уравнений системы на любое действительное число
;
- перестановка местами уравнений системы;
- прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число не равное нулю.
Элементарные преобразования преобразуют данную систему уравнений в эквивалентную систему, т.е. в систему, которая имеет те же решения, что и исходная.
Для решения системы т линейных уравнений с т неизвестными удобно применять метод Гаусса, называемый методом последовательного исключения неизвестных, который основан на применении элементарных преобразований системы. Рассмотрим этот метод.
Предположим, что в системе (6.1.1)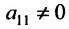
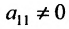
На первом шаге метода Гаусса исключим неизвестное 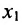
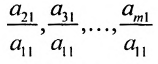
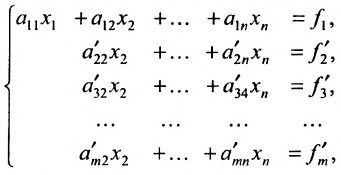
в которой коэффициенты 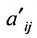
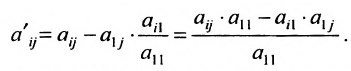
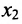
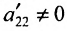
чтобы это условие было выполнено). Для исключения неизвестного 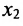
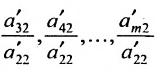
в которой коэффициенты 
Продолжая аналогичные преобразования, систему (6.1.1) можно привести к одному из видов:
или
Совокупность элементарных преобразований, приводящих систему (6.1.1) к виду (6.1.4) или (6.1.5) называется прямым ходом метода Гаусса.
Отметим, что если на каком-то шаге прямого хода метода Гаусса получим уравнение вида:
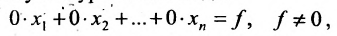
Итак, предположим, что в результате прямого хода метода Гаусса мы получили систему (6.1.4), которая называется системой треугольного вида. Тогда из последнего уравнения находим значение 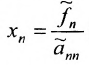
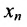
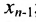
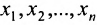
Если же в результате прямого хода метода Гаусса мы получим систему (6.1.5), которая называется системой ступенчатого вида, то из последнего уравнения этой системы находим значение неизвсстного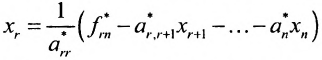
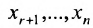
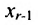
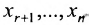
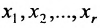
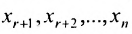
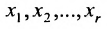
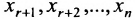
Таким образом, если система (6.1.1) путём элементарных преобразований приводится к треугольному виду (6.1.4), то она имеет единственное решение, если же она приводится к системе ступенчатого вида (6.1.5), то она имеет бесконечное множество решений. При этом неизвестные 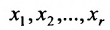
Практически удобнее преобразовывать не саму систему уравнений (6.1.1), а расширенную матрицу системы, соединяя последовательно получающиеся матрицы знаком эквивалентности
Формализовать метод Гаусса можно при помощи следующего алгоритма.
Алгоритм решения системы m линейных уравнений с n неизвестными методом Гаусса
1. Составьте расширенную матрицу коэффициентов системы уравнений так, чтобы 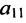
2. Выполните первый шаг метода Гаусса: в первом столбце начиная со второй строки, запишите нули, а все другие элементы вычислите по формуле
Матрица после первого шага примет вид
3. Выполните второй шаг метода Гаусса, предполагая, что 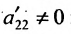
После второго шага матрица примет вид
4. Продолжая аналогичные преобразования, придёте к одному из двух случаев:
а) либо в ходе преобразований получим уравнение вида
тогда данная система несовместна;
б) либо придём к матрице вида:
где 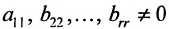
связано с тем, что в процессе преобразований матрицы исключаются строки, состоящие из нулей.
5. Использовав конечную матрицу, составьте систему, при этом возможны два случая:
5.1. r=n:
Система имеет единственное,решение 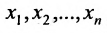
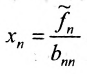
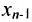
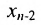
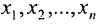
5.2. 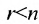
Тогда r неизвестных будут базисными, а остальные (n-r) – свободными. Из последнего уравнения выражаете неизвестное 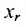
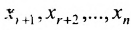
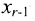
Система имеет в этом случае бесконечное множество решений.
Приведенный алгоритм можно несколько видоизменить и получить алгоритм полного исключения, состоящий в выполнении следующих шагов. На первом шаге:
- составляется расширенная матрица;
- выбирается разрешающий элемент расширенной матрицы
(если
, строки матрицы можно переставить так, чтобы выполнялось условие
);
- элементы разрешающей строки (строки, содержащей разрешающий элемент) оставляем без изменения; элементы разрешающего столбца (столбца, содержащего разрешающий элемент), кроме разрешающего элемента, заменяем нулями;
- все другие элементы вычисляем по правилу прямоугольника: преобразуемый элемент равен разности произведений элементов главной диагонали (главную диагональ образует разрешающий элемент и преобразуемый) и побочной диагонали (побочную диагональ образуют элементы, стоящие в разрешающей строке и разрешающем столбце):
– разрешающий элемент (см. схему).
Последующие шаги выполняем по правилам:
1) выбирается разрешающий элемент 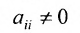
2) элементы разрешающей строки оставляем без изменения;
3) все элементы разрешающего столбца, кроме разрешающего элемента, заменяем нулями; • •
4) все другие элементы матрицы пересчитываем по правилу прямоугольника.
На последнем шаге делим элементы строк на диагональные элементы матрицы, записанные слева от вертикальной черты, и получаем решение системы.
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
Из последней матрицы находим следующее решение системы
уравнении:
Ответ:
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
Система привелась к ступенчатому виду (трапециевидной форме):
в которой неизвестные 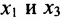
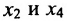
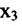
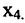
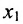
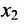
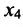
в котором 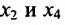
Если в общем решении положить 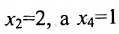
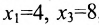
Ответ: система имеет бесконечное множество решений, общее решение которой записывается в виде:
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
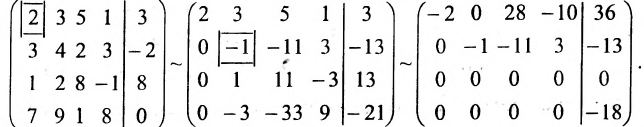
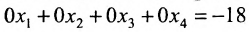
Ответ: система несовместна.
Замечание 1. Если дана система уравнений (6.1.1), в которой число уравнений m равно числу неизвестных n (m=n) и определитель этой системы 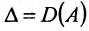
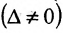
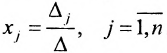
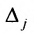
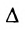
Если же такую систему (m-n) записать в матричной форме AX=F, то её решение можно найти по формуле 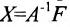
Замечание 2. Используя метод Гаусса, тем самым и алгоритм полного исключения, можно находить обратную матрицу. Для этого составляется расширенная матрица, в которой слева от вертикальной черты записана матрица А, а справа – единичная матрица. Реализовав алгоритм полного исключения, справа от вертикальной черты получаем обратную матрицу, а слева – единичную.
Пример:
Найти обратную матрицу для матрицы:
Решение:
Так как
то обратная матрица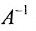
тогда
Покажем, что
ответ
Исследование совместности и определённости системы. Теорема Кронекера-Капелли
Рассмотрим систему (6.1.1) m линейных уравнений с n неизвестными при любых m и n (случай m=n не исключается). Вопрос о совместности системы решается следующим критерием.
Теорема 6.2.1. (критерий Кронкера-Капелли). Для того, чтобы система линейных уравнений(6.1.1) была совместна, необходимо и достаточно, чтобы ранг матрицы А системы был равен рангу расширенной матрицы 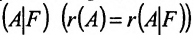
Доказательство и Необходимость:
Предположим, что система (6.1.1) совместна и 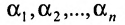
Из этих равенств следует, что последний столбец матрицы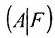
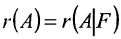
Достаточность. Пусть 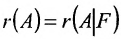
столбцов матрицы А, которые одновременно будут базисными столбцами и матрицы 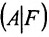
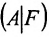
где 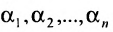
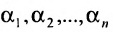
эта система совместна.
Совместная система линейных уравнений (6.1.1) может быть либо определенной, либо неопределенной.
Следующая теорема даст критерий определенности.
Теорема 6.2.2. Совместная система линейных уравнений имеет единственное решение тогда и только тогда, когда ранг матрицы А системы равен числу п ее неизвестных.
Таким образом, если число уравнений m системы (6.1.1) меньше числа ее неизвестных n и система совместна, то ранг матрицы системы 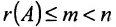
В случае 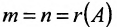
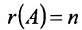
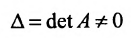
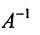
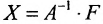
Следует отметить, что, решая систему (6.1.1) методом Гаусса, мы определяем и совместность, и определённость системы.
Пример:
Исследовать на совместность и определённость следующую систему линейных уравнений:
Решение:
Составим расширенную матрицу заданной системы. Определяя её ранг, находим тем самым и ранг матрицы системы. Для нахождения ранга матрицы применим алгоритм метода Гаусса.
Из последней матрицы следует, что ранг расширенной матрицы 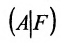
- Заказать решение задач по высшей математике
Однородные системы линейных уравнений
Система линейных уравнений (6.1.1) называется однородной, если все свободные члены 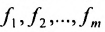
Эта система всегда совместна, так как очевидно, что она имеет нулевое решение
Для однородной системы важно установить, имеет ли она ненулевые решения. Этот факт устанавливается следующей теоремой.
Теорема 6.3.1. Для того, чтобы однородная система имела ненулевые решения, необходимо и достаточно, чтобы ранг г матрицы А системы был меньше числа неизвестных n (r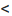
Доказательство. Необходимость. Пусть система (6.3.1) имеет ненулевое решение. Тогда она неопределённая, т.к. имеет еще и нулевое решение. В силу теоремы 6.2.2 ранг матрицы неопределённой системы не может равняться n потому что при r(А)=n система определённая. Следовательно, 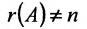
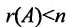
Достаточность. Если 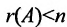
Следствие 1. Если число неизвестных в однородной системе больше числа уравнений, то однородная система имеет ненулевые решения.
Доказательство. Действительно, ранг матрицы системы (6.3.1) не может превышать m. Но так как по условию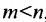
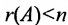
Следствие 2. Для того, чтобы однородная система с квадрат-ной матрицей имела ненулевые решения, необходимо и достаточно, чтобы её определитель 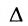
Доказательство. Рассмотрим однородную систему с квадратной матрицей:
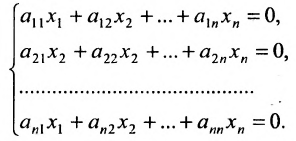
Если определитель матрицы системы 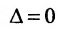
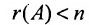
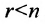
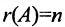
Пример:
Решить систему однородных линейных уравнений:
Решение:
Составим матицу системы и применим алгоритм полного исключения:
Из последней матрицы следует, что 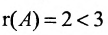
Используя последнюю матрицу, последовательно находим общее решение:
Неизвестные 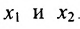
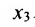
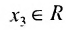
Фундаментальная система решений. Общее решение неоднородной системы линейных уравнений
Рассмотрим систему однородных линейных уравнений
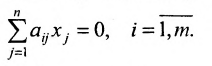
Любое решение
системы m линейных однородных уравнений с n неизвестными можно рассматривать как вектор-строку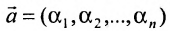
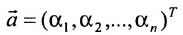
1) сумма двух решений также является решением системы, т.е.
если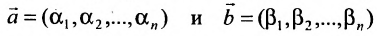
(6.4.1), то и 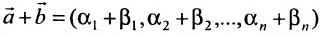
2) произведение решений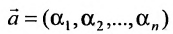
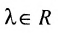
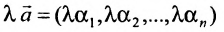
Из приведенных свойств следует, что
3) линейная комбинация решений системы (6.4.1) является решением этой системы.
В частности, если однородная система (6.4.1) имеет хотя бы одно ненулевое решение, то из него умножением на произвольные числа, можно получить бесконечное множество решений.
Определение 6.4.1. Фундаментальной системой решений для системы однородных линейных уравнений (6.4.1) называется линейно независимая система решений, через которую линейно выражается любое решение системы (6.4.1).
Заметим, что если ранг матрицы системы (6.4.1) равен числу неизвестных n (r(А)=n), то эта система не имеет фундаментальной системы решений, так как единственным решением будет нулевое решение, составляющее линейно зависимую систему. Существование и число фундаментальных решений определяется следующей теоремой.
Теорема 6.4.1. Если ранг матрицы однородной системы уравнений (6.4.1) меньше числа неизвестных (r(А)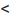
Сформулируем алгоритм построения фундаментальной системы решений:
- Выбираем любой определитель
порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные – нули.
- Свободным неизвестным придаём поочерёдно значения, равные элементам первой, второй и т.д. строк определителя
, и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
- Из полученных n-r решений составляют фундаментальную систему решений.
Меняя произвольно определитель 
Пример:
Найти общее решение и фундаментальную систему решений для однородной системы уравнений:
Решение:
Составим матрицу системы и применим алгоритм полного исключения.
Для последней матрицы составляем систему:
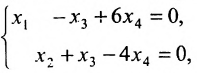
, из которой находим общее решение:
в котором 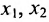
Построим фундаментальную систему решений. Для этого выбираем определитель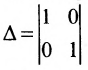
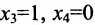
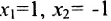
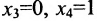
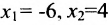
Таким образом, построенные два решения (1; -1; 1; 0) и (-6; 4; 0; 1) составляют фундаментальную систему решений.
Если ранг матрицы системы однородных линейных уравнений (6.4.1) на единицу меньше числа неизвестных: 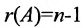
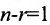
Рассмотрим теперь неоднородную систему m линейных уравнений с n неизвестными (6.1.1). Если в системе (6.1.1) положить 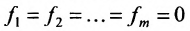
Решения системы (6.1.1) и её приведенной системы удовлетворяют свойствам:
- Сумма и разность любого решения системы (6.1.1) и любого решения её приведенной системы является решением неоднородной системы.
- Все решения неоднородной системы можно получить, прибавляя к одному (любому) её решению поочерёдно все решения её приведенной системы.
Из этих свойств следует теорема.
Теорема 6.4.2. Общее решение неоднородной системы (6.1.1.) определяется суммой любого частного решения этой системы и общего решения её приведенной системы.
Пример:
Найти общее решение системы:
Решение:
Составим расширенную матрицу (A|F) заданной системы и применим алгоритм полного исключения:
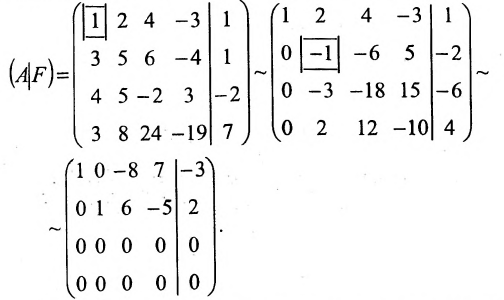
Преобразованной матрице соответствует система уравнений:
из которой находим общее решение системы:
, где 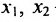
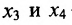
Покажем, что это общее решение определяется суммой любого частного решения заданной системы и общего решения приведенной системы.
Подставляя вместо свободных неизвестных 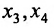
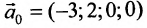
Очевидно, что общее решение приведенной системы имеет вид:
Суммируя частное решение заданной системы и общее решение приведенной системы, получим общее решение (6.4.2) исходной системы.
Отметим, что общее решение системы (6.1.1) можно представить в векторном виде:
где 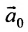
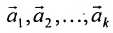
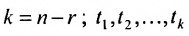
Формула (6.4.4) называется общим решением системы (6.1.1) в векторной форме.
Запишем общее решение системы примера 6.4.1 в векторной форме. Для этого определим фундаментальную систему решений приведенной системы. Возьмём определитель 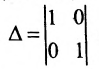
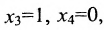
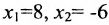
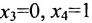
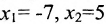
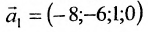
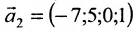
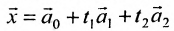
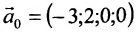
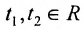
Определение метода Гаусса
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример:
Решить систему уравнений методом Гаусса:
Решение:
Выпишем расширенную матрицу данной системы 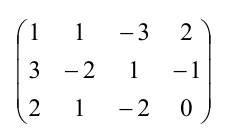
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
б) третью строку умножим на (-5) и прибавим к ней вторую:
В результате всех этих преобразований данная система приводится к треугольному виду:
Из последнего уравнения находим 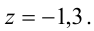
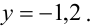
Вычисление метода Гаусса
Этот метод основан на следующей теореме.
Теорема:
Элементарные преобразования не изменяют ранга матрицы.
К элементарным преобразованиям матрицы относят:
- перестановку двух параллельных рядов;
- умножение какого-нибудь ряда на число, отличное от нуля;
- прибавление к какому-либо ряду матрицы другого, параллельного ему ряда, умноженного на произвольное число.
Путем элементарных преобразований исходную матрицу можно привести к трапециевидной форме
где все диагональные элементы 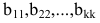
Пример:
Найти ранг матрицы
1) методом окаймляющих миноров;
2 ) методом Гаусса.
Указать один из базисных миноров.
Решение:
1. Найдем ранг матрицы методом окаймляющих миноров. Выберем минор второго порядка, отличный от нуля. Например,
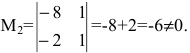
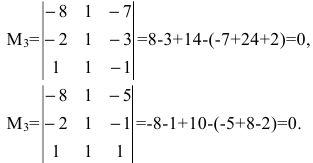
2. Найдем ранг матрицы методом Гаусса. Производя последовательно элементарные преобразования, получим:
- переставили первую и третью строки;
- первую строку умножили на 2 и прибавили ко второй, первую строку умножили на 8 и прибавили к третьей;
- вторую строку умножили на -3 и прибавили к третьей.
Последняя матрица имеет трапециевидную форму и ее ранг равен двум. Следовательно, ранг исходной матрицы также равен двум.
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Дифференциальные уравнения с примерами
- Обратная матрица – определение и нахождение
- Ранг матрицы – определение и вычисление
- Определители второго и третьего порядков и их свойства
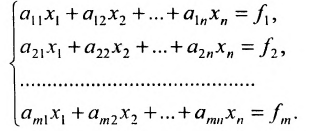
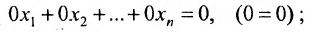
 ;
;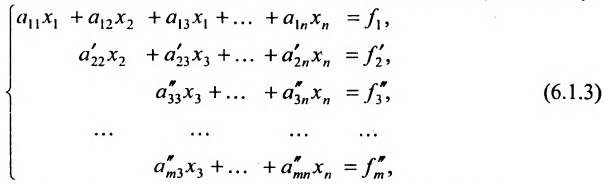
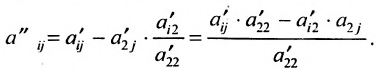
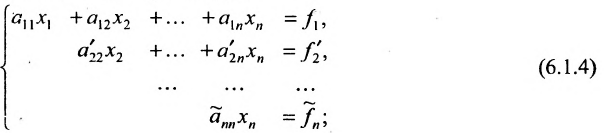
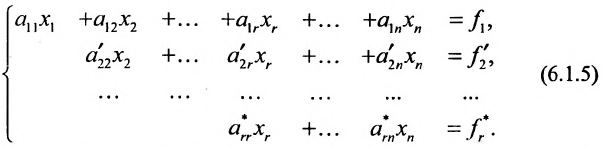

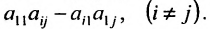
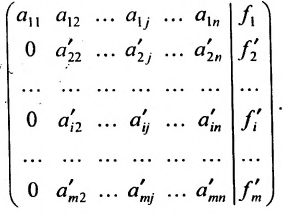
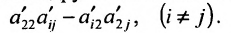

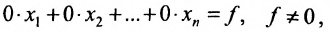
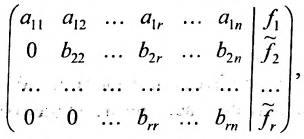
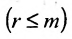
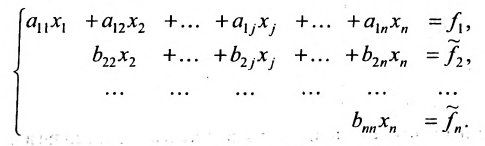
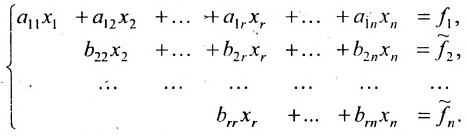
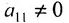 (если
(если 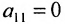 , строки матрицы можно переставить так, чтобы выполнялось условие
, строки матрицы можно переставить так, чтобы выполнялось условие 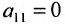 );
);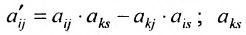 – разрешающий элемент (см. схему).
– разрешающий элемент (см. схему).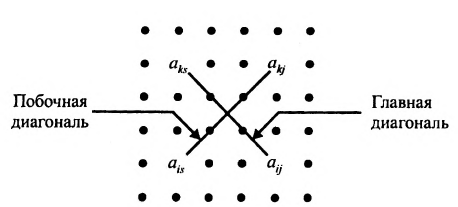
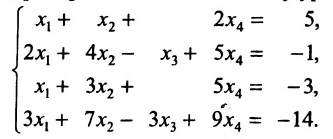


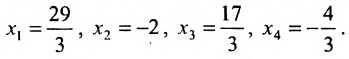
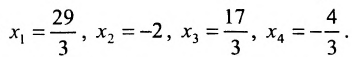
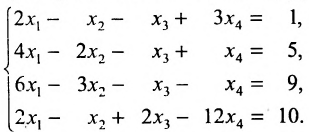

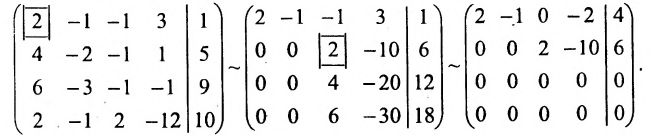

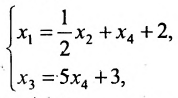
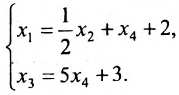
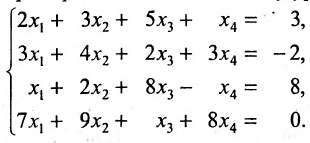
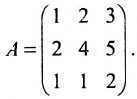
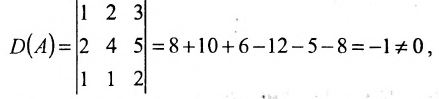

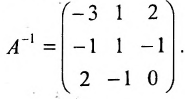
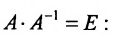
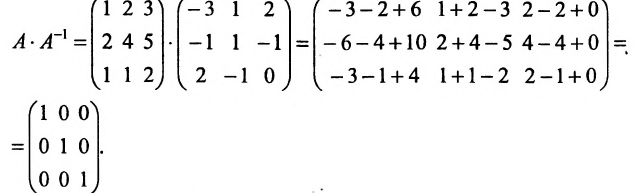
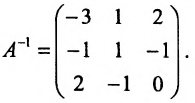
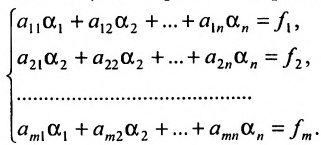
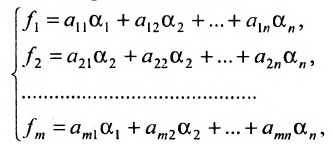
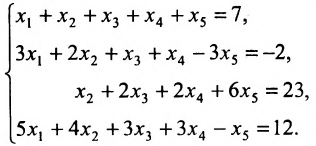

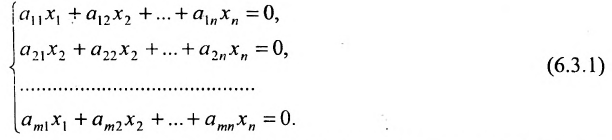
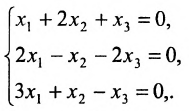
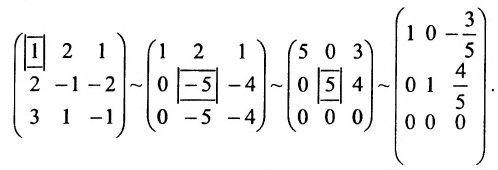
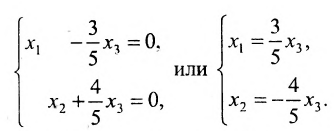
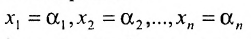
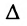 порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные – нули.
порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные – нули.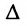 , и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
, и каждый раз из общего решения находим соответствующие значения базисных неизвестных.