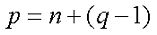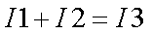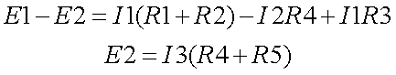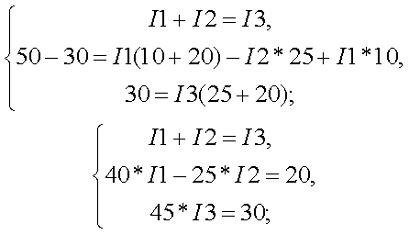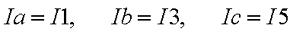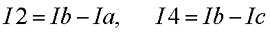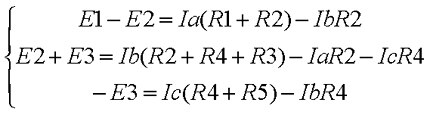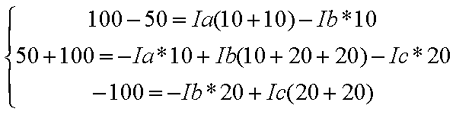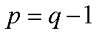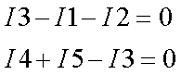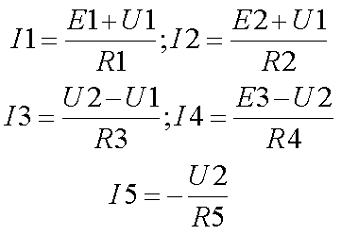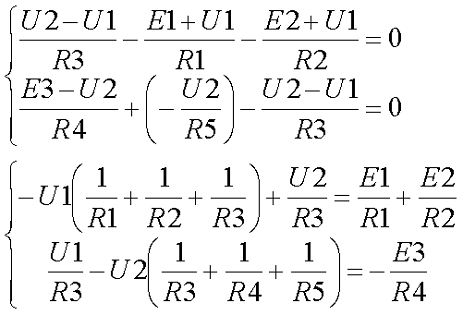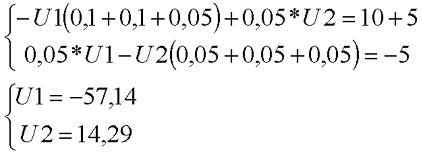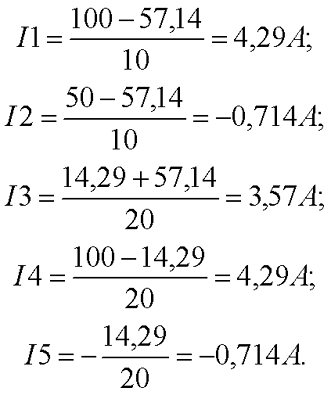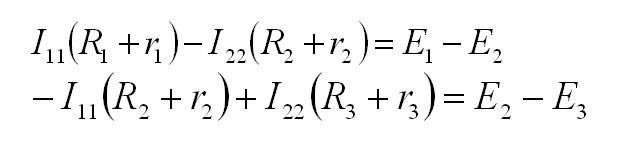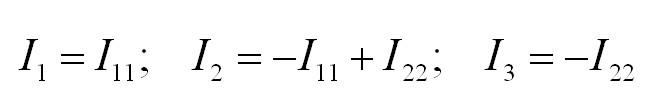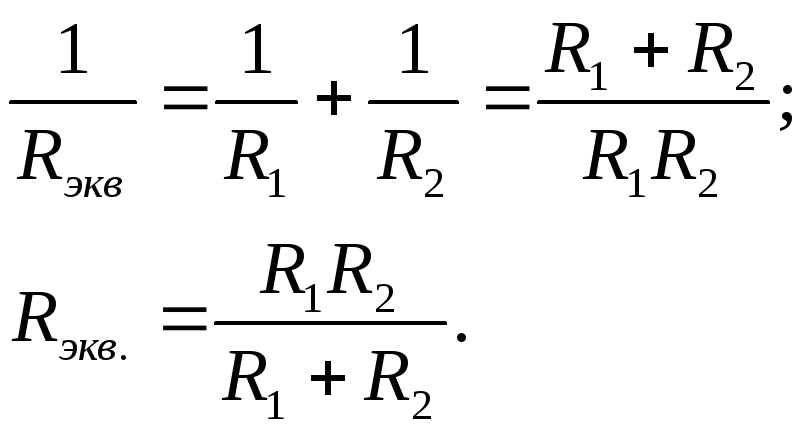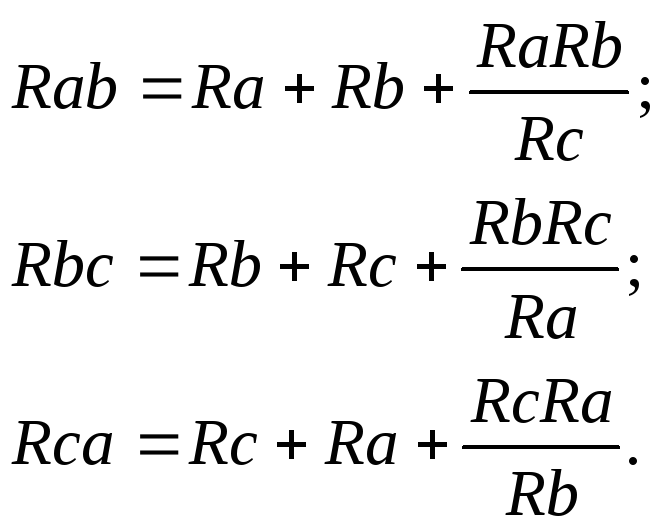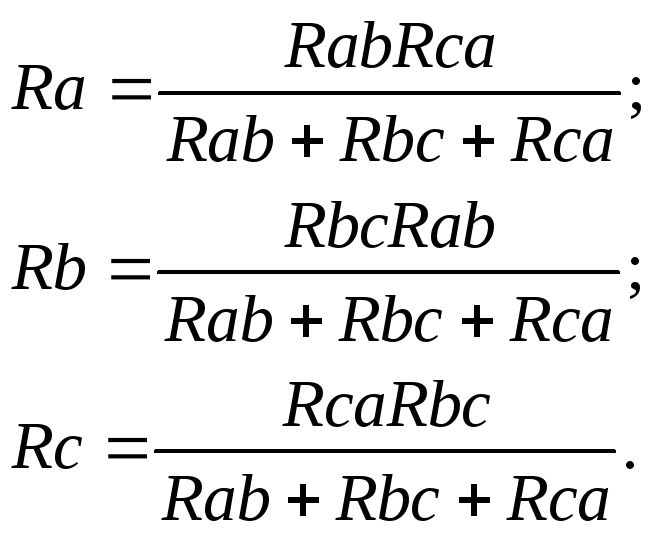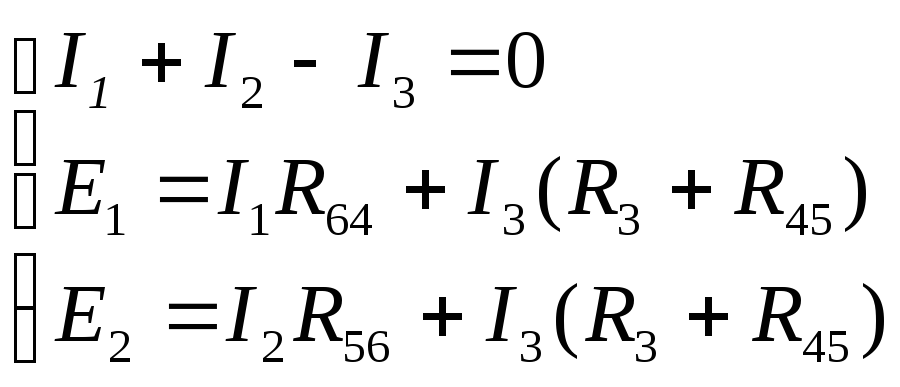Как найти сколько токов в цепи

Расчет электрических цепей

На практике разработан ряд методов для определения и расчета схем с постоянным током, что предоставляет возможность уменьшить трудоемкий процесс вычисления трудных электрических цепей. Основными законами, с помощью которых определяются характеристики практически каждой схемы, являются постулаты Кирхгофа.

Пример сложных электрических цепей

Пути вычисления электрических схем

Расчет электрических цепей разветвляется на множество методов, используемых на практике, а именно: метод эквивалентных преобразований, прием, основанный на постулатах Ома и Кирхгофа, способ наложения, способ контурных токов, метод узловых потенциалов, метод идентичного генератора.

Процесс расчета электрической цепи состоит из нескольких обязательных этапов, позволяющих довольно быстро и точно произвести все расчеты.

Перед тем, как узнать или вычислить необходимые параметры, рассчитываемая электрическая цепь переносится схематически на бумагу, где содержатся символические обозначения входящих в ее состав элементов и порядок их соединения.

Все элементы и устройства подразделяются на три категории:

1. Источники электропитания. Основным признаком данного элемента является превращение неэлектрической энергии в электрическую. Эти источники энергии именуются первичными источниками энергии. Вторичные источники энергии представляют собой такие устройства, на входах и выходах которых присутствует электрическая энергия. К ним относятся выпрямительные приборы или трансформаторы напряжения;
2. Устройства, потребляющие электрическую энергию. Такие элементы преобразовывают электрическую энергию в любую другую, будь то свет, звук, тепло и тому подобные виды;
3. Вспомогательные элементы цепи, к которым относятся провода соединений, аппаратура коммутации, защиты и другие подобные элементы.

Также к основным понятиям электрической схемы относятся:

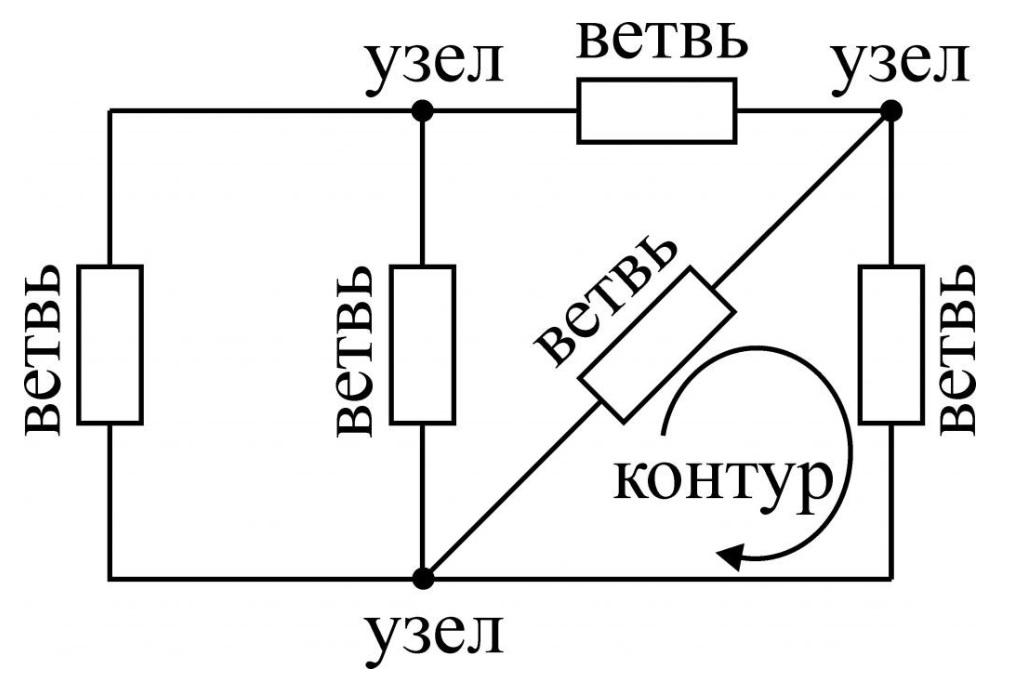
• Ветвь электрической схемы – участок цепи с одним и тем же током. В состав такой ветви могут входить один или несколько последовательно соединенных элементов;
• Узел электрической схемы – точка соединения трех и более ветвей схемы;
• Контур электрической схемы, представляющий собой любой замкнутый путь, проходящий по нескольким ветвям.

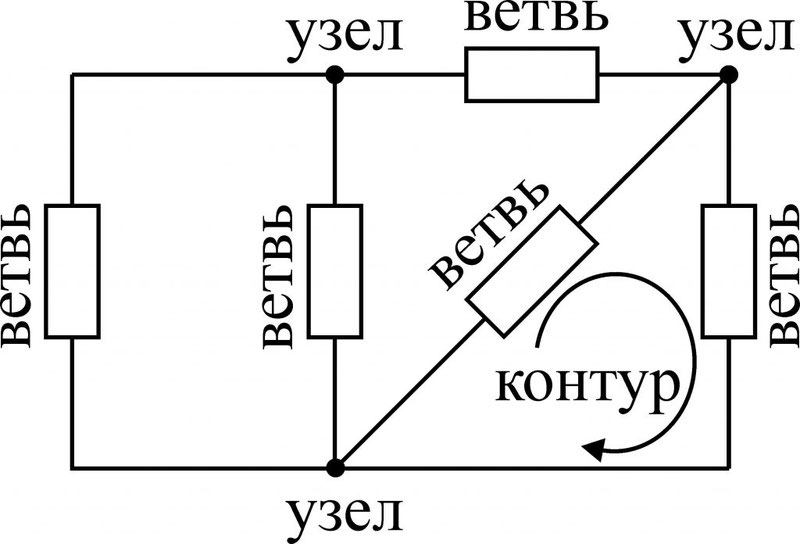
Обозначение ветвей, узлов и контуров на схеме

Метод расчета по законам Ома и Кирхгофа

Данные законы позволяют узнать силу тока и найти взаимосвязь между значениями токов, напряжений, ЭДС всей цепи и единичных участков.

Закон Ома для участка цепи

По закону Ома соотношение тока, напряжения и сопротивления цепи выглядит как:

Исходя из этой формулы, найти силу тока можно по выражению:

• UR – напряжение или падение напряжения на резисторе;
• I – ток в резисторе.

Закон Ома для полной цепи

В законе Ома для полной цепи дополнительно используется величина внутреннего сопротивления источника питания. Найти силу тока с учетом внутреннего сопротивления возможно по выражению:

• E – ЭДС источника питания;
• rо – внутреннее сопротивление источника питания.

Поскольку сложная электрическая цепь, состоящая из нескольких ветвей и имеющая в своей структуре ряд устройств питания, не может быть описана законом Ома, то применяют 1-ый и 2-ой закон Кирхгофа.

Первый закон Кирхгофа

Закон Кирхгофа гласит, что сумма токов, втекающих в узел, равна сумме токов, вытекающих из него, это выглядит как:

∑mIk=0, где m – число ветвей, подведенных к узлу.

Согласно закону Кирхгофа, токи, втекающие в узел, используются со знаком «+», а токи, вытекающие из узла, – со знаком «-».

Второй закон Кирхгофа

Из второго закона Кирхгофа следует, что сумма падений напряжений на всех элементах цепи равна сумме ЭДС цепи, выглядит как:

• n – число источников ЭДС в контуре;
• m – число элементов с сопротивлением Rk в контуре;
• Uk=RkIk – напряжение или падение напряжения на k-том элементе контура.

Перед применением второго закона Кирхгофа следует проверить выполнение следующих требований:

1. Указать относительно положительные направления ЭДС, токов и напряжений;
2. Указать направление обхода контура, описываемого уравнением;
3. Применяя одну из трактовок 2-го закона Кирхгофа, характеристики входящие в уравнение используются со знаком «+», если их относительно положительные направления схожи с обходом контура, и с «-», если они разнонаправленные.

Из 2-го закона Кирхгофа следует выражение баланса мощностей, по которому мощность источников питания в любой момент времени равна сумме мощностей, расходуемых на всех участках цепи. Уравнение баланса мощностей имеет вид:

Метод преобразования электрической цепи

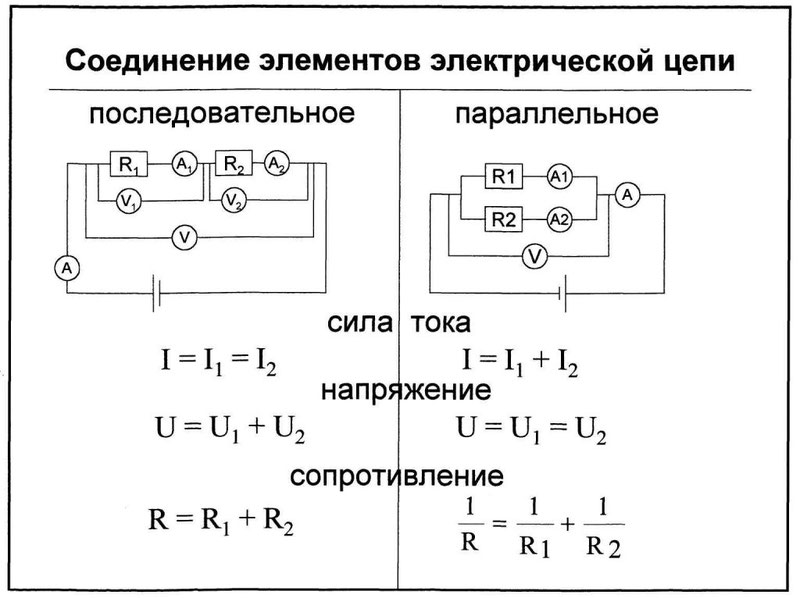
Элементы в электрических цепях могут соединяться параллельно, последовательно, смешанным способом и по схемам «звезда», «треугольник». Расчет таких схем упрощается путем замены нескольких сопротивлений на эквивалентное сопротивление, и дальнейшие вычисления уже проводятся по закону Ома либо Кирхгофа.

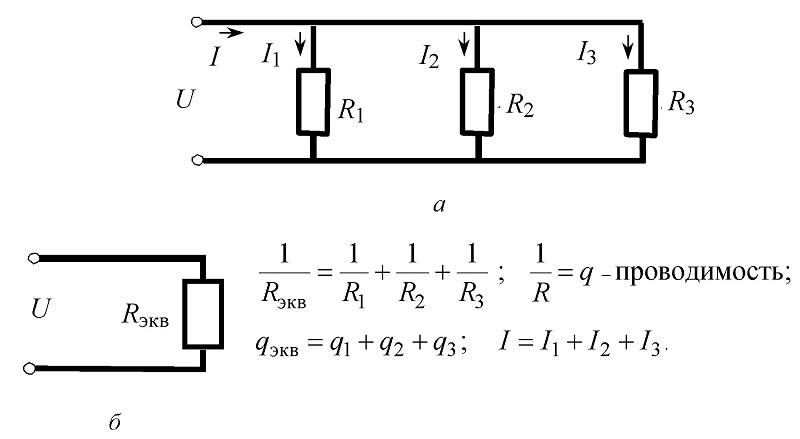
Последовательное и параллельное соединение элементов

Под смешанным соединением элементов подразумевается одновременное присутствие в схеме и последовательного, и параллельного соединения элементов. При этом сопротивление смешанного соединения вычисляется после преобразования схемы в эквивалентную цепь с помощью формул, приведенных на рис. выше.

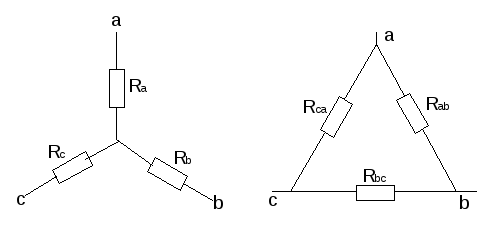
Также встречается соединение элементов «звездой» и «треугольником». Для нахождения эквивалентного сопротивления необходимо первоначально преобразовать схему «треугольник» в «звезду». По картинке ниже, сопротивления равны:

• R1=R12R31/R12+R31+R23,
• R2=R12R23/R12+R31+R23,
• R3=R31R23/R12+R31+R23.

Треугольник и звезда соединений

Дополнительные методы расчета цепей

Все дополнительные методы расчета цепей в той или иной мере являются или основаны на первом и втором законах Кирхгофа. К этим методам относятся:

1. Метод контурных токов – основан на введении дополнительных величин контурных токов, удовлетворяющих 1-му закону Кирхгофа;
2. Метод узловых потенциалов – с его помощью находят потенциалы всех узлов схемы и затем по известным потенциалам токи во всех ветвях. Метод базируется на первом законе Кирхгофа;
3. Метод эквивалентного генератора – этот метод предоставляет решение задачи, как найти ток только в одной или нескольких ветвях. Суть метода в том, что любую электрическую цепь по отношению к исследуемой ветви можно представить в виде эквивалентного генератора;
4. Метод наложения – основан на том, что ток в цепи или ветви схемы равен алгебраической сумме токов, наводимых каждым источником в отдельности.

Основная часть методов расчета направлена на упрощение процедуры определения токов в ветвях схемы. Эти мероприятия проводятся либо упрощением систем уравнений, по которым проводятся расчеты, либо упрощением самой схемы. Основываясь, в первую очередь, на постулаты Кирхгофа, любой из методов отвечает на вопрос: как определить силу тока и напряжение электрической цепи.

Видео

Источник

Расчет электрических цепей

Для вычисления рабочих параметров радиотехнических устройств и отдельных схем применяют специальные методики. После изучения соответствующих технологий результат можно узнать быстро, без сложных практических экспериментов. Корректный расчет электрических цепей пригодится на стадии проектирования и для выполнения ремонтных работ.

Категории элементов и устройств электрической цепи

Для условного изображения определенной цепи применяют специальную схему. Кроме отдельных физических компонентов, она содержит сведения о направлении (силе) токов, уровнях напряжения и другую информацию. Качественная модель показывает реальные процессы с высокой точностью.

Компоненты электрической цепи:

• источник постоянного или переменного тока (Е) – аккумулятор или генератор, соответственно;
• пассивные элементы (R) – резисторы;
• компоненты с индуктивными (L) и емкостными (С) характеристиками;
• соединительные провода.

На рисунке обозначены:

• ветви – участки цепи с одним током;
• узлы – точки соединения нескольких ветвей;
• контур – замкнутый путь прохождения тока.

При решении практических задач выясняют, как узнать силу тока в отдельных ветвях. Полученные значения используют для анализа электрических параметров. В частности, можно определять падение напряжения на резисторе, мощность потребления подключенной нагрузки. При расчете цепей переменного тока приходится учитывать переходные энергетические процессы, влияние частоты.

Метод расчета по законам Ома и Кирхгофа

До изучения технологий вычислений необходимо уточнить особенности типовых элементов при подключении к разным источникам питания. При постоянном токе сопротивлением индуктивности можно пренебречь. Конденсатор эквивалентен разрыву цепи. Также следует учитывать следующие различия разных видов соединений резисторов:

• последовательное – увеличивает общее сопротивление;
• параллельное – распределяет токи по нескольким ветвям, что улучшает проводимость.

Закон Ома для участка цепи

Типовая аккумуляторная батарея легкового автомобиля вырабатывает напряжение U = 12 V. Бортовой или внешний амперметр покажет соответствующее значение при измерении. Соединение клемм проводом недопустимо, так как это провоцирует короткое замыкание. Если жила тонкая (

К сведению. Результат показанного расчета пригодится для поиска подходящего резистора. Следует делать запас в сторону увеличения. По стандарту серийных изделий подойдет элемент с паспортной номинальной мощностью 5 Вт.

На практике приходится решать более сложные задачи. Так, при значительной длине линии нужно учесть влияние соединительных ветвей цепи. Через стальной проводник ток будет протекать хуже, по сравнению с медным аналогом. Следовательно, надо в расчете учитывать удельное сопротивление материала. Короткий провод можно исключить из расчета. Однако в нагрузке может быть два элемента. В любом случае общий показатель эквивалентен определенному сопротивлению цепи. При последовательном соединении Rэкв = R1 + R2 +…+ Rn. Данный метод пригоден, если применяется постоянный ток.

Закон Ома для полной цепи

Для вычисления такой схемы следует добавить внутреннее сопротивление (Rвн) источника. Как найти ток, показывает следующая формула:

Вместо напряжения (U) при расчетах часто используют типовое обозначение электродвижущей силы (ЭДС) – E.

Первый закон Кирхгофа

По классической формулировке этого постулата алгебраическая сумма токов, которые входят и выходят из одного узла, равна нулю:

I1 + I2 + … + In = 0.

Это правило действительно для любой точки соединения ветвей электрической схемы. Следует подчеркнуть, что в данном случае не учитывают характеристики отдельных элементов (пассивные, реактивные). Можно не обращать внимания на полярность источников питания, включенных в отдельные контуры.

Чтобы исключить путаницу при работе с крупными схемами, предполагается следующее использование знаков отдельных токов:

• входящие – положительные (+I);
• выходящие – отрицательные (-I).

Второй закон Кирхгофа

Этим правилом установлено суммарное равенство источников тока (ЭДС), которые включены в рассматриваемый контур. Для наглядности можно посмотреть, как происходит распределение контрольных параметров при последовательном подключении двух резисторов (R1 = 50 Ом, R2 = 10 Ом) к аккумуляторной батарее (Uакб = 12 V). Для проверки измеряют разницу потенциалов на выводах пассивных элементов:

• UR1 = 10 V;
• UR1 = 2 V;
• Uакб = 12 V = UR1 + UR2 = 10 + 2;
• ток в цепи определяют по закону Ома: I = 12/(50+10) = 0,2 А;
• при необходимости вычисляют мощность: P = I2 *R = 0,04 * (50+10) = 2,4 Вт.

Второе правило Кирхгофа действительно для любых комбинаций пассивных компонентов в отдельных ветвях. Его часто применяют для итоговой проверки. Чтобы уточнить корректность выполненных действий, складывают падения напряжений на отдельных элементах. Следует не забывать о том, что дополнительные источники ЭДС делают результат отличным от нуля.

Метод преобразования электрической цепи

Как определить силу тока в отдельных контурах сложных схем? Для решения практических задач не всегда нужно уточнение электрических параметров на каждом элементе. Чтобы упростить вычисления, используют специальные методики преобразования.

Расчет цепи с одним источником питания

Для последовательного соединения пользуются рассмотренным в примере суммированием электрических сопротивлений:

Rэкв = R1 + R2 + … + Rn.

Контурный ток – одинаковый в любой точке цепи. Проверять его можно в разрыве контрольного участка мультиметром. Однако на каждом отдельном элементе (при отличающихся номиналах) прибор покажет разное напряжение. По второму закону Кирхгофа можно уточнить результат вычислений:

E = Ur1 + Ur2 + Urn.

В этом варианте в полном соответствии с первым постулатом Кирхгофа токи разделяются и соединяются во входных и выходных узлах. Показанное на схеме направление выбрано с учетом полярности подключенного аккумулятора. По рассмотренным выше принципам сохраняется базовое определение равенства напряжений на отдельных компонентах схемы.

Как найти ток в отдельных ветвях, демонстрирует следующий пример. Для расчета приняты следующие исходные значения:

• R1 = 10 Ом;
• R2 = 20 Ом;
• R3= 15 Ом;
• U = 12 V.

По следующему алгоритму будут определяться характеристики цепи:

• базовая формула для трех элементов:

Rобщ = R1*R2*R3/(R1*R2 + R2*R3 + R1*R3.

• подставив данные, вычисляют Rобщ = 10 * 20 * 15 / (10*20 + 20*15 +10*15) = 3000 /(200+300+150) = 4,615 Ом;
• I = 12/ 4,615 ≈ 2,6 А;
• I1 = 12/ 10 = 1,2 А;
• I2 = 12/20 = 0,6 А;
• I3 = 12/15 = 0,8 А.

Как и в предыдущем примере, рекомендуется проверить результат вычислений. При параллельном соединении компонентов должно соблюдаться равенство токов на входе и суммарного значения:

I = 1,2 + 0,6 + 0,8 = 2,6 А.

Если применяется синусоидальный сигнал источника, вычисления усложняются. При включении в однофазную розетку 220V трансформатора придется учитывать потери (утечку) в режиме холостого хода. В этом случае существенное значение имеют индуктивные характеристики обмоток и коэффициент связи (трансформации). Электрическое сопротивление (ХL) зависит от следующих параметров:

• частоты сигнала (f);
• индуктивности (L).

Вычисляют ХL по формуле:

Чтобы находить сопротивление емкостной нагрузки, подойдет выражение:

Следует не забывать о том, что в цепях с реактивными компонентами сдвигаются фазы тока и напряжения.

Расчет разветвленной электрической цепи с несколькими источниками питания

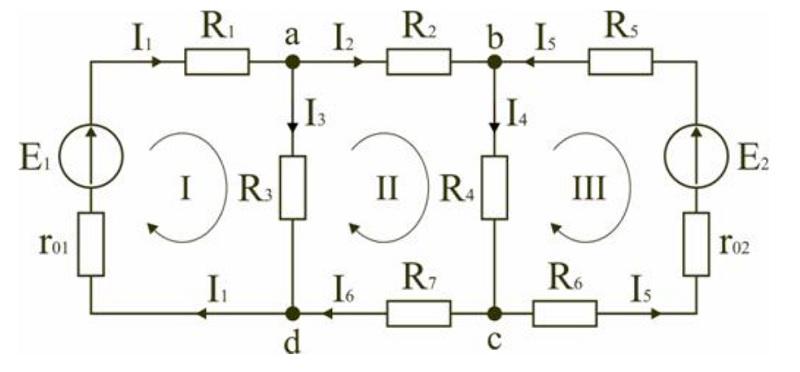
Пользуясь рассмотренными принципами, вычисляют характеристики сложных схем. Ниже показано, как найти ток в цепи при наличии двух источников:

• обозначают компоненты и базовые параметры во всех контурах;
• составляют уравнения для отдельных узлов: a) I1-I2-I3=0, b) I2-I4+I5=0, c) I4-I5+I6=0;
• в соответствии со вторым постулатом Кирхгофа, можно записать следующие выражения для контуров: I) E1=R1 (R01+R1)+I3*R3, II) 0=I2*R2+I4*R4+I6*R7+I3*R3, III) -E2=-I5*(R02+R5+R6)-I4*R4;
• проверка: d) I3+I6-I1=0, внешний контур E1-E2=I1*(r01+R1)+I2*R2-I5*(R02+R5+R6)+I6*R7.

Дополнительные методы расчета цепей

В зависимости от сложности устройства (электрической схемы), выбирают оптимальную технологию вычислений.

Метод узлового напряжения

Основные принципы этого способа базируются на законе Ома и постулатах Кирхгофа. На первом этапе определяют потенциалы в каждом узле. Далее вычисляют токи в отдельных ветвях с учетом соответствующих электрических сопротивлений (отдельных компонентов или эквивалентных значений). Проверку делают по рассмотренным правилам.

Метод эквивалентного генератора

Эта технология подходит для быстрого расчета тока в одной или нескольких контрольных ветвях.

В данной методике общую цепь представляют в виде источника тока с определенным напряжением и внутренним сопротивлением. Далее выполняют вычисления по контрольной ветви с применением стандартного алгоритма.

Видео

Источник

Расчет силы тока по мощности, напряжению, сопротивлению

Бесплатный калькулятор расчета силы тока по мощности и напряжению/сопротивлению – рассчитайте силу тока в однофазной или трехфазной сети в ОДИН КЛИК!

Если вы хотите узнать как рассчитать силу тока в цепи по мощности, напряжению или сопротивлению, то предлагаем воспользоваться данным онлайн-калькулятором. Программа выполняет расчет для сетей постоянного и переменного тока (однофазные 220 В, трехфазные 380 В) по закону Ома. Рекомендуем без необходимости не изменять значение коэффициента мощности (cos φ) и оставлять равным 0.95. Знание величины силы тока позволяет подобрать оптимальный материал и диаметр кабеля, установить надежные предохранители и автоматические выключатели, которые способны защитить квартиру от возможных перегрузок. Нажмите на кнопку, чтобы получить результат.

Смежные нормативные документы:

• СП 256.1325800.2016 «Электроустановки жилых и общественных зданий. Правила проектирования и монтажа»
• СП 31-110-2003 «Проектирование и монтаж электроустановок жилых и общественных зданий»
• СП 76.13330.2016 «Электротехнические устройства»
• ГОСТ 31565-2012 «Кабельные изделия. Требования пожарной безопасности»
• ГОСТ 10434-82 «Соединения контактные электрические. Классификация»
• ГОСТ Р 50571.1-93 «Электроустановки зданий»

Формулы расчета силы тока

Электрический ток — это направленное упорядоченное движение заряженных частиц.
Сила тока (I) — это, количество тока, прошедшего за единицу времени сквозь поперечное сечение проводника. Международная единица измерения — Ампер (А / A).

— Сила тока через мощность и напряжение (постоянный ток): I = P / U
— Сила тока через мощность и напряжение (переменный ток однофазный): I = P / (U × cosφ)
— Сила тока через мощность и напряжение (переменный ток трехфазный): I = P / (U × cosφ × √3)
— Сила тока через мощность и сопротивление: I = √(P / R)
— Сила тока через напряжение и сопротивление: I = U / R

• P – мощность, Вт;
• U – напряжение, В;
• R – сопротивление, Ом;
• cos φ – коэффициент мощности.

Коэффициент мощности cos φ – относительная скалярная величина, которая характеризует насколько эффективно расходуется электрическая энергия. У бытовых приборов данный коэффициент практически всегда находится в диапазоне от 0.90 до 1.00.

Источник

ElectronicsBlog

Обучающие статьи по электронике

Электротехника Часть 5 Методы расчёта электрических цепей

Всем доброго времени суток. В прошлой статье я рассматривал типы соединений приемников энергии в электрических цепях, а так же законы Кирхгофа, которые определяют основные соотношения токов и напряжений в этих цепях. Но кроме знания основных законов электротехники необходимо уметь рассчитывать неизвестные параметры электрических цепей по заданным известным параметрам. Так, например, по известным напряжениям, ЭДС и сопротивлениям необходимо знать какую мощность будет потреблять тот или иной приемник энергии, а так же вся цепь в целом. Этим мы и займёмся в данной статье.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Расчёт электрических цепей с помощью законов Кирхгофа

Существует несколько методов расчёта электрических цепей, которые различаются между собой параметрами, которые необходимо найти, а так же количеством необходимых расчётов.

Вначале я расскажу, как произвести расчёт цепи в общем виде, но в результате размеры вычислений будут неоправданно большими. Данный метод расчёта основан на законах Ома и Кирхгофа и используется при расчётах небольших цепей с малым количеством контуров. Для этого составляют систему уравнений из (q — 1) уравнений для узлов цепи и n уравнений для независимых контуров. Независимые контуры характеризуются тем, что при составлении уравнений для каждого нового контура входит хотя бы одна новая ветвь, не вошедшая в предыдущий контур. Таким образом, количество уравнений в системе уравнений по данному методу расчёта цепи будет определяться следующим выражением

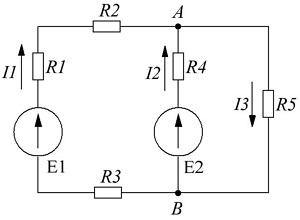
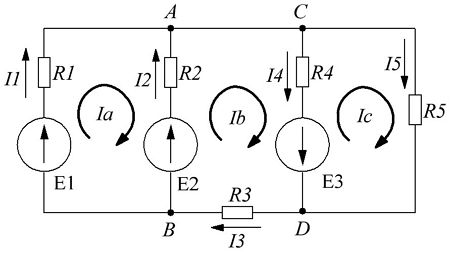
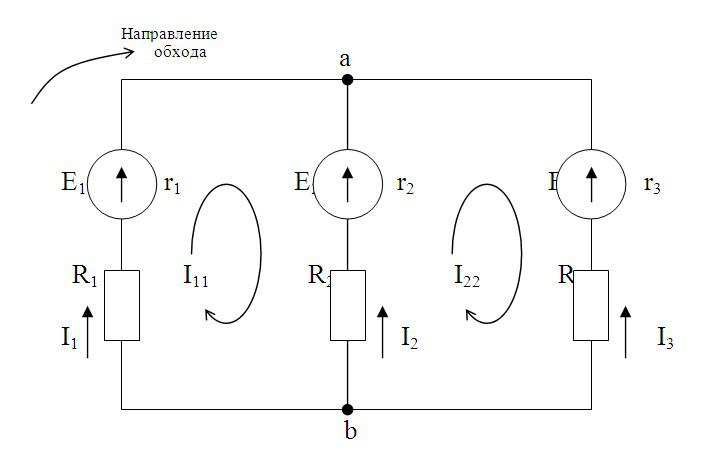
В качестве примера рассчитаем электрическую цепь, приведённую на рисунке ниже

Пример электрической цепи для расчёта по законам Ома и Кирхгофа.

В качестве примера возьмём следующие параметры схемы: E1 = 50 B, E2 = 30 B, R1 = R3 = 10 Ом, R2 = R5 = 20 Ом, R4 = 25 Ом.

Составим уравнение по первому закону Кирхгофа. Так как узла у нас два, то выберем узел А и составим для него уравнение. Я выбрал условно, что токи I1 и I2 втекают в узел, а I3 – вытекает, тогда уравнение будет иметь вид

Составим недостающие уравнения по второму закону Кирхгофа. В схеме у нас два независимых контура: E1R1R2R4E2R3 и E2R4R5, поэтому выбирая произвольное направление контуров составим недостающие два уравнения. Я выбрал обход по ходу часовой стрелке, поэтому уравнения имеют вид

Таким образом, получившаяся система уравнений будет иметь следующий вид

Решив данную систему, получим следующие результаты: I1 ≈ 0,564 А, I2 ≈ 0,103 А, I2 ≈ 0,667 А.

В результате решения системы уравнений по данному методу может оказаться, что токи получились отрицательными. Это значит, что действительное направление токов противоположно по направлению выбранному.

Метод контурных токов

Рассмотренный выше метод расчета электрических цепей при анализе больших и разветвленных цепей приводит к неоправданно трудоемким расчетам, поэтому редко применяется. Более широко используется метод контурных токов, позволяющий значительно сократить количество уравнений. При этом вместо токов в ветвях электрической цепи определяются так называемые контурные токи при помощи второго закона Кирхгофа. Таким образом, количество требуемых уравнений будет равняться числу независимых контуров. В качестве примера рассчитаем цепь изображённую на рисунке ниже

Расчет цепи методом контурных токов.

Если бы мы вели расчёт цепи по методу законов Ома и Кирхгофа, то необходимо было бы решить систему из пяти уравнений. Для расчёта по методу контурных токов необходимо всего три уравнения.

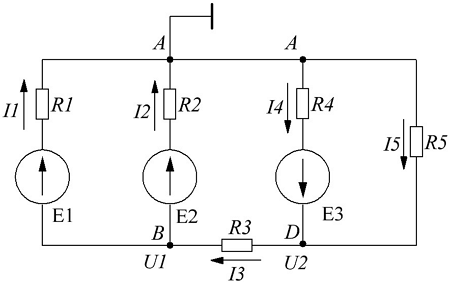
В начале расчёта выделяют независимые контуры, в нашем случае это: E1R1R2E2, E2R2R4E3R3 и E3R4R5. Затем контурам присваивают произвольно направленный контурный ток, который имеет одинаковое направление для всех участков выбранного контура, в нашем случае для первого контура контурный ток будет Ia, для второго – Ib, для третьего – Ic. Как видно из рисунка некоторые контурные токи соответствуют токам в ветвях

Остальные же токи можно найти как разность двух контурных токов

В результате выбора контурных токов можно составить систему уравнений по второму закону Кирхгофа

Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений

В результате решения системы получим Ia = I1 = 4,286 А, Ib = I3 = 3,571 А, Ic = I5 = -0,714 А, I2 = -0,715 А, I4 = 4,285 А. Так же как и в предыдущем случае если токи получаются отрицательными, значит действительное направление противоположно принятому. Таким образом, токи I2 и I5 имеют направление противоположное изображённым на рисунке.

Метод узловых напряжений

Кроме метода контурных токов, для уменьшения трудоемкости расчётов, применяют метод узловых напряжений, при этом возможно еще меньшее число уравнений, так как при этом методе их число достигает

где q – количество узлов в электрической цепи.

Принцип расчёта электрической цепи заключается в следующем:

1. Принимаем один из узлов цепи за базисный и присваиваем ему потенциал равный нулю;
2. Для оставшихся узлов составляем уравнения по первому закону Кирхгофа, заменяя токи в ветвях по закону Ома через напряжение и сопротивление;
3. После решения получившейся системы уравнений вычисляем токи в ветвях по обобщенному закону Ома.

В качестве примера возьмём предыдущую цепь и составим систему уравнений

Схема для решения уравнений методом узловых потенциалов.

В качестве базисного возьмём узел А и заземлим его, для остальных узлов B и D составим уравнения по первому закону Кирхгофа

Примем потенциалы узлов В = U1 и D = U2, тогда токи в ветвях выразятся через обобщённый закон Ома

В результате получившаяся система будет иметь следующий вид

Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений

В результате решения системы уравнений мы пришли к следующим результатам: потенциал в узле В – U1 = -57,14 В, а в узле D – U2 = 14,29 В. Теперь нетрудно посчитать, что токи в ветвях будут равны

Результат решения для токов I2 и I5 получился отрицательным, так как действительное направление токов противоположно направлению, изображённому на рисунке. Данные результаты совпадают с результатами, полученными для этой же схемы при расчёте по методу контурных токов.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Источник

Эта статья для тех, кто только начинает изучать теорию электрических цепей. Как всегда не будем лезть в дебри формул, но попытаемся объяснить основные понятия и суть вещей, важные для понимания. Итак, добро пожаловать в мир электрических цепей!

Хотите больше полезной информации и свежих новостей каждый день? Присоединяйтесь к нам в телеграм.

Электрические цепи

Электрическая цепь – это совокупность устройств, по которым течет электрический ток.

Рассмотрим самую простую электрическую цепь.  Из чего она состоит? В ней есть генератор – источник тока, приемник (например, лампочка или электродвигатель), а также система передачи (провода). Чтобы цепь стала именно цепью, а не набором проводов и батареек, ее элементы должны быть соединены между собой проводниками. Ток может течь только по замкнутой цепи. Дадим еще одно определение:

Электрическая цепь – это соединенные между собой источник тока, линии передачи и приемник.

Конечно, источник, приемник и провода – самый простой вариант для элементарной электрической цепи. В реальности в разные цепи входит еще множество элементов и вспомогательного оборудования: резисторы, конденсаторы, рубильники, амперметры, вольтметры, выключатели, контактные соединения, трансформаторы и прочее.

Кстати, о том, что такое трансформатор, читайте в отдельном материале нашего блога.

По какому фундаментальному признаку можно разделить все цепи электрического тока? По тому же, что и ток! Есть цепи постоянного тока, а есть – переменного. В цепи постоянного тока он не меняет своего направления, полярность источника постоянна. Переменный же ток периодически изменяется во времени как по направлению, так и по величине.

Сейчас переменный ток используется повсеместно. О том, что для этого сделал Никола Тесла, читайте в нашей статье.

Элементы электрических цепей

Все элементы электрических цепей можно разделить на активные и пассивные. Активные элементы цепи – это те элементы, которые индуцируют ЭДС. К ним относятся источники тока, аккумуляторы, электродвигатели. Пассивные элементы – соединительные провода и электроприемники.

Приемники и источники тока, с точки зрения топологии цепей, являются двухполюсными элементами (двухполюсниками). Для их работы необходимо два полюса, через которые они передают или принимают электрическую энергию. Устройства, по которым ток идет от источника к приемнику, являются четырехполюсниками. Чтобы передать энергию от одного двухполюсника к другому им необходимо минимум 4 контакта, соответственно для приема и передачи.

Резисторы – элементы электрической цепи, которые обладают сопротивлением. Вообще, все элементы реальных цепей, вплоть до самого маленького соединительного провода, имеют сопротивление. Однако в большинстве случаев этим можно пренебречь и при расчете считать элементы электрической цепи идеальными.

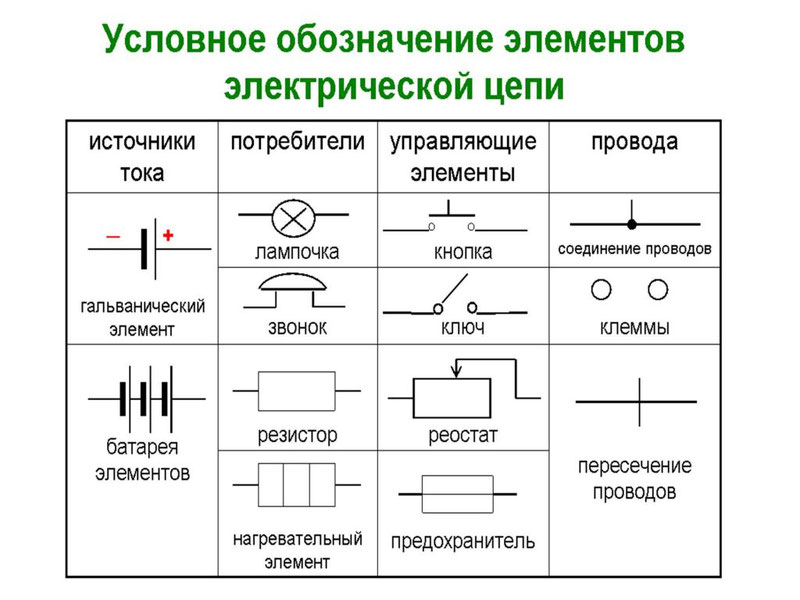
Существуют условные обозначения для изображения элементов цепи на схемах.

Кстати, подробнее про силу тока, напряжение, сопротивление и закон Ома для элементов электрической цепи читайте в отдельной статье.

Вольт-амперная характеристика – фундаментальная характеристика элементов цепи. Это зависимость напряжения на зажимах элемента от тока, который проходит через него. Если вольт-амперная характеристика представляет собой прямую линию, то говорят, что элемент линейный. Цепь, состоящая из линейных элементов – линейная электрическая цепь. Нелинейная электрическая цепь – такая цепь, сопротивление участков которой зависит от значений и направления токов.

Какие есть способы соединения элементов электрической цепи? Какой бы сложной ни была схема, элементы в ней соединены либо последовательно, либо параллельно.

При решении задач и анализе схем используют следующие понятия:

• Ветвь – такой участок цепи, вдоль которого течет один и тот же ток;
• Узел – соединение ветвей цепи;
• Контур – последовательность ветвей, которая образует замкнутый путь. При этом один из узлов является как началом, так и концом пути, а другие узлы встречаются в контуре только один раз.

Чтобы понять, что есть что, взглянем на рисунок:

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Классификация электрических цепей

По назначению электрические цепи бывают:

• Силовые электрические цепи;
• Электрические цепи управления;
• Электрические цепи измерения;

Силовые цепи предназначены для передачи и распределения электрической энергии. Именно силовые цепи ведут ток к потребителю.

Также цепи разделяют по силе тока в них. Например, если ток в цепи превышает 5 ампер, то цепь силовая. Когда вы щелкаете чайник, включенный в розетку, Вы замыкаете силовую электрическую цепь.

Электрические цепи управления не являются силовыми и предназначены для приведения в действие или изменения параметров работы электрических устройств и оборудования. Пример цепи управления – аппаратура контроля, управления и сигнализации.

Электрические цепи измерения предназначены для фиксации изменений параметров работы электрического оборудования.

Расчет электрических цепей

Рассчитать цепь – значит найти все токи в ней. Существуют разные методы расчета электрических цепей: законы Кирхгофа, метод контурных токов, метод узловых потенциалов и другие. Рассмотрим применение метода контурных токов на примере конкретной цепи.

Сначала выделим контуры и обозначим ток в них. Направление тока можно выбирать произвольно. В нашем случае – по часовой стрелке. Затем для каждого контура составим уравнения по 2 закону Кирхгофа. Уравнения составляются так: Ток контура умножается на сопротивление контура, к полученному выражению добавляются произведения тока других контуров и общих сопротивлений этих контуров. Для нашей схемы:

Полученная система решается с подставкой исходных данных задачи. Токи в ветвях исходной цепи находим как алгебраическую сумму контурных токов

Какую бы цепь Вам ни понадобилось рассчитать, наши специалисты всегда помогут справится с заданиями. Мы найдем все токи по правилу Кирхгофа и решим любой пример на переходные процессы в электрических цепях. Получайте удовольствие от учебы вместе с нами!

Методы расчета электрических цепей

Постановка
задачи: в известной схеме цепи с заданными
параметрами необходимо рассчитать
токи, напряжения, мощности на отдельных
участках. Для этого можно использовать
следующие методы:

• преобразования цепи;

• непосредственного применения законов
  Кирхгофа;

• контурных токов;

• узловых потенциалов;

• наложения;

• эквивалентного генератора.

Будем
рассматривать первых два метода.

1. Метод
   преобразования цепи. Суть метода: если
   несколько последовательно или (и)
   параллельно включенных сопротивлений
   заменить одним, то распределение токов
   в электрической цепи не изменится.

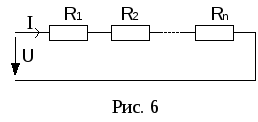
а)
Последовательное соединение резисторов.
Сопротивления включены таким образом,
что начало следующего сопротивления
подключается к концу предыдущего (рис.
6).

Ток
во всех последовательно соединенных
элементах одинаков.

З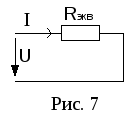аменим
все последовательно соединенные
резисторы одним эквивалентным(рис. 7.).

По
IIзакону Кирхгофа:

;

;

т.е.
при последовательном соединении
резисторов эквивалентное сопротивление
участка цепи равно сумме всех
последовательно включенных сопротивлений.

б)
Параллельное соединение резисторов.
При этом соединении соединяются вместе
одноименные зажимы резисторов (рис. 8).

В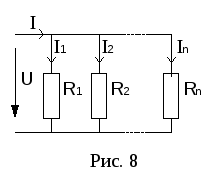се
элементы присоединяются к одной паре
узлов. Поэтому ко всем элементам приложено
одно и тоже напряжениеU.

По Iзакону Кирхгофа:.

По
закону Ома
.
Тогда.

Для
эквивалентной схемы (см рис. 7):
;
.

Величина
,
обратная сопротивлению, называется
проводимостьюG.

;=
Сименс (См).

Ч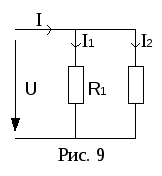астный
случай: параллельно соединены два
резистора (рис. 9).

в)
Взаимное преобразование звезды (рис.10а)
и треугольник сопротивлений (рис. 10б).

–
преобразование звезды сопротивлений
в треугольник:

а)	б)
Рис. 10

–
преобразование “треугольника”
сопротивлений в “звезду”:

1. Метод
   непосредственного применения законов
   Кирхгофа. Порядок расчета:

• Определить
  число ветвей (т.е. токов) и узлов в схеме.

• Произвольно
  выбрать условно-положительные направления
  токов. Общее число уравнений должно
  быть равно числу неизвестных токов.

• Определить,
  сколько уравнений должно быть составлено
  по Iзакону Кирхгофа, а
  сколько – поIIзакону
  Кирхгофа.

• Составить
  уравнения для
  узлов
  поIзакону Кирхгофа и
  длянезависимых
  контуров (отличающихся друг от друга
  хотя бы на одну ветвь) – поIIзакону Кирхгофа.

• Решить
  система уравнений относительно токов.
  Если в результате ток получился
  отрицательным, то его действительное
  направление противоположно выбранному.

• Проверить
  правильность решения задачи, составив
  уравнение баланса мощности и смоделировав
  электрическую цепь средствами
  моделирующего пакета ElectronicsWorkbench.

Примечание:
если есть возможность, то перед
составлением системы уравнений по
законам Кирхгофа, следует преобразовать
“треугольник” сопротивлений в
соответствующую “звезду”.

Пример расчет электрических цепей постоянного тока

Расчет будем выполнять с применением
законов Кирхгофа, предварительно
преобразовав треугольник сопротивлений
в звезду.

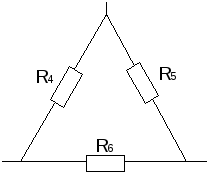
П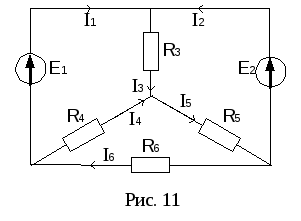ример.
Определить токи в цепи рис. 11, еслиE₁=160
В,E₂=100 В,R₃=100 Ом,R₄=100 Ом,R₅=150 Ом,R₆=40
Ом.

Преобразуем
треугольник сопротивлений R₄
R₅ R₆в звезду сопротивленийR₄₅
R₅₆ R₆₄,
предварительно указав условные
положительные направления токов в цепи
(рис. 12).

Ом;

Ом;

Ом.

а)	б)
Рис. 12

После
преобразования электрическая цепь
примет вид рис. 13 (в непреобразованной
части электрической цепи направления
токов не изменятся).

В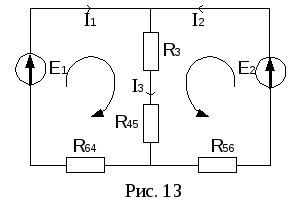полученной электрической цепи 2 узла,
3 ветви, 2 независимых контура, следовательно,
в цепи протекает три тока (по количеству
ветвей) и необходимо составить систему
трех уравнений, из которых поIзакону Кирхгофа – одно уравнение (на 1
меньше, чем узлов в схеме электрической
цепи) и два уравнения – поIIзакону Кирхгофа:

Подставим
в полученную систему уравнений известные
значения ЭДС и сопротивлений:

Решая
систему уравнений любым способом,
определяем токи схемы электрической
цепи рис. 13:

А;А;А.

Переходим
к исходной схеме (см. рис. 11). По IIзакону Кирхгофа:

;

А.

По Iзакону Кирхгофа:

;

А;

;

А.

Т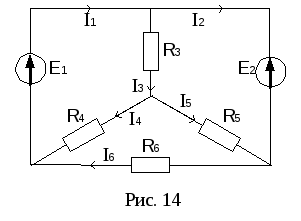окииполучились отрицательными, следовательно,
их действительное направление
противоположно выбранному нами (рис.
14).

Правильность
решения проверяем, составив уравнение
баланса мощности. Мощность источников
(учтем, что ЭДС источника E₂направленно встречно токуI₂,
протекающему через него):

Вт.

Мощность
потребителей:

Погрешность
вычислений в пределах допустимого
(меньше 5%).

Смоделируем
электрическую цепь рис. 11 средствами
моделирующего пакета ElectronicsWorkbench(рис. 15):

Рис.
15

При
сравнении расчетных результатов и
результатов моделирования, можно
увидеть, что они отличаются (различия
не превышают 5%), т.к. измерительные
приборы имеют внутренние сопротивления,
которые моделирующая система учитывает

Соседние файлы в папке Все что скинул препод

• #
• #
• #

  25.03.20169.01 Кб111Задача 1.xlsx

• #

  25.03.201610.02 Кб63зАДАЧА 2.xlsx

• #

  25.03.20168.97 Кб42Звезда с нулем.xlsx

• #
• #
• #

Всем доброго времени суток. В прошлой статье я рассматривал типы соединений приемников энергии в электрических цепях, а так же законы Кирхгофа, которые определяют основные соотношения токов и напряжений в этих цепях. Но кроме знания основных законов электротехники необходимо уметь рассчитывать неизвестные параметры электрических цепей по заданным известным параметрам. Так, например, по известным напряжениям, ЭДС и сопротивлениям необходимо знать какую мощность будет потреблять тот или иной приемник энергии, а так же вся цепь в целом. Этим мы и займёмся в данной статье.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Расчёт электрических цепей с помощью законов Кирхгофа

Существует несколько методов расчёта электрических цепей, которые различаются между собой параметрами, которые необходимо найти, а так же количеством необходимых расчётов.

Вначале я расскажу, как произвести расчёт цепи в общем виде, но в результате размеры вычислений будут неоправданно большими. Данный метод расчёта основан на законах Ома и Кирхгофа и используется при расчётах небольших цепей с малым количеством контуров. Для этого составляют систему уравнений из (q — 1) уравнений для узлов цепи и n уравнений для независимых контуров. Независимые контуры характеризуются тем, что при составлении уравнений для каждого нового контура входит хотя бы одна новая ветвь, не вошедшая в предыдущий контур. Таким образом, количество уравнений в системе уравнений по данному методу расчёта цепи будет определяться следующим выражением

В качестве примера рассчитаем электрическую цепь, приведённую на рисунке ниже

Пример электрической цепи для расчёта по законам Ома и Кирхгофа.

В качестве примера возьмём следующие параметры схемы: E1 = 50 B, E2 = 30 B, R1 = R3 = 10 Ом, R2 = R5 = 20 Ом, R4 = 25 Ом.

1. Составим уравнение по первому закону Кирхгофа. Так как узла у нас два, то выберем узел А и составим для него уравнение. Я выбрал условно, что токи I1 и I2 втекают в узел, а I3 – вытекает, тогда уравнение будет иметь вид

   

2. Составим недостающие уравнения по второму закону Кирхгофа. В схеме у нас два независимых контура: E1R1R2R4E2R3  и E2R4R5, поэтому выбирая произвольное направление контуров составим недостающие два уравнения. Я выбрал обход по ходу часовой стрелке, поэтому уравнения имеют вид

   

Таким образом, получившаяся система уравнений будет иметь следующий вид

Решив данную систему, получим следующие результаты: I1 ≈ 0,564 А, I2 ≈ 0,103 А, I2 ≈ 0,667 А.

В результате решения системы уравнений по данному методу может оказаться, что токи получились отрицательными. Это значит, что действительное направление токов противоположно по направлению выбранному.

Метод контурных токов

Рассмотренный выше метод расчета электрических цепей при анализе больших и разветвленных цепей приводит к неоправданно трудоемким расчетам, поэтому редко применяется. Более широко используется метод контурных токов, позволяющий значительно сократить количество уравнений. При этом вместо токов в ветвях электрической цепи определяются так называемые контурные токи при помощи второго закона Кирхгофа. Таким образом, количество требуемых уравнений будет равняться числу независимых контуров. В качестве примера рассчитаем цепь изображённую на рисунке ниже

Расчет цепи методом контурных токов.

Если бы мы вели расчёт цепи по методу законов Ома и Кирхгофа, то необходимо было бы решить систему из пяти уравнений. Для расчёта по методу контурных токов необходимо всего три уравнения.

В начале расчёта выделяют независимые контуры, в нашем случае это: E1R1R2E2, E2R2R4E3R3 и E3R4R5. Затем контурам присваивают произвольно направленный контурный ток, который имеет одинаковое направление для всех участков выбранного контура, в нашем случае для первого контура контурный ток будет Ia, для второго – Ib, для третьего – Ic. Как видно из рисунка некоторые контурные токи соответствуют токам в ветвях

Остальные же токи можно найти как разность двух контурных токов

В результате выбора контурных токов можно составить систему уравнений по второму закону Кирхгофа

Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений

В результате решения системы получим Ia = I1 = 4,286 А, Ib = I3 = 3,571 А, Ic = I5 = -0,714 А, I2 = -0,715 А, I4 = 4,285 А. Так же как и в предыдущем случае если токи получаются отрицательными, значит действительное направление противоположно принятому. Таким образом, токи I2 и I5 имеют направление противоположное изображённым на рисунке.

Метод узловых напряжений

Кроме метода контурных токов, для уменьшения трудоемкости расчётов, применяют метод узловых напряжений, при этом возможно еще меньшее число уравнений, так как при этом методе их число достигает

где q – количество узлов в электрической цепи.

Принцип расчёта электрической цепи заключается в следующем:

1. Принимаем один из узлов цепи за базисный и присваиваем ему потенциал равный нулю;
2. Для оставшихся узлов составляем уравнения по первому закону Кирхгофа, заменяя токи в ветвях по закону Ома через напряжение и сопротивление;
3. После решения получившейся системы уравнений вычисляем токи в ветвях по обобщенному закону Ома.

В качестве примера возьмём предыдущую цепь и составим систему уравнений

Схема для решения уравнений методом узловых потенциалов.

В качестве базисного возьмём узел А и заземлим его, для остальных узлов B и D составим уравнения по первому закону Кирхгофа

Примем потенциалы узлов В = U1 и D = U2, тогда токи в ветвях выразятся через обобщённый закон Ома

В результате получившаяся система будет иметь следующий вид

Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений

В результате решения системы уравнений мы пришли к следующим результатам: потенциал в узле В – U1 = -57,14 В, а в узле D – U2 = 14,29 В. Теперь нетрудно посчитать, что токи в ветвях будут равны

Результат решения для токов I2 и I5 получился отрицательным, так как действительное направление токов противоположно направлению, изображённому на рисунке. Данные результаты совпадают с результатами, полученными для этой же схемы при расчёте по методу контурных токов.