Как найти сколько треугольников в треугольнике - Сайт, где вы сможете решить свои вопросы

Считать треугольники легко. Но школьники во время тестов и олимпиад тратят на эти задания слишком много времени, а потом не успевают решить задачи, которые приносят много очков. Считают они чаще бессистемно и поэтому путаются.

Во вчерашнем коротком видео мы попросили вас сосчитать треугольники.

Начинать считать треугольники нужно с вершин.

Мы решили показать как быстро и правильно посчитать треугольники на любом чертеже.

Вот наш чертеж.

Как быстро сосчитать треугольники и не запутаться

В нашем случае треугольников много, но ведь бывают чертежи и попроще. И если принцип будет понятен, то вы справитесь и с более сложным рисунком. А рассказываем еще и потому, что вы сможете подсказать своим детям или внукам, как быстро это делать, так как в школьных заданиях, и даже на олимпиадах такие задачи встречаются часто.

В решении таких головоломок требуется, конечно, и умение запоминать то, что уже посчитано.

Вот так считали мы. Но мы делали это в уме. А для вас показываем схематично.

Для того, чтобы быстро посчитать треугольники среди множества пересеченных между собой линий, нужно выбрать и отметить главные точки пересечений. Они и станут вершинами наших треугольников.

У нас получилось 12 вершин.

Теперь считать легко.

На картинке ниже в вершинах указано количество треугольников

Получаем по вершинам

№1 — 6 ▲ + №2 — 5 ▲ + №3 — 5▲ + №4 — 4 ▲ + №5 — 4 ▲ №6 — 3 ▲ + №7 — 3 ▲ + №8 — 2 ▲ + №9 — 1 ▲ + №10 — 2 ▲ + №11 — 3 ▲ + №12 — 4 ▲

Можно посмотреть подробнее

Ответ

Пишите нам! Всем спасибо, успехов и удачи!

Источник

Задача, которую решают единицы: сколько треугольников на картинке?

Если у вас нашлась свободная минутка, то почему бы вам не проверить свои силы и не попробовать решить довольно простую задачу. Хотя простой она может показаться уже после того, как вы узнаете ответ. Итак, сколько треугольников вы можете найти на этой картинке?

Считается, что найти все зашифрованные треугольники могут только люди с высоким IQ. Если вы думаете, что действительно нашли все треугольники, то попробуйте сравнить свой ответ с нашим.

Число треугольников на картинке 24. Эта цифра может показаться невозможной, но это единственно верный ответ.

Считаем треугольники — разбор задания

Неделю назад дал ученикам своих мини-групп задание посчитать все треугольники, из которых состоят два рисунка:

Легкий треугольник

Сложный треугольник

Задание 1.

К выполнению подобных заданий нужно подходить системно. (Именно этому я учу детей, которые собираются поступать в 5 класс математических гимназий и лицеев, на моем математическом кружке и в мини-группах в Новых Черемушках.)

Пронумеруем все элементы легкого треугольника.

Выпишем поочередно треугольники, состоящие из одного элемента, из двух, из трех и т.д.

1. Из 1 элемента: 1, 2, 3, 5 — всего 4 треугольника (некоторые дети автоматически зачисляют в треугольники элементы № 4 и № 6 — это неправильно!).

2. Из 2 элементов: 12, 34, 56, 13, 35, 24 — всего 6 треугольников.

3. Из 3 элементов: 135, 246 — 2 треугольника.

4. Из 4 элементов: 1234 и 3456 — 2 треугольника.

5. Из 5 элементов — ничего нет.

6. Из 6 элементов — единственный 123456.

Итого: 15 треугольников.

Задание 2.

Сложное задание, требующее от детей внимательности, усидчивости и аккуратности в подсчетах. Пронумеруем все элементы легкого треугольника, причем цифр от 1 до 9 нам не хватит. Задействуем 10, 11 и 12.

Выпишем поочередно треугольники, состоящие из одного элемента, из двух, из трех и т.д.

1. Из 1 элемента: все от 1 до 12 — это треугольники. Их 12 штук.

2. Из 2 элементов. Начинаем считать от вершины и движемся по часовой стрелке. 12, 17, 18, 9 11, 11 12, 12 10, 56, 54, 43. Не забудем про внутренние треугольники: 28, 9 10, 36. Насчитали снова 12 штук.

3. Из 3 элементов — отыщем их только во внутреннем треугольнике. 289, 36 10, 823, 9 10 6, 10 98, 632. Их 6 штук.

4. Из 4 элементов: 1234, 1236, 789 10, 789 11, 12 10 63, 12 10 65, 289 11, 4328, 56 10 9. Набрали еще 9 треугольников.

5. Из 5 элементов — ничего не нашел. Кто найдет — напишите, объявлю благодарность.

6. Из 6 элементов: 123456, 789 10 11 12, 12789 11, 12 10 6345, 56 10 9 11 12, 432178 — нарыли еще 6 штук. Плюс центральный: 236 10 98. Итого — 7 треугольников.

7. Ну и самый большой, из 12 элементов — 1 треугольник.

Кратко:
1 — 12
2 — 12
3 — 6
4 — 9
6 — 7
12 — 1

Итого: 47 треугольников. (Огромное спасибо мамам Антона и Маруси, которые помогли мне найти недостающие треугольники из 4-х элементов).

Бедные мои ученики…

Сочувствую. Но если им нужно сдавать вступительные экзамены в наши математические школы Юго-Запада (1533, 1534, 1543, 2007, Л2Ш, 1514 и т.д.) или участвовать в олимпиадах, то такая тренировка мозгов пойдет им только на пользу.

Так что их ждут новые задания. Что-то — полегче, что-то — потяжелее. Поступление в хорошую школу стоит того, чтобы усердно работать над заданиями, чуть-чуть выходящими за рамки школьной программы.

С этой задачкой для первоклашек не могут справиться даже опытные учителя: проверьте свои знания

Эта банальная логическая задача стара как мир. Все очень просто: посчитайте каждый отдельный треугольник, затем сложите все различные комбинации маленьких треугольников и обязательно не забудьте про большую общую фигуру. Вы ведь так делаете? При всей своей простоте, эта задача всегда вызывает массу споров и сотни комментариев с ответами в диапазоне от четырех до 45 (боже, откуда столько?).

Давайте сначала вспомним из школьной программы, что же такое треугольник. В евклидовом пространстве это геометрическая фигура (он же многоугольник с фиксированным числом углов), образованная тремя отрезками (стороны треугольника), которые соединяют три точки (вершины треугольника), не лежащие на одной прямой. Возможно, мы повторно взорвем ваш мозг, но есть так называемый вырожденный треугольник, вершины которого таки лежат на одной прямой. Живите теперь с этим.

Отрезок, соединяющий вершину с точкой на противоположной стороне, называется чевианой. Обычно под чевианой понимают не один такой отрезок, а один из трех отрезков, проведенных из трех разных вершин треугольника и пересекающихся в одной точке. В нашем случае есть две чевианы, которые спускаются из верхнего угла на нижнюю сторону большой фигуры. Благодаря треугольнику появилась тригонометрия, планиметрия, а еще используя эту простую фигуру, люди научились составлять карты, измерять участки и конструировать. Даже «Черный квадрат» Малевича должен был называться «Черный китайский треугольник», и не спрашивайте, почему. Казимир Северинович унес эту тайну с собой на тот свет. В общем, при всей своей простоте полезная штука. Но мы отвлеклись.

Итак, еще раз посмотрим на нашу задачу. Те из вас, кто везде торопится, выдают сразу варианты ответов: шесть треугольников, 16, 22. Многие насчитывают 18 искомых фигур. Кто подотошнее считает, что на изображении нет ни одной прямой линии, а некоторые углы — не углы вовсе. Ну, конечно, это же нарисовано от руки! Для таких тут вообще нет ни одного треугольника. Зануды. Если вы все еще не нашли ответ и пытаетесь прочитать его в этом тексте, то остановитесь и просто посчитайте чертовы треугольники.

Ладно, давайте не будем играть в «Поле Чудес», а посмотрим на задачу с точки зрения науки. Единственный способ образовать треугольники на рисунке — это если верхний угол является частью каждого треугольника. Основание треугольника должно быть одним из трех горизонтальных уровней ниже. Получается, три уровня, на каждом вы можете выбрать базу для шести разных способов построения фигуры. В сумме выходит восемнадцать или три раза по шесть треугольников. Все варианты научного решения так или иначе крутятся вокруг этого способа. И да, вы же не забыли посчитать треугольник у стрелочки? Ладно, это была шутка. Или все же посчитали?

[spoiler title=”источники:”]

Считаем треугольники — разбор задания

http://www.popmech.ru/science/587343-zadacha-dlya-pervoklashki-a-vy-spravites/

[/spoiler]

Источник

Сколько треугольников видно на картинке?

Сначала насчитала 8, потом 9, а потом пошло и поехало. Не уверена что правильно посчитала, но у меня всего получилось 22 треугольника. Интересно сколько их на самом деле. Хорошее упражнение на внимательность.

Давайте попробуем считать треугольники по каким-тот правилам. Итак, треугольников которые имеют общую вершину на самом верху всего 18. Действительно из этой вершины исходят три луча, которые пересекаются с двумя прямыми, образуя на каждом уровне по 6 треугольников (3 маленьких, 2 средних и один большой).

Теперь перейдем к вершине на втором уровне, там можно найти 3 треугольника (большой, средний и маленький). Те же 3 треугольника можно найти на нижнем уровне. Итак всего 24 треугольника: 18+3+3 = 24.

Как вычислить количество треугольников?

Вот я криво нарисовал треугольник и разбил его на несколько маленьких, а затем задумался: можно ли как-нибудь без банального пересчета узнать общее количество получившихся треугольников? Немного подумав я разделил все треугольники на несколько типов: одинарные, двойные и т. д. То есть формула должна быть суммой всех треугольников каждого типа. На рисунке сторона самого большого треугольника поделена на 7 отрезков. Практическим методом я понял, что при любом количестве этих отрезков число одинарных треугольников равно квадрату числа отрезков. То есть, самых маленьких треугольничков на рисунке 49. Так же разобрался с двойными, их количество находится по формуле 3(n-1), где n- опять же число отрезков. К этой сумме можно прибавить число самых больших треугольников — всегда 1. Вот и все: для остальных треугольников не могу закономерности увидеть. Может из здесь присутствующих кто нибудь увидит?
/>

считай не треугольники, а ВЕРХНИЕ/НИЖНИЕ ВЕРШИНЫ (как вариант- ПАРЫ точек, задающих горизонтальное основание)
_________

Сколько есть горизонтальных отрезков длины 1?
1+2+. +(n-1)+n
Каждый, кроме последних n,задает 2 треугольника.
2*(1+2+. +(n-1))+n
________________
Сколько есть горизонтальных отрезков длины 2?
1+2+. +(n-2)+(n-1)
Каждый, кроме последних (n-1) и (n-2),задает 2 треугольника.

только не бросайся сразу складывать.)))

Просто пойми сначала, что можно смотреть на задачу с разных сторон.
____________________

вторая идея тебе:
попробуй идти не от мелкого к крупному, а наоборот- от самого большого размера уменьшать понемногу.

Задачи «на подсчет треугольников»

5.3.2. Опишем проведенную работу при решении задач «на подсчет треугольников». В первых геометрических задачах будет применяться термин «взаимопроникающие фигуры», предложенный И.С. Якиманской. Вслед за ней взаимопроникающими мы называем такие фигуры, которые имеют часть общей площади: одними своими частями они перекрывают друг друга, другими частями не совпадают [196].

Посмотрите на рис. 5.2, а: треугольник АВС можно разделить на составляющие его фигуры: треугольники АЕО, О DC, АОС и четырехугольник BEOD (рис. 5.2, б).

Можно рассмотреть и другие имеющиеся в треугольнике АВС треугольники: ABD, ЕВС, АЕС, ADC (рис. 5.2, в). В этом случае мы получаем «взаимопроникающие» фигуры.

Исследование И.С. Якиманской [196] было направлено на изучение того, как учащийся анализирует геометрический чертеж, какие фигуры выступают для него более явно, бросаются в глаза, а какие трудны для выделения, на что опирается учащийся при рассмотрении чертежа, какие умственные процессы обеспечивают возможность различного видения чертежа. Результаты, полученные И.С. Якиманской, очень интересны, к сожалению, их недостаточно используют при работе с учащимися.

Задачи с взаимопроникающими элементами использовал в своей работе и В. А. Крутецкий. С помощью этих задач он исследовал особенности аналитико-синтетического восприятия геометрических фигур учащимися, в частности умения рассматривать и оценивать взаимопроникающие элементы геометрических фигур с различных точек зрения, выделять элементы фигур и фигуры из фона, включать один и тот же элемент в разные фигуры и соответственно давать им различную интерпретацию.

Рассмотрим некоторые задачи по подсчету треугольников с учетом взаимопроникающих фигур.

Задача 5.8. Сколько отрезков вы видите на рис. 5.3? Назовите их.

Задача 5.9. Сколько треугольников изображено на рис. 5.4? Назовите их.

Задача 5.10. Сколько углов вы видите на рис. 5.5? Назовите их.

В.А. Крутецкий ограничивал исследование тем, что фиксировал, «насколько полный ответ дают испытуемые, какую роль играют „видение» и „рассуждение»» [98].

Учитывая вышеизложенное, рассмотрим, как можно использовать «цепочки задач на подсчет треугольников» для выявления «геометрического зрения», уровней владения приемами анализа и синтеза, алгоритмических способностей учащихся, причем не будем ограничиваться только окончательным ответом, а приведем качественный анализ выполнения задания.

Б.М. Теплов подчеркивал, что «не следует вовсе исключать возможность количественного подхода при исследовании способностей. Он возможен, однако, только в том случае, когда он следует за качественным анализом, вытекает из него, им определяется» [171].

Количественная характеристика применялась нами при оценке:

• геометрического зрения — насколько полно и точно учащийся увидел искомые фигуры; количество выделенных фигур из фона;
• аналитико-синтетической деятельности — наличие и количество «идей» при решении задач, выбор наиболее рационального способа решения;
• алгоритмические способности — количество шагов, приводящих к правильному решению.

Ниже приведены некоторые из предлагаемых учащимся заданий по подсчету треугольников и дан анализ их решения.

Задача 5.11. Сосчитайте, сколько треугольников изображено на рис. 5.6.

Цепочка задач построена таким образом, что при переходе к каждой последующей фигуре увеличивается число искомых треугольников (принцип нарушается при переходе от слу-

чая 5.6, в к случаю, изображенному на рис. 5.6, г, но в случае 5.6, г усложняется «геометрический фон», т. е. появляются такие взаимопроникающие треугольники, которые состоят, например, из треугольника и четырехугольника, а в случае 5.6, в все взаимопроникающие треугольники можно рассматривать состоящими только из треугольников).

Оценка выполнения задания (а)

1. Если учащийся увидел на рис. 5.6, а большой треугольник, состоящий из двух маленьких, т. е. всего три треугольника, то он получает 1 балл.
2. Если учащийся не видит какой-либо из трех треугольников, то он получает 0 баллов.

Оценка выполнения задания (б)

На рис. 5.6, б изображен большой треугольник, состоящий из трех маленьких, всего четыре треугольника. Такое решение оценивается в 1 балл.

Схема рассуждений и ход решения (в)

1. Воспроизведем рис. 5.6, в. Пронумеруем треугольники (рис. 5.7, а). Сосчитаем все маленькие треугольники, их всего шесть (рис. 5.7, б).

2. Сосчитаем треугольники, состоящие из двух маленьких, их всего три (рис. 5.7, в).
3. Сосчитаем треугольники, состоящие из трех маленьких, их всего шесть (рис. 5.7, г).
4. Треугольник, состоящий из шести маленьких треугольников, — один (рис. 5.7, а).

Всего получилось 16 треугольников.

Оценка выполнения задания (в)

1. Учащиеся сосчитали (увидели) все взаимопроникающие треугольники, подсчет вели с помощью алгоритма — 2 балла.
2. Задача решалась без применения алгоритма (какие треугольники учащийся увидел, такие и сосчитал, но нашел больше семи треугольников — 1 балл).
3. Учащийся при решении насчитал меньше семи треугольников, т. е. не увидел взаимопроникающих треугольников, — оценка 0 баллов.

Схема рассуждений и ход решения (г)

1. Сосчитаем треугольники в «нижней» части рис. 5.6, г, их всего шесть, причем все они состоят только из треугольников (рис. 5.8, а, б, в).
2. Добавляем «верхнюю» часть, получаем треугольники, состоящие из треугольников и четырехугольника, решение аналогично решению в случае а, треугольников тоже шесть (рис. 5.9, а, б, в).

Всего получилось: (3 + 2 + 1) + (3 + 2+ 1) = 12 треугольников.

Оценка выполнения задания (г)

1. Учащийся подсчитал все треугольники с помощью алгоритма (выбор алгоритма значения не имеет) — оценка 3 балла.
2. Учащийся применил для решения алгоритм, не позволивший выделить все имеющиеся на рисунке треугольники — оценка 2 балла.
3. Учащиеся, сосчитавшие только треугольники на рис. 5.8, а, в и рис. 5.9, а, в, т. е. не увидевшие взаимопроникающих треугольников, получают 1 балл.

4. Учащиеся, увидевшие на рисунке меньше семи треугольников, получают О баллов.

Схема рассуждений и ход решения (д)

В этой задаче (как, впрочем, и в других) при подсчете числа треугольников без алгоритма есть опасность «потерять» треугольники, поэтому полезно обозначить треугольники цифрами (рис. 5.10).

1. Начнем подсчет с маленьких треугольников, их всего 12 (рис. 5.10).
2. Считаем треугольники, состоящие из трех маленьких (два маленьких треугольника образуют ромб), таких треугольников шесть (рис. 5.11).

3. Четыре, пять, шесть, семь, восемь маленьких треугольников не образуют новых треугольников, а треугольников, состоящих из девяти маленьких треугольников, — два (рис. 5.12).

Всего получилось 12 + 6 + 2 = 20 треугольников.

Оценка выполнения задания (д)

1. Учащиеся, предложившие алгоритм подсчета и сосчитавшие все треугольники, получают 3 балла.
2. Учащиеся, сосчитавшие все треугольники, но не предложившие алгоритм подсчета, получают 2 балла.
3. Учащиеся, увидевшие случаи, изображенные на рис. 5.11 и рис. 5.12, но пропустившие некоторые треугольники, получают 1 балл.
4. Учащиеся, не увидевшие случаи, изображенные на рис. 5.11, 5.12, получают 0 баллов.

Схема рассуждений и ход решения (е)

Эта задача самая сложная в цепочке, выявляющей «уровни видения» взаимопроникающих треугольников, так как в ней появляются треугольники, состоящие из треугольников и пятиугольника. Пронумеруем все элементы пятиугольника (рис. 5.13).

1. Десять маленьких треугольников (1-10) (рис. 5.13).

2. Десять треугольников, состоящих из двух маленьких треугольников (1-2, 2-3,
3-4, 4-5, 5-6, 6-7, 7-8, 8-9, 9-10, 10-1).
3. Пять треугольников, состоящих из трех маленьких треугольников (1-2-3,
3-4-5, 5-6-7, 7-8-9, 9-10-1).
4. Пять треугольников, состоящих из двух маленьких треугольников и пятиугольника (2-11-6, 4-11-8, 6-11-10, 8-11-2,10-11-4).
5. Пять треугольников, состоящих из четырех маленьких треугольников и пятиугольника (1-2-10-11-6, 3-4-2-11-8, 5-6-4-11-10,7-8-6-11-2,9-8-10-11-4).

Всего получилось 10 + 10 + 5 + 5 + 5 = 35 треугольников.

Оценка выполнения задания (д)

1. Учащийся увидел все взаимопроникающие треугольники, предложил алгоритм подсчета (не обязательно рассмотренный нами) — оценка 4 балла.
2. Учащийся увидел треугольники, соответствующие пп. 1, 2, 3, 4 или 1, 2, 3, 5 и какие-то треугольники, соответствующие пп. 4 или 5, — оценка 3 балла.
3. Учащийся увидел треугольники, соответствующие пп. 1, 2, 3, но не увидел ни одного треугольника, соответствующего пп. 4 и 5, — оценка 2 балла.
4. Учащийся увидел какие-то треугольники, соответствующие пп. 1, 2, 3, но не все — оценка 1 балл.
5. Учащийся увидел только треугольники, соответствующие п. 1, — оценка 0 баллов.

При рассмотрении предложенных в предыдущей задаче случаев видно, что можно пользоваться «методом проб и ошибок», но без подключения «анализа» (причем иногда довольно углубленного) успеха добиться трудно.

Задача 5.12. Сосчитайте, сколько треугольников изображено на рис. 5.14.

Ответ: на рис. 5.14, а изображено 13 треугольников; 5.14,6 — 27 треугольников; 5.14, в — 47 треугольников; 5.14, г —27 треугольников; 5.14, д — 32 треугольника; 5.14, е — 48 треугольников.

Источник

Конкурс исследовательских работ и проектов учащихся

общеобразовательных учреждений Республики Дагестан

«Науки юношей питают»

Исследовательская работа

на тему

«Треугольники в моей жизни»

по математике

Автор:

Крымаев Ибрагим Маратович

ученик 6 «в» класса

МКОУ «Гимназия №2 им. А.М.Сайтиева»

г.Хасавюрт

8 928 517-54-44

[email protected]

Научный руководитель:

Чакаева Асма Султановна

МКОУ «Гимназия №2 им.А.М.Сайтиева»

8 928 681-91-53

а[email protected]

Введение:

Треугольник – самая известная и одна из старейших фигур. С виду треугольник очень прост – три вершины и три стороны и ограниченная ими плоскость, но эта фигура породила собой целую науку – тригонометрию. Треугольник – фигура, состоящая из трёх отрезков которые соединяют 3 непересекающихся между собой точки, самая элементарная прямолинейная фигура, упоминания о которой шли ещё в глубокой древности. Фигура довольно часто встречалась в практической жизни, наши предки довольно быстро принялись за её изучение.

Первые упоминания о фигуре были обнаружены на папирусах Древнего Египта. Затем большое внимание к треугольнику проявляли древние Греки: создание теоремы Пифагора и формула . Самый известный математик древности – Пифагор черпал информацию у египтян. Без полученных там знаний он бы не смог создать свою великую теорему, например египтянам было известно о том, что треугольник со сторонами 3, 4, 5 всегда будет являться прямоугольным – основа теоремы Пифагора. Особенный вклад в развитие данной отрасли внёс Эйлер Леонгард , который открыл новые факты о свойствах треугольника, в частности известную теорему Эйлера. Теперь пару слов об одном из самой известной загадке человечества – Бермудском треугольнике. Так называют район в Саргассовом море в котором происходят загадочные исчезновения кораблей и самолётов.Этот район имеет форму треугольника. Версий куда же на самом деле пропадают эти воздушные и морские судна много, начиная от погодных аномалий заканчивая похищением Инопланетных жителей. Власти данного участка земли относятся скептически к таким версиям и утверждают что эти происшествия происходят не чаще чем где либо, якобы, всё это слухи. Что на самом деле происходит в этом треугольнике, вы можете знать из известной книги Чарльза Берлица “Бермудский треугольник”.

Основная часть:

В моем проекте «Практическое применение треугольников в жизни» я хочу доказать, что треугольник и математика окружают нас везде и всегда. Стоит только внимательно присмотреться. Треугольник – это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Эта фигура встречается везде, но не всегда её замечают.

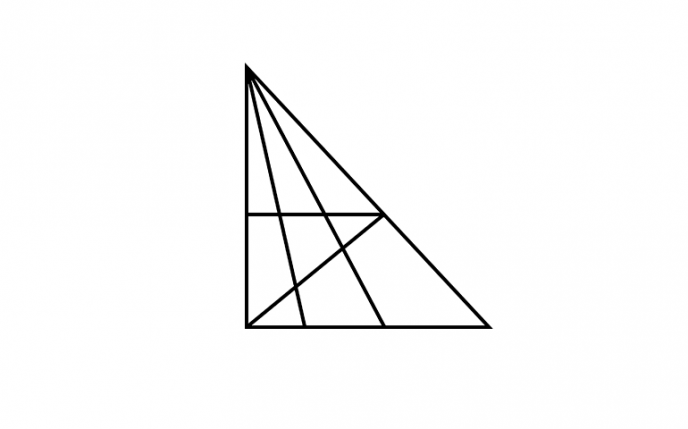
Я давно интересуюсь треугольниками, ещё с начальных классов. Люблю чертить их, находить количество треугольников на которых он разбит. Для себя вывел следующий алгоритм подсчёта треугольников.(см.приложение)

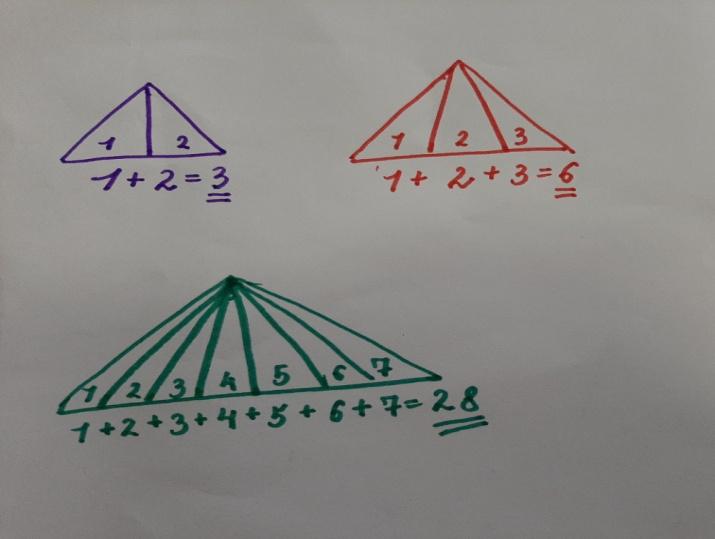
Часто знает и дошкольник,
Что такое треугольник,
А уж вам-то как не знать!
Но совсем другое дело –
Быстро, точно и умело
Треугольники считать.
Например, в фигуре этой
Сколько разных? Рассмотри!
Все внимательно исследуй
И по краю, и внутри!

Мы знакомы с разными многоугольниками: треугольник, четырехугольник, пятиугольник и т.д. Почему же именно треугольник считают символом геометрии? Оказывается, потому, что треугольник – это многоугольник с наименьшим количеством сторон. Действительно, попробуйте построить многоугольник с двумя сторонами и у вас ничего не получится, ведь для того чтобы получился многоугольник нужна третья сторона.

Треугольник Рёло – это область пересечения трех окружностей, построенных из вершин правильного треугольника. Они имеют радиус, равный стороне этого же треугольника. Он относится к разряду простых фигур (как круг), обладающих постоянной шириной. То есть если к нему провести две параллельные опорные прямые, то независимо от выбранного направления, расстояние между ними будет неизменным, в любой точке независимо от их длины. По мнению историков, название это «непростой» простой фигуре дал немецкий механик Франц Рёло, живший с 1829 по 1905 годы. Многие историки сходятся в том, что именно он стал первооткрывателем свойств этой геометрической фигуры. Потому как он первый широко использовал свойства и возможности треугольника Рёло в своих механизмах. Франц Рёло первым дал доскональные определения понятиям «кинетическая пара», «кинетическая цепь». Он впервые показал возможность связи между основами механики и конструирования. То есть связал теорию и практические проблемы конструирования. Что позволило создавать механизмы в совокупности их функциональных возможностей с внешней привлекательностью/эстетичностью. Отсюда Рёло стали считать поэтом механики. Что позволило последователям в корне пересмотреть имеющиеся в ней теории.

Иные исследователи первооткрывателем этой фигуры признают Леонарда Эйлер (18 век), который уже тогда продемонстрировал возможность его создания ее из трех окружностей.

А третьи «увидели» треугольник Рёло в рукописях гениального Леонардо Да Винчи. Манускрипты этого естествоиспытателя, с изображением этой «простой» фигуры, хранятся в Мадридском кодексе и в Институте Франции. Но кто бы ни был первооткрывателем этот «не простой» треугольник получил широкое распространение в современном мире. А именно:

• Сверло Уаттса. В 1914 году Гарри Джеймс Уаттс изобрел уникальный инструмент для высверливания квадратных отверстий. Это сверло, выполнено в форме Треугольника Рёло;

• Двигатель Ванкеля. С 1957 года треугольник Рёло немецкий изобретатель Ванкель Ф. создал уникальный механизм. Где внутри камеры, цилиндрической формы, по сложной траектории передвигается ротор-поршень. Созданный в форме треугольника Рёло. При его постоянном движении, каждая его грань, контактируя со стенками камеры, образует сразу три камеры, названные позже «камерами сгорания».

• Грейферный механизм кинопроекторов. Треугольник Рёло, вписанный в квадрат и двойной параллелограмм лежат в его основе. А нужен он для равномерного продергивания кинопленки во время киносеанса со скоростью в 18 кадров/с без отклонений и задержек;

• в архитектуре. Конструкция из двух дуг треугольника Рёло образует стрельчатую арку готического стиля. А окна в форме Рёло стоят в Брюгге в церкви Богоматери. Как орнамент он присутствует и на оконных решетках швейцарской коммуны Отрив и цистерцианского аббатства.

Следовательно, изобретенный в прошлом веке треугольник Рёло широко используется сегодня. Однако его изучение не стоит на месте. Его свойства, как характеристики простой фигуры, находится в постоянном теоретическом и практическом изучении.

Все вышеизложенные гипотезы из-за отсутствия точно выстроенной научной основы не могут быть приняты за теорию, объясняющую аномалию Бермудского треугольника. Однако в науке было так не один раз: сегодня это не воспринимается нашим разумом, а завтра уже всё принимается как новая теория.

Выявить суть загадочных катастроф, происходящих в печально известном районе Атлантического океана, пролить свет на таинство там происходящего, столько времени, волнующего умы людей, поможет только дальнейшие научные исследования и наблюдения в этих регионах, как и развитие науки в целом.

Выводы:

Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которых человек узнал еще в глубокой древности, поэтому эта фигура всегда имела широкое применения в практической жизни .И даже сейчас мы встречаем треугольники по всюду: в архитектуре, в музыке и даже в медицине. Треугольник – распространённая фигура, также с ним связаны загадки и тайны природы. Без треугольников и в жизни, и в математике просто не обойтись. Это настолько необъятная тема, что чем больше я в нее погружаюсь, тем больше утопаю как в Бермудском треугольнике.

Список литературы:

Энциклопедия для детей. Т. 11. Математика/Главный редактор Э68 М.Д. Аксёнова. – М.: Аванта+, 1998.
Я познаю мир: Детская энциклопедия: Математика/Сост. А. П. Савин, В. В. Станцо, А. Ю. Котова: Под общ. ред. О. Г. Хинн; Худож. А. В. Кардашук, А. Е. Шабельник, А. О. Хоменко. – М.: АСТ, 1995.
И. Н. Бронштейн и К. А. Семендяев, Справочник по математике.1965г.
Шарыгин И. Ф., Ерганжиева Л.Н. Наглядная геометрия: Учебное пособие для учащихся 5 – 6 классов. – М.: МИРОСЭ, 1995.