Как найти сколько углов в выпуклом многоугольнике

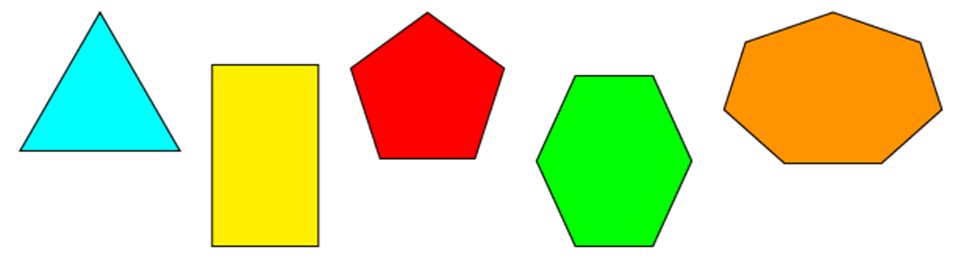
В геометрии многоугольниками называют плоские замкнутые фигуры, состоящие из нескольких прямых отрезков. Суммарная длина всех сторон называется периметром.

Поговорим подробнее о видах многоугольников и их характеристиках.

При изучении темы, что такое многоугольники, применяются следующие термины:

• Вершины многоугольника.
• Стороны замкнутой ломаной.
• Углы, образованные между смежными сторонами.
• Отрезки между несмежными вершинами называются диагоналями.
• Сумма длин всех сторон фигуры является периметром.
• Внутренние углы между соседними сторонами. Число углов равно числу сторон и вершин.

Наименования данных фигур зависят от количества сторон:

• Треугольник – это 3 стороны.
• Четырехугольник имеет 4 стороны.
• Пятиугольник – это 5 сторон и пр.

Все фигуры имеют буквенные обозначения, необходимо правильно проставлять их при вершинах.

Например, обозначение пятиугольника ABCDE будет выглядеть так:

В этом пятиугольнике вершинами являются точки: A, B, C, D и E.

Отрезки: AB, BC, CD, DE и EA являются сторонами пятиугольника.

Виды многоугольников

Различают несколько видов этих фигур: выпуклые, вогнутые, правильные и неправильные.

Какие многоугольники называются выпуклыми и невыпуклыми (вогнутыми)? Чтобы определить, какой многоугольник называется выпуклым, достаточно знать его определение.

Если стороны, при продолжении до прямой линии, не пересекают плоскость, то это выпуклый многоугольник.

Определение невыпуклого многоугольника: если при продолжении сторон прямые линии пересекают плоскость фигуры, то она является вогнутой.

Что такое правильные многоугольники

Выпуклые многоугольники, у которых все стороны и все углы равны, называются правильными.

На рисунке показан правильный многоугольник.

Как найти периметр многоугольника и определить диагонали

Периметром многоугольника называется сумма длин его сторон.

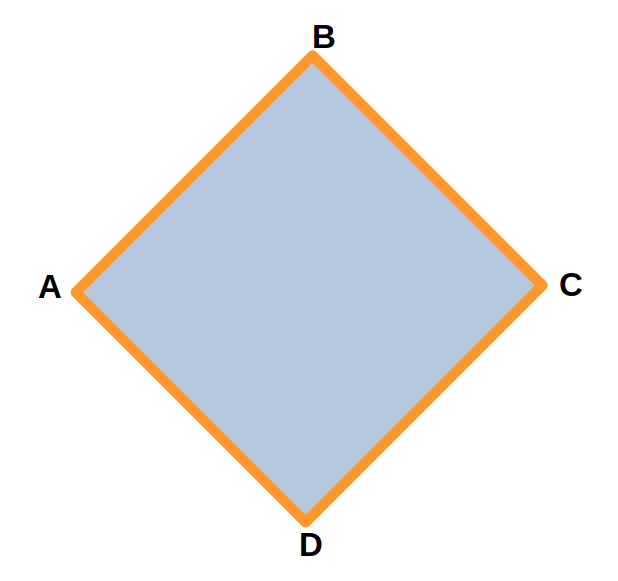
Для четырехугольника ABCD периметр будет равен сумме его сторон: AB + BC + CD + DA.

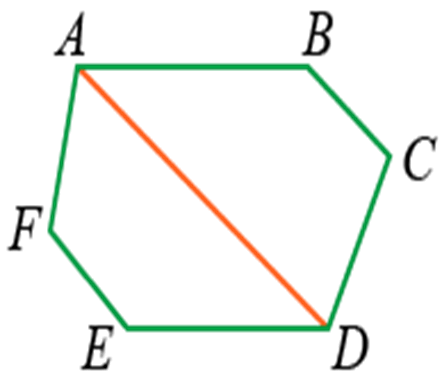
Диагональю многоугольника является отрезок, который соединяет вершины противоположных углов.

Например, отрезок AD будет являться диагональю фигуры ABCDEF:

Свойство треугольников: если треугольник не имеет углов с общими сторонами, диагональ он иметь не может.

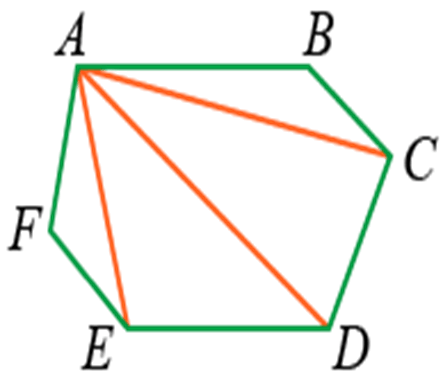
Если из вершин провести несколько диагоналей, то они разделят фигуру на несколько треугольников:

Количество треугольников будет на 2 меньше, чем число сторон:

Если t — количество треугольников, а n — количество сторон, то формула будет выглядеть так: t = n – 2.

Разделение многоугольника диагоналями на несколько треугольников помогает быстро найти площадь.

Чтобы найти площадь многоугольника, нужно разделить его на треугольники, затем найти их площадь и сложить полученные результаты.

Сумма углов выпуклого многоугольника

Научимся находить сумму углов выпуклого четырёхугольника, не только внешних, но и внутренних. Но сначала определим, какие углы называются внутренними углами выпуклого многоугольника.

Внутренним называется угол между смежными сторонами.

Например, ∠ABC является внутренним для ABCDEF.

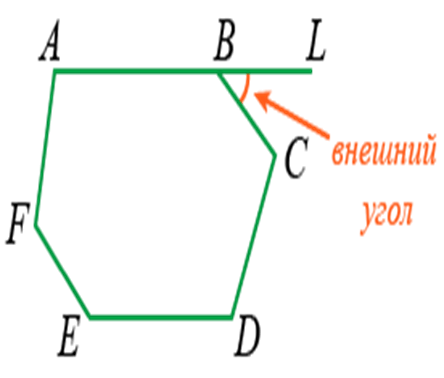
Внешним называют угол между стороной фигуры и линейным продолжением близлежащего отрезка.

Например, ∠LBC является внешним углом для ABCDEF.

Правило: сумма углов выпуклого многоугольника всегда равно числу его сторон. Это определение относится ко всем углам.

Это значит, чтобы найти количество углов, достаточно посчитать количество всех его сторон. Значит сумма углов четырехугольника будет равна четырем.

Сумма внутренних углов

Правило для нахождения суммы углов гласит: чтобы найти сумму всех внутренних углов выпуклого многоугольника, нужно умножить уменьшенное на 2 количество его сторон на 180°.

Обозначения выглядят следующим образом:

• сумма углов – s;
• число сторон – n;
•  два прямых угла (2 · 90 = 180°) – 2d.

Формула многоугольника для нахождения суммы углов: s = 2d · (n – 2).

Найти сумму углов также можно с помощью деления фигуры на треугольники. Она будет равна сумме углов всех треугольников (180° · n).

Пример:

Если у фигуры 4 треугольника, то сумму всех углов находим по следующей формуле: s = 2d (n — 2) = 180 · 4 = 720°.

Это означает, что сумма внутренних углов – это постоянная величина, которая зависит от количества его сторон.

Сумма внешних углов

Определение: Сумму всех внешних углов многоугольника находим по формуле: s = 4d.

Где:

• s — сумма внешних углов;
• 4d — четыре прямых угла (4 · 90 = 360°).

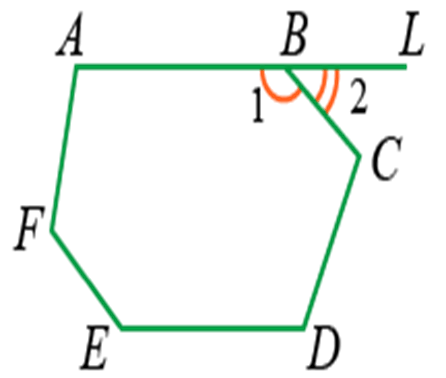
Сумма смежных (внутреннего и внешнего) углов, лежащих при вершине, равна 180° · (2d).

Например, ∠1 и ∠2:

Если имеется n вершин, то сумма внутренних и внешних и углов будет равна 2dn.

Зная основные формулы и определения для многоугольников, можно легко справиться с любой задачей.

Углы многоугольника

• Сумма внутренних углов
• Сумма внешних углов

Внутренний угол многоугольника — это угол, образованный двумя смежными сторонами многоугольника. Например,  ∠ABC  является внутренним углом.

Внешний угол многоугольника — это угол, образованный одной стороной многоугольника и продолжением другой стороны. Например,  ∠LBC  является внешним углом.

Количество углов многоугольника всегда равно количеству его сторон. Это относится и к внутренним углам и к внешним. Несмотря на то, что для каждой вершины многоугольника можно построить два равных внешних угла, из них всегда принимается во внимание только один. Следовательно, чтобы найти количество углов любого многоугольника, надо посчитать количество его сторон.

Сумма внутренних углов

Сумма внутренних углов выпуклого многоугольника равна произведению  180°  и количеству сторон без двух.

s = 2d(n – 2),

где  s  — это сумма углов,  2d  — два прямых угла (то есть  2 · 90 = 180°),  а  n  — количество сторон.

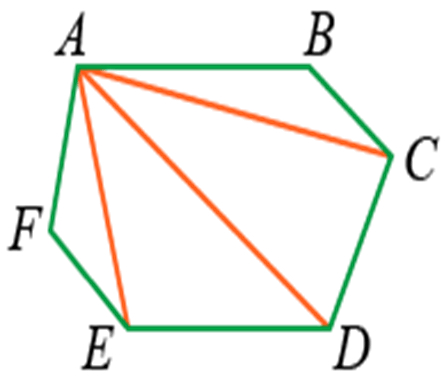
Если мы проведём из вершины  A  многоугольника  ABCDEF  все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:

Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна  180°  (2d),  то сумма углов всех треугольников будет равна произведению  2d  на их количество:

s = 2d(n – 2) = 180 · 4 = 720°.

Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.

Сумма внешних углов

Сумма внешних углов выпуклого многоугольника равна  360°  (или  4d).

s = 4d,

где  s  — это сумма внешних углов,  4d  — четыре прямых угла (то есть 4 · 90 = 360°).

Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна  180°  (2d),  так как они являются смежными углами. Например,  ∠1  и  ∠2:

Следовательно, если многоугольник имеет  n  сторон (и  n  вершин), то сумма внешних и внутренних углов при всех  n  вершинах будет равна  2dn.  Чтобы из этой суммы  2dn  получить только сумму внешних углов, надо из неё вычесть сумму внутренних углов, то есть  2d(n – 2):

s = 2dn – 2d(n – 2) = 2dn – 2dn + 4d = 4d.

Теорема

(о сумме углов выпуклого многоугольника)

Сумма внутренних углов выпуклого многоугольника равна 180º(n-2).

(n — количество сторон многоугольника).

Другой вариант формулировки этой теоремы:

Сумма внутренних углов выпуклого n — угольника равна 180º(n-2).

Дано:

   

—  выпуклый n -угольник.

Доказать:

   

   

Доказательство:

1-й способ

Обозначим внутри многоугольника произвольную точку O.

Соединим точку O с вершинами многоугольника.

Получили n треугольников.

   

   

   

Сумма внутренних углов многоугольника равна сумме углов всех треугольников без углов при вершине O.

Так как сумма углов при вершине O составляет 360º

   

то сумма углов многоугольника равна сумме углов n треугольников минус 360º.

Сумма углов каждого треугольника равна 180º.

Таким образом, искомая сумма углов n угольника равна

   

   

Что и требовалось доказать.

2-й способ

Соединим вершину A1 со всеми остальными вершинами многоугольника. Получили n-2 треугольника.

Сумма всех углов этих треугольников равна сумме углов многоугольника.

Сумма углов углов каждого из треугольников равна 180º.

Следовательно, сумма углов многоугольника

   

   

Что и требовалось доказать.

Цель: Вывести формулу для нахождения суммы углов выпуклого
многоугольника;

• исследовать вопрос о сумме внешних углов многоугольника, взятых по
  одному при каждой вершине;
• формировать положительную мотивацию к познавательной деятельности ;
• развивать логическое мышление ;
• развивать внимание, наблюдательность, умение анализировать чертеж;
• формировать умение применять полученные знания для решения задач;
• развивать коммуникативную культуру учащихся.

Ход урока

Великий русский ученый, гордость Земли Русской,

Михайло Васильевич Ломоносов, сказал: “ Неусыпный труд препятствия
преодолевает”. Я надеюсь, что сегодня на уроке наш с вами труд поможет нам
преодолеть все препятствия.

1. Актуализация опорных знаний. (Фронтальный опрос.)

Презентация. (Слайды 2–4)

– Сформулируйте определение многоугольника, назовите его основные элементы.
– Определение выпуклого многоугольника.
– Приведите примеры известных вам четырехугольников, которые являются выпуклыми
многоугольниками.
– Можно ли треугольник считать выпуклым многоугольником?
– Что такое внешний угол выпуклого многоугольника?

2. Постановка проблемы (выход на тему урока).

Устная фронтальная работа.

Найдите сумму углов данных многоугольников (Слайды 5–6)

– треугольника; прямоугольника:
– трапеции; произвольного семиугольника.

В случае затруднения учитель задает вопросы:

– Сформулируйте определение трапеции.
– Назовите основания трапеции.
– Что можно сказать о паре углов А и Д, каким свойством они обладают?
– Можно ли еще назвать на чертеже пару внутренних односторонних улов?
– Смогли вы найти сумму углов семиугольника? Какой возникает вопрос? (Существует
ли формула для нахождения суммы углов произвольного многоугольника?)

Итак, ясно, что наших знаний на сегодня не достаточно для решения этой
задачи.

Каким образом можно сформулировать тему нашего урока? – Сумма углов
выпуклого многоугольника.

3. Решение проблемы. Чтобы ответить на поставленный вопрос,
давайте проведем небольшое исследование.

Мы уже знаем теорему о сумме углов треугольника. Можем ли мы ее каким либо
образом применить?

– Что для этого надо сделать? (Разбить многоугольник на треугольники.)

– А каким образом многоугольник можно разбить на треугольники? Подумайте над
этим, обсудите и предложите свои самые удачные варианты.

Идет работа в группах, каждая группа работает за отдельным компьютером, на
котором установлена программа “Geo
Gebra”.

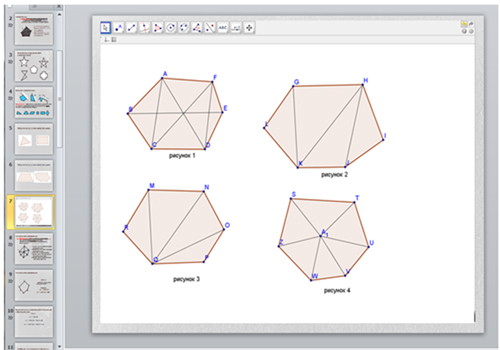
По окончании работы учитель выводит на экран результаты работы групп.
(Слайд 7)

– Давайте проанализируем предложенные варианты и попробуем выбрать самый
оптимальный для нашего исследования.

Определимся с критериями отбора: что мы хотим получить в результате
разбиения? (Сумма всех углов построенных треугольников должна быть равна сумме
углов многоугольника.)

– Какие варианты можно сразу отбросить? Почему?

(Вариант 1, так как сумма углов всех треугольников не равна сумме углов
многоугольника.)

– Какой вариант годиться больше всего? Почему? (Вариант 3.)

Как получили этот вариант? (Провели диагонали из одной вершины многоугольника

чертеж	n – количество вершин многоугольника	Количество диагоналей, проведенных из одной вершины	Количество полученных треугольников
	4
	5
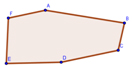	6
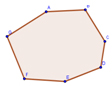	7
	n

– Попробуем установить зависимость между количеством вершин многоугольника,
количеством диагоналей, которые можно провести из одной вершины и количеством
получаемых при этом треугольников.

Каждая группа получает таблицу, которую должны заполнить в процессе
исследования.

После обсуждения в группах дети формулируют полученные выводы:
из одной вершины n-угольника можно
провести n – 3 диагонали, (так как
диагональ нельзя провести к самой выбранной вершине и к двум соседним). При этом
получим n – 2 треугольника.

Следовательно, сумма углов выпуклого многоугольника равна 180⁰(n-2).

– Вернемся к предложенным вариантам разбиения многоугольника на треугольники.

Можно ли использовать для доказательства этой теоремы вариант, предложенный
на рисунке 4?

– Сколько треугольников получается при таком разбиении? (п штук)
– На сколько отличается сумма углов всех треугольников от суммы углов
многоугольника? (На 360⁰)
– Каким образом можно сосчитать сумму углов многоугольника в этом случае?

(180п – 360 = 180 п – 180х2 = 180(п -2) )(Слайд
8)

– Удовлетворяет ли главному требованию, которое мы предъявляли к разбиению,
вариант, предложенный на рисунке 2? (Да.)

– Почему не целесообразно его использование для нахождения суммы углов
многоугольника? (Тяжелее подсчитать количество получаемых треугольников.)

Ну а теперь вернемся к задаче, которую мы не смогли решить вначале урока.

(Дети устно считают сумму углов семиугольника и еще два аналогичных
упражнения.) (Слайд 9 и 10)

4. Применение полученных знаний.

Мы вывели формулу для нахождения суммы внутренних углов выпуклого
многоугольника. А теперь поговорим о сумме внешних углов многоугольника, взятых
по одной при каждой вершине.

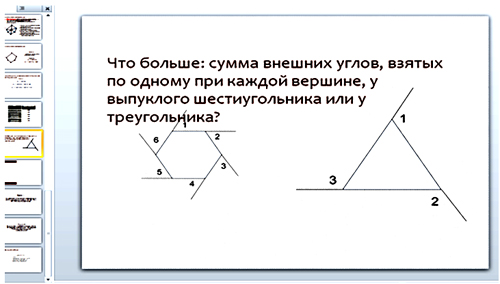
Итак, задача: что больше: сумма внешних углов, взятых по одному при каждой
вершине, у выпуклого шестиугольника или у треугольника? (Слайд 11)

Дети высказывают свои предположения. Учитель предлагает провести исследование
для решения этого вопроса.

Каждая группа получает задание для самостоятельного решения.

Группа 1.

1) Найдите сумму внешних углов, взятых по одному при каждой вершине, у
правильного треугольника.
2) – У треугольника, градусные величины углов которого равны соответственно
70⁰, 80⁰ и 30⁰.

Группа 2.

1) Найдите сумму внешних углов, взятых по одному при каждой
вершине, у прямоугольника.
2) – У четырехугольника, внутренние углы которого равны соответственно 70⁰,
80⁰ и 120⁰ и 90⁰.

Группа 3.

1) Найдите сумму внешних углов, взятых по одному при каждой
вершине, у правильного шестиугольника.
2) – У шестиугольника, внутренние углы которого равны соответственно 170⁰,
80⁰ и 130⁰ , 100⁰ , 70⁰,
170^0.

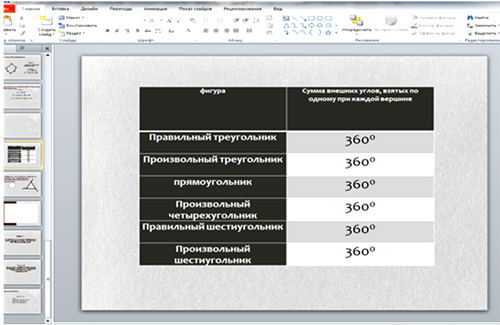
После окончания работы дети сообщают свои результаты, учитель заносит их в
таблицу и демонстрирует на экране. (Слайд 12)

Итак, какой вывод можно сделать из полученных результатов? (Сумма внешних
углов, взятых по одному при каждой вершине, у любого многоугольника равна 360^0.)

А теперь давайте попробуем доказать этот факт для любого н-угольника.

Если возникают трудности, коллективно обсуждается план доказательства:

1. Обозначить внутренние углы многоугольника через
α, β, γ и т.д.
2. Выразить через введенные обозначения градусные меры внешних углов
3. Составить выражение для нахождения суммы внешних углов многоугольника
4. Преобразовать полученное выражение, использовать полученную ранее формулу для
суммы внутренних углов многоугольника.

Доказательство записывается на доске:

(180 – α) + (180 – β) + (180 – γ) + …=
180 п – (α+ β +γ + …) = 180 п – 180(п – 2) =
360

Далее демонстрируется видео: как можно проиллюстрировать этот факт с помощью
картонной модели. (Слайд 13)

5. Закрепление изученного материала. Решение задач.

Задача 1. Существует ли выпуклый многоугольник с такими внутренними
углами: 45⁰, 68⁰, 73⁰ и 56⁰?
Объясните свой ответ.

Решение.

Проведем доказательство от противного. Если у выпуклого многоугольника четыре
острых внутренних угла то среди его внешних углов четырех тупых, откуда следует,
что сумма всех внешних углов многоугольника больше 4*90⁰ = 360⁰.
Имеем противоречие. Утверждение доказано.

Задача 2.

В выпуклом многоугольнике три угла по 80 градусов, а остальные – 150
градусов. Сколько углов в выпуклом многоугольнике?

Решение.

Так как: для выпуклого n-угольника сумма углов равна 180°(n – 2),
то 180(n – 2)=3*80 + x*150, где 3 угла по 80 градусов нам даны по условию
задачи, а количество остальных углов нам пока неизвестно, значит, обозначим их
количество через x.

Однако из записи в левой части мы определили количество углов многоугольника
как n, поскольку из них величины трех углов мы знаем по условию задачи, то
очевидно, что x=n-3.

Таким образом, уравнение будет выглядеть так: 180(n – 2) = 240 + 150(n – 3)

Решаем полученное уравнение

180n – 360 = 240 + 150n – 450

180n – 150n = 240 + 360 – 450

30n = 150

n = 5

Ответ: 5 вершин.

6. Подведение итогов урока.

Итак, давайте подведем итоги. Сформулируйте свои вопросы для ребят из
другой группы по материалам сегодняшнего урока.

Какой вопрос вы считаете наиболее удачным?

Обсудите степень участия каждого члена группы в коллективной работе, назовите
самых активных.

Чья работа в группе была самой результативной?

7. Домашнее задание:

1. Задача.

В многоугольнике три угла по 113 градусов, а остальные равны между собой и их
градусная мера – целое число. Найти количество вершин многоугольника.

2. п.114 стр.169–171, Погорелов А.В. “Геометрия 7–9”.