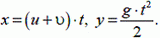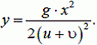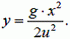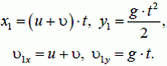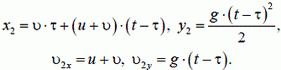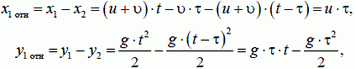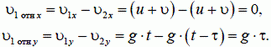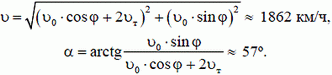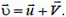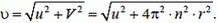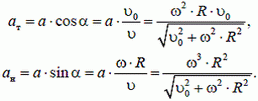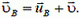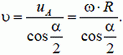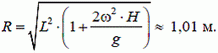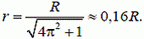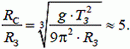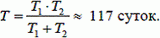Любое движение тела происходит по отношению к другим телам. Физики говорят: «Относительно других тел».
К примеру, человек, едущий в автобусе, относительно автобуса находится в состоянии покоя, а относительно дороги – движется.
Примечание: Когда мы рассматриваем движение тела, мы выбираем систему отсчета, в которой это дело будет двигаться. При этом, тело отсчета мы принимаем за неподвижное тело, относительно которого происходит движение изучаемого тела.
Такие характеристики движения, как:
- перемещение тела;
- траектория, вдоль которой тело двигалось;
- скорость тела;
- ускорение тела;
в разных системах отсчета (СО) будут различаться.
Траектория тела различна в разных системах отсчета
Траектория – это относительная характеристика движения. Потому, что она различается для разных систем отсчета (СО).
В то время, пока самолет летит, точка, лежащая на кончике его винта, относительно самолета движется по окружности (рис. 1), а относительно неподвижного наблюдателя на земле – эта же точка имеет винтовую траекторию.
Рис.1. Траектория кончика винта летящего самолета относительно пилота является окружностью, а относительно поверхности земли – винтовой линией
Например, движение ниппеля велосипедного колеса во время поездки на велосипеде.
В системе отсчета, связанной с:
- велосипедом, траектория ниппеля – это окружность.
- поверхностью земли, траектория ниппеля – это циклоида.
Что такое циклоида
Циклоида – это плоская кривая линия. По такой линии движется точка, лежащая на окружности, когда эта окружность катится по прямой без проскальзывания (рис. 2).
Рис. 2. Когда окружность катится по прямой, точка, лежащая на окружности, описывает циклоиду
Циклоиду называют трансцендентной кривой линией.
Линия трансцендентная, если ее в прямоугольных координатах не получается описать с помощью алгебраического уравнения.
Но с помощью параметра t можно записать отдельно координату x и координату y с помощью таких уравнений:
[ large begin{cases} x = r cdot t — r cdot sin(t) \ y = r — r cdot cos(t) end{cases} ]
Примечания:
- Окружность, которая катится – называется производящей.
- Прямая, по которой катится окружность – направляющая прямая.
- Точки пересечения циклоиды и направляющей прямой – это точки возврата.
- Самые высокие точки на циклоиде, располагающиеся между соседними точками возврата – это вершины циклоиды.
Циклоиду впервые изучил Галилео Галилей. Этот выдающийся итальянский ученый занимался физикой, математикой, астрономией, механикой и философией.
А английский математик и архитектор Кристофер Рен в 1658 году посчитал длину арки циклоиды.
Длина циклоиды равна четырем диаметрам производящей окружности.
Кристофер Рен спроектировал и руководил возведением в Лондоне купола собора Святого Павла.
С помощью циклоиды братья Бернулли решили задачу о скорейшем спуске — брахистохроне. Брахистохрон – с греч. «Краткое время». Они доказали, что по желобу, имеющему форму перевернутой вниз циклоиды шарик скатывается вниз за кратчайшее из возможных время.
Скорость тела различна в разных системах отсчета
Рассмотрим движение человека в едущем по прямому участку пути трамвае (рис. 3).
Рис. 3. Скорость человека относительно трамвая равна 3 километра в час, а относительно земли – 63 километра в час
Скорость трамвая (large vec{v_{text{Трам}}}) 60 километров в час. Предположим, в движущемся вагоне трамвая человек перемещается от задней части трамвая к его передней части, со скоростью (large vec{v_{text{Чел}}}) 3 километра в час.
Тогда скорость человека относительно трамвая будет равна 3 километрам в час, а относительно земли – 63 километрам в час.
[ large begin{cases} overrightarrow{v_{text{относит земли}}} = overrightarrow {v_{text{Трам}}} + overrightarrow {v_{text{Чел}}} \ overrightarrow {v_{text{ относит трам}}} = overrightarrow {v_{text{Чел}}} end{cases} ]
Как переходить из одной системы отсчета в другую
Любое движение, которое мы рассматриваем, а, так же, его характеристики, будут различаться в разных системах отсчета.
Относительно одних тел рассматриваемое тело может покоиться, а вместе с тем, относительно других тел оно может находиться в движении.
Чтобы осуществить переход между системами отсчета, нужно применять закон сложения скоростей и перемещений. Скорость и перемещение – это векторы. Значит, будем складывать их геометрически. То есть, при сложении векторов будем учитывать их направления.
Примечание: Ньютон изучал движение тел. В его теории время протекает одинаково во всех системах отсчета. То есть, в механике Ньютона время – это абсолютная величина.
Представим себе такую картину: На берегу реки сидит и отдыхает девушка (рис. 4). По реке мимо нее проплывает плот (по течению). С плота в это время в воду прыгает молодой человек и вплавь добирается к противоположному берегу реки. После чего, садится на берег и отдыхает.
Рис. 4. Чтобы найти скорость пловца относительно неподвижного наблюдателя, нужно сложить вектор скорости реки и вектор собственной скорости пловца
Перемещение в различных системах отсчета
Сначала запишем перемещение парня в системе отсчета, связанной с девушкой, когда нам известны его перемещение в системе отсчета, связанной с плотом.
Примечание:
- Относительно девушки – значит, в системе отсчета, связанной с девушкой.
- Относительно плота – значит, в системе отсчета, связанной с плотом.
На рисунке перемещение плота и перемещение парня относительно плота обозначены длинными черными стрелками. А перемещение парня относительно сидящей на берегу девушки обозначено длинной синей стрелкой.
Из рисунка видно, что векторы перемещений образуют прямоугольный треугольник.
Сложив вектор переносного и относительного перемещений, получим вектор абсолютного перемещения:
[ large boxed{ overrightarrow{S_{text{абсол}}} = overrightarrow{S_{text{перенос}}} + overrightarrow{S_{text{отн}}} }]
( large overrightarrow{S_{text{перенос}}} ) – вектор перемещения плота;
( large overrightarrow{S_{text{отн}}} ) – вектор перемещения парня относительно плота (собственное перемещение парня);
( large overrightarrow{S_{text{абсол}}} ) – вектор перемещения парня относительно девушки на берегу;
Длину вектора абсолютного перемещения можно найти по теореме Пифагора:
[ large boxed{ left| overrightarrow{S_{text{абсол}}} right| = sqrt{ left(S_{text{перенос}} right)^{2} + left(S_{text{отн}}right) ^{2}} } ]
Скорость в различных системах отсчета
Запишем еще раз формулу для связи перемещений:
[ large overrightarrow{S_{text{абсол}}} = overrightarrow{S_{text{перенос}}} + overrightarrow{S_{text{отн}}} ]
Зная перемещение, и время равномерного движения, можно найти модуль вектора скорости, т. е. длину вектора скорости.
Скорость плывущего плота и скорость парня не изменяются. Поэтому, для связи скорости и перемещения можно применить формулу
[ large S = v cdot t ]
Разделив обе части этого уравнения на время t, получим выражение для скорости равномерного движения:
[ large frac{S}{t} = v ]
Обе части уравнения для перемещений разделим на время t движения.
[ large frac{overrightarrow{S_{text{абсол}}}}{t} = frac{overrightarrow{S_{text{перенос}}}}{t} + frac{overrightarrow{S_{text{отн}}}}{t}]
Полученное выражение можно записать с помощью векторов скоростей:
[ large boxed{ overrightarrow{v_{text{абсол}}} = overrightarrow{v_{text{перенос}}} + overrightarrow{v_{text{отн}}} }]
В частности, на рисунке 4 красными векторами обозначены скорость реки (плота) и скорость парня.
Опишем обозначения, использованные нами в уравнении, связывающем скорости в различных системах отсчета:
( large overrightarrow{v_{text{отн}}} = overrightarrow{v_{text{чел}}} ) – вектор скорости парня;
( large overrightarrow{v_{text{перенос}}} = overrightarrow{v_{text{плота}}} ) – вектор скорости плота (течения реки);
( large overrightarrow{v_{text{абсол}}} ) – вектор скорости парня относительно девушки;
Длину вектора скорости найдем по теореме Пифагора:
[ large boxed{ left| overrightarrow{v_{text{абсол}}} right| = sqrt{ left( v_{text{перенос}}right)^{2} + left(v_{text{отн}}right) ^{2} } }]
Таким образом, до прыжка в воду скорость парня в системе отсчета, связанной с плотом, равнялась нулю (рис. 5).
А в системе отсчета, связанной с отдыхающей на берегу девушкой, скорость парня равнялась скорости течения реки (скорости плота).
Рис. 5. Скорость пловца зависит от выбора системы отсчета, так как в различных системах отсчета скорости будут разными
После прыжка с плота в системе отсчета, связанной с плотом, скорость парня равняется скорости, с которой он плывет к берегу перпендикулярно течению реки.
Ну а в системе отсчета, связанной с девушкой, скорость парня – это векторная сумма скорости течения реки и скорости плавания парня.
Выводы
- Перемещение тела и траектория, вдоль которой тело двигалось, скорость и ускорение тела в разных системах отсчета (СО) будут различаться. В этом заключается относительность движения.
- Перемещение и скорость – это векторы. Поэтому, при переходе из одной системы отсчета в другую, нужно складывать, или вычитать векторы скоростей и перемещений.
- Векторы складываем и вычитаем с помощью геометрии.
- Переносная скорость – это скорость движущейся системы отсчета;
- Относительная скорость – это скорость тела по отношению к движущейся системе отсчета (движущемуся телу отсчета);
- Абсолютная скорость – скорость тела в неподвижной системе отсчета;
- Каждая система отсчета связана со своим телом отсчета.
Человек массой 50 кг прыгает с неподвижной тележки массой 100 кг с горизонтальной скоростью 3 м/с относительно тележки. Какова скорость тележки относительно Земли после прыжка человека? (Ответ дайте в метрах в секунду.)
Спрятать решение
Решение.
Поскольку на систему человек — тележка в горизонтальном направлении не действует никаких сил, для нее в этом направлении выполняется закон сохранения импульса. В системе отсчета, связанной с Землей, в проекции на горизонтальную ось имеем:
Отсюда находим скорость тележки относительно Земли
Ответ: 1.
Какова скорость человека относительно земли?!
Токсик
Знаток
(258),
закрыт
14 лет назад
Какова скорость человека который находится в движущемся объекте (машина, поезд, мотоцикл) по отношению к земле?! И в момент “спрыгивания” на ходу, какова будет скорость человека относительно земли?! Хотелось бы узнать есть ли научные ссылки в интернете?! Мне именно нужно как это выглядит научно и по каким законам физики регулируется. Спасибо за ответ
Дополнен 14 лет назад
Интересует именно теория – как она звучит? Какой закон? И… В какую сторону будет продолжать движение тело человека после того как отделиться от движущегося объекта..?
From Wikipedia, the free encyclopedia
The relative velocity 


Classical mechanics[edit]
In one dimension (non-relativistic)[edit]
Relative motion man on train
We begin with relative motion in the classical, (or non-relativistic, or the Newtonian approximation) that all speeds are much less than the speed of light. This limit is associated with the Galilean transformation. The figure shows a man on top of a train, at the back edge. At 1:00 pm he begins to walk forward at a walking speed of 10 km/h (kilometers per hour). The train is moving at 40 km/h. The figure depicts the man and train at two different times: first, when the journey began, and also one hour later at 2:00 pm. The figure suggests that the man is 50 km from the starting point after having traveled (by walking and by train) for one hour. This, by definition, is 50 km/h, which suggests that the prescription for calculating relative velocity in this fashion is to add the two velocities.
The diagram displays clocks and rulers to remind the reader that while the logic behind this calculation seem flawless, it makes false assumptions about how clocks and rulers behave. (See The train-and-platform thought experiment.) To recognize that this classical model of relative motion violates special relativity, we generalize the example into an equation:
where:
is the velocity of the Man relative to Earth,
is the velocity of the Man relative to the Train,
is the velocity of the Train relative to Earth.
Fully legitimate expressions for “the velocity of A relative to B” include “the velocity of A with respect to B” and “the velocity of A in the coordinate system where B is always at rest”. The violation of special relativity occurs because this equation for relative velocity falsely predicts that different observers will measure different speeds when observing the motion of light. [note 1]
In two dimensions (non-relativistic)[edit]
Relative velocities between two particles in classical mechanics
The figure shows two objects A and B moving at constant velocity. The equations of motion are:
where the subscript i refers to the initial displacement (at time t equal to zero). The difference between the two displacement vectors, 
Hence:
After making the substitutions 

Galilean transformation (non-relativistic)[edit]
To construct a theory of relative motion consistent with the theory of special relativity, we must adopt a different convention. Continuing to work in the (non-relativistic) Newtonian limit we begin with a Galilean transformation in one dimension:[note 2]
where x’ is the position as seen by a reference frame that is moving at speed, v, in the “unprimed” (x) reference frame.[note 3] Taking the differential of the first of the two equations above, we have, 

To recover the previous expressions for relative velocity, we assume that particle A is following the path defined by dx/dt in the unprimed reference (and hence dx′/dt′ in the primed frame). Thus 




where the latter form has the desired (easily learned) symmetry.
Special relativity[edit]
As in classical mechanics, in Special Relativity the relative velocity 
This peculiar lack of symmetry is related to Thomas precession and the fact that two successive Lorentz transformations rotate the coordinate system. This rotation has no effect on the magnitude of a vector, and hence relative speed is symmetrical.
Parallel velocities[edit]
In the case where two objects are traveling in parallel directions, the relativistic formula for relative velocity is similar in form to the formula for addition of relativistic velocities.
The relative speed is given by the formula:
Perpendicular velocities[edit]
In the case where two objects are traveling in perpendicular directions, the relativistic relative velocity 
where
The relative speed is given by the formula
General case[edit]
The general formula for the relative velocity 
where
The relative speed is given by the formula
See also[edit]
- Doppler effect
- Non-Euclidean geometry § Kinematic geometries
- Peculiar velocity
- Proper motion
- Range rate
- Radial velocity
- Rapidity
- Relativistic speed
- Space velocity (astronomy)
Notes[edit]
- ^ For example, replace the “Man” by a photon traveling at the speed of light.
- ^ This result is valid if all motion is restricted to the x-axis, but can be easily generalized by replacing the first equation by
- ^ It is easy to be confused about the minus sign before v, or whether v is defined in the prime or unprimed reference frame. It might help to visualize the fact that if x = vt, then x′ = 0, meaning that a particle that is following the path x = vt is at rest in the primed reference frame.
- ^ Keep in mind that, due to time dilation, dt = dt′ is valid only in the approximation that the speed is much less than that of light.
References[edit]
- ^ Fock 1964 The theory of Space Time and Gravitation, retrieved from https://archive.org/details/TheTheoryOfSpaceTimeGravitation
Further reading[edit]
- Alonso & Finn, Fundamental University Physics ISBN 0-201-56518-8
- Greenwood, Donald T, Principles of Dynamics.
- Goodman and Warner, Dynamics.
- Beer and Johnston, Statics and Dynamics.
- McGraw Hill Dictionary of Physics and Mathematics.
- Rindler, W., Essential Relativity.
- KHURMI R.S., Mechanics, Engineering Mechanics, Statics, Dynamics
External links[edit]
- Relative Motion at HyperPhysics
- A Java applet illustrating Relative Velocity, by Andrew Duffy
- Relatív mozgás (1)…(3) Relative motion of two train (1)…(3). Videos on the portal FizKapu. (in Hungarian)
- Sebességek összegzése Relative tranquility of trout in creek. Video on the portal FizKapu. (in Hungarian)
Данилин В. Кинематика. Относительность движения //Квант. — 1982. — № 10. — С. 48-51.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Раздел механики, в котором движения описываются без исследования причин, их вызывающих, называется кинематикой. Основная задача кинематики заключается в том, чтобы, зная три кинематические величины: перемещение, скорость и ускорение, найти положение тела в любой момент времени.
Всякое движение относительно, поэтому для его описания можно использовать различные системы отсчета. Все они кинематически равноправны, то есть принципиально позволяют решить ту или иную задачу. Трудно дать какие-либо общие рекомендации по выбору системы отсчета, поскольку он определяется, в основном, конкретными условиями данной задачи. В большинстве случаев следует выбирать ту систему, которая наиболее естественна и в которой решение задачи имеет наиболее простой вид. Например, при рассмотрении движения искусственного спутника Земли с точки зрения земного наблюдателя систему отсчета естественно связать с Землей. При анализе движений различных тел внутри спутника с точки зрения космонавта систему отсчета разумно связать с самим спутником, а с точки зрения земного наблюдателя — опять-таки с Землей.
Иногда приходится переходить от одной системы отсчета к другой. В разных системах описания движения могут выглядеть по-разному: могут различаться траектории движения, перемещения, скорости и ускорения тела. Однако при заданных связях между различными системами отсчета описания одного и того же движения всегда можно связать друг с другом.
А теперь поясним сказанное на конкретных задачах. Большинство из них предлагалось на вступительных экзаменах в Московский физико-технический институт.
Задача 1. Два снаряда выпущены горизонтально вперед один вслед за другим с интервалом времени t со скоростью u из орудия, находящегося на самолете, который летит горизонтально со скоростью υ. Пренебрегая сопротивлением воздуха, найдите: 1) уравнение траектории первого снаряда относительно земли; 2) уравнение траектории первого снаряда относительно самолета; 3) как изменяется положение первого снаряда относительно второго (после обоих выстрелов).
В данном случае выбор системы отсчета фактически определен условием задачи.
Направим оси координат следующим образом: ось X — горизонтально, параллельно курсу самолета, ось Y — вертикально вниз. Начало же системы координат каждый раз будем указывать отдельно.
1) Поместим начало координат в точку, в которой находился самолет в момент вылета первого снаряда (разумеется, и самолет, и снаряд считаются материальными точками). Относительно этой неподвижной системы отсчета начальная (горизонтальная) скорость снаряда равна сумме скоростей снаряда относительно самолета и самого самолета, то есть 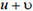
Тогда горизонтальная и вертикальная координаты снаряда в любой момент времени t таковы:
Выражая t из первого равенства и подставляя во второе, получим уравнение траектории снаряда относительно земли:
Это безусловно знакомое всем уравнение параболы. Заметим, что уравнение траектории второго снаряда относительно земли будет точно таким же.
2) В этом случае начало системы отсчета надо связать с самолетом. Относительно него начальная скорость снаряда равна u, поэтому горизонтальная координата снаряда будет изменяться по закону 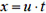
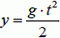
Очевидно, что и здесь траектория движения снаряда — парабола.
3) Для того чтобы описать движение первого снаряда относительно второго, воспользуемся той же системой отсчета, что и для первого случая, то есть поместим начало координат в ту точку, где находился самолет в момент первого выстрела.
Запишем уравнения для координат хi и уi первого снаряда и для соответствующих проекций υ1x и υ1y его скорости:
Здесь время t отсчитывается от момента первого выстрела, но по смыслу задачи оно не меньше интервала τ между выстрелами, то есть 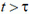
Если наблюдатель связан со вторым снарядом, то относительно него координаты (или проекции скорости) первого снаряда равны разности соответствующих координат (или соответствующих проекций скоростей) первого и второго снарядов в неподвижной системе отсчета:
Итак, после обоих выстрелов снаряды по горизонтали движутся с одинаковыми скоростями, так что расстояние между ними не изменяется и остается равным 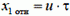
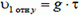
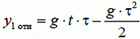
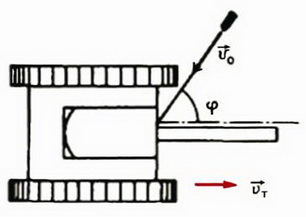
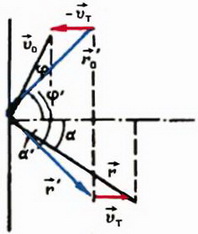
Задача 2. В лобовой щит танка, движущегося со скоростью υт = 54 км/ч, ударяется пуля, летящая со скоростью υ0 = 1800 км/ч под углом φ = 60° к направлению движения танка, и упруго отскакивает от него (рис. 1, а). С какой скоростью 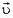
а
б
Рис. 1.
Задачу удобно сначала решить в системе отсчета, связанной с танком, а затем перейти в неподвижную систему отсчета.
Относительно танка скорость пули до удара равна 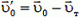
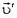
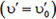
В неподвижной системе отсчета пуля после удара будет двигаться со скоростью
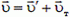
Модуль и направление этой скорости найдем из рисунка 1, б:
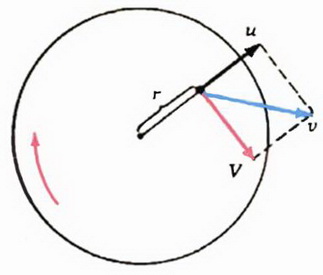
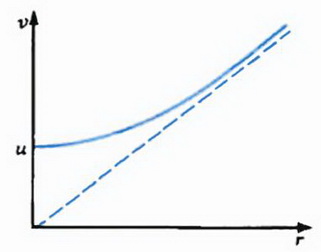
Задача 3. Горизонтальный диск вращается вокруг своей оси, делая п = 5 об/мин. Человек идет вдоль радиуса диска с постоянной скоростью и = 1,5 м/с относительно диска. Как меняется модуль скорости человека относительно земли в зависимости от расстояния r от оси диска? Чему равен модуль этой скорости на расстоянии R = 3 м от оси диска?
а
б
Рис. 2.
В любой точке диска скорость 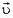
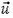
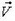
Поскольку модуль V линейной скорости связан с угловой скоростью ω, а значит, и с частотой п вращения диска: 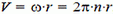
Графически зависимость υ от r представлена на рисунке 2, б.
На расстоянии R от оси диска модуль искомой скорости равен
Задача 4. Колесо радиуса R движется по земле поступательно со скоростью υ0 и вращается с угловой скоростью ω (рис. 3). Найдите тангенциальную и нормальную проекции ускорения некоторой точки А на ободе колеса в неподвижной системе отсчета, связанной с землей.
Напомним, что тангенциальная (касательная) проекция ат ускорения 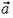
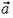
Сначала рассмотрим движение точки А в системе отсчета, связанной с колесом. Здесь эта точка равномерно вращается по окружности радиуса R, так что скорость изменяется только по направлению. Ускорение точки направлено по радиусу к центру колеса и равно по модулю 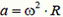
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
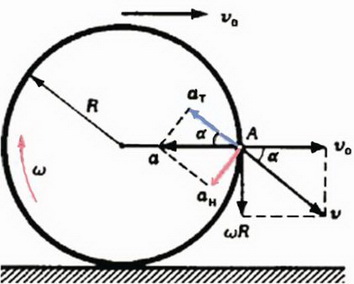
Рис. 3.
Рассмотрим точку А в некоторый момент времени (см. рис. 3). Ее скорость 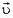

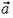
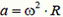
Задача 5*. Тяжелый диск радиуса R скатывается на двух нерастяжимых нитях, намотанных на него (рис. 4). Концы нитей закреплены. Нити при движении диска постоянно натянуты. В некоторый момент угловая скорость диска равна ω, а угол между нитями α. Какова в этот момент скорость центра диска?
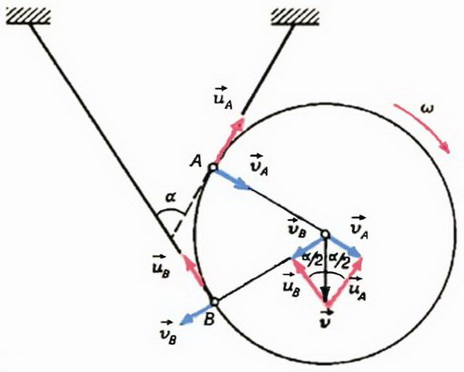
Рис. 4
Выберем две системы отсчета: неподвижную, связанную, например, с землей, и подвижную, связанную с центром диска. Таким образом, задача сводится к тому, чтобы найти скорость подвижной системы отсчета относительно неподвижной.
Пусть в данный момент нити касаются диска в точках А и В. В подвижной системе отсчета (связанной с центром диска) скорости 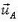
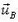
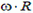
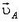
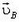
Обозначим скорость центра диска (скорость подвижной системы отсчета), направленную вертикально вниз, через 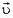
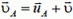
Как видно из рисунка, при сложении соответствующих векторов получаются равные прямоугольные треугольники, из которых
Упражнения
1. Изогнутая трубка длины L = 1 м вращается вокруг вертикальной оси ОО’ с угловой скоростью ω = 0,1 рад/с (рис. 5). Открытый конец трубки направлен вертикально вниз, и из него вытекает вода практически без начальной скорости относительно трубки. На расстоянии Н = 10 м ниже отверстия расположена горизонтальная плоскость. Найдите радиус окружности, которую опишет след струи воды на этой плоскости.
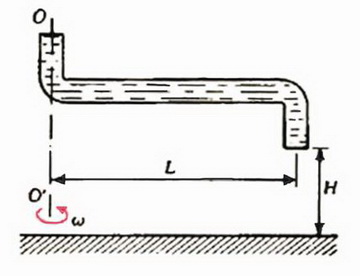
Рис. 5.
2. Гладкий диск радиуса R, плоскость которого горизонтальна, вращается вокруг своей оси. От поверхности диска отрывается небольшое тело, которое без трения скользит по диску. На каком расстоянии от оси оторвалось тело, если за время, пока оно соскользнуло с диска, диск сделал полный оборот?
3. Искусственный спутник Земли запущен с экватора и вращается по круговой орбите в плоскости экватора в направлении вращения Земли. Найдите отношение радиуса орбиты спутника к радиусу Земли, при котором спутник периодически проходит над точкой запуска ровно через двое суток.
4. Как показали радиолокационные измерения, Венера вращается вокруг своей оси в направлении, противоположном ее орбитальному движению. Период осевого вращения Венеры (относительно звезд) Т1 = 243 земных суток. Определите продолжительность солнечных суток на Венере, то есть время Т между двумя последовательными прохождениями Солнца через один и тот же меридиан на этой планете (время от полудня до полудня). Венера обращается вокруг Солнца с периодом Т2 = 225 земных суток.
5. Тяжелый шар радиуса R лежит на горизонтальной плоскости, а в верхней точке шара покоится малое тело. По шару наносят удар, и он начинает двигаться со скоростью υ. На какую высоту подпрыгнет тело после упругого отскока от плоскости? Трением и сопротивлением воздуха пренебречь.
Ответы.
1.
2.
3. 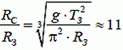
4.
5. 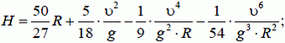
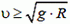




























![{displaystyle {vec {v}}_{mathrm {B|A} }={frac {1}{gamma _{mathrm {A} }left(1-{frac {{vec {v}}_{mathrm {A} }{vec {v}}_{mathrm {B} }}{c^{2}}}right)}}left[{vec {v}}_{mathrm {B} }-{vec {v}}_{mathrm {A} }+{vec {v}}_{mathrm {A} }(gamma _{mathrm {A} }-1)left({frac {{vec {v}}_{mathrm {A} }cdot {vec {v}}_{mathrm {B} }}{v_{mathrm {A} }^{2}}}-1right)right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df4dfe757c619047b27a74f71b219a91abc01113)