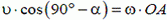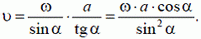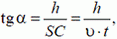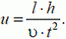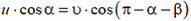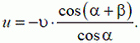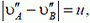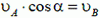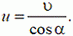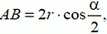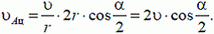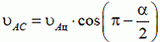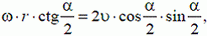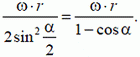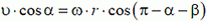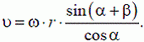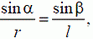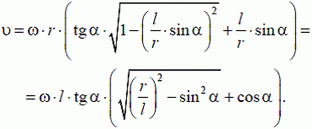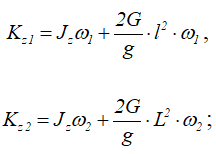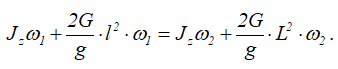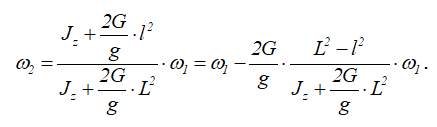Решение с формулами пожалуйста. Угловая скорость стержня? Длинна стержня?
Кул Док
Ученик
(174),
на голосовании
7 лет назад
1)Стержень длиной L=40 см вращается с угловой скоростью вокруг неподвижной оси, проходящей через некоторую точку стержня и перпендикулярной к нему. Если один конец стержня движется со скоростью v = 1,6 м/с, другой со скоростью 3,2 м/с, то угловая скорость стержня равна?
2)Та же самая задача только дано: угловая скорость=8 рад/сек ; один конец v = 0.8 м/с, другой v = 4 м/с. Длинна стержня равна?
Голосование за лучший ответ
ВК
Просветленный
(32923)
7 лет назад
1) w=V1/(L-x)=V2/x
отсюда находится x, потом w
2) аналогично
Кул ДокУченик (174)
7 лет назад
1) непонятно, если находить х отсюда w=V1/(L-x)=V2/x, то v1x=v2(L-x) , v2L=x(v1+v2) , x=v2L/(v1+v2). не выходит.
ВК
Просветленный
(32923)
что не выходит?
1,6/х=3,2/(0,4-х), отсюда находите х, не вижу проблемы.
В
п. 3.1.2 рассмотрен метод решения задачи
скоростей, когда исходными данными
являются скорость полюса и угловая
скорость тела. Но скорость конкретной
точки плоской фигуры можно найти и в
том случае, если известны скорость
полюса и направление искомой скорости
точки. Для этого используем следующую
теорему: при
движении тела проекции скоростей двух
точек этого тела на прямую, проходящую
через точки, равны между собой
(рис. 3.4), т.е.
.
(3.7)
|
Рис. |
Для определения |
Задача
3.2 (12)
|
Рис. |
Стержень АВ (рис. |
Решение
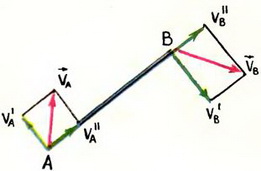
Покажем
для заданного положения стержня
направления скоростей точек А и В.
Проектируя векторы
VА
и
VВ
на линию АВ, получим
.
Откуда
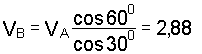
Метод
определения скоростей точек тела с
помощью теоремы о проекциях не
позволяет определить угловую скорость
тела. Метод не дает общей картины
(закономерности) распределения скоростей
в теле для данного момента времени, в
связи с чем трудно определить скорость
точки, направление которой неизвестно
(например,
VС
на рис. 3.5).
Этих
недостатков нет в методе, рассмотренном
в следующем подразделе.
3.1.4. Метод, основанный на использовании мгновенного центра скоростей
|
Рис. |
Мгновенный |
и
;
(3.8)
и
;
и
и
т. п.
Отсюда
и
т.п.
(3.9)
Из
анализа формул (3.8) и (3.9) видно, что для
определения скоростей надо знать
положение МЦС и скорость одной какой-нибудь
точки (последнее нужно для определения
).
Рассмотрим
основные способы нахождения положения
МЦС.
а)
В некоторых случаях удается сразу
указать точку плоской фигуры, скорость
которой в рассматриваемый момент времени
равна нулю. Эта точка и есть МЦС. Так, в
случае качения без скольжения тела по
неподвижной поверхности точка
соприкосновения тела с поверхностью
является мгновенным центром скоростей
(рис. 3.7). Примером служит качение колеса
по рельсу.
б)
Если известны направления скоростей
каких-нибудь двух точек плоской фигуры
в данный момент, то МЦС находится на
пересечении перпендикуляров,
восстановленных в этих точках к
направлениям скоростей (перпендикуляры
АР и ВР на рис. 3.8).
Рис.
3.7
Рис. 3.8
Рис. 3.9
в)
Если скорости точек А и В (рис. 3.9) взаимно
параллельны, а точки лежат на общем
перпендикуляре к скоростям, то МЦС
(точка Р) находится на пересечении
указанного общего перпендикуляра АВ и
прямой 1–1, проведенной через концы
векторов скоростей этих точек. Это
следует из соотношения (3.9).
|
Рис. |
г)
|
Скорости
всех точек фигуры в этом случае одинаковы
по величине и направлению:
VА
=
VB
=
VC
= … .
Отметим,
что при мгновенном поступательном
движении только скорости точек одинаковы,
а их ускорения в общем случае различны.
Укажем
последовательность определения скоростей
с использованием мгновенного центра
скоростей.
1.
Изобразить на чертеже тело (плоскую
фигуру) в заданном положении и найти
мгновенный центр скоростей одним из
рассмотренных выше способов.
2.
Указать направления векторов скоростей
точек фигуры и записать формулы для
вычисления их модулей в соответствии
с (3.8).
3.
Определить угловую скорость по формуле
(3.9), учитывая, что скорость одной
какой-либо точки задана по условию
задачи.
4.
Вычислить искомые модули скоростей
точек по формулам (3.8).
Задача
3.3 (13)
|
Рис. |
Колесо |
Решение
1.
Мгновенным центром скоростей является
точка Р касания колеса с рельсом (см.
способ (а) нахождения МЦС).
2.
Направления векторов скоростей точек
определяются как при вращательном
движении колеса вокруг Р:
VB
ВР;
VD
DР;
VE
EР;
VС
СР.
Их
модули:
;
;
;
.
3.
Учитывая, что скорость точки С задана
(VС
= 2м/с), определим угловую скорость колеса

4.
Вычислим искомые модули скоростей по
написанным выше формулам (п. 2):
м/с;
м/с;
м/с.
Задача
3.4 (12)
Рассмотрим
решение задачи 3.2 с помощью мгновенного
центра скоростей. Дополнительно определим
скорость середины С стержня и его угловую
скорость. Длина стержня 2 м.
Решение
|
Рис. |
1. |
2.
Вектор
VС
направлен перпендикулярно СР.
Запишем
формулы для модулей скоростей:
,
,
.
3.
Определим угловую скорость стержня
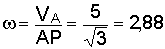
4.
Вычислим искомые модули скоростей по
приведенным выше формулам:
м/с;
м/с.
Соседние файлы в предмете Теоретическая механика
- #
- #
- #
- #
- #
- #
- #
- #
Беляев С.А. Кинематика и связи // Квант. — 1971. — № 2. — С. 44-46.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Кинематика часто рассматривает движение абсолютно твердых тел, то есть тел, расстояния между любыми двумя точками которых остаются постоянными. При этом существуют методы, значительно упрощающие решение кинематических задач. С одним из них мы сейчас познакомимся.
Пусть тела при движении соприкасаются, и скольжение между ними отсутствует. Тогда скорости обоих тел в точке соприкосновения полностью совпадают (рис. 1).
Рис. 1
Если же между телами есть проскальзывание, то совпадают лишь проекции скоростей на перпендикуляр к касательной в точке соприкосновения. При этом достаточно, чтобы касательная существовала хотя бы для одной из скользящих поверхностей (рис. 2).
Рис. 2.
Рассмотрим несколько примеров.
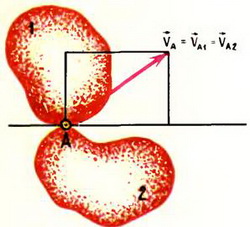
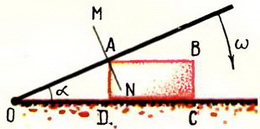
1. Стержень ОА вращается по часовой стрелке с угловой скоростью ω, приводя в движение кирпич ABCD с боковой стороной а (рис. 3). Найти зависимость скорости кирпича υ от угла α.
Решение. Стержень и кирпич соприкасаются в точке А. Следовательно, скорости кирпича и стержня в этой точке в направлении MN 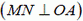
или
Рис. 3.
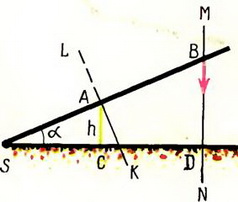
2. Источник света S находится на расстоянии l от экрана MN (рис. 4). В начальный момент времени плоский предмет высоты h начинает равномерно двигаться со скоростью υ от источника к экрану. Найти зависимость скорости движения края тени по экрану от времени.
Рис. 4.
Решение. В данной задаче в роли стержня выступает луч SB. В точке А луч «соприкасается» с предметом, а в точке В с экраном, образуя границу тени. Составим два уравнения, связывающих проекции скоростей в точках А и В: 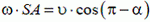
— проекция на MN. Здесь ω — угловая скорость вращения луча. Разделив второе равенство на первое и учитывая, что
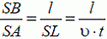
получим
Пусть теперь стержень АВ заданной длины l (рис. 5) движется произвольно. Скорости 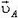
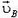
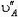
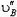
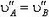
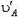
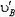
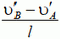
Рис. 5.
Решим две задачи.
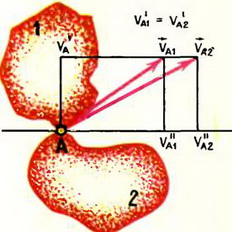
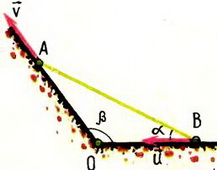
3. Стержень АВ опирается своими концами о стороны тупого угла β (рис. 6). Верхний конец стержня тянут со скоростью υ вдоль стороны АО. Найти зависимость скорости u точки В от угла α.
Рис. 6.
Решение. Так как длина стержня АВ неизменна, проекции скоростей его концов на направление стержня одинаковы:
или
Рассмотрим случай, когда длина стержня изменяется во время движения («стержнем» может служить, например, отрезок, соединяющий две заданные точки, расстояние между которыми меняется). Тогда соотношение, связывающее проекции скоростей концов стержня, принимает вид
где u — скорость изменения длины стержня. (Модуль здесь нужен, так как неизвестно, какая из скоростей больше.)
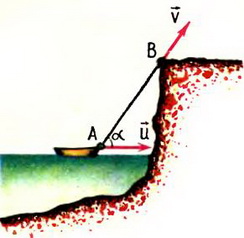
4. Лодку с крутого берега тянут за веревку с постоянной скоростью υ. Найти зависимость скорости лодки u от угла α.
Решение. В данном случае нас интересует часть веревки АВ. Скорость ее сокращения равна υ. Векторы скоростей концов, веревки А и В показаны на рисунке 7.
Рис. 7.
Согласно утверждению, приведенному выше, имеем
или так как 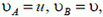
Попробуйте самостоятельно решить подобные задачи.
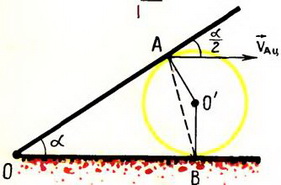
1. Стержень ОА вращается по часовой стрелке с угловой скоростью ω, приводя в движение цилиндр радиуса r (рис. 8). Скольжения между цилиндром и плоскостью нет. Найти зависимость скорости цилиндра υ от угла α.
Рис. 8.
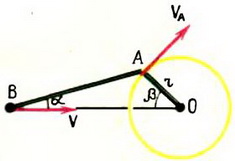
2. Кривошип АО длины r (рис. 9) вращается с угловой скоростью ω, длина шатуна АВ равна l. Найти скорость υ точки В шатуна, если 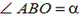
Рис. 9.
3. Шарик, предварительно раскрутив вокруг оси, кладут на горизонтальную поверхность. Коэффициент трения шарика о поверхность отличен от нуля. Под действием силы трения шарик изменяет свое первоначальное вращательное движение и начинает каким-то образом двигаться по поверхности. Описать, как будет происходить это движение.
Ответы
1. (*На рисунке к этой задаче вектор скорости υAц должен быть направлен под углом α/2 к стержню.)
В точке А проекции скоростей цилиндра υAц и стержня υAС на направление АО´ 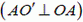
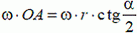
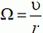
получим
Из условия равенства проекции имеем
или
Откуда
2. Поскольку длина АВ неизменна, проектируя скорости концов шатуна на направление АВ, получим 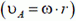
или
Воспользовавшись теоремой синусов
можно найти
Пример решения задачи по разделу динамика на определение угловой скорости вращающейся системы при заданном условии.
Задача
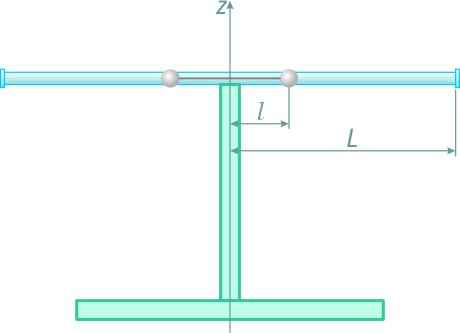
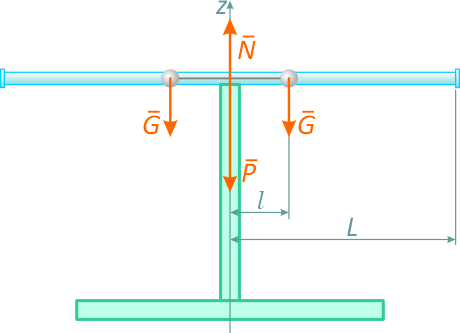
Стержень длиной 2l, вращается в горизонтальной плоскости вокруг неподвижной оси z (рисунок 3.7) с угловой скоростью ω.
По этому стержню, как по направляющей, могут скользить два одинаковых шара, радиусы которых пренебрежимо малы по сравнению с их расстоянием от оси вращения.
Рисунок 3.7
В начальный момент шары связаны нитью и находятся на расстоянии l от оси вращения.
Какова будет угловая скорость системы, если нить, связывающая шары, оборвется и расстояние каждого из шаров от оси вращения станет равным L?
Другие примеры решений >
Помощь с решением задач >
Пример решения
Для определения угловой скорости применим теорему о кинетическом моменте.
Так как внешними силами этой системы являются вес стержня P, вес шаров G и реакция оси вращения N, момент этих сил относительно оси z равен нулю, то на основании следствия 2 теоремы об изменении кинетического момента механической системы будем иметь
Kz1=Kz2,
где Kz1 и Kz2 – кинетические моменты системы при первом и втором положениях шаров. Обозначая момент инерции стержня относительно оси z через Jz и принимая шары за материальные точки массой m=G/g, получаем
следовательно,
Отсюда
Таким образом, угловая скорость этой системы уменьшается под действием внутренних сил.
Другие примеры решения задач>
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Условие задачи:
В магнитном поле с индукцией 0,01 Тл вращается стержень длиной 0,2 м с постоянной угловой скоростью 100 рад/с. Определить ЭДС индукции, возникающую в стержне, если ось вращения проходит через конец стержня параллельно линиям индукции магнитного поля.
Задача №8.4.50 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(B=0,01) Тл, (l=0,2) м, (omega=100) рад/с, (rm E_i-?)
Решение задачи:
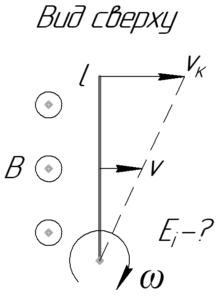
[{{rm E}_i} = Bupsilon l;;;;(1)]
В этой формуле (B) – индукция магнитного поля, (upsilon) – скорость центра масс стержня (т.е. скорость середины проводника), (l) – длина стержня.
На рисунке показано распределение скоростей точек стержня, например, (upsilon_к) – это скорость конца стержня. Очевидно, что точка стержня, находящаяся на оси вращения, имеет нулевую скорость. В этой задаче важно понять, что в формуле (1) используется именно скорость середины стержня (upsilon).
Скорость центра масс стержня (upsilon) легко найти по формуле:
[upsilon = frac{{omega l}}{2};;;;(2)]
Подставим выражение (2) в формулу (1):
[{{rm E}_i} = frac{{Bomega {l^2}}}{2}]
Подставим данные задачи в эту формулу и посчитаем численный ответ:
[{{rm E}_i} = frac{{0,01 cdot 100 cdot {{0,2}^2}}}{2} = 0,02;В]
Ответ: 0,02 В.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.4.49 Поток магнитной индукции в проводящем контуре, содержащем 100 витков
8.4.51 Найти максимальный магнитный поток через прямоугольную рамку, вращающуюся
8.4.52 При равномерном изменении силы тока через катушку из 500 витков в ней возникает







 .
.