как найти скорость тела если известно импульс тела и масса тела ?
El_Nano
Гуру
(2974),
на голосовании
7 лет назад
Голосование за лучший ответ
Допустимое отклонение
Искусственный Интеллект
(111186)
7 лет назад
подели импульс на массу
El_NanoГуру (2974)
7 лет назад
о спасибо тогда еще несколько вопросов электические заряды имеются один +10 другой -20 и они слились что будет? ответ будет же -10 ??
Допустимое отклонение
Искусственный Интеллект
(111186)
Сложно себе представить “слившиеся” заряды, но если ты говоришь о заряде системы из этих двух зарядов, то да, они просто складываются.
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Определение
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2 = m1v1отн2 = m1(v1 – v2)
p1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1 и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103 (кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:
∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар |
|
|
|
Конечная скорость после удара:
v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. |
Абсолютно упругий удар |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. |
Пуля пробила стенку |
|
|
|
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) |
Радиус-вектор тела повернул на 180 градусов |
|
|
|
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой:
|
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:

Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:

Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:

Подставим это выражение во второй закон Ньютона и получим:

Или:

F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:

Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:

Реактивная сила:

Второй закон Ньютона для ракеты:

Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:

Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
![]()
Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел
Определение
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:


Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:

Закон сохранения импульса
Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:

Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
Важно!
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:

Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:

Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17695
 На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?
На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?
а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22730
 Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.
Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.
Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek = 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22520
 Снаряд, имеющий в точке О траектории импульсp0, разорвался на два осколка. Один из осколков имеет импульс −p1
Снаряд, имеющий в точке О траектории импульсp0, разорвался на два осколка. Один из осколков имеет импульс −p1
. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:

Сделаем чертеж:

Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:

Выразим массу груза:

Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 19.9k
Закон cохранения импульса

О чем эта статья:
9 класс, 10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Импульс: что это такое
Как-то раз Рене Декарт (это который придумал ту самую декартову систему координат) решил, что каждый раз считать силу, чтобы описать процессы — как-то лень и сложно.
Для этого нужно ускорение, а оно не всегда очевидно. Тогда он придумал такую величину, как импульс. Импульс можно охарактеризовать, как количество движения — это произведение массы на скорость.
Импульс тела
p — импульс тела [кг · м/с]
m — масса тела [кг]
Закон сохранения импульса
В физике и правда ничего не исчезает и не появляется из ниоткуда. Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:
Закон сохранения импульса
Векторная сумма импульсов тел в замкнутой системе постоянна
А выглядит — вот так:
Закон сохранения импульса
pn — импульс тела [кг · м/с]
Простая задачка
Мальчик массой m = 45 кг плыл на лодке массой M = 270 кг в озере и решил искупаться. Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?
Решение:
Запишем закон сохранения импульса для данного процесса.
— это импульс системы мальчик + лодка до того, как мальчик спрыгнул,
— это импульс мальчика после прыжка,
— это импульс лодки после прыжка.
Изобразим на рисунке, что происходило до и после прыжка.
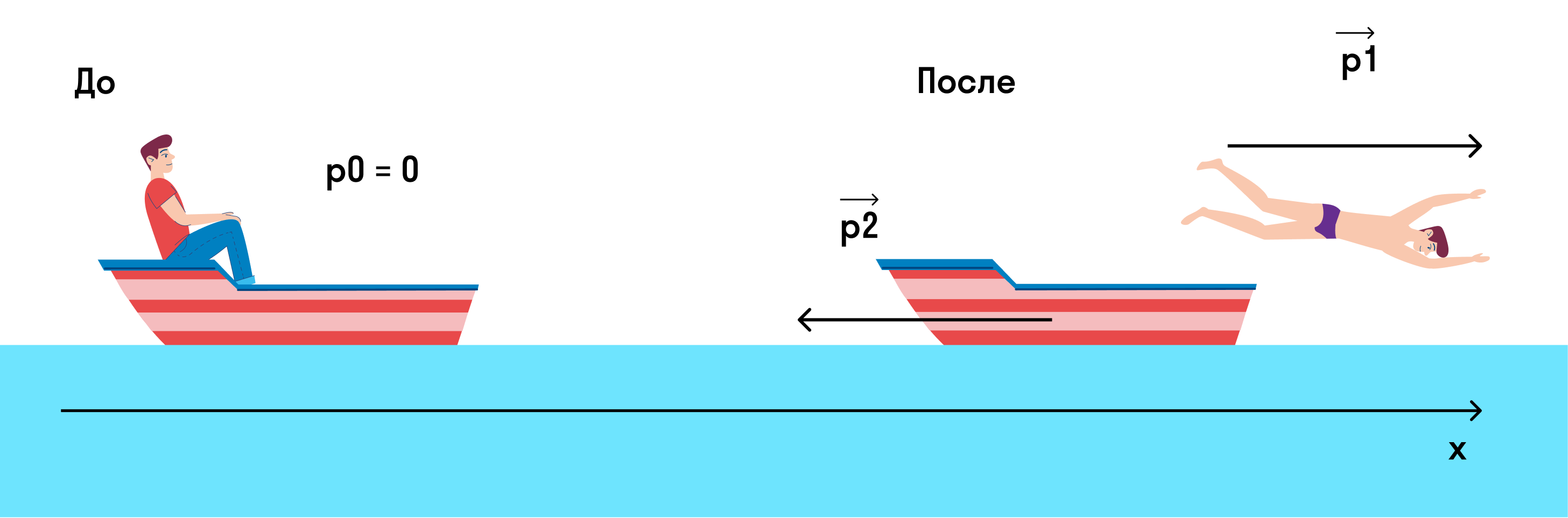
Если мы спроецируем импульсы на ось х, то закон сохранения импульса примет вид
Подставим формулу импульса.
, где:
— масса мальчика [кг]
— скорость мальчика после прыжка [м/с]
— масса лодки [кг]
— скорость лодки после прыжка [м/с]
Выразим скорость лодки :
Подставим значения:
м/с
Ответ: скорость лодки после прыжка равна 0,5 м/с
Задачка посложнее
Тело массы m1 = 800 г движется со скоростью v1 = 3 м/с по гладкой горизонтальной поверхности. Навстречу ему движется тело массы m2 = 200 г со скоростью v2 = 13 м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.
Решение: Для данной системы выполняется закон сохранения импульса:
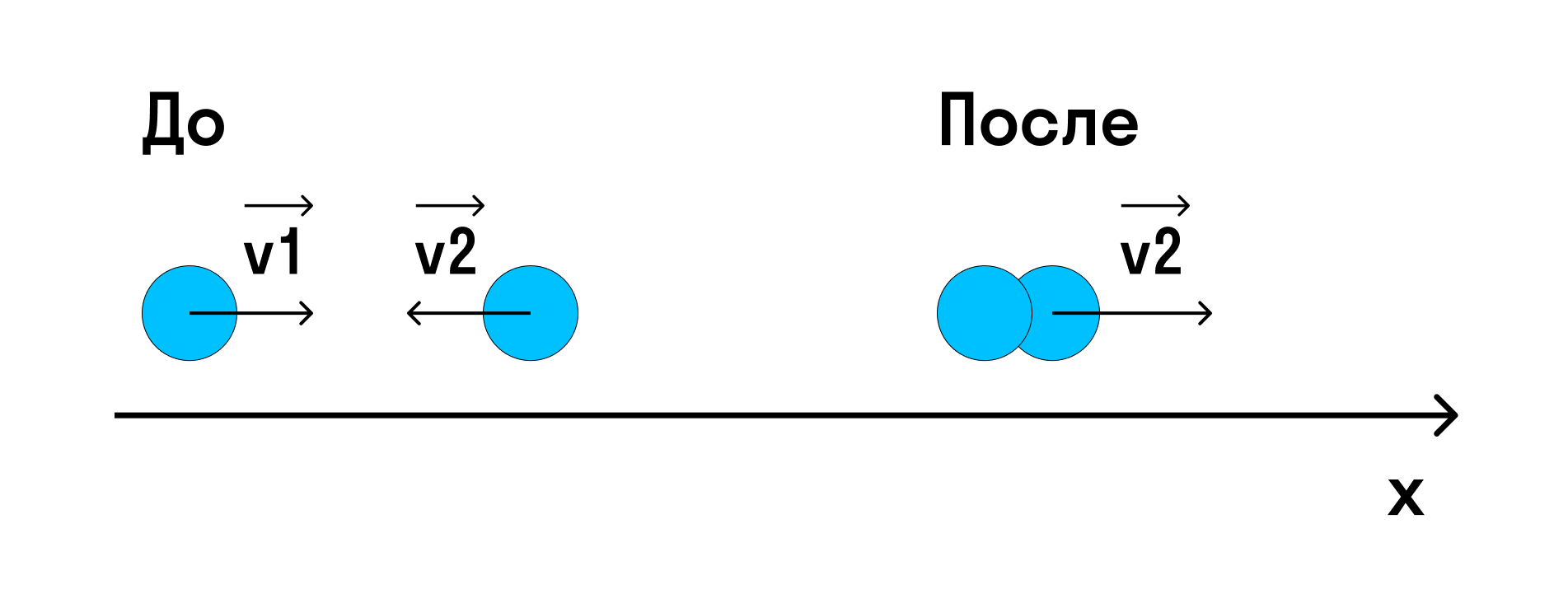
Импульс системы до удара — это сумма импульсов тел, а после удара — импульс «получившегося» в результате удара тела.
Спроецируем импульсы на ось х:
После неупругого удара получилось одно тело массы , которое движется с искомой скоростью:
Отсюда находим скорость тела, образовавшегося после удара:
Переводим массу в килограммы и подставляем значения:
В результате мы получили отрицательное значение скорости. Это значит, что в самом начале на рисунке мы направили скорость после удара неправильно.
Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси X. Это никак не влияет на получившееся значение.
Ответ: скорость системы тел после соударения равна v = 0,2 м/с.
Второй закон Ньютона в импульсной форме
Второй закон Ньютона в импульсной форме можно получить следующим образом. Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.
Запишем второй закон Ньютона, спроецированный на ось х, сонаправленную с направлением движения и ускорением:
Применим выражение для ускорения
В этих уравнениях слева находится величина a. Так как левые части уравнений равны, можно приравнять правые их части
Полученное выражение является пропорцией. Применив основное свойство пропорции, получим такое выражение:
В правой части находится — это разница между конечной и начальной скоростью.
Преобразуем правую часть
Раскрыв скобки, получим
Заменим произведение массы и скорости на импульс:
То есть, вектор – это вектор изменения импульса .
Тогда второй закон Ньютона в импульсной форме запишем так
Вернемся к векторной форме, чтобы данное выражение было справедливо для любого направления вектора ускорения.
Задачка про белку отлично описывает смысл второго закона Ньютона в импульсной форме
Белка с полными лапками орехов сидит на гладком горизонтальном столе. И вот кто-то бесцеремонно толкает ее к краю стола. Белка понимает законы Ньютона и предотвращает падение. Но как?
Решение:
Чтобы к белке приложить силу, которая будет толкать белку в обратном направлении от края стола, нужно создать соответствующий импульс (вот и второй закон Ньютона в импульсной форме подъехал).
Ну, а чтобы создать импульс, белка может выкинуть орехи в сторону направления движения — тогда по закону сохранения импульса ее собственный импульс будет направлен против направления скорости орехов.
Реактивное движение
В основе движения ракет, салютов и некоторых живых существ: кальмаров, осьминогов, каракатиц и медуз — лежит закон сохранения импульса. В этих случаях движение тела возникает из-за отделения какой-либо его части. Такое движение называется реактивным.
Яркий пример реактивного движения в технике — движение ракеты, когда из нее истекает струя горючего газа, которая образуется при сгорании топлива.
Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:
Сила называется реактивной. Это та сила, которая возникает в процессе отделения части тела. Особенностью реактивной силы является то, что она возникает без взаимодействия с внешними телами.
Закон сохранения импульса позволяет оценить скорость ракеты.
vг — скорость горючего,
vр — скорость ракеты.
Отсюда можно выразить скорость ракеты:
Скорость ракеты при реактивном движении
vг — скорость горючего [м/с]
mр — масса ракеты [кг]
vр — скорость ракеты [м/с]
Эта формула справедлива для случая мгновенного сгорания топлива. Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Как измерить скорость объекта, используя закон сохранения импульса
Как известно, дети полны энергии, которая из них «бьет ключом». Чтобы убедиться в этом, достаточно посетить во время переменки коридор средней школы у дверей кабинета, в котором обучаются школьники начальных классов. Постараемся решить гипотетическую задачу, когда первоклассник Петя, имеющий массу 30 кг, мчится со скоростью 3 м/с и сталкивается с неподвижно стоящим одноклассником Колей, который имеет такую же массу — 30 кг. Спрашивается, с какой скоростью будет после столкновения двигаться тандем Коля+Петя.
Чтобы упростить решение задачи, пренебрегаем всеми внешними силами, включая силу трения, считая, таким образом, что наша система является замкнутой.
Согласно закону сохранения импульса, горизонтальные проекции импульсов (начальный импульс — р0; конечный импульс — р1) учеников равны:
Подставляем в формулу массу и начальную скорость Пети, который обладал определенным импульсом (импульс Коли был равен нулю, поскольку он стоял на месте): Поскольку конечный импульс р1 должен быть равен произведению общей массы учеников (mП + mК) на их конечную скорость vПК1, получаем следующую формулу: Из двух последних уравнений получаем равенство: Отсюда конечная скорость учеников будет равна: Подставив значения в формулу получим: Таким образом, тандем Коля+Петя после их столкновения будет двигаться со скоростью 1,5 м/с, что ровно в 2 раза ниже начальной скорости Пети, что, в общем-то, логично, поскольку масса движущихся объектов после столкновения увеличилась ровно в 2 раза.
Как с помощью закона сохранения импульса измерить начальную скорость пули
Никогда не смотрели передачу «Разрушители легенд» (MythBusters), которая с 2003 года идет на канале Discovery Channel? Посмотрите, не пожалеете. В ходе передачи американские специалисты Джейми Хайнеман и Адам Сэвидж, используя свои навыки и опыт, проводят экспериментальную проверку различных слухов, легенд, мифов и прочих «небылиц», выясняя, могут ли они быть реализованы в реальной жизни людей (например, действительно ли бутерброд всегда падает маслом вниз).
В некоторых сериях Джейми и Адам проводят опыты с огнестрельным оружием, например, в одном эксперименте они выясняли, может ли звуковая волна от движения пули разрушить стеклянный бокал.
Давайте на короткое время представим себя на месте разрушителей легенд и в теории измерим скорость пули, вылетающей из ствола винтовки или пистолета.
Для решения задачи будем использовать специальный маятник, который будет отклоняться на определенный угол после попадания в него пули, и закон сохранения импульса.
В начальный момент времени (положение 1) пуля движется с некой начальной скоростью по направлению к мишени, закрепленной на маятнике, которая находится в покое.
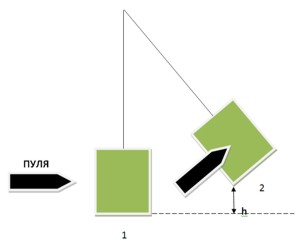
Начальный суммарный импульс пули и мишени равен:
Конечный суммарный импульс пули, застрявшей в мишени (положение 2):
Для простоты эксперимента мы пренебрегаем потерями энергии на преодоление трения при попадании пули в мишень, поэтому, начальный и конечный импульсы системы пуля+мишень равны:
Искомая величина начальной скорости пули будет равна:
Для ее нахождения нам надо знать конечную скорость системы пуля+мишень. В этом нам поможет наш маятник — после попадания пули в мишень, последняя отклонится на определенный угол, поднявшись при этом на высоту h, на которой скорость системы мишень+пуля станет равной нулю. В этой точке кинетическая энергия, которая выражается формулой (m+M)v1 2 /2, преобразуется в потенциальную (m+M)gh. Согласно закону сохранения энергии:
Отсюда выводим формулу для расчета конечной скорости системы мишень+пуля:
Подставляем эту формулу в прежнее выражение для нахождения начальной скорости пули:
Если предположить, что масса пули равна 10 г, а мишень весит 10 кг (10 4 г), при этом после попадания пули в мишень система мишень+пуля отклонилась на некоторый угол, поднявшись на высоту 10 см, то начальная скорость пули будет равна:
Если вам понравился сайт, будем благодарны за его популяризацию 🙂 Расскажите о нас друзьям на форуме, в блоге, сообществе. Это наша кнопочка:

Код кнопки: 
Политика конфиденциальности Об авторе
Импульс тела, закон сохранения импульса
теория по физике 🧲 законы сохранения
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости ( p ↑↓ v ), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p 1отн2— импульс первого тела относительно второго, m1 — масса первого тела, v 1отн2 — скорость первого тела относительно второго, v 1и v 2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
Изменение импульса тела
∆ p — изменение импульса тела, p — конечный импульс тела, p 0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар

Конечный импульс тела:
Модуль изменения импульса тела равен модулю его начального импульса:
Абсолютно упругий удар

Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Пуля пробила стенку

Модуль изменения импульса тела равен разности модулей начального и конечного импульсов:
Радиус-вектор тела повернул на 180 градусов

Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали

Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Угол падения равен углу отражения:
Модуль изменения импульса в этом случае определяется формулой:

Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем: 
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:

Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:

Подставим это выражение во второй закон Ньютона и получим:


F ∆t — импульс силы, ∆ p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:

Реактивное движение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:


Второй закон Ньютона для ракеты:

Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
Выразим ускорение из второго закона Ньютона для ракеты:

Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
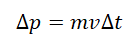
Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:


Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:

Закон сохранения импульса
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
Отсюда скорость равна:

Импульс частицы до столкновения равен − p 1, а после столкновения равен − p 2, причём p1 = p, p2 = 2p, − p 1⊥ − p 2. Изменение импульса частицы при столкновении Δ − p равняется по модулю:
Алгоритм решения
Решение
Запишем исходные данные:

Так как угол α = 90 о , вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δ p = √ p 2 1 + p 2 2
Подставим известные данные:
Δ p = √ p 2 + ( 2 p ) 2 = √ 5 p 2 = p √ 5
pазбирался: Алиса Никитина | обсудить разбор | оценить
 На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?
На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?
а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
источники:
http://prosto-o-slognom.ru/fizika/20_kak_izmerit_skorost_zakon_sohraneniya_impulsa.html
http://spadilo.ru/impuls-tela-zakon-soxraneniya-impulsa/
Закон сохранения импульса
Закон сохранения импульса можно наблюдать повсюду. Он достаточно точно выполняется в реальных условиях, если пренебречь сопротивлением воздуха, силами трения и т.д. Примеры проявления этого закона:
- стрелок ощущает отдачу при выстреле из ружья;
- рыбак переходит с кормы на нос лодки, а лодка при этом движется в противоположную сторону;
- шары сталкиваются на бильярдном столе.
Однако, прежде чем говорить о законе сохранении импульса, рассмотрим понятие замкнутой системы.
Замкнутая система – система тел, на которую со стороны других тел не действуют внешние силы.
Векторная сумма импульсов всех тел, входящих в замкнутую систему, остается постоянной при любых взаимодействиях этих тел между собой внутри системы.
Данный закон является следствием из второго и третьего законов Ньютона. Покажем это.
Возьмем замкнутую систему из двух взаимодействующих тел. Силы F1→ и F2→ – это силы взаимодействия между телами. Третий закон Ньютона гласит, что F2→=-F1→. Пусть тела взаимодействуют во течение времени t. Тогда импульсы сил одинаковы по модулю и противоположны по направлению, как и сами силы.
F2t→=-F1→t.
По второму закону Ньютона:
F1→t=m1v1’→-m1v1→; F2→t=m1v2’→-m1v2→
Здесь v1’→ и v2’→ – скорости тел в конце взаимодействия. Соответственно, скорости без штрихов обозначают эти величины в начальный момент взаимодействия.
Из записанного выше следует соотношение:
m1v1→+m2v2→=m1v1’→+m2v2’→
Это равенство – математическая форма записи закона сохранения импульса. Оно означает, что суммарный импульс системы в результате какого-то взаимодействия не изменился.
Проиллюстрируем закон сохранения импульса на примере соударения шаров разных масс. Один из шаров до удара покоился.
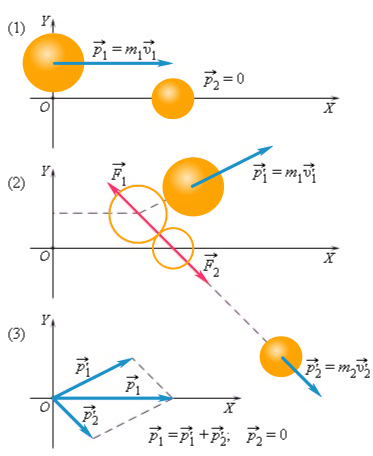
Как видим, после удара векторная сумма импульсов двух шаров равна первоначальному импульсу движущегося шара.
Важно! Закон сохранения выполняется и для проекций векторов на координатные оси.
Закон сохранения импульса позволяет решать задачи и находить скорости тел не зная значений действующих сил.
Рассмотрим снаряд, вылетающий из пушки.
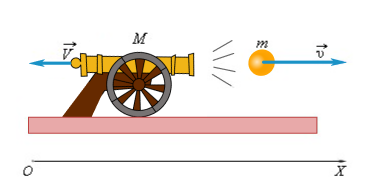
В данном случае взаимодействующие тела – это снаряд и пушка. Сначала тела не движутся. При выстреле снаряд приобретает скорость v→ и летит вперед, а пушка откатывается назад со скоростью V→. Откатывание пушки называется отдачей от выстрела.
По закону сохранения импульса в проекции на ось OX можно записать:
mv-MV=0
V=mvM.
Реактивное движение
Реактивное движение также основано на принципе отдачи. Нагретые газы выбрасываются из сопла реактивного двигателя со скоростью u→. Пусть масса газов равна m, а масса ракеты после истечения газов – M. Рассматривая замкнутую систему “ракета-газы” и применяя к ней закон сохранения импульса, можно вычислить скорость ракеты V после истечения газов.
V=muM
Формула для пушки и снаряда не применима к ракете, так как дает лишь приблизительное представление о движении ракеты, На самом деле вся масса газов выходит из сопла не сразу, а постепенно.
Рассмотрим этот процесс подробнее. Пусть масса ракеты в момент времени t равна M, а сама ракета движется со скоростью v→. В течение малого промежутка времени ∆t из сопла ракеты выбрасывается порция газа с относительной скоростью u→. По истечении времени ∆t ракета будет двигаться со скоростью v+∆v, а масса ракеты станет равной M-∆M.
В момент t+∆t импульс ракеты равен:
M-∆M·v→+∆v→.
Импульс реактивных газов:
∆M·v→+u→.
По закону сохранения импульса:
Mv→=M-∆M·v→+∆v→+∆M·v→+u→.
Или
M∆v→=∆M·u→-∆M·∆v→.
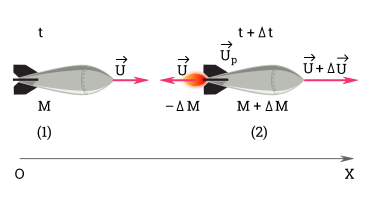
Величиной ∆M·∆v→ можно пренебречь, так как ∆M намного меньше M.
Разделим последнее равенство на ∆t и перейдем к пределу ∆t→0.
M∆v→∆t=∆M·u→∆t (∆t→0)
Ma→=-μu→.
Здесь μ – расход топлива в единицу времени, а -μu→ – реактивная сила тяги. Направление этой силы совпадает с направлением движения ракеты.
Формула Ma→=-μu→ выражает второй закон Ньютона для тела переменной массы. В скалярном виде ее можно переписать так:
Ma=μu.
Конечная скорость ракеты определяется по формуле:
v=ulnM0M.
Это так называемая формула Циолковского, согласно которой конечная скорость ракеты может превышать скорость истечения газов из сопла двигателя. Правда, достижение такой скорости связано с определенными сложностями. Во-первых, такими, как значительный расход топлива.
Для того, чтобы развить первую космическую скорость v=v1=7,9·103 мс при скорости истечения газов u=3·103 мс стартовая масса ракеты должна быть примерно в 14 раз больше конечной массы.
Современное ракетостроение развивается в направлении экономичных многоступенчатых ракет. Сброс отсеков с отработанным топливом позволяет значительно сократить массу ракеты и оптимизировать дальнейший расход топлива для ее разгона.
Импульс. Закон сохранения импульса
Импульс — произведение массы на скорость.

Само по себе это произведение ничего не дает для понимания взаимодействий описываемых импульсом. Немного более понятно о чем речь, когда примерно представляешь себе массу и скорость, и, можно сказать, что эти величины будут на него влиять и это верно. Однако давайте поробуем сделать наше понимание более адекватным тому, что происходит.
Чем импульс отличается от силы?
Сила, воздействуя на тело, пытается изменить его скорость.
Импульс присущ телу просто по факту наличия скорости, поэтому его иногда называют количеством движения.
И когда мы пытаемся остановить или разогнать какое то тело, обладающее импульсом, мы вынуждены, воздействуя на тело, приложить к нему силу.
Закон сохранения импульса
Если некое множество тел изолировано от действия внешних, по отношению к ним, сил, то суммарный импульс тел сохраняется.

- закон также выполняется при условии, если действие внешних сил скомпенсировано
- могут быть внутренние силы, действующие между телами
- если есть внешнии силы, то их сумма будет равна изменению суммарного импульса тел:

Закон сохранения импульса может выполнятся в векторной форме, но также возможно выполнение закона для одной из осей (например Х). Только вдоль нее обязательно либо не должны действовать внешние силы, либо действие их должно быть скомпенсировано.
Векторный вид:

В проекциях на ось Х:

Упругий и неупругий удар
В качестве примера рассмотрим абсолютно упругое и абсолютно неупругое столкновения:
Абсолютно упругое столкновение — столкновение, при котором сохраняется механическая энергия сталкивающихся тел (тела разлетаются в стороны).
Абсолютно неупругое столкновение — столкновение, при котором сталкивающиеся тела слипаются в одно целое.
Абсолютно упругое столкновение
Тело движущееся с одной скоростью врезается в тело движущееся с другой. Тела двигаются в одном направлении. Удар — абсолютно упругий. Внешнии силы отсутствуют или скомпенсированы.



Поскольку считается, что внешнии силы отсутствуют, то выполняется закон сохранения импульса в векторной форме:

В векторной форме не учитываются направления векторов (в уравнении везде плюсы). Для того, чтобы отыскать любую из скоростей можно записать его в виде:

Для получения модулей векторов скоростей (числовое значение скоростей), нужно спроектировать все вектора на горизонтальную ось ОХ. Так как все скорости целиком находятся на горизонтальной оси ОХ, то длина проекций всех векторов полностью равна длинам этих векторов.
Поэтому можно убрать значки векторов и записать в следующем виде:

Поскольку скорость V1| направлена против оси ОХ в ее проекции появляется знак минус.
С помощью последней формулы мы можем найти все величины и скоростей, и масс, в зависимости от того, что дано в условии.
Абсолютно неупругое столкновение
Тело движущееся с одной скоростью врезается в тело движущееся с другой. Тела двигались в одном направлении. Удар — абсолютно неупругий. Внешнии силы отсутствуют или скомпенсированы.

![]()


Все тоже самое. Поскольку считается, что внешнии силы отсутствуют, то выполняется закон сохранения импульса в векторной форме.

Масса после удара двух тел — общая потому, что тела слиплись в результате неупругого соударения (по условию):

Скорости также направлены вдоль оси ОХ, поэтому:

Откуда также можем найти все величины и скоростей, и масс, в зависимости от того, что дано в условии.
Выполнение закона сохранения импульса для оси
Рассмотрим пример, когда закон сохранения импульса не выполняется в векторной форме, но выполняется для оси.
Шар массой m1 врезается под углом в вагон массой m2. Соударение — неупругое. Внешнии силы отсутствуют.

Вертикальная составляющая скорости V1 идет на нагрев, в результате силы трения внутри вагона (если бы его не было, то вагон должен был либо провалиться вниз, либо его должно было бы отпружинить вверх), а горизонтальная составляющая учавствует в законе сохранения импульса вдоль оси ОХ.

Поэтому закон сохранения импульса не выполняется в векторной форме, но выполняется для оси ОХ, т.к. вдоль нее не действуют никакие силы:

Столкновение шаров под углом
Шар, массой m1 налетает на шар массой m2, под углом. Удар — абсолютно упругий. Внешнии силы отсутствуют.

Сложим вектора импульсов до столкновения P и вектора импульсов после столкновения P|, путем параллельного переноса (зеленая пунктирная линия).

Закон сохранения импульса выполнятеся в векторной форме. Для получения скалярных величин (численных значений), существует способ сложения двух векторов называемый теоремой косинусов.

Скалярнае (численное) значение вектора общего импульса:

Общий импульс — неизменен, вследствие закона сохранения импульса. Поэтому и после удара будет тот же самый импульс, но с другими скоростями и углом:

В зависимости от условия задачи, можно рассчитать те или иные скорости или углы, правомерно приравняв эти два уравнения.
