Как найти скорость через плотность тока

Постоянный электрический ток

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: постоянный электрический ток, сила тока, напряжение.

Электрический ток обеспечивает комфортом жизнь современного человека. Технологические достижения цивилизации — энергетика, транспорт, радио, телевидение, компьютеры, мобильная связь — основаны на использовании электрического тока.

Электрический ток — это направленное движение заряженных частиц, при котором происходит перенос заряда из одних областей пространства в другие.

Электрический ток может возникать в самых различных средах: твёрдых телах, жидкостях, газах. Порой и среды никакой не нужно — ток может существовать даже в вакууме! Мы поговорим об этом в своё время, а пока приведём лишь некоторые примеры.

• Замкнём полюса батарейки металлическим проводом. Свободные электроны провода начнут направленное движение от «минуса» батарейки к «плюсу».
Это — пример тока в металлах.

• Бросим в стакан воды щепотку поваренной соли . Молекулы соли диссоциируют на ионы, так что в растворе появятся свободные заряды: положительные ионы и отрицательные ионы . Теперь засунем в воду два электрода, соединённые с полюсами батарейки. Ионы начнут направленное движение к отрицательному электроду, а ионы — к положительному.
Это — пример прохождения тока через раствор электролита.

• Грозовые тучи создают столь мощные электрические поля, что оказывается возможным пробой воздушного промежутка длиной в несколько километров. В результате сквозь воздух проходит гигантский разряд — молния.
Это — пример электрического тока в газе.

Во всех трёх рассмотренных примерах электрический ток обусловлен движением заряженных частиц внутри тела и называется током проводимости.

• Вот несколько иной пример. Будем перемещать в пространстве заряженное тело. Такая ситуация согласуется с определением тока! Направленное движение зарядов — есть, перенос заряда в пространстве — присутствует. Ток, созданный движением макроскопического заряженного тела, называется конвекционным.

Заметим, что не всякое движение заряженных частиц образует ток. Например, хаотическое тепловое движение зарядов проводника — не направленное (оно совершается в каких угодно направлениях), и потому током не является (при возникновении тока свободные заряды продолжают совершать тепловое движение! Просто в этом случае к хаотическим перемещениям заряженных частиц добавляется их упорядоченный дрейф в определённом
направлении).
Не будет током и поступательное движение электрически нейтрального тела: хотя заряженные частицы в его атомах и совершают направленное движение, не происходит переноса заряда из одних участков пространства в другие.

к оглавлению ▴

Направление электрического тока

Направление движения заряженных частиц, образующих ток, зависит от знака их заряда. Положительно заряженные частицы будут двигаться от «плюса» к «минусу», а отрицательно заряженные — наоборот, от «минуса» к «плюсу». В электролитах и газах, например, присутствуют как положительные, так и отрицательные свободные заряды, и ток создаётся их встречным движением в обоих направлениях. Какое же из этих направлений принять за направление электрического тока?

Направлением тока принято считать направление движения положительных зарядов.

Попросту говоря, по соглашению ток течёт от «плюса» к «минусу» (рис. 1; положительная клемма источника тока изображена длинной чертой, отрицательная клемма — короткой).

Рис. 1. Направление тока

Данное соглашение вступает в некоторое противоречие с наиболее распространённым случаем металлических проводников. В металле носителями заряда являются свободные электроны, и двигаются они от «минуса» к «плюсу». Но в соответствии с соглашением мы вынуждены считать, что направление тока в металлическом проводнике противоположно движению свободных электронов. Это, конечно, не очень удобно.

Тут, однако, ничего не поделаешь — придётся принять эту ситуацию как данность. Так уж исторически сложилось. Выбор направления тока был предложен Ампером (договорённость о направлении тока понадобилась Амперу для того, чтобы дать чёткое правило определения направления силы, действующей на проводник с током в магнитном поле. Сегодня эту силу мы называем силой Ампера, направление которой определяется по правилу левой руки) в первой половине XIX века, за 70 лет до открытия электрона. К этому выбору все привыкли, и когда в 1916 году выяснилось, что ток в металлах вызван движением свободных электронов, ничего менять уже не стали.

к оглавлению ▴

Действия электрического тока

Как мы можем определить, протекает электрический ток или нет? О возникновении электрического тока можно судить по следующим его проявлениям.

1. Тепловое действие тока. Электрический ток вызывает нагревание вещества, в котором он протекает. Именно так нагреваются спирали нагревательных приборов и ламп накаливания. Именно поэтому мы видим молнию. В основе действия тепловых амперметров лежит тепловое расширение проводника с током, приводящее к перемещению стрелки прибора.

2. Магнитное действие тока. Электрический ток создаёт магнитное поле: стрелка компаса, расположенная рядом с проводом, при включении тока поворачивается перпендикулярно проводу. Магнитное поле тока можно многократно усилить, если обмотать провод вокруг железного стержня — получится электромагнит. На этом принципе основано действие амперметров магнитоэлектрической системы: электромагнит поворачивается в поле постоянного магнита, в результате чего стрелка прибора перемещается по шкале.

3. Химическое действие тока. При прохождении тока через электролиты можно наблюдать изменение химического состава вещества. Так, в растворе положительные ионы двигаются к отрицательному электроду, и этот электрод покрывается медью.

Электрический ток называется постоянным, если за равные промежутки времени через поперечное сечение проводника проходит одинаковый заряд.

Постоянный ток наиболее прост для изучения. С него мы и начинаем.

к оглавлению ▴

Сила и плотность тока

Количественной характеристикой электрического тока является сила тока. В случае постоянного тока абсолютная величина силы тока есть отношение абсолютной величины заряда , прошедшего через поперечное сечение проводника за время , к этому самому времени:

(1)

Измеряется сила тока в амперах (A). При силе тока в А через поперечное сечение проводника за с проходит заряд в Кл.

Подчеркнём, что формула (1) определяет абсолютную величину, или модуль силы тока.
Сила тока может иметь ещё и знак! Этот знак не связан со знаком зарядов, образующих ток, и выбирается из иных соображений. А именно, в ряде ситуаций (например, если заранее не ясно, куда потечёт ток) удобно зафиксировать некоторое направление обхода цепи (скажем, против часовой стрелки) и считать силу тока положительной, если направление тока совпадает с направлением обхода, и отрицательной, если ток течёт против направления обхода (сравните с тригонометрическим кругом: углы считаются положительными, если отсчитываются против часовой стрелки, и отрицательными, если по часовой стрелке).

В случае постоянного тока сила тока есть величина постоянная. Она показывает, какой заряд проходит через поперечное сечение проводника за с.

Часто бывает удобно не связываться с площадью поперечного сечения и ввести величину плотности тока:

(2)

где — сила тока, — площадь поперечного сечения проводника (разумеется, это сечение перпендикулярно направлению тока). С учётом формулы (1) имеем также:

Плотность тока показывает, какой заряд проходит за единицу времени через единицу площади поперечного сечения проводника. Согласно формуле (2), плотность тока измеряется в А/м2.

к оглавлению ▴

Скорость направленного движения зарядов

Когда мы включаем в комнате свет, нам кажется, что лампочка загорается мгновенно. Скорость распространения тока по проводам очень велика: она близка к км/с (скорости света в вакууме). Если бы лампочка находилась на Луне, она зажглась бы через секунду с небольшим.

Однако не следует думать, что с такой грандиозной скоростью двигаются свободные заряды, образующие ток. Оказывается, их скорость составляет всего-навсего доли миллиметра в секунду.

Почему же ток распространяется по проводам так быстро? Дело в том, что свободные заряды взаимодействуют друг с другом и, находясь под действием электрического поля источника тока, при замыкании цепи приходят в движение почти одновременно вдоль всего проводника. Скорость распространения тока есть скорость передачи электрического взаимодействия между свободными зарядами, и она близка к скорости света в вакууме. Скорость же, с которой сами заряды перемещаются внутри проводника, может быть на много порядков меньше.

Итак, подчеркнём ещё раз, что мы различаем две скорости.

1. Скорость распространения тока. Это — скорость передачи электрического сигнала по цепи. Близка к км/с.

2. Скорость направленного движения свободных зарядов. Это — средняя скорость перемещения зарядов, образующих ток. Называется ещё скоростью дрейфа.

Мы сейчас выведем формулу, выражающую силу тока через скорость направленного движения зарядов проводника.

Пусть проводник имеет площадь поперечного сечения (рис. 2). Свободные заряды проводника будем считать положительными; величину свободного заряда обозначим (в наиболее важном для практики случая металлического проводника это есть заряд электрона). Концентрация свободных зарядов (т. е. их число в единице объёма) равна .

Рис. 2. К выводу формулы

Какой заряд пройдёт через поперечное сечение нашего проводника за время ?

С одной стороны, разумеется,

(3)

С другой стороны, сечение пересекут все те свободные заряды, которые спустя время окажутся внутри цилиндра с высотой . Их число равно:

Следовательно, их общий заряд будет равен:

(4)

Приравнивая правые части формул (3) и (4) и сокращая на , получим:

(5)

Соответственно, плотность тока оказывается равна:

Давайте в качестве примера посчитаем, какова скорость движения свободных электронов в медном проводе при силе тока A.

Заряд электрона известен: Кл.

Чему равна концентрация свободных электронов? Она совпадает с концентрацией атомов меди, поскольку от каждого атома отщепляется по одному валентному электрону. Ну а концентрацию атомов мы находить умеем:

м

Положим мм . Из формулы (5) получим:

м/с.

Это порядка одной десятой миллиметра в секунду.

к оглавлению ▴

Стационарное электрическое поле

Мы всё время говорим о направленном движении зарядов, но ещё не касались вопроса о том, почему свободные заряды совершают такое движение. Почему, собственно, возникает электрический ток?

Для упорядоченного перемещения зарядов внутри проводника необходима сила, действующая на заряды в определённом направлении. Откуда берётся эта сила? Со стороны электрического поля!

Чтобы в проводнике протекал постоянный ток, внутри проводника должно существовать стационарное (то есть — постоянное, не зависящее от времени) электрическое поле. Иными словами, между концами проводника нужно поддерживать постоянную разность потенциалов.

Стационарное электрическое поле должно создаваться зарядами проводников, входящих в электрическую цепь. Однако заряженные проводники сами по себе не смогут обеспечить протекание постоянного тока.

Рассмотрим, к примеру, два проводящих шара, заряженных разноимённо. Соединим их проводом. Между концами провода возникнет разность потенциалов, а внутри провода — электрическое поле. По проводу потечёт ток. Но по мере прохождения тока разность потенциалов между шарами будет уменьшаться, вслед за ней станет убывать и напряжённость поля в проводе. В конце концов потенциалы шаров станут равны друг другу, поле в проводе обратится в нуль, и ток исчезнет. Мы оказались в электростатике: шары плюс провод образуют единый проводник, в каждой точке которого потенциал принимает одно и то же значение; напряжённость
поля внутри проводника равна нулю, никакого тока нет.

То, что электростатическое поле само по себе не годится на роль стационарного поля, создающего ток, ясно и из более общих соображений. Ведь электростатическое поле потенциально, его работа при перемещении заряда по замкнутому пути равна нулю. Следовательно, оно не может вызывать циркулирование зарядов по замкнутой электрической цепи — для этого требуется совершать ненулевую работу.

Кто же будет совершать эту ненулевую работу? Кто будет поддерживать в цепи разность потенциалов и обеспечивать стационарное электрическое поле, создающее ток в проводниках?

Ответ — источник тока, важнейший элемент электрической цепи.

Чтобы в проводнике протекал постоянный ток, концы проводника должны быть присоединены к клеммам источника тока (батарейки, аккумулятора и т. д.).

Клеммы источника — это заряженные проводники. Если цепь замкнута, то заряды с клемм перемещаются по цепи — как в рассмотренном выше примере с шарами. Но теперь разность потенциалов между клеммами не уменьшается: источник тока непрерывно восполняет заряды на клеммах, поддерживая разность потенциалов между концами цепи на неизменном уровне.

В этом и состоит предназначение источника постоянного тока. Внутри него протекают процессы неэлектрического (чаще всего — химического) происхождения, которые обеспечивают непрерывное разделение зарядов. Эти заряды поставляются на клеммы источника в необходимом количестве.

Количественную характеристику неэлектрических процессов разделения зарядов внутри источника — так называемую ЭДС — мы изучим позже, в соответствующем листке.

А сейчас вернёмся к стационарному электрическому полю. Каким же образом оно возникает в проводниках цепи при наличии источника тока?

Заряженные клеммы источника создают на концах проводника электрическое поле. Свободные заряды проводника, находящиеся вблизи клемм, приходят в движение и действуют своим электрическим полем на соседние заряды. Со скоростью, близкой к скорости света, это взаимодействие передаётся вдоль всей цепи, и в цепи устанавливается постоянный электрический ток. Стабилизируется и электрическое поле, создаваемое движущимися зарядами.

Стационарное электрическое поле — это поле свободных зарядов проводника, совершающих направленное движение.

Стационарное электрическое поле не меняется со временем потому, что при постоянном токе не меняется картина распределения зарядов в проводнике: на место заряда, покинувшего данный участок проводника, в следующий момент времени поступает точно такой же заряд. По этой причине стационарное поле во многом (но не во всём) аналогично полю электростатическому.

А именно, справедливы следующие два утверждения, которые понадобятся нам в дальнейшем (их доказательство даётся в вузовском курсе физики).

1. Как и электростатическое поле, стационарное электрическое поле потенциально. Это позволяет говорить о разности потенциалов (т. е. напряжении) на любом участке цепи (именно эту разность потенциалов мы измеряем вольтметром).
Потенциальность, напомним, означает, что работа стационарного поля по перемещению заряда не зависит от формы траектории. Именно поэтому при параллельном соединении проводников напряжение на каждом из них одинаково: оно равно разности потенциалов стационарного поля между теми двумя точками, к которым подключены проводники.
2. В отличие от электростатического поля, стационарное поле движущихся зарядов проникает внутрь проводника (дело в том, что свободные заряды, участвуя в направленном движении, не успевают должным образом перестраиваться и принимать «электростатические» конфигурации).
Линии напряжённости стационарного поля внутри проводника параллельны его поверхности, как бы ни изгибался проводник. Поэтому, как и в однородном электростатическом поле, справедлива формула , где — напряжение на концах проводника, — напряжённость стационарного поля в проводнике, — длина проводника.

Постоянный
электрический ток. Сила и плотность
тока.

Постоя́нный
ток,
DC (англ. direct
current —
постоянный ток) — электрический
ток,
параметры, свойства и направление
которого не изменяются (в различных
смыслах) со временем. Характеризуется
параметрами – Вольт (V), Ампер (А), Ом(R) и
Ватт (W).

Ток,
величина которого постоянна во времени.

• Не
  переменный ток, то есть ток, не меняющий
  своего направления со временем и не
  имеющий частоты (то есть для него частота
  f=0).

• Постоянный
  ток как характеристика питания
  устройств — питание от источника с
  напряжением или током нулевой частоты
  (пример — двигатель
  постоянного тока).

Существуют
источники постоянного тока, ток на
выходе которых не зависит от времени и
сопротивления нагрузки.

Постоянный
ток широко используется в технике:
подавляющее большинство электронных
схем в качестве питания используют
постоянный ток. Переменный
ток используется
преимущественно для более удобной
передачи от генератора до потребителя.

Иногда
в некоторых устройствах постоянный ток
преобразуют в переменный ток
преобразователями (инверторами).

Сила
тока —
скалярная физическая величина,
определяемая отношением заряда Δq,
проходящего через поперечное сечение
проводника за некоторый промежуток
времени Δt, к этому промежутку времени.

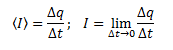
Единицей
силы тока в СИ является ампер (А).

Если
сила тока и его направление со временем
не изменяются, то ток называется
постоянным.

Единица
силы тока — основная единица в СИ 1 А —
есть сила такого неизменяющегося тока,
который, проходя по двум бесконечно
длинным параллельным прямолинейным
проводникам очень маленького сечения,
расположенным на расстоянии 1 м друг от
друга в вакууме, вызывает силу
взаимодействия между ними 2·10-7 Η на
каждый метр длины проводников.

Рассмотрим,
как зависит сила тока от скорости
упорядоченного движения свободных
зарядов.

Выделим
участок проводника площадью сечения S
и длиной Δl (рис. 1). Заряд каждой частицы
q0. В объеме проводника, ограниченном
сечениями 1 и 2, содержится nSΔl частиц,
где n — концентрация частиц. Их общий
заряд 

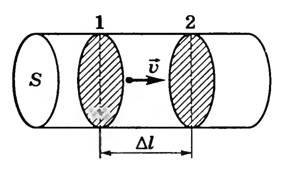
Рис.
1

Если
средняя скорость упорядоченного движения
свободных зарядов ,
то за промежуток времени  все
частицы, заключенные в рассматриваемом
объеме, пройдут через сечение 2. Поэтому
сила тока: 

Таким
образом, сила тока в проводнике зависит
от заряда, переносимого одной частицей,
их концентрации, средней скорости
направленного движения частиц и площади
поперечного сечения проводника.

Заметим,
что в металлах модуль вектора средней
скорости упорядоченного движения
электронов  при
максимально допустимых значениях силы
тока ~ 10-4 м/с, в то время как средняя
скорость их теплового движения ~ 106 м/с.

Плотность
тока j
— это векторная физическая величина,
модуль которой определяется отношением
силы тока I в проводнике к площади S
поперечного сечения проводника, т.е. 

В
СИ единицей плотности тока является
ампер на квадратный метр (А/м2).

Как
следует из формулы (1), .
Направление вектора плотности
тока  совпадает
с направлением вектора скорости
упорядоченного движения  положительно
заряженных частиц. Плотность постоянного
тока постоянна по всему поперечному
сечению проводника.

Сегодня у нас на рассмотрении вопрос касающийся электричества, а именно: с какой скоростью электроны движутся по проводам.

Думаю ни для никого не секрет, что носителями заряда в металле являются свободные электроны, которых там очень много. Если человек задастся сегодняшним вопросом, то может ответить, что скорость электронов в проводнике очень большая, сравнимая со скоростью света. Ведь как только мы переключаем выключатель, чтобы включить свет в комнате, тот в свою очередь появляется мгновенно. Можно простить обывателя за такой вывод, ведь мало кто изучал физику на серьезном уровне.

Сейчас мы с вами разберемся, где зарыта правда. Делать выводы мы будем исходя из классической теории металлов, не учитывая квантовых аспектов. В чем же суть классической теории металлов?

Классическую теорию металлов разработал Пауль Друде. Он предположил, что электроны проводимости в металле ведут себя словно молекулы идеального газа и в промежутках между соударениями движутся свободно. Но в отличие от молекул газа, пробег которых определяется соударениями друг с другом, электроны сталкиваются преимущественно с ионами, образующими кристаллическую решетку металла. Эти столкновения приводят к установлению теплового равновесия между электронами и кристаллической решеткой.

Полагая, что на электронный газ могут быть распространены результаты кинетической теории газов, можно оценить их среднюю скорость теплового движения. Вычисляется она по следующей формуле:

Подставим все величины, температуру примем за комнатную (27 градусов Цельсия или 300 Кельвин)

И мы получаем величину хоть как-то сравнимую со скоростью света (скорость света равняется 3*10^8 м/сек). Но мы посчитали скорость их хаотического, то есть беспорядочного движения. А насколько мы знаем, электрический ток – это упорядоченное движение частиц. Поэтому я предлагаю рассчитать максимально возможную скорость упорядоченного движения электронов.

Чтобы мы могли говорить боле общо, речь вести будем не о токе, а о плотности тока. Это величина равная силе тока, которая проходит через какое-либо поперечное сечение проводника (обозначается она буквой j). Например: пусть по проводу с площадью поперечного сечения 2 мм^2 течет ток силой 1 Ампер. Тогда плотность тока в данном случае будет составлять j= 1/2 = 0,5 А/мм^2. Плотность тока вычисляется по следующей формуле:

Максимально возможная конструктивная плотность тока составляет около 10 А/мм^2, если ток выше этого значения, то медные провода просто начнут плавиться. Ну и среднее значение концентрации электронов в металле составляет около 10^23 в каждом кубическом сантиметре. Выразив все в одной системе единиц и подставив в это уравнение, найдем максимальное значение скорости упорядоченного движения:

И как вы видите она составляет всего 1 мм в секунду! Явно не по этой причине лампочка загорается так быстро. Но мы так и не ответили на вопрос: почему так происходит?

На самом деле ответ на данный вопрос, в отличие от предыдущего, довольно прост. Представьте себе огромную очередь битком набитую людьми. И пусть с конца очереди кто-то большой и массивный начал сильно толкать всех вперед. В этом случае начало очереди довольно быстро придет в движение, хоть и хулиган, который толкал всех сзади, двигался очень медленно.

Тоже самое происходит в проводах: когда электроны от источника начали свое движение, их импульс быстро, практически со скоростью света, передался электронам у приемника. Только в очереди людей вы передаете взаимодействие путем толчков, а электроны взаимодействуют при помощи электромагнитных сил.

Думаю теперь тема полностью раскрыта. Поддержите статью вашим драгоценным лайком, это очень поможет каналу! А также обязательно подписывайтесь на канал, чтобы не пропускать новых выпусков! Всего вам доброго и до скорых встреч!

Тут все достаточно просто, если не учитывать хаотического теплового движения электронов.

За интервал времени Δt через поперечное сечение S проводника пройдут все электроны, находившиеся в объеме SvΔt. Число таких электронов равно nSvΔt (n – концентрация электронов). Через сечение проводника за время Δt пройдет заряд Δq=enSvΔt (e – заряд электрона).

В результате имеем

Количество свободных электронов будет примерно равно количеству атомов в единице объема. Количество атомов в единице объема можно посчитать, разделив плотность на массу одного атома. Массу атома смотрим в таблице или считаем.

Дальше подставляем значения в формулу и получаем результат.

Честно говоря мне лень считать и получать численное значение:) . Тем более, что вопрос звучит КАК рассчитать, т.е. численного ответа можно не писать. Значение будет примерно пара-тройка миллиметров в секунду.

Сила тока I для тока, протекающего через некоторую площадь сечения проводника S эквивалентна производной заряда q по времени t и количественно характеризует электрический ток.

Таким образом выходит, что сила тока — это поток заряженных частиц через некоторую поверхность S.

Электрический ток является процессом движения как отрицательных, так и положительных зарядов.

Перенос заряда одного знака в определенную сторону равен переносу заряда, обладающего противоположным знаком, в обратном направлении. В ситуации, когда ток образуется зарядами и положительного, и отрицательного знаков (dq+ и dq−), справедливым будет заключение о том, что сила тока равна следующему выражению:

I=dq+dt+dq-dt.

В качестве положительного определяют направление движения положительных зарядов. Ток может быть постоянным, когда ни сила тока, ни его направление не претерпевают изменений с течением времени, или, наоборот, переменным. При условии постоянства, формула силы тока может выражаться в следующем виде:

I=q∆t,

где сила тока определена в качестве заряда, который пересекает некоторую поверхность S в единицу времени. В системе СИ роль основной единицы измерения силы тока играет Ампер (А).

1A=1 Кл1 с.

Плотность тока. Связь плотности тока с зарядом и силой тока, напряженностью

Выделим в проводнике, в котором протекает ток, малый объем dV случайной формы. С помощью следующего обозначения υ определим среднюю скорость движения носителей зарядов в проводнике. Пускай n0 представляет собой концентрацию носителей заряда. На поверхности проводника выберем пренебрежительно малую площадку dS, которая расположена ортогонально скорости υ (рис. 1).

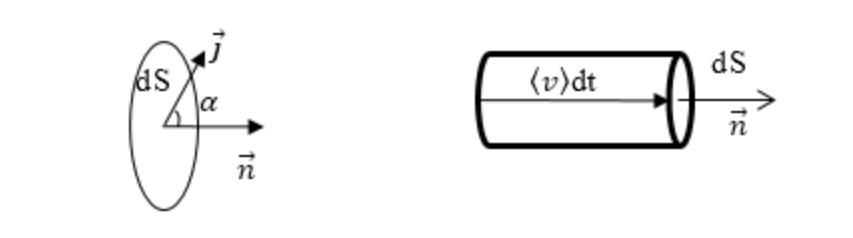
Рисунок 1

Проиллюстрируем на поверхности площадки dS очень короткий прямой цилиндр, имеющий высоту υdt. Весь массив частиц, которые располагались внутри такого цилиндра за время dt пересекут плоскость dS и перенесут через нее, в направлении скорости υ, заряд, выражающийся в виде следующего выражения:

dq=n0qeυdSdt,

где qe=1,6·10-19 Кл является зарядом электрона, другими словами отдельной частицы или же носителя тока. Разделим приведенную формулу на dSdt и получим:

j=dqdSdt,

где j представляет собой модуль плотности электрического тока.

j=n0qeυ,

где j является модулем плотности электрического тока в проводнике, в котором заряд переносится электронами. В случае, если ток появляется как результат движения нескольких типов зарядов, то формула плотности тока может быть определена в виде следующего выражения:

j=∑niqiυii,

где i представляет собой носитель заряда. Плотность тока — это векторная величина. Снова обратим внимание на рисунок 1. Пускай n→ представляет собой единичный перпендикуляр к плоскости dS. В случае, если частицы, переносящие заряд, являются положительными, то переносимый ими заряд в направлении нормали больше нуля. В общем случае переносимый в единицу времени элементарный заряд может быть записана в следующем виде:

dqdt=j→n→dS=jndS.

Формула приведенная выше справедлива также в том случае, когда плоскость площадки dS неортогональная по отношению к вектору плотности тока. По той причине, что составляющая вектора j→, направленная под прямым углом к нормали, через сечение dS электричества не переносит. Исходя из всего вышесказанного, плотность тока в проводнике окончательно запишем, применяя формулу j=n0qeυ в таком виде:

j→=-n0qeυ→.

Таким образом, плотность тока эквивалентна количеству электричества, другими словами заряду, который протекает за одну секунду через единицу сечения проводника. В отношении однородного цилиндрического проводника справедливым будет записать, что:

j=IS∆t,

где S играет роль площади сечения проводника. Плотность постоянного тока равна по всей площади сечения проводника. Для двух разных сечений проводника (S1,S2) с постоянным током справедливо следующее равенство:

j1j2=S2S1.

Основываясь на законе Ома для плотности токов можно записать такое выражение:

j→=λE→,

где λ обозначает коэффициент удельной электропроводности. Определив плотность тока, мы имеем возможность выразить силу тока в следующем виде:

I=∫SjndS,

где интегрирование происходит по всей поверхности S любого сечения проводника. Единица плотности тока Aм2.

Линии тока

Линии, вдоль которых движутся заряженные частицы, носят название линий тока.

Направления движения положительных зарядов также определяются в качестве направлений линий тока. Изобразив линии тока, можно получить наглядное представление о движении электронов и ионов, которые формируют собой ток. Если внутри проводника выделить трубку с током, у которой боковая поверхность состоит из линий тока, то движущиеся заряженные частицы не будут пересекать боковую поверхность данной трубки. Такую трубка представляет собой так называемую трубку тока. К примеру, поверхность металлической проволоки в изоляторе будет определяться как труба тока.