Скорости и ускорения как производные координаты
Зная координату тела (закон, по которому она изменяется) можно очень многое о движении этого тела узнать. Например, скорость – первая производная от координаты. А ускорение – вторая производная, или первая производная скорости. Если в задаче дано еще и время движения тела – то можно полностью описать движение и найти все его характеристики для данного момента времени.
Ускорение
Задача 1.
Точка движется по прямой согласно закону , где
м/с,
м/c
. Определить: среднюю скорость точки в интервале времени от
с до
с, координату точки в тот момент времени, когда скорость тела будет равна нулю.
Средняя скорость – это отношение пройденного пути ко времени. Время движения очевидно: с. А путь можно определить как
:
Чтобы определить скорость, возьмем производную координаты по времени:
Если скорость равна 0, то
Откуда с и
м.
Ответ: м/с,
м.
Задача 2.
Точка движется вдоль оси по закону
. Найти направление движения в моменты времени: а)
с; б)
с. Чему будут равны ускорения в эти моменты времени?
Чтобы определить направление движения, нам надо узнать знак скорости в данные моменты времени. Определим сначала скорость тела как производную координаты:
Тогда
Поэтому в момент времени тело движется в положительном направлении, а в момент времени
– в отрицательном.
Определим ускорение как вторую производную от координаты, или первую производную скорости по времени:
Ответ: м/с, движение по оси,
м/с
,
м/с, движение против оси,
м/с
.
Задача 3.
Тело движется прямолинейно, причем скорость зависит от времени по закону: . Определить зависимость ускорения от времени
. Каково значение ускорения при
с?
Чтобы найти ускорение, возьмем производную скорости:
При имеем:
Ответ: ,
м/с
.
15 мая 2014
Иногда в задаче 6 из ЕГЭ по математике вместо всеми любимых графиков функции или производной дается просто уравнение расстояния от точки до начала координат. Что делать в этом случае? Как по расстоянию найти скорость или ускорение.
На самом деле все просто. Скорость — это производная от расстояния, а ускорение — это производная скорости (или, что то же самое, вторая производная от расстояния). В этом коротком видео вы убедитесь, что такие задачи решаются ничуть не сложнее «классических» заданий 6.
Сегодня мы разберем две задачи на физический смысл производных из ЕГЭ по математике. Эти задания встречаются в части Bи существенно отличаются от тех, что большинство учеников привыкло видеть на пробниках и экзаменах. Все дело в том, что они требуют понимать физический смысл производной функции. В данных задачах речь пойдет о функциях, выражающих расстояния.
Если $S=xleft( t right)$, то $v$ мы можем посчитать следующим образом:
[v={S}’={x}’left( t right)]
Точно так же мы можем посчитать и ускорение:
[a={v}’={{S}’}’={{x}’}’left( t right)]
Эти три формулы – все, что вам потребуется для решения таких примеров на физический смысл производной. Просто запомните, что $v$ — это производная от расстояния, а ускорение — это производная от скорости.
Давайте посмотрим, как это работает при решении реальных задач.
Пример № 1
Материальная точка движется по закону:
[xleft( t right)=-frac{1}{5}{{t}^{5}}+{{t}^{4}}-{{t}^{3}}+5t]
где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, прошедшее с начала движения. Найдите скорость точки (в м/с) в момент времени $t=2c$.
Это означает, что у нас есть функция, задающая расстояние, а нужно посчитать скорость в момент времени $t=2c$. Другими словами, нам нужно найти $v$, т.е.
[v={S}’={x}’left( 2 right)]
Вот и все, что нам нужно было выяснить из условия: во-первых, как выглядит функция, а во-вторых, что от нас требуется найти.
Давайте решать. В первую очередь, посчитаем производную:
[{x}’left( t right)=-frac{1}{5}cdot 5{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]
[{x}’left( t right)=-{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]
Нам требуется найти производную в точке 2. Давайте подставим:
[{x}’left( 2 right)=-{{2}^{4}}+4cdot {{2}^{3}}-3cdot {{2}^{2}}+5=]
[=-16+32-12+5=9]
Вот и все, мы нашли окончательный ответ. Итого, скорость нашей материальной точки в момент времени $t=2c$ составит 9 м/с.
Пример № 2
Материальная точка движется по закону:
[xleft( t right)=frac{1}{3}{{t}^{3}}-4{{t}^{2}}+19t-11]
где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, измеренное с начала движения. В какой момент времени ее скорость была равна 3 м/с?
Взгляните, в прошлый раз от нас требовалось найти $v$ в момент времени 2 с, а в этот раз от нас требуется найти тот самый момент, когда эта скорость будет равна 3 м/с. Можно сказать, что нам известно конечное значение, а по этому конечному значению нам требуется найти исходное.
В первую очередь, вновь ищем производную:
[{x}’left( t right)=frac{1}{3}cdot 3{{t}^{2}}-4cdot 2t+19]
[{x}’left( t right)={{t}^{2}}-8t+19]
От нас просят найти, в какой момент времени скорость будет равна 3 м/с. Составляем и решаем уравнение, чтобы найти физический смысл производной:
[{{t}^{2}}-8t+19=3]
[{{t}^{2}}-8t+16=0]
[{{left( t-4 right)}^{2}}=0]
[t-4=0]
[t=4]
Полученное число означает, что в момент времени 4 с $v$ материальной точки, движущейся по выше описанному закону, как раз и будет равна 3 м/с.
Ключевые моменты
В заключении давайте еще раз пробежимся по самому главному моменту сегодняшней задачи, а именно, по правилу преобразования расстояние в скорость и ускорение. Итак, если нам в задаче прямо описан закон, прямо указывающий расстояние от материальной точки до точки отсчета, то через эту формулу мы можем найти любую мгновенную скорость (это просто производная). И более того, мы можем найти еще и ускорение. Ускорение, в свою очередь, равно производной от скорости, т.е. второй производной от расстояния. Такие задачи встречаются довольно редко, поэтому сегодня мы их не разбирали. Но если вы увидите в условии слово «ускорение», пусть оно вас не пугает, достаточно просто найти еще одну производную.
Надеюсь, этот урок поможет вам подготовиться к ЕГЭ по математике.
Смотрите также:
- Не допускайте таких ошибок, когда видите график производной в задаче 6 из ЕГЭ по математике!
- ЕГЭ 2022, задание 6. Касательная и квадратичная функция с параметром
- Схема Бернулли. Примеры решения задач
- Комбинаторика в задаче B6: средний тест
- Как решать задачи про летающие камни?
- B4: счетчики на электричество
Применение производной в физике и технике
- Скорость и ускорение
- Физические величины как производные от других величин
- Примеры
п.1. Скорость и ускорение
Рассматривая физический смысл производной (см. §42 данного справочника), мы выяснили, что:
Производная функции (y=f(x)) в точке (x_0) равна скорости изменения функции в этой точке.
Например:
Рассмотрим прямолинейное равноускоренное движение.
Уравнение этого движения имеет вид: $$ x(t)=x_0+v_0t+frac{at^2}{2} $$ где (x(t)) – ккордината тела в произвольный момент времени (t, x_0) – начальная координата, (v_0) – начальная скорость, (a=const) – ускорение, действующее на тело.
Чтобы найти скорость тела из этого уравнения, нужно найти производную от координаты по времени: $$ v(t)=x'(t)=left(x_0+v_0t+frac{at^2}{2}right)’=0+v_0cdot 1+frac a2cdot 2t=v_0+at $$ Чтобы найти ускорение, нужно найти производную от скорости: $$ a(t)=v'(t)=x”(t)=(v_0+at)’=0+acdot 1=a=const $$
п.2. Физические величины как производные от других величин
Если рассматривать уравнение процесса (s=f(t)), его производной будет величина $$ f'(t)=lim_{triangle trightarrow 0}frac{triangle s}{triangle t} $$ Такие величины часто встречаются в различных разделах физики и техники.
Исходная величина (процесс)
Производная по времени
Координата (x(t))
Скорость (v(t)=x'(t))
Ускорение (a(t)=v'(t)=x”(t))
Угол поворота (varphi(t))
Угловая скорость (omega(t)=omega'(t))
Угловое ускорение (beta(t)=omega'(t)=varphi”(t))
Масса горючего ракеты (m(t))
Скорость расходования горючего (u(t)=m'(t))
Температура тела (T(t))
Скорость нагрева (v_T(t)=T'(t))
Заряд (q(t))
Сила тока (I(t)=q'(t))
Работа (A(t))
Мощность (N(t)=A'(t))
Магнитный поток (Ф(t))
ЭДС индукции (varepsilon(t)=-Ф'(t))
Число атомов радиоактивного вещества (N(t))
Скорость радиоактивного распада (I(t)=-N'(t))
Конечно же, в физике далеко не обязательно берут производную только по времени.
Например, для теплоты Q(T) теплоемкость равна C(T)=Q'(T), где T – температура.
А для процесса теплопереноса температура u(x,t) в точке с координатой x в момент времени t определяется уравнением теплопроводности: $$ frac{partial u(x,t)}{partial t}-a^2frac{partial^2 u(x,t)}{partial x^2}=f(x,t) $$ и производные берутся по времени (left(frac{partial u}{partial t}right)) и по координате (left(frac{partial u}{partial x}right)), причем по координате берется производная второго порядка (left(frac{partial^2 u}{partial x^2}right)).
Поэтому в физике для производных чаще используются обозначения Лейбница, в которых хорошо видна как функция, так и аргумент.
Например, для производных функции от одной переменной: (frac{partial varphi}{partial t}, frac{partial p}{partial V}, frac{partial Q}{partial T},…)
Для производных функций от многих переменных: (frac{partial u}{partial t}, frac{partial u}{partial x}, frac{partial u}{partial y}, frac{partial u}{partial z},…)
п.3. Примеры
Пример 1. Тело массой 6 кг движется прямолинейно по закону (x(t)=t^2+t+1) (м). Найдите: 1) кинетическую энергию тела через 3 с после начала движения; 2) силу, действующую на тело в это время.
1) Кинетическая энергия равна (E=frac{mv^2}{2})
Скорость тела: (v(t)=x'(t)=(t^2+t+1)’=2t+1)
Через 3 с: (v(3)=2cdot 3+1=7) (м/с)
Подставляем: (E=frac{6cdot 7^2}{2}=147) (Дж)
2) Сила по второму закону Ньютона: (F=ma)
Ускорение тела: (a(t)=v'(t)=(2t+1)’=2) (м/с^2)
Ускорение постоянно.
На тело действует постоянная сила: (F=6cdot 2=12) (Н)
Ответ: 147 Дж; 12 Н
Пример 2. Маховик вращается по закону (varphi (t)=4t-0,5t^2) (рад)
Найдите момент времени, в который маховик остановится.
Угловая скорость: (omega(t)=varphi ‘(t)=(4t-0,5t^2 )’=4-0,5cdot 2t=4-t)
В момент остановки угловая скорость равна 0. Решаем уравнение: $$ 4-t=0Rightarrow t=4 (c) $$ Ответ: 4 c
Пример 3. Ракету запустили вертикально вверх с начальной скоростью 40 м/с. В какой момент времени и на какой высоте ракета достигнет наивысшей точки (g≈10м/с2)?
Выберем начало отсчета на земле ((y_0=0)), направим ось y вверх.
Начальная скорость направлена вверх, её проекция на ось положительна.
Ускорение свободного падения направлено вниз, его проекция отрицательна.
Уравнение движения: $$ y(t)=y_0+v_{0y}t+frac{g_y t^2}{2}=0+40t-frac{10t^2}{2}=40t-5t^2 $$ В верхней точке траектории ракета останавливается, её скорость равна 0.
Найдем скорость: $$ v(t)=y'(t)=40-5cdot 2t=40-10t $$ Найдем момент остановки в верхней точке: $$ 40-10t_0=0Rightarrow t_0=frac{40}{10}=4 (c) $$ Найдем высоту подъема в верхней точке: $$ H_{max}=y(t_0)=40cdot 4-5cdot 4^2=80 (м) $$ Ответ: 4 с, 80 м
Пример 4. Через поперечное сечение проводника проходит заряд (q(t)=ln(t+1)) (Кл). В какой момент времени сила тока в проводнике равна 0,1 А?
Сила тока: $$ I(t)=q'(t)=(ln(t+1))’=frac{1}{t+1} $$ По условию: $$ frac{1}{t_0+1}=0,1Rightarrow t_0+1=frac{1}{0,1}=10Rightarrow t_0=9 (c) $$ Ответ: 9 c
Пример 5. Колесо вращается так, что угол его поворота пропорционален квадрату времени. Первый оборот оно сделало за 8 с. Найдите угловую скорость через 48 с после начала вращения.
По условию угол поворота (varphi (t)=At^2)
Один оборот (2pi) радиан был сделан за 8 с. Получаем уравнение: (Acdot 8^2=2pi)
Находим коэффициент (A=frac{2pi}{8^2}=frac{pi}{32})
Уравнение движения (varphi(t)=frac{pi}{32}t^2) (рад)
Угловая скорость (omega(t)=varphi ‘(t)=left(frac{pi}{32}t^2right)’=frac{pi}{32}cdot 2t=frac{pi}{16}t) (рад/с)
Через 48 секунд (omega(48)=frac{pi}{16}cdot 48=3pi) рад/с – полтора оборота в секунду.
Ответ: (3pi) рад/с
Пример 6. Для нагревания 1 кг жидкости от 0°С до t°C необходимо (Q(t)=1,7t+at^2+bt^3) Дж теплоты.
Известно, что теплоемкость жидкости при температуре 100°С равна 1,71 Дж/К, а для нагревания 1 кг этой жидкости 0°С до 50°C требуется 85,025 Дж теплоты. Найдите коэффициенты a и b.
Теплоемкость: (C(t)=Q'(t)=1,7cdot 1+acdot 2t+bcdot 3t^2=1,7+2at+3bt^2)
По условию: begin{gather*} C(100)=1,7+2acdot 100+3bcdot 100^2-1,71\ 200a+30000b=0,01 end{gather*} Кроме того: begin{gather*} Q(50)=1,7cdot 50+acdot 50^2+bcdot 50^3=85,025\ 2500a+125000b=0,025 end{gather*} Получаем линейную систему: begin{gather*} begin{cases} 200a+30000b=0,01 |:2\ 2500a+125000b=0,025 |:25 end{cases} Rightarrow begin{cases} 100a+15000b=0,005\ 100a+5000b=0,001 end{cases} \ 15000b-5000b=0,005-0,001\ 10000b=0,004\ b=4cdot 10^{-3}cdot 10^{-4}=4cdot 10^{-7} left(frac{Дж}{K^3}right)\ a=frac{0,001-5000b}{100}=frac{10^{-3}-5cdot 10^3cdot 4cdot 10^{-7}}{100}=frac{10^{-3}-2cdot 10^{-3}}{100}=-frac{10^{-3}}{100}\ a=-10^{-5} left(frac{Дж}{K^2}right) end{gather*} Ответ: (a=-10^{-5}frac{Дж}{K^2}; b=4cdot 10^{-7}frac{Дж}{K^3})
Пример 7*. Лестница длиной 5 м стояла вертикально. Потом её нижний конец стали перемещать по полу с постоянной скоростью (v=2) м/с. С какой по абсолютной величине скоростью в зависимости от времени опускается верхний конец лестницы? Постройте график полученной функции.
 |
Лестница со стенами образует прямоугольный треугольник, для которого справедлива теорема Пифагора: $$ x^2(t)+y^2(t)=5^2 $$ Нижний конец движется с постоянной скоростью, его уравнение движения по полу: $$ x(t)=vt=2t $$ Отсюда получаем уравнение движения верхнего конца по стенке: begin{gather*} y^2(t)=25-x^2(t)=25-(2t)^2=25-4t^2\ y(t)=sqrt{25-4t^2} end{gather*} |
Время (tgeq 0) имеет ограничение сверху (25-4t^2geq 0Rightarrow t^2leq frac{25}{4}Rightarrow 0leq tleq 2,5 (с))
Скорость скольжения верхнего конца по стенке: begin{gather*} u_y(t)=y'(t)=left(sqrt{25-4t^2}right)’=frac{1}{2sqrt{25-4t^2}}cdot (25-4t^2)’=frac{-8t}{2sqrt{25-4t^2}}\ u_y(t)=-frac{4t}{sqrt{25-4t^2}} end{gather*} Знак «-» указывает на направление скорости вниз и связан с уменьшением координаты (y(t)) со временем. Абсолютная величина найденной скорости: begin{gather*} u(t)=|u_y(t)|=frac{4t}{sqrt{25-4t^2}} end{gather*} 1) ОДЗ: (0leq tleq 2,5)
2) Четность – нет, т.к. функция определена только на положительных t.
Периодичность – нет.
3) Асимптоты:
1. Вертикальная
Рассмотрим односторонние пределы begin{gather*} lim_{trightarrow +0}left(frac{4t}{sqrt{25-4t^2}}right)=frac05=0\ lim_{trightarrow 2,5-0}left(frac{4t}{sqrt{25-4t^2}}right)=frac{10}{0}=+infty end{gather*} При подходе к правой границе (t=2,5) слева функция стремится к (+infty).
В точке (t=2,5) – вертикальная асимптота.
2. Горизонтальных асимптот нет, т.к. ОДЗ ограничено интервалом.
3. Наклонных асимптот нет.
4) Первая производная begin{gather*} u'(t)=4cdotfrac{1cdotsqrt{25-4t^2}-tcdotfrac{-8t}{2sqrt{25-4t^2}}}{25-4t^2}=4cdotfrac{25-4t^2+8t^2}{2(25-4t^2)^{frac32}}=frac{2(4t^2+25)}{(25-4t^2)^{frac32}} end{gather*} (u'(t)gt 0) на всей ОДЗ, функция возрастает.
5) Вторая производная begin{gather*} u”(t)=frac{2(4t^2+25)}{(25-4t^2)^{frac32}}=2cdotfrac{8tcdot(25-4t^2)^{frac32}-(4t^2+25)cdot frac32sqrt{25-4t^2}cdot (-8t)}{(25-4t^3)}=\ =2cdotfrac{8tcdot(25-4t^2)+8tcdotfrac32cdot (4t^2+25)}{(25-4t^2)^{frac52}}=8tcdotfrac{50-8t^2+12t^2+75}{(25-4t^2)^{frac52}}=frac{8t(4t^2+25)}{(25-4t^2)^{frac52}} end{gather*} (u”(t)gt 0) на всей ОДЗ, функция выпуклая вниз.
6) Пересечение с осями
В начале координат: (t=0, u=0)
7) График
Ответ: (u(t)=frac{4t}{sqrt{25-4t^2}})
Пример 8. Под действием нагрузки деталь с поперечным сечением в виде прямоугольника площадью 17 см2 начинает деформироваться. Одна из сторон прямоугольника растет с постоянной скоростью 1 см/ч, а вторая – уменьшается со скоростью 0,5 см/ч. Найдите скорость изменения площади поперечного сечения через 45 мин после начала деформации, если известно, что в этот момент его площадь равна 20 см2.
Длина первой стороны в зависимости от времени: (a(t)=a_0+1cdot t) (см),
время – в часах.
Длина второй стороны: (b(t)=b_0-0,5cdot t).
Площадь в начальный момент: (S_0=a_0 b_0=17 (см^2))
Площадь в произвольный момент t: begin{gather*} S(t)=a(t)cdot b(t)=(a_0+t)(b_0-0,5t)=a_0 b_0+(-0,5a_0+b_0)t-0,5t^2=\ =17+(-0,5a_0+b_0)t-0,5t^2 end{gather*} По условию при (t=45 мин=frac34 ч): begin{gather*} Sleft(frac34right)=17+(-0,5a_0+b_0)cdotfrac34-0,5cdotleft(frac34right)^2=20\ (-0,5a_0+b_0)cdotfrac34=20-17+frac{9}{32}=3+frac{9}{32}\ (-0,5a_0+b_0)=frac43left(3+frac{9}{32}right)=4+frac38=4frac38 end{gather*} Получаем: begin{gather*} S(t)=17+4frac38t-0,5t^2 end{gather*} Скорость изменения площади: begin{gather*} S'(t)=0+4frac38cdot 1-0,5cdot 2t=4frac38-t end{gather*} Через 45 мин: begin{gather*} S’left(frac34right)=4frac38-frac34=3+frac{11}{8}-frac34=3+frac{11-6}{8}=3frac58=3,625 (см^2/ч) end{gather*} Ответ: 3,625 см2/ч
Определение скорости при координатном способе
задания
движения
Воспользуемся
уравнением (4)
и возьмем от него производную по времени
.
(8)
В
(8)
при единичных векторах стоят проекции
вектора скорости на координатные оси
.
(9)
Проекции
скорости на координатные оси определяются
как первые производные по времени от
соответствующих координат.
Зная
проекции, можно найти модуль вектора и
его направление
,
(10)
.
(11)
Определение
скорости при естественном способе
задания
движения
Пусть
дана траектория материальной точки и
закон изменения криволинейной координаты.
Предположим, при t1
точка имел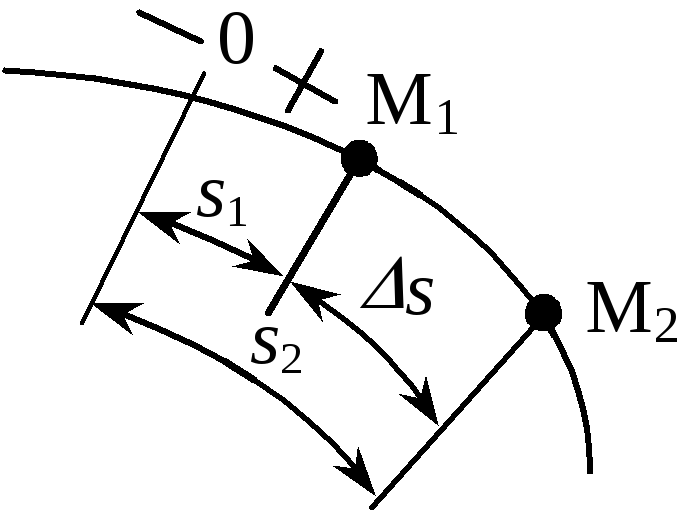
координатуs1,
а при t2
– координату s2.
За время
координата
получила приращение
,
тогда средняя скорость точки
.
Для
нахождения скорости в заданный момент
времени перейдем к пределу
,
.
(12)
Вектор
скорости точки при естественном способе
задания движения определяется как
первая производная по времени от
криволинейной координаты.
Ускорение точки
Под
ускорением материальной точки понимают
векторную величину, характеризующую
быстроту изменения вектора скорости
точки по величине и направлению с
течением времени.
Ускорение точки при векторном способе
задания движения
Рассмотрим
точку в два момента времени t1
()
иt2
(),
тогда– приращение времени,
– приращение скорости.
Вектор
всегда
лежит в плоскости движения и направлен
в сторону вогнутости траектории.
П
ускорением точки
за время t
понимают
величину
.
(13)
Для
нахождения ускорения в заданный момент
времени перейдем к пределу
,
.
(14)
Ускорение
точки в данный момент времени определяется
как вторая производная по времени от
радиус-вектора точки или первая
производная от вектора скорости по
времени.
Вектор
ускорения расположен в соприкасающейся
плоскости и направлен в сторону вогнутости
траектории.
Ускорение точки при координатном способе задания движения
Воспользуемся
уравнением связи векторного и координатного
способов задания движения
.
И возьмем от него
вторую производную
,
.
(15)
В
уравнении (15)
при единичных векторах стоят проекции
вектора ускорения на координатные оси

(16)
Проекции
ускорения на координатные оси определяются
как первые производные по времени от
проекций скорости или как вторые
производные от соответствующих координат
по времени.
Модуль и направление
вектора ускорения можно найти по
следующим выражениям
,
(17)
,
,
.
(18)
Ускорение точки при естественном способе задания движения
П
точка движется по криволинейной
траектории. Рассмотрим два ее положения
в моменты времениt
(s,
M,
v)
и t1
(s1,
M1,
v1).
Ускорение
при этом определяется через его проекции
на оси естественной системы координат,
движущейся вместе с точкой M.
Оси при этом направлены следующим
образом:
M
– касательная, направлена вдоль касательной
к траектории, в сторону положительного
отсчета расстояния,
Mn
– главная нормаль, направлена по нормали,
лежащей в соприкасающейся плоскости,
и направлена в сторону вогнутости
траектории,
Mb
– бинормаль, перпендикулярна плоскости
Mn
и образует с первыми осями правую тройку.
Так
как вектор ускорения лежит в соприкасающейся
плоскости, то ab=0.
Найдем проекции ускорения на другие
оси.
.
(19)
Спроектируем
(19)
на координатные оси
,
(20)
.
(21)
Проведем
через точку M1
оси параллельные осям в точке M
и найдем проекции скорости:
M:
,
Mn:
,
(22)
где – так называемый угол смежности.
Подставляем
(22)
в (20)
.
При
t0
0,
cos1,
тогда
.
(23)
Касательное
ускорение точки определяется первой
производной по времени от скорости или
второй производной по времени от
криволинейной координаты.
Касательное
ускорение характеризует изменение
вектора скорости по величине.
Подставим
(22)
в (21)
.
Умножим
числитель и знаменатель на s
чтобы получить известные пределы
,
(24)
где(первый
замечательный предел),
,
,
,
где
– радиус кривизны траектории.
Подставляя
вычисленные пределы в (24),
получим
.
(25)
Нормальное
ускорение точки определяется отношением
квадрата скорости к радиусу кривизны
траектории в данной точке.
Нормальное
ускорение характеризует изменение
вектора скорости по направлению и всегда
направлено в сторону вогнутости
траектории.
Окончательно
получим проекции ускорения материальной
точки на оси естественной системы
координат и модуль вектора

(26)
.
(27)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
02.04.2015390.66 Кб2316.doc
- #
- #
- #
- #
- #
- #
- #
- #
- #
В КИМах ЕГЭ по математике содержатся задачи, в ходе решения которых необходимо знать и понимать физический смысл производной. Также встречаются задачи, связанные с движением какой-то определённой точки, которая представлена в виде уравнения, и необходимо найти его скорость в момент движения. Представим, что движение точки (назовём её – х) на координатной оси происходит в определённое время (время обозначим, как t). Получаем, что скоростью в определённый момент времени будет являться производная координат по времени. Так мы находим механический смыл производной.
V (t) = x (t)
а (t) = v (t).
То есть физическим смыслом производной является скорость. Для решения задач на данную тему необходимо знать производные, рассмотрим их:
– х = 1;
– x^2 = 2x;
– √х = 1 / 2√x;
– 1 / x = – 1 / x^2;
– sin x = cos x;
– tg x = 1 / cos^2 x;
– e^x = e^x;
– ln x = 1 / x и другие.
Рассмотрим пример решения задачи. Материальная точка х (t) = 6t^2 – 48t + 17, здесь: х является расстоянием от точки в метрах, t – временем, измеряем в секундах.
Найти: скорость движения точки в момент времени, равный девяти секундам.
Решение: помним, что физическим смыслом производной является скорость. Находим закон измерения скорости согласно формуле: v (t) = x (t) = 12t – 48 м / с.
Получаем: v (9) = 12 * 9 – 48 = 60 м / с.
Ответ: скорость движения в момент временя, равный девяти секундам, будет равна 60 метров в секунду.
Перейдём к рассмотрению второй темы для разбора ЕГЭ по математике, эта тебя является уравнением касательной к графику функции.
Итак, если прямая проходит через точку, имеющую координаты х0, f (x0), а угол наклона у этой прямой равняется производной функции в этой точке, такая прямая является касательной к графику. Нужно иметь в виду, что если нет производной графика в точке, то не будет и самой касательной.
Рассмотрим задачу по данной теме: для того чтобы задать любую прямую, следует использовать формулу6 у = kx + b. Коэффициент k определяет угол расположения для прямой на оси ОХ. Если коэффициент будет больше нуля, то угол наклона, соответственно, будет острым. Если коэффициент будет меньше нуля, то есть отрицательный, то угол между ОХ и касательной будет тупым.
Для задания уравнения касательной, следует использовать следующую формулу: y = f (x0) * (x – x0) + f (x0). Переходим к подробному рассмотрению. Проведём аналогию среди уравнений для прямой и касательной. Для того, чтобы найти коэффициент k, нужно найти производную в точке, которую мы рассматриваем.
Находим уравнение прямой для следующей функции у = х^3 в точке x0 = 3.
Во-первых, нужно найти производную этой функции: у = 3х^2.
Во-вторых, у (3) = 3 * 3^2 = 27.
В-третьих, находим значение данной функции в точке f(0). f(3) = 3^3 = 27.
В-четвёртых, составляем уравнение для касательной по следующей формуле: у = 27 * (х – 3) + 27.
Делаем преобразования: у = 27 * (х – 3) + 27 = 27х – 81 + 27 = 27х – 54.
Далее, уравнение к касательной: у = 27ч – 54.
Таким образом, не нужны большие усилия для того, чтобы найти уравнение к касательной, важно ориентироваться в формулах. Поэтому в процессе подготовки к ЕГЭ по математике её следует запомнить либо выучить.
Итак, переходим к рассмотрению темы производной суммы, разности, произведения и частного. Существует несколько правил и формул, рассмотрим их:
– Производная суммы (разности) у двух функций будет равна сумме (разности) производных этих функций, то есть: (u +- v) = г +- v;
– Производная произведения двух функций будет равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго:
(u * v) = u * v +- u * v;
– Производная частного двух функций u(x) / v (x), если v (x) не равняется нулю и равна дроби, у которой числитель является разностью произведений производной числителя на знаменатель и числителя на производную знаменателя.
Рассмотрим пример решения одной из задач, содержащихся в заданиях ЕГЭ по математике, касающуюся нахождения суммы производной: у = х2 + 4ч + 3у = х2 + 4ч +3.
Решение: многочлен есть сумма трёх функций, далее: у = (х2 + 4х + 3) = (х2) + (4х) + (3)у = (х2 + 4ч + 3) = х2 + 4х + 3.
Производную от первого слагаемого находит по правилу: (x^p) = px^(p – 1).
(х2) = 2х (х2) = 2х.
Для того, чтобы найти производную второго слагаемого, нужно вывести константу за знак производной: (х) = 1 (х) = 1, (4х) = 4 (х) = 4 (4х) = 4 (х) = 4.
Третье слагаемое: (3) = 0 * 3 = 0.
Получаем: у = (х2 + 4х + 3) = (х2) + (4х) – (3) = 2х + 4 + 0 = 2х + 4.
Ответ: 2х + 4.
Подобным образом в ЕГЭ по математике решаются задачи на нахождения производной разности, произведения и частного.
Далее мы рассмотрим тему производной основных элементарных функций.
К элементарным функциям относят степенные, показательные, логарифмические, а также тригонометрические функции и их различные комбинации.
Показательная функция f(x) = a^x, при этом а не равна нулю. Данная функция задана на числовой прямой, её производная имеется в каждой точке. Любую показательную функцию можно выразить через показательную функцию с основанием у по формуле: а^x = e^xln a, также е^xln a = (e^ln a)^x. При применении дифференцирования сложной функции, получаем: (е^kx +b ) = ke^kx + b. Производной для а^x будет (a^x) = a^ln a.
Производная логарифмической функции х, имеющую любое основание, можно выразить через логарифмическую функцию с основанием е с применением формулы перехода x = ln ln x / ln ln a.
Производная функции lnx выражается следующей формулой: (lnx) = 1 / x, x больше нуля.
Применяем правило дифференцирования сложной функции и получаем: (ln (kx + b)) = k / kx + b).
(log a x) = 1 / x * ln a.
(log a x) = 1 * ln a.
Для производных тригонометрических функций характерны следующие неравенства:
(sin x) = cos x,
(cos x) = sin x.
Рассмотрим пример решения: f (x) = 3 ln x
3 ln x = 3 / x.
Ответ: 3 / х.
Переходим к рассмотрению заключительной темы данной статьи. Рассмотрим понятие второй производной.
Второй производной называют производную от производной первого порядка. Её обозначают как: f(x) d^2 y / dx^2.
Рассмотрим примеры решения подобных задач.
- у = х^4
у = (х^4) = 4x^3.
Далее вычисляем вторую производную: у = (у) = (4х^3) = 4 * (x^3) = 4 * 3x^2 = 12x.
Ответ: вторая производная функции равна 12х.
- у = cos 2x
y = (cos 2x) = – sin 2x * (2x) = – 2sin 2x.
у = (у) = (-2sin 2x) = – 2 (sin 2x) = – 2cos 2x *(2x) = – 4 cos 2x.
Ответ: производная второй функции равна – 4cos 2x.
Таким образом, мы рассмотрели темы, которые содержаться в разделе начала математического анализа ЕГЭ по математике, изучив теоретический, а также практический материал, изложенный в данной статье, вы будете готовы в сдаче единого государственного экзамена по данному предмету. Также рекомендуем просмотреть доступные демонстрационные варианты КИМов, это поможет вам знать примерную структуру, формулировку, а также уровень сложности заданий.






