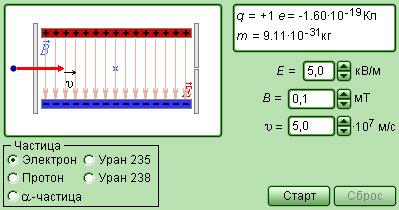
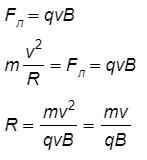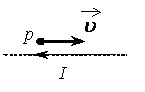Решение задач – обязательная практика в жизни всех студентов-технарей. В сегодняшней статье разберемся, как решать задачи на силу Лоренца.
Если вам скучно читать про решение задач, переходите в наш телеграм-канал. Там найдется интересная информация и новости для всех специальностей. А еще, у нас есть второй канал, где мы рассказываем об акциях нашего сервиса и дарим приятные скидки. Проверьте — и не упустите выгоду!
Задачи по теме «сила Лоренца»
Даже если вы не новичок, прежде чем решать задачи, прочтите общую памятку и на всякий случай держите под рукой полезные формулы.
Задача на силу Лоренца №1
Условие
Электрон с энергией 300 эВ движется перпендикулярно линиям индукции однородного магнитного поля напряженностью 465 А/м. Определить силу Лоренца, скорость и радиус траектории электрона.
Решение
Скорость электрона можно найти из формулы кинетической энергии:
Eк=m·v22v=2Eкm
Сила Лоренца является центростремительной силой, значит, по второму закону Ньютона, можно записать:
Магнитная индукция равна напряженности, умноженной на магнитную постоянную. Подставив ранее найденное выражение для скорости в формулу для радиуса и силы Лоренца, запишем:
R=m2Eктqμ0H=2Eктqμ0HFл=q2Eктμ0H
Теперь осталось только подставить значения и вычислить:
v=2·4,8·10-169,1·10-31=3,25·107 мсFл=4·3,14·10-7·465·1,6·10-19·3,25·107=3·10-15НR=2·4,8·10-16·9,1·10-314·3,14·10-7·465·1,6·10-19=0,32 м
Ответ: v=3,25·107 мс; Fл=3·10-15Н; R=0,32 м.
Задача на силу Лоренца №2
Условие
Альфа-частица влетает в магнитное поле с индукцией 1 Тл перпендинулярно силовым линиям. Найти момент импульса частицы относительно центра окружности, по которой она будет двигаться.
Решение
Когда частица влетает в поле перпендикулярно силовым линиям, на нее начинает действовать сила Лоренца, которая выполняет роль центростремительной силы. Радиус окружности, по которой будет двигаться частица:
R=mvQBm=6,65·10-27 кг – масса альфа частицыQ=2e=3,2·10-19Кл – заряд альфа частицы
Момент импульса частицы относительно центра окружности найдем по формуле:
L=mvR=m2v2QB=6,65·10-272·0,35·10723,2·10-19·1=5,42·10-21кг·м2с
Ответ: 5,42·10-21 кг·м2с.
Задача на силу Лоренца №3
Условие
В однородном магнитном поле с индукцией В = 0,5 Тл вращается с частотой n = 10 с-1 стержень длиной l = 20 см. Ось вращения параллельна линиям индукции и проходит через один из концов стержня перпендикулярно его оси. Определите разность потенциалов U на концах стержня.
Решение
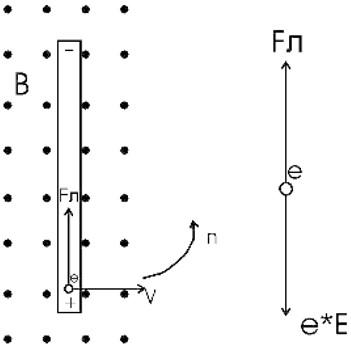
Рассмотрим физическую суть процессов, проходящих в стержне. Когда стержень движется в магнитном поле, в нем возникает ЭДС индукции, которая обусловлена действием силы Лоренца на заряды стержня.
Под действием этой силы в стержне происходит разделение зарядов: свободные электроны перемещаются вверх и между концами стержня возникает разность потенциалов.
Заряды на концах стержня создают поле E, препятствующее дальнейшему разделению зарядов. В какой-то момент сила Лоренца уравновесится с силой возникающего поля:
Fл=e·ЕЕ=Fле=evBe=vB
Скорость нижнего конца стержня, а значит, и скорость электронов в нем, можно найти, зная частоту вращения и длину стержня:
v=2π·n·l
C учетом этого, перепишется выражения для напряженности электрического поля:
Е=2πnlB
Индуцируемая разность потенциалов, по определению, равна:
U=Е·lU=2πnl2B=2·3,14·10-1·0,22·0,5=1,3В
Ответ: 1,3 В.
Задача на силу Лоренца №4
Условие
Какая сила действует на заряд 0,005 Кл, движущийся в магнитном поле с индукцие 0,5 Тл со скоростью 150 м/с под углом 45 градусов к вектору магнитной индукции?
Решение
Это простейшая задача на определение силы Лоренца. Вспомним формулу и запишем, что на заряд действует сила Лоренца, равная:
F=q·v·B·sinα
Подставим значения и вычислим:
F=0,005·150·0,5·22=0,26 Н
Ответ: 0,26 Н.
Задача на силу Лоренца №5
Условие
На тело с зарядом 0,8 мКл, движущееся в магнитном поле, со стороны поля действует сила, равная 32Н. Какова скорость тела, если вектор магнитного поля перпендикулярен ей?
Решение
Это классическая задача на применение формулы силы Лоренца. Так как векторы скорости и магнитной индукции перпендикулярны, можно записать:
F=qvBsinα=qvBv=FqB=320,8·10-3·2=20·103 мс
Ответ: 20000 м/с.
Проходите магнитостатику? Вам также может быть интересно:
- Задачи на закон Био-Савара-Лапласа.
- Задачи на теорему о циркуляции магнитного поля.
Вопросы на тему «Сила Лоренца»
Вопрос 1. Что такое сила Лоренца?
Ответ. Сила Лоренца — это сила, с которой магнитное поле действует на заряженную частицу, движущуюся в нем.
Сила Лоренца действует только на движущиеся заряды.
Вопрос 2. Как определить направление силы Лоренца?
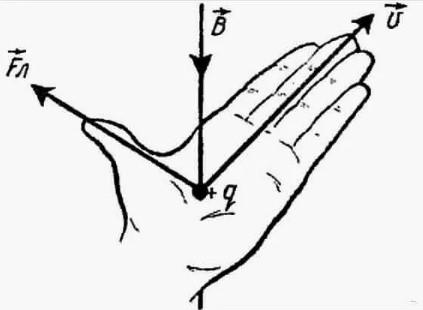
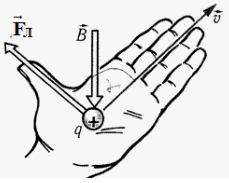
Ответ. Направление силы Лоренца определяется по правилу левой руки:
Если левую руку расположить так, чтобы составляющая вектора В, перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движении положительного заряда (= против движения отрицательного заряда), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца.
Вопрос 3. Зависит ли сила Лоренца от знака заряда?
Ответ. Да, зависит. Для противоположных зарядов сила Лоренца будет направлена в противоположные стороны.
Вопрос 4. Совершает ли сила Лоренца работу?
Ответ. Нет. Сила Лоренца не совершает работу, т.к., являясь перпендикулярной вектору скорости частицей, может изменить лишь направление скорости, но не ее значение. Работа силы Лоренца всегда равна нулю!
Вопрос 5. По какой траектории движется частица, попадающая в магнитное поле, перпендикулярное вектору скорости?
Ответ. Частица, влетающая в магнитное поле перпендикулярно линиям магнитной индукции, будет двигаться в этом поле по окружности определенного радиуса под действием силы Лоренца.
Нужна помощь в решении задач и других заданий по учебе? Профессиональный сервис для студентов посодействует, обращайтесь в любое время!
Как вывести скорость из формулы Лоренца?
Вы зашли на страницу вопроса Как вывести скорость из формулы Лоренца?, который относится к
категории Физика. По уровню сложности вопрос соответствует учебной
программе для учащихся 10 – 11 классов. В этой же категории вы найдете ответ
и на другие, похожие вопросы по теме, найти который можно с помощью
автоматической системы «умный поиск». Интересную информацию можно найти в
комментариях-ответах пользователей, с которыми есть обратная связь для
обсуждения темы. Если предложенные варианты ответов не удовлетворяют,
создайте свой вариант запроса в верхней строке.
На чтение 8 мин. Просмотров 27.2k. Опубликовано 18 ноября
Обновлено 18 ноября
Нигде еще школьный курс физики так сильно не перекликается с большой наукой, как в электродинамике. В частности, ее краеугольный камень – воздействие на заряженные частицы со стороны электромагнитного поля, нашло широкое применение в электротехнике.
Содержание
- Формула силы Лоренца
- Определение и формула силы Лоренца
- Направление силы Лоренца
- Следствия свойств силы Лоренца
- Формула силы Лоренца при наличии магнитного и электрического полей
- Единицы измерения силы Лоренца
- Понятие напряженности электрического поля
- Напряженность электрического поля
- Примеры задачи
- Задача 1
- Задача 2
- Задача 3
Формула силы Лоренца
Формула описывает взаимосвязь магнитного поля и основных характеристик движущегося заряда. Но сперва нужно разобраться, что же оно собой представляет.
Определение и формула силы Лоренца
В школе очень часто показывают опыт с магнитом и железными опилками на бумажном листе. Если расположить его под бумагой и слегка потрясти, то опилки выстроятся по линиям, которые принято называть линиями магнитной напряженности. Говоря простыми словами, это силовое поле магнита, которое окружает его подобно кокону. Оно замкнуто само на себя, то есть не имеет ни начала, ни конца. Это векторная величина, которая направлена от южного полюса магнита к северному.
Если бы в него влетела заряженная частица, то поле воздействовало бы на него очень любопытным образом. Она бы не затормозилась и не ускорилась, а всего лишь отклонилась в сторону. Чем она быстрее и чем сильнее поле, тем больше на нее действует эта сила. Ее назвали силой Лоренца в честь ученого-физика, впервые открывшего это свойство магнитного поля.
Вычисляют ее по специальной формуле:
FЛ=qvB,
здесь q – величина заряда в Кулонах, v – скорость, с которой движется заряд, в м/с, а B – индукция магнитного поля в единице измерения Тл (Тесла).
Направление силы Лоренца
Ученые заметили, что есть определенная закономерность между тем, как частица влетает в магнитное поле и тем, куда оно ее отклоняет. Чтобы ее было легче запомнить, они разработали специальное мнемоническое правило. Для его запоминания нужно совсем немного усилий, ведь в нем используется то, что всегда под рукой – рука. Точнее, левая ладонь, в честь чего оно носит название правила левой руки.
Итак, ладонь должна быть раскрыта, четыре пальца смотрят вперед, большой палец оттопырен в сторону. Угол между ними составляет 900. Теперь необходимо представить, что магнитный поток представляет собой стрелу, которая впивается в ладонь с внутренней стороны и выходит с тыльной. Пальцы при этом смотрят туда же, куда летит воображаемая частица. В таком случае большой палец покажет, куда она отклонится.
Интересно!
Важно отметить, что правило левой руки действует только для частиц со знаком «плюс». Чтобы узнать, куда отклонится отрицательный заряд, нужно четыре пальца направить в сторону, откуда летит частица. Все остальные манипуляции остаются прежними.
Следствия свойств силы Лоренца
Тело влетает в магнитном поле под каким-то определённым углом. Интуитивно понятно, что его величина имеет какое-то значение на характер воздействия на него поля, здесь нужно математическое выражение, чтобы стало понятнее. Следует знать, что как сила, так и скорость являются векторными величинами, то есть имеют направление. То же самое относится и к линиям магнитной напряженности. Тогда формулу можно записать следующим образом:
FЛ=qvBsinα,
sin α здесь – это угол между двумя векторными величинами: скоростью и потоком магнитного поля.
Как известно, синус нулевого угла также равен нулю. Получается, что если траектория движения частицы проходит вдоль силовых линий магнитного поля, то она никуда не отклоняется.
В однородном магнитном поле силовые линии имеют одинаковое и постоянное расстояние друг от друга. Теперь представим, что в таком поле перпендикулярно этим линиям движется частица. В этом случае сила Лоуренса заставит двигаться ее по окружности в плоскости, перпендикулярной силовым линиям. Чтобы найти радиус этой окружности, нужно знать массу частицы:
R=mvqB
Значение заряда не случайно взято как модуль. Это означает, что неважно, отрицательная или положительная частица входит в магнитное поле: радиус кривизны будет одинаков. Изменится только направление, в котором она полетит.
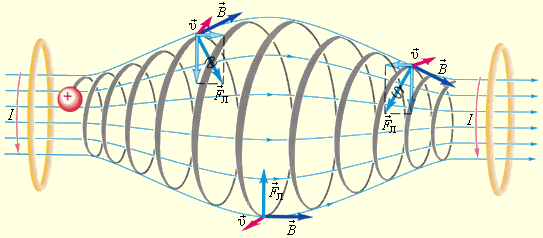
Во всех остальных случаях, когда заряд имеет определенный угол α с магнитным полем, он будет двигаться по траектории, напоминающей спираль с постоянным радиусом R и шагом h. Его можно найти по формуле:
R=mvsinαqB
h=2mvcosαqB
Еще одним следствием свойств этого явления является тот факт, что она не совершает никакой работы. То есть она не отдает и не забирает энергию у частицы, а лишь меняет направление ее движения.
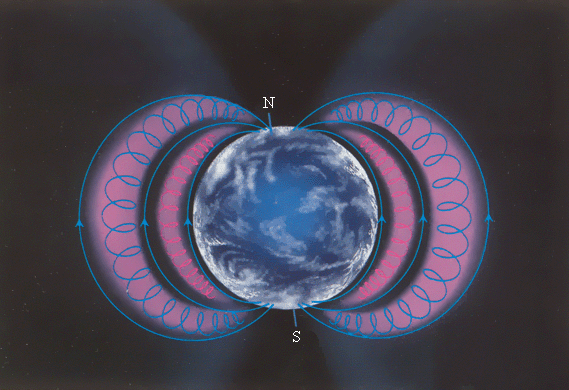
Самая яркая иллюстрация этого эффекта взаимодействия магнитного поля и заряженных частиц – это северное сияние. Магнитное поле, окружающее нашу планету, отклоняет заряженные частицы, прилетающие от Солнца. Но так как оно слабее всего на магнитных полюсах Земли, то туда проникают электрически заряженные частицы, вызывая свечение атмосферы.
Центростремительное ускорение, которое придается частицам, используется в электрических машинах – электродвигателях. Хотя уместнее здесь говорить о силе Ампера – частном проявлении силы Лоуренса, которая воздействует на проводник.
Принцип действия ускорителей элементарных частиц также основан на этом свойстве электромагнитного поля. Сверхпроводящие электромагниты отклоняют частицы от прямолинейного движения, заставляя их двигаться по кругу.
Самое любопытное заключается в том, что сила Лоренца не подчиняется третьему закону Ньютона, который гласит, что всякому действию есть свое противодействие. Связано это с тем, что Исаак Ньютон верил, что всякое взаимодействие на любом расстоянии происходит мгновенно, однако это не так. На самом деле оно происходит с помощью полей. К счастью, конфуза удалось избежать, так как физикам удалось переработать третий закон в закон сохранения импульса, который выполняется в том числе и для эффекта Лоуренса.
Формула силы Лоренца при наличии магнитного и электрического полей
Магнитное поле имеется не только у постоянных магнитов, но и у любого проводника электричества. Только в данном случае помимо магнитной составляющей, в ней присутствует еще и электрическая. Однако даже в этом электромагнитном поле эффект Лоуренса продолжает свое воздействие и определяется по формуле:
FЛ=qE+vB
где v – скорость электрически заряженной частицы, q – ее заряд, B и E – напряженности магнитного и электрических полей поля.
Единицы измерения силы Лоренца
Как и большинство других физических величин, которые действуют на тело и изменяют его состояние, она измеряется в ньютонах и обозначается буквой Н.
Понятие напряженности электрического поля
Электромагнитное поле на самом деле состоит из двух половин – электрической и магнитной. Они точно близнецы, у которых все одинаково, но вот характер разный. А если приглядеться, то во внешности можно заметить небольшие различия.
То же самое касается и силовых полей. Электрическое поле тоже обладает напряженностью – векторной величиной, которая является силовой характеристикой. Она воздействует на частицы, которые в неподвижности находятся в нем. Само по себе оно не является силой Лоренца, ее просто нужно принимать во внимание, когда вычисляется воздействие на частицу в условиях наличия электрического и магнитного полей.
Напряженность электрического поля
Напряженность электрического поля воздействует только на неподвижный заряд и определяется по формуле:
E=Fq
Единицей измерения является Н/Кл или В/м.
Примеры задачи
Задача 1
На заряд в 0,005 Кл, который движется в магнитном поле с индукцией 0,3 Тл, действует сила Лоренца. Вычислить ее, если скорость заряда 200 м/с, а движется он под углом 450 к линиям магнитной индукции.
| Дано:
q = 0,005 Кл B = 0,3 Тл v = 200 м/с α = 450 |
Решение:
В условиях задачи нет упоминания электрического поля, поэтому силу Лоренца можно найти по следующей формуле: FЛ=qvBsinα=0,005×200×0,3×sin 450 =0,3×22=0,21 Н |
Задача 2
Определить скорость тела, имеющего заряд и которое движется в магнитном поле с индукцией 2 Тл под углом 900. Величина, с которой поле воздействует на тело, равна 32 Н, заряд тела – 5 × 10-3 Кл.
| Дано:
q = 0,005 Кл B = 2 Тл FЛ = 32 Н α = 900 |
Решение:
Чтобы найти скорость заряда, необходимо несколько видоизменить формулу для нахождения силы Лоренца: FЛ=qvBsinαv=FЛqBsinα v=320,005×2×sin900=320,01×1=32000мс=32 км/с |
Задача 3
Электрон движется в однородном магнитном поле под углом 900 ее силовым линиям. Величина, с которой поле воздействует на электрон, равна 5 × 10-13 Н. Величина магнитной индукции равна 0,05 Тл. Определить ускорение электрона.
| Дано:
q = -1,6 × 10-19 Кл B = 0,05 Тл FЛ = 5 × 10-13 Н α = 900 |
Решение:
В этой задаче сила Лоренца ко всему прочему еще и заставляет двигаться электрон по окружности. Поэтому здесь под ускорением следует понимать центростремительное ускорение: aц=v2R На данный момент неизвестны ни скорость электрона, ни радиус окружности, по которой он движется. v=FЛqBsinα=5×10-13-1,6×10-19×0,05∙sin900=6×107мс R=mvqB=9×10-31×6×107-1,6×10-19×0,05=6,8×10-3мс |
aц=v2R=6×10726,8×10-3=5×1017мс2
Электродинамика оперирует такими понятиями, которым трудно подобрать аналогию в обычном мире. Но это совсем не значит, что их невозможно постичь. С помощью различных наглядных экспериментов и природных явлений процесс познания мира электричества может стать по настоящему захватывающим.
Содержание:
- Определение и формула силы Лоренца
- Направление силы Лоренца
- Следствия свойств силы Лоренца
- Формула силы Лоренца при наличии магнитного и электрического полей
- Единицы измерения силы Лоренца
- Примеры решения задач
Определение и формула силы Лоренца
Определение
Сила $bar{F}$ , действующая на движущуюся заряженную частицу в магнитном поле, равная:
$$bar{F}=q[bar{v} times bar{B}](1)$$
называется силой Лоренца (магнитной силой).
Исходя из определения (1) модуль рассматриваемой силы:
$$F=q v B sin alpha(2)$$
где $bar{v}$ – вектор скорости частицы, q – заряд частицы,
$bar{B}$ – вектор магнитной индукции поля в точке нахождения заряда,
$alpha$ – угол между векторами
$bar{v}$ и
$bar{B}$. Из выражения (2) следует, что если заряд движется параллельно
силовым линиям магнитного поля,то сила Лоренца равна нулю. Иногда силу Лоренца стараясь выделить, обозначают, используя индекс:
$bar{F}_L$
Направление силы Лоренца
Сила Лоренца (как и всякая сила) – это вектор. Ее направление перпендикулярно вектору скорости
$bar{v}$ и вектору
$bar{B}$ (то есть перпендикулярно плоскости, в которой находятся векторы скорости и магнитной
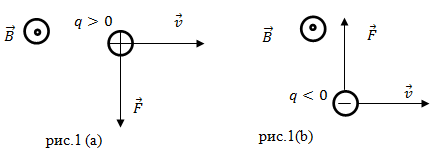
индукции) и определяется правилом правого буравчика (правого винта) рис.1 (a). Если мы имеем дело с отрицательным зарядом,
тонаправление силы Лоренца противоположно результату векторного произведения
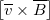
вектор $bar{B}$ направлен перпендикулярно плоскости рисунков на нас.
Следствия свойств силы Лоренца
Так как сила Лоренца направлена всегда перпендикулярно направлению скорости заряда, то ее работа над частицей равна нулю. Получается,
что воздействуя на заряженную частицу при помощи постоянного магнитного поля нельзя изменить ее энергию.
Если магнитное поле однородно и направлено перпендикулярно скорости движения заряженной частицы, то заряд под воздействием
силы Лоренца будет перемещаться по окружности радиуса R=const в плоскости, которая перпендикулярна вектору магнитной индукции.
При этом радиус окружности равен:
$$R=frac{m gamma v}{|q| B}(3)$$
где m – масса частицы,|q|- модуль заряда частицы,
$gamma=frac{1}{sqrt{1-frac{v^{2}}{c^{2}}}}$ – релятивистский множитель Лоренца, c – скорость света в вакууме.
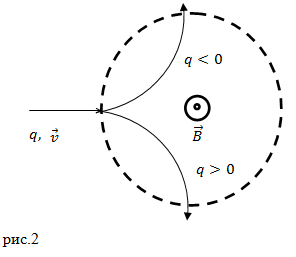
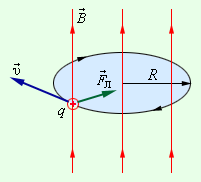
Сила Лоренца – это центростремительная сила. По направлению отклонения элементарной заряженной частицы в магнитном поле делают вывод о ее знаке (рис.2).
Формула силы Лоренца при наличии магнитного и электрического полей
Если заряженная частица перемещается в пространстве, в котором находятся одновременно два поля (магнитное и
электрическое), то сила, которая действует на нее, равна:
$$bar{F}=q bar{E}+q[bar{v} times bar{B}](4)$$
где $bar{E}$ – вектор напряженности электрического поля в точке, в которой находится заряд.
Выражение (4) было эмпирически получено Лоренцем. Сила
$bar{F}$, которая входит в формулу (4) так же называется силой Лоренца
(лоренцевой силой). Деление лоренцевой силы на составляющие: электрическую
$(bar{F} = q bar{E})$ и магнитную
$(bar{F}=q[bar{v} times bar{B}])$ относительно, так как связано с выбором инерциальной системы отсчета.
Так, если система отсчета будет двигаться с такой же скоростью
$bar{v}$, как и заряд, то в такой системе сила Лоренца, действующая на частицу, будет равна нулю.
Единицы измерения силы Лоренца
Основной единицей измерения силы Лоренца (как и любой другой силы) в системе СИ является: [F]=H
В СГС: [F]=дин
Примеры решения задач
Пример
Задание. Какова угловая скорость электрона, который движется по окружности в магнитном поле с индукцией B?
Решение. Так как электрон (частица имеющая заряд) совершает перемещение в магнитном поле, то на
него действует сила Лоренца вида:
$$bar{F}=q[bar{v} times bar{B}](1.1)$$
где q=qe – заряд электрона. Так как в условии сказано, что электрон движется по окружности, то это означает, что
$bar{v} perp bar{B}$, следовательно, выражение для модуля силы Лоренца примет вид:
$$F=q v B(1.2)$$
Сила Лоренцаявляется центростремительной и кроме того, по второму закону Ньютона будет в нашем случае равна:
$$F=m a_{n}=m frac{v^{2}}{R}(1.3)$$
Приравняем правые части выражений (1.2) и (1.3), имеем:
$$q v B=m frac{v^{2}}{R}(1.4)$$
Из выражения (1.3) получим скорость:
$$v=frac{q B R}{m}(1.5)$$
Период обращения электрона по окружности можно найти как:
$$T=frac{2 pi R}{v}=frac{2 pi m}{q B}(1.6)$$
Зная период, можно найти угловую скорость как:
$$omega=frac{2 pi}{T}=frac{q_{e} B}{m}$$
Ответ. $omega=frac{q_{e} B}{m}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Заряженная частица (заряд q, масса m) со скоростью vвлетает в область, где имеется электрическое поле
напряженностью E и магнитное поле с индукцией B. Векторы $bar{E}$ и
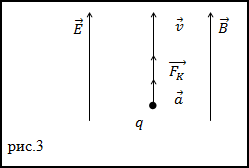
$bar{B}$ совпадают по направлению. Каково ускорение частицы в моментначалаперемещения в полях, если
$bar{v} uparrow bar{B} uparrow bar{E}$?
Решение. Сделаем рисунок.
На заряженную частицу действует сила Лоренца:
$$bar{F}=q bar{E}+q[bar{v} times bar{B}](2.1)$$
Магнитная составляющая имеет направление перпендикулярное вектору скорости ($bar{v}$) и вектору
магнитной индукции ($bar{B}$).
Электрическая составляющая сонаправлена с вектором напряжённости ($bar{E}$) электрического поля.
В соответствии со вторым законом Ньютона имеем:
$$bar{F}=q bar{E}+q[bar{v} times bar{B}]=m bar{a}(2.2)$$
Получаем, что ускорение равно:
$$frac{q bar{E}+q[bar{v} times bar{B}]}{m}=bar{a}(2.3)$$
Если скорость заряда параллельна векторам $bar{E}$ и
$bar{B}$, тогда $[bar{v} times bar{B}]=0$, получим:
$$bar{a}=frac{q bar{E}}{m}$$
Ответ. $bar{a}=frac{q bar{E}}{m}$
Читать дальше: Формула силы натяжения нити.
Сила Лоренца
теория по физике 🧲 магнетизм
Сила Лоренца — сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.
Модуль силы Лоренца обозначается как FЛ. Единица измерения — Ньютон (Н).
Модуль силы Лоренца численно равен отношению модуля силы F, действующий на участок проводника длиной l, к числу N заряженных частиц, упорядоченно движущихся на этом участке проводника:
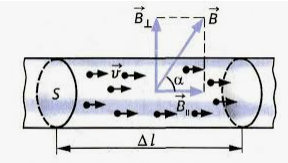
Рассмотрим отрезок тонкого прямого проводника с током. Пусть длина отрезка ∆l и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля → B можно считать неизменным в пределах этого отрезка проводника.
Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (число зарядов в единице объема) и скоростью их упорядоченного движения v следующей формулой:
Модуль силы, действующей со стороны магнитного поля на выбранные элемент тока, равен:
F = | I | Δ l B sin . α
Подставляя сюда выражение, полученное для силы тока, получим:
F = | q n v S | Δ l B sin . α = | q | n v S Δ l B sin . α
Учтем, что число заряженных частиц в рассматриваемом объеме равно произведению величины этого объема на концентрацию самих частиц:
F = | q | v N B sin . α
Следовательно, на каждый движущийся заряд действует сила Лоренца, равная:
F Л = F N . . = | q | v N B sin . α N . . = | q | v B sin . α
α — угол между вектором скорости движущегося заряда и вектором магнитной индукции.
Пример №1. Определить силу, действующую на заряд 0,005 Кл, движущийся в магнитном поле с индукцией 0,3 Тл со скоростью 200 м/с под углом 45 o к вектору магнитной индукции.
F Л = | q | v B sin . α = 0 , 005 · 200 · 0 , 3 · √ 2 2 . . ≈ 0 , 2 ( Н )
Направление силы Лоренца
Сила Лоренца перпендикулярна вектору магнитной индукции и вектору скорости движущегося заряда. Ее направление определяется с помощью правила левой руки:
Если левую руку расположить так, чтобы составляющая магнитной индукции → B , перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца.
Пример №2. Протон p имеет скорость → v , направленную горизонтально вдоль прямого длинного проводника с током I (см. рисунок). Куда направлена действующая на протон сила Лоренца?
В точке, в которой находится протон, вектор магнитной индукции направлен в сторону от наблюдателя. Это следует из правила буравчика. Теперь применим правило левой руки. Для этого четыре пальца левой руки направим в сторону движения протона — вправо. Ладонь развернем в сторону наблюдателя, чтобы линии магнитной индукции входили в нее перпендикулярно. Теперь отставим на 90 градусов большой палец. Он показывает вверх. Следовательно, сила Лоренца, действующая на протон, направлена вверх.
Работа силы Лоренца
Поскольку вектор силы Лоренца направлен перпендикулярно скорости движения заряда, угол между перемещением этого заряда и этой силы равен 90 о . Работа любой силы определяется формулой:
Но так как косинус 90 о равен 0, сила Лоренца не совершает работу. Это значит, что сила Лоренца не влияет на модуль скорости перемещения заряда. Но она может менять вектора его скорости.
Полная сила, действующая на заряд
При решении задач, в которых заряженная частица находится одновременно в электрическом и магнитном полях, нужно учитывать, что не нее действует сразу две силы. Со стороны магнитного поля — сила Лоренца. Со стороны электрического поля — сила → F э л , действующая на неподвижный заряд, помещенный в данную точку поля. Она равна произведению этого заряда на напряженность электрического поля:
Следовательно, полная сила, действующая на заряд, равна:
→ F = → F э л + → F л = q → E + | q | → v → B sin . α
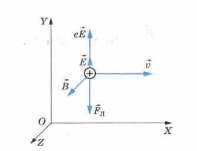
Пример №3. В пространстве, где существует одновременно однородное и постоянное электрическое и магнитное поля, по прямолинейной траектории движется протон. Известно, что напряженность электрического поля равна → E . Какова индукция → B магнитного поля?
Прямолинейное движение протона возможно в двух случаях:
- Вектор → E направлен вдоль траектории движения протона. Тогда вектор → B также должен быть направлен вдоль этой траектории, и его модуль может быть любым, так как магнитное поле на частицу действовать не будет.
- Векторы → E , → B и → v взаимно перпендикулярны, и сила, действующая на протон со стороны электрического поля, равна по модулю и противоположна по направлению силе Лоренца, действующей на протон со стороны магнитного поля (см. рисунок).
Заряд протона равен модулю заряда электрона — e . Сложим силы, действующие на протон по оси ОУ:
В скалярной форме:
Протон ускоряется постоянным электрическим полем конденсатора, напряжение на обкладках которого 2160 В. Затем он влетает в однородное магнитное поле и движется по дуге окружности радиуса 20 см в плоскости, перпендикулярной линиям магнитной индукции. Каков модуль вектора индукции магнитного поля? Начальной скоростью протона в электрическом поле пренебречь. Ответ выразить в мТл, округлив до десятых.
Формула силы Лоренца
Определение и формула силы Лоренца
Сила $bar$ , действующая на движущуюся заряженную частицу в магнитном поле, равная:
называется силой Лоренца (магнитной силой).
Исходя из определения (1) модуль рассматриваемой силы:
$$F=q v B sin alpha(2)$$
где $bar$ – вектор скорости частицы, q – заряд частицы, $bar$ – вектор магнитной индукции поля в точке нахождения заряда, $alpha$ – угол между векторами $bar$ и $bar$. Из выражения (2) следует, что если заряд движется параллельно силовым линиям магнитного поля,то сила Лоренца равна нулю. Иногда силу Лоренца стараясь выделить, обозначают, используя индекс: $bar_L$
Направление силы Лоренца
Сила Лоренца (как и всякая сила) – это вектор. Ее направление перпендикулярно вектору скорости $bar$ и вектору $bar$ (то есть перпендикулярно плоскости, в которой находятся векторы скорости и магнитной индукции) и определяется правилом правого буравчика (правого винта) рис.1 (a). Если мы имеем дело с отрицательным зарядом, тонаправление силы Лоренца противоположно результату векторного произведения 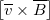
вектор $bar$ направлен перпендикулярно плоскости рисунков на нас.
Следствия свойств силы Лоренца
Так как сила Лоренца направлена всегда перпендикулярно направлению скорости заряда, то ее работа над частицей равна нулю. Получается, что воздействуя на заряженную частицу при помощи постоянного магнитного поля нельзя изменить ее энергию.
Если магнитное поле однородно и направлено перпендикулярно скорости движения заряженной частицы, то заряд под воздействием силы Лоренца будет перемещаться по окружности радиуса R=const в плоскости, которая перпендикулярна вектору магнитной индукции. При этом радиус окружности равен:
где m – масса частицы,|q|- модуль заряда частицы, $gamma=frac<1><sqrt<1-frac>>>>$ – релятивистский множитель Лоренца, c – скорость света в вакууме.
Сила Лоренца – это центростремительная сила. По направлению отклонения элементарной заряженной частицы в магнитном поле делают вывод о ее знаке (рис.2).
Формула силы Лоренца при наличии магнитного и электрического полей
Если заряженная частица перемещается в пространстве, в котором находятся одновременно два поля (магнитное и электрическое), то сила, которая действует на нее, равна:
где $bar$ – вектор напряженности электрического поля в точке, в которой находится заряд. Выражение (4) было эмпирически получено Лоренцем. Сила $bar$, которая входит в формулу (4) так же называется силой Лоренца (лоренцевой силой). Деление лоренцевой силы на составляющие: электрическую $(bar = q bar)$ и магнитную $(bar=q[bar times bar])$ относительно, так как связано с выбором инерциальной системы отсчета. Так, если система отсчета будет двигаться с такой же скоростью $bar$, как и заряд, то в такой системе сила Лоренца, действующая на частицу, будет равна нулю.
Единицы измерения силы Лоренца
Основной единицей измерения силы Лоренца (как и любой другой силы) в системе СИ является: [F]=H
Примеры решения задач
Задание. Какова угловая скорость электрона, который движется по окружности в магнитном поле с индукцией B?
Решение. Так как электрон (частица имеющая заряд) совершает перемещение в магнитном поле, то на него действует сила Лоренца вида:
где q=qe – заряд электрона. Так как в условии сказано, что электрон движется по окружности, то это означает, что $bar perp bar$, следовательно, выражение для модуля силы Лоренца примет вид:
Сила Лоренцаявляется центростремительной и кроме того, по второму закону Ньютона будет в нашем случае равна:
Приравняем правые части выражений (1.2) и (1.3), имеем:
Из выражения (1.3) получим скорость:
Период обращения электрона по окружности можно найти как:
Зная период, можно найти угловую скорость как:
Ответ. $omega=frac B>$
Задание. Заряженная частица (заряд q, масса m) со скоростью vвлетает в область, где имеется электрическое поле напряженностью E и магнитное поле с индукцией B. Векторы $bar$ и $bar$ совпадают по направлению. Каково ускорение частицы в моментначалаперемещения в полях, если $bar uparrow bar uparrow bar$?
Решение. Сделаем рисунок.
На заряженную частицу действует сила Лоренца:
Магнитная составляющая имеет направление перпендикулярное вектору скорости ($bar$) и вектору магнитной индукции ($bar$). Электрическая составляющая сонаправлена с вектором напряжённости ($bar$) электрического поля. В соответствии со вторым законом Ньютона имеем:
Получаем, что ускорение равно:
Если скорость заряда параллельна векторам $bar$ и $bar$, тогда $[bar times bar]=0$, получим:
Сила Лоренца
Сила Лоренца. Определение и формула
Сила Ампера, воздействующая на часть проводника длиной Δ l с некоторой силой тока I , находящийся в магнитном поле B , F = I · B · Δ l · sin α может выражаться через действующие на конкретные носители заряда силы.
Пускай заряд носителя обозначается как q , а n является значением концентрации носителей свободного заряда в проводнике. В этом случае произведение n · q · υ · S , в котором S представляет собой площадь поперечного сечения проводника, эквивалентно току, протекающему в проводнике, а υ – это модуль скорости упорядоченного движения носителей в проводнике:
Формула силы Ампера может записываться в следующем виде:
F = q · n · S · Δ l · υ · B · sin α .
По причине того, что полное число N носителей свободного заряда в проводнике сечением S и длиной Δ l равняется произведению n · S · Δ l , действующая на одну заряженную частицу сила равняется выражению: F Л = q · υ · B · sin α .
Найденная сила носит название силы Лоренца. Угол α в приведенной формуле эквивалентен углу между вектором магнитной индукции B → и скоростью ν → .
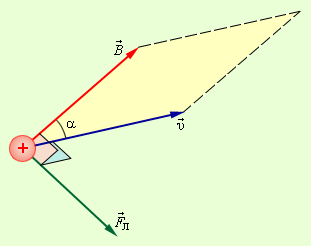
Направление силы Лоренца, которая воздействует частицу с положительным зарядом, таким же образом, как и направление силы Ампера, находится по правилу буравчика или же с помощью правила левой руки. Взаимное расположение векторов ν → , B → и F Л → для частицы, несущей положительный заряд, проиллюстрировано на рис. 1 . 18 . 1 .
Рисунок 1 . 18 . 1 . Взаимное расположение векторов ν → , B → и F Л → . Модуль силы Лоренца F Л → численно эквивалентен произведению площади параллелограмма, построенного на векторах ν → и B → и заряда q .
Сила Лоренца направлена нормально, то есть перпендикулярно, векторам ν → и B → .
Сила Лоренца не совершает работы при движении несущей заряд частицы в магнитном поле. Данный факт приводит к тому, что модуль вектора скорости в условиях движения частицы так же не меняет своего значения.
Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость ν → лежит в плоскости, которая направлена нормально по отношению к вектору B → , то частица будет совершать движение по окружности некоторого радиуса, рассчитывающегося с помощью следующей формулы:
Сила Лоренца в данном случае применяется в качестве центростремительной силы (рис. 1 . 18 . 2 ).
Рисунок 1 . 18 . 2 . Круговое движение заряженной частицы в однородном магнитном поле.
Для периода обращения частицы в однородном магнитном поле будет справедливо следующее выражение:
T = 2 π R υ = 2 π m q B .
Данная формула наглядно демонстрирует отсутствие зависимости заряженных частиц заданной массы m от скорости υ и радиуса траектории R .
Применение силы Лоренца
Приведенное снизу соотношение представляет собой формулу угловой скорости движения заряженной частицы, происходящего по круговой траектории:
ω = υ R = υ q B m υ = q B m .
Оно носит название циклотронной частоты. Данная физическая величина не имеет зависимости от скорости частицы, из чего можно сделать вывод, что и от ее кинетической энергии она не зависит.
Данное обстоятельство находит свое применение в циклотронах, а именно в ускорителях тяжелых частиц (протонов, ионов).
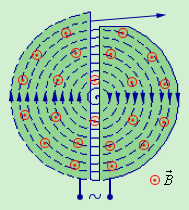
На рисунке 1 . 18 . 3 приводится принципиальная схема циклотрона.
Рисунок 1 . 18 . 3 . Движение заряженных частиц в вакуумной камере циклотрона.
Дуант – это полый металлический полуцилиндр, помещенный в вакуумную камеру между полюсами электромагнита в качестве одного из двух ускоряющих D -образного электрода в циклотроне.
К дуантам приложено переменное электрическое напряжение, чья частота эквивалентна циклотронной частоте. Частицы, несущие некоторый заряд, инжектируются в центре вакуумной камеры. В промежутке между дуантами они испытывают ускорение, вызываемое электрическим полем. Частицы, находящиеся внутри дуантов, в процессе движения по полуокружностям испытывают на себе действие силы Лоренца. Радиус полуокружностей возрастает с увеличением энергии частиц. Как и во всех других ускорителях, в циклотронах ускорение заряженной частицы достигается путем применения электрического поля, а ее удержание на траектории с помощью магнитного поля. Циклотроны дают возможность ускорять протоны до энергии, приближенной к 20 М э В .
Однородные магнитные поля используются во многих устройствах самых разных типов назначений. В частности, они нашли свое применение так называемых масс-спектрометрах.
Масс-спектрометры – это такие устройства, использование которых позволяет нам измерять массы заряженных частиц, то есть ионов или ядер различных атомов.
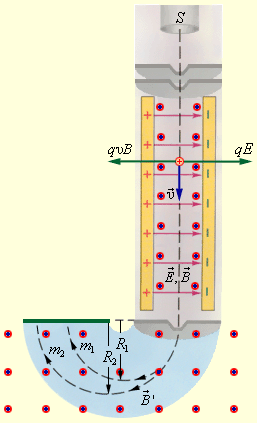
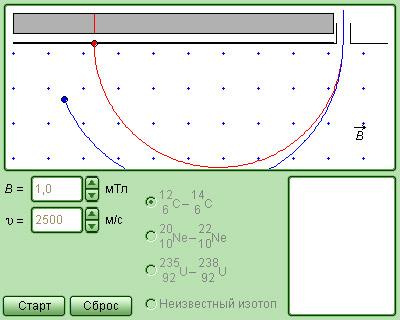
Данные приборы используются для разделения изотопов (ядер атомов с одинаковым зарядом, но разными массами, к примеру, Ne 20 и Ne 22 ). На рис. 1 . 18 . 4 изображен простейшая версия масс-спектрометра. Вылетающие из источника S ионы проходят через несколько малых отверстий, которые в совокупности формируют узкий пучок. После этого они попадают в селектор скоростей, где частицы движутся в скрещенных однородных электрическом, создающимся между пластинами плоского конденсатора, и магнитном, возникающим в зазоре между полюсами электромагнита, полях. Начальная скорость υ → заряженных частиц направлена перпендикулярно векторам E → и B → .
Частица, которая движется в скрещенных магнитном и электрическом полях, испытывает на себе воздействия электрической силы q E → и магнитной силы Лоренца. В условиях, когда выполняется E = υ B , данные силы полностью компенсируют воздействие друг друга. В таком случае частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, которые движутся со скоростью υ = E B .
После данных процессов частицы с одинаковыми значениями скорости попадают в однородное магнитное поле B → камеры масс-спектрометра. Частицы под действием силы Лоренца движутся в камере перпендикулярной магнитному полю плоскости. Их траектории представляют собой окружности с радиусами R = m υ q B ‘ . В процессе измерения радиусов траекторий при известных значениях υ и B ‘ , мы имеем возможность определить отношение q m . В случае изотопов, то есть при условии q 1 = q 2 , масс-спектрометр может разделить частицы с разными массами.
С помощью современных масс-спектрометров мы имеем возможность измерять массы заряженных частиц с точностью, превышающей 10 – 4 .
Рисунок 1 . 18 . 4 . Селектор скоростей и масс-спектрометр.
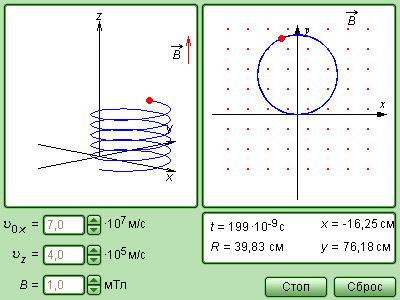
Магнитное поле
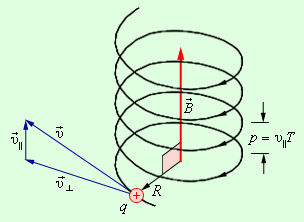
В случае, когда скорость частицы υ → имеет составляющую υ ∥ → вдоль направления магнитного поля, подобная частица в однородном магнитном поле будет совершать спиралевидное движение. Радиус такой спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ ┴ вектор υ → , а шаг спирали p – от модуля продольной составляющей υ ∥ (рис. 1 . 18 . 5 ).
Рисунок 1 . 18 . 5 . Движение заряженной частицы по спирали в однородном магнитном поле.
Исходя из этого, можно сказать, что траектория заряженной частицы в каком-то смысле «навивается» на линии магнитной индукции. Данное явление используется в технике для магнитной термоизоляции высокотемпературной плазмы – полностью ионизированного газа при температуре порядка 10 6 K . При изучении управляемых термоядерных реакций вещество в подобном состоянии получают в установках типа «Токамак». Плазма не должна касаться стенок камеры. Термоизоляция достигается путем создания магнитного поля специальной конфигурации. На рисунке 1 . 18 . 6 в качестве примера проиллюстрирована траектория движения несущей заряд частицы в магнитной «бутылке» (или ловушке).
Рисунок 1 . 18 . 6 . Магнитная «бутылка». Заряженные частицы не выходят за ее пределы. Необходимое магнитное поле может быть создано с помощью двух круглых катушек с током.
Такое же явление происходит в магнитном поле Земли, которое защищает все живое от потока несущих заряд частиц из космического пространства.
Быстрые заряженные частицы из космоса, по большей степени от Солнца, «перехватываются» магнитным полем Земли, вследствие чего образуются радиационные пояса (рис. 1 . 18 . 7 ), в которых частицы, будто в магнитных ловушках, перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за доли секунды.
Исключением являются полярные области, в которых часть частиц прорывается в верхние слои атмосферы, что может приводить к возникновению таких явлений, как «полярные сияния». Радиационные пояса Земли простираются от расстояний около 500 к м до десятков радиусов нашей планеты. Стоит вспомнить, что южный магнитный полюс Земли находится поблизости с северным географическим полюсом на северо-западе Гренландии. Природа земного магнетизма до сих пор не изучена.
Рисунок 1 . 18 . 7 . Радиационные пояса Земли. Быстрые заряженные частицы от Солнца, в основном электроны и протоны, попадают в магнитные ловушки радиационных поясов.
Возможно их вторжение в верхние слои атмосферы, служащее причиной возникновения «северных сияний».
Рисунок 1 . 18 . 8 . Модель движения заряда в магнитном поле.
Рисунок 1 . 18 . 9 . Модель Масс-спектрометра.
Рисунок 1 . 18 . 10 . Модель селектора скоростей.
[spoiler title=”источники:”]
http://www.webmath.ru/poleznoe/formules_21_29_sila_lorenca.php
http://zaochnik.com/spravochnik/fizika/magnitnoe-pole/sila-lorentsa/
[/spoiler]