Скорость материальной точки

4.3
Средняя оценка: 4.3
Всего получено оценок: 278.
4.3
Средняя оценка: 4.3
Всего получено оценок: 278.
Кинематика – это раздел механики, описывающий движение тел без рассмотрения причин этого движения. Одной из характеристик движения является скорость. Рассмотрим ее более подробно.
Материальная точка в Системе Отсчета
При изучении движения необходимо уметь определять положение тела в пространстве. Для этого используются понятие Системы Отсчета и понятие Материальной точки.
Сперва необходимо задаться некоторым базисом – телом, относительно которого будут определяться положение других тел. Такое тело называется Телом Отсчета.
С Телом Отсчета связывается система координат – от одной до трех осей, которые однозначно определяют положение изучаемого тела относительно тела отсчета.
Наконец, поскольку движение всегда происходит во времени, необходима система измерения времени. Некоторый момент принимается за нулевой, кроме того, определяется единица измерения времени.
Тело Отсчета, система координат, связанная с ним и система измерения времени вместе называются Системой Отсчета.

Система координат может задавать положение геометрических точек. А поскольку геометрические размеры и форма тела во многих случаях (но не всегда) не имеют значения, появляется возможность заменить рассматриваемое тело одной точкой. Движение описывается для этой одной точки, а движенbями остальных точек тела пренебрегают. Вся масса тела приписывается этой одной точке. Такая точка называется «материальной».
Скорость движения материальной точки
Движение материальных точек состоит в изменении их положения в Системе Отсчета с течением времени. Изучение этого явления показывает, что оно совершается с разной быстротой. За один и тот же промежуток времени разные материальные точки могут проходить разные расстояния. Поэтому вводится специальная величина для количественной характеристики этой быстроты – скорость.
Скорость материальной точки обозначается латинской буквой $v$ и равна отношению пройденного пути $S$ ко времени его прохождения:
$v = { S over t}$
Чем больше путь, пройденный точкой за некоторое время, тем больше скорость этой точки.
Из формулы скорости материальной точки можно получить единицу скорости. Поскольку единицей расстояния в системе СИ являются метры, а единицей времени – секунды, то единицей скорости являются метры в секунду.
Средняя и мгновенные скорости
Скорость может быть различной не только у разных тел, но и у одного и того же тела в разные моменты времени. Для описания движения, при котором скорость меняется, используются два метода.
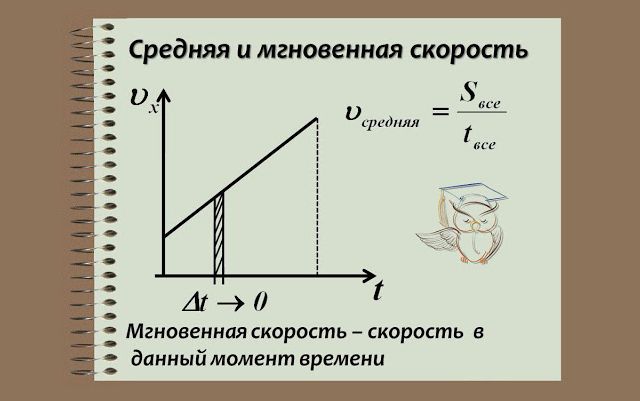
Во-первых, мы можем пренебречь изменением скорости на рассматриваемом участке. Разделив общую длину пути $S_{общ}$ на время его прохождения $t_{общ}$, мы получим среднюю скорость:
$$v_{ср}= {S_{общ}over t_{общ}}$$
Во-вторых, мы можем разбить весь путь на много участков. Даже если скорость тела при прохождении участка менялась, то чем меньше такой участок, тем меньше будет изменение скорости. В пределе каждый участок длиной $ΔS$, пройденный за время $Δt$ «стягивается» в точку, скорость прохождения которой постоянна. Скорость, найденная таким методом, называется мгновенной:
$$v_{мгнов}= {ΔSover {Δt}}, при ΔS rightarrow 0,Δtrightarrow 0$$
Мгновенная скорость используется там, где необходимо знать точное значение скорости в конкретном месте пути. Средняя скорость используется там, где важно знать общий результат прохождения рассматриваемого пути.

Что мы узнали?
Скорость материальной точки равна отношению пройденного пути за время его прохождения. Скорость бывает средней и мгновенной. В системе СИ скорость измеряется в метрах в секунду.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.3
Средняя оценка: 4.3
Всего получено оценок: 278.
А какая ваша оценка?
В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
Поскольку при
движении материальной точки изменяется
ее положение относительно выбранной
системы отсчета, то возникает важный
вопрос: Как быстро это положение
изменяется? Физической величиной, с
помощью которой отвечают на этот вопрос,
является скорость.
Скоростью
материальной
точки
![]()
называется
вектор, равный производной радиус-вектора
по времени:
![]()
(1.5)
или в проекциях
на декартовы координатные оси
![]()
,
![]()
,
![]()
,
(1.6)
![]()
.
Так как хорда
![]()
(рис 1.2), стягивающая дугу траектории
l12,
в пределе при
![]()
![]()
совпадает с касательной, то вектор
скорости направлен по касательной к
траектории в сторону движения материальной
точки.
В частности, если
модуль скорости
![]()
,
то такое движение называется равномерным.
Если детальная
характеристика движения за промежуток
времени
несущественна, то используют средние
величины:
– средний вектор
скорости
![]()
,
(1.7)
– модуль скорости
![]()
, (1.8)
– средняя
скорость
![]()
,
(1.9)
где S
– путь, пройденный материальной точкой
за время t.
Обратите внимание на то, что
![]()
–
скалярная величина. В общем случае
произвольного движения материальной
точки
![]()
.
Часто полезно
бывает знать, с какой скоростью изменяется
со временем
расстояние между
материальной точкой и началом координат
(как быстро изменяется модуль радиус-вектора
![]()
),
и с какой скоростью изменяется направление
радиус-вектора относительно осей
координат системы отсчета? Ответить на
эти вопросы проще всего, если воспользоваться
естественной формой представления
радиус-вектора
![]()
,
(1.10)
которая учитывает
тот факт, что у любого вектора есть две
естественные характеристики: величина
и направление.
Здесь
![]()
– орт вектора
,
то есть вектор, модуль которого равен
единице
![]()
,
а направление совпадает с направлением
радиус-вектора
![]()
.
Используя (1.5) и
(1.10), получим
![]()
.
(1.11)
В соотношении
(1.11) вектор
![]()
представлен в виде двух составляющих,
первая из которых
![]()
(1.12)
характеризует
скорость изменения модуля радиус-вектора
и направлена вдоль
|
|
.
(1.13)
характеризует в сторону его поворота. Действительно,
то |
(угол поворота
радиус-вектора
за время
![]()
).
При этом
![]()
,
значит при
![]()
.
Поэтому
![]()
.
Здесь надо учесть, что
![]()
.
Таким образом,
![]()
;
![]()
.
Выводы:
Скорость материальной точки – есть
производная радиус-вектора по времени,
характеризует быстроту изменения
радиус-вектора как по модулю, так и по
направлению, направлена по касательной
к траектории движения.
Контрольные
вопросы
1.4. Покажите,
что
![]()
.
1.5. Может ли при
прямолинейном движении выполняться
условие
![]()
.
При каком движении выполняется равенство
между этими величинами?
1.6. Что вы можете
сказать о характере движения и виде
траектории, если: а)
![]()
;
б)
![]()
;
в)
![]()
,
![]()
;
г)
![]()
,
![]()
;
д)
![]()
,
![]()
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Определение и формула скорости
- Скорость в разных системах координат
- Частные случаи формул для вычисления скорости
- Единицы измерения скорости
- Примеры решения задач
Определение и формула скорости
Определение
Мгновенной скоростью (или чаще просто скоростью) материальной точки называется физическая величина равная первой производной от радиус–вектора
$bar{r}$ точки по времени (t). Обозначают скорость обычно буквой v.
Это векторная величина. Математически определение вектора мгновенной скорости записывается как:
$$bar{v}=frac{d bar{r}}{d t}=dot{bar{r}}(1)$$
Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения.
Модуль скорости можно определить как первую производную от длины пути (s) по времени:
$$v=frac{d s}{d t}=dot{s}(2)$$
Скорость характеризует быстроту перемещения в направлении движения точки по отношениюк рассматриваемой системе координат.
Скорость в разных системах координат
Проекции скорости на оси декартовой системы координат запишутся как:
$$v_{x}=dot{x} ; v_{y}=dot{y} ; v_{z}=dot{z}(3)$$
Следовательно, вектор скоростив декартовых координатах можно представить:
$$bar{v}=dot{x} bar{i}+dot{y} bar{j}+dot{z} bar{k}(4)$$
где $bar{i}, bar{j}, bar{k}$ единичные орты. При этом модуль вектора скорости находят при помощи формулы:
$$v=sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}}(5)$$
В цилиндрических координатах модуль скорости вычисляют при помощи формулы:
$$v=sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}}(6)$$
в сферической системе координат:
$$v=sqrt{(r)^{2}+(r dot{theta})^{2}+(r dot{varphi} sin theta)^{2}}(7)$$
Частные случаи формул для вычисления скорости
Если модуль скорости не изменяется во времени, то такое движение называют равномерным (v=const).
При равномерном движении скорость можно вычислить, применяя формулу:
$$v=frac{s}{t}(8)$$
где s– длина пути, t – время, за которое материальная точка преодолела путь s.
При ускоренном движении скорость можно найти как:
$$bar{v}=int_{t_{1}}^{t_{2}} bar{a} d t(9)$$
где $bar{a}$ – ускорение точки,
$t_{1} leq t leq t_{2}$ – отрезок времени, в течение которого рассматривается скорость.
Если движение является равнопеременным, то применяется следующая формула для вычисления скорости:
$$bar{v}=bar{v}_{0}+bar{a} t$$
где $bar{v}_0$ – начальная скорость движения,
$bar{a} = const$ .
Единицы измерения скорости
Основной единицей измерения скорости в системе СИ является: [v]=м/с2
В СГС: [v]=см/с2
Примеры решения задач
Пример
Задание. Движение материальной точки А задано уравнением:
$x=2 t^{2}-4 t^{3}$ . Точка начала свое движение при
t0=0 c.Как будет двигаться рассматриваемая точка по отношению к оси X в момент времени t=0,5 с.
Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для
этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:
$$v=frac{d x}{d t}=4 t-12 t^{2}(1.1)$$
Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1.1) указанный в условии момент
времении сравним результат с нулем:
$$v(t=0,5)=4 cdot 0,5-12(0,5)^{2}=-1 lt 0$$
Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.
Ответ. Против оси X.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Скорость материальной точки является функцией от времени вида:
$$v=10left(1-frac{t}{5}right)$$
где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии
10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.
Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой:
$$x=int_{0}^{t} v d t=int_{0}^{t} 10left(1-frac{t}{5}right) d t=10 t-frac{10 t^{2}}{2 cdot 5}=10 t-t^{2}(2.1)$$
Для ответа на первый вопрос задачи подставим в выражение (2.1) время t=10 c, имеем:
$$x=10 cdot 10-(10)^{2}=0(m)$$
Для того чтобы определить в какой момент времени точка будет находиться на расстоянии 10 м от начала координат
приравняем выражение (2.1) к 10 и решим, полученное квадратное уравнение:
$$
begin{array}{c}
10 t-t^{2}=10(2.2) \
t_{1}=5+sqrt{15} approx 8,8(c) ; t_{2}=5-sqrt{15} approx 1,13(c)
end{array}
$$
Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала координат, когда x=-10. Решим квадратное уравнение:
$$10 t-t^{2}=-10(2.3)$$
При решении уравнения (2.3) нам подойдет корень равный:
$$t_{3}=5+6=11 (c)$$
Ответ. 1) $x=0 mathrm{~m}$ 2) $t_{1}=8,8 mathrm{c}, t_{2}=1,13 c, t_{3}=11 c$
Читать дальше: Формула средней скорости.
Как найти скорость материальной точки?
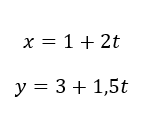
Кинематическое
уравнение движения материальной точки имеет вид: x = 1 + 2t; y = 3 + 1,5t. Координаты x и
y
выражены
в метрах, время – в секундах. Чему равна скорость материальной точки?
Решение.
Если
материальная точка движется в одной плоскости, то ее положение описывается
зависимостями x(t) и y(t), причем при равномерном движении x(t) = x0 + vxt , а y(t) = y0 – начальные координаты
материальной точки, vx
и
vy
–
проекции скорости, материальной точки на оси x и
y. В данной задаче vx = 2 м/с ; vy = 1,5 м/с. Откуда
находим модуль скорости движения материальной точки.
Ответ:
v = 2,5 м/с.
Источник: Пособие-репетитор для подготовки к централизованному тестированию. С.Н.Капельян, Л.А.Аксенович.

