Как найти скорость движения кпд

Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.

Работы силы, формула

Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).

Работа силы — это скалярное произведение вектора силы на вектор перемещения.

Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:

Векторный вид записи

[ large boxed{ A = left( vec{F} , vec{S} right) }]

Для решения задач правую часть этой формулы удобно записывать в скалярном виде:

[ large boxed{ A = left| vec{F} right| cdot left| vec{S} right| cdot cos(alpha) }]

( F left( H right) ) – сила, перемещающая тело;

( S left( text{м} right) ) – перемещение тела под действием силы;

( alpha ) – угол между вектором силы и вектором перемещения тела;

Работу обозначают символом (A) и измеряют в Джоулях. Работа – это скалярная величина.

В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.

Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.

Рассмотрим несколько случаев, следующих из формулы:

1. Когда угол между силой и перемещением острый, работа силы положительная;
2. А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
3. Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!

Работа — разность кинетической энергии

Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.

Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.

( E_{k1} left(text{Дж} right) )  – начальная кинетическая энергия машины;

( E_{k2} left(text{Дж} right) )  – конечная кинетическая энергия машины;

( m left( text{кг}right) ) – масса автомобиля;

( displaystyle v left( frac{text{м}}{c}right) ) – скорость, с которой машина движется.

Кинетическую энергию будем вычислять, используя формулу:

[ large E_{k} = m cdot frac{v^{2}}{2} ]

[ large E_{k1} = 1000 cdot frac{1^{2}}{2} = 500 left(text{Дж} right) ]

[ large E_{k2} = 1000 cdot frac{10^{2}}{2} = 50000 left(text{Дж} right) ]

Теперь найдем разницу кинетической энергии в конце и вначале разгона.

[ large boxed{ A = Delta E_{k} }]

[ large Delta E_{k} = E_{k2} — E_{k1} ]

[ large Delta E_{k} = 50000 – 500 = 49500 left(text{Дж} right) ]

Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.

Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.

[ large boxed{ A = Delta E }]

Работа силы тяжести — разность потенциальной энергии

Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.

Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.

( E_{p1} left(text{Дж} right) )  – начальная потенциальная энергия яблока;

( E_{p2} left(text{Дж} right) )  – конечная потенциальная энергия яблока;

Примечание: Работу можно рассчитать через разность потенциальной энергии тела.

Потенциальную энергию будем вычислять, используя формулу:

[ large E_{p} = m cdot g cdot  h]

( m left( text{кг}right) ) – масса яблока;

Величина ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения.

( h left( text{м}right) ) – высота, на которой находится яблоко относительно поверхности земли.

Начальная высота яблока над поверхностью земли равна 3 метрам

[ large E_{p2} = 0,2 cdot 10 cdot  3 = 6 left(text{Дж} right) ]

Потенциальная энергия яблока на столе

[ large E_{p1} = 0,2 cdot 10 cdot  1 = 2 left(text{Дж} right) ]

Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.

[ large Delta E_{p} = E_{p2} — E_{p1} ]

[ large Delta E_{p} = 2 – 6 = — 4 left(text{Дж} right) ]

Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!

Чтобы работа получилась положительной, в правой части формулы перед ( Delta  E_{p}) дополнительно допишем знак «минус».

[ large boxed{ A = — Delta E_{p} }]

Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.

Примечания:

1. Если тело падает на землю, работа силы тяжести положительна;
2. Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
3. Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
4. Работа силы тяжести не зависит от траектории, по которой двигалось тело;
5. Работа для силы (displaystyle F_{text{тяж}}) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.

Рисунок 4 иллюстрирует факт, что для силы (displaystyle F_{text{тяж}}) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.

Мощность

В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.

Примечание: Символ (vec{N}) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.

Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).

Расчет работы осуществляем, используя любую из формул:

[ large A = Delta E_{k} ]

[ large A = Delta E_{p} ]

[ large A = F cdot S cdot cos(alpha) ]

Разделив эту работу на время, в течение которого она совершалась, получим мощность.

[ large boxed{ P = frac{A}{Delta t} }]

Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.

Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.

Еще одна формула для расчета мощности

Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:

[ large P = left( vec{F} , vec{v} right) ]

Формулу можно записать в скалярном виде:

[ large P = left| vec{F} right| cdot left| vec{v} right| cdot cos(alpha) ]

( F left( H right) ) – сила, перемещающая тело;

( displaystyle v left( frac{text{м}}{c} right) ) – скорость тела;

( alpha ) – угол между вектором силы и вектором скорости тела;

Когда векторы (vec{F}) и (vec{v}) параллельны, запись формулы упрощается:

[ large boxed{ P = F cdot v }]

Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).

КПД

КПД – коэффициент полезного действия. Обычно обозначают греческим символом (eta) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.

Примечания:

1. Процент – это дробь, у которой в знаменателе число 100.
2. КПД — это либо правильная дробь, или дробь, равная единице.

Вычисляют коэффициент (eta) для какого-либо устройства, механизма или процесса.

[ large boxed{ eta = frac{ A_{text{полезная}}}{ A_{text{вся}}} }]

(eta) – КПД;

( large A_{text{полезная}} left(text{Дж} right)) – полезная работа;

(large A_{text{вся}} left(text{Дж} right)) – вся затраченная для выполнения работы энергия;

Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.

[ large boxed{ eta leq 1 }]

Величина (eta) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:

[ large boxed{ eta = frac{ P_{text{полезная}}}{ P_{text{вся затраченная}}} }]

Выводы

1. Сила, приложенная к телу и перемещающая его, совершает работу;
2. Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
3. Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
4. Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
5. Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
6. Мы совершаем работу против силы тяжести, когда поднимаем тело над землей. При этом наша работа положительная, а работа силы тяжести — отрицательная;
7. Сила тяжести — это консервативная сила. Поэтому, работа силы (displaystyle F_{text{тяж}}) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
8. Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
9. Коэффициент полезного действия обозначают греческим символом (eta) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
10. КПД — это либо правильная дробь, или дробь, равная единице.
11. Можно вычислять КПД, подставляя в формулу работу, или мощности

Лекция. Тема: Работа. Мощность. КПД.

1.Изучаем теоретический материал. (записываем основные определения и формулы)

   Работа А – скалярная физическая величина, измеряемая произведением модуля силы, действующей на тело, на модуль его перемещения под действием этой силы и на косинус угла между векторами силы и перемещения:

Здесь: 

 модуль перемещения тела, под действием силы   ,

 работа, которую совершила сила 

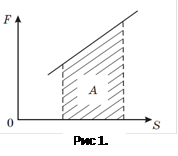
На графиках в осях F-S (рис.1) работа силы численно равна площади фигуры, ограниченной графиком, осью перемещения и прямыми, параллельными оси силы.

Если на тело действует несколько сил, то в формуле работы F – это не равнодействующая ma всех этих сил, а именно та сила, которая и совершает работу. Если локомотив тянет вагоны, то этой силой является сила тяги локомотива, если на канате поднимают тело, то этой силой является сила натяжения каната. Это может быть и сила тяжести и сила трения, если в условии задачи речь идет о работе именно этих сил.

 

Мощность

Для характеристики работоспособности и быстроты соверше­ния работы введено понятие мощности.

Мощность — работа, выполненная в единицу времени:

             

Единицы измерения мощности: ватты, киловатты,

                                      

Мощность при поступательном движении (рис. 16.1)

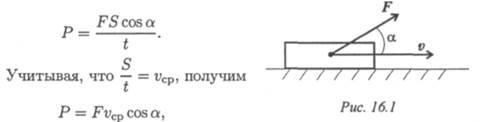
где F — модуль силы, действующей на тело; v_cp — средняя скорость движения тела.

Средняя мощность при поступательном движении равна про­изведению модуля силы на среднюю скорость перемещения и на ко­синус угла между направлениями силы и скорости.

Мощность при вращении (рис. 16.2) Тело движется по дуге радиуса

           

Р = М_врω_ср  где ω_ср — средняя угловая скорость.

Мощность силы при вращении равна произведению вращающе­го момента на среднюю угловую скорость.

Если при выполнении работы усилие машины и скорость дви­жения меняются, можно определить мощность в любой момент вре­мени, зная значения усилия и скорости в данный момент.

Коэффициент полезного действия

Каждая машина и механизм, совершая работу, тратит часть энергии на преодоление вредных сопротивлений.

Таким образом, машина (механизм) кроме полезной работы совершает еще и дополнительную работу.

Отношение полезной работы к полной работе или полезной мощности ко всей затраченной мощности называется коэффициентом по­лезного действия (КПД):

              

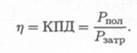
Полезная работа (мощность) расходуется на движение с заданной скоростью и определяется по формулам:

                 

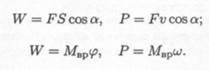
      Затраченная мощность больше полезной на величину мощности, идущей на  преодоление трения в звеньях машины, на утечки и тому подобные потери.

Чем выше КПД, тем совершеннее машина.

  2. Разбираем примеры решения  задач. (даны задачи)

Пример 1. Определение работы.

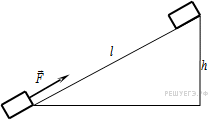
Тело мас­сой 2 кг под дей­стви­ем силы F пе­ре­ме­ща­ет­ся вверх по на­клон­ной плос­ко­сти на рас­сто­я­ние   Рас­сто­я­ние тела от по­верх­но­сти Земли при этом уве­ли­чи­ва­ет­ся на   .

Век­тор силы F на­прав­лен па­рал­лель­но на­клон­ной плос­ко­сти, мо­дуль силы F равен 30 Н. Какую ра­бо­ту при этом пе­ре­ме­ще­нии в си­сте­ме от­сче­та, свя­зан­ной с на­клон­ной плос­ко­стью, со­вер­ши­ла сила F? Уско­ре­ние сво­бод­но­го па­де­ния при­ми­те рав­ным   , ко­эф­фи­ци­ент тре­ния 

 Решение: Ра­бо­та силы опре­де­ля­ет­ся как ска­ляр­ное про­из­ве­де­ние век­то­ра силы и век­то­ра пе­ре­ме­ще­ния тела. Сле­до­ва­тель­но, сила F при подъ­еме тела вверх по на­клон­ной плос­ко­сти со­вер­ши­ла ра­бо­ту.

Ответ: 

Пример 2. Определение мощности.

Определить потребную мощность мотора лебедки для подъема груза весом 3 кН на высоту 10 м за 2,5 с (рис. 16.3). КПД механизма лебедки 0,75.

                           Решение

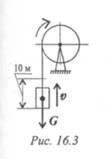
1. Мощность мотора используется на подъем груза с заданной скоростью и преодоление вредных сопротивлений механизма лебедки.

Полезная мощность определяется по формуле Р = Fvcosα. В данном случае α = 0; груз движется поступательно.

                                                     S     10

2. Скорость подъема груза v = —; v = — = 4 м/с.

                                                      T   2,5

3. Необходимое усилие равно весу груза (равно­мерный подъем).

4. Полезная мощность Р = 3000 ∙ 4 = 12 000 Вт.

5. Полная мощность, затрачиваемая мотором,

                            

Пример 3. Определение КПД.Судно движется со скоростью 56 км/ч (рис. 16.4). Двигатель развивает мощность 1200 кВт. Определить силу сопротивления воды движению судна. КПД машины 0,4.

Решение

      1. Определяем полезную мощность, используемую на движение с заданной скоростью: 

              

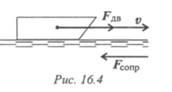
2. По формуле для полезной мощности можно определить движу­щую силу судна с учетом условия α = 0. При равномерном движении движущая сила равна силе сопротивления воды: F дв = F_conp .

Сила сопротивления воды движению судна F_сопр = 48 кН.

Пример 5. Точильный камень прижимается к обрабатываемой детали с силой 1,5 кН (рис. 16.5). Какая мощность затрачивается на обработку де­тали, если коэффициент трения материа­ла камня о деталь 0,28; деталь вращается со скоростью 100 об/мин, диаметр детали 60 мм.

                Решение

1. Резание осуществляется за счет трения между точильным камнем и обра­батываемой деталью:

3. Угловая   скорость вращения детали

4. Мощность, необходимая для обработки детали:

3.Закрепление материала. Пройти тесты по теме. ссылка https://multiurok.ru/tests/35174/

4. Домашнее задание. (с помощью теоретического материала и примера решения задач решить предложенные задачи самостоятельно).

Вопрос 1. Подвесной лодочный мотор развивает мощность 22000 Вт. Какую работу (МДж) может совершить мотор при перевозке груза за 30 минут?

Вопрос 2. Какую мощность (кВт) развивает подъемный кран, равномерно поднимая груз массой 2,5 т на высоту 15 м за 2,5 мин?

Вопрос 3. Механическая лопата, приводимая в движение электродвигателем мощностью 3,68 кВт, поднимает 180 т песка на высоту 6 м в течение 1 ч. Каков КПД установки?

Вопрос 4. Сколько времени (ч) должен работать насос мощностью 50 кВт, чтобы из шахты глубиной 150 м откачать воду объемом 200 м³?

Вопрос 5. Двигатель насоса, развивая некоторую мощность, поднимает 200 м³ воды на высоту 10 м за 5 мин. КПД двигателя 40 %. Найдите мощность (кВт) двигателя.

Вопрос 6. Трактор на пахоте преодолевает силу сопротивления 10 кН, развивая мощность 36 кВт. С какой скоростью движется трактор?

Вопрос 7. Электровоз при движении со скоростью 54 км/ч потребляет мощность 600 кВт. Определите силу тяги (кН) электровоза, если его КПД равен 75%.

Коэффицие́нт поле́зного де́йствия (КПД) — характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии. Определяется отношением полезно использованной энергии к суммарному количеству энергии, полученному системой; обозначается обычно η («эта»)^[1]. КПД является безразмерной величиной и часто выражается в процентах. Часто применяется в переносном смысле как метафора эффективности чего-либо без привязки к расчётам.

Определение[править | править код]

Математически КПД определяется как

где А — полезная работа (энергия), а Q — затраченная энергия.

Если КПД выражается в процентах, эту формулу иногда записывают в виде

.

Здесь умножение на не несёт содержательного смысла, поскольку . В связи с этим второй вариант записи формулы менее предпочтителен (одна и та же физическая величина может быть выражена в различных единицах независимо от формул, где она участвует).

В силу закона сохранения энергии и в результате неустранимых потерь энергии КПД реальных систем всегда меньше единицы, то есть невозможно получить полезной работы больше или столько, сколько затрачено энергии.

КПД теплово́го дви́гателя — отношение совершённой полезной работы двигателя к энергии, полученной от нагревателя. КПД теплового двигателя может быть вычислен по следующей формуле

,

где  — количество теплоты, полученное от нагревателя,  — количество теплоты, отданное холодильнику. Наибольшим КПД среди циклических машин, оперирующих при заданных температурах нагревателя T₁ и холодильника T₂, обладают тепловые двигатели, работающие по циклу Карно; этот предельный КПД равен

.

Другие похожие показатели[править | править код]

Не все показатели, характеризующие эффективность энергетических процессов, соответствуют вышеприведённому описанию. Даже если они традиционно или ошибочно называются «коэффициент полезного действия», они могут иметь другие свойства, в частности, превышать 100 %.

КПД котлов[править | править код]

КПД котлов на органическом топливе традиционно рассчитывается по низшей теплоте сгорания; при этом предполагается, что влага продуктов сгорания покидает котёл в виде перегретого пара. В конденсационных котлах эта влага конденсируется, теплота конденсации полезно используется. При расчёте КПД по низшей теплоте сгорания он в итоге может получиться больше единицы. В данном случае корректнее было бы считать его по высшей теплоте сгорания, учитывающей теплоту конденсации пара; однако при этом показатели такого котла трудно сравнивать с данными о других установках.

Тепловые насосы и холодильные машины[править | править код]

Достоинством тепловых насосов как нагревательной техники является возможность получать больше теплоты, чем расходуется энергии на их работу. Холодильная машина может отвести от охлаждаемого конца больше теплоты, чем затрачивается энергии на организацию процесса.

Эффективность машин характеризует холодильный коэффициент^[en]

,

где  — тепло, отбираемое от холодного конца (в холодильных машинах холодопроизводительность);  — затрачиваемая на этот процесс работа (или электроэнергия).

Для тепловых насосов используют термин коэффициент трансформации

,

где  — тепло конденсации, передаваемое теплоносителю;  — затрачиваемая на этот процесс работа (или электроэнергия).

В идеальной машине , отсюда для идеальной машины

Наилучшими показателями производительности для холодильных машин обладает обратный цикл Карно: в нём холодильный коэффициент

,

где ,  — температуры горячего и холодного концов, K^[2]. Данная величина, очевидно, может быть сколь угодно велика; хотя практически к ней трудно приблизиться, холодильный коэффициент может превосходить единицу. Это не противоречит первому началу термодинамики, поскольку, кроме принимаемой в расчёт энергии A (напр., электрической), в тепло Q идёт и энергия, отбираемая от холодного источника.

Примечания[править | править код]

Литература[править | править код]

• Пёрышкин А. В. Физика. 8 класс. — Дрофа, 2005. — 191 с. — 50 000 экз. — ISBN 5-7107-9459-7..