
1 — платиновая проволока с нанесённым на неё слоем серебра; 2 — щель, формирующая пучок атомов серебра; 3 — пластинка, на которой осаждаются атомы серебра; П и П1 — положения полосок осажденного серебра при неподвижном приборе и при вращении прибора.
Опыт Штерна — физический эксперимент, впервые поставленный немецким физиком Отто Штерном в 1920 году, и ставший одним из первых практических доказательств состоятельности молекулярно-кинетической теории строения вещества. В нём были непосредственно измерены скорости теплового движения молекул и подтверждено наличие распределения молекул газов по скоростям.
Для проведения опыта Штерном был подготовлен прибор, состоящий из двух цилиндров разного радиуса, ось которых совпадала и на ней располагалась платиновая проволока с нанесённым слоем серебра. В пространстве внутри цилиндров посредством непрерывной откачки воздуха поддерживалось достаточно низкое давление. При пропускании электрического тока через проволоку достигалась температура плавления серебра, из-за чего серебро начинало испаряться и атомы серебра летели к внутренней поверхности малого цилиндра равномерно и прямолинейно со скоростью 


,
где 


Найденная таким образом скорость движения атомов серебра совпала со скоростью, рассчитанной по законам молекулярно-кинетической теории (584 м/с), а тот факт, что получившаяся полоска была размытой, свидетельствовал в пользу того, что скорости атомов различны и распределены по некоторому закону — закону распределения Максвелла: атомы, двигавшиеся быстрее, смещались относительно полосы, полученной в состоянии покоя, на меньшие расстояния, чем те, которые двигались медленнее. При этом опыт давал лишь приблизительные сведения о характере распределения Максвелла, более точное экспериментальное подтверждение относится к 1930 году (опыт Ламмерта).
Литература[править | править код]
- Краткий словарь физических терминов / Сост. А. И. Болсун, рец. М. А. Ельяшевич. — Мн.: Вышэйшая школа, 1979. — С. 388. — 416 с. — 30 000 экз.
- Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика. Теплота. Молекулярная физика. — 12-е изд. — М.: Физматлит, 2001. — ISBN 5-9221-0135-8.
- Савельев И. В. Курс общей физики. — Т. 1. Механика. Молекулярная физика и термодинамика. — С. 320.
- Штерна опыт — статья из Большой советской энциклопедии.
Скорость движения молекул впервые была определена в 1920 году немецким физиком Штерном. Опыт Штерна заключается в следующем. По общей оси двух цилиндров, вращавшихся с одинаковой угловой скоростью, натянута посеребренная платиновая проволока O, которая накаливается электрическим током (рис. 77). При температуре 1200°C молекулы серебра испаряются с поверхности проволоки и часть их вылетает через узкую щель, прорезанную вдоль внутреннего цилиндра (щель a на рисунке).
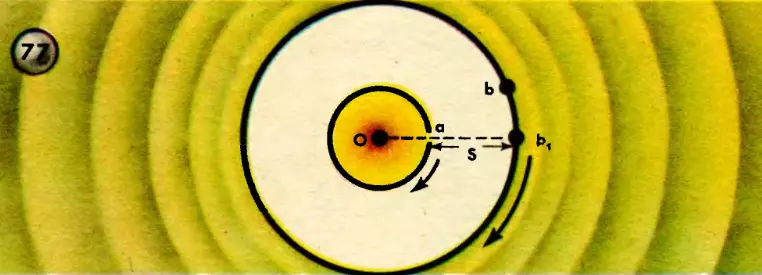
На холодной стенке внешнего цилиндра частицы серебра осаждаются в виде серебряной полоски. Однако за то время, в течение которого частица пролетает расстояние s между цилиндрами. Стенки их поворачиваются на некоторый угол (точка b на стенке внешнего цилиндра переходит в положение b1). Измеряя этот угол, можно подсчитать время поворота внешнего цилиндра, а следовательно, и время t движения частицы от щели до стенки второго цилиндра. Отсюда легко определить и скорость молекулы серебра:
v = s/t
Измеренная таким способом скорость молекул оказалась близкой к теоретически рассчитанной и для серебра заключалась в пределах от 50 до 625 м/с.
Значение этого опыта состоит в том, что его результаты совпали с результатами, полученными теоретически на основании молекулярно-кинетической теории; таким образом, правильность выводов теории подтвердилась.
Ниже приводятся средние скорости молекул некоторых газов и паров, полученные теоретически (при 0°C и 760 мм рт. ст.).
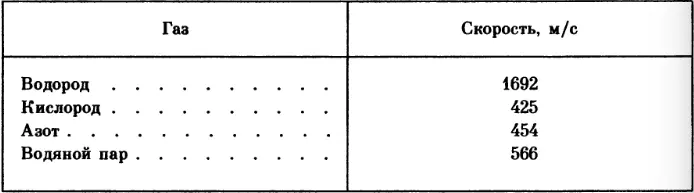
Как видите, эти скорости громадны. Их можно сравнивать лишь со скоростями пуль и артиллерийских снарядов.
Опыт Штерна
В 1920 г. немецкий физик Отто Штерн экспериментальным путем определил скорость движения молекул, подтвердил правильность основ молекулярно-кинетической теории газов.
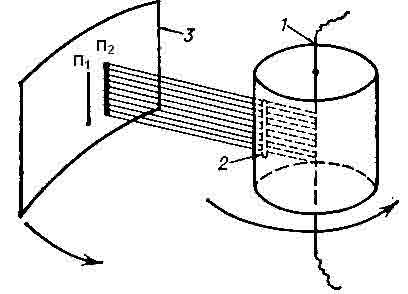
В опыте использовали разреженные пары серебра,получаемые при испарении слоя серебра, нанесённого на платиновую проволоку (1), нагревавшуюся электрическим током. Для получения пучка летящих атомов в цилиндре была сделана узкая щель (2). Атомы серебра осаждались на латунной пластинке (3) в иде узкой полоски, образуя серебряное изображение щели (П1). Затем прибор приводился в быстрое вращение вокруг оси. При этом атомы попадали в др. место пластинки (П2): пока они пролетали расстояние от щели до пластинки, пластинка смещалась.
Полученные в опыте значения наиболее вероятной скорости хорошо согласуются с теоретическим значением, полученным на основе распределения Максвелла.
Интересная статья? Поделитесь ею пожалуйста с другими:
Обновлено: 14.05.2023
Предположение, что молекулы тела могут иметь любую скорость, сначала теоретически доказал в 1856 году английский физик Дж. Максвелл. Он считал, что скорость молекул в данный момент времени является случайной, и поэтому их распределение по скоростям носит статистический характер (распределение Максвелла).
Установленный им характер распределения молекул по скоростям графически представлен кривой, изображенной на рис. 1.17. Наличие у нее максимума (бугра) свидетельствует о том, что скорости большинства молекул приходятся на определенный интервал. Она несимметричная, поскольку молекул с большими скоростями меньше, чем с небольшими.
Быстрые молекулы определяют течение многих физических процессов при обычных условиях. Например, благодаря им происходит испарение жидкостей, ведь при комнатной температуре большинству молекул недостаточно энергии, чтобы разорвать связь с другими молекулами (она намного выше (3 / 2) • kT), а у молекул с высокими скоростями она достаточная.
Распределение молекул по скоростям Максвелла на протяжении продолжительного времени оставалось экспериментально неподтвержденным, и лишь в 1920 году немецкий ученый О. Штерн сумел экспериментально измерить скорости теплового движения молекул.

Этот урок посвящен изучению того, каким способом можно измерить скорость молекул газа. Мы рассмотрим один из самых известных экспериментов в этой области – опыт Штерна.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока “Измерение скоростей молекул газа”
На прошлых уроках мы вывели уравнение, позволяющее связать среднюю кинетическую энергию молекул и температуру.
Как вы знаете, средняя кинетическая энергия молекул равна половине произведения массы молекулы и среднего значения квадрата скорости молекул:

Таким образом, зная температуру газа, мы можем найти среднее значение квадрата скорости его молекул:

Расчеты говорят о том, что при 0 о С, средняя скорость молекул азота достигает 500 м/с, а средняя скорость молекул водорода — 1800 м/с. Во второй половине 19 века это привело некоторых физиков в замешательство. Ведь всем хорошо известно, что запахи распространяются сравнительно медленно. Как же тогда получается, что молекулы газа двигаются с огромными скоростями, а само облако газа двигается в сотни раз медленнее?
Ответ на этот вопрос достаточно простой: молекулы двигаются беспорядочно, а потому их перемещения в сотни раз меньше пройденного пути. В качестве аналогии мы опять можем привести футбол. За один матч футболисты пробегают более десяти километров, однако, все это время они остаются в пределах футбольного поля, размеры которого равны 120 х 60 м.
Кроме расчетов скоростей молекул газа с помощью теории, существуют экспериментальные методы измерения скоростей. На сегодняшнем уроке, мы рассмотрим опыт Штерна, проведенный в 1920 году. Этот опыт был одним из первых экспериментальных подтверждений состоятельности молекулярно-кинетической теории.

Прибор Штерна представляет собой два коаксиальных цилиндра (то есть эти цилиндры обладают общей осью симметрии).
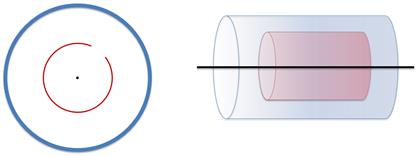
Из цилиндров откачан весь воздух. Вдоль оси малого цилиндра натянута тонкая платиновая проволока, покрытая серебром, а также в малом цилиндре имеется небольшая щель.
По проволочке пропускают электрический ток, с целью заставить серебро испаряться. В результате испарения, малый цилиндр заполняется газом из атомов серебра.
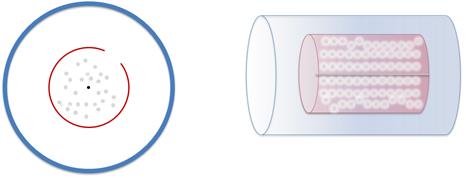
Разумеется, часть этих атомов пролетают через щель и оседают на внутренней стенке большого цилиндра. Этот слой серебра имеет определенное положение — прямо напротив щели в малом цилиндре.
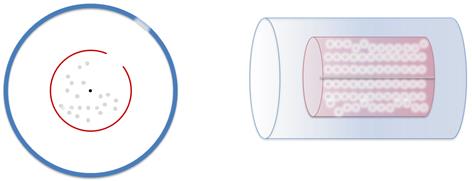
После этого, цилиндры приводят во вращение с одинаковой угловой скоростью и большой частотой (около 1500 об/с). Теперь атомы будут осаждаться не прямо напротив щели, поскольку за то время, пока они проходят расстояние от стенки малого цилиндра до стенки большого цилиндра, цилиндры поворачиваются на некоторый угол. Более того, слой серебра будет немного размытый из-за того, что не все атомы серебра двигаются с одинаковыми скоростями.
Обозначим за R радиус большого цилиндра, а радиус малого цилиндра — за r. Обозначим за d расстояние от конца радиуса, проходящего через центр щели до наибольшей концентрации атомов серебра после начала вращения. (Дело в том, что не все атомы имеют одинаковую скорость, поэтому, не все они попадают в одну и ту же точку). Поэтому, расстоянию d будет соответствовать средняя скорость атомов серебра:

Запишем теперь, что расстояние d равно:

Изучая криволинейное движение, мы убедились, что скорость вращения можно выразить через радиус вращения и частоту:

Из полученного выражения выразим время:

А теперь, это время подставим в формулу для средней скорости:

Таким образом, получили выражение, в котором средняя скорость задана через радиусы цилиндров, частоту вращения и расстояние d. Конечно же, радиусы цилиндров и расстояние d можно измерить. Частоту вращения задает сам экспериментатор, поэтому, она тоже известна. Модули скоростей, измеренные подобным способом, совпадают с теоретическим значением в пределах экспериментальной ошибки. Это говорит о том, что теоретическая формула, по которой мы вычисляли скорость, оказалась верна. Следовательно, верно и уравнение, связывающее среднюю кинетическую энергию молекул и температуру тела по абсолютной шкале Кельвина:
В середине XIX века была сформулирована молекулярно-кинетическая теория, но тогда не было никаких доказательств существования самих молекул. Вся теория базировалась на предположении о движении молекул, но как измерить скорость их движения, если они невидимы?
Теоретики первыми нашли выход. Из уравнения молекулярно-кинетической теории газов известно, что
Получена формула для расчета среднеквадратичной скорости, но масса молекулы неизвестна. Запишем по-другому значение υкв:
Например, при плотности азота, равной 1,25 кг/м, 3 , при t = 0 °С и P = 1 атм, скорости молекул азота . Для водорода: .
При этом интересно отметить, что скорость звука в газе близка к скорости молекул в этом газе , где γ – коэффициент Пуассона. Это объясняется тем, что звуковые волны переносятся молекулами газа.

Рис. 2.1
Платиновая нить А, покрытая снаружи серебром, располагается вдоль оси коаксиальных цилиндров S1, S3,. Внутри цилиндров поддерживается низкое давление порядка Па. При пропускании тока через платиновую нить она разогревается до температуры выше точки плавления серебра (961,9 °С). Серебро испаряется, и его атомы через узкие щели в цилиндре S1, и диафрагме S2, летят к охлаждаемой поверхности цилиндра S1, на которой они осаждаются. Если цилиндры S1, S3 и диафрагма не вращаются, то пучок осаждается в виде узкой полоски D на поверхности цилиндра S3. Если же вся система приводится во вращение с угловой скоростью то изображение щели смещается в точку D´ и становится расплывчатым.
Пусть l – расстояние между D и D´, измеренное вдоль поверхности цилиндра S3, оно равно где – линейная скорость точек поверхности цилиндра S3, радиусом R; – время прохождения атомами серебра расстояния . Таким образом, имеем откуда – можно определить величину скорости теплового движения атомов серебра. Температура нити в опытах Штерна равнялась 1200 °С, что соответствует среднеквадратичной скорости . В эксперименте для этой величины получилось значение от 560 до 640 м/с. Кроме того, изображение щели D´ всегда оказывалось размытым, что указывало на то, что атомы Ag движутся с различными скоростями.
В 1920 г. О. Штерн разработал метод атомных (молекулярных) пучков и с его помощью экспериментально измерил скорость теплового движения молекул газа, а также проверил распределение Максвелла. Установка Штерна состояла из двух коаксикальных цилиндров, на оси которых находилась платиновая проволока, покрытая слоем серебра. (рис. 1). В приборе создавался высокий вакуум. При пропускании по проволоке тока она раскалялась и с ее поверхности испарялись атомы серебра, которые вылетали через узкую щель, проделанную во внутреннем цилиндре, и достигали стенки наружного цилиндра (в точке A на рис. 1).
В результате образовывалась узкая серебряная полоска, являющаяся изображением щели. Затем весь прибор приводился во вращение вокруг оси цилиндров с постоянной угловой скоростью , при этом полоска смещалась в сторону противоположную вращению на величину =AA’. Смещение возникало, потому что за время t пролета атомом серебра расстояния R-r цилиндр успевал повернуться на угол = /R = t. Откуда определялось время t = /R, знание которого позволяло найти скорость атома серебра через измеримые параметры опыта:
Как следовало ожидать, полоска серебра в положении А’ оказывалась размытой из-за того, что атомы серебра имеют разные скорости: более быстрым атомам соответствуют меньшие, а более медленным – большие смещения . Исследуя зависимость плотности серебра в размытой части от расстояния до точки A, нетрудно оценить распределение атомов серебра по скоростям. Полученное распределение хорошо согласовывалось со значениями, вычисленными по формуле .
Более совершенный метод по проверке закона Максвелла был реализован в 1929 г. Ламертом. В высоком вакууме вращаются, насаженные на общую ось, два круглых диска 1 и 2 с радиальными узкими прорезями (рис. 2), смещенными друг относительно друга на угол . Напротив прорези диска 1 находилась тигельная печь 3 с исследуемым веществом и диафрагма 4. Вся установка приводилась во вращение с постоянной угловой скоростью. Очевидно, атомы, вылетевшие со скоростью v из печи, достигают мишени 5, если время их пролета расстояния между дисками t1 = l/v совпадает со временем t2 поворота диска 2 на угол , т.е. t2 = /. Из условия t1 = t2 находим v = l/. Меняя угловую скорость вращения , можно выделить атомы с различными скоростями. Улавливая атомы, движущиеся с различными скоростями в течение равных промежутков времени, можно по толщине (плотности) осадка на мишени определить их относительное количество в пучке и тем самым проверить закон распределения Максвелла. Обработка экспериментальных результатов, полученных на установке Ламерта, показала полное согласие их с законом Максвелла.
Понимание того, что в основе строения любого вещества лежит существование мельчайших частиц – атомов и молекул, находящихся в непрерывном движении и активном взаимодействии между собой, – возникло в XIX веке. В разработке молекулярно-кинетической теории на бумаге участвовали физики Рудольф Клаузиус, Людвиг Больцман и особенно Джеймс Максвелл. Вскоре последовали и подтверждающие её практические исследования. Важнейшим из них является опыт Штерна, проведенный в 1920 году.

Гений эксперимента
Кроме классического эксперимента по измерению скорости теплового движения частиц, известен опыт Штерна-Герлаха, в результате которого было доказано существование спина – момента импульса атомного ядра или атома. Этот эксперимент, проведенный в 1922 году совместно с Вальтером Герлахом (1889-1979), стал важнейшим доказательством основных постулатов квантовой теории.
Описание прибора
Эксперимент 1920 года, результатом которого стало доказательство распределения скоростей теплового движения молекул, был осуществлен с помощью технически несложной установки. Основой прибора послужили два коаксиальных (соосных) цилиндра разного диаметра, внутри которых путём откачки воздуха была создана область низкого давления. На общей оси расположена проволока из платины с тонким серебряным напылением. При подключении к концам проводника электрического тока происходит нагревание проволоки до температуры, превышающей точку плавления серебра. Возникает испарение атомов металла, которые начинают прямолинейное равномерное движение к внутренней поверхности маленького цилиндра.
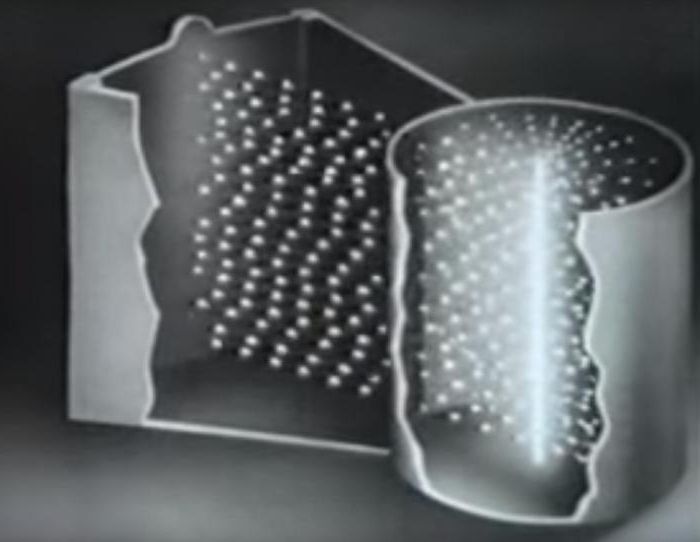
Измерение скорости молекулярного движения
Главный показатель, который сделал видимым опыт Штерна, — скорость молекул V. Было установлено, что средняя скорость, с которой двигаются при испарении атомы серебра при нагревании спирали до 1200 °C, – от 560 до 650 м/с.
Для измерения её Штерн получил все необходимые данные:
• S – смещение полосы серебра при вращении от того положения, которое она занимала в состоянии покоя;
• L – путь, пройденный атомами (расстояние между внутренними поверхностями цилиндров);
• U – скорость перемещения точек поверхности внешнего цилиндра;
• t – время пролета атомов.
Результат, экспериментально полученный немецким физиком — V = S / U = L / V = UL / S — совпал со значениями, полученными в результате рассмотрения молекулярно-кинетической теории. Средняя скорость движения молекул серебра, определенная теоретически, была равна 584 м/с.

Это стало доказательством справедливости постулатов, сформулированных её основоположниками, видное место среди которых занимает Джеймс Максвелл.
Закон распределения Максвелла
Кратко опыт Штерна можно определить как визуализацию распределения скорости теплового движения атомов и молекул. При осаждении серебра на стенках внешнего цилиндра, когда система находится в состоянии покоя, получалась полоска с достаточно четкими краями. При вращении цилиндров она выходила размытой.

Причина этого – различие в скорости движения атомов, испускаемых при испарении серебряного покрытия проволоки. Более быстрые частицы осаждались с меньшим смещением от прорези в малом цилиндре, а те, что двигались медленнее, успевали преодолеть большее расстояние. Соотношение скоростей укладывается в пропорцию, предсказанную вычислениями Максвелла. Кривая поперечного сечения полученного напыления совпадает по форме с графическим выражением формул, послуживших основой молекулярно-кинетической теории.
Теория, проверенная практикой
Большое значение, которое имеет экспериментальная физика, опыт Штерна показывает особенно наглядно. Умение найти способ доказательства правильности теоретических постулатов особенно ценно, когда предметом научных исследований становятся объекты, неразличимые невооруженным глазом.
Последующая история науки, когда физика вступила в фазу исследования строения атома в период поиска элементарных частиц, доказала это. Одним из пионеров нового течения был немецкий физик, гениальный экспериментатор Отто Штерн.
Читайте также:
- Биография бокова ахмеда кратко
- Выявить связь видового богатства с различными факторами кратко
- Сша в период от войны за независимость до гражданской войны кратко
- Прорыв линии зигфрида кратко
- Церковь сен дени кратко
Информацией можно воспользоваться на уроке физики, если для этого в курсе окажется свободное время или можно предложить разобраться с опытом Штерна учащимся на факультативных занятиях. Очень полезная информация для любознательных.
Опыт Штерна © Исакова М.А., 2021

Опыт Штерна
© Исакова М.А., 2021
Принципиальные элементы в приборе для определения скоростей молекул:

Принципиальные элементы в приборе для определения скоростей молекул:
Отто Штерном проведён опыт, благодаря которому рассчитаны скорости движения молекул газа и подтверждено распределение молекул газа по скоростям

1920 год – Отто Штерном проведён опыт, благодаря которому рассчитаны скорости движения молекул газа и подтверждено распределение молекул газа по скоростям.
В центе прибора – платиновая нить, покрытая слоем серебра.
По нити пропускается ток – идёт нагрев до температуры плавления серебра.
to
пл
Испаряющиеся молекулы серебра вылетают через щель и оседают.
щель
щель
наружный цилиндр
внутренний цилиндр
Наружный цилиндр приводится во вращение с угловой скоростью ω

Наружный цилиндр приводится во вращение с угловой скоростью ω.
В центе прибора – платиновая нить, покрытая слоем серебра.
to
пл
щель
щель
наружный цилиндр
ω
φ
Определяются радиусы цилиндров и частота вращения наружного цилиндра и делается расчёт.
Замеряется угол φ, до области наиболее яркого напыления серебра.
R1
R2
S S – расстояние по дуге до области максимального насыщения серебром t – время движения частиц между цилиндрами

S
S – расстояние по дуге до области максимального насыщения серебром
t – время движения частиц между цилиндрами R1 и R2
U – скорость вращения точек
цилиндра №2
V – скорость движения большинства молекул паров серебра
ω
S / U ꟷ для точек наружного цилиндра t = (

t = S/U ꟷ для точек наружного цилиндра
t = (R2 – R1)/ V ꟷ для атомов «большинства»серебра
U = ω٠ R2
S/(ω٠ R2) = (R2 – R1)/ V
V = (ω٠ R2)٠ (R2 – R1)/ S
То, что пятно «размыто» по стенке цилиндра, значит, что молекулы движутся с разными скоростями –
подтверждение «распределения Максвелла».
Как определить скорости полёта молекул в газе – опыт Штерна.

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
Введите ваш emailВаш email
