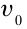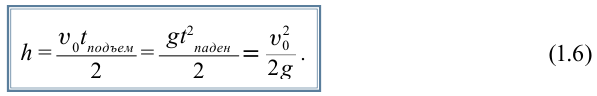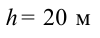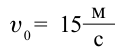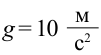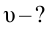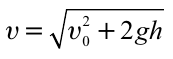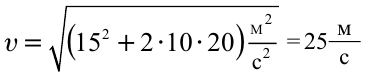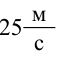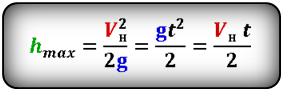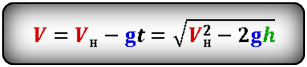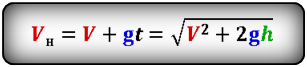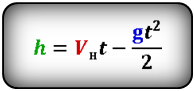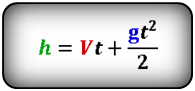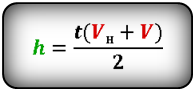Преподаватель который помогает студентам и школьникам в учёбе.
Вертикальное движение тел в физике – формулы и определение с примерами
Вертикальное движение тел:
Если держать в руках какой-либо предмет, а затем отпустить его, то предмет из-за притяжения Земли начнет двигаться прямо к ее поверхности. Такое движение тел называется вертикальное движение вниз. С этим движением вы ознакомились на уроках физики в 7 классе. В этой теме мы рассмотрим вертикальное движение вниз с точки зрения принципа независимости движений.
Когда тело двигается вертикально, на него действует одна или несколько сил (сила тяжести, сила сопротивления воздуха, сила Архимеда). В случае движения тел вверх (вертикально) в целях упрощения задачи мы не учитываем силу сопротивления воздуха и силу Архимеда.
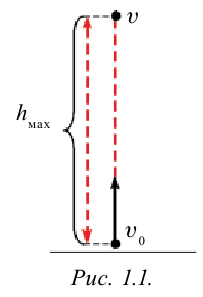
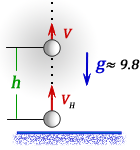
Понаблюдаем за движением какого-либо предмета, подбросив его вверх в вертикальном направлении (рис. 1.1.). Если бы тело двигалось вверх только со скоростью
Движение тела, брошенного вертикально вверх, является равнозамедленным движением.
Скорость тела через время 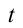
Тело останавливается при достижении самой верхней точки 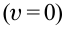
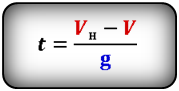
Приравнивая левую сторону выражения (1.4) нулю, находим выражение для определения времени, необходимого для подъема тела:
Максимальная высота подъема тела определяется выражением:
В условиях, когда сопротивление воздуха ничтожно мало и можно его не учитывать, время подъема брошенного вверх тела будет равно времени падения вниз 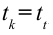
Тело, брошенное вертикально вниз, совершает равномерно ускоренное движение. Здесь скорость тела через время 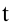
Уравнение движения тела, брошенного вертикально вниз, запишем следующим образом:
Первым закономерности вертикального движения тел экспериментальным способом начал изучать великий итальянский ученый Г. Галилей. На основе проведенных опытов были обнаружены две закономерности вертикального падения тел. Во-первых, вертикальное падение тела является прямолинейным равноускоренным движением, во-вторых, все тела при свободном падении двигаются с постоянным ускорением.
Если учесть, что свободное падение тел является равноускоренным движением, то все уравнения прямолинейного равноускоренного движения в этом случае также действительны, т.е. можно заменить ускорение 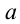
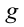
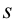
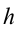
Из-за того, что свободное падение происходит равноускоренно, а движение вертикально вверх – равнозамедленно, среднюю скорость движения тела можно определить из следующего выражения:
Образец решения задачи:
Начальная скорость предмета, падающего с крыши здания высотой
20 м, равна 15 м/сек. Чему равняется его скорость в момент столкновения
с землей?
Дано:
Найти:
Формула:
Решение:
Ответ:
Таблица 1
| Уравнения равноускоренного движения |
Уравнения движения при свободном падении |
|---|---|
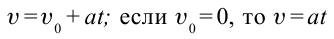 |
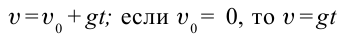 |
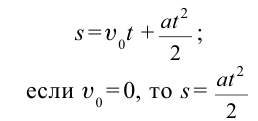 |
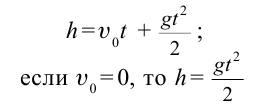 |
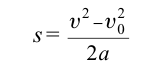 |
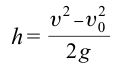 |
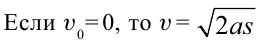 |
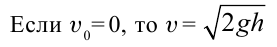 |
- Неравномерное движение по окружности
- Равномерное движение по окружности
- Взаимная передача вращательного и поступательного движения
- Движение горизонтально брошенного тела
- Опыты Фарадея в физике
- Электромагниты и их применение в физике
- Колебательный контур в физике
- Исследовательские методы в физике
Когда объект падает с определенной высоты, сила тяжести в значительной степени влияет на его достижение. скорость. Итак, ясно, что высота — это сущность, влияющая на движение.
Свободно падающий объект сначала достигает нуля скорость, и когда он начинает двигаться вниз, он набирает скорость. Предположим, мы знаем единственную высоту падающего объекта, как найти скорость с высотой, а также вместе с высотой, как другие объекты влияют на скорость, объясняется в этом посте.
Как найти скорость по высоте?
Рассмотрим книгу, которую держат на столе на высоте h от земли. Когда книга падает со стола, скорость падения книги на землю определяется скоростью. Поскольку книга находится на высоте h, как найти скорость с высотой?
Мы знаем, что скорость можно вычислить, зная расстояние, пройденное телом, и время, затрачиваемое им на преодоление этого расстояния. Математически это можно записать как,
В приведенном выше примере нам предоставлена высота h. высота тела связана с потенциалом энергия. Таким образом, основное уравнение неверно.
Учитывая потенциальную энергию, которой обладает книга до того, как она упадет, выражение можно записать в виде
PE = мгч.
Но книга находится в движении; следовательно, потенциальная энергия теперь превращается в кинетическую энергию, как
Таким образом, потенциальная энергия и кинетическая энергия равны по закону сохранения энергии. Следовательно, уравнение можно записать в виде
Преобразовав уравнение, мы получим скорость как
v2 = 2гх
В приведенном выше уравнении g — это ускорение свободного падения. Любой объект, падающий с определенной высоты, находится под влиянием гравитации и постоянно ускоряется из-за гравитации.
Как найти скорость через ускорение и высоту?
Мы знаем, как найти скорость с ускорением и расстоянием из предыдущей статьи. Но мы дали с ускорением и высотой, тогда как найти скорость с ускорением и высотой вместо расстояния?
Ускорение и скорость пропорциональны друг другу, поскольку производная скорости по времени есть ускорение. Если у нас есть средства ускорения, при интегрировании ускорения мы можем получить скорость. Но в данном случае у нас есть ускорение и высота. Обсудим, как найти скорость с высотой, если задано ускорение.
Предположим, что мяч находится на определенной высоте над землей. Мяч падает с высоты «h», и он начинает ускоряться на «а» в направлении ускорения под действием силы тяжести; это означает, что мяч падает с высоты h в направлении силы тяжести.
Поскольку и ускорение, и ускорение свободного падения имеют одно и то же направление, общее ускорение тела равно сумме обоих ускорений тела и ускорения свободного падения A = g+a. Теперь скорость мяча можно рассчитать, используя уравнение движения.
Мы знаем из кинематического уравнения движения, что расстояние, пройденное телом, можно записать в терминах математического уравнения как
Но у нас есть высота мяча и ускорение. Расстояние можно записать через высоту как
Начальное положение мяча, когда он начинает двигаться, и конечное положение мяча определяют расстояние.
Следовательно, x = h – 0, т. е. x=h, можно сказать, что расстояние по вертикали – это высота. Теперь подставив x = h, мы получим уравнение вида
Преобразовывая приведенное выше уравнение, мы имеем
Уравнение, полученное выше, дает скорость мяча с учетом ускорения и высоты.
Приведем другой пример, если снаряд движется к земле с высоты h и его ускорение больше, чем ускорение свободного падения, так как снаряд преодолевается за счет трения о воздух, то уравнение скорости будет вычисляться как
В уравнениях кинематики скорость определяется выражением
v2 = 2Ах
Где х – расстояние. Но здесь х = h, тогда
v2 = 2Ач
Рассмотрим другой случай; если подбросить мяч в воздух, то после достижения высоты h мяч начнет ускоряться вниз под действием силы тяжести; движение называется движение снаряда; как в этой ситуации найти скорость через ускорение и высоту? Движение мяча в воздухе показано на рисунке ниже.
Из приведенного выше рисунка высота объекта равна h, а расстояние — это не высота, но у нас есть высота в терминах расстояния с использованием уравнения движения снаряда. Связь между расстоянием и высотой можно записать как
Подставив значение расстояния в уравнение движения, получим
Преобразовывая уравнение, мы получаем скорость как
Как найти начальную скорость, зная ускорение и высоту?
Начальная скорость может быть получена из ускорения и высоты, учитывая уравнение движения.
Тело ускоряется, значит, должно быть изменение скорости тела в данном случае, что также говорит о том, что изначально тело имеет некоторую скорость, которая продолжает меняться со временем. Таким образом, чтобы найти Начальная скорость, нам нужно знать конечную скорость тела.
Когда мы подбрасываем мяч в воздух, он достигает определенной высоты h с определенной скоростью и приобретает ускорение а. Изначально; мяч движется со скоростью vi. Наконец, скорость будет vf. Уравнение начальной скорости запишем с помощью уравнения движения мяча, которое можно рассчитать следующим образом.
Скорость может быть
Конечная скорость мяча определяется как vf, следовательно, из средней скорости.
Но на высоте h мяч приобретает нулевую конечную скорость, падая обратно на землю под действием силы тяжести.
Но мы не знаем, сколько времени потребуется мячу, чтобы достичь высоты h, поэтому мы можем использовать ускорение. Первоначально мяч ускоряется против силы тяжести; его ускорение станет отрицательным.
Мы знаем, конечная скорость равно нулю, то
Таким образом, мы получаем фактор времени как
Подставляя в уравнение средней начальной скорости, получаем
Преобразовывая уравнение, получаем
Мы можем вычислить начальную скорость, когда конечная скорость отлична от нуля. Рассмотрим уравнение
В приведенном выше уравнении подставив значение t как
т = (vf+vi) / а
Получаем уравнение в виде
(vf+vi) (вf-vi) = 2ah
Приведенное выше уравнение можно записать как
vf2-vi2 = 2ah
Переставляя условия, чтобы получить начальную скорость как
vi2 = Vf2– 2 часа
Как рассчитать скорость по высоте и времени?
При вертикальном движении путь, пройденный телом, равен высоте, с которой тело начинает движение.
Скорость можно рассчитать, используя высоту и время. Расстояние, пройденное телом с время всегда описывает скорость тела. Физические объекты, такие как ускорение и высота, также способствуют нахождению скорости.
Мы можем вычислить скорость по высоте и времени тремя способами.
- При вертикальном движении тела
- При метательном движении тела
- График зависимости роста от времени
При вертикальном движении тела
Если баскетбольный мяч падает из корзины на высоте h и ускоряется в направлении силы тяжести, то скорость можно определить как
Но ускорение задается
Подставляя значение a и заменяя член расстояния высотой h, мы получаем
При перестановке членов скорость с высотой и временем равна
По движению снаряда
Рассмотрим другой пример; баскетболист бросает мяч в корзину, стоящую на расстоянии d от корзины. Мяч делает движение снаряда добраться до корзины; то мы можем рассчитать скорость следующим образом:
Общее выражение скорости дается выражением
Мяч проходит расстояние d на высоте h; если пренебречь трением, расстояние можно записать как
Подставляя значение x в общее уравнение скорости, получаем
График зависимости роста от времени
Если мы построим график с высотой по оси y и временем по оси x, график называется графиком высота-время.
Мы можем рассчитать скорость по графику высота-время. Наклон графика высота-время дает скорость тела.
Из приведенного выше графика наклон определяется выражением
Из графика AB параллелен высоте h, а BC параллелен времени t; следовательно, мы можем сказать, что
АВ = h и ВС = t;
Из определения скорости мы можем сказать, что наклон есть не что иное, как скорость. Таким образом, наклон равен скорости.
Как найти скорость по высоте и массе?
Хотя масса не влияет на скорость, она вносит энергию и силу, необходимые телу для достижения определенной скорости.
Высота и масса — это объекты, связанные с объектом. потенциальная энергия. Масса также вносит вклад в кинетическую энергию, приобретаемую объектом при движении. Зная массу, давайте поймем, как найти скорость с высотой.
Объект на определенной высоте обладает потенциалом, который заставляет тело двигаться, и он равен кинетической энергии тела при движении.
Поскольку и потенциальная энергия, и кинетическая энергия равны, мы можем их приравнять.
Ep= Ek
Кинетическая энергия тела равна
Преобразовывая уравнение, получаем
В начале мы сказали, что потенциальная энергия = кинетическая энергия,
Поэтому уравнение можно переписать как
В общем случае потенциальная энергия равна Е.p= мгх.
Ответ, который мы получили из потенциальной энергии, можно подставить в приведенное выше уравнение, чтобы получить скорость тела.
Как найти скорость с учетом высоты и силы тяжести?
Когда вы бросаете камень в воздух, он падает на землю под действием силы тяжести. Это общий процесс. Но заметили ли вы, что скорость мяча? Скорость камня при движении вниз немного меньше скорости того же камня при падении назад.
Приведенное выше утверждение поясняет, что скорость может меняться и под действием силы тяжести. Гравитация вступает в действие, когда тело находится на определенной высоте; поскольку гравитация является силой притяжения, она пытается поднять тело на высоту к земле, поэтому, основываясь на этих данных, как найти скорость через высоту и расстояние?
В предыдущем разделе обсуждался один из способов нахождения скорость с высотой и силой тяжести. Обсудим, как найти скорость по высоте и расстоянию, рассматривая кинематическое уравнение движения.
Высота всегда равна расстоянию из кинематического уравнения расстояния. Следовательно, мы можем рассматривать расстояние как высоту. Таким образом, уравнение будет
Если камень движется в направлении силы тяжести, то ускорение происходит только благодаря силе тяжести; следовательно, уравнение можно переписать как
Переставив члены, уравнение будет
Приведенное выше уравнение дает скорость с высотой и силу тяжести с временным фактором. Если тело движется с ускорением против силы тяжести, то
г = -г
Как найти скорость по высоте и углу?
Когда тело начинает падать с некоторой высоты на поверхность, оно образует с точкой падения некоторый угол θ. Угол, создаваемый объектом, помогает нам найти ответ на вопрос, как найти скорость с высотой.
Компания смещение тела в вертикальном положении – высота. Вертикальную составляющую скорости можно записать как
v = v sinθ
Если тело вырабатывает некоторые горизонтальное смещение, то скорость
v = v cos θ
Из уравнения движения вертикальную и горизонтальную скорости можно записать как
vx = v cosθ
vy = v sinθ-gt; где g – ускорение свободного падения
На максимальной высоте vy= 0 = v sinθ –gt
v sinθ = gt
Когда тело падает под углом θ и движется со скоростью v, его дальность действия определяется выражением
Поэтому, используя значение R,
Следовательно, скорость можно переписать как
Решенные задачи о том, как рассчитать скорость с высотой
Задача 1) Мяч падает с высоты 15 м и достигает земли с определенной скоростью. Вычислите скорость мяча.
Решение:
Нам предоставляется только высота h = 15м.
Поскольку мяч движется к земле, движение происходит за счет ускорения силы тяжести g. Величина ускорения свободного падения g = 9.8 м/с.2. Скорость мяча
Подставляя значения h и g;
v = 17.14 м / с.
Задача 2) Вычислите начальную скорость камня, падающего с высоты 3 м, и его ускорение 2 м/с.2, и, следовательно, найти время, за которое камень достигнет земли.
Решение:
Приведенные данные: Высота h = 3м
Ускорение камня a = 2 м/с2.
Скорость камня определяется выражением
v = 3.46 м / с.
Время, необходимое камню, чтобы достичь земли, определяется уравнением
t = 1.79 с.
Задача 3) Тело массой 3 кг падает с высоты 7 м, ускоряясь под действием силы тяжести. Вычислите скорость объекта.
Решение:
Даны данные – масса объекта m = 3кг.
Высота, с которой упал предмет, h = 7 м.
Ускорение свободного падения g = 9.8 м/с.2.
Поскольку движение объекта обусловлено массой, высотой и гравитацией, то совершаемая работа равна потенциальной энергии. это дано
Ep = мгх
Объект движется, поэтому объект обладает кинетической энергией; это представлено формулой,
Из закона сохранения энергии, когда объект начинает двигаться, его потенциальная энергия теперь называется кинетической энергией.
Поэтому Еp = Ek
Потенциальная энергия Еp = 3 × 9.8 × 7
Ep = 205.8 Дж
Подставив Ep = Ek = 205.8 Дж.
v2 = 137.2
v = 11.71 м / с.
Задача 4) Спортсмен стреляет толканием ядра в воздух в вертикальном направлении, и ему требуется время 3 секунды, чтобы упасть на землю вертикально с высоты 7 м от земли. Рассчитайте скорость, с которой толкатель ядра возвращается на землю.
Решение:
Приведенные данные – высота от земли h = 7 м.
Время, необходимое для достижения земли = 3 секунды.
Скорость определяется выражением
v = 2.33 м / с.
Задача 5) Тело массой 4 кг падает с высоты 11 м над землей под углом 20°. Вычислите скорость тела. (Примите ускорение свободного падения равным 10 м/с.2)
Решение:
Приведены данные – масса тела m = 4 кг.
Высота h = 11 м.
Угол θ = 20°.
Ускорение свободного падения g = 10 м/с.2.
Скорость определяется выражением
v = 43.45 м / с.
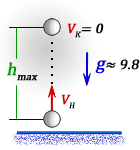
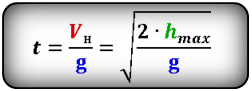
1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту
h max
– максимальная высота достигнутая телом за время t
Vк – конечная скорость тела на пике, равная нулю
Vн – начальная скорость тела
t – время подъема тела на максимальную высоту h
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула максимальной высоты (h max):
Формула времени за которое тело достигло максимальную высоту (t):
2. Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести
h – расстояние пройденное телом за время t
Vн – начальная скорость тела
V – скорость тела в момент времени t
t – время подъема за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула скорости тела в момент времени t (V):
Формула начальной скорости тела (Vн):
Формулы высоты тела в момент времени t (h):
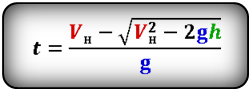
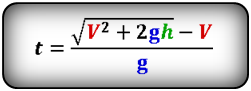
Формулы времени, за которое тело достигло высоту h (t):
- Подробности
-
Опубликовано: 04 августа 2015
-
Обновлено: 13 августа 2021
Содержание материала
- Прямолинейное равномерное движение
- Скалярные величины (определяются только значением)
- Векторные величины (определяются значением и направлением)
- Проецирование векторов
- Уравнение движения
- Видео
- Средняя скорость по перемещению. Средняя путевая скорость
- Равномерное движение
- График скорости (проекции скорости)
- График перемещения (проекции перемещения)
- О том, как решить основную задачу механики
- Скорость не меняется движение равномерное
- Равномерное движение в направлении противоположном оси
- Относительность механического движения
- Правило сложения перемещений
- Правило сложения скоростей
- Относительная скорость
- Движение по вертикали
- Задачи
Прямолинейное равномерное движение
Движение по прямой, при котором тело проходит равные участки пути за равные промежутки времени называют прямолинейным равномерным. Это любое движение с постоянной скоростью.
Например, если у вас ограничение скорости на дороге 60 км/ч и у вас нет никаких препятствий на пути, то вы скорее всего будете двигаться прямолинейно равномерно.
Мы можем охарактеризовать это движение следующими величинами.
Скалярные величины (определяются только значением)
- Время — в международной системе единиц СИ измеряется в секундах [с].
- Путь — длина траектории (линии, по которой движется тело). В случае прямолинейного равномерного движения — длина отрезка [м].
Векторные величины (определяются значением и направлением)
- Скорость — характеризует быстроту перемещения и направление движения материальной точки [м/с].
- Перемещение — вектор, проведенный из начальной точки пути в конечную [м].
Проецирование векторов
Векторное описание движения полезно, так как на одном чертеже всегда можно изобразить много разнообразных векторов и получить перед глазами наглядную «картину» движения.
Однако всякий раз использовать линейку и транспортир, чтобы производить действия с векторами, очень трудоёмко. Поэтому эти действия сводят к действиям с положительными и отрицательными числами — проекциями векторов.
Если вектор сонаправлен с осью, то его проекция равна длине вектора. А если вектор противоположно направлен оси — проекция численно равна длине вектора, но отрицательна. Если вектор перпендикулярен — его проекция равна нулю.
Скорость может определяться по перемещению и пути, только это будут две разные характеристики. Скорость — это векторная физическая величина, характеризующая быстроту перемещения, а средняя путевая скорость — это отношение длины пути ко времени, за которое путь был пройден.
Скорость
— скорость [м/с] — перемещение [м] — время [с]
В чем разница между перемещением и путем?
Перемещение — это вектор, проведенный из начальной точки в конечную, а путь — это длина траектории.

Задача
Найдите, с какой средней путевой скоростью должен двигаться автомобиль, если расстояние от Санкт-Петербурга до Великого Новгорода в 210 километров ему нужно пройти за 2,5 часа. Ответ дайте в км/ч.
Решение:
Возьмем формулу средней путевой скорости
V ср.путевая = S/t
Подставим значения:
V ср.путевая = 210/2,5 = 84 км/ч
Ответ: автомобиль будет двигаться со средней путевой скоростью равной 84 км/ч
Уравнение движения
Одна из основных задач механики — определение положения тела относительно других тел в данный момент времени. Для решения этой задачи помогает уравнение движения, то есть зависимость координаты тела от времени х = х(t).
Уравнение движения
x(t) = x + vxt
x(t) — искомая координата в момент времени t [м] x — начальная координата [м] vx — скорость тела в данный момент времени [м/с] t — момент времени [с]
Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:
Уравнение движения при движении против оси
x(t) = x − vxt
x(t) — искомая координата в момент времени t [м] x — начальная координата [м] vx — скорость тела в данный момент времени [м/с] t — момент времени [с]
Видео
Средняя скорость по перемещению. Средняя путевая скорость
Хочешь, покажу фокус?
Смотри.
Из горной пещеры вылетает дракон, а за ним в ту же секунду выбегает доблестный рыцарь. Дракон хочет разрушить замок, находящийся от пещеры на расстоянии 7 километров. Задача рыцаря – добраться до замка первым и остановить дракона.
Рыцарь скачет на лошади прямо к замку по равнине в течении 20 минут. Он обнаруживает, что мост через реку на пути к замку разрушен, поэтому решает переплыть реку, и (спасибо его хорошей подготовке) у него уходит лишь 5 минут на то, чтобы снять с себя доспехи и сделать это. Затем в течении 10 минут он продолжает движение к замку.
Дракон после вылета из пещеры движется вперед и вверх, на это у него уходит 15 минут. На какой-то высоте он останавливается, потому что видит стаю пролетающих мимо уток. Драконы, динозавры, птицы… Смекаешь, да? Он решает поиграться со своими «родственниками», на что у него уходит 15 минут. Затем он вспоминает о замке и стремительно пикирует к нему на протяжении 5 минут.
Давай всё это изобразим для наглядности:
Дракон и рыцарь совершили одинаковые перемещения, так? 7 км, ведь они оказались у замка, двигаясь из пещеры.
Давай посчитаем время каждого в пути. И для дракона, и для рыцаря оно составило 35 минут. Они прибыли к замку одновременно.
Так что ж получается… Они совершили одинаковое перемещение за одинаковый промежуток времени.
Но их траектории были очень различны! И двигались они по-разному!
Для того, чтобы описать это, существует средняя скорость по перемещению.
Средняя скорость тела – векторная физическая величина, равная отношению перемещения тела на определенном участке траектории ко времени, за которое оно совершено.
Можно в виде формулы: ({{vec{V}}_{cp}}=frac{{vec{S}}}{t})
Средняя скорость дракона и рыцаря по перемещению одинакова, ведь они пришли одновременно в одно и то же место.
Есть подвох, о котором тебе на математике не рассказали. Ты все время работал не с этой средней скоростью. А с этой:
Средняя путевая скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.
Понял, да? Путевая – про путь, а не про перемещение. Средняя путевая скорость совпадает (по модулю) со средней скоростью по перемещению только в том случае, если тело двигалось по прямой в одном направлении.
Средняя путевая скорость дракона сильно отличается от средней путевой скорости рыцаря.
Если не помнишь, в чем отличие пути от перемещения, советую посмотреть основные определения кинематики!
Равномерное движение
Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.
Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:
Проекция вектора скорости на ось ОХ:
Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:
График скорости (проекции скорости)
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
График скорости при равномерном движении – прямая, параллельная оси времени. График 1 лежит над осью ( t ), тело движется по направлению оси ОХ. Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.
Перемещение при равномерном движении – это величина, равная произведению скорости на время:
Проекция вектора перемещения на ось ОХ:
График перемещения (проекции перемещения)
График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:
График перемещения при равномерном движении – прямая, выходящая из начала координат. График 1 лежит над осью ( t ), тело движется по направлению оси ОХ. Графики 2 и 3 лежат под осью ( t ), тело движется против оси ОХ.
По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Координата тела при равномерном движении рассчитывается по формуле:
График координаты представляет собой зависимость координаты от времени: ( x=x(t) ).
График координаты при равномерном движении – прямая. График 1 направлен вверх, тело движется по направлению оси ОХ:
График 2 параллелен оси ОХ, тело покоится. График 3 направлен вниз, тело движется против оси ОХ:
О том, как решить основную задачу механики
Мы помним, что основная задача механики – указать положение тела в пространстве в любой момент времени, не только в настоящем, но и в будущем.
Мы узнали это, когда только начали изучать кинематику.
Итак, что нужно знать для того, чтобы найти положение тела в пространстве?
Неплохо было бы знать, где оно находилось в начале своего движения, его начальные координаты. Ведь нам важно, откуда мы выдвигаемся в путь.
Зависят ли начальные координаты тела от времени? Совсем нет: мы просто принимаем то, что тело где-то есть.
А еще нам важно знать, как далеко оказалось тело от своего начального положения и куда вообще двигалось. Важно знать перемещение этого тела.
Давай опробуем свои силы! Думаю, мы уже готовы решить главную задачу!
Рассмотрим какое-то тело. Оно подвигалось, изменило свое положение, оказалось в другой точке.
Назовем ее конечной и постараемся найти ее координаты, то есть узнать положение тела после совершенного им перемещения.
Помним, что перемещение – вектор, поэтому изобразим его:
Скорость не меняется движение равномерное
Разберём равномерное движение в направлении оси (рис. 2а).
Начальная координата тела – это точка (x_{0}), а конечная координата — точка (x) на оси Ox. В точку «x» тело переместится к конечному времени «t».
Красной стрелкой обозначено направление, в котором тело движется.
Примечание: Тело движется туда, куда направлен вектор его скорости.
Рис.2. Тело движется равномерно в направлении оси Ox – рис а). Зависимость координаты от времени – это возрастающая прямая x(t) – рис. б). График скорости в) – это горизонтальная прямая, а график ускорения г) лежит на оси времени, так как ускорение равно нулю
Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).
Уравнение, описывающее изменение координаты выглядят так:
[ x = x_{0} + v cdot t ]
Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:
[ v = v_{0} = const ]
Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:
[ a = 0 ]
Равномерное движение в направлении противоположном оси
Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).
Рис.3. Тело движется равномерно противоположно направлению оси Ox – рис. а). Такому движению соответствуют: убывающая зависимость координаты от времени – рис б), отрицательная проекция скорости на ось – рис. в) и, нулевое ускорение – рис. г)
Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.
Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.
Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.
А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.
Относительность механического движения
Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.
Правило сложения перемещений
Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:
где ( S ) — перемещение тела относительно неподвижной системы отсчета; ( S_1 ) — перемещение тела относительно подвижной системы отсчета; ( S_2 ) — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.
Правило сложения скоростей
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:
где ( v ) — скорость тела относительно неподвижной системы отсчета; ( v_1 ) — скорость тела относительно подвижной системы отсчета; ( v_2 ) — скорость подвижной системы отсчета относительно неподвижной системы отсчета.
Относительная скорость
Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.
Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела. Определим скорость первого тела относительно второго ( v_{12} ):
Определим скорость второго тела относительно первого ( v_{21} ):
Следует помнить, что траектория движения тела и пройденный путь тоже относительны.
Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:
Если скорости направлены под углом ( alpha ) друг к другу, то относительная скорость рассчитывается по теореме косинусов:
Движение по вертикали
Движение по вертикали — это частный случай равноускоренного движения. Дело в том, что на Земле тела падают с одинаковым ускорением — ускорением свободного падения. Для Земли оно приблизительно равно 9,81 м/с2, а в задачах мы и вовсе осмеливаемся округлять его до 10 (физики просто дерзкие).
Вообще в значении ускорения свободного падения для Земли очень много знаков после запятой. В школе обычно дают значение: g = 9,8 м/с2. В экзаменах ОГЭ и ЕГЭ в справочных данных дают g = 10 м/с2.
И кому же верить?
Все просто: для кого решается задача, тот и главный. В экзаменах берем g = 10 , в школе при решении задач (если в условии задачи не написано что-то другое) берем g = 9,8 м/с2.
Частным случаем движения по вертикали (частным случаем частного случая, получается) считается свободное падение — это равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.
Помните о том, что свободное падение — это не всегда движение по вертикали из состояния покоя. Если мы бросаем тело вверх, то начальная скорость, конечно же, будет.
Задачи
Задача 1. Пассажирский поезд тормозит с ускорением 0,2 м/с2. На каком расстоянии от места включения тормоза скорость поезда станет равной 5 м/с, если перед торможением скорость была 15 м/с?
Решение. Скорость поезда уменьшается, поэтому ускорение направлено против начальной скорости. При прямолинейном движении (без поворотов) перемещение поезда равно расстоянию, которое он пройдет, т.е. s = s. Ось 0Х направим по направлению начальной скорости (рис. 1), поэтому
1 Способ. Из уравнения 
Перемещение находим из уравнения 

2 Способ. Используются υ0, υ, a и s (надо найти).
Теги
Движение тела, брошенного вертикально вверх
Тело, брошенное вертикально вверх, движется равномерно замедленно с начальной скоростью u0 и ускорением
a = -g.
Перемещение тела за время t представляет собой высоту подъема h.
Для этого движения справедливы формулы:
Если:
u0 — начальная скорость движения тела ,
u — скорость падения тела спустя время t,
g — ускорение свободного падения, 9.81 (м/с²),
h — высота на которую поднимется тело за время t,
t — время,
То, движение тела, брошенного вертикально вверх описывается следующими формулами:
Высота подъема тела за некоторое время, зная конечную скорость
[ h = frac{u_0 + u}{2} t ]
Высота подъема тела за некоторое время, зная ускорение свободного падения
[ h = u_0 t – frac{g t^2}{2} ]
Скорость тела через некоторое время, зная ускорение свободного падения
[ u = u_0 – gt ]
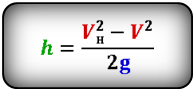
Скорость тела на некоторой высоте, зная ускорение свободного падения
[ u = sqrt{ u_0^2 – 2gh} ]
Максимальная высота подъема тела, зная первоначальную скорость и ускорение свободного падения
Тело, брошенное вертикально вверх, достигает максимальной высоты в тот момент, когда его скорость обращается в ноль. Поднявшись на максимальную высоту тело начинает свободное падение вниз.
[ h_{max} = frac{u_0^2}{2g} ]
Время подъема на максимальную высоту подъема тела, зная первоначальную скорость и ускорение свободного падения
[ t_{hmax} = frac{u_0}{g} ]
Примечание к статье: Движение тела, брошенного вертикально вверх
- Сопротивление воздуха в данных формулах не учитывается.
- Ускорение свободного падения имеет приведенное значение (9.81 (м/с²)) вблизи земной поверхности. Значение g на других расстояниях от поверхности Земли изменяется!
Движение тела, брошенного вертикально вверх |
стр. 409 |
|---|