Содержание:
- § 1 Движение с отставанием
- § 2 Решение задач
- § 3 Краткие итоги по теме урока
§ 1 Движение с отставанием
Решая задачи на движение, мы сталкиваемся со взаимосвязанными понятиями «скорость», «время» и «расстояние». Так, чтобы найти скорость, необходимо расстояние разделить на время: ʋ = S : t. Чтобы найти время, надо расстояние разделить на скорость: t = S : ʋ. А чтобы найти расстояние, можно скорость умножить на время:
S = ʋ · t.
При решении задач на движение с отставанием используют еще одно понятие «скорость удаления».
Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени. Обозначается латинской буквой ʋуд..
Чтобы найти скорость удаления, зная скорости объектов, надо найти разность этих скоростей: ʋуд. = ʋ1 – ʋ2. Чтобы найти скорость удаления, зная время и расстояние, необходимо расстояние разделить на время: ʋуд. = S : t.
§ 2 Решение задач
Рассмотрим взаимосвязь понятий «скорость», «время» и «расстояние» при решении задач на движение с отставанием.
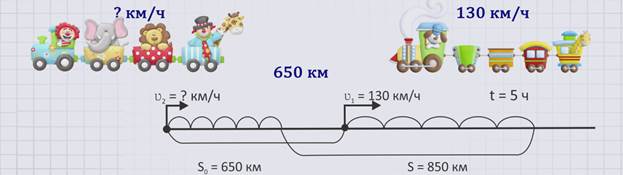
ЗАДАЧА 1. От двух станций, расстояние между которыми 650 км, одновременно в одном направлении вышли два поезда. Скорость одного из них – 130 км/час. Какова скорость второго, если через 5 часов второй поезд будет отставать от первого на 850 км?
Изобразим движение поездов на схеме.
Скорость первого поезда обозначим буквой ʋ1 = 130 км/ч. Скорость второго поезда обозначим буквой ʋ2 = ? км/ч. Время в пути обозначим буквой t = 5 ч. Расстояние, которое было изначально между поездами – буквой S0 = 650 км, а расстояние, которое стало между ними через 5 часов – буквой S = 850 км.
Чтобы найти неизвестную скорость ʋ2, необходимо знать скорость первого поезда, а она нам известна и равна 130 км/ч, и скорость удаления, которая не указана в условии задачи, так как ʋ2 = ʋ1 – ʋуд..Из условия задачи нам известно расстояние S = 850 км, первоначальное расстояние между поездами S0 = 650 км и время t = 5 ч. Если мы найдем, на сколько расстояние между поездами стало больше (обозначим эту разницу буквой S2), то сможем найти и скорость удаления, так как ʋуд. = S2 : t. Найдем разницу между расстояниями S и S0: S2 = S – S0 = 850 – 650 = 200 км. Теперь можем вычислить скорость удаления поездов: ʋуд. = S2 : t = 200 : 5 = 40 км/ч. Теперь, найдя скорость удаления, мы можем найти скорость второго поезда. ʋ2 = ʋ1 – ʋуд. = 130 – 40 = 90 км/ч. Получили, что скорость второго поезда равна 90 км/ч.
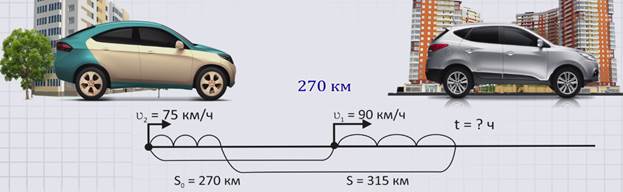
ЗАДАЧА 2. Расстояние между двумя городами 270 км. Из них одновременно в одном направлении выехали две машины. Первая машины ехала со скоростью 90 км/ч, а вторая машина ехала со скоростью 75 км/ч и отставала от первой. Сколько часов они были в пути, если в конце пути расстояние между ними стало 315 км?
Изобразим движение машин на схеме.
Скорость первой машины обозначим буквой ʋ1 = 90 км/ч. Скорость второй машины обозначим буквой ʋ2 = 75 км/ч. Расстояние между городами обозначим буквой S0 = 270 км, а расстояние, которое стало между машинами в конце пути – буквой S. Время – буквой t = ? часов.
Чтобы ответить на поставленный вопрос задачи, необходимо знать расстояние S2 (а именно разницу между расстояниями S0 и S) и скорость удаления, так как t = S2 : ʋуд.. Поскольку расстояния S0 и S нам известны из условия задачи, найдем их разность: S2 = S – S0 = 315 – 270 = 45 км. Зная скорости машин, мы можем найти скорость удаления. ʋуд. = ʋ1 – ʋ2 = 90 – 75 = 15 км/ч. Теперь, найдя расстояние S2 и скорость удаления ʋуд., мы можем ответить на поставленный вопрос задачи. t = S2 : ʋуд. = 45 : 15 = 3 ч. Получили, что машины были в пути 3 часа.
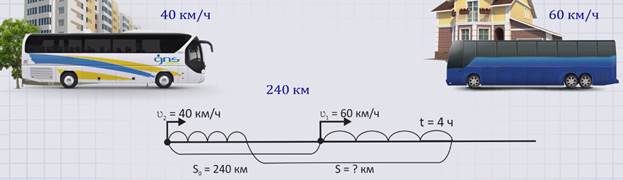
ЗАДАЧА 3. Из поселка и города в одном направлении, одновременно выехали два автобуса. Один автобус ехал со скоростью 40 км/ч, а другой – 60 км/ч. Сколько километров станет между ними через 4 часа, если изначально между ними было 240 км?
Покажем движение автобусов на схеме.
Скорость первого автобуса обозначим буквой ʋ1 = 60 км /ч. Скорость второго автобуса обозначим буквой ʋ2 = 40 км/ч. Расстояние, которое было изначально между автобусами, обозначим буквой S0 = 240 км. Расстояние, которое станет между автобусами через 4 часа – буквой S = ? км, а время – буквой t = 4 часа.
Чтобы ответить на вопрос задачи, необходимо знать первоначальное расстояние между автобусами, время и скорость удаления, так как S = ʋуд. · t + S0. Поскольку первоначальное расстояние между автобусами и время известны из условия задачи, надо найти скорость удаления. Используя такие данные задачи, как скорости автобусов, можем найти скорость удаления: ʋуд. = ʋ1 – ʋ2 = 60 – 40 = 20 км/ч. Теперь, зная скорость удаления, можем найти расстояние, которое станет между автобусами через 4 часа: S = ʋуд. · t + S0 = 20 · 4 + 240 = 80 + 240 = 320 км. Получили, что 320 км станет между автобусами через 4 часа.
§ 3 Краткие итоги по теме урока
При решении задач на движение с отставанием, следует помнить, что в задачах такого типа выполняются следующие условия:
1) Объекты начинают свое движение одновременно в одном направлении и находятся в пути одинаковое количество времени, причем один объект отстает от другого; время обозначается латинской буквой t = (S – S0) : ʋуд;
2) Расстояние S0 – это первоначальное расстояний между двумя объектами; расстояние S – это расстояние, которое станет между объектами через определенное количество времени t; S = S0 + ʋуд. · t;
3) Объекты удаляются с определенной скоростью – скоростью удаления, которая обозначается латинской буквой ʋуд. = (S – S0) : t или ʋуд. = ʋ1 – ʋ2.
Список использованной литературы:
- Петерсон Л.Г. Математика. 4 класс. Часть 2. / Л.Г. Петерсон. – М.: Ювента, 2014. – 96 с.: ил.
- Математика. 4 класс. Методические рекомендации к учебнику математики «Учусь учиться» для 4 класса / Л.Г. Петерсон. – М.: Ювента, 2014. – 280 с.: ил.
- Зак С.М. Все задания к учебнику математики для 4 класса Л.Г. Петерсон и комплекту самостоятельных и контрольных работ. ФГОС. – М.: ЮНВЕС, 2014.
- CD-ROM. Математика. 4 класс. Сценарии уроков к учебнику к 2 части Петерсон Л.Г. – М.: Ювента, 2013.
Использованные изображения:
Цели:
- Вывести формулы зависимости расстояния, скорости и времени движения при движении с отставанием;
- Развивать математическую речь, мышление, внимание, память, умение обобщать и делать выводы, самостоятельность;
- Воспитывать уважение к товарищам, аккуратность.
Оборудование: формулы движения, компьютер, проектор, экран.
Ход урока
I. Организационный момент.
II. Актуализация знаний:
– Над задачами какого типа мы работали с вами на предыдущих уроках? (на движение)
Работа по схемам и формулам.
– Посмотрите на схему задачи. Как называется этот вид движения? (движение в противоположных направлениях)
– Определите, какая формула подходит. (2)
На экране:

(слайд 1)
– Как называется этот вид движения? (встречное движение)
– Определите, какая формула подходит. (3)
На экране:
(слайд 2)
– Как называется этот вид движения? (движение вдогонку)
– Определите, какая формула подходит. (1)
На экране:
(слайд 3)
III. Фиксация затруднения в деятельности и постановка проблемы:
1) Сравните задачи:
а) «Из пунктов А и В одновременно в одном направлении выехали два поезда. Скорость первого поезда 80 км/ч, расстояние между пунктами 120 км. Найдите скорость второго поезда, если встреча произойдёт через 4 часа».
На экране:
(слайд 4)
– Какое это движение? (вдогонку)
– Скорость второго поезда будет больше или меньше скорости первого поезда? (больше)
– Какую формулу будем использовать? (S= Uсбл.∙t)
– Как решим?
Решают на доске и в тетради:
- 120:4=30(км/ч) – скорость сближения.
- 80+30=110(км/ч) – скорость второго поезда.
Ответ: 110 км/ч скорость второго поезда.
б) «Миша начал догонять Борю, когда расстояние между ними было 100 м. Миша идёт со скоростью 80 м/мин. Найдите скорость Бори, если мальчики встретились через 5 минут».
На экране:
(слайд 5)
– Это, какое движение? (вдогонку)
– У какого мальчика скорость больше? (у Миши)
– Как решить эту задачу?
Решают на доске и в тетради:
- 100:5=20(м/мин.) – скорость сближения.
- 80-20=60 (м/мин.) – скорость Бори.
Ответ: 60 м/мин. скорость Бори.
2) Почему в первой задаче скорость находится сложением, а во второй – вычитанием? (В первой задаче надо найти скорость догоняющего поезда – она больше, поэтому находим сложением. Во второй задаче мы находим скорость мальчика, которого догоняют. Она меньше, поэтому надо вычитать.)
3) Поменяйте данные скоростей в последней задаче. Что получается? (новая задача – движение с отставанием)
Меняются данные на схеме к задаче.
На экране:
(слайд 5)
– Подойдёт ли наше решение к новой задаче? (нет, т.к. встречи не будет)
– Сумеем ли мы решить новую задачу? Что необходимо вывести для её решения? (формулу зависимости между расстоянием, скоростью и временем движения)
IV. Определение темы и цели урока:
– Так какова тема нашего урока? (задачи на движение с отставанием)
– Наша цель на уроке: вывести формулу зависимости расстояния от скорости и времени при движении с отставанием.
V. Построение проекта выхода из затруднения:
1) №1 (с. 101) решают письменно в тетрадях.
Учащиеся изображают движение по числовому лучу и находят расстояние между ними через 4 часа.
– Чему равно расстояние между ними через 4 часа? (16 км)
– Как найти это расстояние с помощью вычислений, не выполняя построения?
Решение: (6-2)∙4=16
– Вычитая 2 из 6, что мы находим? (скорость удаления)
2) №2 (с. 101) работа в учебнике и на доске.
Учитель читает задачу до вопросов, учащиеся рассматривают схему.
– Как изменяется расстояние между ними за 1 час? (увеличивается на 3 ед./ч)
– Чему оно будет равно через 1 час? (8 ед.), 2часа? (11 ед.), 3 часа? (14 ед.)
– Сможет ли вертолёт догнать самолёт? Почему?
– Продолжите построение на луче, и заполним таблицу:
На доске: Uуд.=4-1=3(ед./ч)
| t, час | d, ед. |
| 0 | 5 |
| 1 | 5+(4-1)∙1=8 |
| 2 | 5+(4-1)∙2=11 |
| 3 | 5+(4-1)∙3=14 |
| t | 5+(4-1) t |
– О какой скорости мы говорим в этой задаче? (удаления) Как её найти? (4-1)
Заполняется таблица:
– Что обозначает 0 часов? (начало пути)
– Какое между ними было расстояние? (5км)
– Как найти, какое стало через 1 час? 2 часа? 3 часа? t часов?
– А теперь, используя таблицу, выведем формулу зависимости расстояния d между вертолётом и самолётом от времени движения t.
– Что такое 5 ед.? (do)
– Что такое 4-1? (U1-U2=Uуд.)
– Что такое t? (время)
– Кто запишет получившуюся формулу? (d=do+( U1-U2)∙t)
– Как её ещё можно записать? (d=do+ Uуд.∙t)
– Знакома ли нам эта формула? При каком движении? (при противоположном направлении)
3) На основе полученных формул найдите:
На доске:
do=d-Uуд.∙t
t=(d-do):Uуд.
Uуд.=(d-do):t
VI. Первичное закрепление:
№3 (с. 101) 1 ученик чертит схему на доске и объясняет:
Решение:
(32-25)∙6=42
Ответ: 42 км будет между ними через 6 часов.
VII. Физминутка.
VIII. Закрепление пройденного:
№ 6 (с.102): устно составляют задачи, самостоятельно решают.
– Охарактеризуйте данную задачу. (на одновременное движение с отставанием)
– Какую формулу будете использовать? (d=do+ Uуд.∙t)
– Что может двигаться со скоростью 30 км/ч? 60 км/ч?
Первую задачу решают коллективно, остальные по рядам самостоятельно. Дети, решившие первыми, проверяют у учащихся своего ряда.
– Составьте задачи.
Примеры задач:
а) Из двух городов, расстояние между которыми 100 км, одновременно в одном направлении выехали две лодки. Скорость первой 60 км/ч, второй – 30 км/ч. Какое расстояние между ними будет через 3 часа?
100+(60-30)∙3=190
Ответ: 190 км.
б) Из двух городов, расстояние между которыми 100 км, одновременно в одном направлении выехали две лодки. Скорость первой 60 км/ч, второй – 30 км/ч.
Через какое время расстояние между ними будет 190 км?
(190-100):(60-30)=3
Ответ: через 3 часа.
в) Из двух городов, расстояние между которыми 100 км, одновременно в одном направлении выехали две лодки. Скорость первой 60 км/ч. Через 3 часа расстояние между ними было 190 км. С какой скоростью движется вторая лодка?
60-(190-100):3=30
Ответ: 30 км/ч.
г) Из двух городов, расстояние между которыми 100 км, одновременно в одном направлении выехали две лодки. Скорость первой 60 км/ч, второй – 30 км/ч. Через 3 часа расстояние между ними было 190 км. Какое расстояние между ними было в начале пути?
190-(60-30)∙3=100
Ответ: 100км.
IX. Итог:
На экране:
(слайд 6)
– Произойдёт ли встреча? (нет)
– Как называется этот вид движения? (движение с отставанием)
– По какой формуле будете решать такие задачи? (d=do+ Uуд.∙t)
X. Д/з:
- №4 (с. 102) – решение задачи,
- №9 (с.103) 1р.-а), 2р.-б), 3р.-в) – решение уравнений.
Приложение.
После долгой прогулки по парку Юра и Яра выехали в противоположных направлениях на автомобилях. Скорость автомобиля Юры — (75) км/ч, а скорость автомобиля, на котором едет Яра — (58) км/ч. Как и с какой скоростью изменится расстояние между ними?
Рассмотрим схему движения Юры и Яры.
Юра и Яра удаляются друг от друга, значит, расстояние между ними увеличивается.
Чтобы найти, с какой скоростью они удаляются друг от друга, рассмотрим правило вычисления скорости удаления.
Получается, что скорость удаления автомобилей Юры и Яры: (75 + 58 = 133) км/ч.
Рассмотрим ещё один пример.
Юра и Яра ехали на автомобилях в одном направлении, но с разной скоростью. Юра ехал первым со скоростью (69) км/ч, а Яра ехала следом со скоростью (46) км/ч. Уменьшится или увеличится расстояние между ними и с какой скоростью?
Рассмотрим схему движения Юры и Яры.
Скорость автомобиля Юры больше, чем автомобиля, на котором едет Яра, значит, расстояние между ними увеличивается. Перед нами движение с отставанием.
Чтобы найти, с какой скоростью удаляются друг от друга Юра и Яра, рассмотрим правило вычисления скорости удаления во время движения с отставанием.
Получается, что скорость удаления автомобилей Юры и Яры: (69) (– 46 = 23) км/ч.
Расстояние, на которое объекты удаляются друг от друга за единицу времени, называется скоростью удаления.
Сделаем вывод:
при движении в противоположных направлениях скорость удаления равна сумме скоростей:
vуд.=v1+v2
.
При движении с отставанием скорость удаления равна разности скоростей:
vуд.=v1
−v2
.
Содержание материала
- Задачи на скорость сближения
- Видео
- Скорость сближения
- Задачи на течение реки
- Скорость
- Задача на движение объектов в одном направлении
- Движение в противоположных направлениях
- Относительное движение
- Примеры решения задач
Задачи на скорость сближения
Скорость сближения — это скорость, с которой объекты сближаются друг с другом.
Чтобы найти скорость сближения двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача 1. Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?
Решение: Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на:
40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:
60 — 40 = 20 (км/ч) — это скорость сближения автомобилей.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:
160 : 20 = 8 (ч).
Решение задачи по действиям можно записать так:
1) 40 · 4 = 160 (км) — расстояние между автомобилями,
2) 60 — 40 = 20 (км/ч) — скорость сближения автомобилей,
3) 160 : 20 = 8 (ч).
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 2. Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:
5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:
5 : 1 = 5 (ч).
Решение задачи по действиям можно записать так:
1) 5 — 4 = 1 (км/ч) — это скорость сближения пешеходов,
2) 5 : 1 = 5 (ч).
Ответ: Через 5 часов второй пешеход догонит первого.
Видео
Скорость сближения
Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м, а второго — 105 м/м, то скорость сближения будет составлять 100 + 105, то есть 205 м/м. Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.
Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:
205 × 3 = 615 метров
Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.
Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров
100 × 3 = 300 метров
А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метров
105 × 3 = 315 метров
Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:
300 м + 315 м = 615 м
Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами
Решение
Найдем скорость сближения велосипедистов
10 км/ч + 12 км/ч = 22 км/ч
Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения
22 × 2 = 44 км
Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.
Найдем расстояние, пройденное первым велосипедистом:
10 × 2 = 20 км
Найдем расстояние, пройденное вторым велосипедистом:
12 × 2 = 24 км
Сложим полученные расстояния:
20 км + 24 км = 44 км
Ответ: расстояние между населенными пунктами составляет 44 км.
Задача 2. Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?
Решение
Найдем скорость сближения велосипедистов:
14 км/ч + 16 км/ч = 30 км/ч
За один час расстояние между велосипедистами уменьшается на 30 километров. Чтобы определить через сколько часов они встретятся, нужно расстояние между населенными пунктами разделить на скорость сближения:
60 : 30 = 2 часа
Значит велосипедисты встретились через два часа
Ответ: велосипедисты встретились через 2 часа.
Задача 3. Из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу выехали одновременно два велосипедиста. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.
Решение
Определим расстояние пройденное первым велосипедистом. Как и второй велосипедист в пути он провел 2 часа. Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи
12 × 2 = 24 км
За два часа первый велосипедист прошел 24 км. За один час он прошел 24:2, то есть 12 км. Изобразим это графически
Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км). Так мы определим сколько километров прошел второй велосипедист:
56 км − 24 км = 32 км
Второй велосипедист, как и первый провел в пути 2 часа. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
32 : 2 = 16 км/ч
Значит скорость второго велосипедиста составляет 16 км/ч.
Ответ: скорость второго велосипедиста составляет 16 км/ч.
Задачи на течение реки
Теперь, когда ты отлично решаешь задачи «на суше», перейдем в воду, и рассмотрим страаашные задачи, связанные с течением.
Особенность этих задач в том, что к скорости, с которой движется тело по воде добавляется (или вычитается) скорость течения реки.
Давай разберемся.
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Задача на движение объектов в одном направлении
В предыдущей теме мы рассматривали задачи в которых объекты (люди, машины, лодки) двигались либо навстречу другу другу либо в противоположных направлениях. При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.
В первом случае мы находили скорость сближения — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшалось на определенное расстояние
Движение в противоположных направлениях
Если два объекта движутся в противоположных направлениях, то они удаляются. Чтобы найти скорость удаления, надо сложить скорости этих объектов:

Скорость удаления больше скорости любого из них.
Задача 1
Из поселка вышли одновременно в противоположных направлениях два пешехода. Средняя скорость одного пешехода – 5 км/ч, другого – 4 км/ч. Через сколько часов расстояние между ними будет 27 км ?
Решение:
Чтобы найти время движения пешеходов, нужно знать расстояние и скорость пешеходов. Мы знаем, что за каждый час один пешеход удаляется от поселка на 5 км, а другой пешеход удаляется от поселка на 4 км. Можем найти их скорость удаления.
1. (км/ч)
Мы знаем скорость удаления и знаем все расстояние – 27 км. Можем найти время, через которое пешеходы удалятся друг от друга на 27 км, для этого нужно расстояние разделить на скорость.
2. (ч)
Ответ: Через три часа расстояние между переходами будет 27 км.
Задача 2
Из поселка вышли одновременно в противоположных направлениях два пешехода. Через 3 часа расстояние между ними было 27 км. Первый пешеход шел со скоростью 5 км/ч. С какой скоростью шел второй пешеход ?

Решение:
Чтобы узнать скорость второго пешехода, надо знать расстояние, которое он прошел, и его время в пути. Чтобы узнать, какое расстояние прошел второй пешеход, надо знать, какое расстояние прошел первый пешеход и общее расстояние. Общее расстояние мы знаем. Чтобы найти расстояние, которое прошел первый пешеход, надо знать его скорость и его время в пути. Средняя скорость движения первого пешехода – 5 км/ч, его время в пути – 3 часа. Если среднюю скорость умножить на время в пути, получим расстояние, которое прошел пешеход:
1. (км)
Мы знаем общее расстояние и знаем расстояние, которое прошел первый пешеход. Можем теперь узнать, какое расстояние прошел второй пешеход.
2. (км)
Теперь мы знаем расстояние, которое прошел второй пешеход, и время, проведенное им в пути. Можем найти его скорость.
3. (км/ч)
Ответ: Скорость второго пешехода – 4 км/ч.
Задача 3
Товарный и пассажирский поезда движутся в противоположных направлениях. Скорость товарного 45 км/ч, скорость пассажирского — 70 км/ч. Сейчас между ними 20 км. Какое расстояние будет между ними через 2 часа ?
Решение:
1) 70+45=115 (км/ч) скорость удаления поездов
2) 115∙2=230 (км) пройдут поезда вместе за 2 часа
3) 230+20=250 (км) такое расстояние между поездами будет через 2 часа.
Ответ: Через 2 часа расстояние между поездами составит 250 км.
Задача 4
Из одного пункта одновременно в противоположных направлениях выехали два мотоциклиста. Скорость одного из них — 60 км/ч, скорость другого — 40 км/ч. Через какое время расстояние между ними станет равным 300 км?

Решение:
1) 60+40=100 (км/ч) скорость удаления мотоциклистов
2) 300:100=3 (ч) через такое время расстояние между ними будет 300 км.
Ответ: Расстояние между мотоциклистами станет 300 км через 3 часа.
Относительное движение
Если какие-то тела движутся друг относительно друга, часто бывает полезно посчитать их относительную скорость. Она равна:
- сумме скоростей, если тела движутся навстречу друг другу;
- разности скоростей, если тела движутся в одном направлении.
Примеры решения задач
Два туриста на велосипедах отправились в одно и то же время из разных пунктов в точку назначения. Время в пути первого велосипедиста составило 2 ч. Для того чтобы прибыть в точку назначения одновременно с первым туристом, второму велосипедисту потребовалось проехать каждый последующий км пути на 1 мин быстрее по сравнению с предыдущим. Расстояние, которое преодолел второй турист на велосипеде больше на 6 км, чем путь первого туриста. Требуется определить скорости первого и второго велосипедистов.
Решение
Предположим, что первый турист на велосипеде преодолевал каждый км пути за х мин. Тогда его скорость равна 60/х км/ч. В таком случае, скорость второго велосипедиста составит 60/(х-1) км/ч. Составим уравнение:
60/(х–1)*2–(60/х)*2=6
х1=5
х2=–4
Второй корень является посторонним.
Ответ: скорость первого велосипедиста 12 км/ч, второй велосипедист двигался со скоростью 15 км/ч.
Теги
Зная различные методы решения систем линейных уравнений, вы овладеваете прекрасным инструментом, который помогает решать различные виды текстовых задач. И сегодня я хотел бы вам показать, как решается при помощи систем линейных уравнений задачи на движение, рассмотрим на одном примере все этапы. Вспомним основные формулы и понятия:
Пример: Велосипедист ехал 2ч по лесной дороге и 1 ч по шоссе, всего он проехал 40 км. Скорость его по шоссе была на 4 км/ч больше, чем скорость на лесной дороге. С какой скоростью велосипедист ехал по шоссе и с какой по лесной дороге?
Решение:
1. Пусть х км/ч – скорость велосипедиста в лесу, тогда у км/ч – скорость велосипедиста при движении по шоссе.
2. Следовательно, за два часа езды по лесной дороге велосипедист прошел расстояние 2х км, а за 1 час езды по шоссе он прошел расстояние у км.
3. Тогда поусловию задачи получаем:
2х + у = 40 км.
4. Читаем дальше задачу: ” Скорость его на шоссе была на 4 км/ч больше, чем скорость на лесной дороге” . Получаем:
у = х + 4 км/ч.
5. Составим систему уравнений:
Перенесем х в правую сторону с противоположным знаком,получим:
Теперь домножим второе уравнение системы на (-1):
Тогда получаем:
Теперь давайте применим “метод сложения” для решения данной системы. Сложим первое и второе уравнения системы:
В результате получили, что х= 12 км/ч , то есть мы нашли скорость велосипедиста в лесу.
Теперь найдем у, подставив наш х во второе уравнение системы и получим:
Окончательно получаем следующие ответы: велосипедист ехал по лесной дороге со скоростью 12 км/ч, а по шоссе со скоростью 16 км/ч.
Ответ: 12 км/ч; 16 км/ч.
Всем спасибо за внимание!)