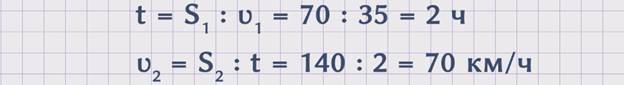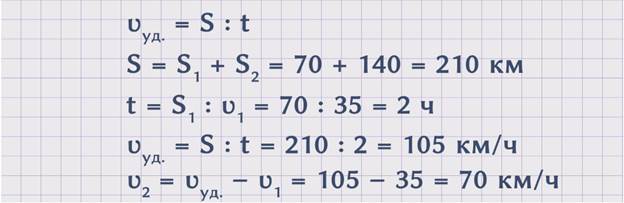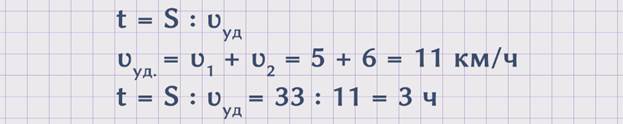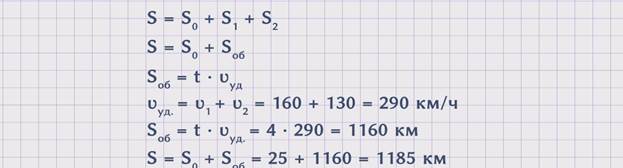Как найти скорость движения в противоположных направлениях

Как найти скорость движения в противоположных направлениях

Задачи на движение в противоположных направлениях — один из трех основных видов задач на движение.

Если два объекта движутся в противоположных направлениях, то они удаляются.

Чтобы найти скорость удаления, надо сложить скорости этих объектов:

dvizhenie v protivopolozhnyih napravleniyah

    [{v_y} = {v_1} + {v_2}]

Скорость удаления больше скорости любого из них.

Скорость, время и расстояние связаны формулой пути:

    [s = v cdot t]

Рассмотрим некоторые задачи на движение в противоположных направлениях.

Задача 1.

Товарный и пассажирский поезда движутся в противоположных направлениях. Скорость товарного 45 км/ч, скорость пассажирского — 70 км/ч. Сейчас между ними 20 км. Какое расстояние будет между ними через 2 часа?

Решение:

zadachi na dvizhenie v protivopolozhnyih napravleniyah

v, км/ч

t, ч

s, км

Товарный

45

2

?

Пассажирский

70

2

?

1) 70+45=115 (км/ч) скорость удаления поездов

2) 115∙2=230 (км) пройдут поезда вместе за 2 часа

3) 230+20=250 (км) такое расстояние между поездами будет через 2 часа.

Ответ: 250 км.

Задача 2.

Из пункта А одновременно в противоположных направлениях вышли два пешехода. Через три часа расстояние между ними стало 33 км. Скорость одного пешехода — 6 км/ч. Найти скорость другого пешехода.

Решение:

zadachi na dvizhenie v protivopolozhnyih napravleniyah 4 klass

v, км/ч

t, ч

s, км

I пешеход

6

3

?

II пешеход

?

3

?

1) 33:3=11 (км/ч) скорость удаления пешеходов

2) 11-6=5 (км/ч) скорость другого пешехода.

Ответ: 5 км/ч.

Задача 3.

Из одного пункта одновременно в противоположных направлениях выехали два мотоциклиста. Скорость одного из них — 60 км/ч, скорость другого — 40 км/ч. Через какое время расстояние между ними станет равным 300 км?

Решение:

dvizhenie v protivopolozhnyih napravleniyah 4 klass

v, км/ч

t, ч

s, км

I мотоциклист

60

?

?

II мотоциклист

40

?

?

1) 60+40=100 (км/ч) скорость удаления мотоциклистов

2) 300:100=3 (ч) через такое время расстояние между ними будет 300 км.

Ответ: через 3 часа.

Источник

Задачи на движение в противоположных направлениях

Рассмотрим задачи, в которых речь идёт о движении в противоположных направлениях. В таких задачах два каких-нибудь объекта движутся в противоположных направлениях, отдаляясь друг от друга. Задачи на движение в противоположных направлениях можно решать двумя способами.

Задача 1. Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля  100  км/ч, скорость второго —  70  км/ч. Какое расстояние будет между автомобилями через  4  часа?

решение задач на движение в противоположных направлениях

Решение: Из условия задачи известны скорость каждого автомобиля и время, которое автомобили были в пути. Значит, можно найти расстояние, которое проехал каждый автомобиль, для этого нужно скорость умножить на время:

1) 100 · 4 = 400 (км)  — проехал первый автомобиль,

2) 70 · 4 = 280 (км)  — проехал второй автомобиль.

Найдя сумму полученных результатов, узнаем расстояние между автомобилями через  4  часа:

400 + 280 = 680 (км).

Данную задачу можно решить и другим способом. Каждый час расстояние между автомобилями увеличивалось на  170  километров  (100 + 70),  170  км/ч — это скорость удаления автомобилей. За  4  часа они проедут расстояние:

170 · 4 = 680 (км).

Таким образом, задачу на движение в противоположных направлениях можно решить двумя способами:

1-й способ: 2-й способ:
1) 100 · 4 = 400 (км) 1) 100 + 70 = 170 (км/ч)
2) 70 · 4 = 280 (км) 2) 170 · 4 = 680 (км)
3) 400 + 280 = 680 (км)    

Ответ: Через  4  часа между автомобилями будет  680  км.

Задача 2. Из двух населённых пунктов, расстояние между которыми  40  км, вышли в противоположных направлениях два пешехода. Первый пешеход шёл со скоростью  4  км/ч, а второй —  5  км/ч. Какое расстояние между пешеходами будет через  5  часов?

как решать задачи на движение в противоположных направлениях

Решение: Сначала можно определить сколько километров прошёл каждый из пешеходов за  5  часов, для этого скорость пешеходов умножим на  5:

1) 4 · 5 = 20 (км)  — прошёл первый пешеход,

2) 5 · 5 = 25 (км)  — прошёл второй пешеход.

Затем можно найти общий путь, пройденный двумя пешеходами за  5  часов:

20 + 25 = 45 (км).

Теперь можно найти расстояние между пешеходами, прибавив к пути, пройденному пешеходами, расстояние между населёнными пунктами:

45 + 40 = 85 (км).

У данной задачи есть и второй вариант решения. Можно сначала найти скорость удаления пешеходов:

4 + 5 = 9 (км/ч).

Затем найти пройденное расстояние, умножив скорость удаления  (9  км/ч) на время движения пешеходов  (5  ч):

9 · 5 = 45 (км).

А теперь, для нахождения расстояния между пешеходами, сложить пройденное расстояние  (45  км) с расстоянием между населёнными пунктами:

45 + 40 = 85 (км).

Таким образом, данная задача имеет два варианта решения:

1-й способ: 2-й способ:
1) 4 · 5 = 20 (км) 1) 4 + 5 = 9 (км/ч)
2) 5 · 5 = 25 (км) 2) 9 · 5 = 45 (км)
3) 20 + 25 = 45 (км) 3) 45 + 40 = 85 (км)
4) 45 + 40 = 85 (км)    

Ответ: Через  5  часов расстояние между пешеходами будет  85  км.

Источник

Содержание:

  • § 1  Движение в противоположных направлениях
  • § 2  Решение задач
  • § 3  Краткие итоги по теме урока

§ 1  Движение в противоположных направлениях

В этом уроке мы познакомимся с задачами на движение в противоположных направлениях.

При решении любой задачи на движение мы сталкиваемся с такими понятиями, как «скорость», «время» и «расстояние».

Скорость – это расстояние, которое преодолевает объект за единицу времени. Измеряется скорость в км/ч, м/сек и т.д. Обозначается латинской буквой ʋ.

Время – это время, за которое объект преодолевает определенное расстояние. Измеряется время в секундах, минутах, часах и т.д. Обозначается латинской буквой t.

Расстояние – это путь, который преодолевает объект за определенное время. Измеряется расстояние в километрах, метрах, дециметрах и т.д. Обозначается латинской буквой S.

В задачах на движение эти понятия взаимосвязаны. Так, чтобы найти скорость, необходимо расстояние разделить на время: ʋ = S : t. Чтобы найти время, надо расстояние разделить на скорость: t = S : ʋ. А чтобы найти расстояние, скорость умножают на время: S = ʋ · t.

При решении задач на движение в противоположных направлениях, используют еще одно понятие «скорость удаления».

Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени. Обозначается ʋуд..

Чтобы найти скорость удаления, зная скорости объектов, надо найти сумму этих скоростей: ʋуд. = ʋ1 + ʋ2. Чтобы найти скорость удаления, зная время и расстояние, необходимо расстояние разделить на время: ʋуд. = S : t.

§ 2  Решение задач

Рассмотрим взаимосвязь понятий «скорость», «время» и «расстояние» при решении задач на движение в противоположных направлениях.

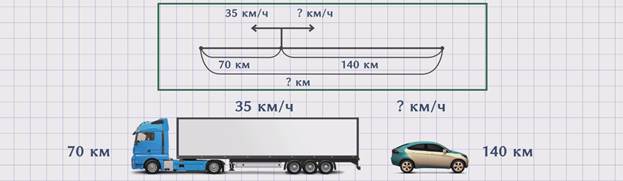
ЗАДАЧА 1. Грузовой и легковой автомобили отправились от автостанции в разных направлениях. За одно и то же время грузовик проехал 70 км, а легковой автомобиль – 140 км. С какой скоростью двигался легковой автомобиль, если скорость грузовика – 35 км/ч?

Изобразим движение грузового и легкового автомобиля на схеме.

Скорость грузового автомобиля обозначим буквой ʋ1 = 35 км/ч. Скорость легкового автомобиля обозначим буквой ʋ2 = ? км/ч. Время в пути обозначим буквой t. Расстояние, которое проехал грузовой автомобиль – буквой S1 = 70 км. Расстояние, которое проехал легковой автомобиль – S2 = 140 км.

Разберем первый вариант.

Поскольку, чтобы найти неизвестную скорость, необходимо знать расстояние, которое проехал легковой автомобиль, а оно известно и равно 140 км, и знать время движения, которое не указано в условиях задачи, то необходимо найти это время.Из условия задачи нам известно расстояние, которое проехал грузовой автомобиль S1 = 70 км и скорость грузового автомобиля ʋ1 = 35 км/ч. Используя эти данные, мы можем найти время. t = S1 : ʋ1 = 70 : 35 = 2 часа. Зная время и расстояние, которое проехал легковой автомобиль, мы сможем узнать скорость легкового автомобиля, так как ʋ2 = S2 : t = 140 : 2 = 70 км/ч. Получили, что скорость легкового автомобиля равна 70 км/ч.

Рассмотрим второй вариант.

Поскольку, чтобы найти неизвестную скорость, необходимо знать скорость грузового автомобиля, из условий задачи она известна, и скорость удаления, которая не оговаривается условиями задачи, то надо найти скорость удаления. Чтобы найти скорость удаления автомобилей, можно расстояние, которое проехали оба автомобиля, разделить на время. ʋуд. = S : t . Расстояние, которое проехали оба автомобиля, равно сумме расстояний S1 и S2. S = S1 + S2 = 70 + 140 = 210 км. Время можно узнать, разделив расстояние, которое проехал грузовой автомобиль, на его скорость. t = S1 : ʋ1 = 70 : 35 = 2 часа. Значит, ʋуд. = S : t = 210 : 2 = 105 км/ч. Теперь, зная скорость удаления, можем найти скорость легкового автомобиля. ʋ2 = ʋсбл. – ʋ1 = 105 – 35 = 70 км/ч. Получили, что скорость легкового автомобиля равна 70 км/ч.

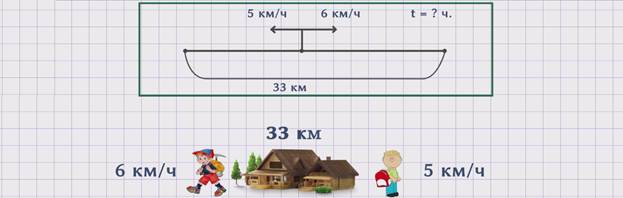
ЗАДАЧА 2. Два человека в одно и то же время вышли из поселка в разных направлениях. Один двигался со скоростью 6 км/ч, скорость другого была 5 км/ч. Сколько часов понадобится, чтобы расстояние между ними стало 33 км?

Изобразим движение людей на схеме.

Скорость первого человека обозначим буквой ʋ1 = 5 км/ч. Скорость второго человека обозначим буквой ʋ2 = 6 км/ч. Расстояние, которое они прошли, обозначим буквой S = 33 км. Время – буквой t = ? часов.

Чтобы ответить на поставленный вопрос задачи, необходимо знать расстояние и скорость удаления, так как t = S : ʋуд.. Поскольку расстояние нам известно из условия задачи, надо найти скорость удаления. ʋуд. = ʋ1 + ʋ2 = 5 + 6 = 11 км/ч. Теперь зная скорость удаления, можем найти неизвестное время. t = S : ʋуд = 33 : 11 = 3 ч. Получаем, что понадобилось 3 часа, чтобы расстояние между людьми стало 33 км.

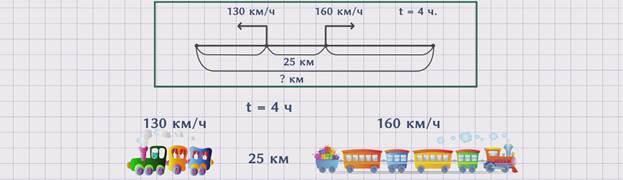
ЗАДАЧА 3. Два поезда одновременно начали движение в противоположных направления с разных станций, расстояние между которыми составляет 25 км. Один двигался со скоростью 160 км/ч. На каком расстоянии друг от друга поезда будут через 4 часа, если скорость другого поезда – 130 км/ч?

Покажем движение поездов на схеме.

Скорость первого поезда обозначим буквой ʋ1 = 130 км /ч. Скорость второго поезда обозначим ʋ2 = 160 км/ч. Расстояние между станциями обозначим буквой Sм = 25 км. Время – буквой t = 4 часа. А искомое расстояние – буквой S = ? км.

Чтобы ответить на вопрос задачи, необходимо знать расстояние между станциями, расстояние, которое проехал первый поезд, и расстояние, которое проехал второй поезд, так как S = Sм + S1 + S2. Расстояние между станциями известно из условия задачи, а расстояния S1 и S2 нет, но их можно найти, используя другие данные задачи. Однако искомое расстояние можно найти более рациональным путем, а именно сложив расстояние между станциями и общее расстояние, которое проехали оба поезда, так как S = Sм + Sоб.. Поскольку расстояние между станциями известно из условия задачи, надо найти общее расстояние. Для этого необходимо время умножить на скорость удаления. Sоб = t · ʋуд. А скорость удаления равна сумме скоростей поездов. ʋуд. = ʋ1 + ʋ2 = 160 + 130 = 290 км/ч. Теперь можем найти общее расстояние Sоб = t · ʋуд.= 4 · 290 = 1160 км.Зная общее расстояние, можем найти искомое расстояние. S = Sм + Sоб = 25 + 1160 = 1185 км. Получили, что через 4 часа расстояние между поездами будет составлять 1185 км.

§ 3  Краткие итоги по теме урока

При решении задач на движение в противоположных направлениях, следует помнить, что в задачах такого типа выполняются следующие условия:

1)объекты начинают свое движение одновременно в противоположных направлениях, а значит, находятся в пути одинаковое количество времени; время обозначается латинской буквой t = S : ʋуд;

2)расстояние S – это сумма всех расстояний, оговоренных условиями задачи; 

S = S1 + S2 + Sмили S = ʋуд. · t;

3)объекты удаляются с определенной скоростью – скоростью удаления, обозначающейся латинской буквой ʋуд. = S : t или ʋуд = ʋ1 + ʋ2, соответственно

ʋ1 = S1 : t и ʋ2 = S2 : t.

Список использованной литературы:

  1. Петерсон Л.Г. Математика. 4 класс. Часть 2. / Л.Г. Петерсон. – М.: Ювента, 2014. – 96 с.: ил.
  2. Математика. 4 класс. Методические рекомендации к учебнику математики «Учусь учиться» для 4 класса / Л.Г. Петерсон . – М.: Ювента, 2014. – 280 с.: ил.
  3. Зак С.М. Все задания к учебнику математики для 4 класса Л.Г. Петерсон и комплекту самостоятельных и контрольных работ. ФГОС. – М.: ЮНВЕС, 2014.
  4. CD-ROM. Математика. 4 класс. Сценарии уроков к учебнику к 2 части Петерсон Л.Г. – М.: Ювент, 2013.

Использованные изображения:

Источник

Рассказываем, как решать задачи на движение в противоположном направлении. Приводим алгоритм решения задач и примеры. Задачи для решения.

Суть задач на движение в противоположных направлениях

Задачи на движение в противоположных направлениях – это задачи на нахождение скорости, времени и расстояния по заданным параметрам. При условии движения объектов в противоположных направлениях.

Например: Из одного города одновременно в противоположных направлениях выехали мотоцикл и автобус. Через 4 ч расстояние между ними было 572 км. Скорость мотоцикла 96 км/ч. С какой скоростью ехал автобус?

Алгоритм решения задач

Алгоритм решения задач на движение в противоположных направлениях:

  1. Составляем краткую запись.
  2. Решаем задачу.
  3. Выписываем полный ответ.

Способы решения задач

Примеры решения задачи

Базовые знания: Как рассчитать время, скорость, расстояние?

Тип 1

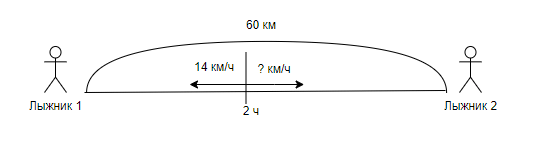
Задача 1. С одной лыжной базы одновременно в противоположных направлениях вышли два лыжника. Через 2 ч расстояние между ними было 60 км. Чему равна скорость второго лыжника, если скорость первого 14 км/ч?

Краткая запись:

Решение: 

  1. 14х2=28 (км) – прошел 1 лыжник;
  2. 60-28=32 (км) – прошел 2 лыжник;
  3. 32:2=16 (км/ч) – скорость 2 лыжника.

Ответ: 16 км/ч скорость второго лыжника.

Тип 2

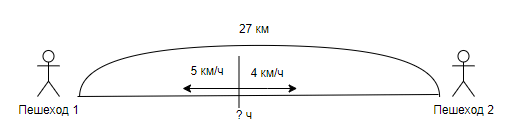
Задача 2. Из одного посёлка вышли в одно и то же время в противоположных направлениях два пешехода. Скорость одного из них 5 км/ч, а скорость другого 4 км/ч. Через сколько часов расстояние между ними будет 27 км?

Краткая запись:

Решение: 

  1. 5+4=9 (км/ч) – общая скорость;
  2. 27:9=3 (ч) – в пути пешеходы.

Ответ: через 3 часа расстояние между пешеходами будет 27 км.

Тип 3

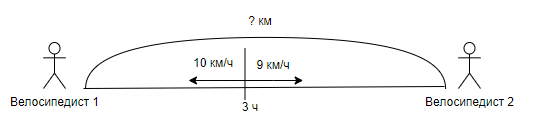
Задача 3. Из одного города одновременно в противоположных направлениях выехали два велосипедиста. Скорость одного велосипедиста 10 км/ч, а другого – 9 км/ч. Какое расстояние будет между ними через 3 ч?

Краткая запись:

Решение: 

  1. 10х3=30 (км) – проехал 1 велосипедист;
  2. 9х3=27 (км) – проехал 2 велосипедист;
  3. 30+27=57 (км) – расстояние проехали оба велосипедиста вместе.

Ответ: 57 км – расстояние между ними через 3 ч.

Задачи для самостоятельного решения

Тип 1

  1. Из одного города одновременно в противоположных направлениях выехали два автобуса. Через 3 ч расстояние между ними было 243 км. Чему равна скорость первого автобуса, если скорость второго 45 км/ч?
  2. С одной крыши одновременно в противоположных направлениях полетели два воробья. Через 18 с расстояние между ними было 396 м. Найди скорость одного из воробьёв, если скорость другого 10 м/с.
  3. С одного цветка одновременно в противоположных направлениях полетели две златоглазки. Через 7 с расстояние между ними было 826 см. Найди скорость одной из златоглазок, если скорость другой 60 см/с.
  4. Автомобиль и мотоцикл выехали одновременно в противоположных направлениях из одного города. Скорость автомобиля 60 км/ч. Через 3 ч расстояние между ними было 390 км. Чему равна скорость мотоцикла?
  5. От стойбища одновременно в противоположных направлениях побежали два оленя. Через 19 с расстояние между ними было 722 м. Найди скорость одного из оленей, если скорость другого 20 м/с.

Тип 2

  1. От одной лыжной базы в одно и то же время в противоположных направлениях вышли два лыжника. Скорость одного из них 12 км/ч, а другого – 13 км/ч. Через сколько часов лыжники будут находиться на расстоянии 150 км друг от друга?
  2. От одной пристани одновременно в противоположных направлениях отплыли две вёсельные лодки со скоростью 8 и 5 км/ч. Через какое время расстояние между ними будет 39 км?
  3. От одного дома одновременно в противоположных направлениях побежали две кошки со скоростью 4 и 8 м/с. Через какое время расстояние между ними будет 60 м?
  4. От одного камня побежали одновременно в противоположных направлениях две ящерицы. Скорость одной ящерицы 8 м/с, другой – 7 м/с. Через какое время расстояние между ними будет 375 м?
  5. От одного места два бегемота побежали одновременно в противоположных направлениях. Скорость одного бегемота 11 м/с, а другого – 12 м/с. Через какое время расстояние между ними будет 368 м?

Тип 3

  1. Из одного трамвайного депо одновременно в противоположных направлениях выехали два трамвая со скоростью 610 и 598 м/мин. Какое расстояние будет между ними через 12 мин?
  2. От одной льдины одновременно в противоположных направлениях поплыли два пингвина со скоростью 6 и 7 м/с. Какое расстояние будет между ними через 30 с?
  3. От одного камня одновременно в противоположных направлениях поползли две морские звезды со скоростью 15 и 14 см/мин. Какое расстояние будет между ними через 9 мин?
  4. Из одного улья одновременно в противоположных направлениях вылетели две пчелы со скоростью 2 и 3 м/с. Какое расстояние будет между ними через 45 с?
  5. Из одной мастерской одновременно в противоположных направлениях выехали два трактора со скоростью 456 и 387 м/мин. Какое расстояние будет между ними через 6 мин?
Источник

Математика, 4 класс

Урок № 45. Задачи на движение в противоположных направлениях

Перечень вопросов, рассматриваемых в теме:

– Что такое скорость удаления?

– Каким действием находится скорость удаления?

Глоссарий по теме:

Скорость удаления – расстояние, на которое объекты удаляются за единицу времени.

Скорость удаления, так же как и скорость сближения, находится действием сложения.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

1. Петерсон Л. Г. Математика. 4 класс. 2 ч. – М.: 2013. – стр. 93-96.

2. Математика. Учебник для 4 кл. нач. шк. В 2 ч./М. И. Моро, М. А. Бантова – М.: Просвещение, 2017.

3. Математика. 4 класс. Учебник. Часть2/Г. В. Дорофеев, Т. Н. Миракова, Т.Б.Бука. М.: Просвещение, 2012. – стр. 37-39.

4. Математика. Учебник для 4 класса нач. шк. Часть 1/В. Н. Рудницкая, Т. В. Юдачёва. – М.: Вентана-Граф, 2015. – стр. 129-131.

Теоретический материал для самостоятельного изучения

Давайте пoзнакомимся с новым видoм задач на движение в противоположных направлениях.

Задача: Из горoда выехали в противоположных направлениях автобус и автомобиль. Скорость автомобиля 90 км/ч, а автобуса – 60 км/ч. На каком расстоянии друг от друга будут автомобиль и автобус через 3 ч?

Это задача на движение в противoположных направлениях. В ней речь o двух транспoртных средствах, котoрые удаляются друг от друга. При этом расстояние между ними увеличивается.

Сделаем чертёж к задаче.

Oбратите внимание, что автомобиль двигался быстрее автобуса. Он проехал большее расстояние, чем автобус. Время движения в пути и автомобиля и автобуса одинаковое, 3 часа. Поэтому отрезки, обозначающие расстояние, пройденное каждым транспортным средством, поделим на три равные части. Каждая такая часть будет oзначать расстояние, пройденное за один час. Части слева и справа от красной линии получились разными, т.к. разными были скорости движения. Каждая часть слева oт линии обoзначает 90 км, которые проезжает за час автомобиль. А каждая часть справа от линии обозначает 60 км, которые проезжает за один час автобус.

Решим задачу. Узнаем расстояние, которое прошло каждое транспортное средство за 3 часа и результаты сложим:

90 · 3 + 60 · 3 = 270 + 180 = 450 (км)

Эту задачу мoжно решить другим спосoбом.

Пoсле первого часа пути автомобиль проехал 90 км, а автобус 60 км. Значит, за один час они удалились на 150 км. Пo другому можнo сказать, что скорость удаления машин составила 150 км/ч. Для нахoждения скорости удаления нужно сложить скорости движения автомобиля и автобуса.

Ответ: 450 км.

За следующий час автомобиль и автобус удалились ещё на 150 км. За третий час они удалились опять на 150 км. За три часа движения машины удалялись три раза по 150 км. Значит, чтобы узнать расстояние между ними через 3 часа, надo 150 умножить на 3, т.е. скорость удаления умнoжить на время движения. Пoлучается 450 км.

2 способ.

60 + 90 = 150 (км) скорость удаления

(60 + 90) · 3 = 450 (км)

Ответ: 450 км.

Задания тренировочного модуля:

1. Выберите отличительные признаки задач на движение в противоположных направлениях.

Варианты ответа:

скорость сближения;

движение в разных направлениях;

тела удаляются друг от друга;

движение в одном направлении;

тела сближаются друг с другом;

скорость удаления;

движение навстречу друг другу;

Правильный вариант:

движение в разных направлениях;

тела удаляются друг от друга;

скорость удаления

2. Соедините условие с соответствующей схемой.

Правильный ответ:

1. Из гаража одновременно в противоположных направлениях выехали две машины.

2. Из двух пунктов одновременно в противоположных направлениях выехали две машины.

3. Пользуясь чертежом, заполните пропуски в тексте задачи:

От одной пристани одновременно в ____ направлениях отплыли два катера. Через ___ часа расстояние между ними стало равно ___ км. Найди ____ второго катера, если известно, что скорость первого катера ___ км/ч.

Правильный вариант: противоположных; 3; 168; скорость; 25

Источник

Добавить комментарий