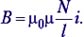Как найти скорость электромагнитной волны формула - Сайт, где вы сможете решить свои вопросы

Роман Алексеевич Лалетин

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Эмпирический способ нахождения скорости электромагнитных волн

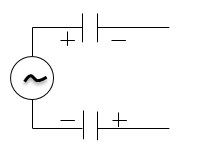
Скорость распространения электромагнитных волн эмпирически определяют, изучая стоячие волны, которые получают, например, в цепи, которая изображена на рис. 1, где выход генератора соединен с проводами линии через конденсаторы. Когда генератор работает, между проводами появляются колебания напряжения, а, значит, существуют колебания электрического поля, то есть возникает электромагнитная волна.

Рисунок 1.

Для понимания об интенсивности колебаний в различных точках линии включают лампы накаливания. В таких опытах можно показать, что стоячие волны в линии появляются только при определенной частоте генератора, когда она совпадает с частотой собственных колебаний линии.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Измеряя расстояния ($triangle x$) между соседними узлами или пучностями в стоячей волне, определяется $frac{1}{2}$ длины волны ($lambda $). При этом, известно, что:

где $nu $ — частота генератора. Измерив $nu $, легко найти скорость распространения электромагнитной волны. Опыты показали, что скорость электромагнитной волны ($v$) совпадает со скоростью света. В воздухе она приблизительно равна $v=c=3cdot {10}^8frac{м}{с}.$

Вывод скорости распространения электромагнитных волн из теории Максвелла

Раньше, чем электромагнитные волны были получены в экспериментах, Максвелл вычислил скорость этих волн, используя свою теорию поля. Рассмотри плоскую электромагнитную волну (одномерная задача, означающая, что $overrightarrow{E }и overrightarrow{H }зависят только от одной координаты, допустим x$), которая распространяется в однородной среде ($j_x=j_y=j_z=0, при varepsilon =const, mu =const$). В таком случае система уравнений Максвелла в скалярном виде будет записана как:

Исключим из уравнений Максвелла электрическое поле. С этой целью используем формулу, связывающую индукцию магнитного поля и его напряженность:

«Скорость распространения электромагнитных волн» 👇

и продифференцируем второе уравнение системы (2) по времени, получим:

Первое уравнение системы (2) продифференцируем по $x$, и используем уравнение:

в результате имеем:

Сравним уравнения (4) и (6), запишем:

Уравнение (7) есть волновое уравнение, следовательно, коэффициент, который стоит при $frac{{partial }^2H}{partial x^2}$ – квадрат скорости распространения электромагнитной волны:

$c$- скорость света. В вакууме скорость электромагнитных волн будет выражена как:

Замечание

Теория Максвелла предсказала, что скорость распространения электромагнитных волн в вакууме равна скорости света – этот факт доказывает, что свет имеет электромагнитную природу.

Замечание 1

Основные процессы при распространении волн в проводах происходят не внутри проводов, а в окружающей их среде. Следовательно, если среда вне провода изменится, то скорость электромагнитных волн будет другой, длина волны при неизменной частоте генератора станет другой.

В справедливости формулы (8) легко убедиться на опыте, если часть двухпроводной линии, которая первоначально была в воздухе погрузить в воду. Для воды $mu approx 1, varepsilon >1,$ следовательно, скорость электромагнитных волн в воде меньше, чем в воздухе, значит расстояние между соседними узлами (пучностями) станет меньше.

Следует учитывать, что $mu и varepsilon $ зависят от частоты. Поэтому при нахождении скорости применяя формулу (8) следует использовать их значения, соответствующие частоте колебаний в электромагнитной волне.

Пример 1

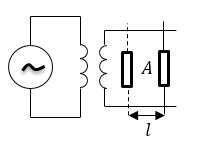
Задание: Параллельные провода (рис.2) находятся в некотором веществе, магнитная проницаемость которого равна $1$, диэлектрическая проницаемость не равна $1$. Они посредством индуктивности соединены с генератором. При высокой частоте колебаний $nu $ в системе устанавливаются стоячие электромагнитные волны. Вдоль проводов перемещают газоразрядную трубку $А$, по интенсивности ее свечения определили положения пучностей напряженности электрического поля, расстояние между которыми оказались равны $triangle x$. Какова диэлектрическая проницаемость вещества?

Рисунок 2.

Решение:

Стоячие электромагнитные волны появляются как результат интерференции волн, которые распространяются по двухпроводной линии от генератора в прямом направлении с волнами, которые отражаются концами линии. При высокой частоте электромагнитных колебаний основные процессы, которые связаны с распространением волн, происходят в среде, которая окружает провода.

В соответствии с теорией Максвелла скорость электромагнитных волн в среде равна:

[v=frac{c}{sqrt{varepsilon mu }}left(1.1right).]

По условию задачи для данного вещества $mu =1$, диэлектрическая проницаемость выразится из (1.1) как:

[varepsilon =frac{c^2}{v^2}left(1.2right).]

Скорость электромагнитных волн связана с длинной волны как:

[v=lambda nu left(1.3right).]

Расстояние между соседними пучностями в стоячей волне равно половине длины волны ($triangle x=frac{1}{2}lambda $), в таком случае имеем:

[varepsilon =frac{c^2}{{(lambda nu )}^2}=frac{c^2}{{4triangle x^2nu }^2}.]

Ответ: $varepsilon =frac{c^2}{{4triangle x^2nu }^2}.$

Пример 2

Задание: Какова скорость распространения электромагнитной волны в концентрическом кабеле, в котором пространство между внешним и внутренним проводами заполнено диэлектриком с проницаемостью $varepsilon ?$ Считайте, что потерями в кабеле можно пренебречь.

Решение:

Согласно теории Максвелла, скорость распространения электромагнитных волн в веществе равна:

[v=frac{c}{sqrt{varepsilon mu }}left(2.1right).]

Магнитную проницаемость среды можно считать равной единице, тогда выражение (2.1) перепишем в виде:

[v=frac{c}{sqrt{varepsilon }}.]

Ответ: $v=frac{c}{sqrt{varepsilon }}.$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Конкурс “Я иду на урок”

Проф. В. В.
Майер,
< varaksina_ei@list.ru >, ГГПИ им. В.Г.Короленко, г. Глазов, Удмуртская Респ.

Энергия и скорость электромагнитной волны

Урок 4-й из серии уроков на тему «Электромагнитные волны». См. № 24/08; 2, 4/09

Цели обучения: ввести понятие плотности энергии электромагнитной волны; вычислить скорость электромагнитной волны; измерить скорость распространения электромагнитной волны в воздухе и воде.

Цели развития: совершенствовать физическое мышление учащихся; развивать память путём вывода известных учащимся формул; углублять способности анализировать результаты эксперимента; развивать умения перехода от теории к эксперименту, делать количественные оценки, в опытах определять значения физических величин.

Цели воспитания: воспитывать восторг перед дерзостью и силой человеческого ума, обеспечившего измерение гигантского значения скорости света; восхищение физической наукой, простейшими средствами раскрывающей жгучие тайны природы.

Дидактические средства:

Мякишев Г.Я. Физика: Учеб. для 11 кл. общеобразоват. учреждений / Г.Я.Мякишев, Б.Б.Буховцев. – М.: Просвещение, 2004.
Касьянов В.А. Физика. 11 кл.: Учебн. для 11 кл. общеобразоват. учеб. заведений. – М.: Дрофа, 2002.
Электронная версия опорного конспекта урока; видеофрагменты демонстрационных опытов.
Комплект для изучения электромагнитных волн (выпускается ЗАО НПК «Компьютерлинк»), кювета с водой.

4.1. Введение

Учитель. Основная задача сегодняшнего урока заключается в теоретическом и экспериментальном обосновании того факта, что электромагнитная волна распространяется с определённой скоростью и при распространении переносит энергию. Скорость электромагнитной волны громадна, но мы научимся измерять её в разных средах. Начать урок лучше всего с повторения пройденного.

4.2. Энергия электромагнитной волны

Учитель. Вспомните вывод формулы для плотности энергии электрического поля.

Учащиеся. Если напряжение на плоском конденсаторе равно u, то напряжённость электрического поля в нём E = u/l. Так как ёмкость конденсатора С = ε₀εS/l. (1.2) и объём, занятый полем между пластинами конденсатора V = Sl, то из формулы (W_E = Cu²/2) (1.5) плотность энергии электрического поля

Учитель. Теперь получите выражение для плотности энергии магнитного поля. Напомню, что проще всего это сделать, рассмотрев магнитное поле соленоида.

Учащиеся. Индуктивность соленоида длиной l и площадью S, обмотка которого содержит N витков, равна 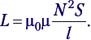Если по соленоиду идёт ток силой i, то индукция магнитного поля в нём

Выражая отсюда i и вместе с L подставляя в формулу (1.6) для энергии магнитного поля W_B = Li²/2, получаем

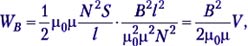
где V = Sl – объём соленоида, в котором в основном сосредоточено магнитное поле. Отсюда плотность энергии магнитного поля

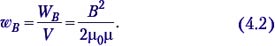
Учитель. Тогда плотность энергии в электромагнитной волне

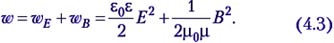
Так как в электромагнитной волне электрическое и магнитное поля совершенно равноправны, причём одно поле порождает другое и наоборот, то плотности энергии этих полей должны быть равны. Приравнивая два слагаемых последней формулы, получаем

Несмотря на равноправие электрического и магнитного полей, одно из них обнаружить в электромагнитной волне проще, чем другое. Какое именно и почему?

Учащиеся. Проще обнаружить электрическое поле, т.к. оно непосредственно вызывает в проводнике электрический ток. Магнитное поле обнаруживают по создаваемому им вихревому электрическому полю, которое вызывает ток в замкнутом проводнике.

Учитель. Замеченная вами особенность носит общий характер, так как именно электрическое поле волны в основном взаимодействует с веществом. Поэтому полную плотность энергии электромагнитной волны (4.3) удобнее выражать через напряженность ее электрического поля:

ω = ε₀εE². (4.5)

4.3. Скорость перемещения электрического и магнитного полей

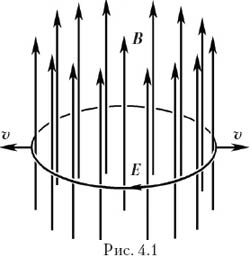
Учитель. Представим, что в площади круга радиусом r создано однородное магнитное поле индукцией B (рис. 4.1). Пусть площадь, занятая этим полем, равномерно растёт так, что радиус круга увеличивается со скоростью υ = dr/dt. Что отсюда следует?

Учащиеся. Вокруг магнитного поля возникает вихревое электрическое поле, радиус которого также растёт со скоростью υ. Согласно закону Фарадея (1.1), поскольку магнитный поток Φ = BS, ЭДС индукции в контуре радиусом r по модулю равна

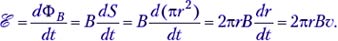
Тогда напряжённость вихревого электрического поля, равная отношению ЭДС индукции 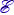ЭДС к длине контура 2πr выражается формулой:

Учитель. При выводе этого соотношения мы не пользовались ничем, кроме закона Фарадея, следовательно, можно предположить, что оно справедливо для любых переменных электрического и магнитного полей. Это позволяет найти скорость электромагнитной волны. Попробуйте!

4.4. Скорость электромагнитной волны в вакууме

Учащиеся. Из последней формулы видно, что E/B = υ. тогда формула (4.4) даёт, что скорость электромагнитной волны

Учитель. В эту формулу входят фундаментальные константы ε₀ и μ₀, поэтому разумно вычислить величину

Учащиеся. Так как ε₀ = 8,85 · 10¹² Кл²/(м² · Н)
и μ₀ = 2,56 · 10^-7 Н/А², то, подставив эти значения в формулу (4.8), получаем с = 3 · 10⁸ м/с.

Учитель. Таким образом, с в формуле (4.8) есть не что иное, как скорость света в вакууме, и формулу (4.7) можно переписать в виде

где величина

называется абсолютным показателем преломления, или просто показателем преломления вещества. Осталось найти способ, позволяющий измерить скорость электромагнитной волны в разных средах.

Учащиеся. Для этого можно измерить длину волны λ и, зная частоту генератора ν, вычислить скорость электромагнитной волны

υ = λ/T = λν (4.11)

Учитель. Для измерения длины волны используем интерференцию волн. Подобный опыт мы уже делали на прошлом уроке, когда параллельно приёмному диполю располагали проводящий стержень. Вместо стержня возьмём металлический лист и расположим его параллельно излучающему диполю. Тогда на приёмном диполе будут интерферировать две электромагнитные волны: идущая непосредственно от излучающего диполя и отражённая от листа (рис. 4.2). Перемещая отражатель поступательно в направлении распространения электромагнитной волны, отметим два таких его положения, при которых яркость лампы приёмного диполя минимальна. Вспомните опыты по интерференции звука и в проделанном сейчас эксперименте найдите длину электромагнитной волны.

Учащиеся. Расстояние между двумя положениями отражателя, при которых лампа приёмного диполя гаснет, равно половине длины электромагнитной волны. Измерения показывают, что эта величина составляет
35 см, значит, длина волны излучения генератора λ = 0,7 м. Так как частота генератора ν = 430 МГц = 4,3 · 10⁸ Гц, то скорость элетромагнитной волны в воздухе υ = λν = 3 · 10⁸ м/с, такая же, как в вакууме! Поэтому показатель преломления воздуха n практически равен 1.

4.5. Скорость электромагнитной волны в веществе

Учитель. Обратите внимание, что длины излучающего и приёмного диполей равны половине длины электромагнитного излучения. Случайно ли это?

Учащиеся. Чтобы получить ответ, нужно попробовать изменить длины диполей и посмотреть, что из этого получится.

Учитель. Диполем с лампой, длина которого может регулироваться, я замыкаю клеммы генератора, при этом его лампа ярко светится, а лампа приёмного диполя не горит (рис. 4.3, а). Постепенно увеличиваю длину диполя, соединённого с генератором. Что вы наблюдаете?

Учащиеся. При определённой длине диполя, подключённого к генератору, яркость его лампы становится минимальной, а яркость лампы приёмного диполя – максимальной (рис. 4.3, б). Опыт очень убедительно свидетельствует, что соединённый с генератором диполь излучает электромагнитную волну, и это приводит к уменьшению энергии электрического тока в нём. Измерения показывают, что длина диполя, при которой его излучение максимально, равна 35 см, т.е. половине длины электромагнитной волны.

Учитель. Снабдим генератор полуволновым излучающим диполем и будем изменять длину приёмного диполя. Сделайте вывод из этого опыта.

Учащиеся. При изменении длины приёмного диполя свечение его лампы максимально, когда она также равна половине длины электромагнитной волны. Значит, наиболее эффективны полуволновые излучающий и приёмный диполи. Наверное, в этих опытах наблюдается резонанс… В самом деле – резонанс, ведь всякий диполь – это открытый колебательный контур!

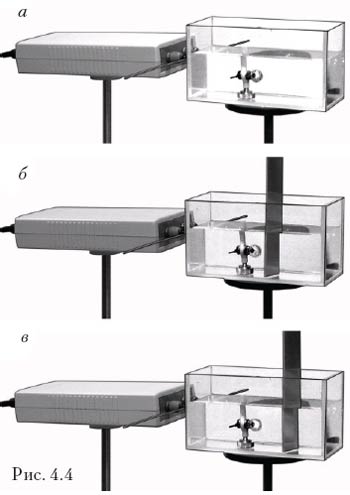
Учитель. Подумайте, как убедиться, что скорость электромагнитной волны в веществе отличается от скорости света в вакууме? Подскажу, что в качестве исследуемого вещества удобнее всего взять воду, поскольку её диэлектрическая проницаемость велика.

Учащиеся. Так как магнитная проницаемость воды практически равна 1, то, согласно формуле (4.9), скорость электромагнитной волны в воде 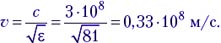Тогда, по формуле (4.11), длина волны λ = υ/ν = 7,7 см. Выходит, что в воде нужно использовать полуволновые диполи длиной примерно 3,8 см.

Учитель. Пусть излучающий диполь находится в воздухе. Вблизи него я помещаю пластиковый сосуд с водой и ввожу в воду короткий диполь с лампой, длина которого 4 см. Вы видите, что лампа загорается (рис. 4.4, а). Перемещаю за приёмным диполем металлическую полоску, и вы наблюдаете, что лампа приёмного диполя периодически гаснет и загорается (рис. 4.4, б, в). Что отсюда следует?

Учащиеся. Опыт подтверждает наше предположение: действительно длина и скорость распространения электромагнитной волны в воде в 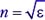раз меньше, чем в воздухе. Но ведь известно, что показатель преломления воды равен не 9, а 1,33!

Учитель. Дело в том, что существует явление дисперсии: скорость электромагнитной волны в веществе зависит от её частоты. Частота видимого света порядка 10¹⁴ Гц, на такой частоте диэлектрическая проницаемость воды равна не 81, а 1,77.

4.6. Заключение

Учитель. Что нового вы узнали на этом уроке? Чему вы научились? Что произвело на вас наибольшее впечатление?

Учащиеся. Мы узнали, чему равны плотность энергии электромагнитной волны и скорость её распространения в вакууме и в веществе. Научились вычислять отношение напряжённости электрического поля к индукции магнитного поля, на опыте определять длину электромагнитной волны и её скорость в разных средах. Наибольшее впечатление произвели опыты с изменением длины излучающего диполя и с коротким приёмным диполем в воде.

Учитель. Как обычно, домашнее задание даётся тем, кому интересно его выполнять, или тем, кто хочет повторить пройденное, узнать новое, углубить свои знания и умения. Материал для выполнения задания вы найдёте в учебниках физики и в электронной версии опорного конспекта урока.

Дайте определение и напишите формулу для плотности энергии электромагнитной волны. [В.А.Касьянов, § 47.]
Как выражается скорость света в вакууме через электрическую и магнитную постоянные? [Опорный конспект.]
Как связаны векторы напряжённости электрического поля, индукции магнитного поля и скорости распространения электромагнитной волны? [Опорный конспект.]
Опишите опыты по измерению скорости электромагнитной волны в различных средах. [Опорный конспект.]
Каков физический смысл абсолютного показателя преломления вещества? [Опорный конспект.]
Напряжённость электрического поля в области приёмного диполя равна 10 В/м. Найдите плотность энергии электромагнитной волны, а также плотности энергий электрического и магнитного полей в этой области. [Опорный конспект.]
Гармоническая электромагнитная волна распространяется в воздухе и на некотором расстоянии от генератора создаёт электрическое поле, амплитуда напряжённости которого 10 В/м. Найдите амплитуду индукции магнитного поля в этой области. Какое поле проще экспериментально обнаружить в электромагнитной волне: электрическое или магнитное? [Опорный конспект.]

Продолжение

следует

Источник

Скорость электромагнитной волны

v – скорость
c – скорость света
ε – диэлектрическая постоянная (проницаемость)
μ – относительная магнитная проницаемость

Найти

Известно, что:

Вычислить ‘v‘

Скорость света в вакууме

c – скорость света
ε0 – электрическая постоянная
μ0 – магнитная постоянная

Найти

Известно, что:

Вычислить ‘c‘

Длина электромагнитной волны

λ – длина волны
c – скорость света
T – период

Найти

Известно, что:

Вычислить ‘λ‘

Длина электромагнитной волны

λ – длина волны
c – скорость света
ν – частота

Найти

Известно, что:

Вычислить ‘λ‘

Объёмная (пространственная) плотность электромагнитной волны

ω – объёмная (пространственная) плотность
E – электрическое поле
B – магнитная индукция
v – скорость
ε0 – электрическая постоянная
μ0 – магнитная постоянная

Найти

Известно, что:

Вычислить ‘ω‘

Длина электромагнитной волны

λ – длина волны
v – скорость
ν – частота

Найти

Известно, что:

Вычислить ‘λ‘

Радиолокация: расстояние

s – расстояние
c – скорость света
t – время

Найти

Известно, что:

Вычислить ‘s‘

Источник

Вывод формулы для скорости электромагнитной волны в веществе

Страница 2 из 2

Формирование понятия об электромагнитном поле явилось важным этапом развития физики. Максвелл не только высказал гипотезу о существовании электромагнитного поля, но и теоретически вывел систему уравнений, описывающих это поле. Он показал, что скорость распространения электромагнитной волны является величиной конечной и в вакууме равна скорости света.

Из уравнений Максвелла следует, что в простейшем случае векторы переменного электромагнитного поля удовлетворяют следующим соотношениям:

и , (1)

где – волновое число (2)

w – циклическая частота колебаний тока,

ɛ и µ – соответственно диэлектрическая и магнитная проницаемости однородной и изотропной диэлектрической среды, в которой рассматривается данное электромагнитное поле,

– электрическая постоянная,

– магнитная постоянная.

Согласно уравнениям (1) электромагнитное поле будет одинаковым для всех моментов времени t и координат х, удовлетворяющих соотношению

. (3)

Это означает, что значение электромагнитного поля (,), которое существовало в начальный момент времени t=0 в точке х=0, через время t˃0 окажется на расстоянии

(4)

от начала координат.

Другими словами, возникнув в данной точке, возмущение электромагнитного поля тут же начинает распространяться от неё с некоторой скоростью. Скорость, с которой распространяется возмущение электромагнитного поля, называется скоростью электромагнитной волны. Эта скорость может быть найдена с помощью соотношения (4):

. (5)

или с учётом формулы (2), получим

[1] (6)

Для углубленного изучения учащимися темы «Электромагнитные волны» предлагается и другой способ вывода формулы скорости электромагнитной волны в веществе.

Известно, что импеданс электрического поля в вакууме выражается формулой

, (7)

где – постоянная Кулона.

Также известно, что импеданс магнитного поля в вакууме выражается формулой

=120p Ом [2] . (8)

Используя выражение (7) и учитывая, что, будем иметь:

. (9)

С другой стороны

. (10)

Используя выражения (8), (9) и (10), получим

или ,

отсюда . (11)

Электромагнитные волны распространяются в различных средах с конечной скоростью

. (12)

Используя выражения (11) и (12), получим конечную скорость электромагнитной волны в веществе:

. (13)

Задача 1. Вычислить скорость электромагнитной волны в воде.

Дано:

ɛ=81

µ=0,999991

Решение:

Воспользуемся формулой (13):

– ?

Ответ: .

Литература

1. Громов С. В. Физика. 10 кл. Учебник для общеобразовательных учреждений. М. Просвещение, 2002. 290 с.

2. Акопов В. В. О импедансе электростатического и магнитного поля в вакууме. Открытый педагогический форум – 2011 «Новая школа».

Есть вопрос? Задайте его Вашему персональному менеджеру. Служба поддержки призвана помочь пользователям в решении любых проблем, связанных с вопросами публикации своих работ и другими аспектами работы издательства «Проблемы науки».

Источник

Электромагнитные колебания и волны Основные формулы

Формула Томсона

Период
собственных колебаний в контуре без
активного сопротивления

–
индуктивность контура;

– электроемкость контура.

Связь длины электромагнитной волны с периодом т и частотой колебаний

–
скорость электромагнитной волны в
вакууме.

Скорость электромагнитной волны в среде с диэлектрической проницаемостью и магнитной проницаемостью

Пример.
Колебательный контур,
состоящий из воздушного конденсатора
с двумя пластинами площадью 0,01 м²
каждая и катушки с индуктивностью 1
мкГн. Резонирует на длину волны 10 м.
Определить расстояние между пластинами
конденсатора.

Дано:

Решение:

Электроемкость
плоского конденсатора
,
откуда

(1)

Из
формулы Томсона

находим электроемкость

(2)

Из
соотношения

найдем

(3)

Подставляя
(3) в (2). А затем полученное выражение в
(1), получим для d

Вычисления:

Проверка
размерностей:

Ответ:

Задачи для самостоятельного решения

Катушка
индуктивностью 1 мГн и конденсатор
электроемкостью 500 мкФ соединены
параллельно. Найти период колебаний в
контуре.
Колебательный
контур состоит из параллельно соединенных
конденсатора электроемкостью 1 мкФ и
катушки индуктивностью 1 мГн. Найти
частоту колебаний.
Индуктивность
колебательного контура равна 0,5 мГн.
Какова должна быть электроемкость
контура, чтобы он резонировал на длину
волны 300 м.?
На
какую длину волны будет резонировать
контур, состоящий из катушки индуктивностью
4 мкГн и конденсатора электроемкостью
1 нФ?
Определить
скорость электромагнитных волн в
парафине, если его диэлектрическая
проницаемость

и магнитная проницаемость
.
Найти
диапазон длин волн радиоприемника,
если во входном колебательном контуре
индуктивность L=0,1 мГн, а
емкость меняется от 10^-12 Ф до10^-10
Ф.

5.
оптика

Геометрическая оптика и фотометрия Основные формулы

Закон
отражения света

–
угол падения;

– угол отражения.

Закон
преломления света

–
угол падения;

– угол преломления;

– относительный показатель преломления
второй среды относительно первой;

и

– абсолютные показатели преломления
первой и второй сред.

Предельный
угол полного внутреннего отражения

Оптическая
сила тонкой линзы D

f
– фокусное расстояние линзы;

– абсолютный показатель преломления
вещества линзы;

– абсолютный показатель среды;

– относительный показатель преломления
вещества линзы относительно среды;
радиусы выпуклых поверхностей линзы

и

берутся со знаком плюс, вогнутых со
знаком минус.

Формула
тонкой линзы

a
– расстояние от оптического центра
линзы до предмета; b
– расстояние от оптического центра до
изображения; если фокус мнимый (линза
рассеивающая), то фокусное расстояние
f<0.